Abstract
Camouflage is a natural or artificial process that prevents an object from being detected, while camouflage breaking is a countering process for the identification of the concealed object. We report that a perfectly camouflaged object can be retrieved from the background and detected with stereo-vision-assisted three-dimensional (3D) imaging. The analysis is based on a binocular neuron energy model applied to general 3D settings. We show that a perfectly concealed object with background interference can be retrieved with vision stereoacuity to resolve the hidden structures. The theoretical analysis is further tested and demonstrated with distant natural images taken by a drone camera, processed with a computer and displayed using autostereoscopy. The recovered imaging is presented with the removal of background interference to demonstrate the general applicability for camouflage breaking with stereo imaging and sensing.
1. Introduction
Camouflage is a natural concealment capability used by animals to hunt and to avoid being hunted [1,2]. The making and breaking of camouflage become important for achieving advantages in various confrontation circumstances [3,4]. Camouflage is usually achieved by a combination of structures, colors and illuminations to hide the identity of an object in the background [5,6]. There has been consistent interest in the subject of camouflage and camouflage breaking, as the topic is not only scientifically interesting but technologically important. Among the various techniques for camouflage breaking, 3D convexity, machine learning and artificial intelligence have been widely studied [7,8]. It has been suggested that breaking camouflage is one of the major functions of 3D perception [9,10]. Hence, binocular stereo matching [11], deep learning [12] and multi-view stereo vision [13] are applied for camouflage breaking. Nevertheless, the capability of digital computer 3D analysis is not in any way as powerful as human stereo vision, as the human brain has a natural advantage in processing 3D stereo imaging by performing automatic feature point detection, matching and intelligent stereo-vision perception. For general 3D imaging, holography [14] is also a powerful technique, recording and displaying the interference between the reference light and the object light. It is then necessary to re-examine the effect of human stereopsis on camouflage breaking by comparing its similarities with holography and to analyze its impact in real-world applications.
In this work, we show with a vision neuron energy model [15,16,17] that 3D structures hidden deep in the background can be retrieved with binocular vision via stereoacuity. A vision neuron energy model was first proposed to depict how creatures with stereo vision encode information in the visual cortex [18]. Various biological experiments verified its validity, as presented in the references [19]. This theoretical analysis is applied to a case where the object is completely submerged in its background. The results show that the submerged object can be recovered if the recorded images are correctly perceived with human vision’s stereopsis. A field experiment is carried out with natural images taken by a drone camera. These image data are processed with a computer, displayed by autostereoscopy [20,21] and perceived with vision. The removal of the background to show the concealed object clearly demonstrates the general applicability of the novel technique for camouflage breaking.
2. Theoretical Analysis
The theoretical analysis presented in this work is based on the vision neuron energy model proposed by Ohzawa et al. [15,16,17]. We present here how the human brain discerns depth information through neural networks. Figure 1 clearly illustrates the process of using the vision neuron energy model to explain how the human brain obtains depth information. First, the left eye and right eye receive similar but slightly different images. Second, the disparity, as discussed below, is derived from the left-eye and right-eye images. The two images can be sent to stereopsis for display, and they can also be analyzed with digital procedures, as we shall discuss below.
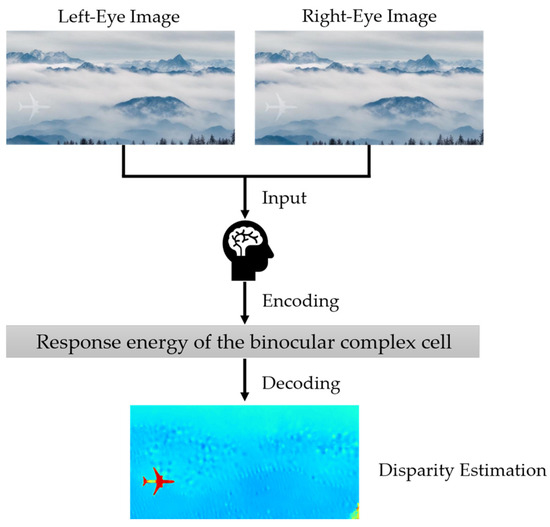
Figure 1.
The vision neuron energy model explains how the human brain perceives depth.
The binocular energy unit for a thin object located in a plane can be written as follows [17]:
where is the position of the receptive field and is equal to the filter of the input signal by its corresponding receptive field.
The response energy of the binocular unit can be described in terms of amplitude and phase signals as follows:
where is the amplitude and is the phase difference between the left and right signals.
Usually, the images received by the left and right eyes are similar, but they are displaced by a distance known as disparity.
Let the objects be located at different distances from the observer, which will induce disparity responses of different magnitudes. Therefore, we can express Equation (3) as follows:
where should be summed up for all different layers in the object space.
Equation (3) shows that the images received by the left and right eyes are correlated, with the contribution from each eye and from the crossed term described as the third term of Equation (3). It is interesting to note that the energy model of binocular vision is similar to digital holographic [14] imaging in the sense that it consists of the contributions from the two input channels and from the interference term between the left and right images.
It is evident that the response energy of the binocular unit is related to the disparity, and different disparities represent different layers in object space. By varying the disparity (measured in pixels in the left and right images in the display), we obtain the corresponding response energy values. When it reaches its maximum value with varying phase difference, the disparity at this point is considered to be the disparity between the left and right images [22].
For conventional 2D images, the object depth information is superimposed along the depth direction, and an object can be swamped with camouflage background which can be placed before or after the object.
There are two ways to obtain the global 3D picture for object space. The first one is to input the left and right images to a stereopsis display, which can be visualized with human eyes, thus directly generating a 3D scene for camouflage breaking. The second one is to compare the left and right images to obtain well-defined disparity. The partial image in a plane described with the disparity can be simulated by convoluting this depth map with the image input.
To analyze the stereo vision with the energy model, it is important to note how the lateral and longitudinal spatial resolutions are related to the stereo vision. Stereoacuity is defined as a human’s visual ability to resolve the smallest depth difference measured with angular difference, described as [23,24]:
The parameters for stereoacuity are shown in Figure 2, where is the interocular separation of the observer, represents the distance of the fixed peg from the eye, and means the position difference.
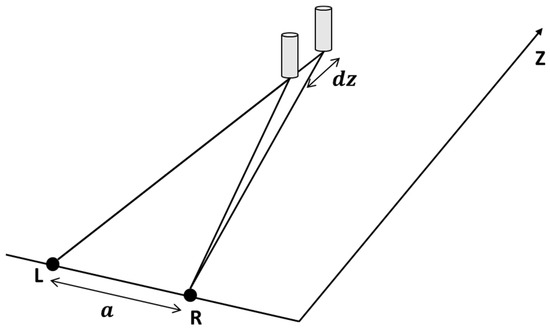
Figure 2.
The architecture of stereoacuity measurement with respect to the observer’s interocular separation.
For objects captured with a camera and displayed on stereopsis, images can be magnified with optics and stereopsis screen size. Considering the total magnification factor and the baseline difference, the stereoacuity can be approximated by Equation (8) [23,24]:
where is the magnification (the ratio of the display FOV and the camera FOV), is the effective interocular separation (the ratio of the baseline and the interocular separation).
An interesting but rarely discussed topic is how stereoacuity is affecting the lateral resolution of the image. In general, the depth-resolved measurement should enhance the lateral resolution in a similar way as with a confocal configuration, while the rejection of the out-of-focus component is expected to increase the lateral resolution [25,26,27].
3. Results and Discussion
As a first step, we examine a case where a “car” is completely hidden in the background. The “car” is placed with a small depth difference from the background so that it has nonzero disparity, where the background is assumed to have zero disparity. Figure 3a,b show images received with the left and right eyes. On the other hand, when these left and right images are perceived with stereopsis, a concealed car becomes prominent, which can be visualized with a 3D display. The derived digital disparity map is also shown in Figure 3c. The appearance of the pattern with stereopsis is a conventional technique for the screening of stereoacuity [28] and it is an indication of how binocular viewing can be applied to conveniently perceive the object that is not perceivable with a single eye.

Figure 3.
Camouflage breaking with a car concealed under trees: (a) the planar image by the left eye; (b) the planar image by the right eye; (c) the recovered car based on the disparity estimation.
For the test of camouflage breaking in a natural scene, a field experiment is carried out to show the retrieval of an object with stereoacuity-assisted image sensing. The difficulty of 3D remote sensing with stereopsis arises from the required large baseline distance, which is studied in this work with a drone equipped with a single camera. For the purpose of executing stereoacuity functioning, an experimental architecture similar to Figure 2 is carried out and left and right images are selected from a video taken by the flying camera. The key parameters to be considered are the relative positions of the object in its background and the baseline of the two positions to provide the stereo-viewing so that the object can be resolved with stereoacuity measurement. It is noticed that a 3D object can be resolved with the finest human stereoacuity, as small as 5 arc sec [29]. Assuming, for example, an object located 100 m away from the camera is 1 m away from its background, it can be estimated that the baseline of the dual cameras must be approximately 57 cm apart. With the recorded navigating speed of the drone, it is straight forward to choose left and right images from the video format to meet the requirement of the baseline length.
To meet the sensing requirement, a drone (DJI Mavic2 pro: 28 mm equivalent lens on the 1-inch CMOS sensor, Shenzhen, Guangdong) equipped with a Hasselblad L1D-20c camera is employed to take the video for the scene, and the two images from selected positions are employed as the input for the left- and right-eye images. The flying altitude of the drone is 90 m. The dual images are transmitted to an autostereoscopic display for 3D viewing at a viewing distance of 90 cm. The autostereoscopic display is a directional backlight illuminated liquid crystal display with a feature size of 24 inches, a contrast ratio of 1000:1, a refresh rate of 120 Hz, and single-eye resolution at 1920 P × 1080 P (Type MID-FD24VT) [20,21]. With this autostereoscopic display, the 3D scene is clearly visible. For the convenience of 3D perception, we convert the left and right images by coding them with blue and red, so that the images can be perceived with a 3D anaglyph.
The use of an autostereoscopic display makes it possible to study the difference between 2D and 3D perception. In 2D mode, the left and right eyes perceive a planar image. With 3D perception, the left and right images are delivered to the left and right eyes, respectively. It becomes evident that 3D perception provides detailed object structures due to the perception of the layered structures of the scene assisted with stereoacuity. In 2D mode, the information of different depths is intermixed, giving rise to the opportunity for camouflaging. With 3D perception, the concealed object can be retrieved with binocular vision.
In order to further view the effect of stereopsis on the resolved 3D object (compared with Figure 4a), an image is synthesized using disparity discriminated image pixels as input information. Detailed structures can be observed with stereo vision concentrating on a specific layer in object space. By enhancing the image structure in one particular layer while removing structures from other layers, the lateral structures of the scene are substantially enhanced.

Figure 4.
Left- (a) and right (b)-eye images and stereo anaglyph (c) synthesized by drone images taken at an altitude of 90 m above the ground. The baseline distance between the left and right views is approximately 7 m. The tree leaves obscured in 2D are made prominent with 3D.
Figure 5a shows the energy response, in which binocular vision focuses on the ground layer, while Figure 5b illustrates the situation when two eyes are focusing on the top tree layer, within which the tree branches and leaves are clearly visible.
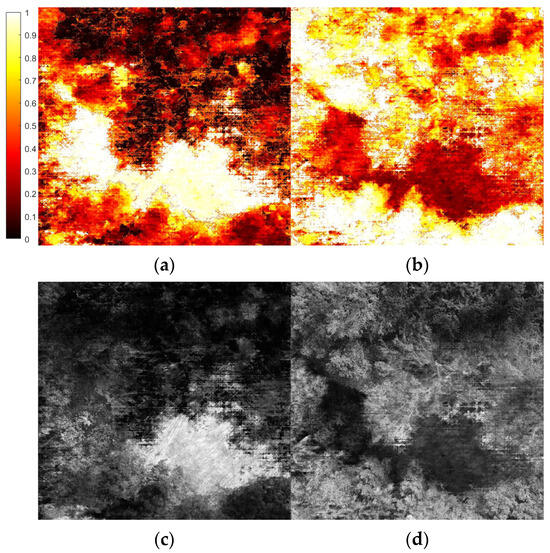
Figure 5.
The energy response for the scene with two eyes focusing on the ground (a) and focusing on the tree (b). (c,d) are structures recovered, respectively, corresponding to (a,b) based on the disparity estimation.
Figure 5c is obtained by dot multiplication of the energy pattern at a particular height of the tree with the input from Figure 4a. Similarly, Figure 5d is the result of multiplying the energy pattern with Figure 4a. A prominent difference is clearly visible in the comparison of these two cases, showing substantially enhanced camouflage breaking capability. With the binocular energy model, Figure 5c,d show the corresponding sectioning of the 3D scene corresponding to patterns at different altitudes. The sectioning images are in accordance with the direct perception shown in Figure 4c. Compared with the corresponding region of the original image presented in Figure 4a, neither ground nor tree characteristics can be identified with the original image, which proves that camouflage breaking can be realized for stereo vision and stereo-vision-based optical imaging.
To better illustrate the advantages of layered discrimination with the energy model, we select a sub-region in Figure 4a marked by a green square, which is amplified in Figure 6. It becomes clear that the image structures indistinct from a bright background can be sectioned. The 2D image sections focusing on the ground and on the tree branches are clearly visible.

Figure 6.
(a) The perceived 2D image pattern and (b,c) the sectioning image patterns focused on the ground and on the top of the trees.
4. Conclusions
In conclusion, three different scenarios are applied to demonstrate the validity of the study for camouflage breaking: (1) camouflage breaking is theoretically analyzed and numerically simulated with binocular visual processing; (2) stereoacuity-based sensing is directly applied to a field experiment, as shown in Figure 5 and Figure 6; (3) the recovery of the concealed object with a neuron energy model can be visualized with digital processing of the images from the field experiment. All of these efforts demonstrate the robustness of stereo vision for camouflage breaking. We anticipate that the proposed and demonstrated technique has immediate applications for scientific research and technological applications.
Author Contributions
H.Y. carried out field measurements and image analysis; J.L. conducted the theoretical analysis, energy model simulation, and image reconstruction; L.C. conducted the theoretical analysis of energy models and field experimental measurements; Y.L. conducted project coordination and data analysis; J.Z. proposed the project and wrote the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Chinese National Science Foundation (NOS. 61991452); the Guangdong key Project (No. 2020B301030009); and the Ministry of Science and Technology (No. 2021YFB2802204).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
Author Jianying Zhou was employed by the company Guangzhou Midstereo Ltd., National University Science and Technology Park. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Mondal, A. Camouflage design, assessment and breaking techniques: A survey. Multimed. Syst. 2022, 28, 141–160. [Google Scholar] [CrossRef]
- Stevens, M.; Merilaita, S. Animal camouflage: Current issues and new perspectives. Philos. Trans. R. Soc. B 2009, 364, 423–427. [Google Scholar] [CrossRef] [PubMed]
- Lamdouar, H.; Xie, W.; Zisserman, A. The making and breaking of camouflage. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 832–842. [Google Scholar]
- Cuthill, I.C. Camouflage. J. Zool. 2019, 308, 75–92. [Google Scholar] [CrossRef]
- Tankus, A.; Yeshurun, Y. Convexity-based visual camouflage breaking. Comput. Vis. Image Underst. 2001, 82, 208–237. [Google Scholar] [CrossRef]
- Stevens, M.; Ruxton, G. The key role of behaviour in animal camouflage. Biol. Rev. 2019, 94, 116–134. [Google Scholar] [CrossRef]
- Fan, D.; Ji, G.; Sun, G.; Cheng, M.; Shen, J.; Shao, L. Camouflaged object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 2777–2787. [Google Scholar]
- Ji, G.; Fan, D.; Chou, Y.; Dai, D.; Liniger, A.; Van, G. Deep gradient learning for efficient camouflaged object detection. Mach. Intell. Res. 2023, 20, 92–108. [Google Scholar] [CrossRef]
- Julesz, B. Foundations of Cyclopean Perception; The University of Chicago Press: Chicago, IL, USA, 1971. [Google Scholar]
- Wardle, S.; Cass, J.; Brooks, K.; David, A. Breaking camouflage: Binocular disparity reduces contrast masking in natural images. J. Vis. 2010, 10, 38. [Google Scholar] [CrossRef][Green Version]
- Geiger, A.; Roser, M.; Urtasun, R. Efficient large-scale stereo matching. In Asian Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Chen, J.; Kira, Z.; Cho, Y. Deep learning approach to point cloud scene understanding for automated scan to 3D reconstruction. J. Comput. Civ. Eng. 2019, 33, 04019027. [Google Scholar] [CrossRef]
- Seitz, S.; Curless, B.; Diebel, J. A comparison and evaluation of multi-view stereo reconstruction algorithms. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06), New York, NY, USA, 17–22 June 2006; IEEE: Piscataway, NJ, USA, 2006; Volume 1, pp. 519–528. [Google Scholar]
- Zhai, Y.; Huang, H.; Sun, D. End-to-end infrared radiation sensing technique based on holography-guided visual attention network. Opt. Laser Eng. 2024, 178, 108201. [Google Scholar] [CrossRef]
- Ohzawa, I.; Deangelis, G.; Freeman, R. Encoding of binocular disparity by complex cells in the cat’s visual cortex. J. Neurophysiol. 1997, 77, 2879–2909. [Google Scholar] [CrossRef]
- Fleet, D.; Wagner, H.; Heeger, D. Neural encoding of binocular disparity: Energy models, position shifts and phase shifts. Vis. Res. 1996, 36, 1839–1857. [Google Scholar] [CrossRef] [PubMed]
- Hibbard, P. Binocular energy responses to natural images. Vis. Res. 2008, 48, 1427–1439. [Google Scholar] [CrossRef] [PubMed]
- Ohzawa, I.; DeAngelis, G.; Freeman, R. Stereoscopic depth discrimination in the visual cortex: Neurons ideally suited as disparity detectors. Science 1990, 249, 1037–1041. [Google Scholar] [CrossRef]
- Haefner, R.; Cumming, B. Adaptation to natural binocular disparities in primate V1 explained by a generalized energy model. Neuron 2008, 57, 147–158. [Google Scholar] [CrossRef]
- He, Y.; Chen, X.; Zhang, G.; Fan, Y.; Liu, X.; Deng, D.; Yan, Z.; Liang, H.; Zhou, J. A directionally illuminated pixel-selective flickering-free autostereoscopic display. Displays 2024, 82, 102651. [Google Scholar] [CrossRef]
- Zhang, A.; Chen, X.; Wang, J.; He, Y.; Zhou, J. Directionally Illuminated Autostereoscopy with Seamless Viewpoints for Multi-Viewers. Micromachines 2024, 15, 403. [Google Scholar] [CrossRef]
- Yu, L. Stereo Matching with Cortical Disparity Detection Mechanisms. Ph.D. Thesis, Institute of Automation, Chinese Academy of Sciences, Beijing, China, 2008. [Google Scholar]
- Jennings, J.; Charman, W. Depth resolution in stereoscopic systems. Appl. Opt. 1994, 33, 5192–5196. [Google Scholar] [CrossRef] [PubMed]
- Kytö, M.; Nuutinen, M.; Oittinen, P. Method for measuring stereo camera depth accuracy based on stereoscopic vision. Proc. SPIE 2011, 7864, 168–176. [Google Scholar]
- Webb, R. Confocal optical microscopy. Rep. Prog. Phys. 1996, 59, 427. [Google Scholar] [CrossRef]
- Xie, X.; Chen, Y.; Yang, K.; Zhou, J. Harnessing the point-spread function for high-resolution far-field optical microscopy. Phys. Rev. Lett. 2014, 113, 263901. [Google Scholar] [CrossRef]
- Yang, L.; Xie, X.; Wang, S.; Zhou, J. Minimized spot of annular radially polarized focusing beam. Opt. Lett. 2013, 38, 1331–1333. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhong, J.; Cheng, M.; Li, J.; Ma, K.; Hu, X.; Li, N.; Liang, H.; Zhu, Z.; Zhou, J.; et al. A novel clinical dynamic stereopsis assessment based on autostereoscopic display system. Ann. Transl. Med. 2022, 10, 656. [Google Scholar] [CrossRef] [PubMed]
- McKee, S. The spatial requirements for fine stereoacuity. Vis. Res. 1983, 23, 191–198. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).