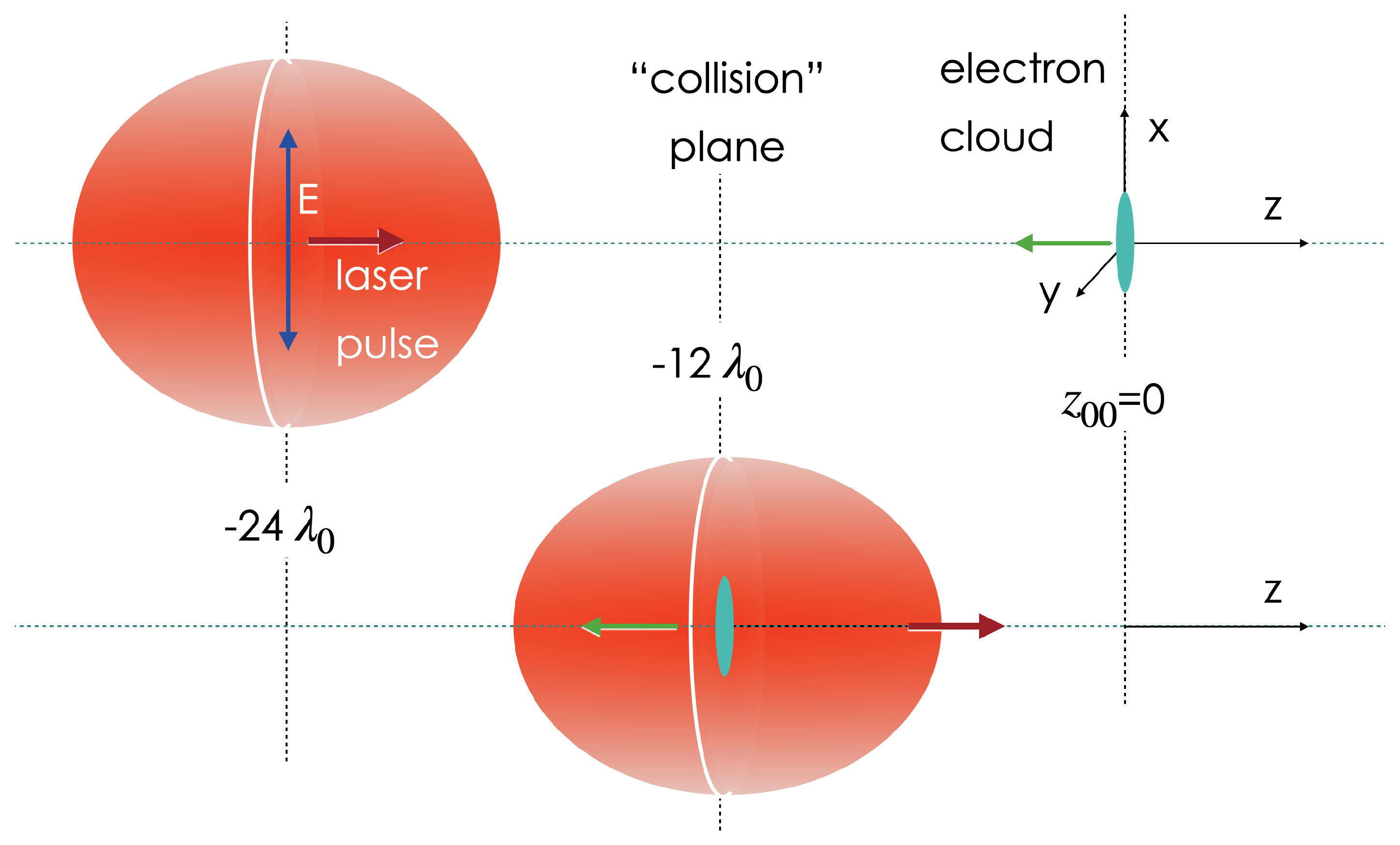
Figure 1.
Schematic representation of the studied process. Initially, the laser and the electron bunch are counter-propagating. The laser moves towards the positive Z-axis, and the electron bunch moves initially in the opposite direction. The upper figure shows the initial position with the electron bunch centered at and the laser pulse peak at (19.2 ). Neglecting the interaction before this point is a reasonable assumption. Since the electron’s initial speed is very close to c, the electron would cross the laser pulse close to . However, for extreme intensities, as we will describe, the trajectory of the electrons will be significantly modified.
Figure 1.
Schematic representation of the studied process. Initially, the laser and the electron bunch are counter-propagating. The laser moves towards the positive Z-axis, and the electron bunch moves initially in the opposite direction. The upper figure shows the initial position with the electron bunch centered at and the laser pulse peak at (19.2 ). Neglecting the interaction before this point is a reasonable assumption. Since the electron’s initial speed is very close to c, the electron would cross the laser pulse close to . However, for extreme intensities, as we will describe, the trajectory of the electrons will be significantly modified.
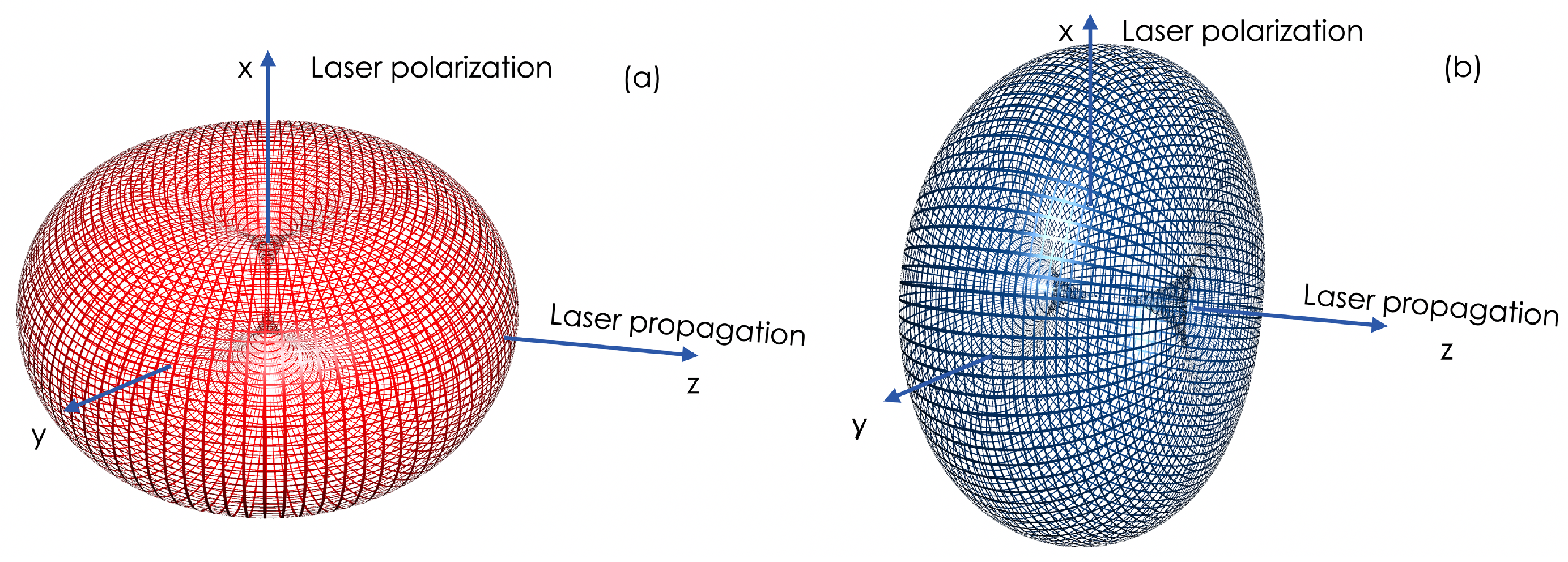
Figure 2.
Schematic representation of the TS radiation pattern. Electrons driven exclusively by the laser polarization radiate mainly in the YZ plane (a). However, electrons driven by the laser magnetic field radiate mostly in the XY plane (b). Comparing Thomson radiation along these two planes provides relevant information on RR-induced dynamics. The YZ pattern, driven by the laser electric field, corresponds to even harmonics of the fundamental frequency. The XY radiation, due to coupling with the laser magnetic field, also shows strong even harmonics. Relativistic distortion of these donut shapes is not depicted for simplicity.
Figure 2.
Schematic representation of the TS radiation pattern. Electrons driven exclusively by the laser polarization radiate mainly in the YZ plane (a). However, electrons driven by the laser magnetic field radiate mostly in the XY plane (b). Comparing Thomson radiation along these two planes provides relevant information on RR-induced dynamics. The YZ pattern, driven by the laser electric field, corresponds to even harmonics of the fundamental frequency. The XY radiation, due to coupling with the laser magnetic field, also shows strong even harmonics. Relativistic distortion of these donut shapes is not depicted for simplicity.
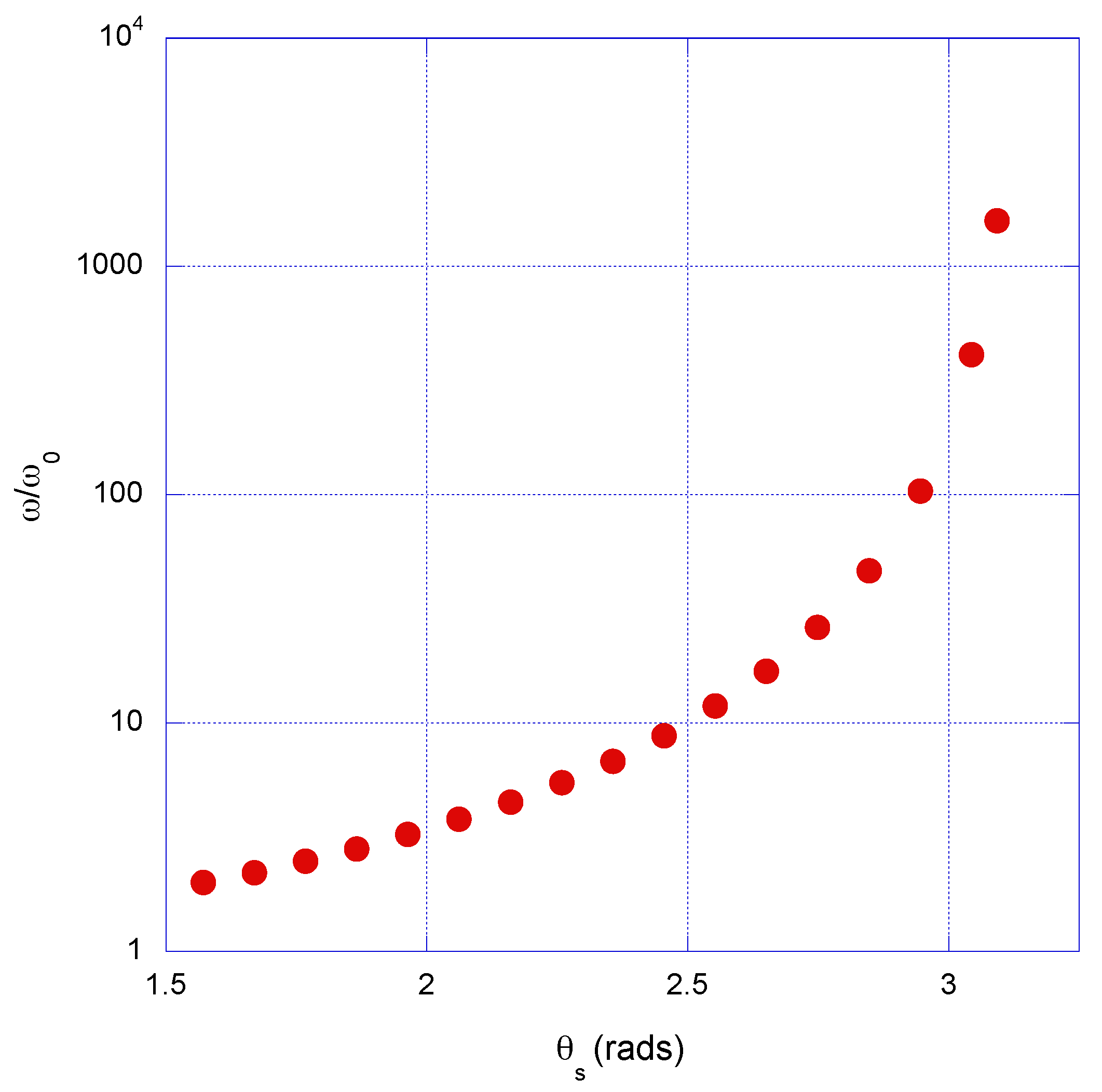
Figure 3.
Spectral location of the Thomson scattered main peak (i.e., ), X-polarization, spectra averaged for an electron sample aimed at the central part of the laser pulse, including RR, as a function of . Scattering is computed in the YZ plane. Notice the extremely fast increase in the (blue-shifted) peak frequency with the scattering angle as the angle approaches (this corresponds to light scattered counter-propagating with respect to the laser).
Figure 3.
Spectral location of the Thomson scattered main peak (i.e., ), X-polarization, spectra averaged for an electron sample aimed at the central part of the laser pulse, including RR, as a function of . Scattering is computed in the YZ plane. Notice the extremely fast increase in the (blue-shifted) peak frequency with the scattering angle as the angle approaches (this corresponds to light scattered counter-propagating with respect to the laser).
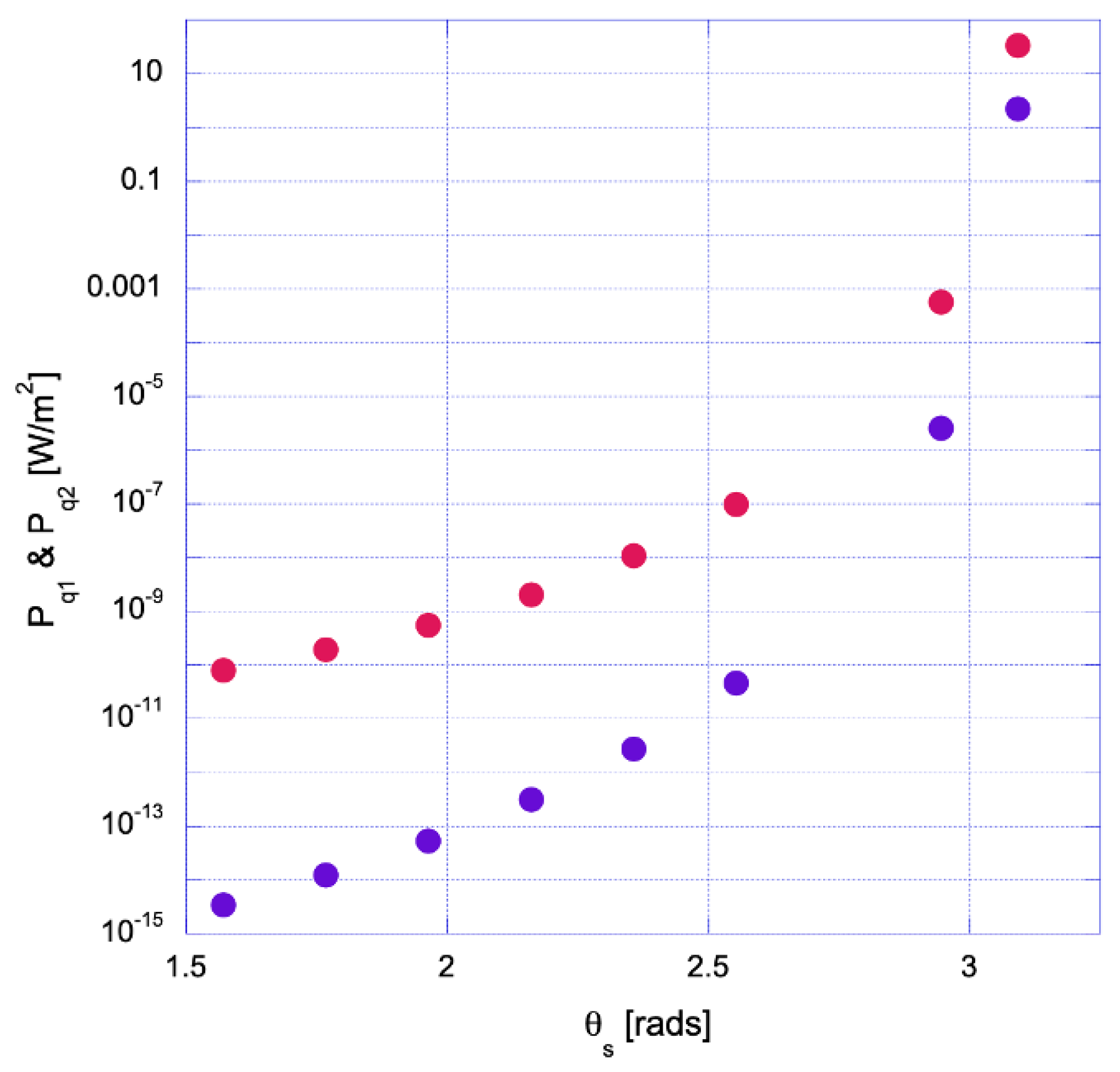
Figure 4.
Integrated spectral power, X-polarization in red and the other orthogonal quadrature in blue, averaged for an electron sample aimed at the central part of the laser pulse, including RR, as a function of the scattering angle. Scattering plane is YZ. Notice that for a scattering angle of , the light is nearly completely polarized along the X-axis, and notice how the two orthogonal contributions become more balanced as the scattering angle approaches .
Figure 4.
Integrated spectral power, X-polarization in red and the other orthogonal quadrature in blue, averaged for an electron sample aimed at the central part of the laser pulse, including RR, as a function of the scattering angle. Scattering plane is YZ. Notice that for a scattering angle of , the light is nearly completely polarized along the X-axis, and notice how the two orthogonal contributions become more balanced as the scattering angle approaches .
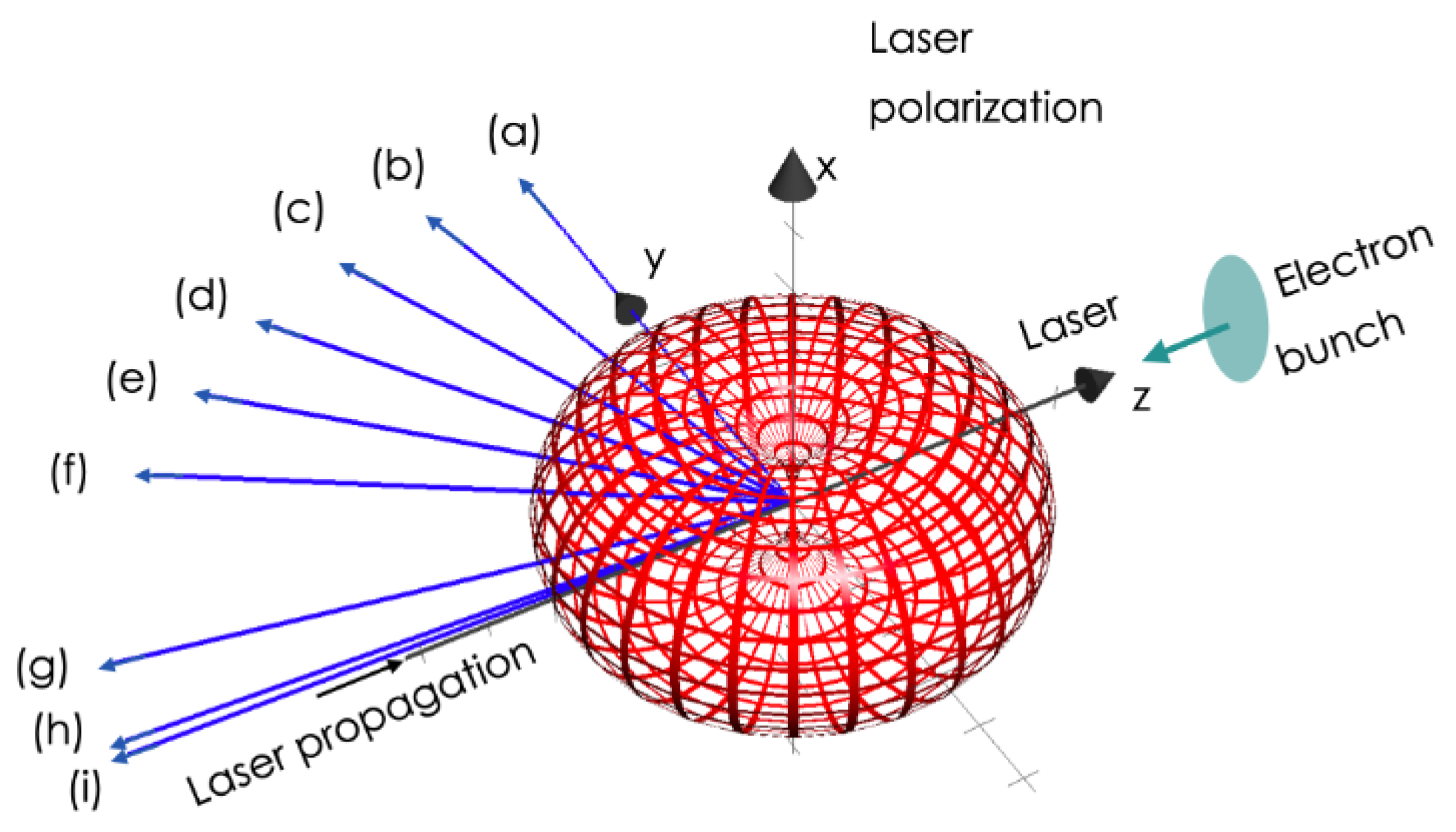
Figure 5.
Schematic representation of the angles where the TS spectra have been calculated. Labels (a–i) refer to the directions of observation of the spectra shown in the next figure.
Figure 5.
Schematic representation of the angles where the TS spectra have been calculated. Labels (a–i) refer to the directions of observation of the spectra shown in the next figure.
Figure 6.
Averaged TS spectra including RR for several scattering angles in the YZ plane; see main text for details. (a–i) Scattering angles are, respectively, , , , , , , , , and . Observe that the last one, (i), corresponds to scattering almost perfectly counter-propagating to the laser pulse. The colors red and blue are the same as in the previous figure, with quadrature in red (polarization along the electric field) and quadrature in blue.
Figure 6.
Averaged TS spectra including RR for several scattering angles in the YZ plane; see main text for details. (a–i) Scattering angles are, respectively, , , , , , , , , and . Observe that the last one, (i), corresponds to scattering almost perfectly counter-propagating to the laser pulse. The colors red and blue are the same as in the previous figure, with quadrature in red (polarization along the electric field) and quadrature in blue.
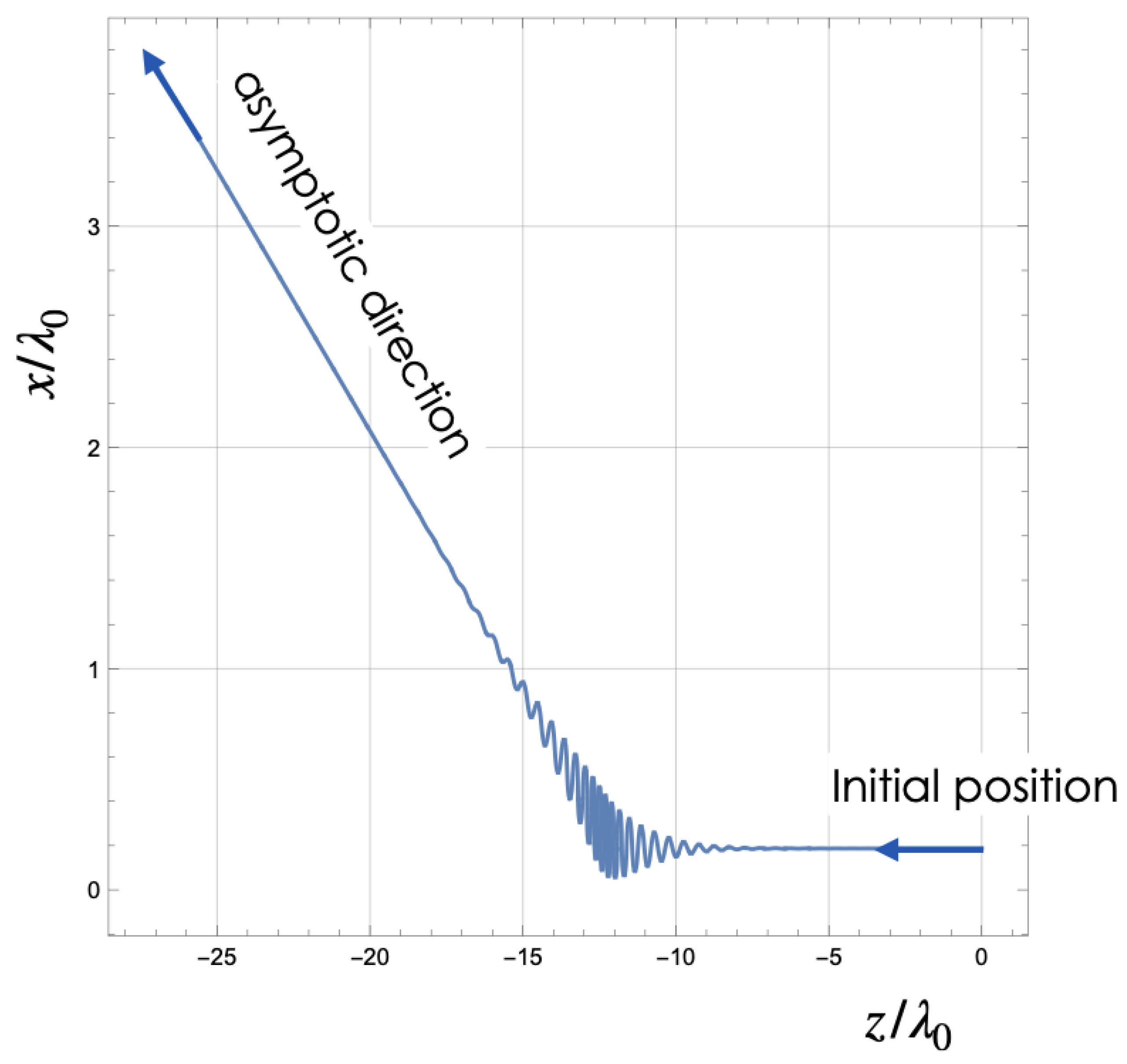
Figure 7.
Projection of a sample trajectory onto the XZ plane, including RR. The electron is initially located at , moves from right to left, strongly interacts with the laser pulse around , and gets deflected, eventually becoming a free electron. The center of the laser pulse was initially at and propagates from left to right along the Z axis.
Figure 7.
Projection of a sample trajectory onto the XZ plane, including RR. The electron is initially located at , moves from right to left, strongly interacts with the laser pulse around , and gets deflected, eventually becoming a free electron. The center of the laser pulse was initially at and propagates from left to right along the Z axis.
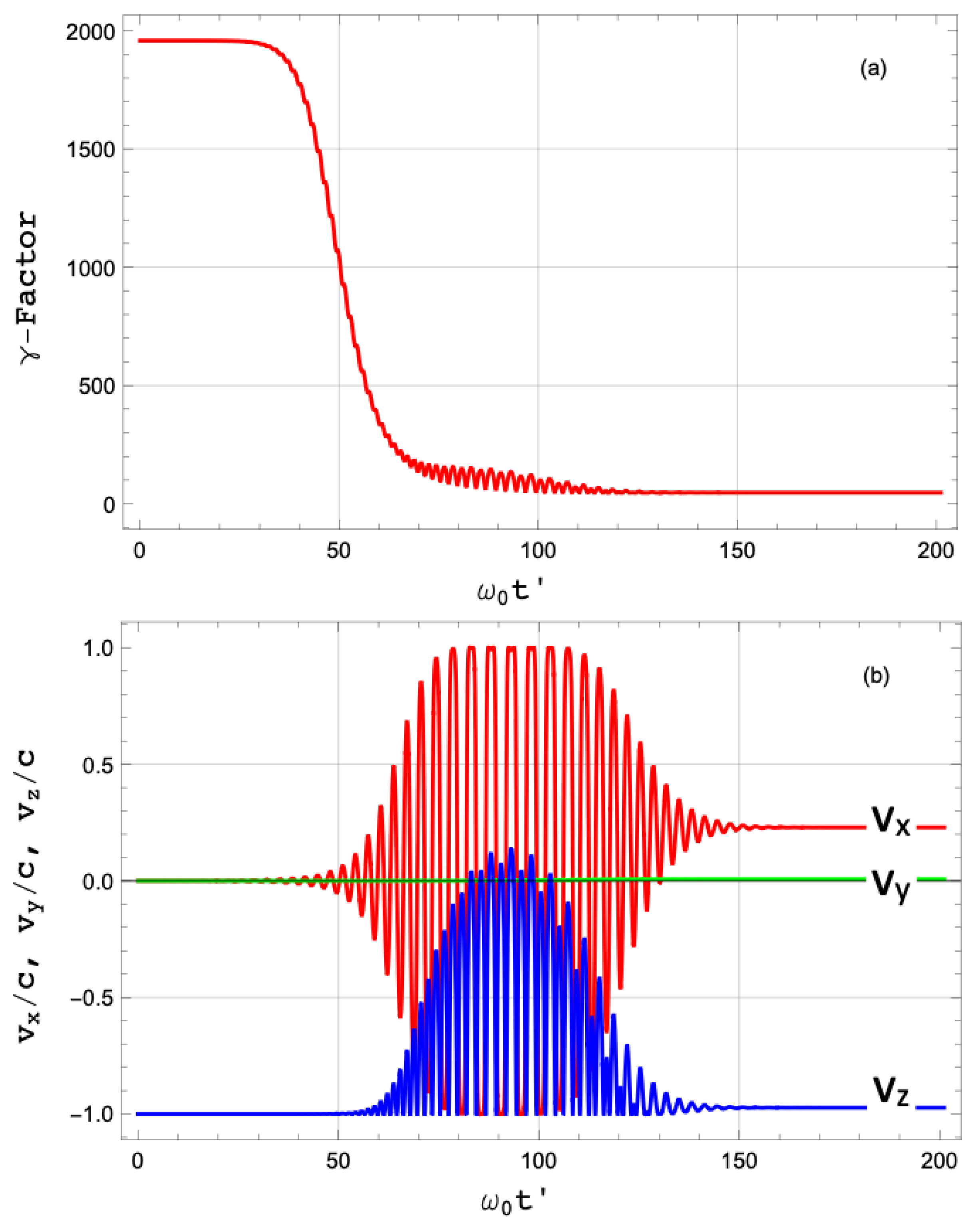
Figure 8.
Time evolution of the relativistic
factor (
a) and the normalized velocity (
b) for the sample trajectory in
Figure 7. The significant reduction in the
factor (i.e., the electron energy) due to RR is evident, along with substantial perturbations in
and
. Color code in (
b): red, green, and blue correspond to
,
, and
, respectively.
Figure 8.
Time evolution of the relativistic
factor (
a) and the normalized velocity (
b) for the sample trajectory in
Figure 7. The significant reduction in the
factor (i.e., the electron energy) due to RR is evident, along with substantial perturbations in
and
. Color code in (
b): red, green, and blue correspond to
,
, and
, respectively.
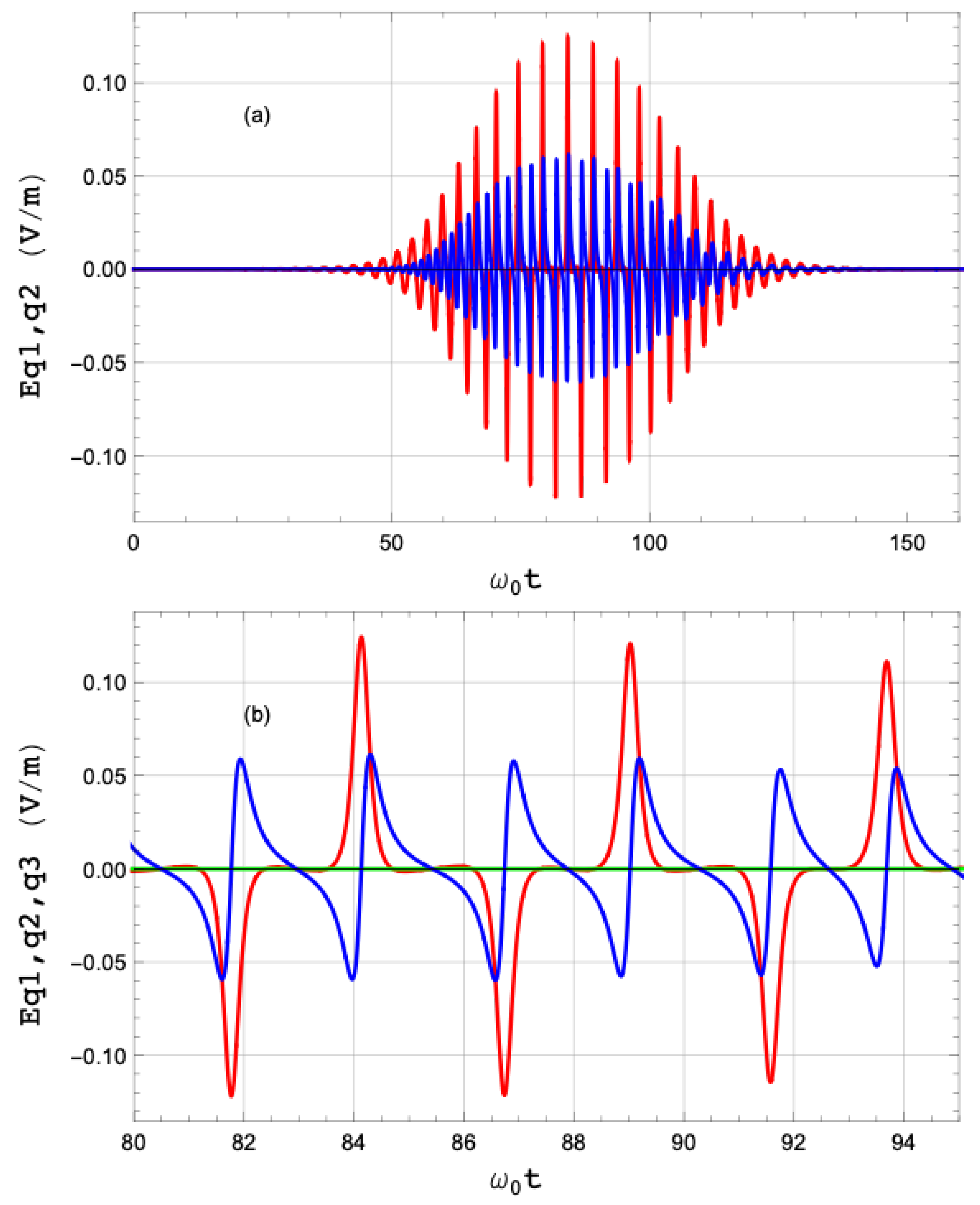
Figure 9.
Radiated electric field at the detector in the time domain (a) and a close-up (b) displaying the spike structure under the radiated pulse envelope. The scattering plane is YZ. The electric field component parallel to the X axis is shown in red, while the other component is in blue. In (b), the component along the scattering vector is also displayed in green and is negligible compared to the other components.
Figure 9.
Radiated electric field at the detector in the time domain (a) and a close-up (b) displaying the spike structure under the radiated pulse envelope. The scattering plane is YZ. The electric field component parallel to the X axis is shown in red, while the other component is in blue. In (b), the component along the scattering vector is also displayed in green and is negligible compared to the other components.
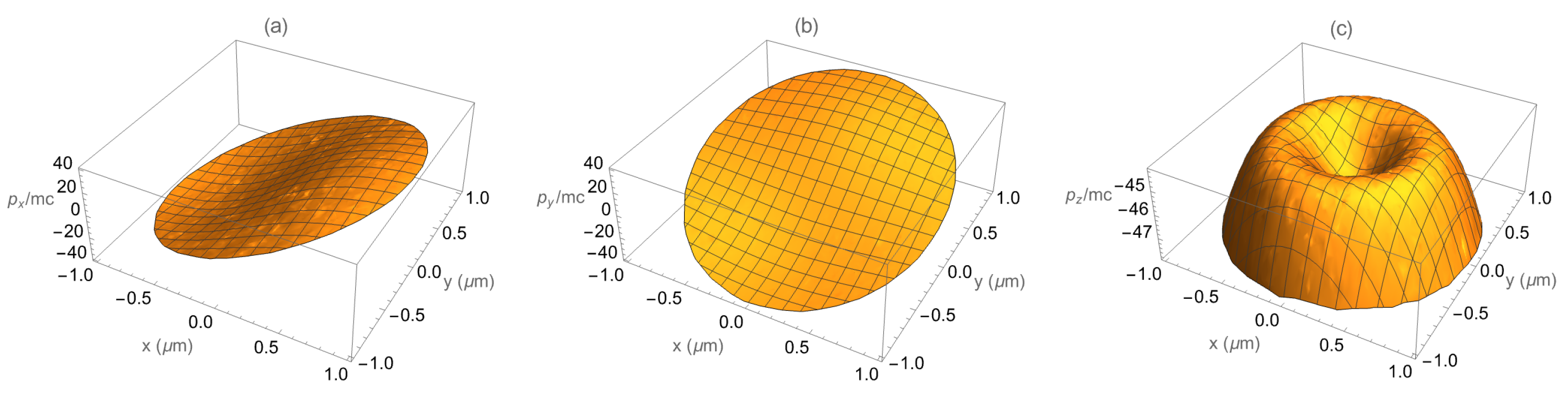
Figure 10.
Asymptotic momentum components for counter-propagating 1 GeV electrons, including RR. (a–c) correspond respectively to the asymptotic distributions of , and . The sample contains 4096 electrons randomly distributed up to , with . The laser is in the mode, X polarized, with a peak intensity of .
Figure 10.
Asymptotic momentum components for counter-propagating 1 GeV electrons, including RR. (a–c) correspond respectively to the asymptotic distributions of , and . The sample contains 4096 electrons randomly distributed up to , with . The laser is in the mode, X polarized, with a peak intensity of .
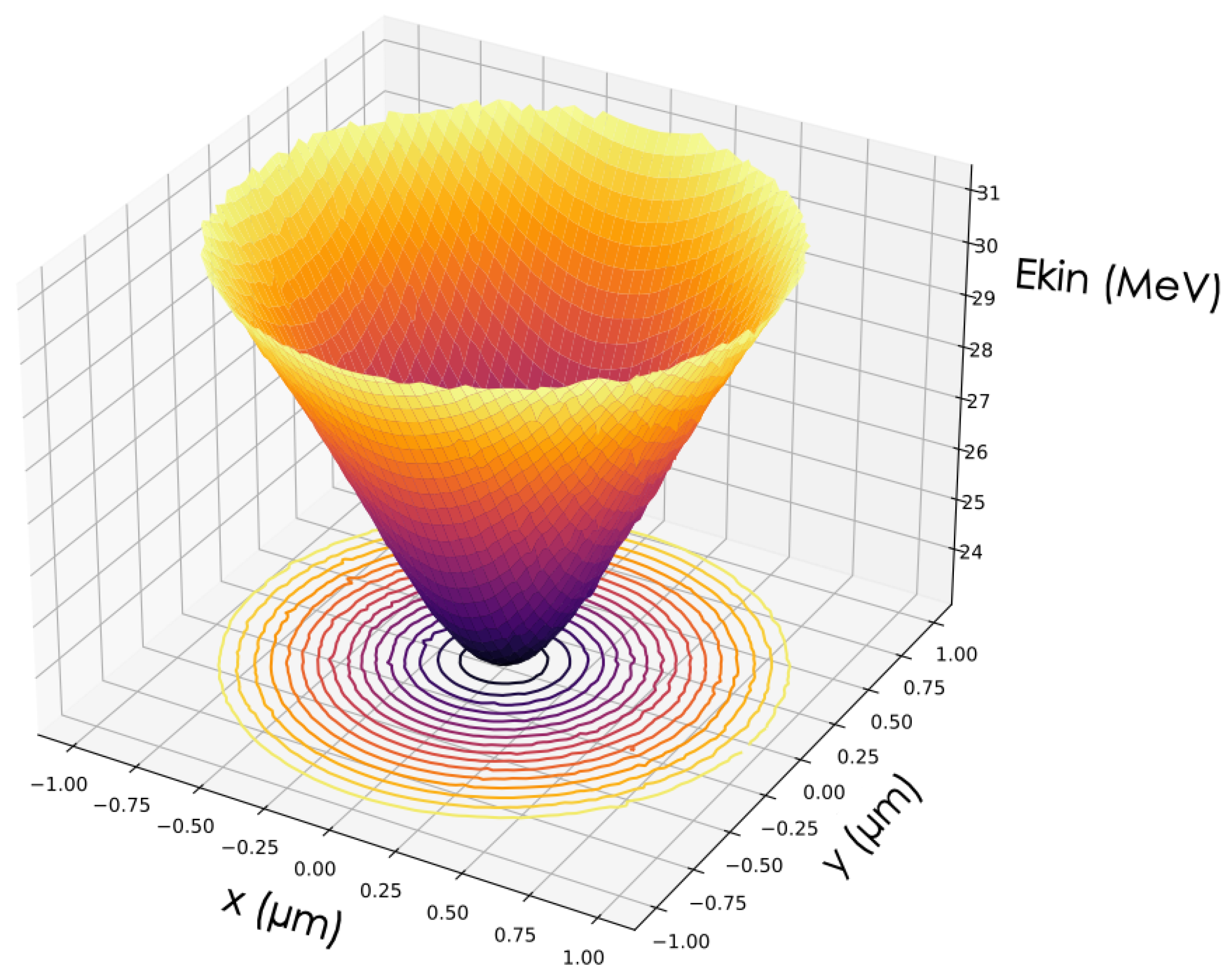
Figure 11.
Asymptotic kinetic energy for counter-propagating 1 GeV electrons with RR. The sample includes 4096 electrons randomly distributed up to , with . The laser is in the mode, X polarized, with a peak intensity of . A strong reduction in kinetic energy is predicted under these conditions with RR. Contour plots of iso-energy show an approximate circular symmetry around the laser propagation axis.
Figure 11.
Asymptotic kinetic energy for counter-propagating 1 GeV electrons with RR. The sample includes 4096 electrons randomly distributed up to , with . The laser is in the mode, X polarized, with a peak intensity of . A strong reduction in kinetic energy is predicted under these conditions with RR. Contour plots of iso-energy show an approximate circular symmetry around the laser propagation axis.
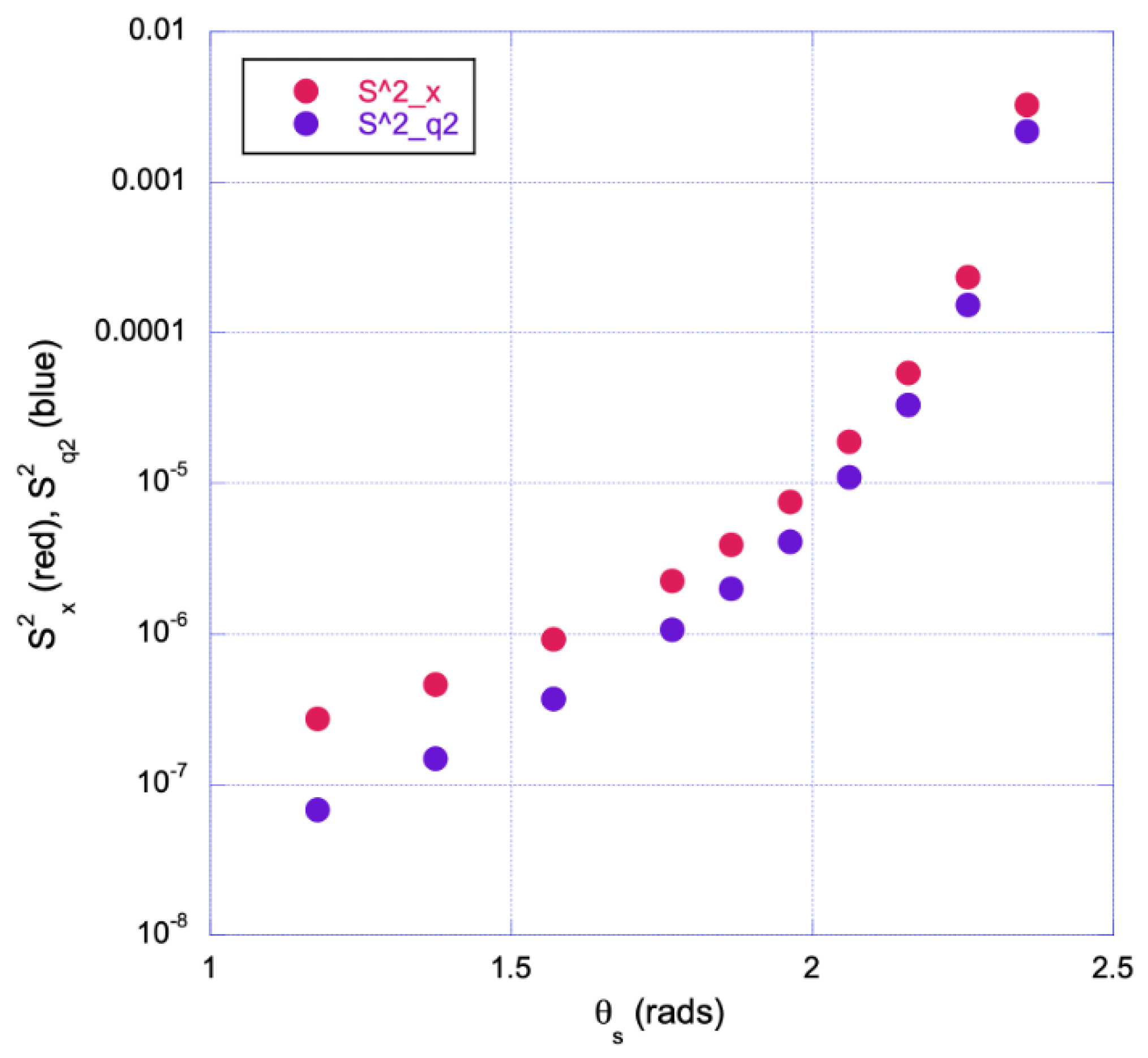
Figure 12.
Integrated spectral power: X-polarization in red and the orthogonal quadrature (q2) in blue, averaged over electron samples (typically 2048 or 4096 at each scattering angle) aimed at the central part of the laser pulse, including RR, as a function of the scattering angle. The scattering plane is YZ. Notice the rapid increase in integrated power with the scattering angle.
Figure 12.
Integrated spectral power: X-polarization in red and the orthogonal quadrature (q2) in blue, averaged over electron samples (typically 2048 or 4096 at each scattering angle) aimed at the central part of the laser pulse, including RR, as a function of the scattering angle. The scattering plane is YZ. Notice the rapid increase in integrated power with the scattering angle.
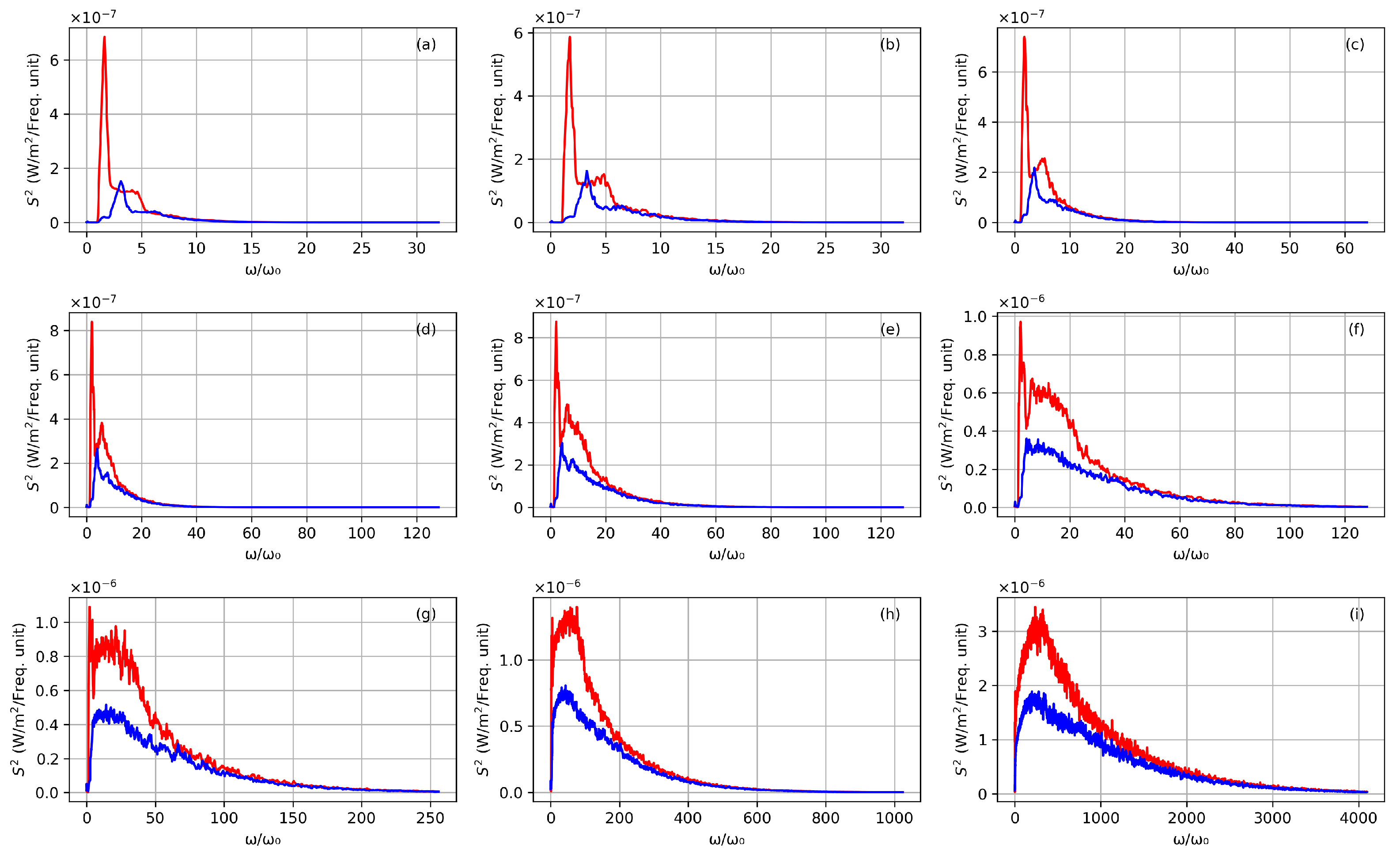
Figure 13.
Averaged TS spectra. The scattering plane is YZ. Scattering angles for (a–i) are respectively , , , , , , , , and . A spectrum extending up to is obtained for .
Figure 13.
Averaged TS spectra. The scattering plane is YZ. Scattering angles for (a–i) are respectively , , , , , , , , and . A spectrum extending up to is obtained for .
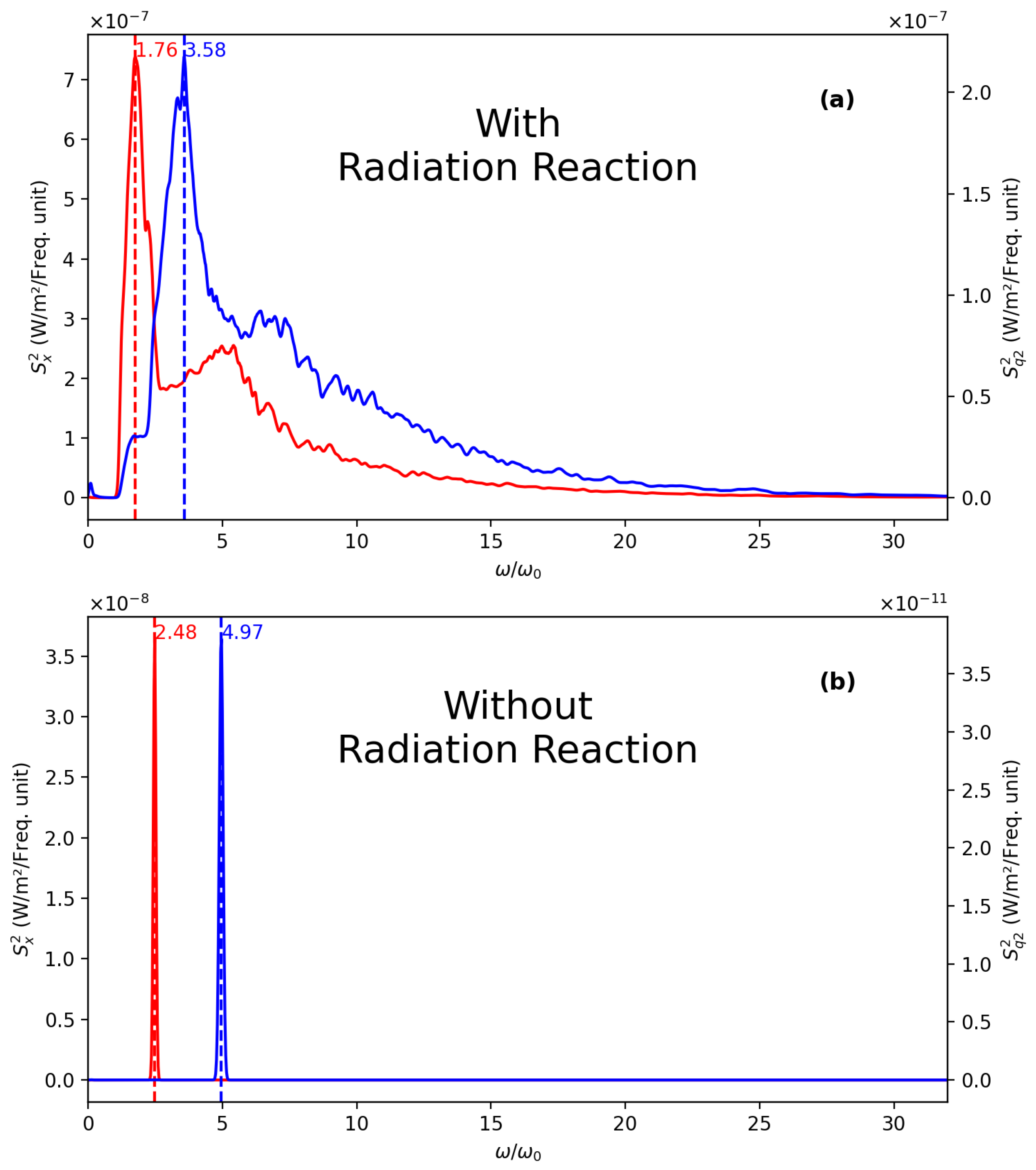
Figure 14.
Comparison of TS spectra (X-quadrature in red, q2-quadrature in blue) with (a) and without (b) RR. The scattering angle is . The shape, amplitude, and power ratio of the two quadratures are altered by RR, which can help distinguish and detect RR signatures in the spectra. See more details in the main text.
Figure 14.
Comparison of TS spectra (X-quadrature in red, q2-quadrature in blue) with (a) and without (b) RR. The scattering angle is . The shape, amplitude, and power ratio of the two quadratures are altered by RR, which can help distinguish and detect RR signatures in the spectra. See more details in the main text.
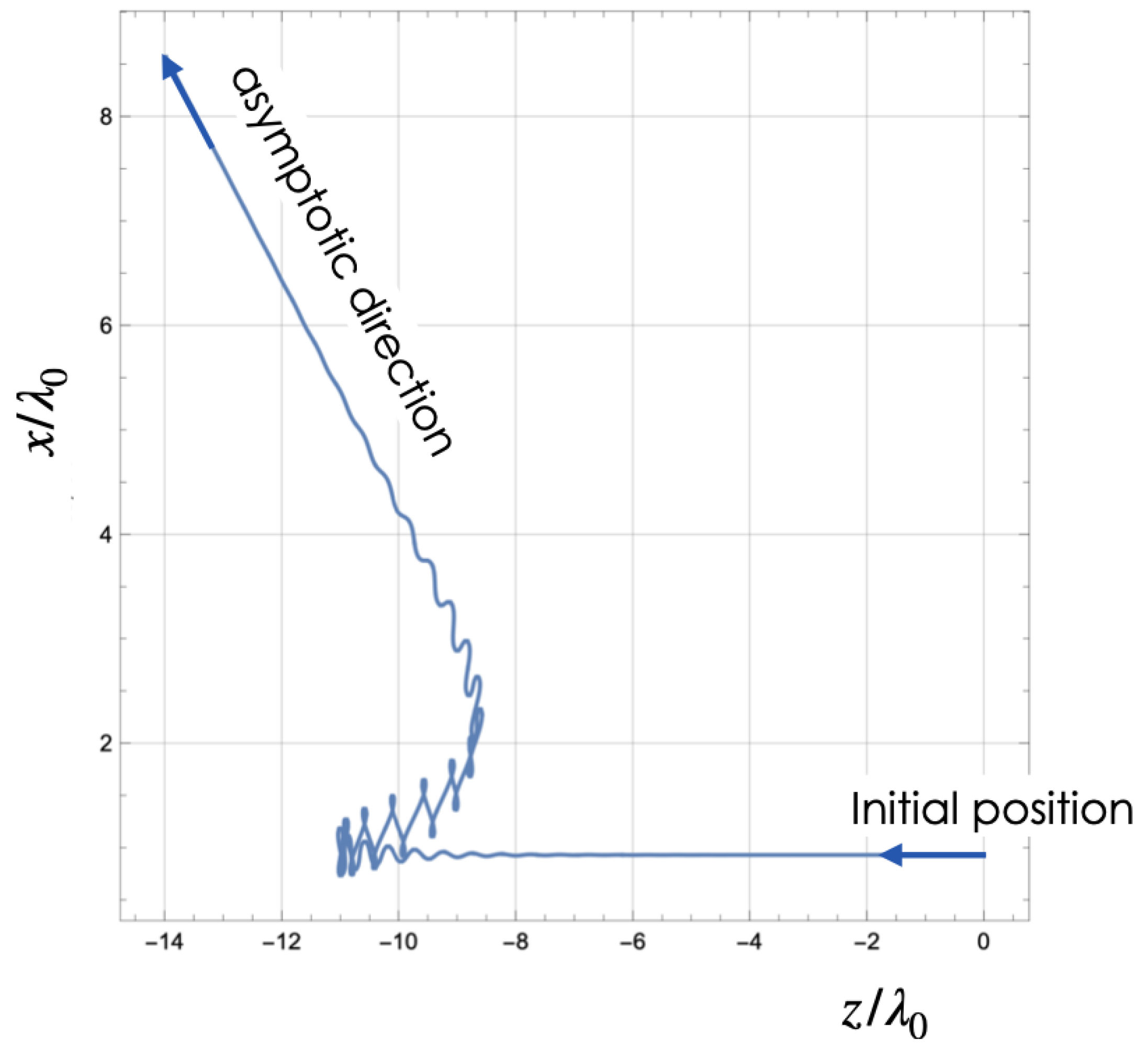
Figure 15.
Projection of a sample trajectory onto the X-Z plane, including RR. The electron, initially at , moves from right to left, interacts strongly with the laser pulse around , and is deflected nearly from its initial direction. Note the reversal in electron motion after deceleration (curly part moving towards the positive side of the z-axis).
Figure 15.
Projection of a sample trajectory onto the X-Z plane, including RR. The electron, initially at , moves from right to left, interacts strongly with the laser pulse around , and is deflected nearly from its initial direction. Note the reversal in electron motion after deceleration (curly part moving towards the positive side of the z-axis).
Figure 16.
Time evolution of the relativistic
factor (
a) and normalized velocity (
b) for the trajectory shown in
Figure 15. The strong reduction in
due to RR is evident, along with substantial perturbations in
and
, and to a lesser extent in
. Note that
reverses from counter-propagating to co-propagating at various points in the trajectory. In (
b), the color code is as follows: red, green, and blue represent
,
, and
, respectively.
Figure 16.
Time evolution of the relativistic
factor (
a) and normalized velocity (
b) for the trajectory shown in
Figure 15. The strong reduction in
due to RR is evident, along with substantial perturbations in
and
, and to a lesser extent in
. Note that
reverses from counter-propagating to co-propagating at various points in the trajectory. In (
b), the color code is as follows: red, green, and blue represent
,
, and
, respectively.
Figure 17.
Radiated electric field at the detector in the time domain (a) and a close-up view (b) showing the structure of spikes under the radiated pulse envelope. The scattering plane is Y-Z. The electric field component parallel to the X-axis is shown in red, while the other component is shown in blue. In (b), the component along the scattering vector is also displayed (in green), which is negligible compared to the other components.
Figure 17.
Radiated electric field at the detector in the time domain (a) and a close-up view (b) showing the structure of spikes under the radiated pulse envelope. The scattering plane is Y-Z. The electric field component parallel to the X-axis is shown in red, while the other component is shown in blue. In (b), the component along the scattering vector is also displayed (in green), which is negligible compared to the other components.
Figure 18.
Three-dimensional asymptotic distributions of (a), (b), and (c) as functions of the initial transverse position of the electrons. The panels show 4096 sample electrons, uniformly and randomly distributed up to .
Figure 18.
Three-dimensional asymptotic distributions of (a), (b), and (c) as functions of the initial transverse position of the electrons. The panels show 4096 sample electrons, uniformly and randomly distributed up to .
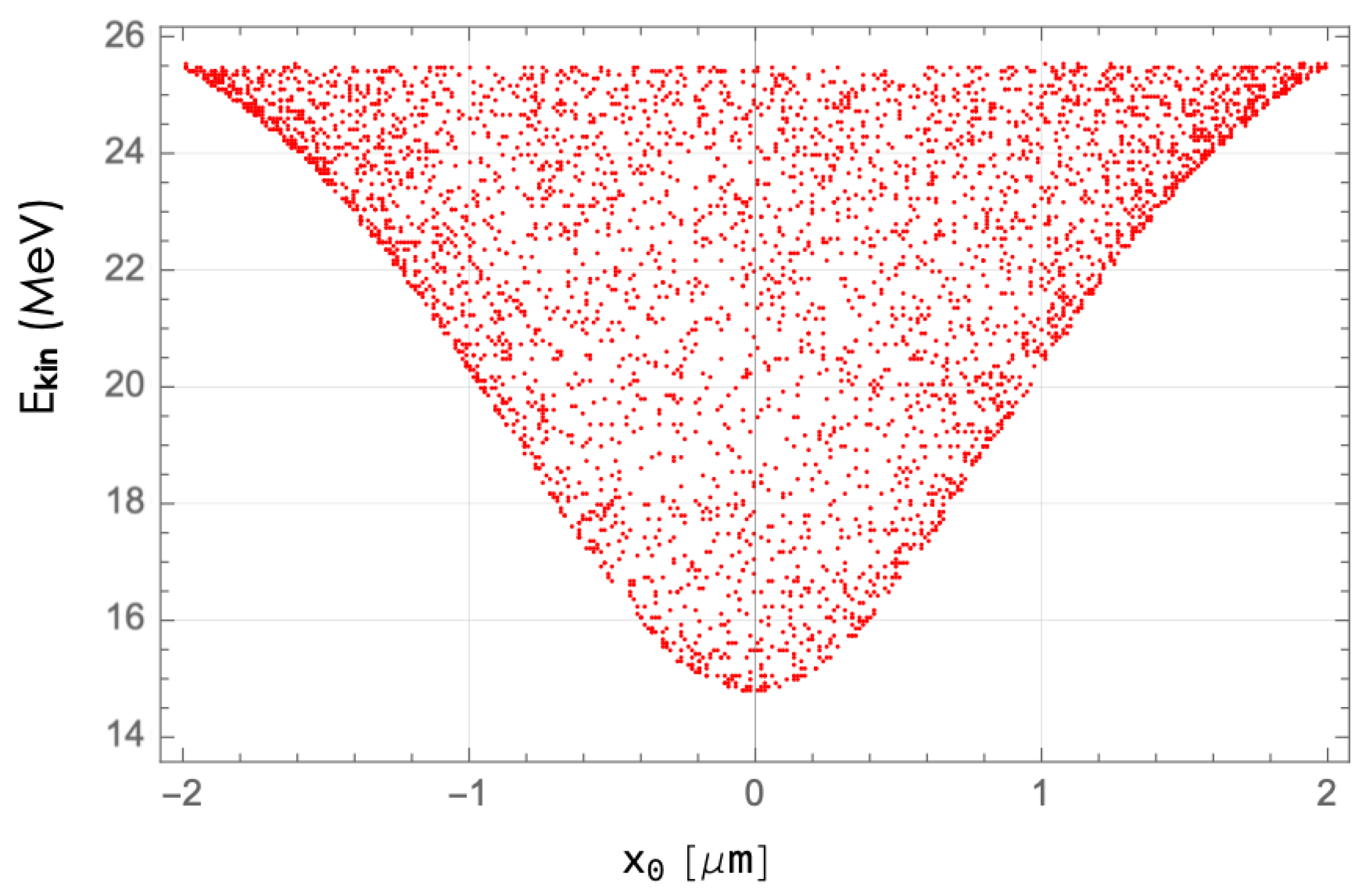
Figure 19.
Asymptotic distribution of projected onto the X-axis. The panel includes 4096 sample electrons, uniformly and randomly distributed up to . RR accounts for up to 98.5% loss of the initial kinetic energy for electrons near the center of the mode laser axis.
Figure 19.
Asymptotic distribution of projected onto the X-axis. The panel includes 4096 sample electrons, uniformly and randomly distributed up to . RR accounts for up to 98.5% loss of the initial kinetic energy for electrons near the center of the mode laser axis.
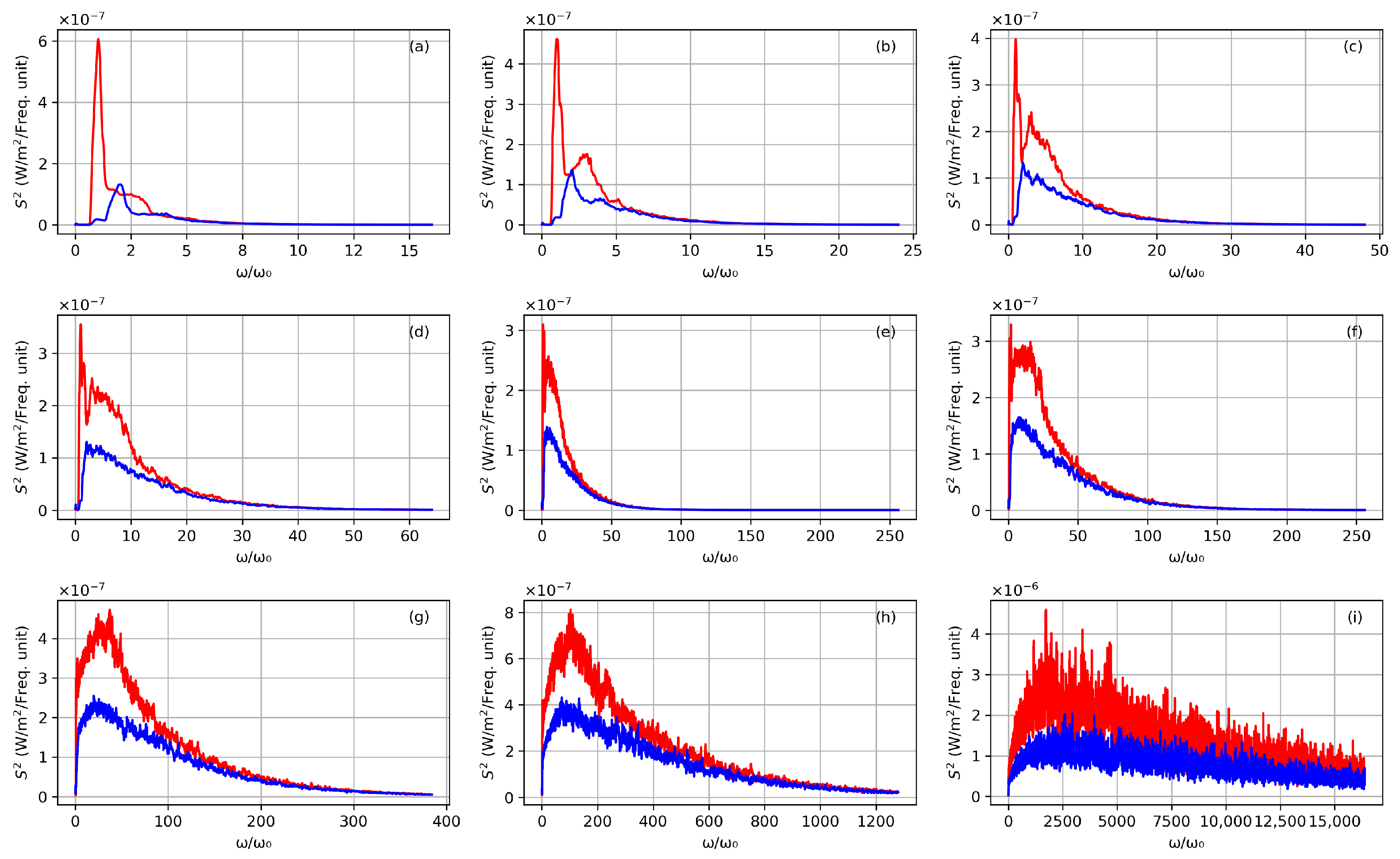
Figure 20.
Averaged TS spectra. The scattering plane is YZ, and scattering angles for (a–i) are, respectively, , , , , , , , , and . An extremely broad spectrum, extending well beyond , is obtained for .
Figure 20.
Averaged TS spectra. The scattering plane is YZ, and scattering angles for (a–i) are, respectively, , , , , , , , , and . An extremely broad spectrum, extending well beyond , is obtained for .
Figure 21.
Visualization of the scattering process on a unit momentum sphere. Each point on the sphere’s surface represents the asymptotic direction of electron scattering; dot colors indicate asymptotic energy, with dark blue representing minimum and red representing maximum energy.
Figure 21.
Visualization of the scattering process on a unit momentum sphere. Each point on the sphere’s surface represents the asymptotic direction of electron scattering; dot colors indicate asymptotic energy, with dark blue representing minimum and red representing maximum energy.
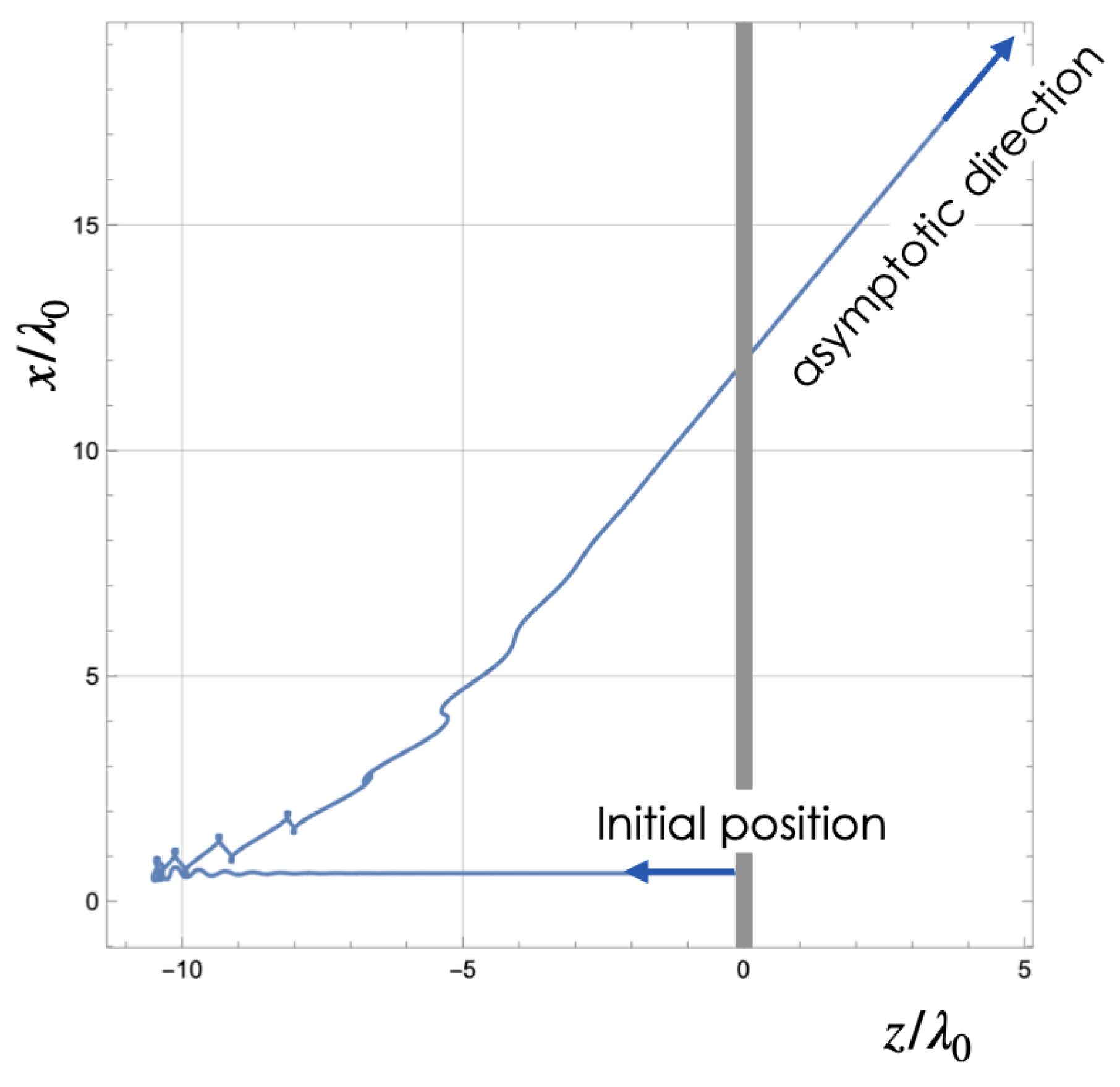
Figure 22.
Projection of a sample trajectory onto the XZ plane, including RR. The electron is initially located at , moves from right to left, strongly interacts with the laser pulse around , and is deflected at an angle larger than with respect to its initial direction. The (or ) component changes from counter-propagating to co-propagating. The thick gray line indicates the initial position of the electron bunch. For this extreme intensity, the electron trajectory is reversed.
Figure 22.
Projection of a sample trajectory onto the XZ plane, including RR. The electron is initially located at , moves from right to left, strongly interacts with the laser pulse around , and is deflected at an angle larger than with respect to its initial direction. The (or ) component changes from counter-propagating to co-propagating. The thick gray line indicates the initial position of the electron bunch. For this extreme intensity, the electron trajectory is reversed.
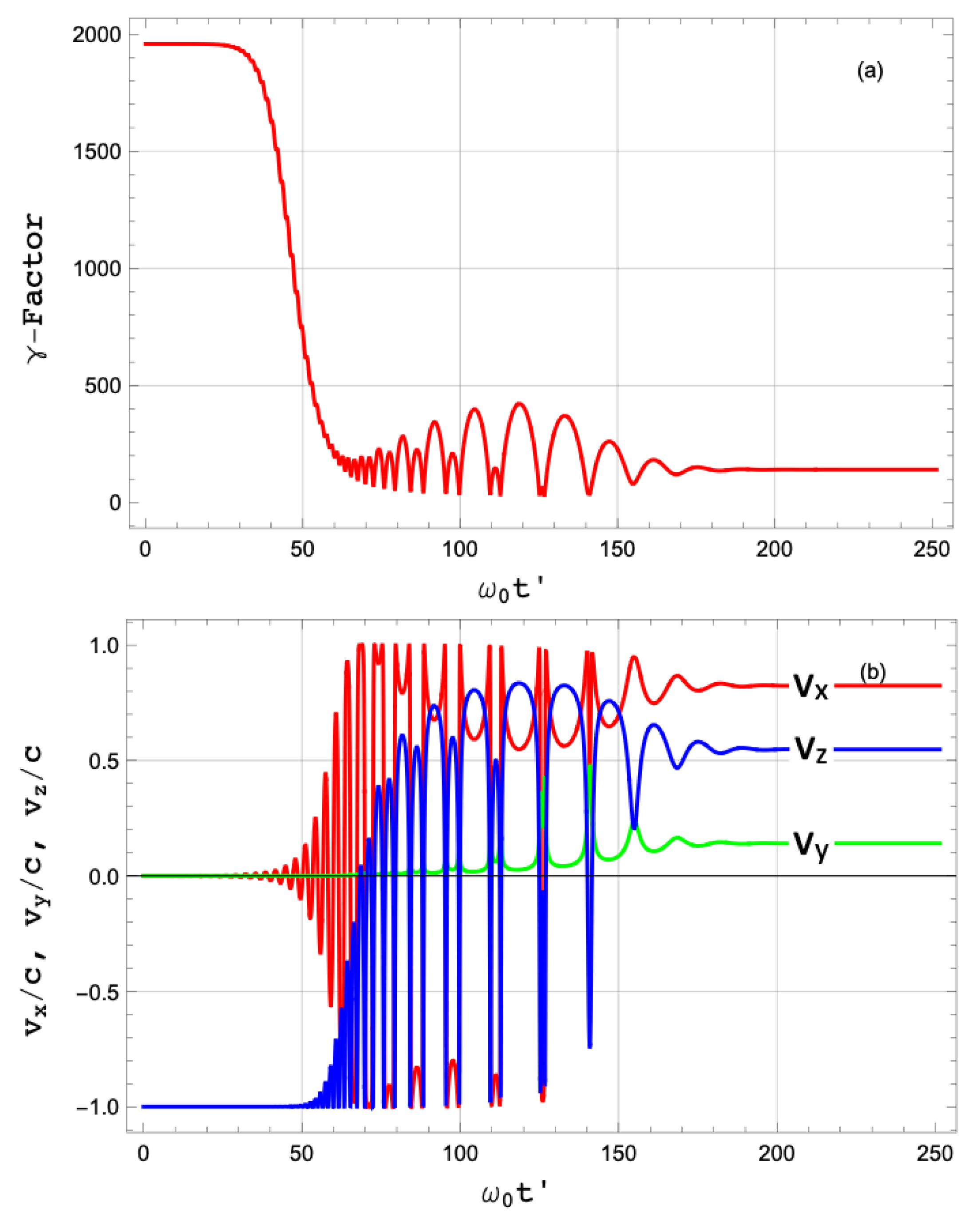
Figure 23.
Time evolution of the relativistic
factor (
a) and of the normalized velocity (
b) for the sample trajectory in
Figure 22. The strong reduction in
due to RR is apparent, as well as the large perturbations on
and
, and also to some extent on
. Note that
asymptotically reverses from counter-propagating to co-propagating. Color code in (
b) is red, green, and blue corresponding to
,
, and
, respectively.
Figure 23.
Time evolution of the relativistic
factor (
a) and of the normalized velocity (
b) for the sample trajectory in
Figure 22. The strong reduction in
due to RR is apparent, as well as the large perturbations on
and
, and also to some extent on
. Note that
asymptotically reverses from counter-propagating to co-propagating. Color code in (
b) is red, green, and blue corresponding to
,
, and
, respectively.
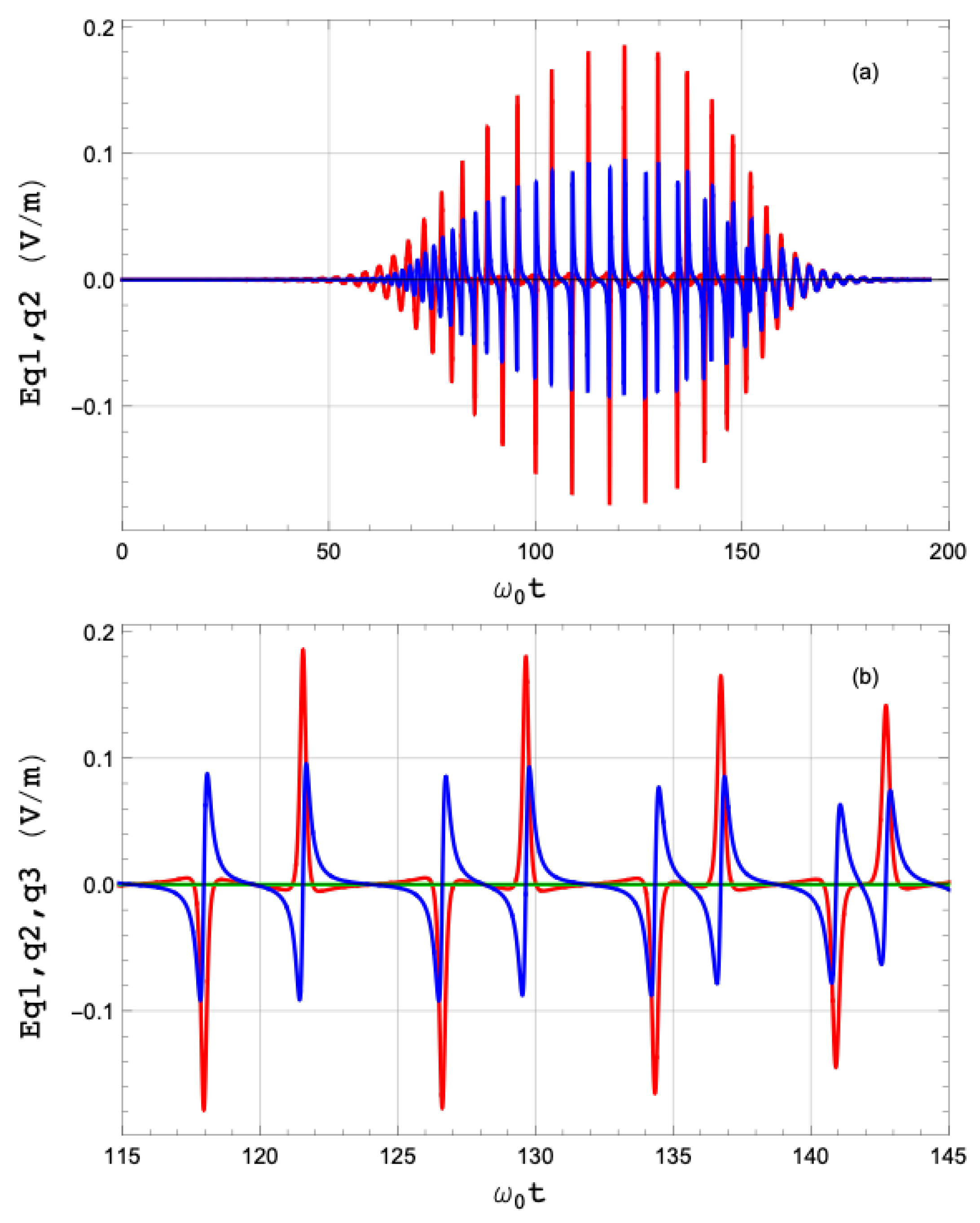
Figure 24.
Radiated electric field at the detector in the time domain (a) and a close-up (b) displaying the structure of the spikes under the radiated pulse envelope. The scattering plane is YZ. The electric field component parallel to the X axis is displayed in red, the other one in blue. In (b), the component along the scattering vector is also displayed (in green), showing it to be negligible compared to the other components. Note the highly asymmetric shape of the electric pulse envelope in this particular case.
Figure 24.
Radiated electric field at the detector in the time domain (a) and a close-up (b) displaying the structure of the spikes under the radiated pulse envelope. The scattering plane is YZ. The electric field component parallel to the X axis is displayed in red, the other one in blue. In (b), the component along the scattering vector is also displayed (in green), showing it to be negligible compared to the other components. Note the highly asymmetric shape of the electric pulse envelope in this particular case.
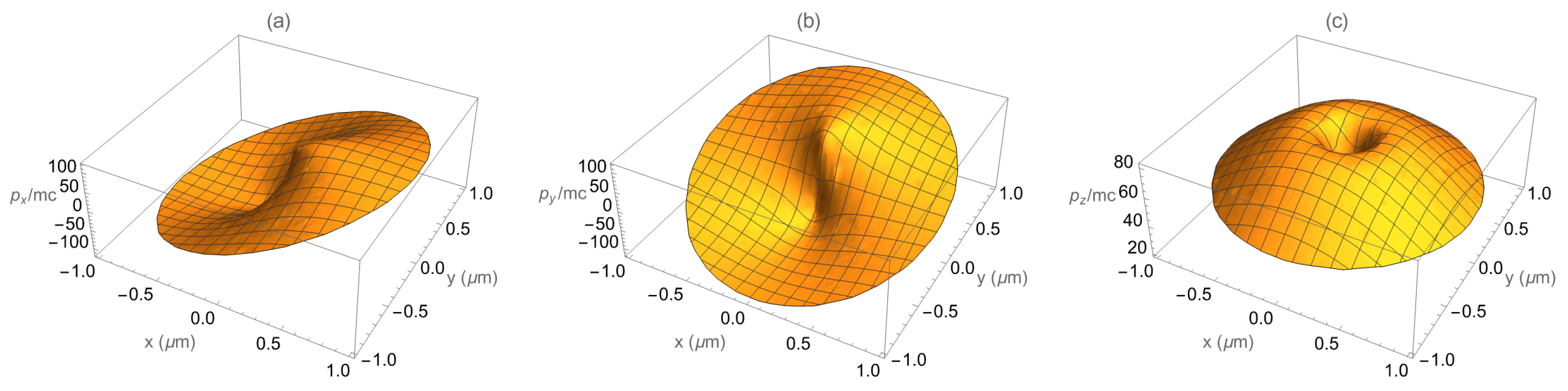
Figure 25.
Three-dimensional asymptotic normalized momentum components for counter-propagating 1 GeV electrons. (a–c) correspond respectively to the asymptotic distributions of , and . The sample includes 4096 electrons randomly distributed up to , where is 4 m. The laser is in the mode, X polarized, with a peak intensity of . Close to the center of the laser mode, RR accounts for up to 99 percent energy loss.
Figure 25.
Three-dimensional asymptotic normalized momentum components for counter-propagating 1 GeV electrons. (a–c) correspond respectively to the asymptotic distributions of , and . The sample includes 4096 electrons randomly distributed up to , where is 4 m. The laser is in the mode, X polarized, with a peak intensity of . Close to the center of the laser mode, RR accounts for up to 99 percent energy loss.
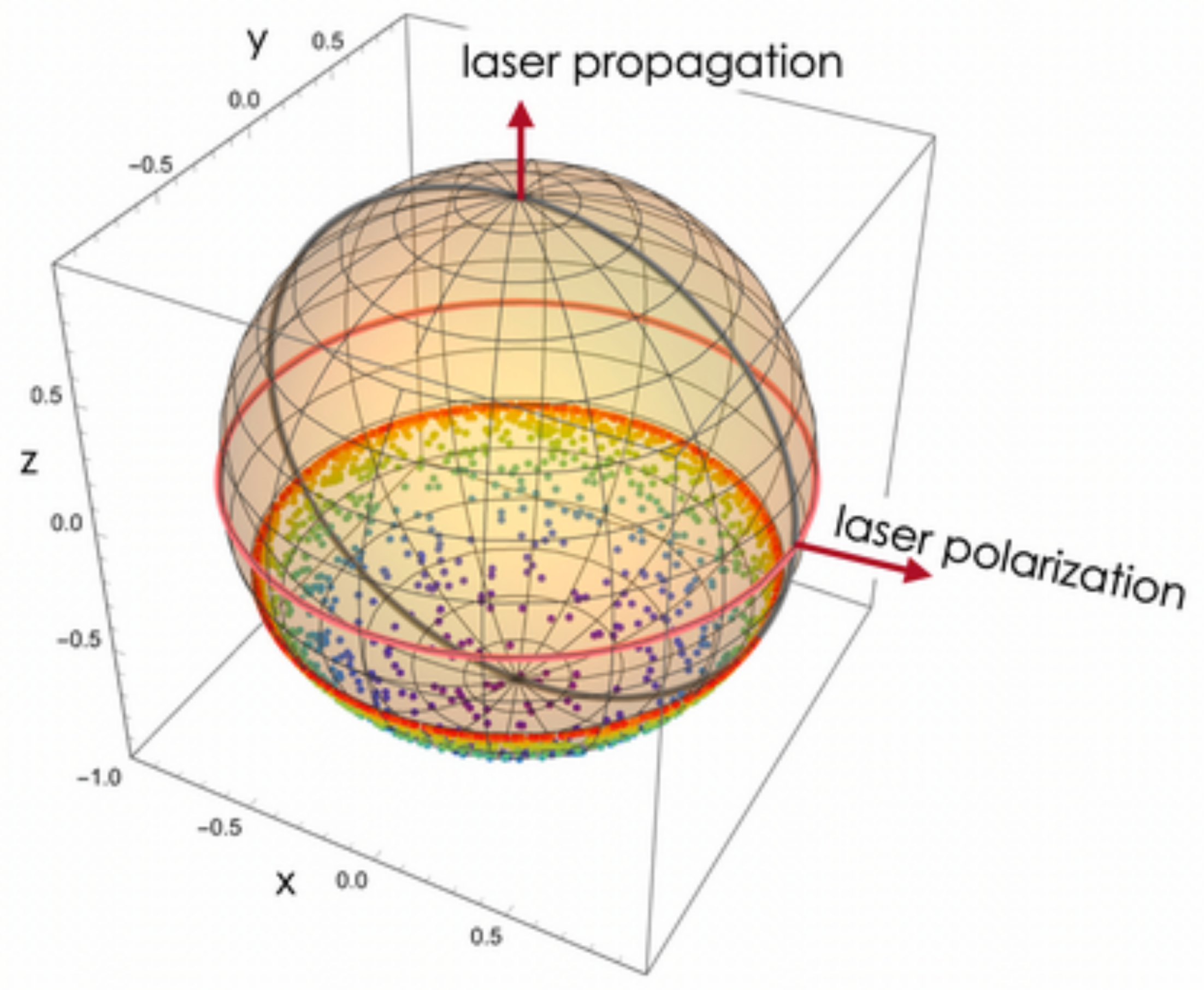
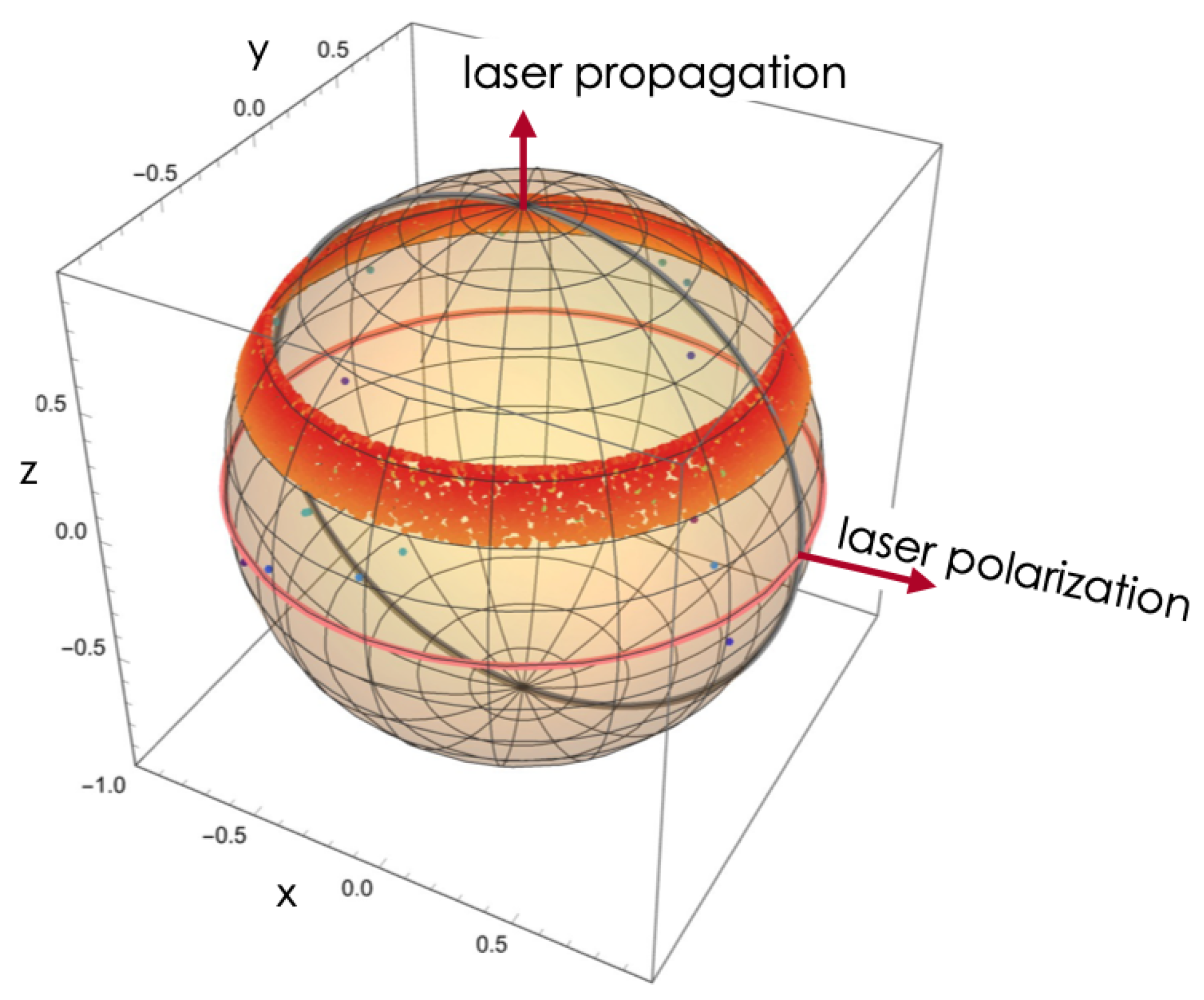
Figure 26.
Asymptotic velocity distribution (final velocity of the electrons) depicted over the unit sphere. The pink circle is the equator of the unit sphere and the gray circle crosses the unit sphere poles. The value of the final velocity is given by the color scale. The orange dotted ribbon indicates the multiple trajectories with asymptotic speeds that have been reversed, i.e., points towards the positive values of z.
Figure 26.
Asymptotic velocity distribution (final velocity of the electrons) depicted over the unit sphere. The pink circle is the equator of the unit sphere and the gray circle crosses the unit sphere poles. The value of the final velocity is given by the color scale. The orange dotted ribbon indicates the multiple trajectories with asymptotic speeds that have been reversed, i.e., points towards the positive values of z.
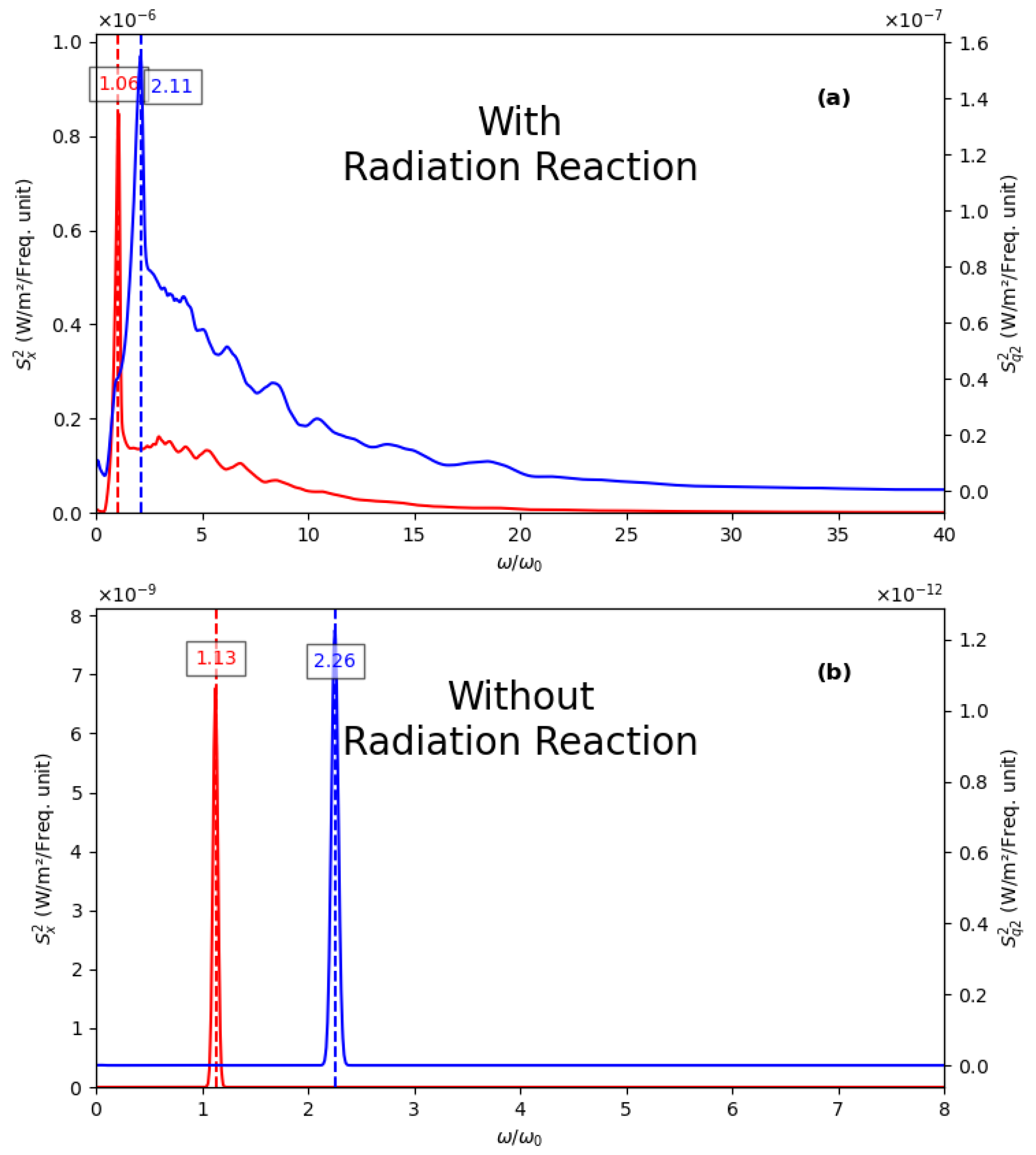
Figure 27.
A comparison of TS spectra (X-quadrature in red, q2-quadrature in blue) with (a) and without (b) RR. The scattering angle is in this case. The shape, amplitude, and power ratio of the two quadratures are altered by RR, which can help distinguish and detect RR signatures in the spectra. See more details in the main text.
Figure 27.
A comparison of TS spectra (X-quadrature in red, q2-quadrature in blue) with (a) and without (b) RR. The scattering angle is in this case. The shape, amplitude, and power ratio of the two quadratures are altered by RR, which can help distinguish and detect RR signatures in the spectra. See more details in the main text.