High-Sensitivity Refractive Index Sensing Based on an SNPNS Composite Structure
Abstract
1. Introduction
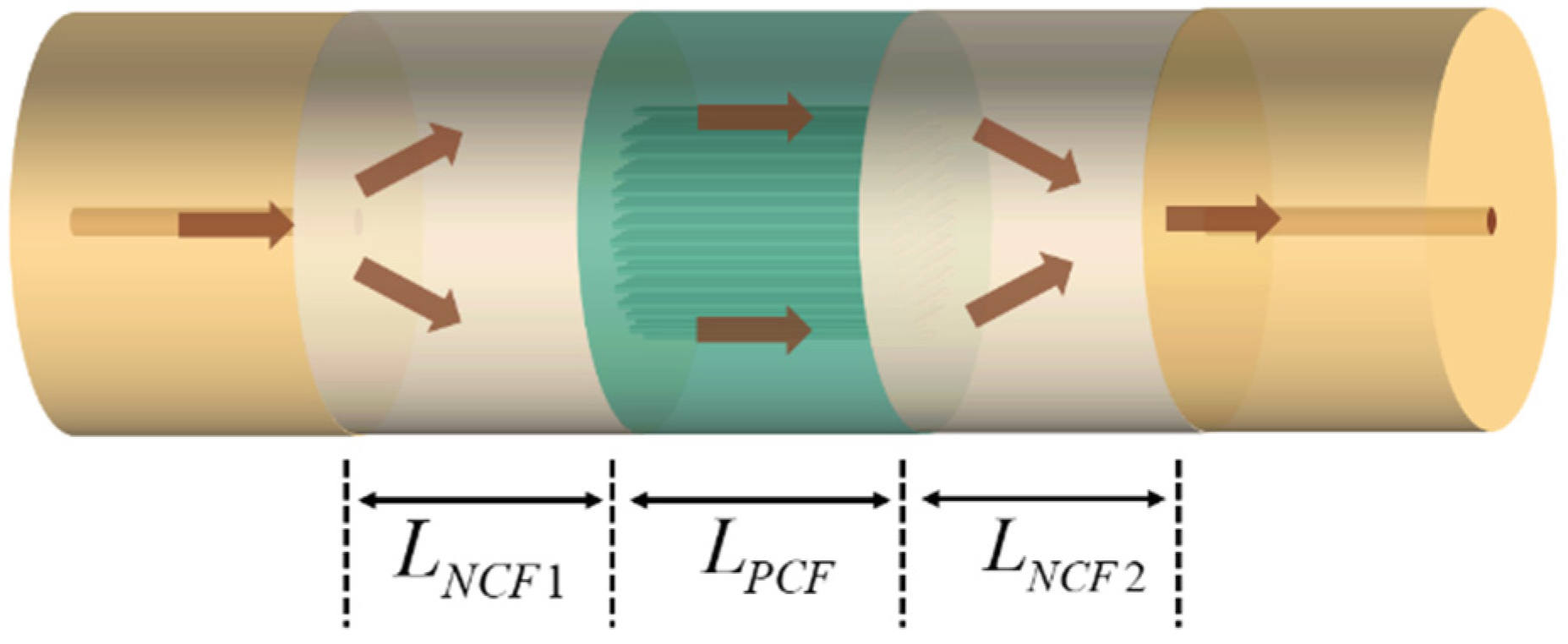
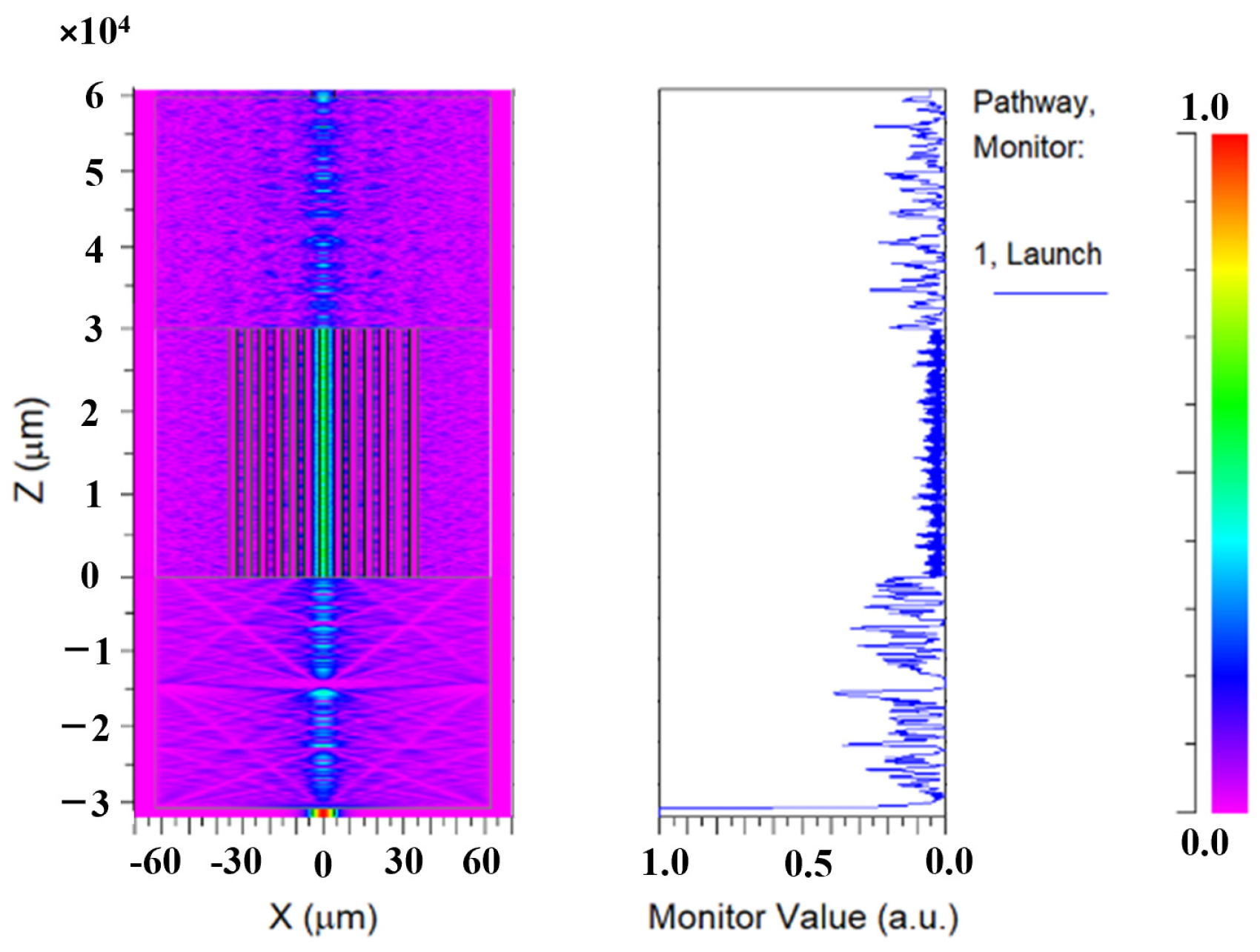
2. Sensor Fabrication and Principle
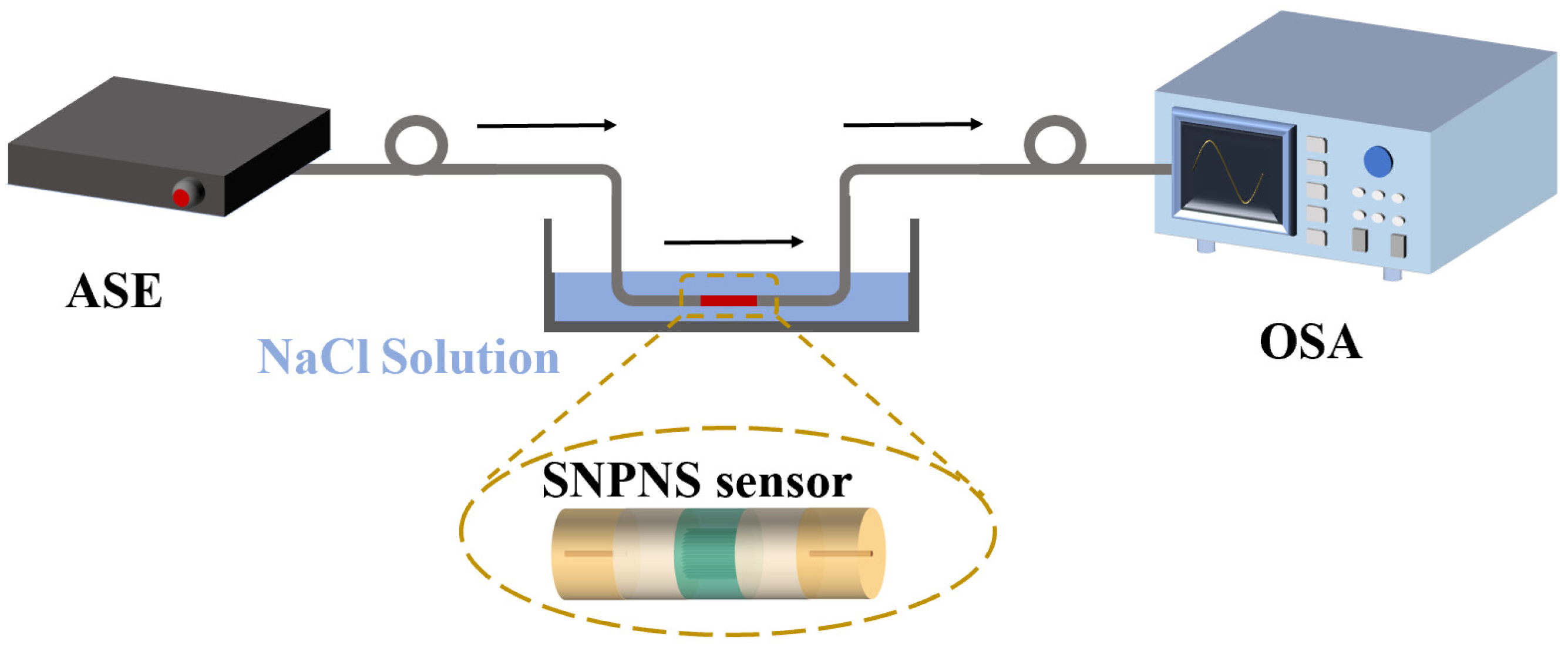
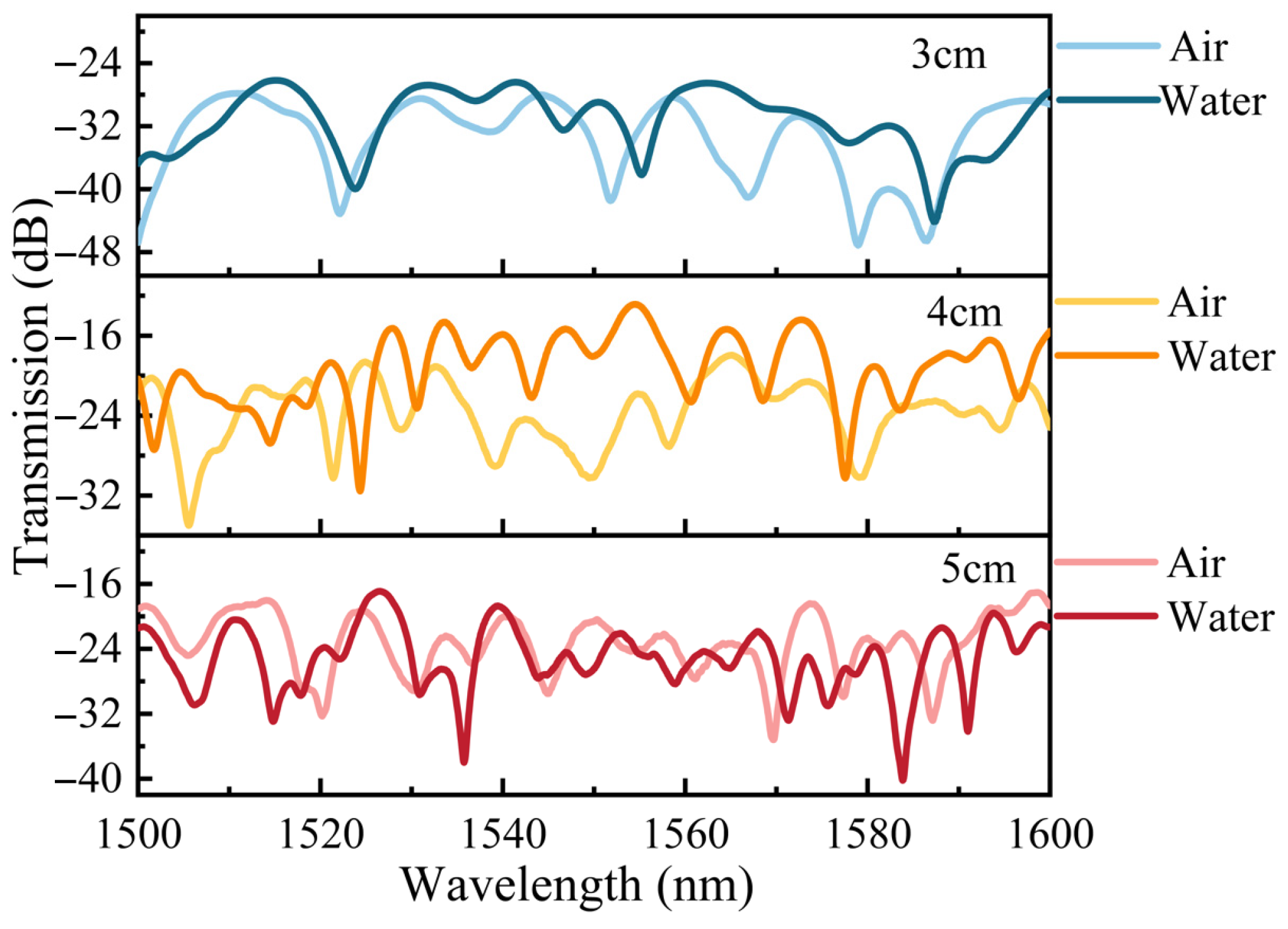
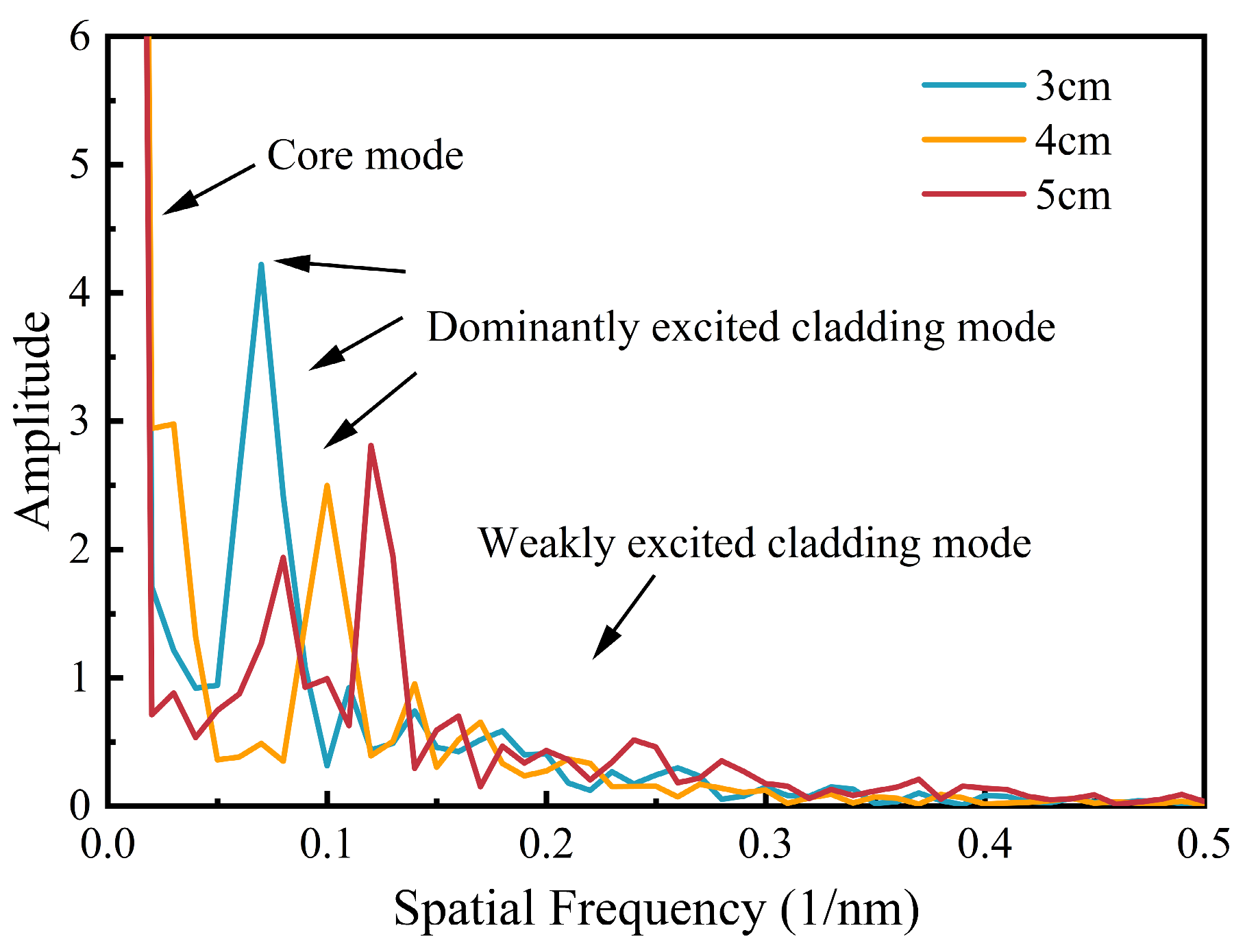
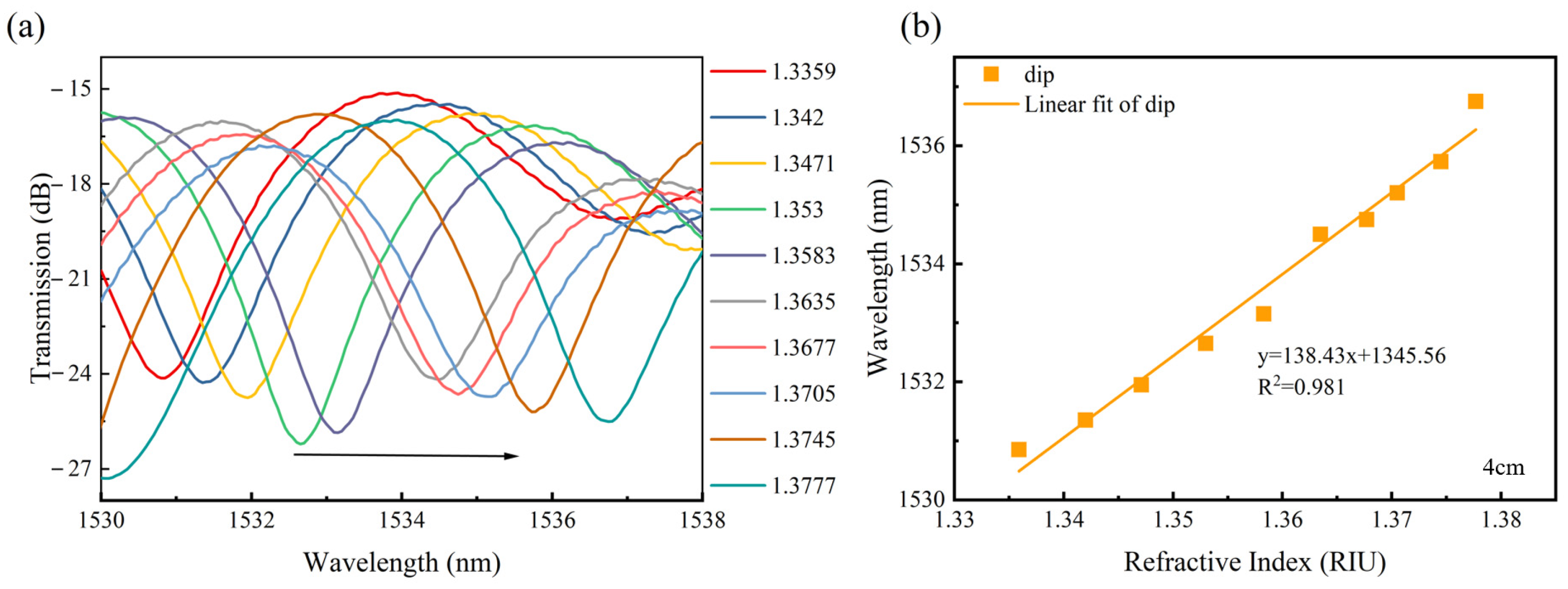
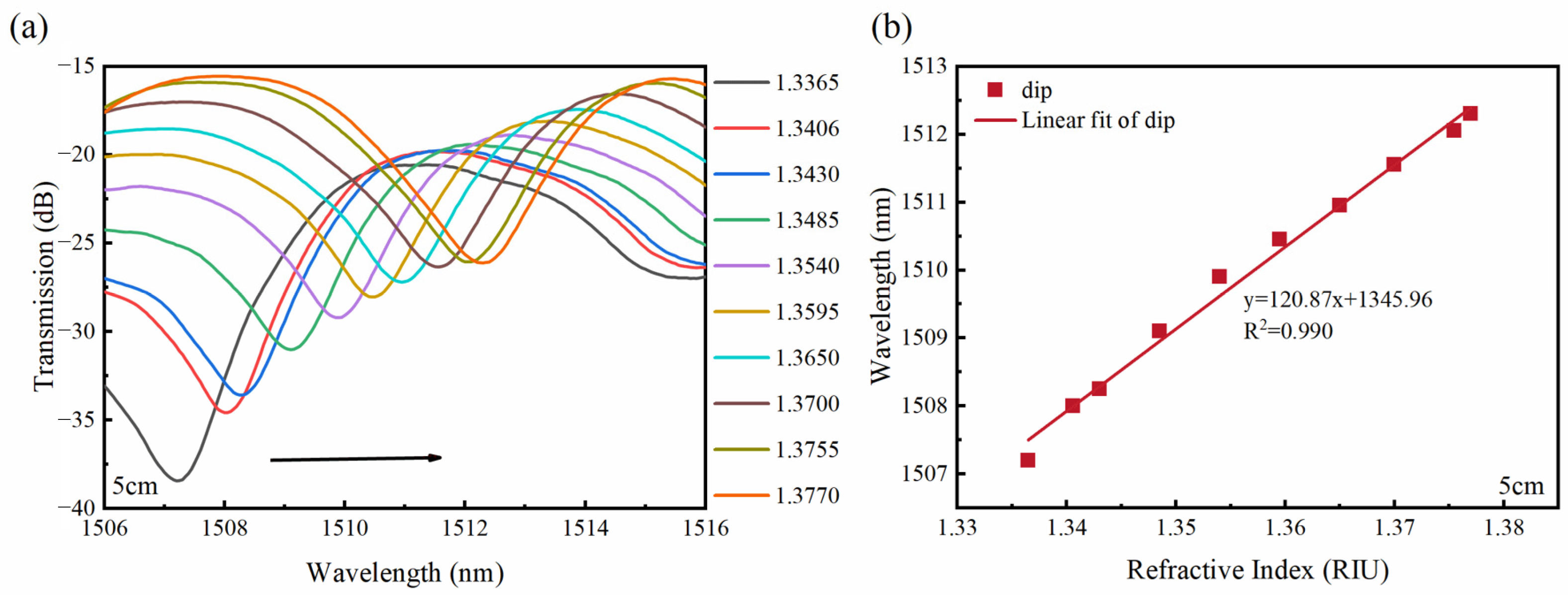
3. Experimental Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Joe, H.E.; Yun, H.; Jo, S.H.; Jun, M.; Min, B. A review on optical fiber sensors for environmental monitoring. Int. J. Precis. Eng. Man. GT 2018, 5, 173–191. [Google Scholar] [CrossRef]
- Chaudhary, V.S.; Kumar, D.; Kumar, S. Gold-immobilized photonic crystal fiber-based SPR biosensor for detection of malaria disease in human body. IEEE Sen. J. 2021, 21, 17800–17807. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, C.; Wang, J.; Li, N.; Song, Y.; Wu, H.; Liu, Y. A fiber Bragg grating sensor based on cladding mode resonance for label-free biosensing. Biosensors 2023, 13, 97. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Wang, G.; Yu, X.; Fan, Y.; Chen, X.; Liu, S. Label-free DNA hybridization detection using a highly sensitive fiber microcavity biosensor. Sensors 2024, 24, 278. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; He, T.; Chen, M.; Zhang, Z.; Tong, R. Ultra-short fiber Bragg grating composed of cascaded microchannels in a microprobe for refractive index measurement. J. Lightwave Technol. 2023, 41, 2555–2561. [Google Scholar] [CrossRef]
- Upadhyay, C.; Dhawan, D. Fiber Bragg grating refractive index sensor based on double D-shaped fiber. Opt. Quantum Electron. 2023, 55, 271. [Google Scholar] [CrossRef]
- Qi, L.; Zhao, C.L.; Yuan, J.; Ye, M.; Wang, J.; Zhang, Z.; Jin, S. Highly reflective long period fiber grating sensor and its application in refractive index sensing. Sens. Actuators B 2014, 193, 185–189. [Google Scholar] [CrossRef]
- Li, H.C.; Liu, J.; He, X.; Yuan, J.; Wu, Q.; Liu, B. Long-period fiber grating based on side-polished optical fiber and its sensing application. IEEE Trans. Instrum. Meas. 2023, 72, 7001109. [Google Scholar] [CrossRef]
- Liu, D.; Mallik, A.K.; Yuan, J.; Yu, C.; Farrell, G.; Semenova, Y.; Wu, Q. High-sensitivity refractive index sensor based on a tapered small core single-mode fiber structure. Opt. Lett. 2015, 40, 4166–4169. [Google Scholar] [CrossRef]
- Lu, Z.; Liu, C.; Ren, J.; Chen, L.; Li, C.; Zhou, W. Temperature-insensitive high-sensitivity refractive index sensor based on tapered no core fiber. Meas. Sci. Technol. 2023, 34, 084001. [Google Scholar] [CrossRef]
- Islam, N.; Arif, M.F.H.; Yousuf, M.A.; Asaduzzaman, S. Highly sensitive open channel-based PCF-SPR sensor for analyte refractive index sensing. Results Phys. 2023, 46, 106266. [Google Scholar] [CrossRef]
- Chaudhary, V.S.; Kumar, D.; Kumar, S. Au-TiO2 coated photonic crystal fiber based SPR refractometric sensor for detection of cancerous cells. IEEE Trans. Nanobiosci. 2023, 22, 562–569. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Qiao, X.; Guo, T.; Wang, R.; Zhang, J.; Weng, Y.; Rong, Q.; Hu, M.; Feng, Z. Temperature-independent refractive index measurement based on Fabry-Perot fiber tip sensor modulated by Fresnel reflection. Chin. Opt. Lett. 2012, 10, 050603. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, Y.; Zheng, J. Investigation of an inline fiber Mach-Zehnder interferometer based on hybrid joints of core-offset and peanut-shape for refractive index sensing. Opt. Fiber Technol. 2023, 81, 103521. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, X.; Cai, L. A highly sensitive Mach–Zehnder interferometric refractive index sensor based on core-offset single mode fiber. Sens. Actuators A 2015, 223, 119–124. [Google Scholar] [CrossRef]
- Yu, F.; Xue, P.; Zheng, J. Study of a large lateral core-offset in-line fiber modal interferometer for refractive index sensing. Opt. Fiber Technol. 2019, 47, 107–112. [Google Scholar] [CrossRef]
- Dong, R.X.; Sun, X.Y.; Chu, D.K.; Yin, K.; Luo, Z.; Wang, C.; Hu, Y.W.; Duan, J.A. Microcavity Mach–Zehnder interferometer sensors for refractive index sensing. IEEE Photonics Technol. Lett. 2016, 28, 2285–2288. [Google Scholar] [CrossRef]
- Cui, J.; Gunawardena, D.S.; Cheng, X.; Htein, L.; Leong, C.Y.; Lau, A.P.T.; Tam, H.Y. In-line open-cavity Mach-Zehnder interferometric refractive-index sensors based on inter-mode and inter-core-mode interferences. Opt. Lasers Eng. 2024, 172, 107880. [Google Scholar] [CrossRef]
- Azab, M.Y.; Hameed, M.F.O.; Mahdiraji, G.A.; Adikan, M.; Obayya, S.S.A. Experimental and numerical characterization of a D-shaped PCF refractive index sensor. Opt. Quantum Electron. 2022, 54, 846. [Google Scholar] [CrossRef]
- Wu, D.; Zhao, Y.; Li, J. PCF taper-based Mach–Zehnder interferometer for refractive index sensing in a PDMS detection cell. Sens. Actuators B 2015, 213, 1–4. [Google Scholar] [CrossRef]
- Liu, F.; Guo, X.; Zhang, Q.; Fu, X. Dual-hole photonic crystal fiber intermodal interference based refractometer. Opt. Commun. 2017, 405, 147–151. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, B.T.; Kong, L.X.; Zhan, Y. Comparative analyses of bi-tapered fiber Mach–Zehnder interferometer for refractive index sensing. IEEE Trans. Instrum. Meas. 2017, 66, 2483–2489. [Google Scholar] [CrossRef]
- Zhao, Y.; Xia, F.; Hu, H.F.; Chen, M.Q. A novel photonic crystal fiber Mach–Zehnder interferometer for enhancing refractive index measurement sensitivity. Opt. Commun. 2017, 402, 368–374. [Google Scholar] [CrossRef]
- Li, X.G.; Zhao, Y.; Cai, L.; Wang, Q. Simultaneous measurement of RI and temperature based on a composite interferometer. IEEE Photonics Technol. Lett. 2016, 28, 1839–1842. [Google Scholar] [CrossRef]
- Dong, X.; Zeng, L.; Chu, D.; Sun, X.; Duan, J. Highly sensitive refractive index sensing based on a novel Mach-Zehnder interferometer with TCF-PCF composite structure. Infrared Phys. Technol. 2022, 123, 104134. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, X.; Cai, L.; Yang, Y. Refractive index sensing based on photonic crystal fiber interferometer structure with up-tapered joints. Sens. Actuators B 2015, 221, 406–410. [Google Scholar] [CrossRef]
- Wang, Q.; Kong, L.; Dang, Y.; Xia, F.; Zhang, Y.; Zhao, Y.; Hu, H.; Li, J. High sensitivity refractive index sensor based on splicing points tapered SMF-PCF-SMF structure Mach-Zehnder mode interferometer. Sens. Actuators B Chem. 2016, 225, 213–220. [Google Scholar] [CrossRef]
- Ding, J.F.; Zhang, A.P.; Shao, L.Y.; Yan, J.H.; He, S. Fiber-taper seeded long-period grating pair as a highly sensitive refractive-index sensor. IEEE Photonics Technol. Lett. 2005, 17, 1247–1249. [Google Scholar] [CrossRef]
- Tripathi, S.M.; Bock, W.J.; Mikulic, P. A wide-range temperature immune refractive-index sensor using concatenated long-period-fiber-gratings. Sens. Actuators B 2017, 243, 1109–1114. [Google Scholar] [CrossRef]
- Garg, R.; Tripathi, S.M.; Thyagarajan, K.; Bock, W.J. Long period fiber grating based temperature-compensated high performance sensor for bio-chemical sensing applications. Sens. Actuators B Chem. 2013, 176, 1121–1127. [Google Scholar] [CrossRef]
- Chen, J.; Cui, S.; Zhang, S.; Liu, A. Refractive index sensors based on a chirped core long-period fiber grating. IEEE Photonics Technol. Lett. 2024, 36, 771–774. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, Y.; Hu, H.; Yang, Y.; Lei, M.; Wang, S. High-sensitive Mach-Zehnder interferometers based on no-core optical fiber with large lateral offset. Sens. Actuators A Phys. 2018, 281, 9–14. [Google Scholar] [CrossRef]
- Li, L.; Zhang, Y.; Han, B.; Lv, R.; Zhao, J.; Zhao, Y. Highly Sensitive and Regulatable Optical Fiber Vernier Sensor Based on Two Integrated Parallel MZIs. J. Light. Technol. 2024, 42, 6318–6325. [Google Scholar] [CrossRef]
- Tian, Z.; Yam, S.S.-H.; Barnes, J.; Bock, W.; Greig, P.; Fraser, J.M.; Loock, H.-P.; Oleschuk, R.D. Refractive index sensing with Mach-Zehnder interferometer based on concatenating two single-mode fiber tapers. IEEE Photon. Technol. Lett. 2008, 20, 626–628. [Google Scholar] [CrossRef]
- Wang, Q.; Wei, W.; Guo, M.; Zhao, Y. Optimization of cascaded fiber tapered Mach-Zehnder interferometer and refractive index sensing technology. Sens. Actuators B Chem. 2016, 222, 159–165. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, M.W.; Wang, D.N.; Liu, S.J.; Lu, P.X. Fiber in-line Mach-Zehnder interferometer fabricated by femtosecond laser micromachining for refractive index measurement with high sensitivity. J. Opt. Soc. Am. B 2010, 27, 370–374. [Google Scholar] [CrossRef]
- Gao, S.C.; Zhang, W.G.; Zhang, H.; Zhang, C.L. Reconfigurable and ultra-sensitive in-line Mach-Zehnder interferometer based on the fusion of microfiber and microfluid. Appl. Phys. Lett. 2015, 106, 084103. [Google Scholar] [CrossRef]
- Gao, S.; Zhang, W.; Bai, Z.; Zhang, H.; Geng, P.; Lin, W.; Li, J. Ultrasensitive refractive index sensor based on microfiber-assisted u-shape cavity. IEEE Photonics Technol. Lett. 2013, 25, 1815–1818. [Google Scholar] [CrossRef]



| Parameter | Values |
|---|---|
| Cladding diameter (μm) | 125 |
| Air hole diameter (μm) | 2.576 |
| Air hole pitch (μm) | 5.6 |
| Core diameter (μm) | 8.3 |
| Structures | Sensitivity (nm/RIU) | RI Range | Reference |
|---|---|---|---|
| Tapered PCF | 51.902 | 1.3411–1.3737 | [20] |
| MMF–PCF MZI | 108 | 1.333–1.374 | [24] |
| TCF–PCF MZI | 119.29 | 1.3333–1.3735 | [25] |
| HTCR–PCF–HTCR MZI | 181.96 | 1.3333–1.3574 | [23] |
| Up-tapered MZI | 252 | 1.333–1.379 | [26] |
| Tapered SMF–PCF–SMF | 260.8/243.4 | 1.3333–1.3737 | [27] |
| SNPNS MZI | 176.90 | 1.3365–1.3767 | This work |
| Structures | Sensitivity (nm/RIU) | RI Range | Reference |
|---|---|---|---|
| Tapered LPFG | 178.87 | 1.3333–1.3624 | [28] |
| etched, DRLPFGs | 2577/4681 | 1.333–1.343 | [29] |
| etched, DRLPFGs | 2500 | 1.333–1.353 | [30] |
| CC–LPFG | >600 | 1.42 | [31] |
| Bent SMF-peanut shape- SMF- core-off section-SMF | −167.27 | 1.333–1.373 | [14] |
| SMF–NCF-offset NCF–NCF–SMF | −11,078.8 | 1.3320–1.3355 | [32] |
| SMF–MMF-offset SSHF–SMF–MMF–SMF | −101,622 | 1.3311–1.3335 | [33] |
| Two cascaded SMF tapers | 1570 | 1.315–1.3618 | [34] |
| Two cascaded SMF tapers | 1548.4 | 1.3333–1.3792 | [35] |
| V-shape | 1437.61 | 1.3333–1.3459 | [17] |
| Rectangular-shape | 1489.10 | 1.3371–1.3407 | [17] |
| U-shape | 1584.47 | 1.31–1.335 | [36] |
| SMF-microfiber-SMF | 1537 | 1.44 | [37] |
| SMF-microfiber-SMF | 1376.03 | 1.4444–1.4462 | [38] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, D.; Zhou, J.; Yu, X.; Sun, Y. High-Sensitivity Refractive Index Sensing Based on an SNPNS Composite Structure. Photonics 2024, 11, 941. https://doi.org/10.3390/photonics11100941
Wu D, Zhou J, Yu X, Sun Y. High-Sensitivity Refractive Index Sensing Based on an SNPNS Composite Structure. Photonics. 2024; 11(10):941. https://doi.org/10.3390/photonics11100941
Chicago/Turabian StyleWu, Di, Jingwen Zhou, Xiang Yu, and Yue Sun. 2024. "High-Sensitivity Refractive Index Sensing Based on an SNPNS Composite Structure" Photonics 11, no. 10: 941. https://doi.org/10.3390/photonics11100941
APA StyleWu, D., Zhou, J., Yu, X., & Sun, Y. (2024). High-Sensitivity Refractive Index Sensing Based on an SNPNS Composite Structure. Photonics, 11(10), 941. https://doi.org/10.3390/photonics11100941





