Efficient Inverse Design of Large-Scale, Ultrahigh-Numerical-Aperture Metalens
Abstract
1. Introduction
2. Methods
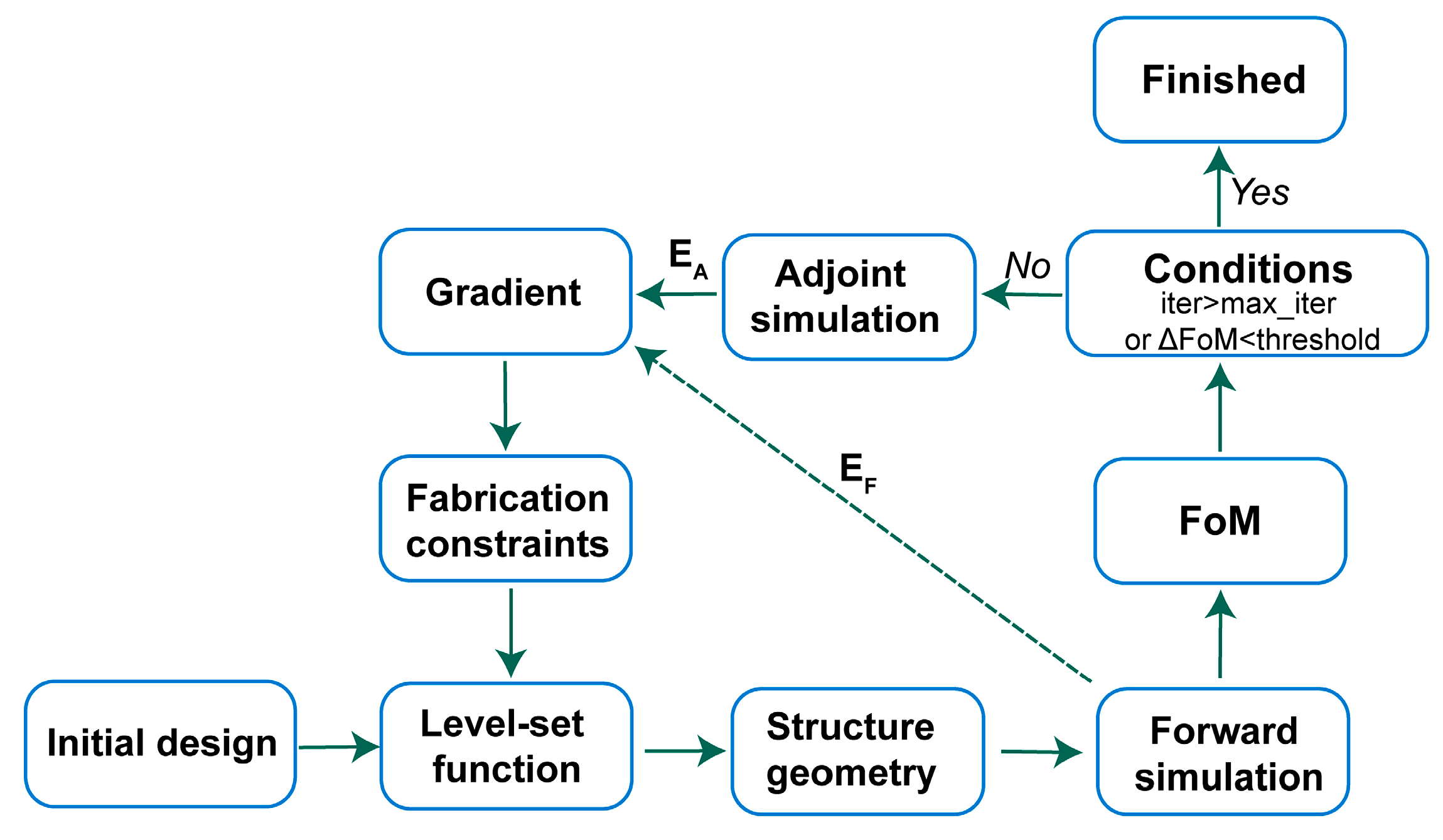
2.1. Adjoint-Based Level-Set Optimization Method
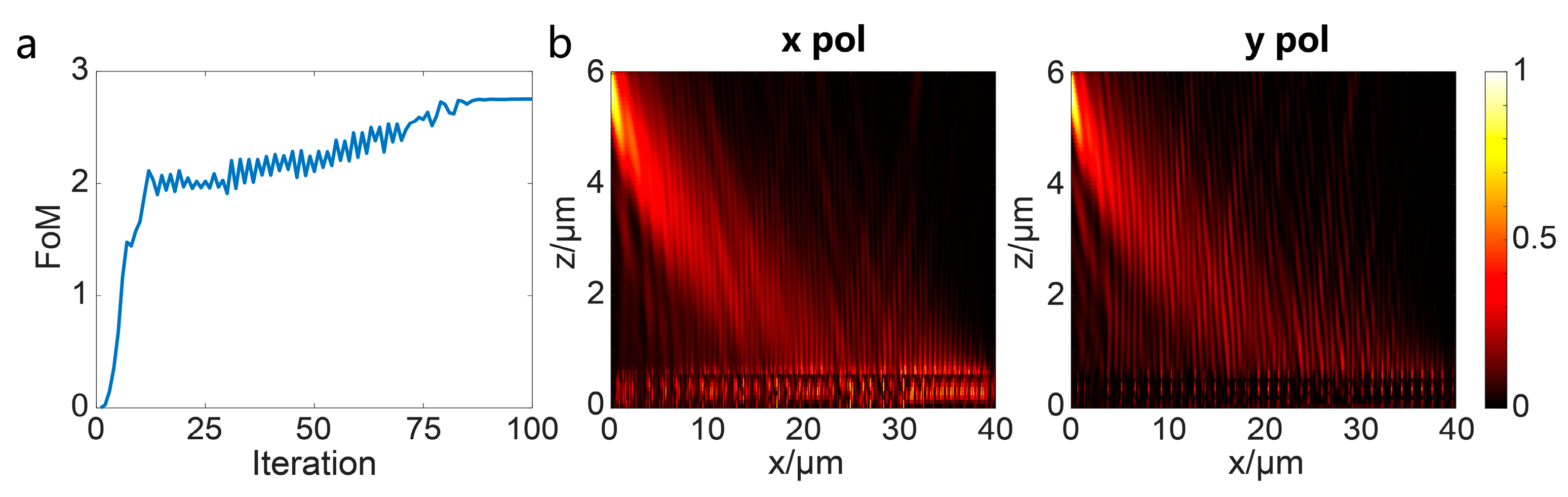
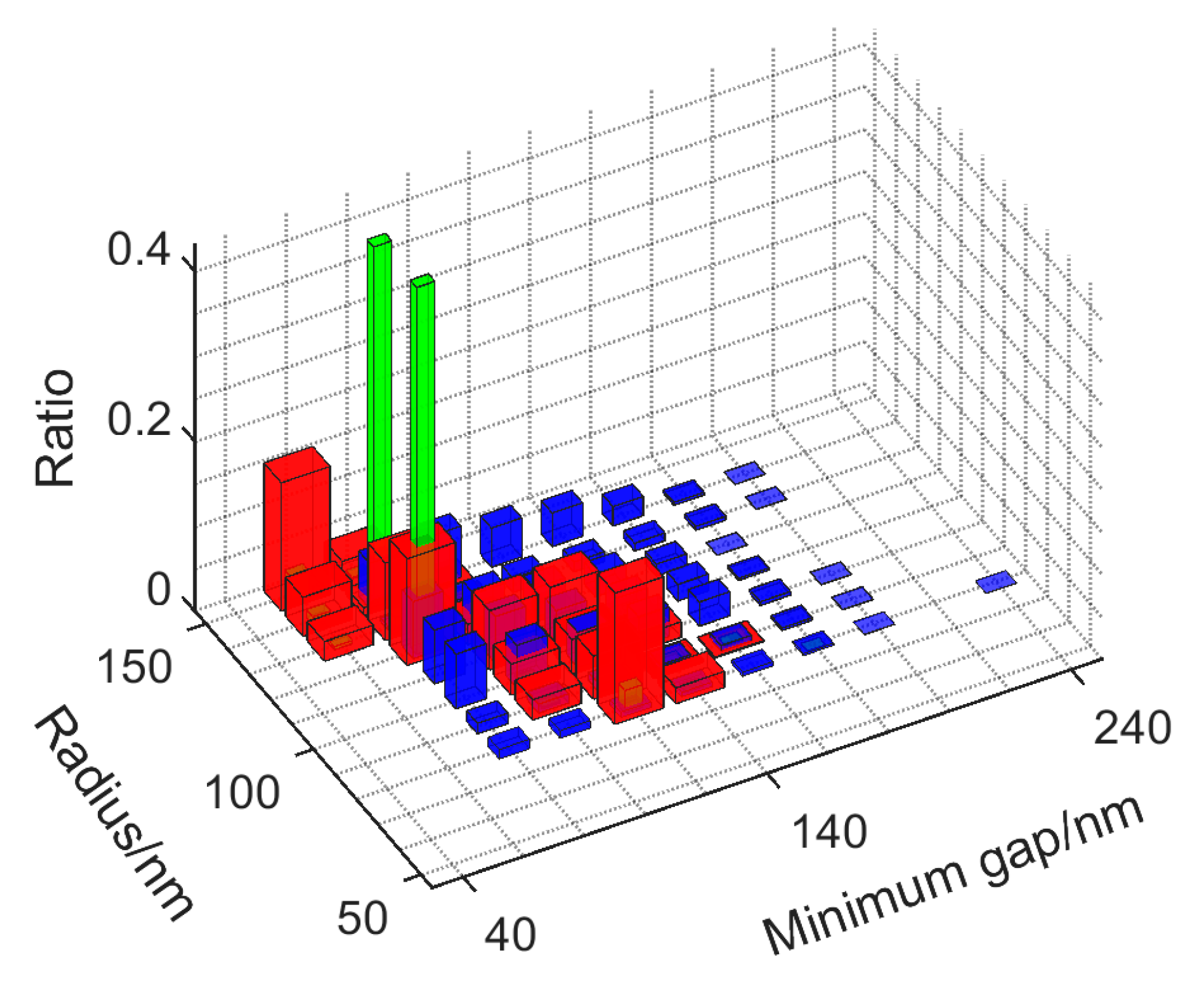
2.2. Large-Scale Design
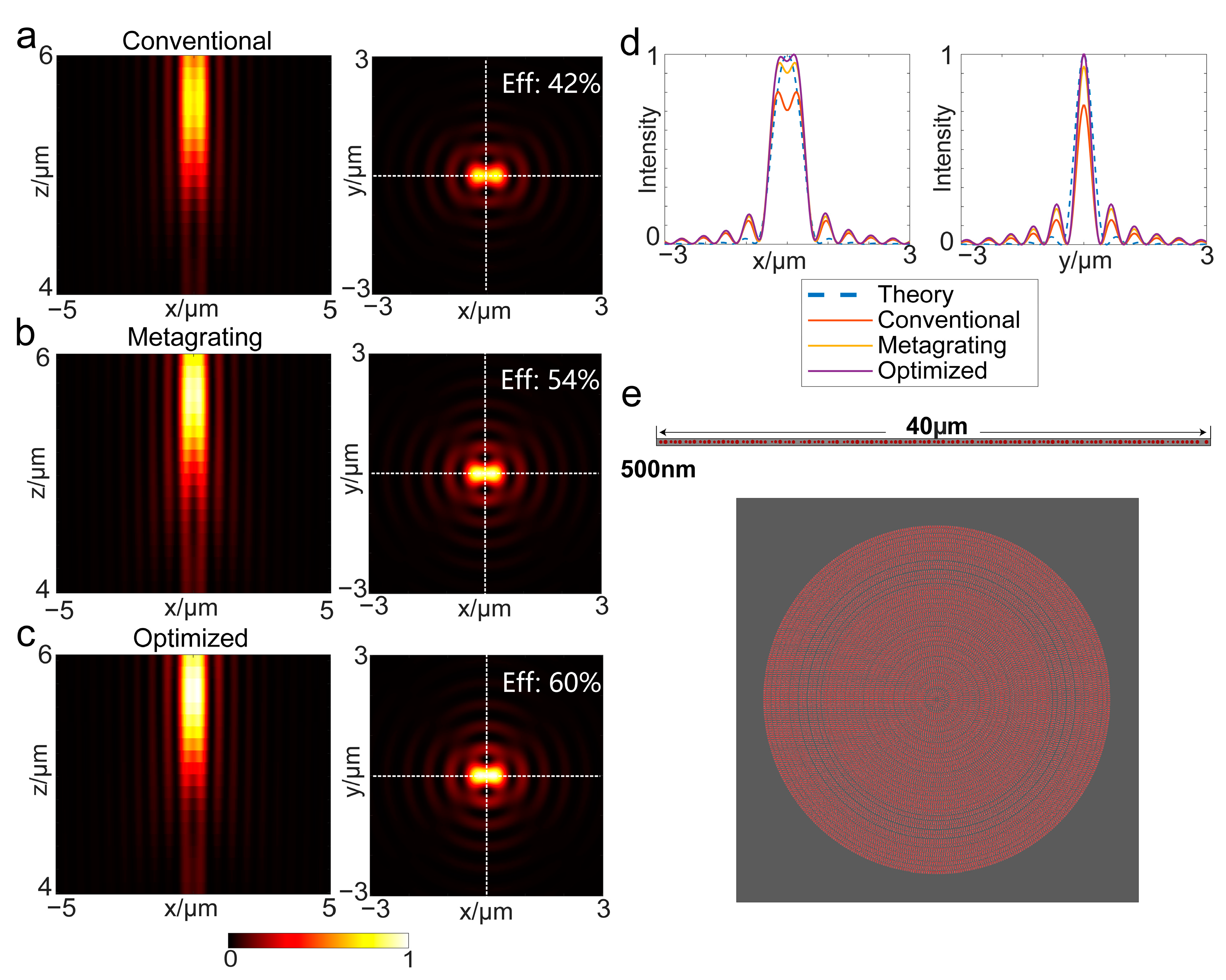
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. The Design of the Metalens Using the Phase Mapping Method
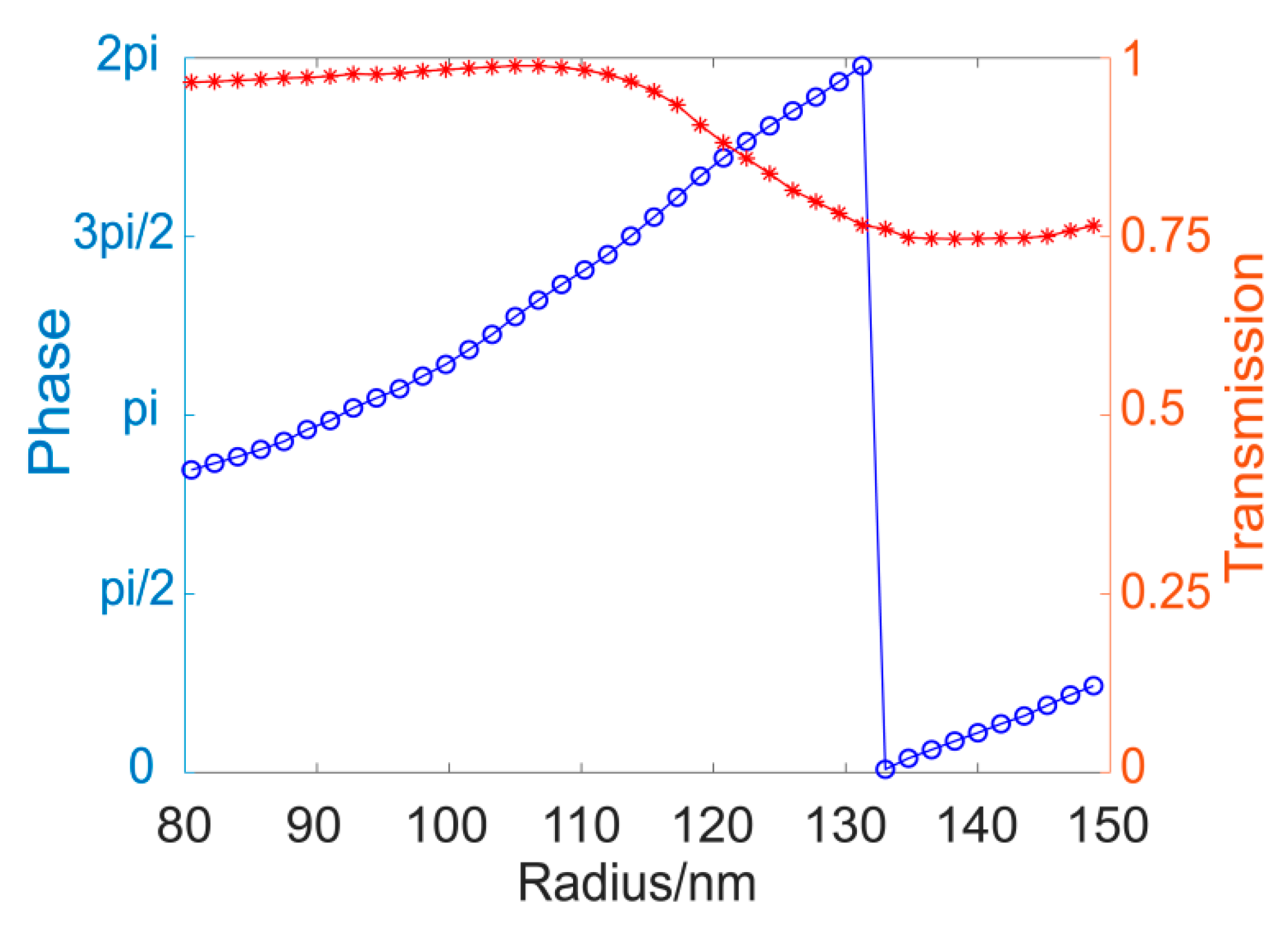

Appendix B. The Design of the Metalens Using the Metagrating Method
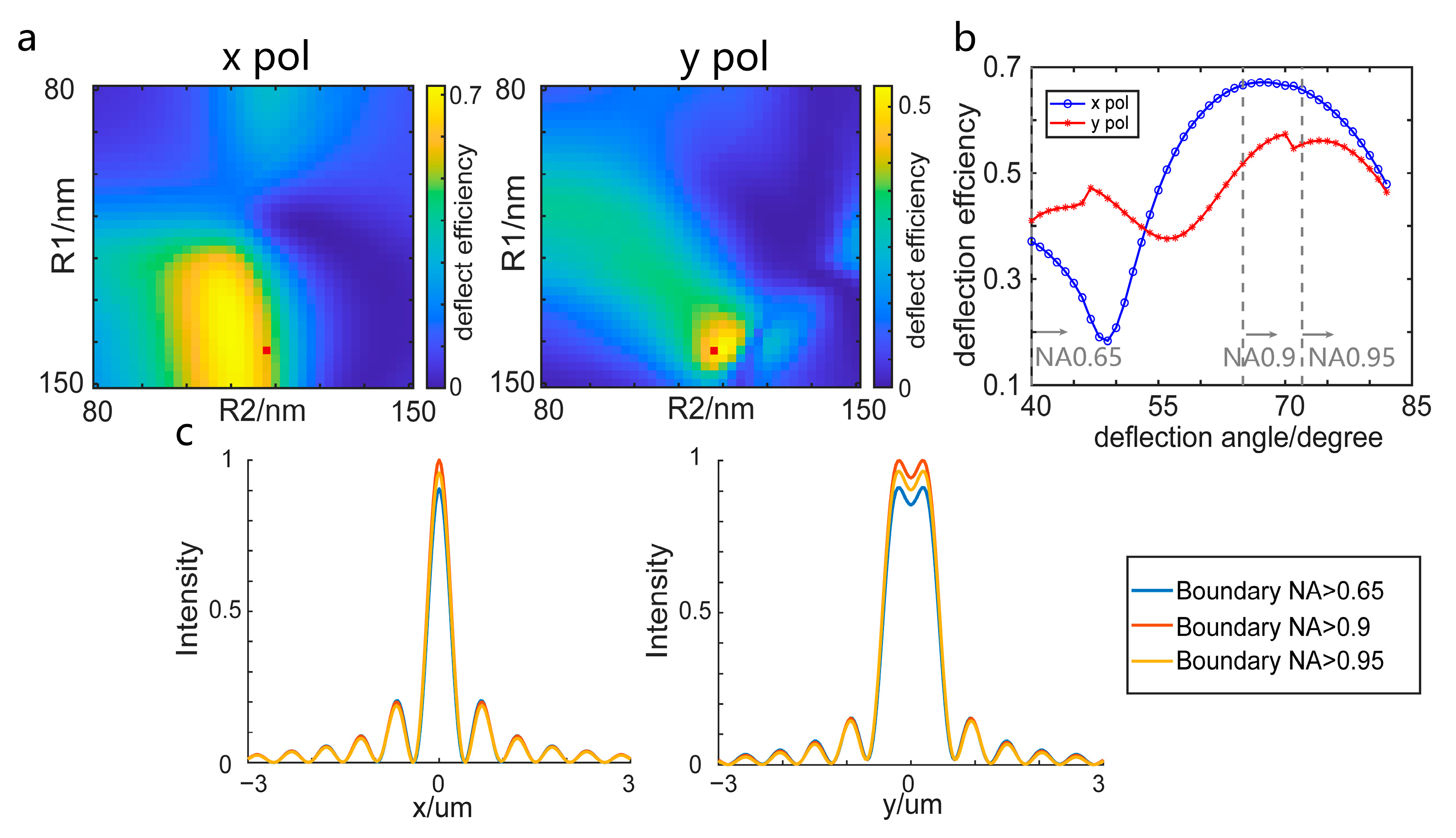
Appendix C. The Field Distribution in the Metalenses
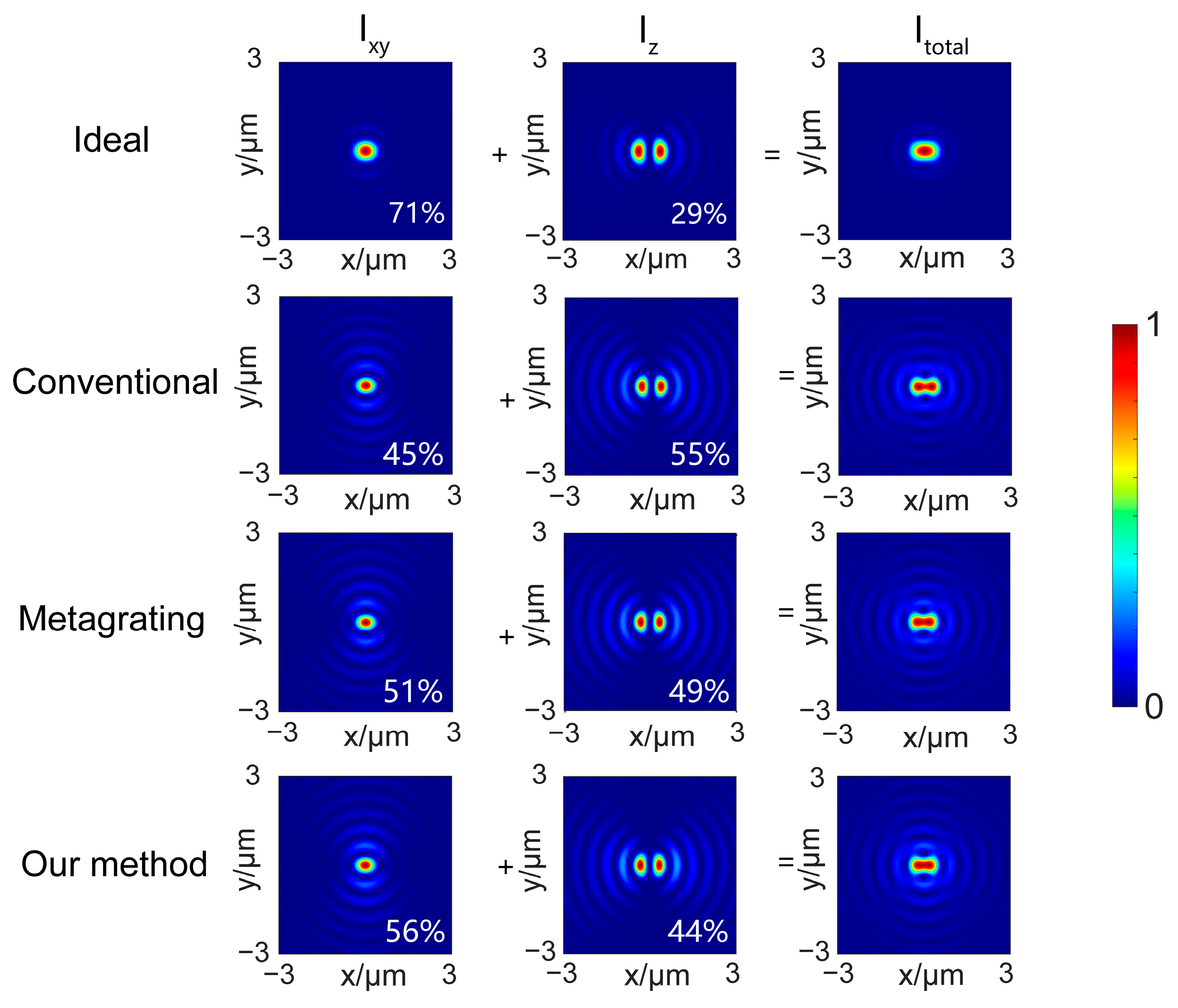
Appendix D. The Iz and Ixy Components of the Focal Spot
References
- Khorasaninejad, M.; Chen, W.T.; Devlin, R.C.; Oh, J.; Zhu, A.Y.; Capasso, F. Metalenses at visible wavelengths: Diffraction-limited focusing and subwavelength resolution imaging. Science 2016, 352, 1190–1194. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Wu, P.C.; Su, V.; Lai, Y.; Chen, M.; Kuo, H.Y.; Chen, B.H.; Chen, Y.H.; Huang, T.; Wang, J.; et al. A broadband achromatic metalens in the visible. Nat. Nanotechnol. 2018, 13, 227–232. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Ye, X.; Gao, S.; Chen, Y.; Zhao, Y.; Huang, C.; Qiu, K.; Zhu, S.; Li, T. Planar wide-angle-imaging camera enabled by metalens array. Optica 2022, 9, 431–437. [Google Scholar] [CrossRef]
- Juodėnas, M.; Strandberg, E.; Grabowski, A.; Gustavsson, J.; Šípová-Jungová, H.; Larsson, A.; Käll, M. High-angle deflection of metagrating-integrated laser emission for high-contrast microscopy. Light Sci. Appl. 2023, 12, 251. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.T.; Park, J.; Marchioni, J.; Millay, S.; Yousef, K.M.A.; Capasso, F. Dispersion-engineered metasurfaces reaching broadband 90% relative diffraction efficiency. Nat. Commun. 2023, 14, 2544. [Google Scholar] [CrossRef]
- Yin, Y.; Jiang, Q.; Wang, H.; Liu, J.; Xie, Y.; Wang, Q.; Wang, Y.; Huang, L. Multi-Dimensional Multiplexed Metasurface Holography by Inverse Design. Adv. Mater. 2024, 36, 2312303. [Google Scholar] [CrossRef]
- He, G.; Zheng, Y.; Zhou, C.; Li, S.; Shi, Z.; Deng, Y.; Zhou, Z. Multiplexed manipulation of orbital angular momentum and wavelength in metasurfaces based on arbitrary complex-amplitude control. Light Sci. Appl. 2024, 13, 98. [Google Scholar] [CrossRef]
- Kim, G.; Kim, Y.; Yun, J.; Moon, S.; Kim, S.; Kim, J.; Park, J.; Badloe, T.; Kim, I.; Rho, J. Metasurface-driven full-space structured light for three-dimensional imaging. Nat. Commun. 2022, 13, 5920. [Google Scholar] [CrossRef]
- Zou, X.; Zhang, Y.; Lin, R.; Gong, G.; Wang, S.; Zhu, S.; Wang, Z. Pixel-level Bayer-type colour router based on metasurfaces. Nat. Commun. 2022, 13, 3288. [Google Scholar] [CrossRef]
- Zhang, X.G.; Sun, Y.L.; Zhu, B.; Jiang, W.X.; Yu, Q.; Tian, H.W.; Qiu, C.; Zhang, Z.; Cui, T.J. A metasurface-based light-to-microwave transmitter for hybrid wireless communications. Light Sci. Appl. 2022, 11, 126. [Google Scholar] [CrossRef]
- Liu, Z.; Guo, T.; Tan, Q.; Hu, Z.; Sun, Y.; Fan, H.; Zhang, Z.; Jin, Y.; He, S. Phase Interrogation Sensor Based on All-Dielectric BIC Metasurface. Nano Lett. 2023, 23, 10441–10448. [Google Scholar] [CrossRef] [PubMed]
- Zaidi, A.; Rubin, N.A.; Meretska, M.L.; Li, L.W.; Dorrah, A.H.; Park, J.; Capasso, F. Metasurface-enabled single-shot and complete Mueller matrix imaging. Nat. Photonics 2024, 18, 704–712. [Google Scholar] [CrossRef]
- Zheng, Z.; Smirnova, D.; Sanderson, G.; Cuifeng, Y.; Koutsogeorgis, D.C.; Huang, L.; Liu, Z.; Oulton, R.; Yousefi, A.; Miroshnichenko, A.E.; et al. Broadband infrared imaging governed by guided-mode resonance in dielectric metasurfaces. Light Sci. Appl. 2024, 13, 249. [Google Scholar] [CrossRef] [PubMed]
- Lin, X.; Rivenson, Y.; Yardimci, N.T.; Veli, M.; Luo, Y.; Jarrahi, M.; Ozcan, A. All-optical machine learning using diffractive deep neural networks. Science 2018, 361, 1004–1008. [Google Scholar] [CrossRef]
- Luo, X.; Hu, Y.; Ou, X.; Li, X.; Lai, J.; Liu, N.; Cheng, X.; Pan, A.; Duan, H. Metasurface-enabled on-chip multiplexed diffractive neural networks in the visible. Light Sci. Appl. 2022, 11, 158. [Google Scholar] [CrossRef]
- Liang, H.; Martins, A.; Borges, B.V.; Zhou, J.; Martins, E.R.; Li, J.; Krauss, T.F. High performance metalenses: Numerical aperture, aberrations, chromaticity, and trade-offs. Optica 2019, 6, 1461–1470. [Google Scholar] [CrossRef]
- An, S.; Zheng, B.; Shalaginov, M.Y.; Tang, H.; Li, H.; Zhou, L.; Dong, Y.; Haerinia, M.; Agarwal, A.M.; Rivero-Baleine, C.; et al. Deep Convolutional Neural Networks to Predict Mutual Coupling Effects in Metasurfaces. Adv. Opt. Mater. 2022, 10, 2102113. [Google Scholar] [CrossRef]
- Cai, H.; Srinivasan, S.; Czaplewski, D.A.; Martinson, A.B.F.; Gosztola, D.J.; Stan, L.; Loeffler, T.; Sankaranarayanan, S.K.R.S.; López, D. Inverse design of metasurfaces with non-local interactions. NPJ Comput. Mater. 2020, 6, 116. [Google Scholar] [CrossRef]
- Liang, H.; Lin, Q.; Xie, X.; Sun, Q.; Wang, Y.; Zhou, L.; Liu, L.; Yu, X.; Zhou, J.; Krauss, T.F.; et al. Ultrahigh Numerical Aperture Metalens at Visible Wavelengths. Nano Lett. 2018, 18, 4460–4466. [Google Scholar] [CrossRef]
- Miller, O.D. Photonic Design: From Fundamental Solar Cell Physics to Computational Inverse Design. Ph.D. Thesis, UC Berkeley, Berkeley, CA, USA, 2012. [Google Scholar]
- Chung, H.; Miller, O.D. High-NA achromatic metalenses by inverse design. Opt. Express 2020, 28, 6945–6965. [Google Scholar] [CrossRef]
- Mansouree, M.; McClung, A.; Samudrala, S.; Arbabi, A. Large-Scale Parametrized Metasurface Design Using Adjoint Optimization. ACS Photonics 2021, 8, 455–463. [Google Scholar] [CrossRef]
- Zhang, J.; Liang, H.; Long, Y.; Zhou, Y.; Sun, Q.; Wu, Q.; Fu, X.; Martins, E.R.; Krauss, T.F.; Li, J.; et al. Metalenses with Polarization-Insensitive Adaptive Nano-Antennas. Laser Photon. Rev. 2022, 16, 2200268. [Google Scholar] [CrossRef]
- Phan, T.; Sell, D.; Wang, E.W.; Doshay, S.; Edee, K.; Yang, J.; Fan, J.A. High-efficiency, large-area, topology-optimized metasurfaces. Light Sci. Appl. 2019, 8, 48. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Mao, C.; Gershnabel, E.; Chen, M.; Fan, J.A. Large-Area, High-Numerical-Aperture, Freeform Metasurfaces. Laser Photon. Rev. 2024, 18, 2300988. [Google Scholar] [CrossRef]
- Paniagua-Domínguez, R.; Yu, Y.F.; Khaidarov, E.; Choi, S.; Leong, V.; Bakker, R.M.; Liang, X.; Fu, Y.H.; Valuckas, V.; Krivitsky, L.A.; et al. A Metalens with a Near-Unity Numerical Aperture. Nano Lett 2018, 18, 2124–2132. [Google Scholar] [CrossRef]
- Caselles, V.; Catté, F.; Coll, T.; Dibos, F. A geometric model for active contours in image processing. Numer. Math. 1993, 66, 1–31. [Google Scholar] [CrossRef]
- Santosa, F. A level-set approach for inverse problems involving obstacles. ESAIM COCV 1996, 1, 17–33. [Google Scholar] [CrossRef]
- Lalau-Keraly, C.M.; Bhargava, S.; Miller, O.D.; Yablonovitch, E. Adjoint shape optimization applied to electromagnetic design. Opt. Express 2013, 21, 21693–21701. [Google Scholar] [CrossRef]
- Mansouree, M.; Arbabi, A. Metasurface Design Using Level-Set and Gradient Descent Optimization Techniques. In Proceedings of the 2019 International Applied Computational Electromagnetics Society Symposium (ACES), Nanjing, China, 8–12 August 2019. [Google Scholar]
- Dong, L.; Kong, W.; Wang, C.; Pu, M.; Liu, X.; Luo, Y.; Luo, X. Quasi-continuous metasurface for high-efficiency beam deflection based on multi-objective level-set optimization. Opt. Mater. Express 2022, 12, 3667–3678. [Google Scholar] [CrossRef]
- Bao, H.; Zhang, F.; Pu, M.; He, Q.; Xu, M.; Guo, Y.; Li, L.; Ma, X.; Li, X.; Luo, X. Field-Driven Inverse Design of High-Performance Polarization-Multiplexed Meta-devices. Laser Photon. Rev. 2024, 18, 2301158. [Google Scholar] [CrossRef]
- Shen, Y.; Wong, N.; Lam, E.Y. Level-set-based inverse lithography for photomask synthesis. Opt. Express 2009, 17, 23690–23701. [Google Scholar] [CrossRef] [PubMed]
- Saad-Falcon, A.; Howard, C.; Romberg, J.; Allen, K. Level set methods for gradient-free optimization of metasurface arrays. Sci. Rep. 2024, 14, 16674. [Google Scholar] [CrossRef] [PubMed]
- Dainese, P.; Marra, L.; Cassara, D.; Portes, A.; Oh, J.; Yang, J.; Palmieri, A.; Rodrigues, J.R.; Dorrah, A.H.; Capasso, F. Shape optimization for high efficiency metasurfaces: Theory and implementation. arXiv 2024, arXiv:2405.03930. [Google Scholar]
- Bertsekas, D.P. Constrained Optimization and Lagrange Multiplier Methods; Academic Press: Cambridge, MA, USA, 1982. [Google Scholar]
- Sell, D.; Yang, J.; Doshay, S.; Yang, R.; Fan, J.A. Large-Angle, Multifunctional Metagratings Based on Freeform Multimode Geometries. Nano Lett. 2017, 17, 3752–3757. [Google Scholar] [CrossRef] [PubMed]
- Richards, B.; Wolf, E.; Gabor, D. Electromagnetic diffraction in optical systems, II. Structure of the image field in an aplanatic system. Proc. R. Soc. Lond. Ser. A 1959, 253, 358–379. [Google Scholar]
- Gao, J.; Yan, S.; Zhou, Y.; Liang, G.; Zhang, Z.; Wen, Z.; Chen, G. Polarization-conversion microscopy for imaging the vectorial polarization distribution in focused light. Optica 2021, 8, 984–994. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Liu, Y.; Liang, H.; Li, J. Efficient Inverse Design of Large-Scale, Ultrahigh-Numerical-Aperture Metalens. Photonics 2024, 11, 940. https://doi.org/10.3390/photonics11100940
Zhou Y, Liu Y, Liang H, Li J. Efficient Inverse Design of Large-Scale, Ultrahigh-Numerical-Aperture Metalens. Photonics. 2024; 11(10):940. https://doi.org/10.3390/photonics11100940
Chicago/Turabian StyleZhou, Yongle, Yikun Liu, Haowen Liang, and Juntao Li. 2024. "Efficient Inverse Design of Large-Scale, Ultrahigh-Numerical-Aperture Metalens" Photonics 11, no. 10: 940. https://doi.org/10.3390/photonics11100940
APA StyleZhou, Y., Liu, Y., Liang, H., & Li, J. (2024). Efficient Inverse Design of Large-Scale, Ultrahigh-Numerical-Aperture Metalens. Photonics, 11(10), 940. https://doi.org/10.3390/photonics11100940




