Compact Partially End-Pumped Innoslab Laser Based on Micro-Cylindrical Lens Array Homogenizer
Abstract
1. Introduction
2. Experimental Setup
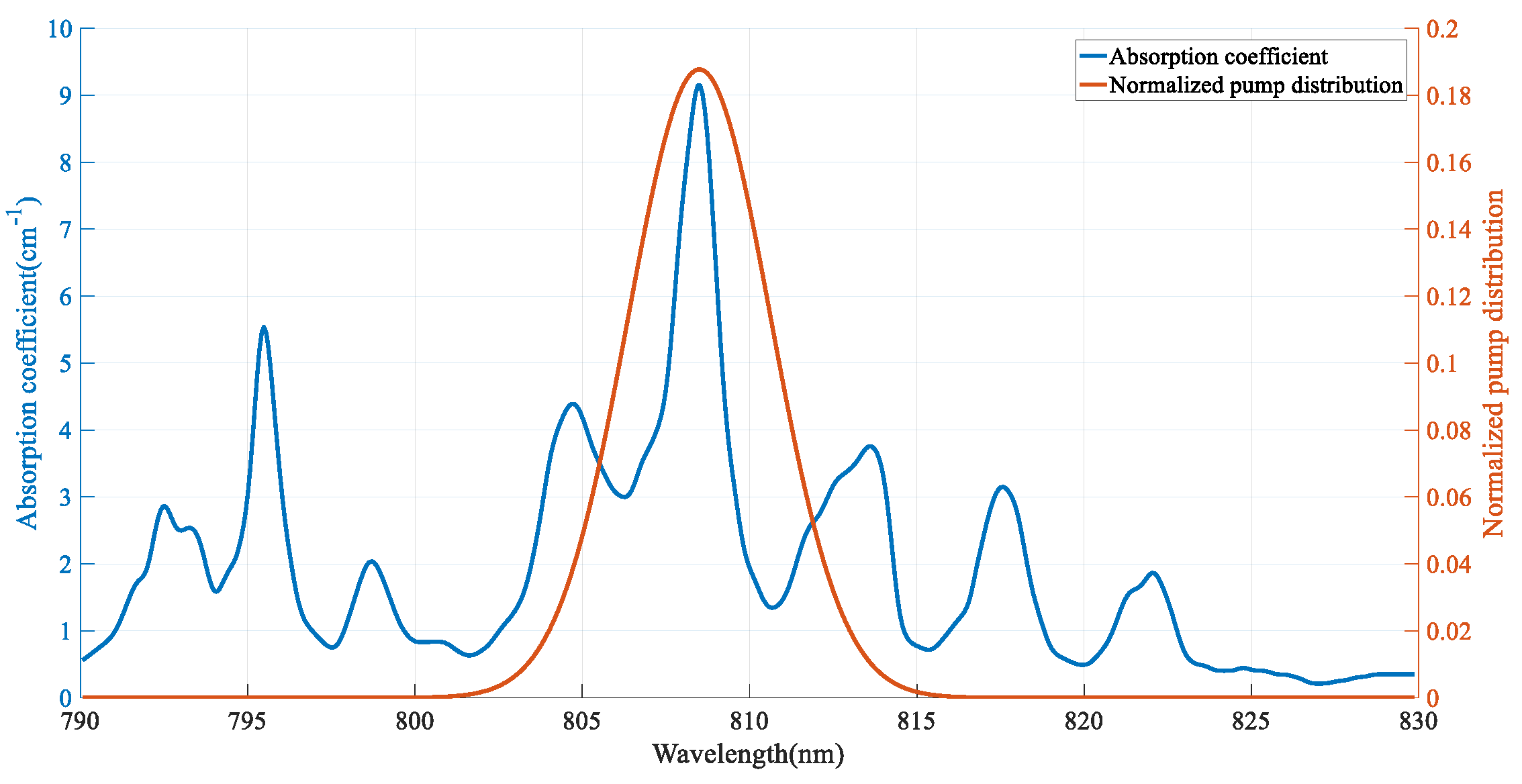
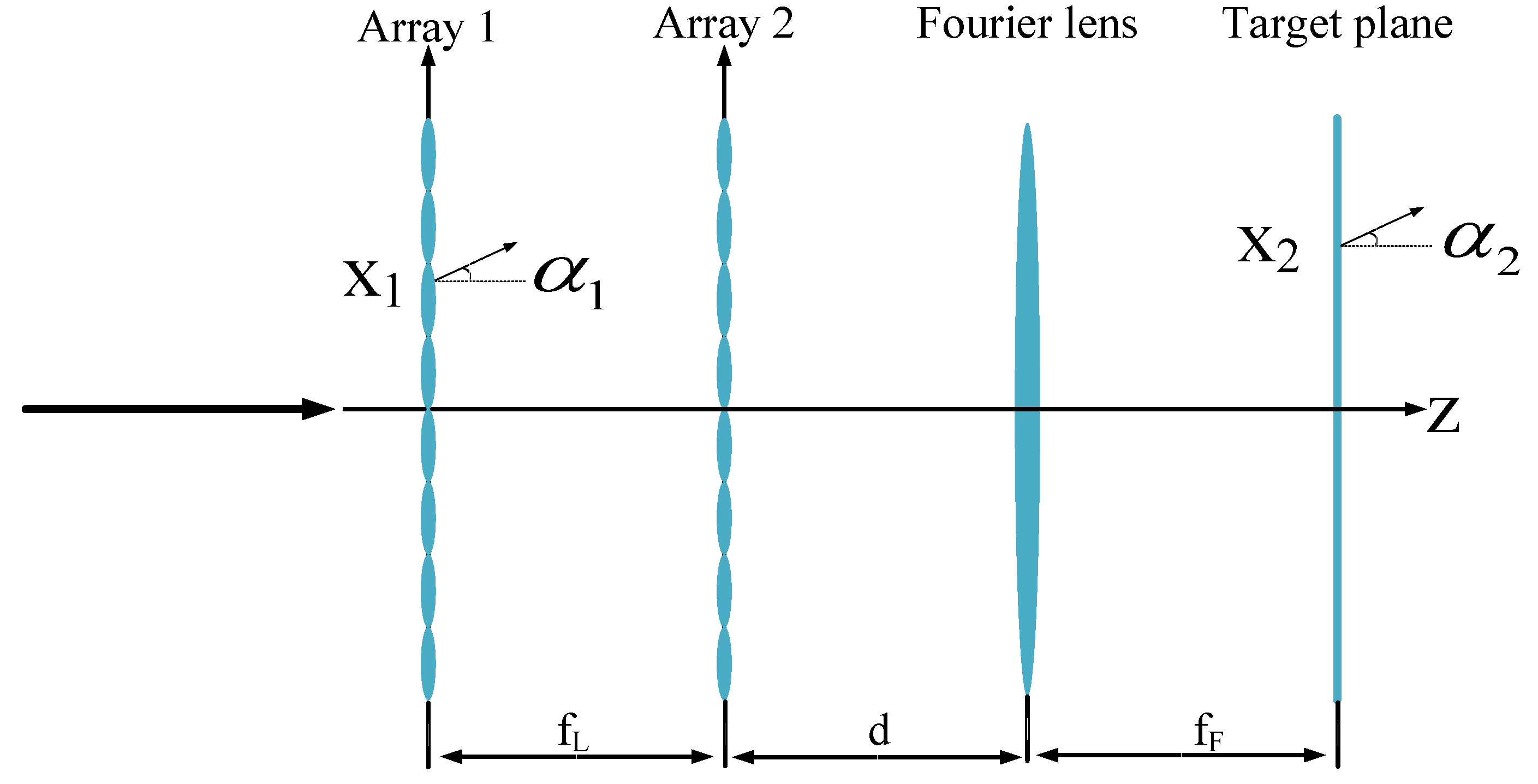
3. Micro-Cylindrical Lens Array Homogenizer
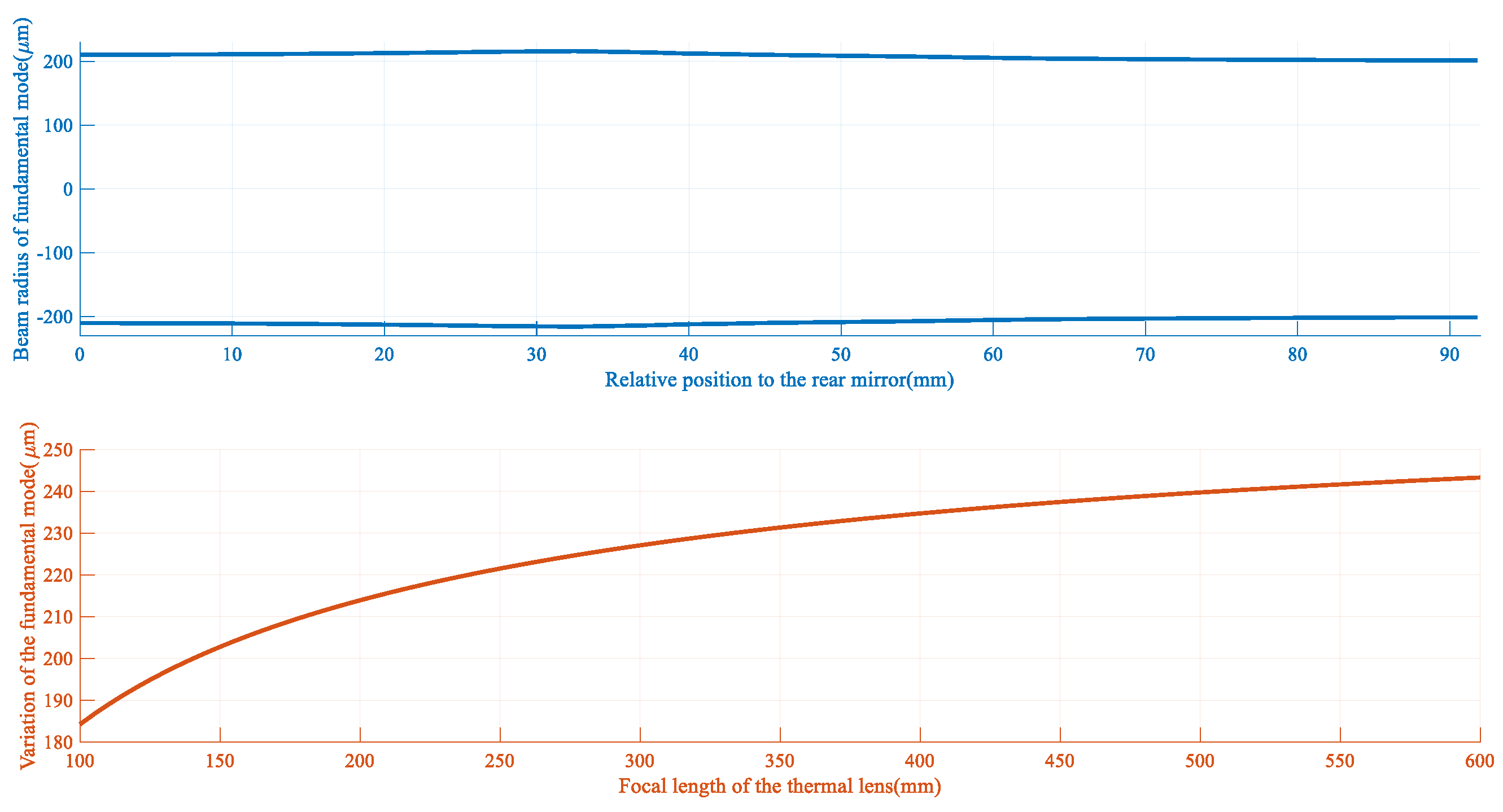
4. Laser Dynamics Modeling
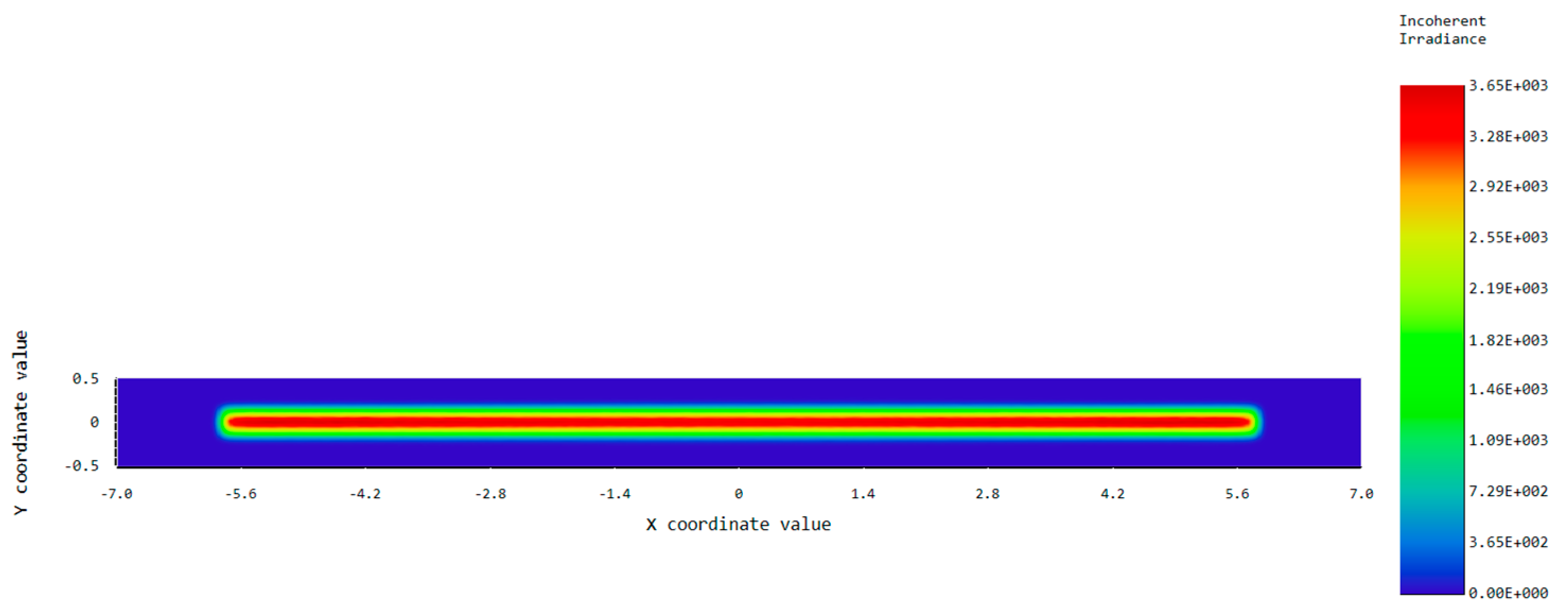
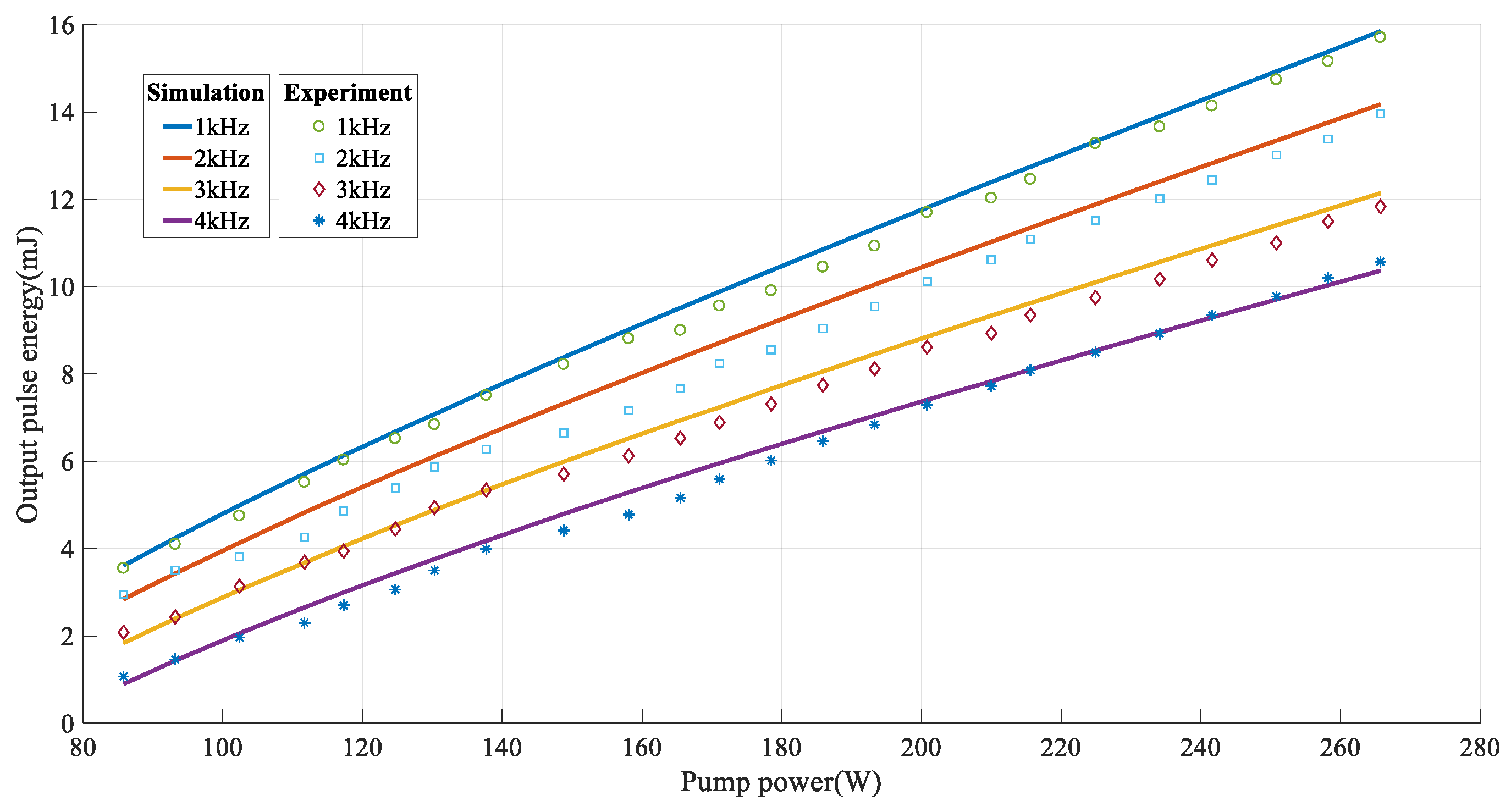
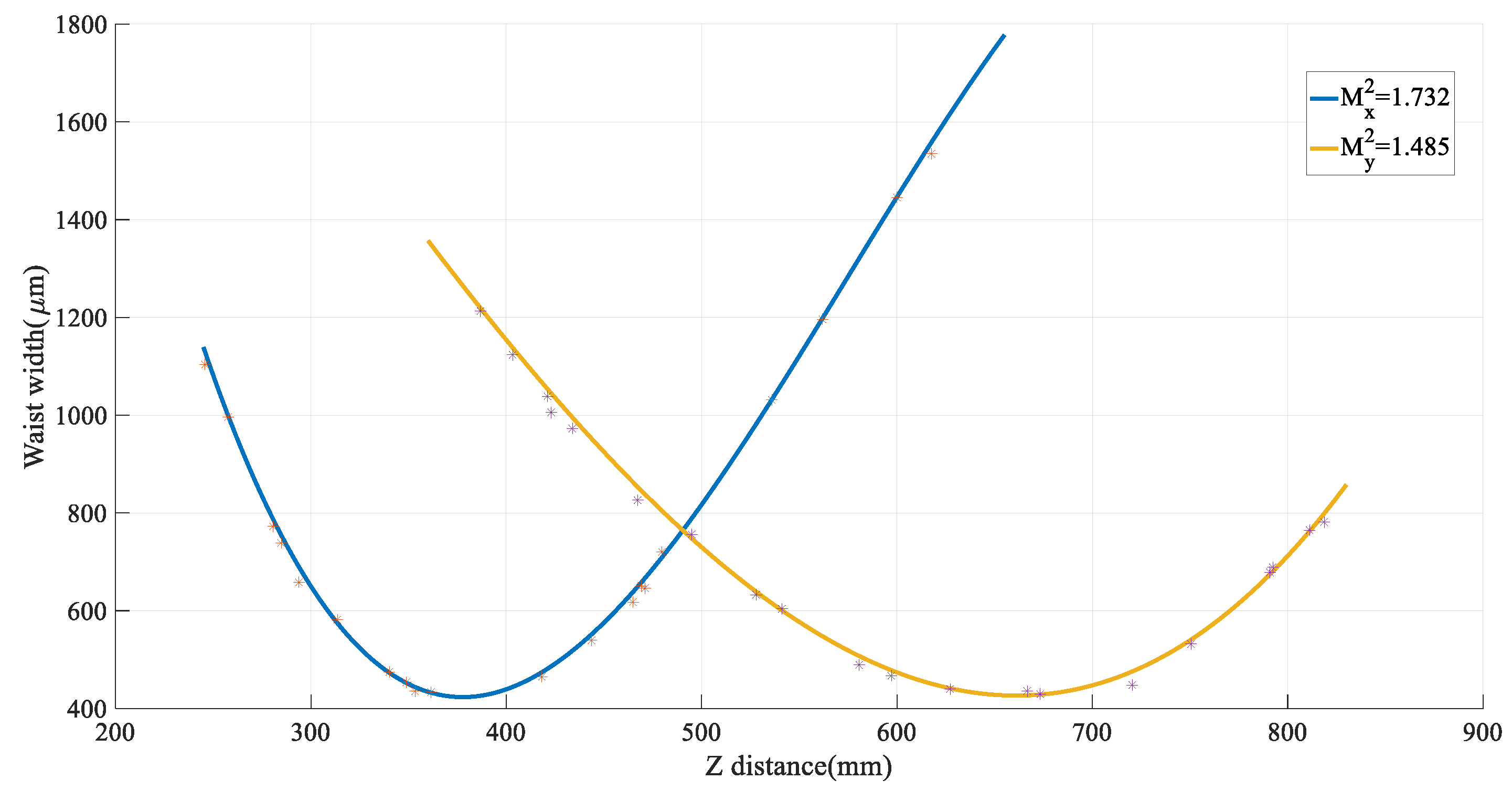
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Du, K.M.; Li, D.J.; Shi, P.; Fu, S.J.; Haas, C.R.; Liu, X.M.; Qi, B.S.; Chen, J.; Schell, A. The unique features and application examples of INNOSLAB lasers. In Proceedings of the ICALEO® 2009: 28th International Congress on Laser Materials Processing, Laser Microprocessing and Nanomanufacturing, Orlando, FL, USA, 2–5 November 2009; AIP Publishing: New York, NY, USA, 2009; pp. 861–867. [Google Scholar]
- Du, K. Unique performances and favourable applications of INNOSLAB lasers. In Proceedings of the SPIE—Solid State Lasers XVIII: Technology and Devices, San Jose, CA, USA, 25–29 January 2009; Volume 7193, pp. 607–616. [Google Scholar]
- Russbueldt, P.; Hoffmann, D.; Hofer, M.; Lohring, L.; Luttmann, J.; Meissner, A.; Wei, J. Innoslab amplifiers. IEEE J. Sel. Top. Quantum Electron. 2014, 21, 447–463. [Google Scholar] [CrossRef]
- Poprawe, R.; Gillner, A.; Hoffmann, H.D.; Kaierle, S.; Loosen, P.; Meiners, W.; Noll, R.; Willenborg, E. Disk, fiber, rod, slab: New laser concepts open new application perspectives. In Proceedings of the SPIE 7138, Photonics, Devices, and Systems IV, Prague, Czech Republic, 27–29 September 2008; Volume 7138, pp. 47–58. [Google Scholar]
- Li, D.J.; Ma, Z.; Haas, R.; Schell, A.; Simon, J.; Zhu, P.; Shi, P.; Du, K.M. Diode-end-pumped double Nd: YLF slab laser with high energy, short pulse width, and diffraction-limited quality. Opt. Lett. 2008, 33, 1708–1710. [Google Scholar] [CrossRef] [PubMed]
- Li, D.J.; Ma, Z.; Haas, R.; Schell, A.; Diart, R.; Shi, P.; Hu, P.X.; Loosen, P.; Du, K.M. Diode-pumped efficient slab laser with two Nd: YLF crystals and second-harmonic generation by slab LBO. Opt. Lett. 2007, 32, 1272–1274. [Google Scholar] [CrossRef] [PubMed]
- Ma, Z.; Li, D.J.; Hu, P.X.; Schell, A.; Shi, P.; Haas, R.; Wu, N.L.; Du, K.M. Monolithic Nd: YVO4 slab oscillator-amplifier. Opt. Lett. 2007, 32, 1262–1264. [Google Scholar] [CrossRef] [PubMed]
- Mao, Y.F.; Zhang, H.L.; Cui, J.H.; Yuan, J.H.; Hao, X.L.; Yi, J. 25 mJ, 5 KHz, 3 ns, Nd: YAG discrete path slab amplifier using a hybrid resonator. Appl. Opt. 2017, 56, 2741–2744. [Google Scholar] [CrossRef] [PubMed]
- Sang, S.H.; Zhang, H.L.; Mao, Y.F.; Zhang, X.; Zou, J.Y.; Xin, J.G.; Xing, J.C.; Jiang, Y. Compact, high-average-power, nanosecond multi-pass Nd: YVO4 Innoslab amplifier. Appl. Phys. B 2015, 121, 131–134. [Google Scholar] [CrossRef]
- Mao, Y.F.; Zhang, H.L.; Zhang, X.L.; Hao, J.H.; Xing, J.C.; Xin, J.G.; Yi, J. 8.4 mJ, 10kHz, 3.6 ns, Nd: YVO4 slab amplifier. Opt. Express 2016, 24, 11017–11022. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Li, D.J.; Shi, P.; Haas, R.; Du, K.M. Highly efficient third-harmonic generation with electro-optically Q-switched diode-end-pumped Nd: YVO4 slab laser. Opt. Commun. 2007, 272, 192–196. [Google Scholar] [CrossRef]
- Li, D.J.; Fu, S.J.; Liu, X.M.; Shi, P.; Chen, J.; Shell, A.; Qi, B.S.; Haas, C.R.; Wang, J.X.; Du, K.M. Recent progresses in INNOSLAB lasers and their harmonic generation. In Solid State Lasers XIX—Technology and Devices; SPIE: Philadelphia, PA, USA, 2010; Volume 7578. [Google Scholar]
- Schnitzler, C.; Schmidt, G.; Du, K.M.; Loosen, P.; Poprawe, R.; Marshall, C. Improving the brightness of a diode end pumped slab laser by a new pumping scheme. In Topical Meeting on Advanced Solid-State Lasers; Optica Publishing Group: San Jose, CA, USA, 2001; Volume 50, pp. 5–10. [Google Scholar]
- Slimani, M.; Liu, J.; Xin, J.; Chen, J. Beam shaping of high power diode laser stack into homogeneous line. Front. Optoelectron. 2014, 7, 102–106. [Google Scholar] [CrossRef]
- Duan, Y.; Song, C.; Mao, Y. >300 W laser-diode dual-end-pumped Nd: YVO4 Innoslab laser. Laser Phys. 2016, 26, 095006. [Google Scholar] [CrossRef]
- Liu, L.; Zhou, S.H.; Liu, Y.; Wang, Z.; Wang, G.; Zhao, H. The 5.2kW Nd: YAG Slab Amplifier Chain Seeded by Nd: YVO4 Innoslab Laser. Chin. Phys. Lett. 2017, 34, 064202. [Google Scholar] [CrossRef]
- Gao, Q.; Zhang, H.; Fayyaz, J. Laser diode partially end-pumped electro-optically Q-switched Yb: YAG slab laser. Chin. Opt. Lett. 2019, 17, 111405. [Google Scholar] [CrossRef]
- Kanchanavaleerat, E.; Cochet-Muchy, D.; Kokta, M.; Stone-Sundberg, J.; Sarkies, P.; Sarkies, J.; Sarkies, J. Crystal growth of high doped Nd: YAG. Opt. Mater. 2004, 26, 337–341. [Google Scholar] [CrossRef]
- Degnan, J.J. Theory of the Optimally Coupled Q-Switched Laser. IEEE J. Quantum Electron. 1989, 25, 214–220. [Google Scholar] [CrossRef]








| Parameters | Value |
|---|---|
| Number of Bars | 6 |
| Number of emitters in the slow direction | 25 |
| Width of emitters | 200 μm |
| Pitch of emitters | 400 μm |
| Bar-to-Bar Spacing | 1.9 mm |
| Fast-Axis Divergence (90%) after FAC | ≤8 mrad |
| Slow-Axis Divergence (90%) | 8° |
| Focal length of the micro-cylindrical lens | 6.6 mm |
| Diameter of the micro-cylindrical lens | 1.9 mm |
| The focal length of the Fourier lens in the slow axis | 61 mm |
| The focal length of the Fourier lens in the fast axis | 57 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, X.; Zhao, X.; Chen, J.; Wu, Y.; Fu, Y.; Cheng, G.; Chen, X.; Liu, P.; Shang, L.; Fan, G.; et al. Compact Partially End-Pumped Innoslab Laser Based on Micro-Cylindrical Lens Array Homogenizer. Photonics 2024, 11, 932. https://doi.org/10.3390/photonics11100932
Sun X, Zhao X, Chen J, Wu Y, Fu Y, Cheng G, Chen X, Liu P, Shang L, Fan G, et al. Compact Partially End-Pumped Innoslab Laser Based on Micro-Cylindrical Lens Array Homogenizer. Photonics. 2024; 11(10):932. https://doi.org/10.3390/photonics11100932
Chicago/Turabian StyleSun, Xinhui, Xiaonan Zhao, Jinxin Chen, Yajun Wu, Yibin Fu, Gang Cheng, Xi Chen, Pan Liu, Linhao Shang, Guangqiang Fan, and et al. 2024. "Compact Partially End-Pumped Innoslab Laser Based on Micro-Cylindrical Lens Array Homogenizer" Photonics 11, no. 10: 932. https://doi.org/10.3390/photonics11100932
APA StyleSun, X., Zhao, X., Chen, J., Wu, Y., Fu, Y., Cheng, G., Chen, X., Liu, P., Shang, L., Fan, G., Gao, H., Xiang, Y., & Zhang, T. (2024). Compact Partially End-Pumped Innoslab Laser Based on Micro-Cylindrical Lens Array Homogenizer. Photonics, 11(10), 932. https://doi.org/10.3390/photonics11100932






