Femtosecond Third-Order Nonlinear Electronic Responses of 2D Metallic NbSe2
Abstract
1. Introduction
2. Materials and Methods
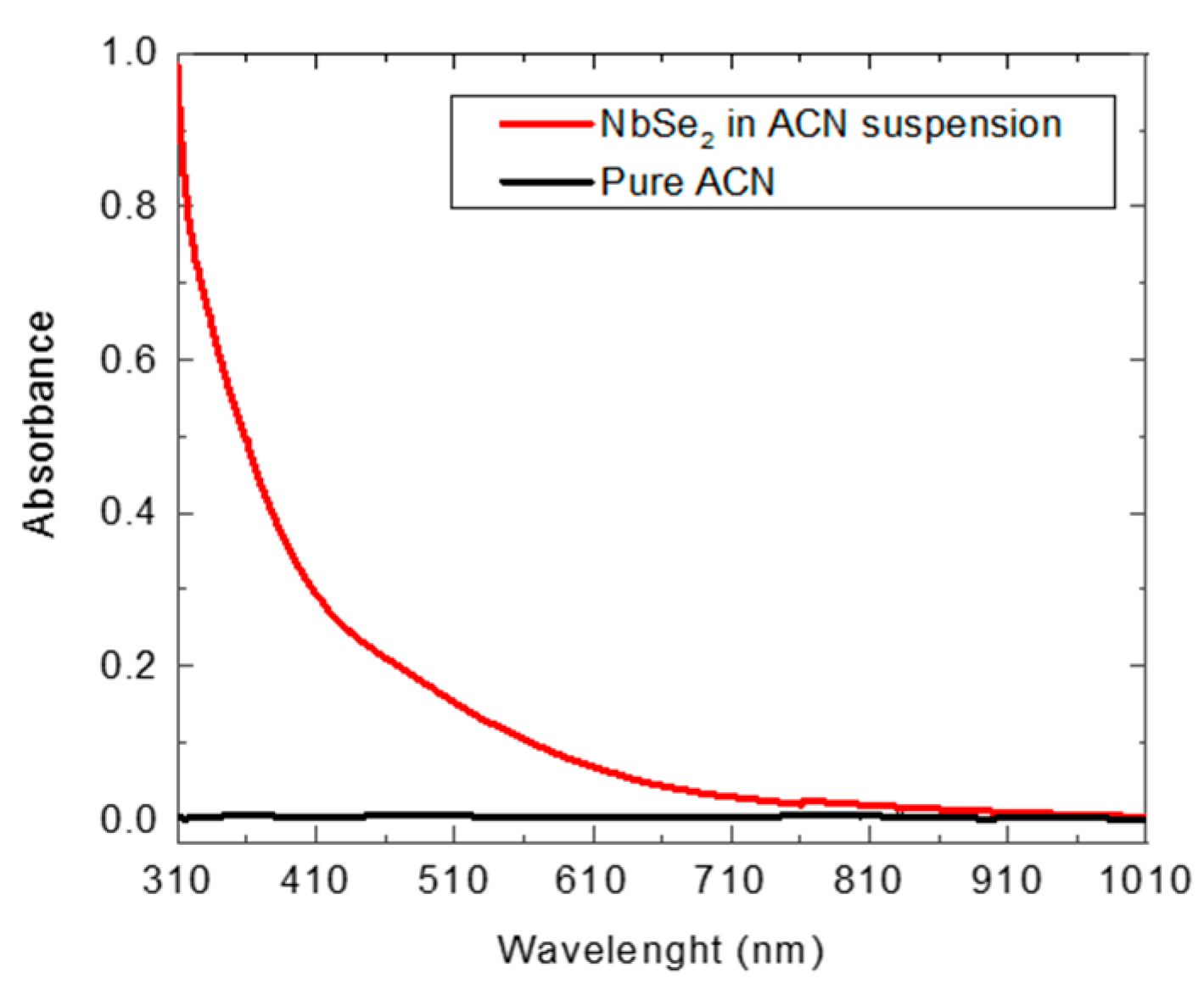
2.1. Two-Dimensional Metallic NbSe2
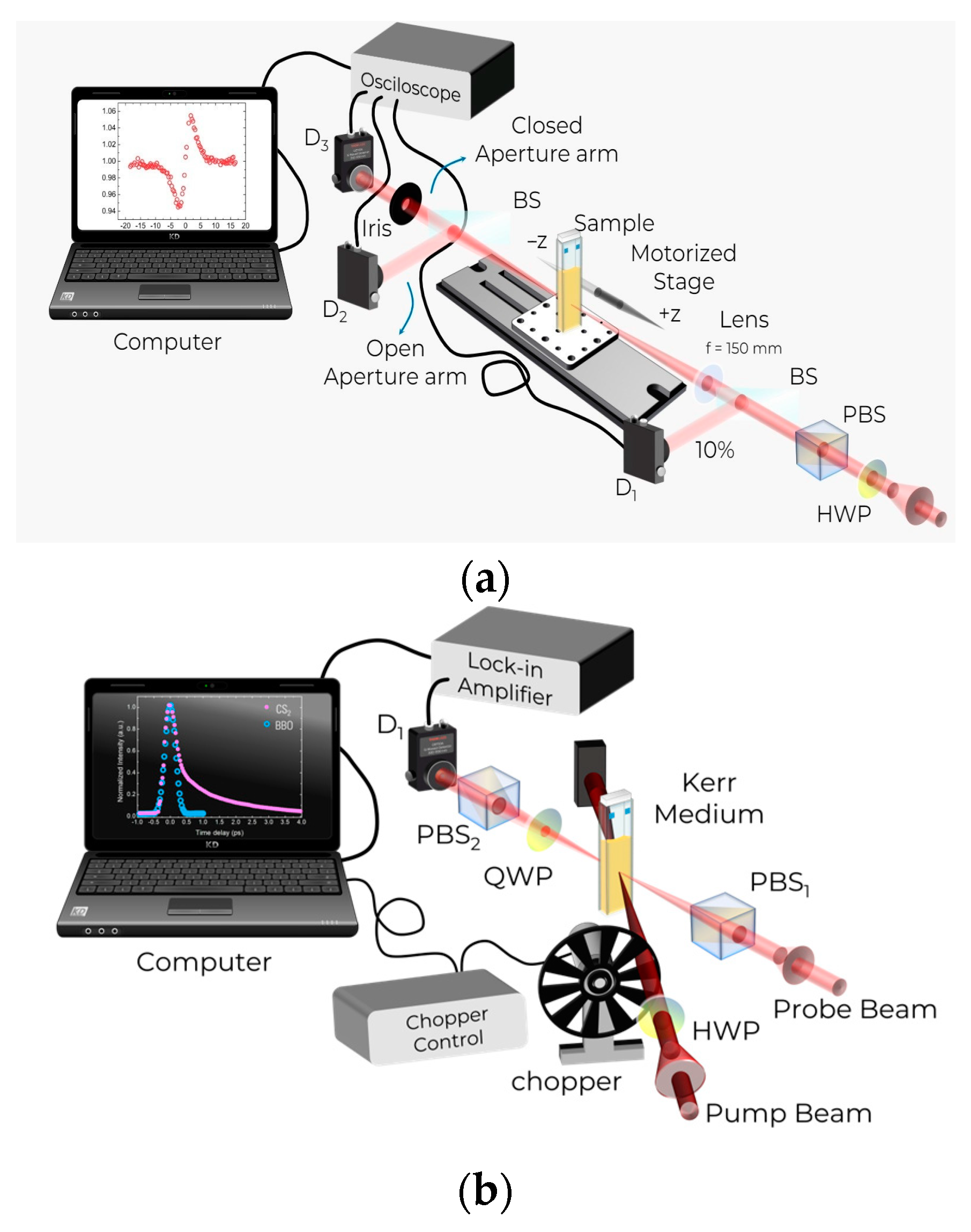
2.2. Z-Scan Technique and Setup
2.3. Optical Kerr Gate Technique and Setup
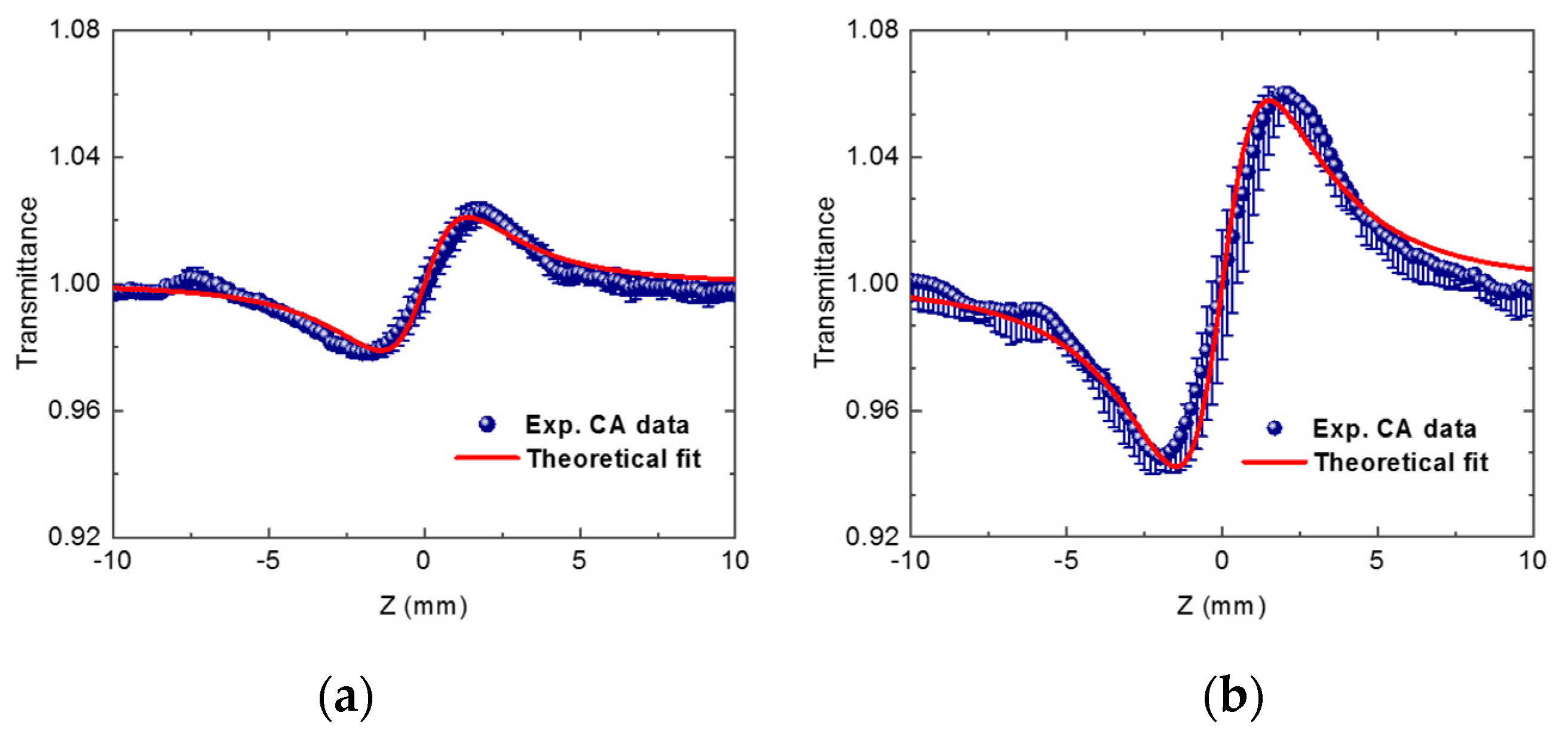
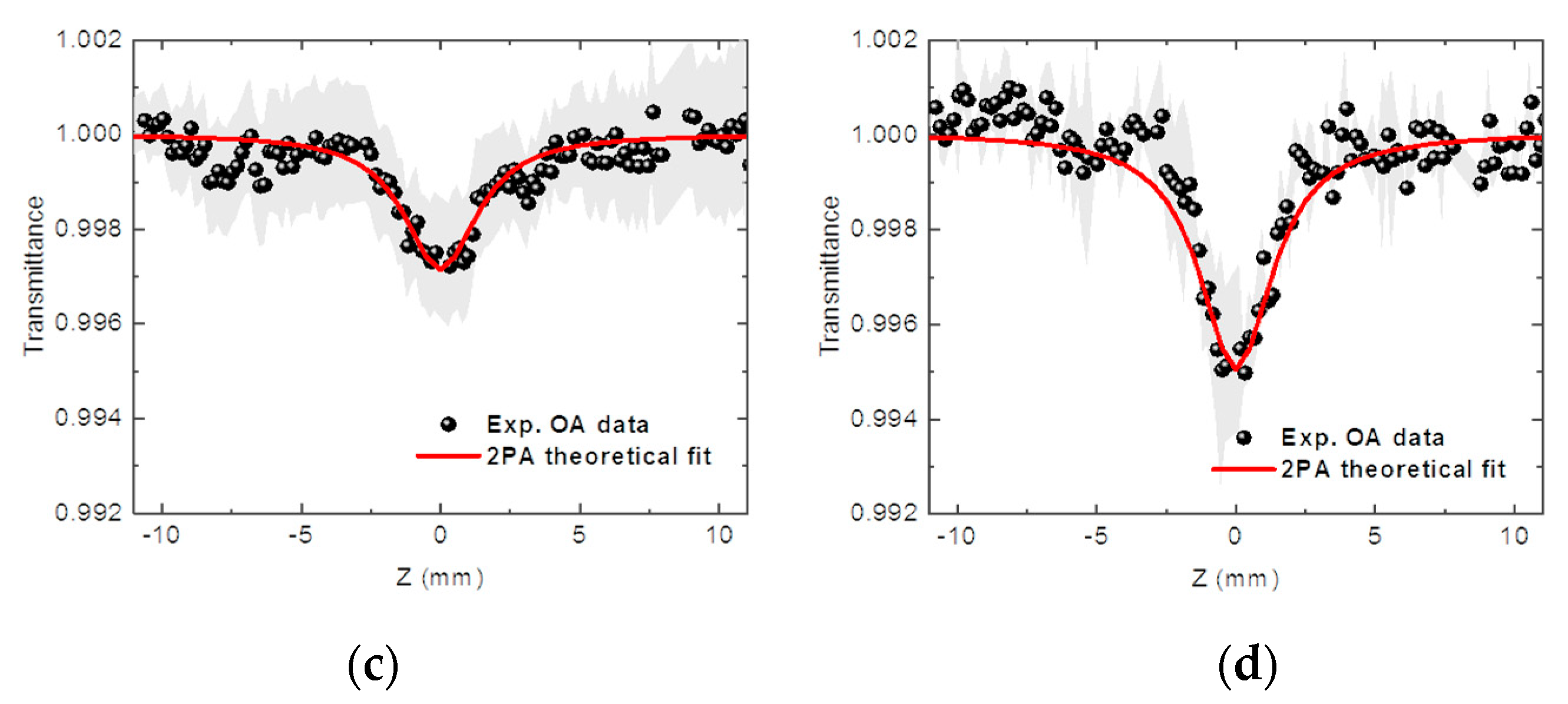
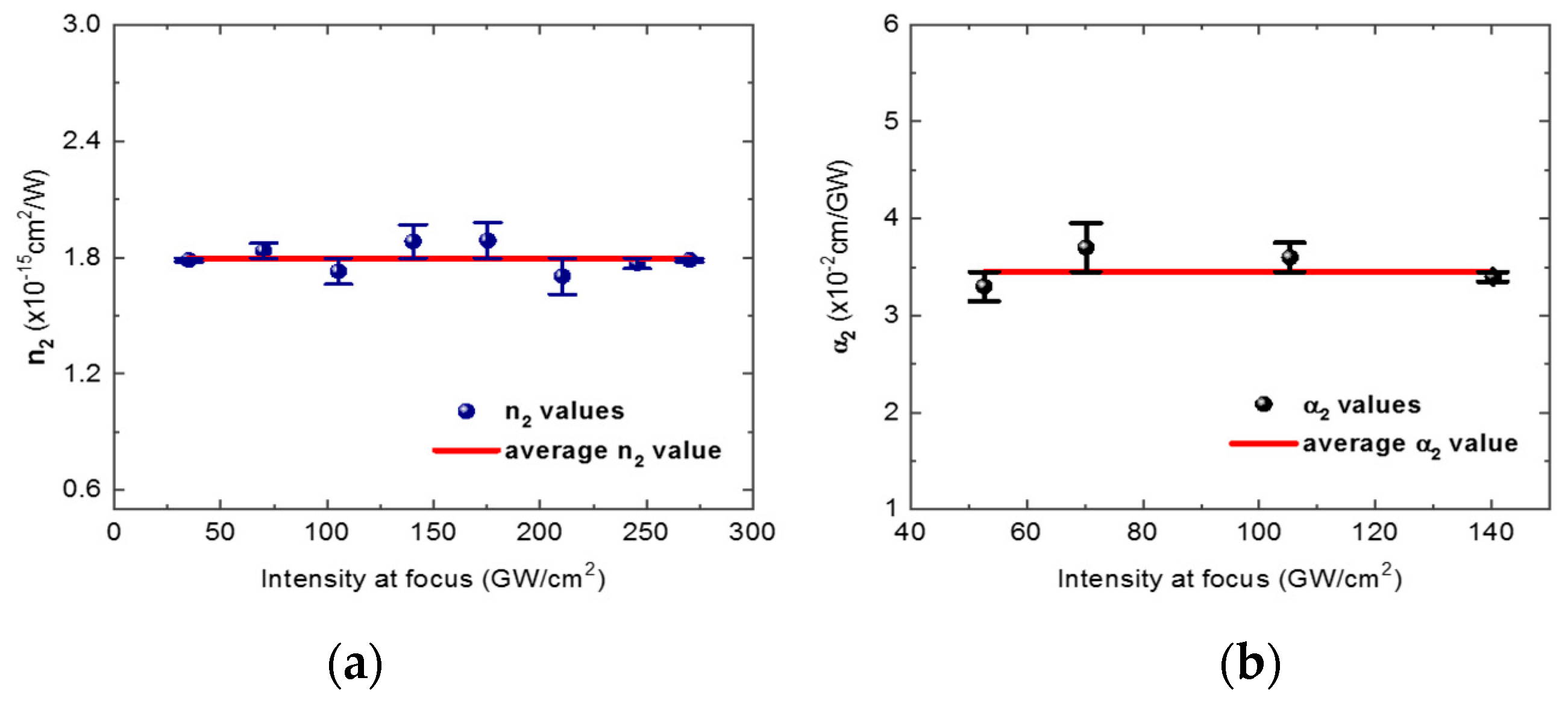
3. Results
4. Theory and Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alam, S.; Chowdhury, M.A.; Shahid, A.; Alam, R.; Rahim, A. Synthesis of Emerging Two-Dimensional (2D) Materials—Advances, Challenges and Prospects. Flat. Chem. 2021, 30, 100305. [Google Scholar] [CrossRef]
- Song, L.; Song, M.; Lu, Z.; Yu, G.; Liang, Z.; Hou, W.; Liao, Q.; Song, Y. Recent Advances of Preparation and Application of Two-Dimension van Der Waals Heterostructure. Coatings 2022, 12, 1152. [Google Scholar] [CrossRef]
- Lei, Y.; Zhang, T.; Lin, Y.C.; Granzier-Nakajima, T.; Bepete, G.; Kowalczyk, D.A.; Lin, Z.; Zhou, D.; Schranghamer, T.F.; Dodda, A.; et al. Graphene and beyond: Recent Advances in Two-Dimensional Materials Synthesis, Properties, and Devices. ACS Nanosci. Au 2022, 2, 450–485. [Google Scholar] [CrossRef] [PubMed]
- Han, S.A.; Bhatia, R.; Kim, S.W. Synthesis, Properties and Potential Applications of Two-Dimensional Transition Metal Dichalcogenides. Nano Converg. 2015, 2, 17. [Google Scholar] [CrossRef]
- Yin, P.; Jiang, X.; Huang, R.; Wang, X.; Ge, Y.; Ma, C.; Zhang, H. 2D Materials for Nonlinear Photonics and Electro-optical Applications. Adv. Mater. Interfaces 2021, 8, 2100367. [Google Scholar] [CrossRef]
- Joseph, S.; Mohan, J.; Lakshmy, S.; Thomas, S.; Chakraborty, B.; Thomas, S.; Kalarikkal, N. A review of the synthesis, properties, and applications of 2D transition metal dichalcogenides and their heterostructures. Mater. Chem. Phys. 2023, 297, 127332. [Google Scholar] [CrossRef]
- McCreary, A.; Kazakova, O.; Jariwala, D.; Al Balushi, Z.Y. An outlook into the flat land of 2D materials beyond graphene: Synthesis, properties and device applications. 2D Mater. 2021, 8, 013001. [Google Scholar] [CrossRef]
- Moody, G.; Sorger, V.J.; Blumenthal, D.J. Post-2000 Nonlinear Optical Materials and Measurements: Data Tables and Best Practices. J. Phys. Photonics 2023, 5, 035001. [Google Scholar]
- Autere, A.; Jussila, H.; Dai, Y.; Wang, Y.; Lipsanen, H.; Sun, Z. Nonlinear Optics with 2D Layered Materials. Adv. Mater. 2018, 30, e1705963. [Google Scholar] [CrossRef]
- Zhou, L.; Fu, H.; Lv, T.; Wang, C.; Gao, H.; Li, D.; Deng, L.; Xiong, W. Nonlinear Optical Characterization of 2D Materials. Nanomaterials 2020, 10, 2263. [Google Scholar] [CrossRef]
- Ahmed, S.; Jiang, X.; Wang, C.; Kalsoom, U.E.; Wang, B.; Khan, J.; Muhammad, Y.; Duan, Y.; Zhu, H.; Ren, X.; et al. An Insightful Picture of Nonlinear Photonics in 2D Materials and Their Applications: Recent Advances and Future Prospects. Adv. Opt. Mater. 2021, 9, 2001671. [Google Scholar] [CrossRef]
- Gomes, A.S.; Campos, C.L.; de Araújo, C.B.; Maldonado, M.; da Silva-Neto, M.L.; Jawaid, A.M.; Busch, R.; Vaia, R.A. Intensity-Dependent Optical Response of 2D LTMDs Suspensions: From Thermal to Electronic Nonlinearities. Nanomaterials 2023, 13, 2267. [Google Scholar] [CrossRef]
- Maldonado, M.; da Silva Neto, M.L.; Vianna, P.G.; Ribeiro, H.B.; Gordo, V.O.; Carvalho, I.C.; Menezes, L.d.S.; de Araújo, C.B.; de Matos, C.J.S.; Seixas, L.; et al. Femtosecond Nonlinear Optical Properties of 2D Metallic NbS2 in the near Infrared. J. Phys. Chem. C 2020, 124, 15425–15433. [Google Scholar]
- Carvalho, A.J.; Campos, C.L.; Valente, D.; Jawaid, A.M.; Busch, R.; Vaia, R.A.; Gomes, A.S. Near-Infrared Ultrafast Third-Order Nonlinear Optical Response of 2D NbS2, NbSe2, ZrTe2, and MoS2. Opt. Lett. 2023, 48, 2297–2300. [Google Scholar] [CrossRef] [PubMed]
- Liang, C.; Wang, E.; Li, X.; Wang, J.; Liu, Y.; Chen, B.; Chen, H.; Liu, Y.; Peng, X. Optical limiting performances of transitional metal dichalcogenides MX2 (M = V, Nb, Ta; X = S, Se) with ultralow initial threshold and optical limiting threshold. Chin. Opt. Lett. 2022, 20, 021901. [Google Scholar] [CrossRef]
- Jia, Y.; Liao, Y.; Wu, L.; Shan, Y.; Dai, X.; Cai, H.; Xiang, Y.; Fan, D. Nonlinear optical response, all optical switching, and all optical information conversion in NbSe2 nanosheets based on spatial self-phase modulation. Nanoscale 2019, 11, 4515–4522. [Google Scholar] [CrossRef]
- Wang, B.; Ma, B.; Wang, K.; Zhang, H.; Zhang, Z.; Song, T.; Wang, S.; Chen, M.; Li, S.; Wang, Q.; et al. Fractal Growth of 2D NbSe2 for Broadband Nonlinear Optical Limiting. Adv. Funct. Mater. 2024, 34, 2401490. [Google Scholar] [CrossRef]
- Bautista, J.E.; Campos, C.L.; da Silva-Neto, M.L.; de Araujo, C.B.; Jawaid, A.M.; Busch, R.; Vaia, R.A.; Gomes, A.S.L. Intensity-Dependent Thermally Induced Nonlinear Optical Response of Two-Dimensional Layered Transition-Metal Dichalcogenides in Suspension. ACS Photonics 2023, 10, 484–492. [Google Scholar] [CrossRef]
- Silva-Guillén, J.Á.; Ordejón, P.; Guinea, F.; Canadell, E. Electronic structure of 2H-NbSe the CDW state single-layers. 2D Mater. 2016, 3, 035028. [Google Scholar] [CrossRef]
- Ugeda, M.M.; Bradley, A.J.; Zhang, Y.; Onishi, S.; Chen, Y.; Ruan, W.; Ojeda-Aristizabal, C.; Ryu, H.; Edmonds, M.T.; Tsai, H.-Z.; et al. Characterization of collective ground states in single-layer NbSe2. Nat. Phys. 2016, 12, 92–97. [Google Scholar] [CrossRef]
- Jawaid, A.; Che, J.; Drummy, L.F.; Bultman, J.; Waite, A.; Hsiao, M.-S.; Vaia, R.A. Redox Exfoliation of Layered Transition Metal Dichalcogenides. ACS Nano 2017, 11, 635–646. [Google Scholar] [CrossRef] [PubMed]
- Jawaid, A.M.; Ritter, A.J.; Vaia, R.A. Mechanism for Redox Exfoliation of Layered Transition Metal Dichalcogenides. Chem. Mater. 2020, 32, 6550–6565. [Google Scholar] [CrossRef]
- Sheik-Bahae, M.; Said, A.A.; Wei, T.-H.; Hagan, D.J.; Van Stryland, E.W. Sensitive measurement of optical nonlinearities using a single beam. IEEE J. Quantum Electron. 1990, 26, 760–769. [Google Scholar] [CrossRef]
- de Araújo, C.B.; Gomes, A.S.; Boudebs, G. Techniques for nonlinear optical characterization of materials: A review. Rep. Prog. Phys. 2016, 79, 036401. [Google Scholar] [CrossRef]
- Gomes, A.S.L.; Falcão Filho, E.L.; Rativa, D.; de Araujo, R.E.; de Araújo, C.B. Thermally managed eclipse Z-scan. Opt. Express 2007, 15, 1712. [Google Scholar] [CrossRef]
- Moysés, R.M.; Barbano, E.C.; Misoguti, L. Discrimination of thermal, molecular orientation, and pure electronic refractive nonlinearities using the polarization-resolved Z-scan technique. JOSA B 2023, 40, C60–C66. [Google Scholar] [CrossRef]
- Couris, S.; Renard, M.; Faucher, O.; Lavorel, B.; Chaux, R.; Koudoumas, E.; Michaut, X. An experimental investigation of the nonlinear refractive index (n2) of carbon disulfide and toluene by spectral shearing interferometry and z-scan techniques. Chem. Phys. Lett. 2003, 369, 318–324. [Google Scholar] [CrossRef]
- Iliopoulos, K.; Potamianos, D.; Kakkava, E.; Aloukos, P.; Orfanos, I.; Couris, S. Ultrafast third order nonlinearities of organic solvents. Opt. Express 2015, 23, 24171–24176. [Google Scholar] [CrossRef]
- Silva-Guillén, J.Á.; Ordejón, P.; Guinea, F.; Canadell, E. Electronic structure of 2H-NbSe2 single-layers in the CDW state. 2D Mater. 2016, 3, 035028. [Google Scholar] [CrossRef]
- van Loon, E.G.; Rösner, M.; Schönhoff, G.; Katsnelson, M.I.; Wehling, T.O. Competing Coulomb and electron-phonon interactions in NbS2. Quantum Mater. 2018, 3, 32. [Google Scholar] [CrossRef]

| Material | Technique | (cm2/W) | (cm/GW) | Ref. |
|---|---|---|---|---|
| NbSe2 | Z-Scan a | This work | ||
| OKG b | Not observed | |||
| NbS2 | Z-Scan | [13] | ||
| OKG | Not observed | [14] | ||
| ACN | Z-Scan | Negligible | [13] | |
| CS2 | Z-Scan | [27] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Campos, C.L.A.V.; Gonçalves, I.; Bautista, J.E.Q.; Carvalho, A.; Jawaid, A.M.; Busch, R.; Vaia, R.; Gomes, A.S.L. Femtosecond Third-Order Nonlinear Electronic Responses of 2D Metallic NbSe2. Photonics 2024, 11, 930. https://doi.org/10.3390/photonics11100930
Campos CLAV, Gonçalves I, Bautista JEQ, Carvalho A, Jawaid AM, Busch R, Vaia R, Gomes ASL. Femtosecond Third-Order Nonlinear Electronic Responses of 2D Metallic NbSe2. Photonics. 2024; 11(10):930. https://doi.org/10.3390/photonics11100930
Chicago/Turabian StyleCampos, Cecília L. A. V., Igor Gonçalves, Jessica E. Q. Bautista, Alyson Carvalho, Ali M. Jawaid, Robert Busch, Richard Vaia, and Anderson S. L. Gomes. 2024. "Femtosecond Third-Order Nonlinear Electronic Responses of 2D Metallic NbSe2" Photonics 11, no. 10: 930. https://doi.org/10.3390/photonics11100930
APA StyleCampos, C. L. A. V., Gonçalves, I., Bautista, J. E. Q., Carvalho, A., Jawaid, A. M., Busch, R., Vaia, R., & Gomes, A. S. L. (2024). Femtosecond Third-Order Nonlinear Electronic Responses of 2D Metallic NbSe2. Photonics, 11(10), 930. https://doi.org/10.3390/photonics11100930






