Gold Nanoparticles at a Liquid Interface: Towards a Soft Nonlinear Metasurface

Abstract

Optical second-harmonic generation (SHG) is achieved using adsorbed gold nanoparticles (AuNPs) with an average diameter of 16 nm at the aqueous solution–air interface in reflection. A detailed analysis of the depth profile of the SHG intensity detected shows that two contributions appear in the overall signal, one arising from the aqueous solution–air interface that is sensitive to the AuNP surface excess and one arising from the bulk aqueous phase. The latter is an incoherent signal also known as hyper-Rayleigh scattering (HRS). The results agree with those of an analysis involving Gaussian beam propagation optics and a Langmuir-like isotherm. Discrepancies are revealed for the largest AuNP concentrations used and indicate a new route for the design of soft metasurfaces.

1. Introduction

Frequency conversion, a process achieved routinely in nonlinear optics at the macroscopic scale, requires new devices at the nanoscale to enhance efficiency. This process is achieved with metasurfaces offering opportunities in physics, chemistry, material science, or life sciences, for instance in applications of characterization methods or sensing [1]. Metasurfaces are two-dimensional structures not found in nature composed of an array of sub-wavelength-sized elements, usually called meta-atoms, engineered to manipulate electromagnetic waves to achieve specific properties. Metasurfaces currently find applications in holography, beam steering, or imaging, for instance. Despite the diversity of metasurfaces obtained owing to the availability of materials and fabrication methods, some issues remain to be addressed, notably flexibility or reconfiguration. One promising design is the use of liquid interfaces to introduce soft metasurfaces [2]. Liquid interfaces can be polarized either externally using a potentiostat or chemically using a well-defined choice of supporting electrolytes to drive charge transfer reactions such as ion transfer, assisted ion transfer, or even heterogeneous dark or photo-electron transfer reactions [3,4]. The polarization can also be used to control the adsorption of not only molecules [5,6] but also of nanoparticles [7,8,9,10,11]. These controlled adsorption phenomena are very important for the control of the functionalization of these interfaces by molecular catalysts to drive for an oxygen reduction reaction, for example, [12,13,14] or by nanoparticles to reduce aqueous protons to hydrogen [15,16]. In this context, the structuring of liquid interfaces via the adsorption of metallic nanoparticles is highly desired for its ability to simultaneously allow the benefits from the optical properties of these particles to be combined with the adsorptive control offered by the intrinsic interfacial properties of the liquid phase [17].

The plasmonic effects introduced via the adsorption of plasmonic nanoparticles can be observed at polarized liquid–liquid interfaces both in reflectivity [18] and photo-current measurements [19]. This is a first step towards linear soft metasurfaces. However, it is important to propose new possibilities for these interfaces, perhaps with accompanying active functions like reactivity [20]. Due to their natural propensity to enhance electromagnetic fields, combined with their surface optical sensitivity, plasmonic nanoparticles are also effective platforms for nonlinear optical spectroscopy techniques. This propensity has been shown via investigations of liquid interfaces like liquid–air or liquid–liquid interfaces, for example [21,22,23,24]. The simplest of the nonlinear optical processes is second-harmonic generation (SHG), whereby two photons at a fundamental frequency are converted into a single photon at the harmonic frequency [21,25]. Within electric dipole approximation, SHG is forbidden to occur in bulk centrosymmetric media and can only arise from interfaces between two such media where the centrosymmetry is broken [26]. However, incoherent SHG, also known as hyper–Rayleigh scattering (HRS), is still allowed to occur within centrosymmetric bulk media, but is generally not considered when coherent SHG is concerned because of its weak efficiency [27,28].

SHG experiments performed at liquid interfaces have already demonstrated their potential for use in structural studies, by yielding the surface coverage, surface molecular orientation or surface polarity through intensity, and light-polarization- or wavelength-dependent measurements, for example [29,30]. Moreover, time-resolved studies have unraveled the characteristic durations for the dynamics of molecular processes to appear at the interface as well as for the kinetics of interfacial reactions to be observed [6,31,32,33,34]. Hence, the use of liquid interfaces is an intuitive method that can be used to design nonlinear soft metasurfaces. SHG is usually performed on flat, large-area liquid interfaces [35]. The use of curved surfaces has seldom been investigated in SHG because the interface itself may act as an optical element modifying the laser beam’s physical properties. Nevertheless, experiments on droplets, vesicles, and microspheres have been reported, as the aforementioned problems can be circumvented with the use of tight focusing conditions, for instance with microscope objectives. Indeed, the use of a droplet’s curved surface may represent an asset for the design of soft metasurfaces. Nanoscale droplets have also been investigated but require a different approach, usually considered through Mie theory [36].

SHG has been used to investigate metallic nanoparticles, especially of gold and silver [37], the optical responses of which are dominated by the collective excitation of the conduction band electrons in the visible part of the spectrum. The latter is known as localized surface plasmon resonance (LSPR). The origin and the different field contributions involved in the SHG response have been extensively discussed, and different materials have been used [38]. The field of linear and nonlinear flat metasurfaces is now well established. However, few works have reported on SHG studies of metallic nanoparticles adsorbed at liquid interfaces [39]. In the present work, we design soft nonlinear metasurfaces for use with SHG via the adsorption of gold nanoparticles (AuNPs) at an aqueous solution–air interface. We first determine the nature of the SHG signal retrieved using depth profiling and then determine the relationship between the SHG intensity and the AuNP average surface density.

2. Experimental Methods

2.1. Chemicals

All chemicals were used as received without further purification. All aqueous solutions were prepared with ultra-pure water (Millipore Milli-Q, specific resistivity 18.2 MΩ·cm). Potassium gold(III) chloride (KAuCl₄, 98%) and sodium citrate dihydrate (Na₃C₆H₅O₇·2H₂O, 98%) were purchased from Sigma-Adrich and Acros, respectively.

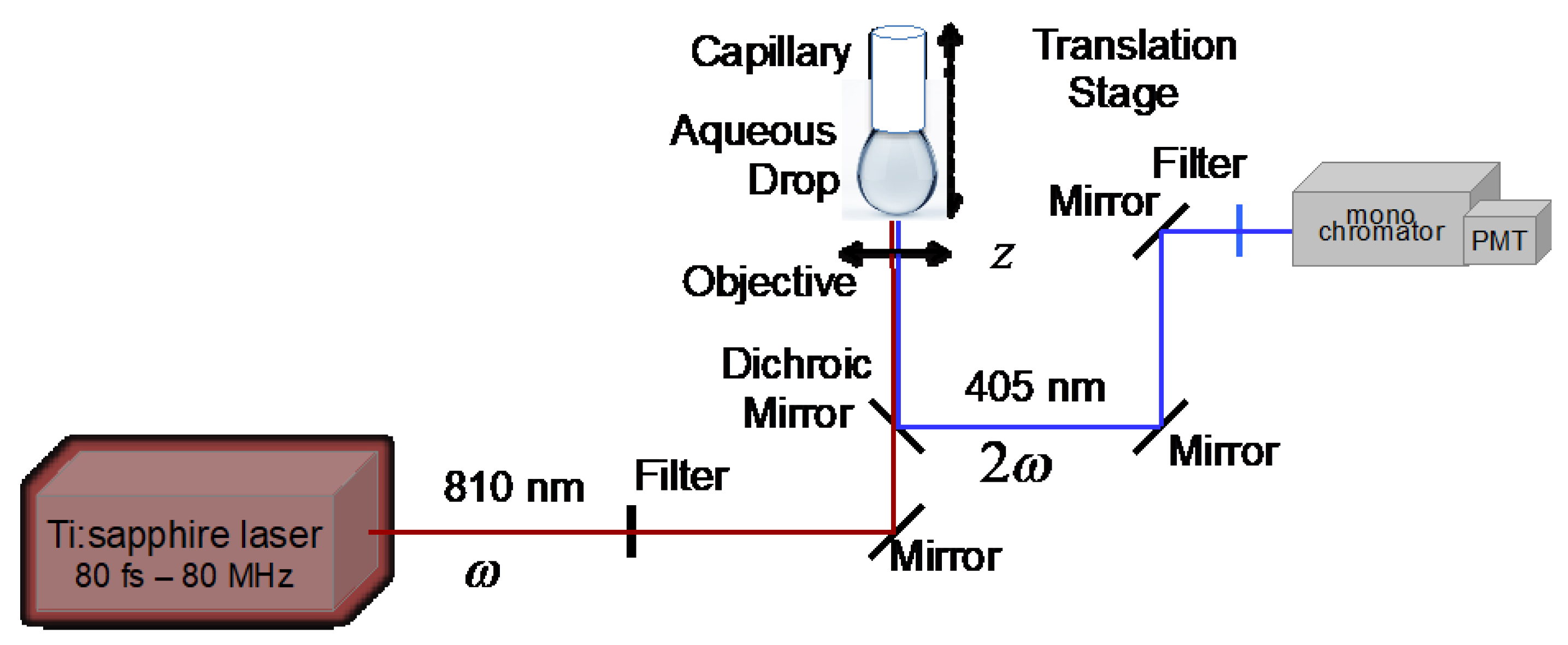
2.2. Acquisition of Longitudinal SHG Intensity Profiles at AuNP-Modified Aqueous Solution–Air Interfaces

The experimental set-up is outlined in Figure 1. A mode-locked Ti:sapphire laser (Spectra Physics, Tsunami, Santa Clara, USA) tuned to a wavelength of 810 nm and delivering pulses with a duration of about 80 femtoseconds at a repetition rate of 80 MHz was used as the laser source. The laser beam was focused at the surface of a 2 mm diameter hanging droplet with a microscope objective (Olympus, X20, NA 0.40), and a low-pass filter was used to remove any residual light at the harmonic frequency generated before the cell. The fundamental beam was also chopped at a frequency slightly different from 50 Hz to allow a gated photon counting regime to remove the background photons. The second-harmonic photons produced by the aqueous droplets containing AuNPs were collected through a monochromator (Jobin-Yvon, TRIAX series 190) and detected by a sensitive photomultiplier. The scattered fundamental photons were removed with a high-pass filter placed before the monochromator. The drop was obtained using a vertical thin capillary held by a manual piston burette (Metrohm) filled with the aqueous AuNP solution. This system allowed for the control of the size of the drop manually. However, the AuNP concentration of the solution could not be set continuously and was therefore changed manually for each profile. The capillary was held on a translation stage (Physik Instrumente), permitting longitudinal scanning of the drop in the laser beam along the propagation direction. For each experiment, the drop was initially placed 0.5 mm above the microscope objective, the working distance of which was 1.2 mm.

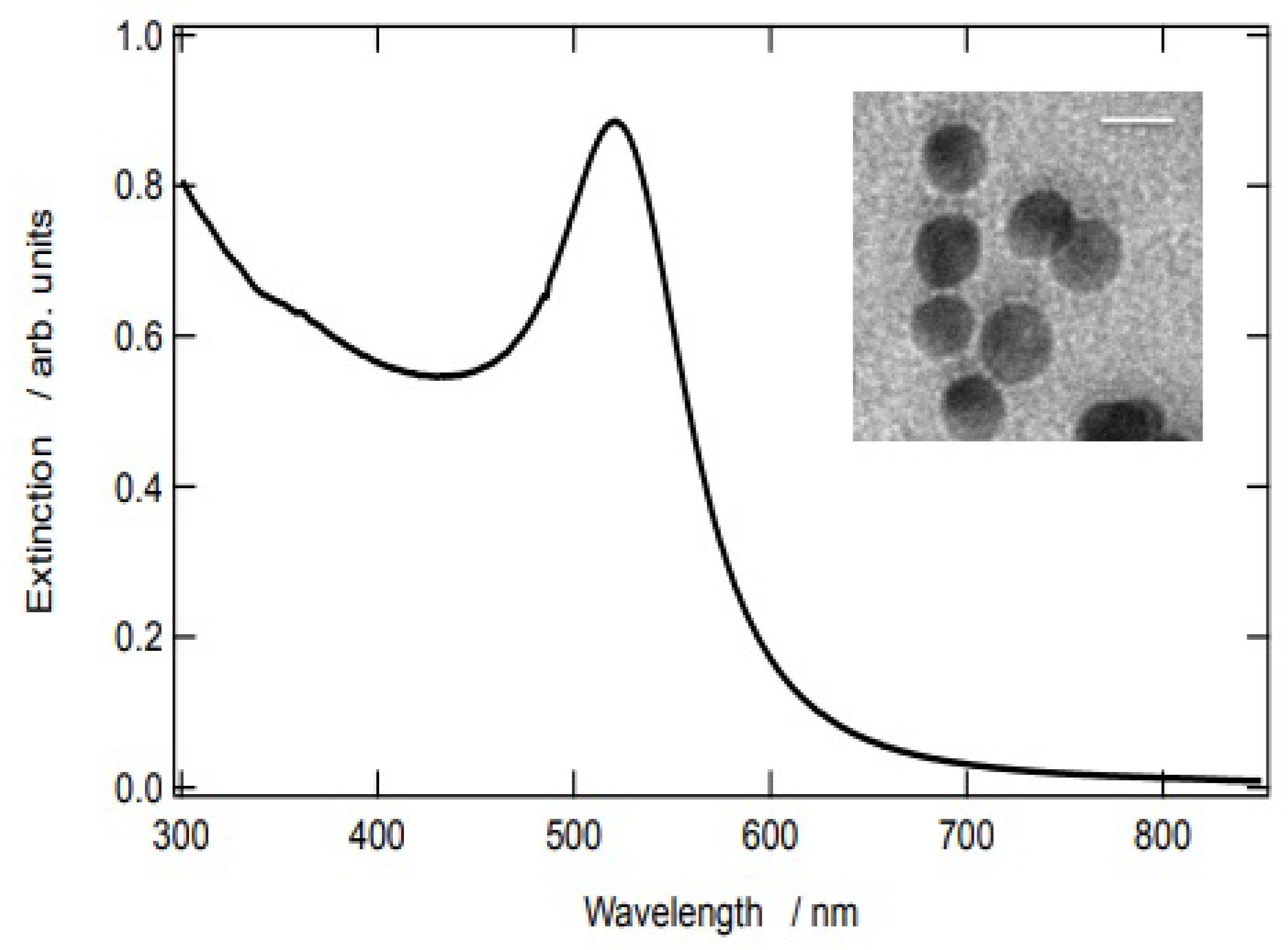
2.3. Synthesis and Characterization of AuNPs

AuNPs were synthesized following Turkevich’s method [40]. Briefly, an aqueous solution of 0.27 mM KAuCl₄ (95 mL) was heated to its boiling point, and a 1% sodium citrate solution (5 mL) was added under vigorous stirring. Subsequently, the solution was heated for 1 h, and the resultant red solution was left to cool to room temperature. Transmission electronic microscopy (TEM) was used to determine the size distribution of the nanoparticles. The particles had an average diameter of 16 nm with a standard deviation of ca. 10%. The extinction spectrum of the 2 nM solution is provided in Figure 2 alongside a TEM picture.

3. Results and Discussion

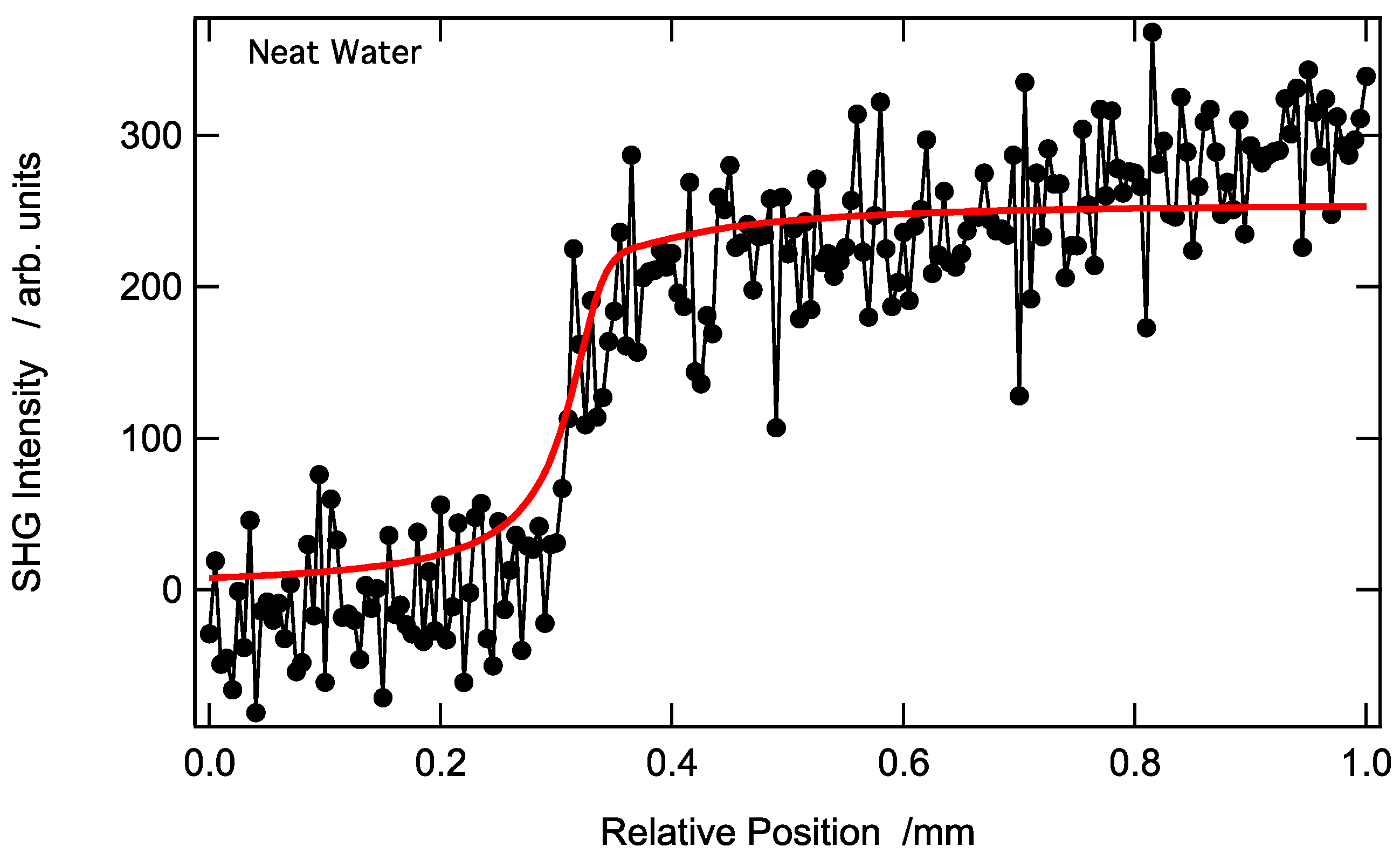
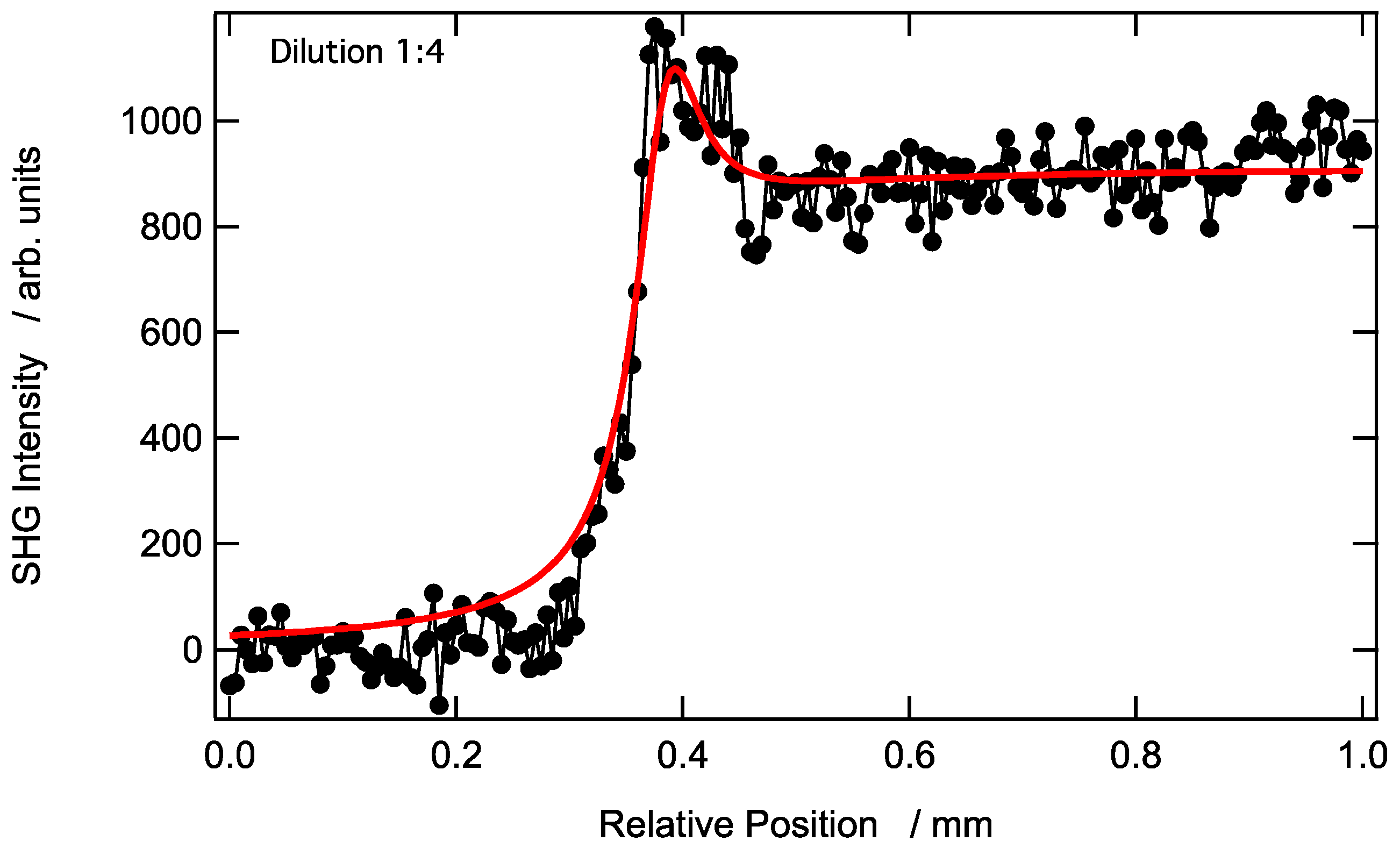
3.1. Longitudinal SHG Intensity Profile at a AuNP-Modified Aqueous Solution–Air Interface Prepared Using a Diluted Aqueous Solution of AuNPs

Second-harmonic photons produced at a wavelength of λ = 405 nm were generated by irradiating a 2 mm diameter aqueous droplet containing a diluted solution of AuNPs with femtosecond laser pulses at λ = 810 nm and collected in retro-reflected mode with the same objective. The position of the interfacial region was moved incrementally through the beam focus, produced with the microscope objective, in a longitudinal direction along the laser beam propagation pathway. Two distinct regions were identified in the resulting SHG intensity profile depending on the position of the beam waist, i.e., the beam portion of the highest intensity, for the neat water solution–air interface, a region of vanishing SHG intensity when the beam focus was in the air, and a region of non-vanishing SHG intensity when the beam focus was in the solution volume; see Figure 3.

In particular, it is noted that the SHG signal captured in the absence of AuNPs was rather weak, leading to considerable noise. A region of high intensity at z > 0.40 mm, indicating the presence of an SHG signal, was seen with the beam waist positioned in the bulk aqueous phase. A region of vanishing intensity at z < 0.40 mm, indicating the absence of SHG, was seen when the beam waist was located in air. See Figure 3 for the neat aqueous solution–air interface and Figure 4 to observe the low concentration of the aqueous solution with respect to the AuNPs.

The localization of the beam waist at the interface was hence determined to be at location z_I = 0.40 mm on the longitudinal displacement scale, as shown in Figure 3 and Figure 4. The SHG signal collected in the bulk aqueous phase remained constant irrespective of the movement of the beam waist away from the interface into the region of higher intensity. Thus, this SHG contribution originated from the bulk itself and is attributed to incoherent SHG or HRS produced within the aqueous phase and subsequently collected via the microscope objective in retro-reflection. However, at position z_I = 0.40 mm, a peak was observed that corresponded to the interface contribution, a spatial region where the centrosymmetry was broken.

3.2. Longitudinal SHG Intensity Profile at a AuNP-Modified Aqueous Solution–Air Interface Prepared Using an Undiluted (Stock) Aqueous Solution of AuNPs

Metallic nanoparticles are known to lead to intense SHG, owing to their large first hyperpolarizability. Indeed, the latter is much higher than that reported for molecular organic chromophores, although the nanoparticle sizes should be taken into account for comparison [41,42].

The experimental SHG response recorded for a AuNP-modified aqueous solution–air interface, using a 2 nM stock solution measuring 16 nm in diameter AuNPs, is shown in Figure 5. In agreement with previous reports of HRS from aqueous AuNP solutions, the incoherent SHG response collected in the bulk of the undiluted droplet was significantly higher than that collected from a diluted droplet (see Figure 4). This feature stemmed from the linear dependence of the incoherent SHG intensity on the AuNP concentration. Adsorbed AuNPs at the interface produced an intense SHG signal that was observed in a thin spatial domain corresponding to a position where the interface was at, or near, the position of the beam waist. Note that NPs made from other materials like dielectric materials, and preferentially non-centrosymmetric materials, would also provide similar features, although metallic nanoparticles like AuNPs have large efficiency with respect to the process of SHG. Analogous to the description in Figure 3 and Figure 4, no SHG signal is measured when the beam waist is in the air phase at a distance far enough from the liquid interface. However, the width of the SHG surface response is rather broad in the presence of a larger surface excess of AuNPs at the aqueous–air interface in comparison to that for the diluted aqueous droplet; see Figure 5 and a discussion below.

3.3. Theoretical Model to Describe SHG Intensity Generated at AuNP-Modified Aqueous Solution–Air Interfaces

A theoretical framework within which the SHG intensity profiles resulting from a neat aqueous solution–air interface, as well as from adsorbed AuNPs at an aqueous solution–air interface, was thus developed. Within this theoretical model, the interface is defined as a region of finite thickness, e, a thickness smaller than the fundamental wavelength. We assume that the incoherent SHG signal arising from the bulk aqueous phase cannot interfere with other SHG contributions, for example from the interface, as it is an incoherent contribution. The bulk contribution is indeed fully incoherent as the medium is centrosymmetric but undergoes instantaneous orientation fluctuations. Indeed, AuNPs are close to spherical but not strictly so (see Figure 2 and the TEM insert), and therefore possess a specific orientation. However, due to Brownian motion, this orientation differs from one NP to another and fluctuates over time. This contribution is therefore fully incoherent and is named hyper-Rayleigh scattering. The interfacial SHG signal thus arises from a very thin spatial region, thinner than the wavelength of the incoming fundamental beam. The phase of the electric field amplitude can be neglected as the integration length is of the order of 1 nm for molecular interfaces and 16 nm for adsorbed AuNPs. The fundamental laser beam was taken as a simple TEM00 Gaussian beam of intensity I(r,z) with a radial coordinate, r, and a longitudinal z dependence. In deriving the model, z₀ is taken as the position of the beam waist relative to the interface itself located at z_I and e is the interfacial thickness. Also, $\beta \left(z\right)$ is the first quadratic hyperpolarizability of water or AuNPs and $N\left(z\right)$ is the number of water or AuNPs per unit volume. The brackets, <…>, indicate orientational averaging. In the liquid phase, water or AuNPs are assumed to take on a random distribution, thereby neglecting correlation, whereas at the interface, this random orientation is no longer pertinent, and an orientational distribution breaking the centrosymmetry is introduced. Indeed, although AuNPs are close to spherical, when they sit at the interface, a nonlinear response results from their interaction with the interface. The orientationally averaged surface and bulk hyperpolarizabilities must therefore be distinguished with a longitudinal $z$ dependence. Likewise, the molecule number density must also possess a similar longitudinal coordinate dependence to distinguish the surface and bulk densities.

Several further assumptions were also applied to the model, describing SHG intensity generated at AuNP-modified aqueous solution–air interfaces. First, the theory for SHG from Gaussian beams was assumed. Therefore, because the confocal parameter of the SHG wave was smaller than that of the fundamental wave by a factor of $\sqrt{2}$ [43], the harmonic beam was considered fully recaptured via reflection through the microscope objective. Second, the propagation of the harmonic beam was considered using the standard ABCD matrix optics for Gaussian beams. Thus, within the approximation of a Gaussian beam, the SHG intensity, $I_{SHG}\left(z\right)$, is given by Equation (1):

$$I_{SHG}\left(z_0\right)=g{\int }_0^r{\int }_{-\infty }^{+\infty }〈p\left(z\right)p^{*}\left(z\right)〉{e^{-\kappa N\left(z\right)z}I}^2\left(r,z\right)dzrdr$$

(1)

with $p\left(z\right)={\sum }_{i=1}^{N\left(z\right)}{\beta }_i\left(z\right)$, where $g$ is a general constant and $N\left(z\right)Adz$ is the number of molecules in the slab of thickness $dz$ and area A, the latter corresponding to the laser beam transverse section. Here, we use scalar quantities, as it is assumed that the polarization states at the fundamental and harmonic frequencies are fixed, thereby defining the exact combination of the tensor elements involved. Nevertheless, it is not necessary to define those further at this stage. Finally, the Gouy phase, is neglected because of the small thickness of the interface with respect to the fundamental wavelength, as is the spatial phrase, and the harmonic light produced in the bulk phase is considered fully incoherent here. Also, $\kappa =2\kappa \left(\omega \right)+\kappa \left(2\omega \right)$ is the effective molar extinction coefficient introduced to take into account the possibility of extinction of the fundamental and harmonic waves with the $\kappa \left(\omega \right)$ and $\kappa \left(2\omega \right)$ molar extinction coefficients, respectively. Then, neglecting self-absorption, integrating Equation (1) over the radial $r$ and longitudinal $z$ coordinates yields the following:

$$I_{SHG}\left(z\right)=GN〈{\beta }_V^2〉\left[{\displaystyle \frac{N_S^2}{N}}{\displaystyle \frac{〈{\beta }_S^2〉}{〈{\beta }_V^2〉}}\left\{atan\left({\displaystyle \frac{z}{z_R}}\right)-atan\left({\displaystyle \frac{z-e}{z_R}}\right)\right\}+\left\{{\displaystyle \frac{\pi }{2}}-atan\left({\displaystyle \frac{z-e}{z_R}}\right)\right\}\right]$$

(2)

where z_R is the Rayleigh parameter of the fundamental beam after it is focused through the microscope objective and propagates across the aqueous solution–air interface. The determination of $z_R$ may be performed using the conventional ABCD formalism for Gaussian beams, but can be also extracted via adjustments to the experimental data, as the latter bear information on the interfacial structure. A Rayleigh parameter of z_R = 0.035 mm was assumed in the liquid phase, and the interface thickness was set to same diameter as the AuNPs of 16 nm. Likewise, the general constant, $G$, resulted from the integration of Equation (1) and embedded all remaining constants.

The major parameter of the model, namely $\alpha =N_S^2〈{\beta }_S^2〉/N〈{\beta }_V^2〉$, is the ratio of the surface to bulk hyperpolarizabilities multiplied by their corresponding molecular or nanoparticle concentrations. However, at the surface, because molecules are oriented a particular way, the concentration dependence is squared due to the coherent effects. Also, due to the method, the interfacial width is convoluted with the Gaussian beam waist, whereas the interfacial thickness is expected to be in the nanometer range. Our theoretical model, as proposed, reproduces the experimental results of the AuNP-modified solution–air interface prepared using a diluted AuNP solution rather accurately (see Figure 4) but some deviations appear for the undiluted AuNP solution (see Figure 5).

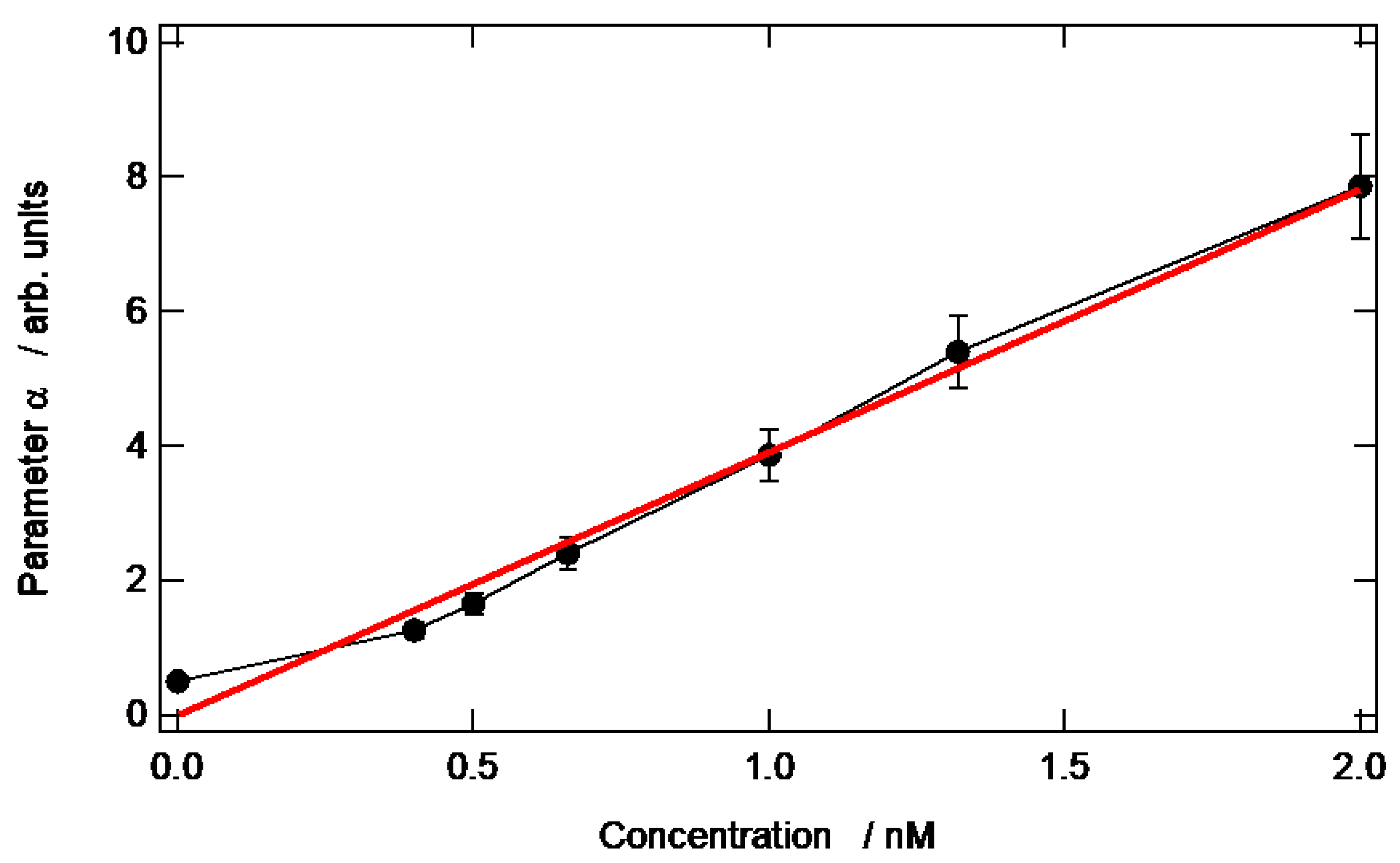
3.4. Evolution of the α Parameter as a Function of the AuNP Concentration in the Aqueous Droplet

The influence of the AuNP concentration in the aqueous droplet on the HRS intensity and the consequent evolution of the α parameter was investigated by carrying out a series of dilutions of the 2 nM stock solution. The α parameter for the neat aqueous solution and each AuNP concentration investigated, obtained via the fitting of the theoretical model to the experimental data, is reported in Figure 6. A linear increase with the AuNP concentration at the interface was observed in the α parameter.

The HRS intensity is known to scale linearly with the AuNP concentration in the aqueous droplet. However, at the interface, the bulk phase centrosymmetry is broken in a direction normal to the interface, and the surface contribution is coherent at this point. Hence, the orientational averaging procedure of $〈p\left(z\right)p^{*}\left(z\right)〉$ must differ from that in the bulk phase. Therefore, this coherent contribution provides an $N_S^2$ dependence to the α parameter. Using a simple Langmuir-like isotherm of the form $N_S=KN/(1+K)$ with constant $K$, a linear dependence of the α parameter as a function of the bulk concentration, $N$, is indeed recovered at low values of the product $KN$. Low values for this product are expected because the AuNPs are known to be negatively charged and therefore do not have a propensity to adsorb easily at interfaces in the absence of a specific driving force. Interestingly, the slope of the line in Figure 6 provides the product of this constant, $K$, multiplied by the ratio of the hyperpolarizabilities, namely $K^2〈{\beta }_S^2〉/〈{\beta }_V^2〉.$ Therefore, this ratio only depends on the surface and bulk hyperpolarizabilities, as well as their orientational averaging and the Langmuir constant.

3.5. The Limits of the Values Obtained from the Adjustment Procedure

As a final analysis, we discuss the limits of the values obtained from the adjustment procedure. In particular, the Gaussian beam Rayleigh parameter z_R is assumed to be constant, as determined via the properties of the optical constant of the liquid phase and optical elements like the objective. However, it is known that due to the presence of metallic nanoparticles, it is possible that higher-order nonlinear optical processes come into play, particularly Kerr effects and nonlinear refraction. Hence, it is possible that the Rayleigh parameter z_R may change with concentration. This might be the reason why the results of adjustment procedure are not in very good agreement with the experimental data in Figure 5 on the decreasing edge of the SHG intensity profile. Interestingly, the rising edge of the profile remains well described with an invariant Rayleigh parameter, z_R. It is also worth noting that the extinction of the 2 nM aqueous solution of 16 nm diameter AuNPs was 0.56 for a 1 cm optical path length at 405 nm and 0 at 800 nm; see Figure 2. Hence, in these experiments, extinction certainly played some kind of role, notably in the absorption of SHG light by the AuNPs themselves. However, it is unlikely to have been uniquely responsible for the decreasing edge of the SHG intensity profile. This point is further supported by the observation of a plateau in the SHG intensity profile for the deepest beam waist positions. If extinction had played the main role alone, the SHG intensity would have been lost altogether for these beam waist positions. Further work is therefore required to reveal the microscopic structure of these AuNP-modified aqueous–air interfaces and their observed thickening in their SHG response. The proposed experimental approach herein provides an adequate method to achieve this goal.

This system, consisting of adsorbed plasmonic AuNPs at a liquid interface, provides a new platform for nonlinear optics and, in particular, SHG. It appears that the SHG beam, captured in retro-reflection, is simply controlled through the volume concentration of the AuNPs and the detailed structure of the interface. This feature opens up perspectives in the design of liquid interfaces as soft metasurfaces for nonlinear optics [44] as there are other possibilities to externally control the structure of the interface, for example through the application of an external electric potential or a second beam, with applications in areas like sensing [45].

4. Conclusions

The SHG intensity profile of metallic AuNPs adsorbed at the aqueous solution–air interface is reported for different nanoparticle bulk concentrations. The obtained responses consist of an interfacial contribution superposed on the incoherent contribution from the bulk volume. A simple theoretical model is derived to account for these observations. The major parameter of this model is the ratio between the contributions from the surface to the bulk volume. The presence of AuNPs at the interface induces a strong SHG response that is then easily disentangled from that of the volume. Furthermore, in agreement with the results of our theoretical model, the surface response is such that the α parameter varies linearly with the bulk volume concentration of AuNPs in the aqueous droplet, a regime in which the number of particles per unit surface at the interface is rather small. Interestingly, at high AuNP concentrations, deviation from the model is identified, opening up a possible avenue in which to investigate the microscopic structure of these interfaces.