PTFE-Based Circular Terahertz Dielectric Waveguides
Abstract
1. Introduction
2. Electric Permittivity Measurement of Materials
3. Analysis and Simulation
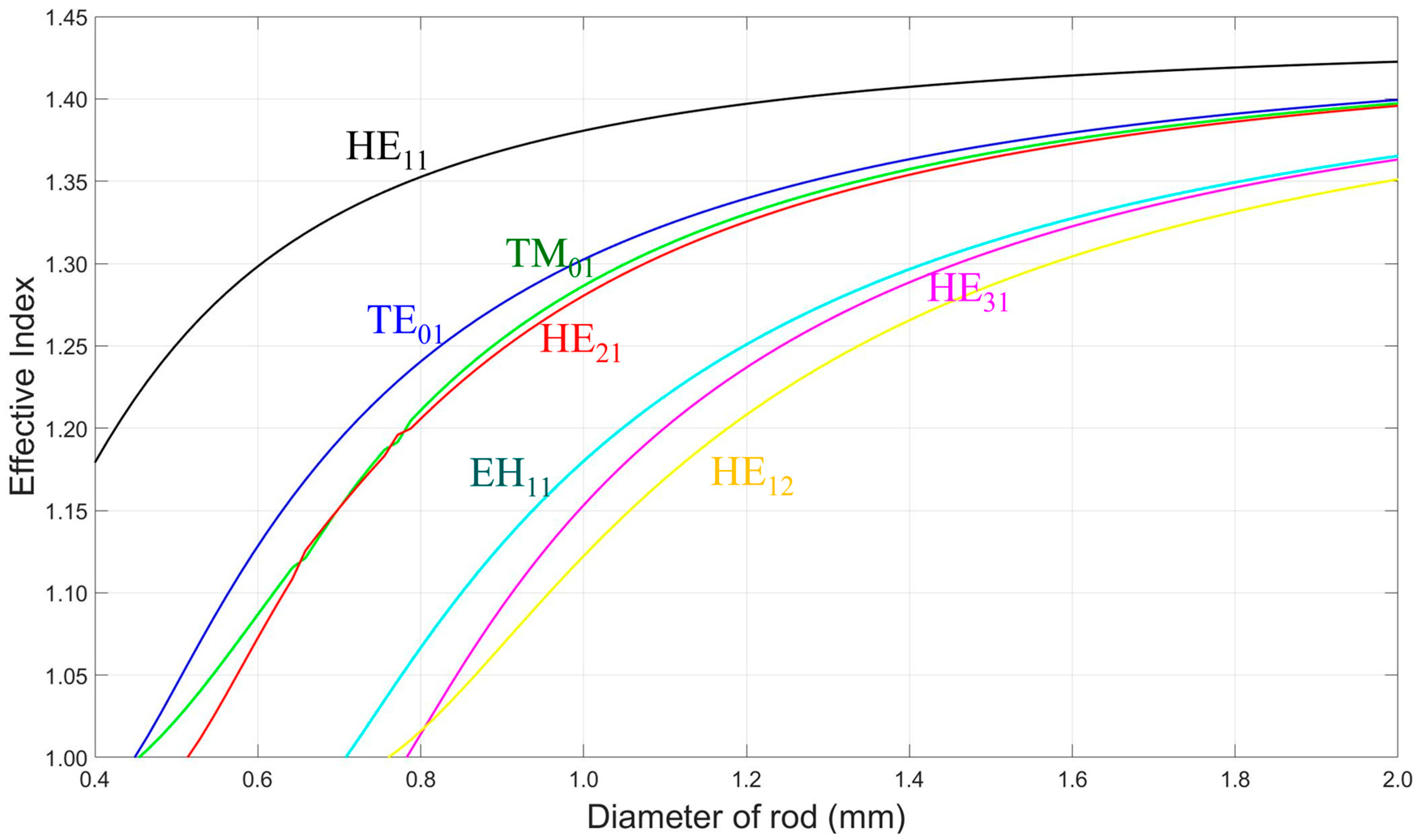
3.1. Propagation Modes
3.2. Energy Confinement
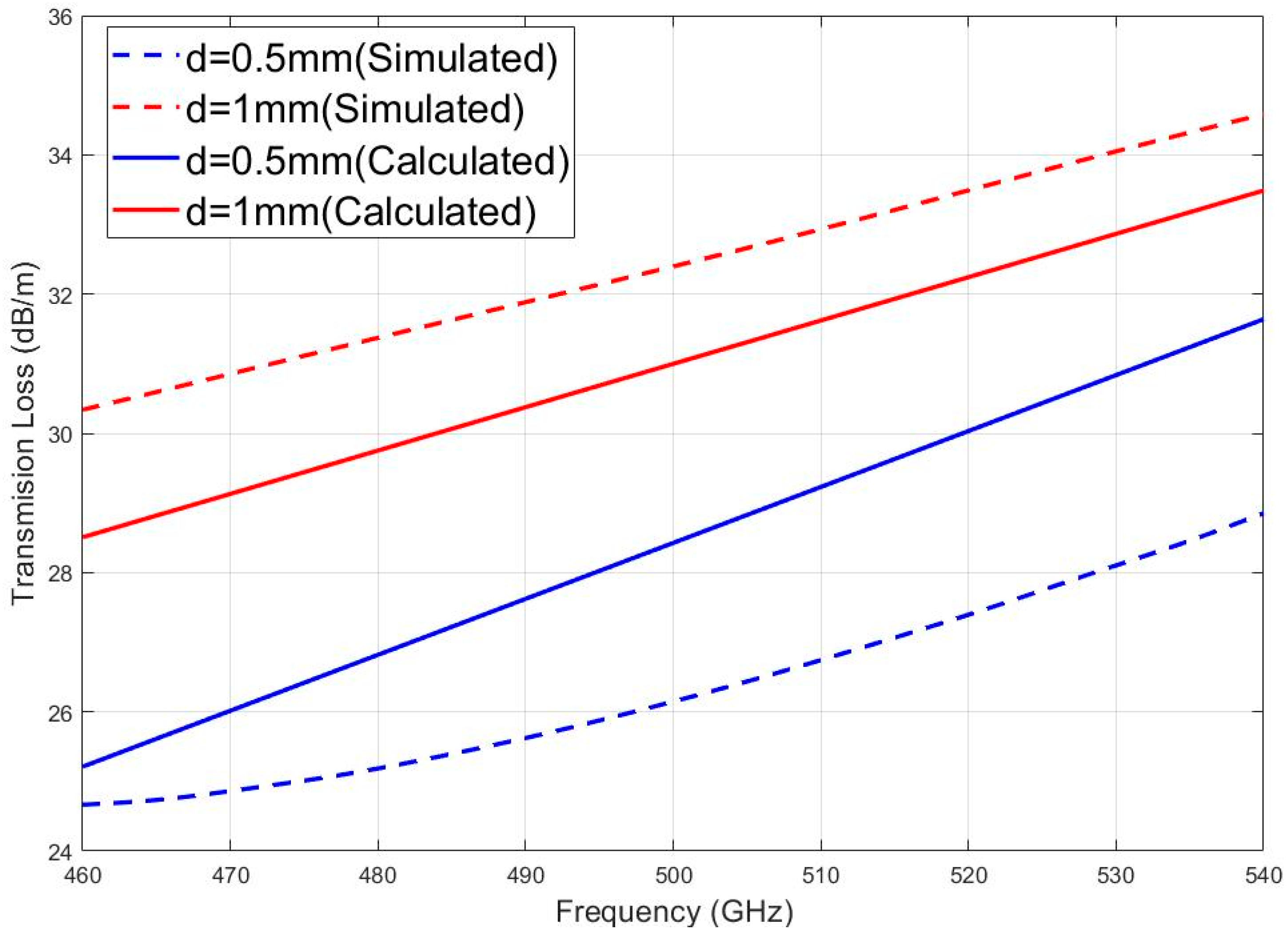
3.3. Transmission Loss
3.4. Bending Loss
4. Key Issues in the Practical Use of Dielectric Waveguides
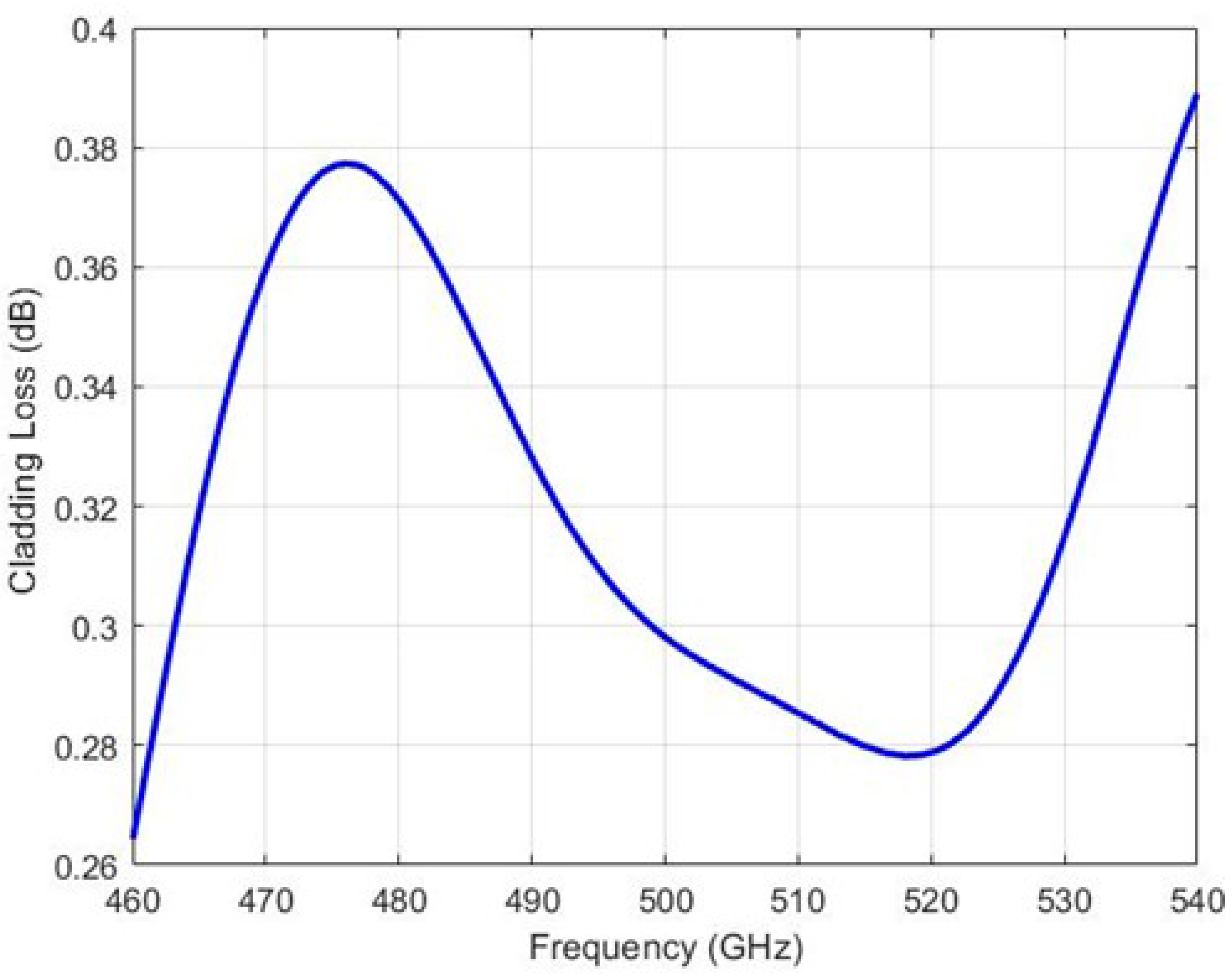
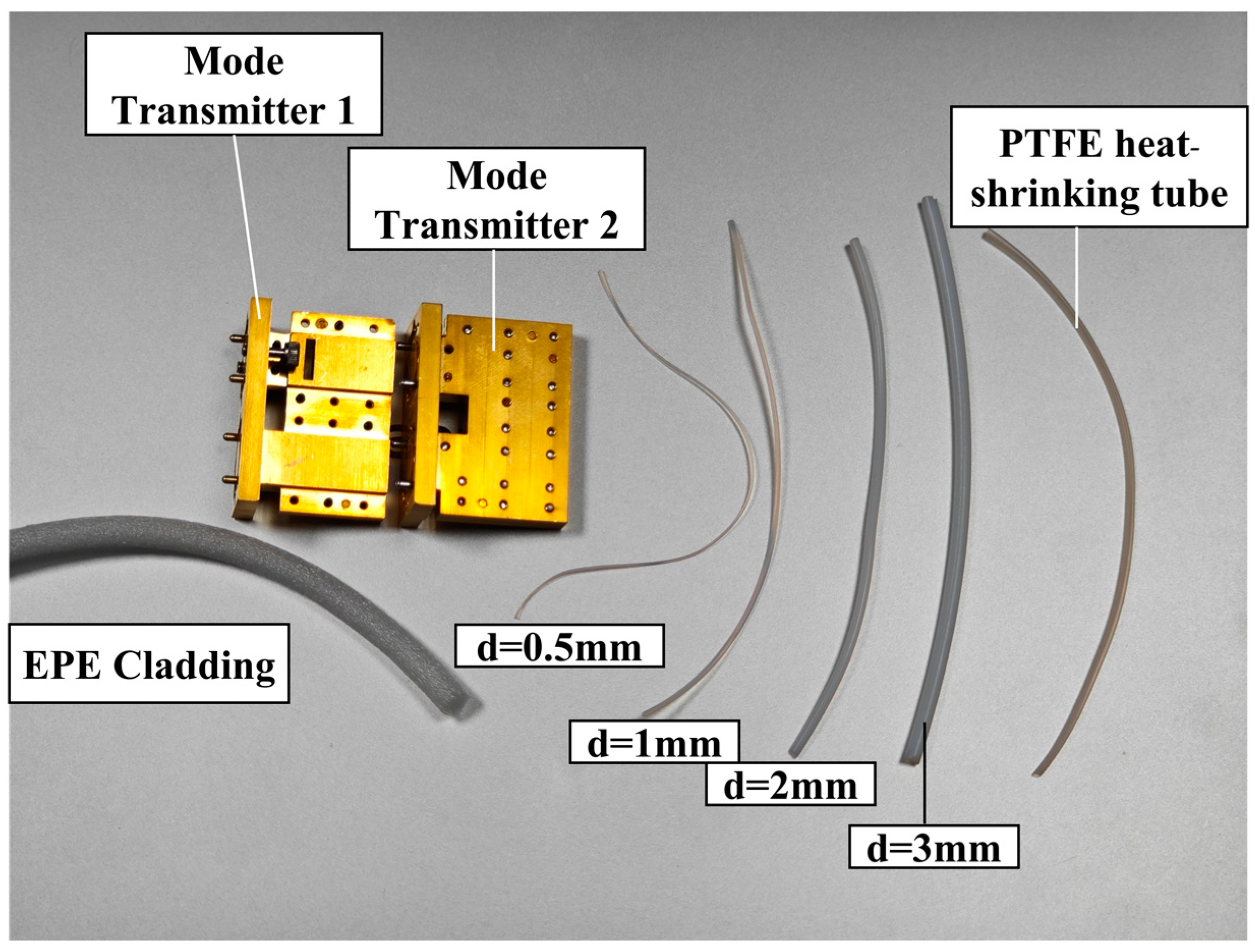
4.1. Cladding
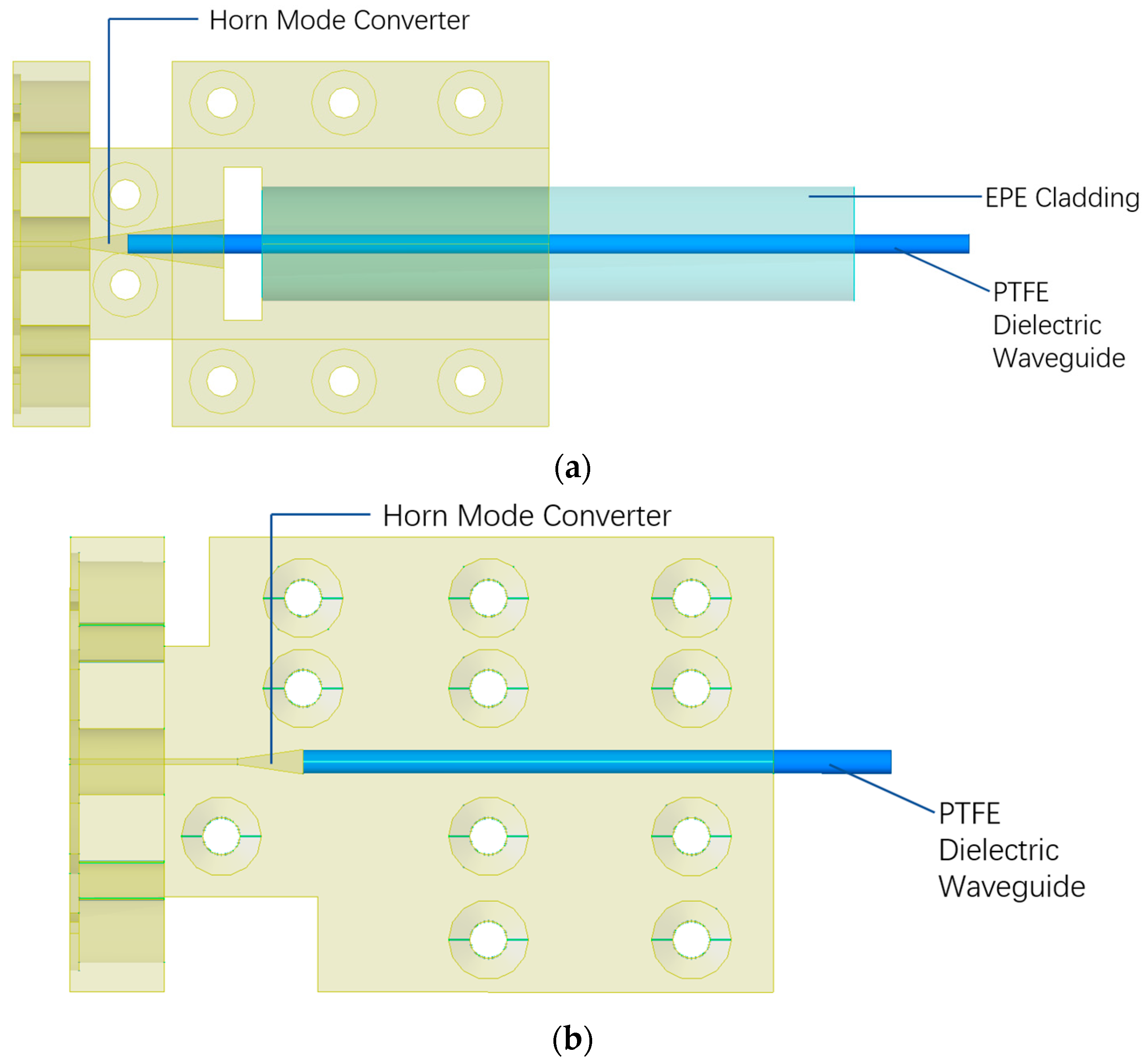
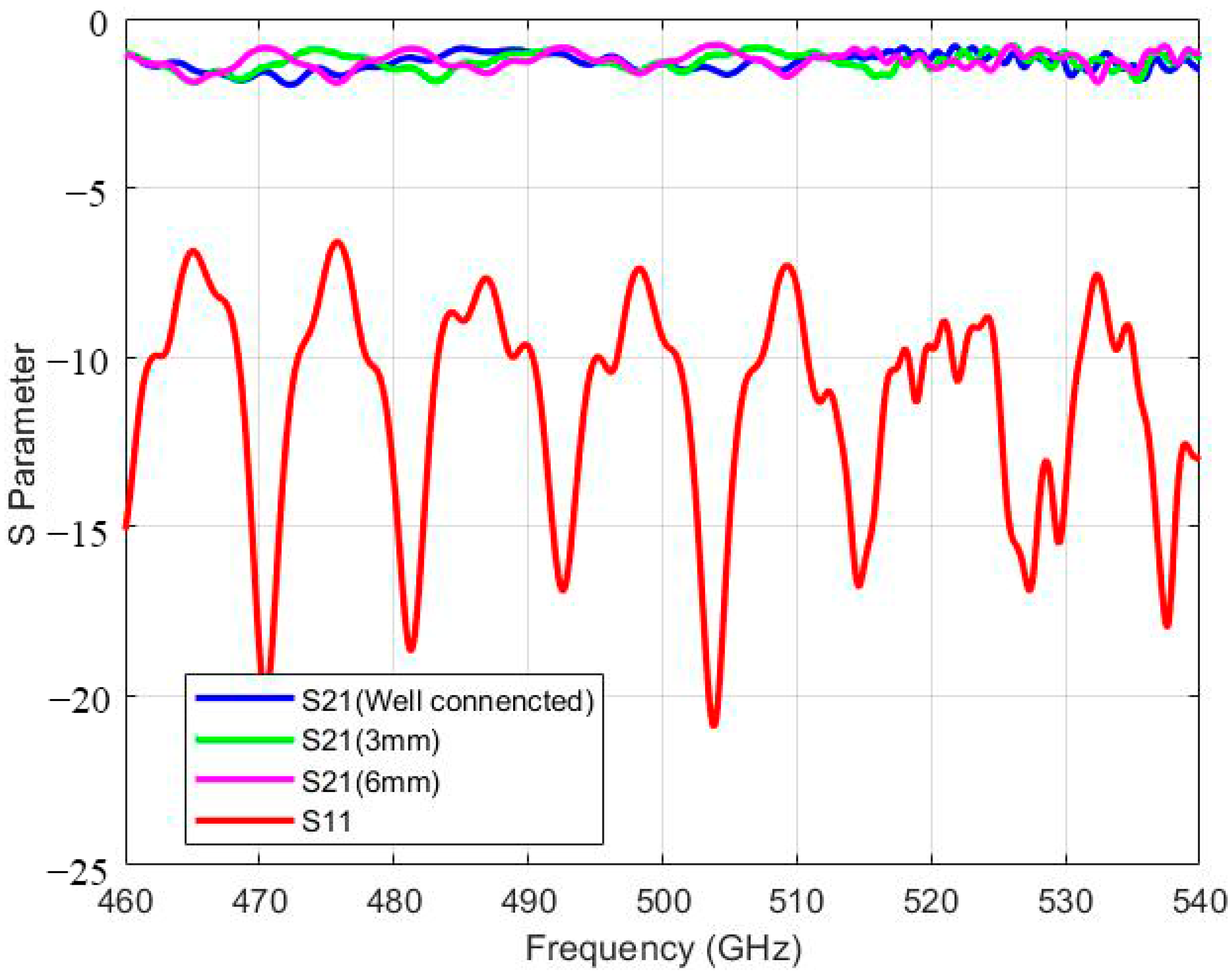
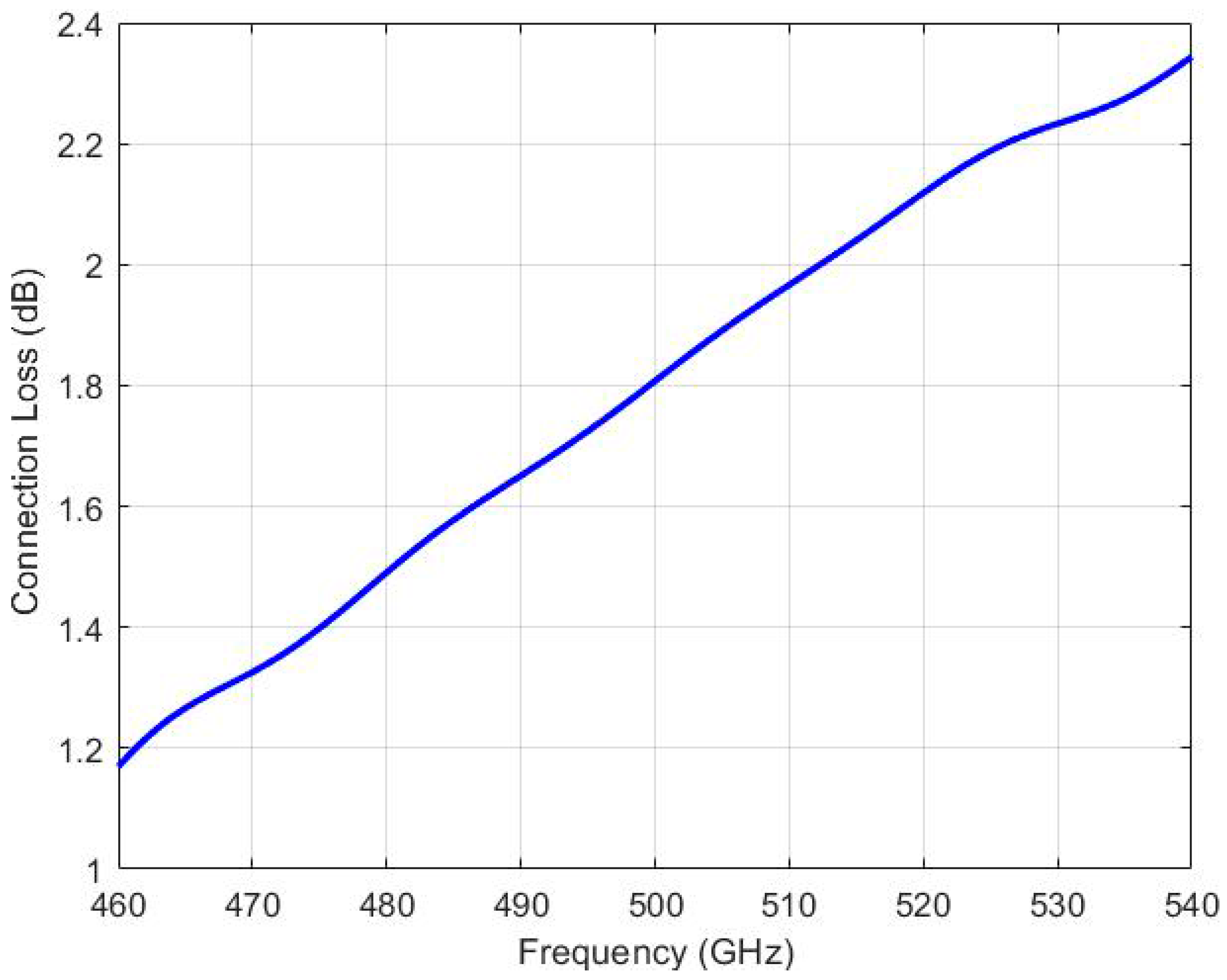
4.2. Metal Waveguide–Dielectric Waveguide Connection
4.3. Interconnection between Dielectric Waveguides
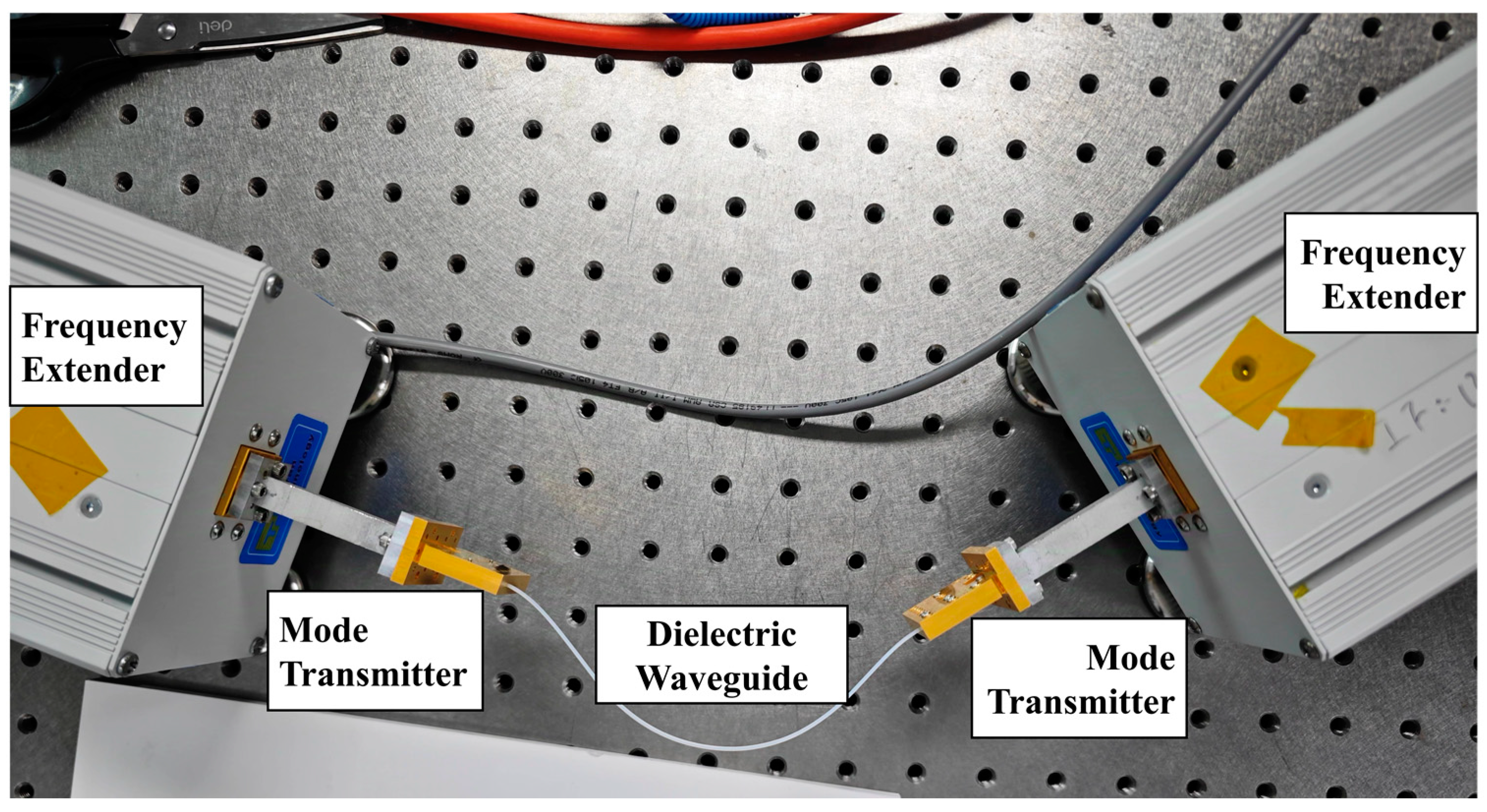
5. Measurement and Result
5.1. Measurement Settings
5.2. Transmission Loss
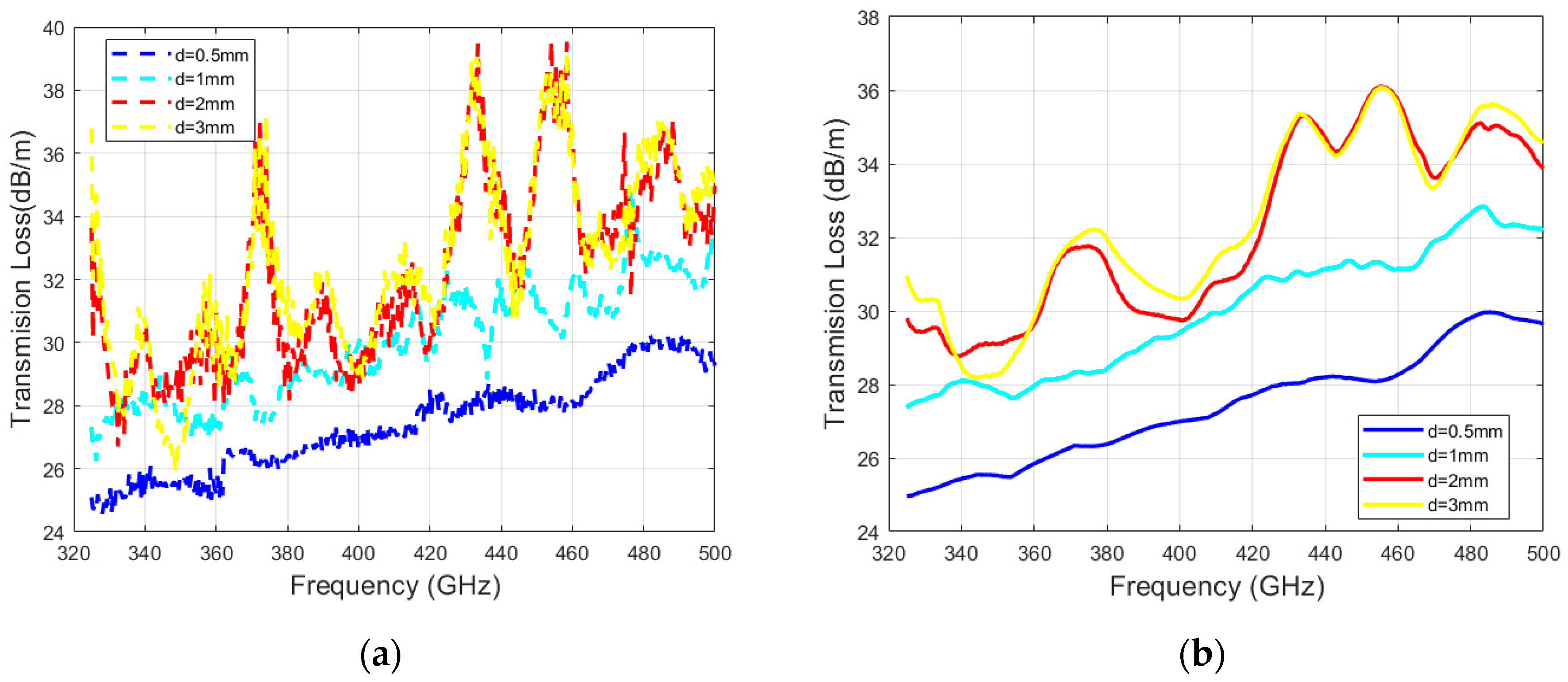
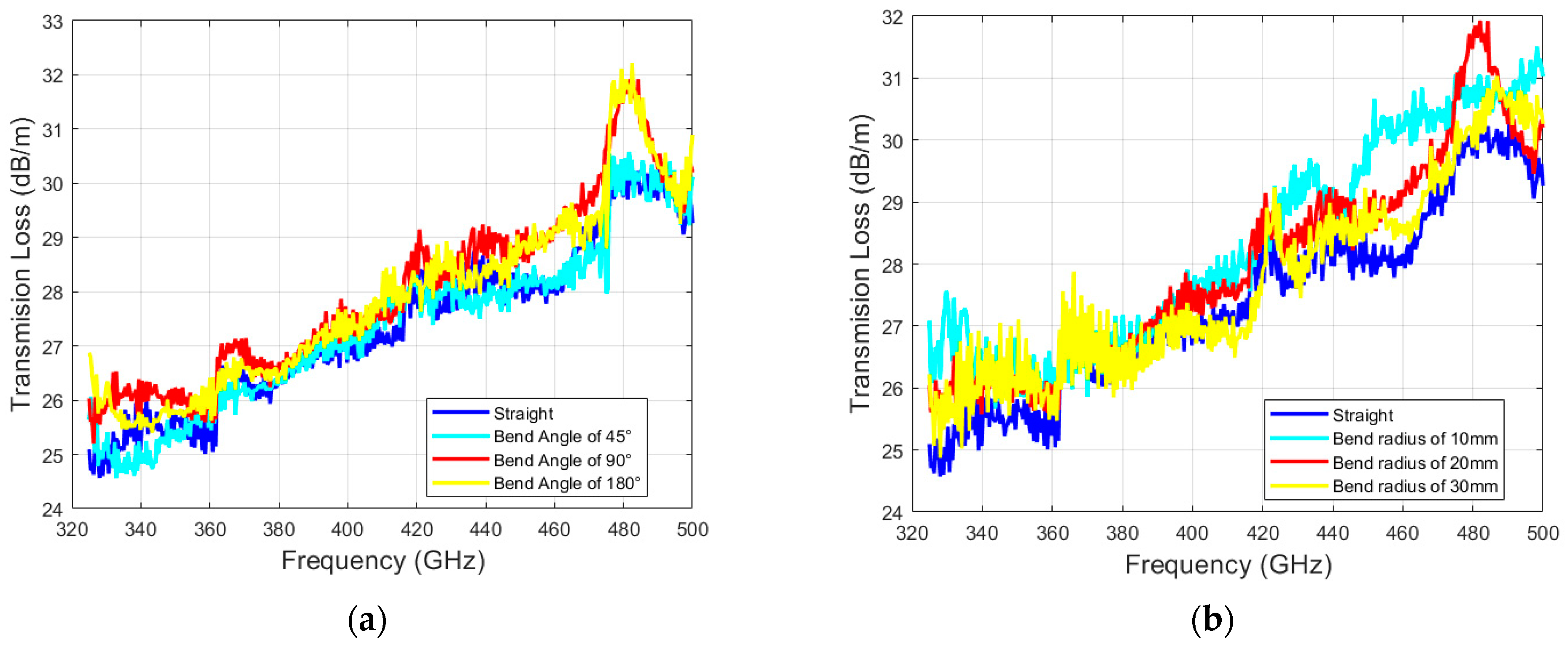
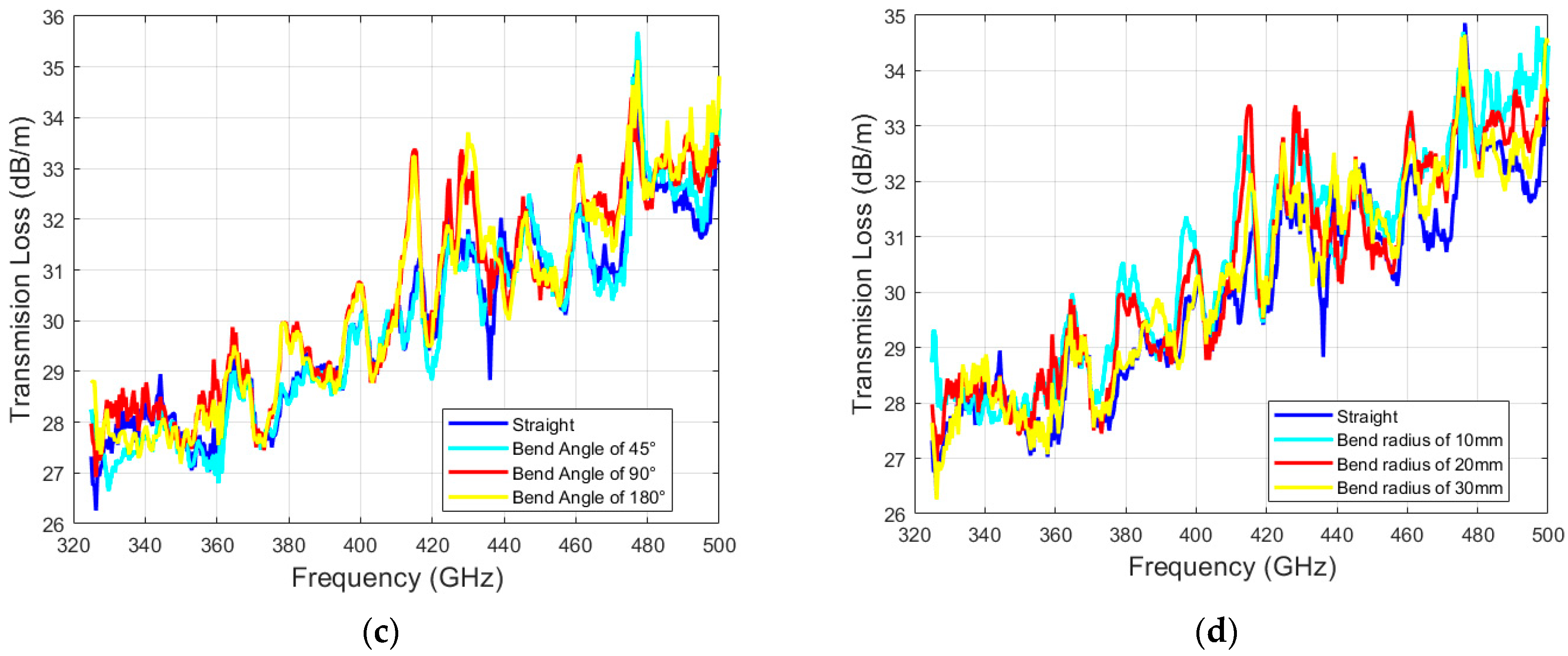
5.3. Bending Loss
5.4. Insertion Loss of the Mode Transmitter
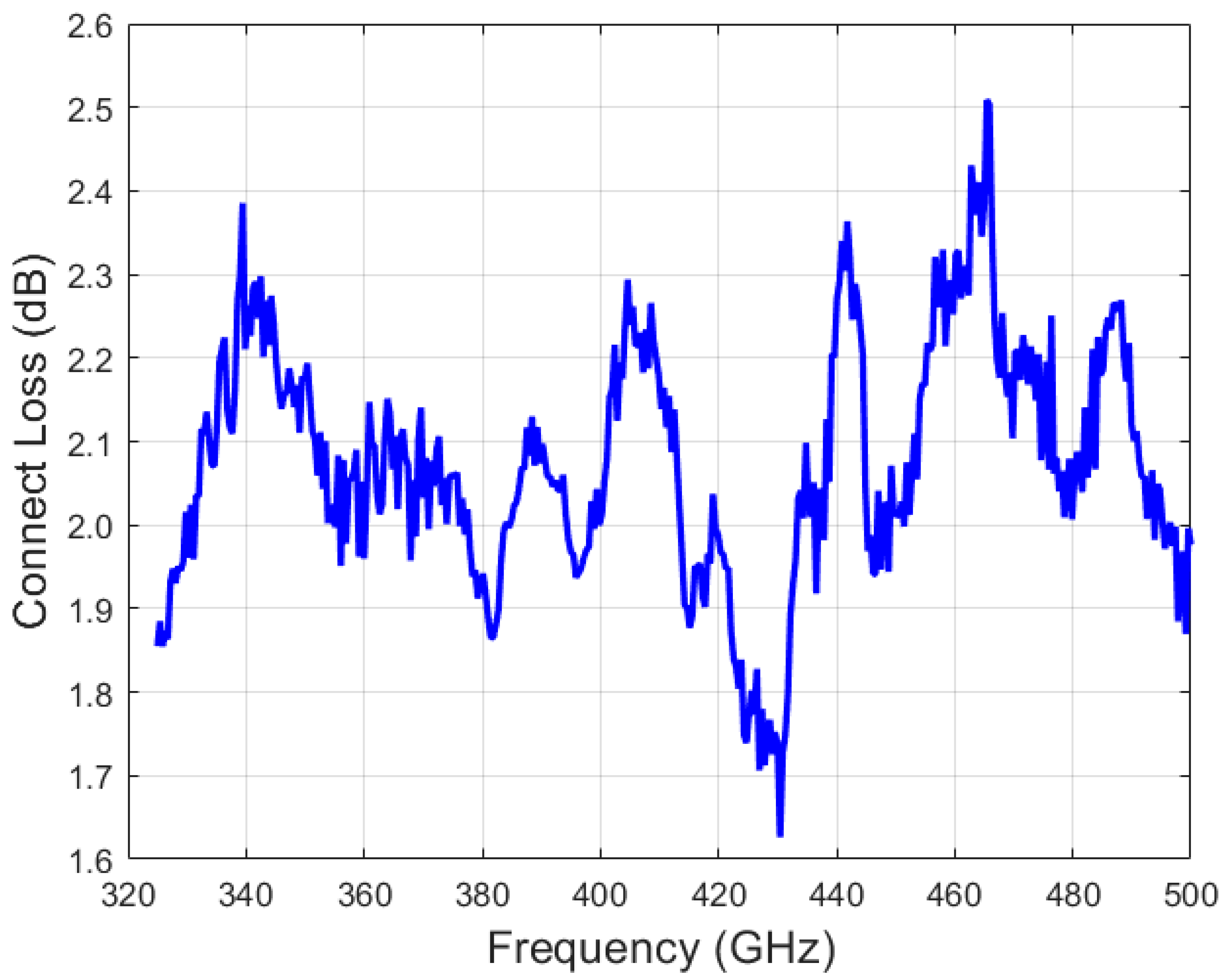
5.5. Interconnection between Dielectric Waveguides
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Siegel, P.H. Terahertz technology. IEEE Trans. Microw. Theory Tech. 2002, 50, 910–928. [Google Scholar] [CrossRef]
- Sleiman J, B. Terahertz Imaging and Spectroscopy: Application to Defense and Security in Front of the Examination Panel. Ph.D. Thesis, Université de Bordeaux, Bordeaux, French, 2016. [Google Scholar]
- Burford, N.M.; El-Shenawee, M.O.; Neal, C.B.O.; Olejniczak, K.J. Terahertz Imaging for Nondestructive Evaluation of Packaged Power Electronic Devices. Int. J. Emerg. Technol. Adv. Eng. 2014, 4, 395–401. [Google Scholar]
- Piesiewicz, R.; Kleine-Ostmann, T.; Krumbholz, N.; Mittleman, D.; Koch, M.; Schoebel, J.; Kurner, T. Short-Range Ultra-Broadband Terahertz Communications: Concepts and Perspectives. IEEE Antennas Propag. Mag. 2007, 49, 24–39. [Google Scholar] [CrossRef]
- Ducournau, G.; Szriftgiser, P.; Pavanello, F.; Peytavit, E.; Zaknoune, M.; Bacquet, D.; Beck, A.; Akalin, T.; Lampin, J.-F.; Lampin, J.-F. THz Communications using Photonics and Electronic Devices: The Race to Data-Rate. J. Infrared Millim. Terahertz Waves 2015, 36, 198–220. [Google Scholar] [CrossRef]
- Ducournau, G.; Pavanello, F.; Beck, A.; Tohme, L.; Blin, S.; Nouvel, P.; Peytavit, E.; Zaknoune, M.; Szriftgiser, P.; Lampin, J.F. High-definition television transmission at 600 GHz combining THzphotonics hotspot and high-sensitivity heterodyne receiver. Electron. Lett. 2014, 50, 413–415. [Google Scholar] [CrossRef]
- Katyba, G.M.; Zaytsev, K.I.; Dolganova, I.N.; Chernomyrdin, N.V.; Ulitko, V.E.; Rossolenko, S.N.; Shikunova, I.A.; Kurlov, V.N. Sapphire waveguides and fibers for terahertz applications. Prog. Cryst. Growth Charact. Mater. 2021, 67, 100523. [Google Scholar] [CrossRef]
- Barh, A.; Pal, B.P.; Agrawal, G.P.; Varshney, R.K.; Rahman, B.M.A. Specialty Fibers for Terahertz Generation and Transmission: A Review. IEEE J. Sel. Top. Quantum Electron. 2016, 22, 365–379. [Google Scholar] [CrossRef]
- Islam, M.S.; Cordeiro, C.M.; Franco, M.A.; Sultana, J.; Cruz, A.L.; Abbott, D. Terahertz optical fibers. Opt. Express 2020, 28, 16089–16117. [Google Scholar] [CrossRef]
- Mitrofanov, O.; James, R.; Fernández, F.A.; Mavrogordatos, T.K.; Harrington, J.A. Reducing transmission losses in hollow THz waveguides. IEEE Trans. Terahertz Sci. Technol. 2011, 1, 124–132. [Google Scholar] [CrossRef]
- Geiger, M.; Hitzler, M.; Saulig, S.; Iberle, J.; Hügler, P.; Waldschmidt, C. A 160-GHz radar with flexible antenna used as a sniffer probe. IEEE Sens. J. 2017, 17, 5104–5111. [Google Scholar] [CrossRef]
- Hondros, D.; Debye, P. Electromagnetische wellen in dielektrischen drahtes. Ann. Der Phys. 1910, 32, 465. [Google Scholar] [CrossRef]
- Agrawal, G.P. Fiber-Optic Communication Systems, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2002. [Google Scholar]
- Argyros, A. Microstructures in polymer fibres for optical fibres, terahertz waveguides, and fibre-based metamaterials. ISRN Opt. 2013, 2013, 785162. [Google Scholar] [CrossRef]
- Knight, J.C.; Broeng, J.; Birks, T.A.; Russel, P.S.J. Photonic band gap guidance in optical fibers. Science 1998, 282, 1476–1478. [Google Scholar] [CrossRef] [PubMed]
- Russell, P. Photonic crystal fibers. Science 2003, 299, 358–362. [Google Scholar] [CrossRef]
- Knight, J.C. Photonic crystal fibres. Nature 2003, 424, 847–851. [Google Scholar] [CrossRef]
- Mei, S.; Kong, D.; Wang, L.; Ma, T.; Zhu, Y.; Zhang, X.; He, Z.; Huang, X.; Zhang, Y. Suspended graded-indexporous core POF for ultra-flat near-zero dispersion terahertz transmission. Opt. Fiber Technol. 2019, 52, 101946. [Google Scholar] [CrossRef]
- Couny, F.; Benabid, F.; Roberts, P.J.; Light, P.S.; Raymer, M.G. Generation and photonic guidance of multi-octaveoptical-frequency combs. Science 2007, 318, 1118–1121. [Google Scholar] [CrossRef]
- Sultana, J.; Islam, M.S.; Cordeiro, C.M.B.; Dinovitser, A.; Koushik, M.; Ng, B.W.-H.; Abbott, D. Terahertzhollow core antiresonant fiber with metamaterial cladding. Fibers 2020, 8, 14. [Google Scholar] [CrossRef]
- Chen, L.J.; Chen, H.W.; Kao, T.F.; Lu, J.Y.; Sun, C.K. Low-loss subwavelength plastic fiber for terahertz waveguiding. Opt. Lett. 2006, 31, 308–310. [Google Scholar] [CrossRef]
- Dolatsha, N.; Saiz, N.; Arbabian, A. Fully packaged millimetre-wave dielectric waveguide with multimodal excitation. Electron. Lett. 2015, 51, 1339–1341. [Google Scholar] [CrossRef]
- Dey, U.; Hesselbarth, J. Millimeter-wave Chip-to-Chip Interconnect Using Plastic Wire Operating in Single and Dual Mode. In Proceedings of the 2018 IEEE/MTT-S International Microwave Symposium—IMS, Philadelphia, PA, USA, 10–15 June 2018; pp. 1549–1552. [Google Scholar] [CrossRef]
- Nallappan, K.; Cao, Y.; Xu, G.; Guerboukha, H.; Nerguizian, C.; Skorobogatiy, M. Dispersion-limited versus power-limited terahertz communication links using solid core subwavelength dielectric fibers. Photonics Res. 2020, 8, 1757–1775. [Google Scholar] [CrossRef]
- Li, Y.; Liao, S.; Xue, Q.; Che, W. Transmission Characteristics of Flexible Low-Loss Solid Circular Polymer Dielectric Waveguides for Sub-THz Applications. J. Infrared Millim. Terahertz Waves 2023, 44, 110–133. [Google Scholar] [CrossRef]
- Chen, H.; Chen, H.; Zhang, C.; Che, W.; Xue, Q. Sub-terahertz Dual-polarized Low-loss Transmission System Using COC-Based Dielectric Waveguide. J. Infrared Millim. Terahertz Waves 2024, 45, 141–158. [Google Scholar] [CrossRef]
- Zhu, H.T.; Wu, K. Complex permittivity measurement of dielectric substrate in sub-THz range. IEEE Trans. Terahertz Sci. Technol. 2020, 11, 2–15. [Google Scholar] [CrossRef]
- Yeh, C.; Shimabukuro, F.I. The Essence of Dielectric Waveguides; Springer: New York, NY, USA, 2008. [Google Scholar]
- Olszewski, J.; Szpulak, M.; Urbanczyk, W. Effect of coupling between fundamental and cladding modes on bending losses in photonic crystal fibers. Opt. Express 2005, 13, 6015–6022. [Google Scholar] [CrossRef]








| Ref. | Working Frequency (GHz) | Transmission Loss (dB/m) | Material |
|---|---|---|---|
| [22] | 75 | 3 | PE |
| [23] | 62–103 | 1.4–6 | HDPE |
| [24] | 128 | 1.01–2.4 | PTFE |
| [25] | 88–140 | 0.5–4.8 | PP |
| [26] | 90–100 | 2.33 | PTFE |
| Material | Dielectric Constant | Loss Tangent |
|---|---|---|
| PMMA | 2.59 | 0.02 |
| HDPE | 2.36 | 0.0003 |
| PC | 2.74 | 0.015 |
| PP | 2.26 | 0.0004 |
| PTFE | 2.07 | 0.0004 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Zhang, D.; Zhu, H. PTFE-Based Circular Terahertz Dielectric Waveguides. Photonics 2024, 11, 921. https://doi.org/10.3390/photonics11100921
Li H, Zhang D, Zhu H. PTFE-Based Circular Terahertz Dielectric Waveguides. Photonics. 2024; 11(10):921. https://doi.org/10.3390/photonics11100921
Chicago/Turabian StyleLi, Hao, Dehai Zhang, and Haotian Zhu. 2024. "PTFE-Based Circular Terahertz Dielectric Waveguides" Photonics 11, no. 10: 921. https://doi.org/10.3390/photonics11100921
APA StyleLi, H., Zhang, D., & Zhu, H. (2024). PTFE-Based Circular Terahertz Dielectric Waveguides. Photonics, 11(10), 921. https://doi.org/10.3390/photonics11100921





