Abstract
Coherent diffractive imaging is an optical methodology that encodes information about an object within the diffraction intensity. Here, we introduce a diffractive optical encryption system that utilizes multiple wavelengths and multiple distances, significantly expanding the size of the secret key space and enhancing the overall security of the system by incorporating these parameters as keys. The system adopts single optical path design, compact structure and is easy to implement, overcoming the disadvantage of single key space of traditional encryption system. This system can encrypt images into a series of diffraction intensity maps (i.e., ciphertexts), and exhibits a high sensitivity to minor variations in wavelength or distance during the process of decryption, showing excellent anti-cracking ability. Furthermore, the system also has considerable robustness, ensuring that the information still can be effectively recovered even in instances of partial loss. Numerical simulation results are presented to demonstrate feasibility and effectiveness of the proposed method. Our study provides novel concepts and methodologies to the advancement of optical encryption technology, while also offering significant technical assistance to the domain of information security.
1. Introduction
In recent years, with the rapid development of Internet data storage and transmission technology, information security has become the focus of modern society. Among this topic, digital images have emerged as significant media for information transmission on the Internet because of their convenient transmission and the substantial volume of information they can convey. Consequently, image encryption technology represents a significant area of investigation within the domain of information security. The optical encryption schemes apply optical technology for image encryption, including interference, diffraction, Fourier transform and a series of optical transformation processes, to encrypt the plaintext pictures to be transmitted into ciphertext. Optical processing approaches possess some marked advantages, including the capability for parallel processing, simple optical strategy and adjustable degrees of freedom. Parameters such as light amplitude, phase and wavelength can produce different secret keys during the interference and diffraction process of light, thus increasing the security and coding capacity of the system.
In 1995, Refregier and Javidi introduced the double random phase encoding technique (DRPE) as a method for image encryption within the framework of the 4f optical system [1]. This method involves using a random phase mask for modulation on the input surface and the spectral surface of the 4f optical system, which is performed on the Fourier transform domain. Further, there are some variations of this approach that have been reported, featuring the expansion of initial DRPE work into different transform domains, comprising the domains such as fractional Fourier transform [2,3] and Fresnel transform [4]. Recently, other optical encryption works have been studied intensely. For example, the interferometry method has been used in optical encryption systems [5,6], Tay et al. proposed a color image encryption scheme based on interference [7] and Zhu et al. proposed using polarized light for optical information encryption [8]. Due to the high complexity of interference-based structures, single path interferenceless method [9,10], also called coherent diffraction imaging (CDI), has attracted much attention in optical encryption [11,12]. J. H et al. reported the potential application of diffractive optics in free space optical systems based on engineering surfaces [13]. Despite reports of attacks against the diffraction imaging encryption system [14], no complex images or multiple images were attacked. Therefore, the research on multiple-image encryption techniques is more challenging and its recent progress is more inspiring. For example, Situ et al. proposed a multi-image encryption system for wavelength reuse [15], Shi et al. have reported that securing a complex-valued image is achievable for the 4f encryption system via ptychography [16], Wu and Clemente et al. encrypted multiple images based on computational ghost imaging [17], G. Luan et al. reported an optical double-image crosstalk-free encryption scheme that employs equal modulus decomposition and random masks [18] and Yi et al. demonstrated a binary-tree encryption strategy for multiple images to resist attacks [19]. Additionally, asymmetric encryption by optical Kerr nonlinearities [20], the angle multiplexing method [21] and optical orbital angular momentum (OAM) holography [22], have also emerged to improve the image security in succession.
In conventional multi-image encryption systems, a single variable (such as wavelength, distance or probe in ptychography) is usually used as the encryption parameter, which makes the key space relatively limited and it cannot withstand several types of attacks [23]. To overcome these weakness, here, we present a novel diffraction optical encryption system, referred to as DRPE, which utilizes multiple wavelengths and varying distances to enhance the encryption performance of multi-image encryption systems. The scheme, which works by utilizing multiple wavelengths and distances, generates the corresponding multiple ciphertext masks and private keys, and the classical random phase mask has also been introduced in our proposal. In this case, multiple distances refer to different optical paths that have varying diffraction distances. When compared with single variable-based encryption systems, our scheme greatly expands the key space, which can strengthen the security and prevent attacks. In addition, compared with the existing interference-based works, our encryption scheme is designed utilizing a single optical path, wherein a CCD camera captures multiple diffraction intensity patterns at various wavelengths and distances, which serve as the ciphertext. At the same time, the iterative phase retrieval algorithm is employed in the image decryption process to extract plaintext information from ciphertext. This algorithm is distinguished by its fast convergence and lack of stagnation problems, which significantly improves the efficiency of the decryption process. Simulation results and the safety performance analysis demonstrate the feasibility and effectiveness of the proposal.
2. Basic Principle
2.1. Encryption Process
The optical schematic diagram of the proposed encryption system is illustrated in Figure 1. This system is lensless, which can avoid the constraints associated with lens numerical aperture and the impact of optical aberrations. Consequently, the encryption system facilitates the acquisition of high-resolution and high-quality images. In contrast to a single-image encryption system that relies on diffraction imaging, the proposed encryption system employs a multi-channel architecture. In the encryption procedure, during the encryption process, each channel of the plaintext is encrypted by the multiple random phase masks. In each channel, plane waves of different wavelengths are used to illuminate the original plaintext image at different positions of the optical axis, so as to obtain the ciphertext at different diffraction distances. In order to address the challenges posed by the stagnation of iterative algorithms during the decryption process, which adversely affects the quality of decrypted images, we simultaneously select three wavelengths and two diffraction distances as secret keys. This approach enhances the key space and increases the data redundancy of the ciphertext, thereby enabling the system to recover high-quality plaintext images during decryption. As shown in Figure 1b, let the distribution of the images to be encrypted be , RPM1 and RPM2 be the random phase masks in the encryption process and, respectively, and represent the recording planes at different diffraction distances. Considering the propagation of light in free space, the diffraction propagation between the input plane, the RPM plane and the recording plane can be expressed by Fresnel’s approximation [24].
where denotes light wavelength, denotes the wave number and d denotes the distance of the axial diffraction propagation. For the purpose of simplifying the formula, Fr is used to represent Fresnel diffraction transmission. The plaintext images passing through diffraction transmitted at different distances after modulation by two random phase masks are recorded for their intensity distribution by the CCD. The recorded diffraction intensity distributions can be expressed as:
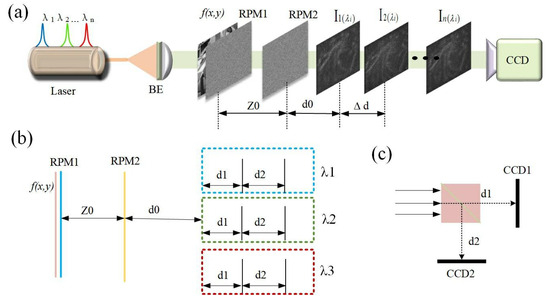
Figure 1.
(a) The schematic of the proposed encryption system. (b) The flowchart of obtaining ciphertext. (c) The BS used to avoid mechanical errors.
Here, n = 1, 2, 3; i = 1, 2, i.e., When the wavelength of light and the diffraction distance are systematically varied, the CCD records a series of corresponding diffraction intensity maps, which serve as the ciphertext within the encryption framework. This process effectively finalizes the encryption of the image file, with the secret key comprising the associated diffraction distance, random phase mask and wavelength. Furthermore, to mitigate errors arising from mechanical movements, the optical configuration can be adopted as shown in Figure 1c. In this configuration, a beam splitter is employed to divide the light, after which two CCD cameras are strategically placed on separate recording planes. This arrangement can simultaneously capture diffraction images at different distances.
2.2. Decryption Process
According to the optical path design of the encryption system, a total of six diffraction intensity maps of the images to be encrypted are collected as ciphertexts. In the decryption process, the iterative recovery algorithm is used to extract the encrypted image from the ciphertext. The detailed decryption process is as follows:
Step 1: A random complex amplitude is generated as the initial value of the original image By substituting into the above encryption system, a corresponding ciphertext is obtained whose intensity distribution is as follows:
Step 2: The recorded intensity was used as the amplitude constraint, then
Step 3: The updated is reverse transmitted to the original image plane to obtain the updated :
where and , respectively, denote the complex conjugation of the random phase mask.
Step 4: Repeat steps 2–3 until all the obtained diffraction patterns have been incorporated into the iterative operation as amplitude constraints, then, an iterative process is completed.
Step 5: Repeat steps 2–4 until a fixed number of iterations have been completed or the iteration error is less than a specified threshold. The iterative error is calculated as follows:
where denotes the ciphertext after one iteration of . The decryption process is a gradual convergence process, meaning that the error decreases gradually during each iteration. When the iteration error is less than a certain threshold (e.g., 0.0001), the iteration process can be terminated. According to the above decryption algorithm, the flow chart of the decryption process of the system is shown in Figure 2.
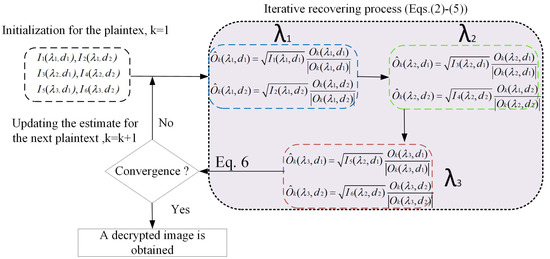
Figure 2.
The flowchart of the decryption process.
As can be seen from the flow chart in the above decryption process, not only two phase mask plates RPM1 and RPM2 are required, but also the diffraction distance and wavelength need to be simultaneously used to complete the decryption. Combining the diffraction distance and working wavelength into the encryption system during the diffraction process can increase the key space and improve the security of the system.
3. Simulation Verification
In order to verify the feasibility and effectiveness of the proposed encryption scheme, a simulation analysis was conducted based on matlab simulation. Here, the grayscale image with pixel size of 512 × 512 was taken as the original encrypted image, as shown in Figure 3a, and the pixel size of the CCD is 5.5 μm. The wavelengths for three channels are set at 457 nm, 532 nm and 633 nm, and the two diffraction distances are designated as d1 = 20 cm and d2 = 23 cm, respectively. In the numerical experiment, the CCD is placed on the recording plane at different distances according to the optical path configurations illustrated in Figure 1. When the working wavelengths are changed, the diffraction pattern of the wavelength at different diffraction distances (i.e., the ciphertext) can be recorded at the same time. It is worth noting that in the image encryption process of this system, RPM1 and RPM2 serve as phase masks that are randomly distributed within the range of 0–2, as shown in Figure 3b,c. In this case, PRM1 is positioned subsequent to the encrypted image, with a separation distance of Z0 = 100 mm between RPM1 and RPM2. Consequently, in our optical diffraction encryption system, a total of six diffraction patterns (Figure 3(d1–f2)) are generated as the ciphertext, including two recording distances and three wavelengths. It is evident that the information contained within the encrypted image has been entirely obscured within the ciphertext.

Figure 3.
Simulation results based on a multiple wavelengths and multiple distances DPRE system. (a) Plaintext image to be encrypted. (b) RPM1. (c) RPM2. (d1–f2) Ciphertext image at different wavelengths and distances.
The decryption procedure involves utilizing the ciphertext images to retrieve the plaintext information in accordance with the proposed iterative phase inversion algorithm. Figure 4a shows the decrypted images of plaintext with the correct secret keys. As can be seen, the content of original image can be recovered with high quality. Since the decryption quality of the image cannot be accurately judged by the naked eye, the correlation coefficient (i.e., CC) can be used to evaluate the similarity between the plaintext and the decrypted image. The calculation formula is as follows:
where and , respectively, denote the original image and the decrypted image, denotes the cross-covariance of and , and denotes standard deviation. A correlation coefficient value approaching 1 indicates a greater similarity between the decrypted image and the original image, thereby reflecting high robustness of the image (i.e., the better the recovery quality is). In addition, to measure the quality of decryption images in the iterative process, we define the sum of square error (SSE) as:
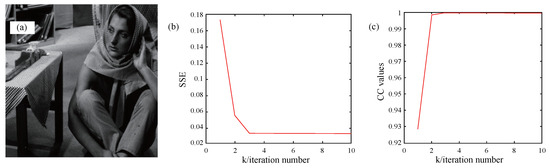
Figure 4.
Decrypted images. (a) Recovered image. (b) The SSE curve varies with the number of iterations. (c) The CC values with the number of iterations.
As can be seen from Figure 4a–c of the decryption results, the encryption system only needs dozens of iterations to recover high-quality decrypted images. The above simulation results show that the encryption system has the characteristics of fast iteration speed and high recovery accuracy.
4. Analysis and Discussion
Many simulations have been performed to check the validity of our proposed encryption system. Now we will proceed to evaluate the security of this scheme. In our approach, we incorporate additional key parameters that are represented in a two-dimensional framework of wavelength and distance into the existing double random phase coding encryption system. Consequently, we focus on analyzing the sensitivity of the new keys (i.e., distance and wavelength) to verify the safety of the system. When testing the sensitivity of one key parameter, we will make a tiny alteration to its correct value while other keys hold their correct values.
Firstly, the decryption effect of the wavelength offset is analyzed. Figure 5a,b represent the decrypted image and the corresponding CC values during the decryption process when one of the wavelengths is offset by nm. The correlation coefficient between the final recovered image and the original image is determined to be 0.61, indicating that the plaintext information cannot be accurately retrieved with a high degree of accuracy. As seen in Figure 5c, the CC value varies with different wavelength offsets. The CC values approximate to 1 only when the wavelength has no deviation, but they decrease sharply when the wavelength deviates from the correct value. It can be seen that the larger the wavelength offset, the worse the decryption effect. Similarly, we also analyzed the effect of the deviation in distance on the decryption process. Figure 5d,e present the decrypted image and the corresponding CC values during the decryption process when a distance is offset by mm. In this case, a significant portion of the information contained within the ciphertext is irretrievable. Figure 5f depicts the CC value of the recovered image at different distances shifts. It is evident that minor distance discrepancies can lead to considerable noise in the reconstructed image, thereby significantly deteriorating the signal-to-noise ratio of the resultant image. The simulation results indicate that the use of an incorrect key can significantly effect the quality of decrypted images, and their CC value curve shapes indicated that the tested scheme is sensitive to deviations of these keys. As the deviation of the secret key error increases, the efficiency of the decryption process decreases. Even slight variations in the secret key may impede the successful retrieval of clear plaintext images, indicating that the innovative secret key derived from wavelength and distance provides improved security.
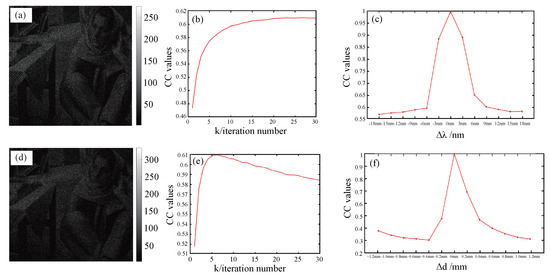
Figure 5.
Simulation result: (a,b) The decrypted images and the CC values varying with the number of iterations when the wavelength offset is nm. (c) The CC values curves with different wavelengths offsets. (d,e) The decrypted images and the CC values varying with the number of iterations when the distance offset = 0.2 mm. (f) The CC values curves with different distances of offsets.
Considering that some ciphertext images will suffer noise or occlusion attacks during ciphertext transmission, here, in order to evaluate the feasibility of the proposed method, we simulated the occlusion effect by cutting out the ciphertext by different percentages. The original ciphertext image is clipped with 10%, 20%, 30% and 50% occlusion, as shown in Figure 6a–d, respectively, and then these ciphertext images with different proportions of occlusion employed the decryption process. The corresponding decryption results are shown in Figure 6(a1–d1), respectively. It can be seen from the above recovered results that a greater degradation in the quality of the recovered images correlates with an increased proportion of missing ciphertext information. Although the loss of information in ciphertext images will reduce the quality of the decrypted image, most of the plaintext information can still be recovered, which shows that the encryption system proposed in this paper has a good performance in robustness. In addition, we also investigated the effects of noise attacks on the encryption system by adding salt and pepper noise and Gaussian noise. Figure 7a,c show the ciphertexts with salt and pepper noise and Gaussian noise added, respectively. And the corresponding CC values for the reconstruction results are 0.92 and 0.93, respectively. All the decrypted images in the figure are distinguishable. Therefore, the proposed method is robust against salt and pepper noise and Gaussian noise.

Figure 6.
Robustness verification results: (a–d) Ciphertext images with 10%, 20%, 30% and 50% occlusion. (a1–d1) Decrypted images from the above ciphertexts.

Figure 7.
(a,b) The ciphertext with salt and pepper noise added and its decrypted image. (c,d) The ciphertext with Gaussian noise added and its decrypted image.
5. Conclusions
In conclusion, we propose a diffractive optical encryption system based on multiple wavelengths and multiple distances, which is a multi-variable optical encryption system based on a single optical path of coherent diffraction. Specifically, the wavelengths, the phase masks and the distances serve as the key space, greatly improving the security of the encryption system. For the encryption, the ciphertext images are generated by combining multiple diffraction patterns corresponding to various wavelengths and distances, utilizing a diffraction-imaging system. In the decryption process, only when all the keys are correct, can the original secret image be successfully extracted by an iterative retrieval algorithm. Here, in our study, three different illuminating wavelengths and two diffraction distances serve as additional keys to significantly reinforce the security. Numerical simulation results validate the advantages of the proposal. The proposal scheme is novel and has three major advantages. First, our proposal has a larger key space and key complexity, if more wavelengths and positions are used in the proposed encryption system. Second, our setup is single path. No reference wave is required, making the method easy to implement in practical experiments. Third, the newly introduced secret keys exhibit a high degree of sensitivity, thereby substantially augmenting the security of the encryption system. This scheme is immune to information leakage and different types of attacks. In addition, it should be noted that there is a trade-off between the accuracy of decryption and the efficiency of decryption in multiple-image encryption systems. Therefore, future research should focus on the development of single-shot techniques to enhance the efficiency of these encryption systems.
Author Contributions
Conceptualization, Y.W. and H.D.; methodology, Y.W. and H.D.; software, Y.W.; validation, Y.L.; investigation, Y.W. and H.D.; resources, Y.L.; data curation, Y.W.; writing—original draft preparation, H.D.; writing—review and editing, Y.L. and Y.H.; visualization, H.D. and Y.W.; supervision, Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China under Grant 62305220 and Shanghai Sailing Program 23YF1429300.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available on request from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Refregier, P.; Javidi, B. Optical image encryption based on input plane and Fourier plane random encoding. Opt. Lett. 1995, 20, 767–769. [Google Scholar] [CrossRef] [PubMed]
- Unnikrishnan, G.; Joseph, J.; Singh, K. Optical encryption by double-random phase encoding in the fractional Fourier domain. Opt. Lett. 2000, 25, 887–889. [Google Scholar] [CrossRef] [PubMed]
- Sui, L.; Duan, K.; Liang, J.; Hei, X. Asymmetric double-image encryption based on cascaded discrete fractional random transform and logistic maps. Opt. Express 2014, 22, 10605–10621. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Xu, W.; Wang, S.; Wu, S. Asymmetric optical cryptosystem based on modulus decomposition in Fresnel domain. Opt. Commun. 2017, 402, 302–310. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, B. Asymmetric optical Optical image encryption based on interference. Opt. Lett. 2008, 33, 2443–2445. [Google Scholar] [CrossRef]
- Li, J.; Li, J.; Shen, L.; Pan, Y.; Li, R. Optical image encryption and hiding based on a modified Mach-Zehnder interferometer. Opt. Express 2014, 22, 4849–4860. [Google Scholar] [CrossRef] [PubMed]
- Tay, C.; Quan, C.; Chen, W.; Fu, Y. Color image encryption based on interference and virtual optics. Opt. Laser Tech. 2010, 42, 409–415. [Google Scholar] [CrossRef]
- Zhu, N.; Wang, Y.; Liu, J.; Xie, J.; Zhang, H. Optical image encryption based on interference of polarized light. Opt. Express 2009, 17, 13418–13424. [Google Scholar] [CrossRef]
- Yang, L.; Yang, J.; Wang, H.; Wang, Y.; Huang, T.; Zhang, W.; Di, J.; Zhong, L. Single shot interferenceless coded aperture correlation holography via a learnable Wiener deconvolution network. Opt. Lasers Eng. 2024, 178, 108227–108232. [Google Scholar] [CrossRef]
- Yang, L.; Yang, J.; Huang, T.; Rosen, J.; Wang, Y.; Wang, H.; Lu, X.; Zhang, W.; Di, J.; Zhong, L. Accelerating quad Airy beams-based point response for interferenceless coded aperture correlation holography. Opt. Lett. 2024, 49, 4429–4432. [Google Scholar] [CrossRef]
- Chen, W.; Chen, X.; Sheppard, C.J.R. Optical image encryption based on diffractive imaging. Opt. Lett. 2010, 35, 3817–3819. [Google Scholar] [CrossRef] [PubMed]
- Qin, Y.; Wang, Z.; Gong, Q. Diffractive-imaging-based optical image encryption with simplified decryption from single diffraction pattern. Appl. Opt. 2014, 53, 4094–4099. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Mengu, D.; Tzarouchis, D.C.; Edwards, B.; Engheta, N.; Ozcan, A. Diffractive optical computing in free space. Nat. Commun. 2024, 15, 1525–1545. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Xiao, Y.; Chen, W. Vulnerability to machine learning attacks of optical encryption based on diffractive imaging. Opt. Lasers Eng. 2020, 125, 105858. [Google Scholar] [CrossRef]
- Situ, G.; Zhang, J. Multiple-image encryption by wavelength multiplexing. Opt. Lett. 2005, 30, 1306–1308. [Google Scholar] [CrossRef]
- Shi, Y.; Li, T.; Wang, Y.; Gao, Q.; Zhang, S.; Li, H. Optical image encryption via ptychography. Opt. Lett. 2013, 38, 1425–1427. [Google Scholar] [CrossRef]
- Clemente, P.; Durán, V.; Torres-Company, V.; Tajahuerce, E.; Lancis, J. Optical encryption based on computational ghost imaging. Opt. Lett. 2010, 35, 2391–2393. [Google Scholar] [CrossRef]
- Luan, G.; Quan, C. Optical phase-truncation-based double-image encryption using equal modulus decomposition and random masks. Sci. Rep. 2024, 14, 7155–7159. [Google Scholar] [CrossRef]
- Yi, J.; Tan, G. Binary-tree encryption strategy for optical multiple-image encryption. Appl. Opt. 2016, 55, 5280–5291. [Google Scholar] [CrossRef]
- César, C.; Araceli, V.M.; Hilario, M.; David, T.; Gina, G.; Lizbeth, M.C.; Carlos, T. Asymmetric encryption by optical Kerr nonlinearities exhibited by electrochromic NiO thin films. Opt. Express 2022, 30, 39849–39859. [Google Scholar]
- Chang, H.; Wang, Y.; Chen, C. Angle Multiplexing Optical Image Encryption in the Fresnel Transform Domain Using Phase-Only Computer-Generated Hologram. Photonics 2020, 7, 1. [Google Scholar] [CrossRef]
- Zhang, N.; Xiong, B.; Zhang, X.; Yuan, X. Holographic Encryption Applications Using Composite Orbital Angular Momentum Beams. Photonics 2022, 9, 605. [Google Scholar] [CrossRef]
- Zhang, Y.S.; Xiao, D.; Wen, W.Y.; Liu, H. Vulnerability to chosen-plaintext attack of a general optical encryption model with the architecture of scrambling-then-double random phase encoding. Opt. Lett. 2013, 38, 4506–4509. [Google Scholar] [CrossRef] [PubMed]
- Goodman, J.W. Introduction to Fourier Optics; Roberts and Company Publishers: Greenwood Village, CO, USA, 2005. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).