Simulation and Experimental Research of V-Crack Testing of Rail Surfaces Based on Laser Ultrasound
Abstract
1. Introduction
2. Theory and Numerical Simulation
2.1. Basic Principles
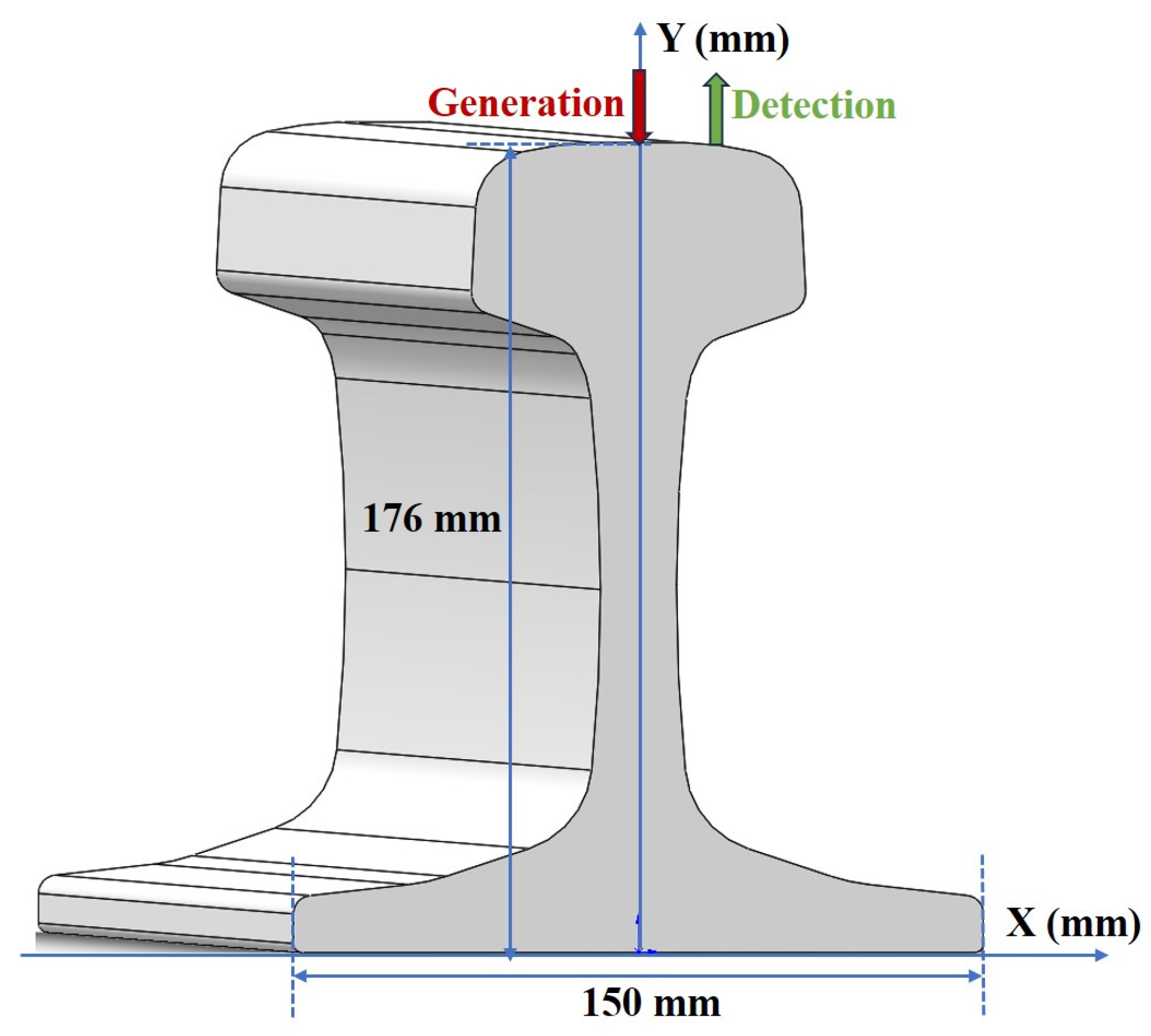
2.2. Numerical Simulation
3. Simulation Results and Analysis
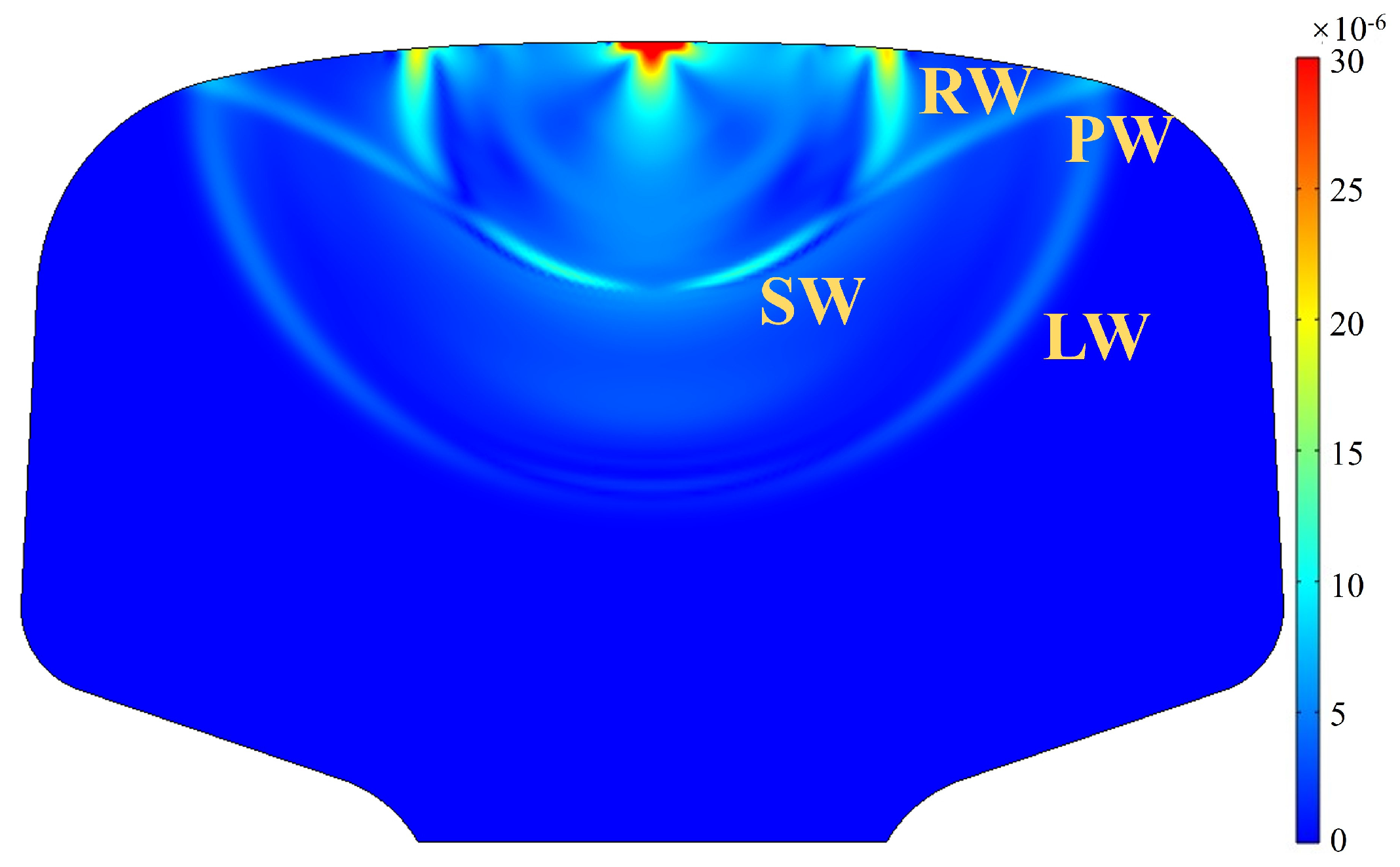
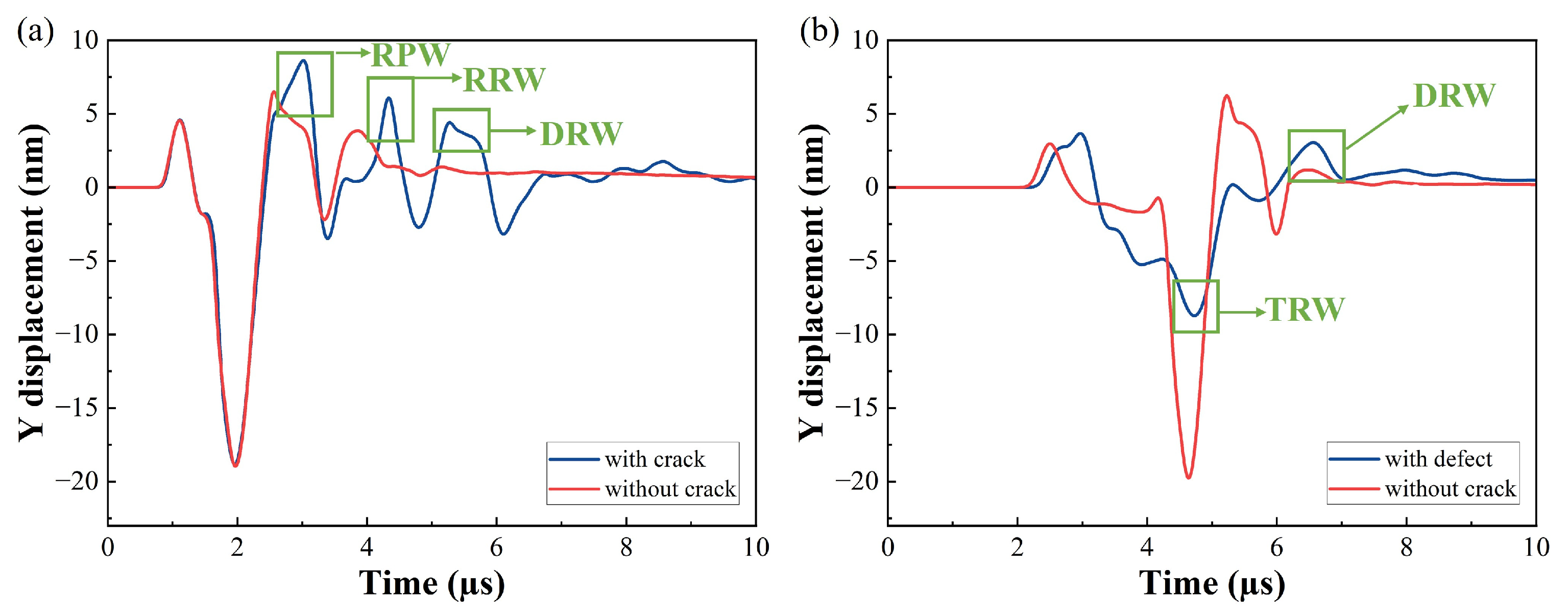
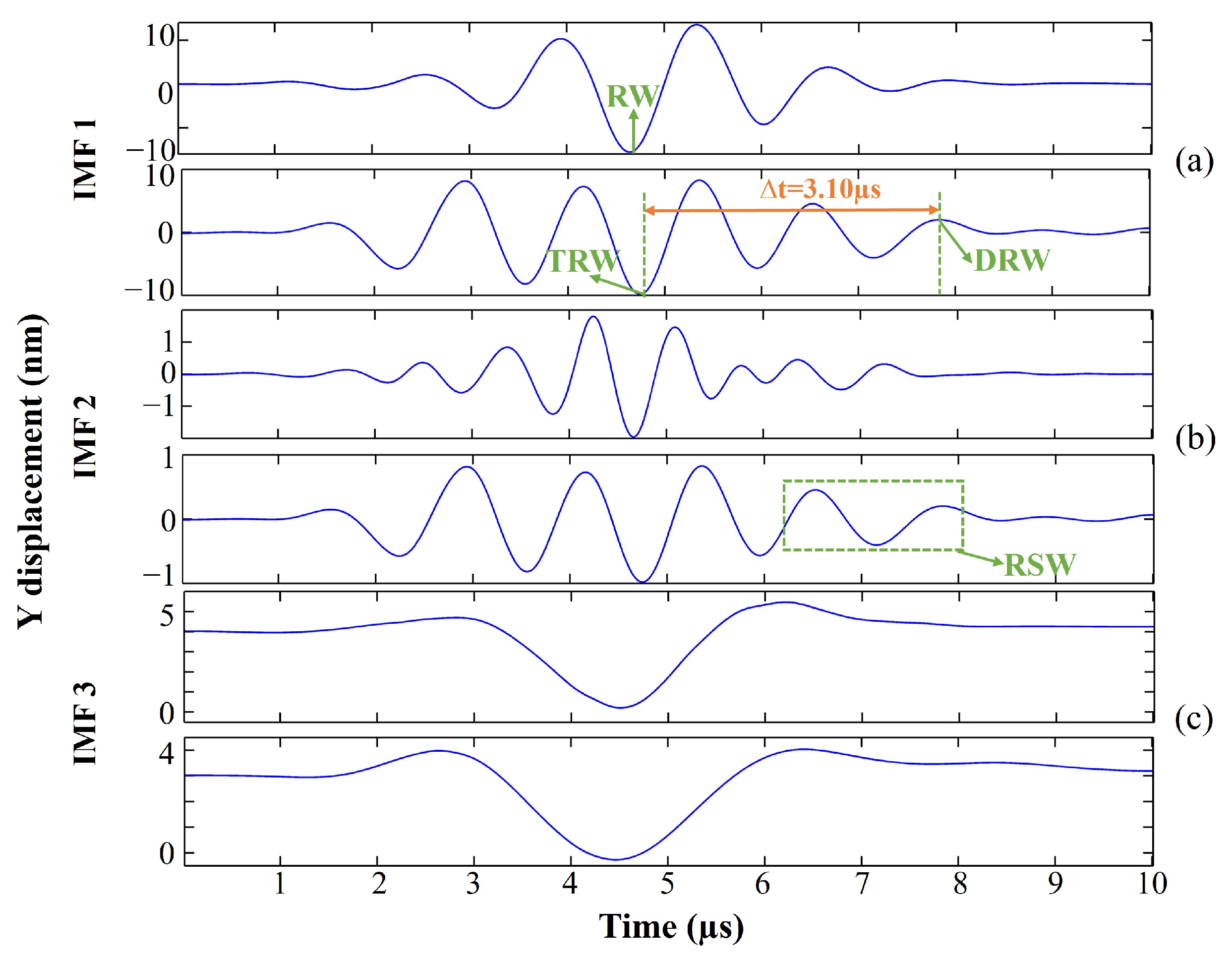
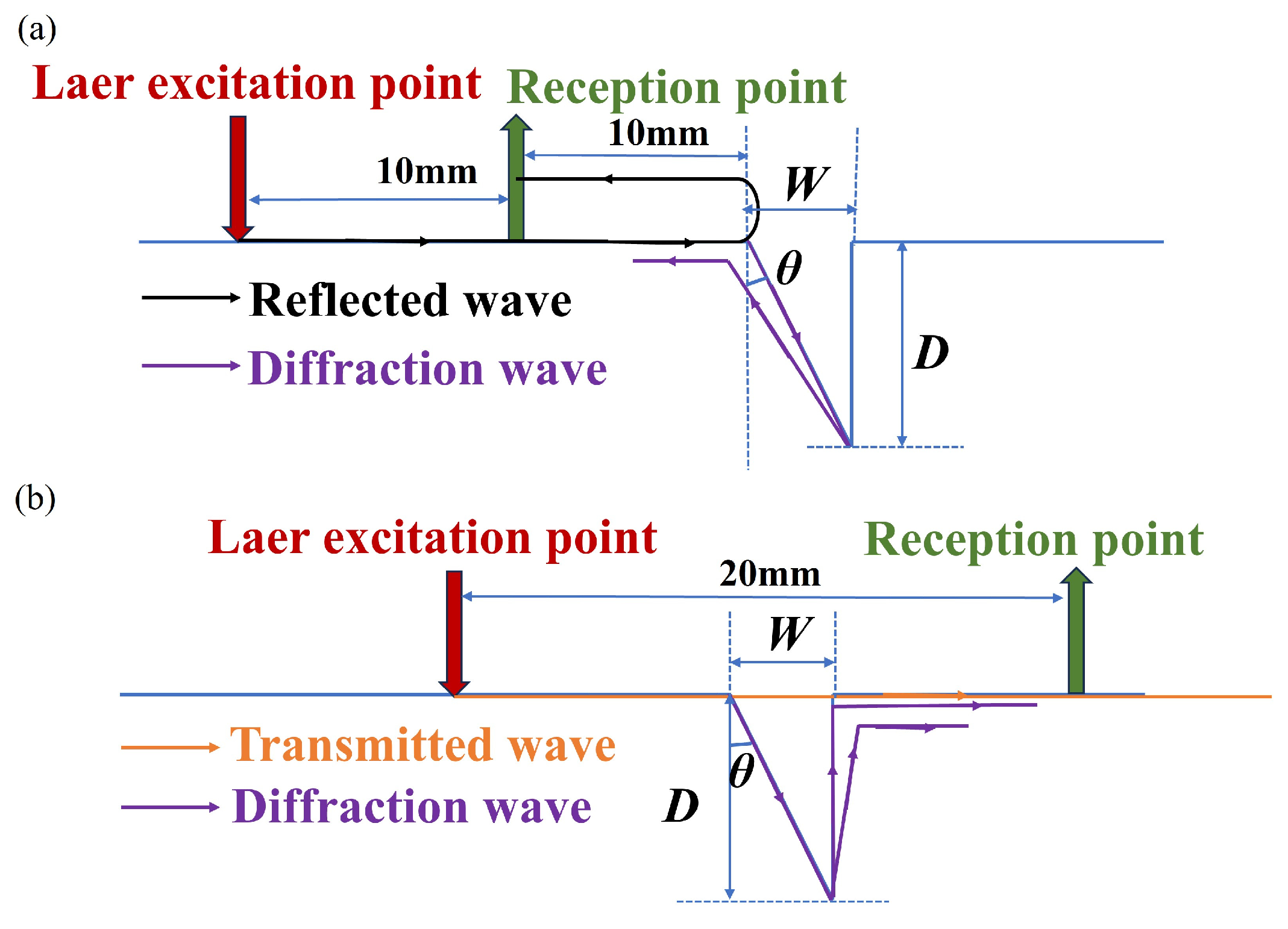
3.1. Determination of Crack Location
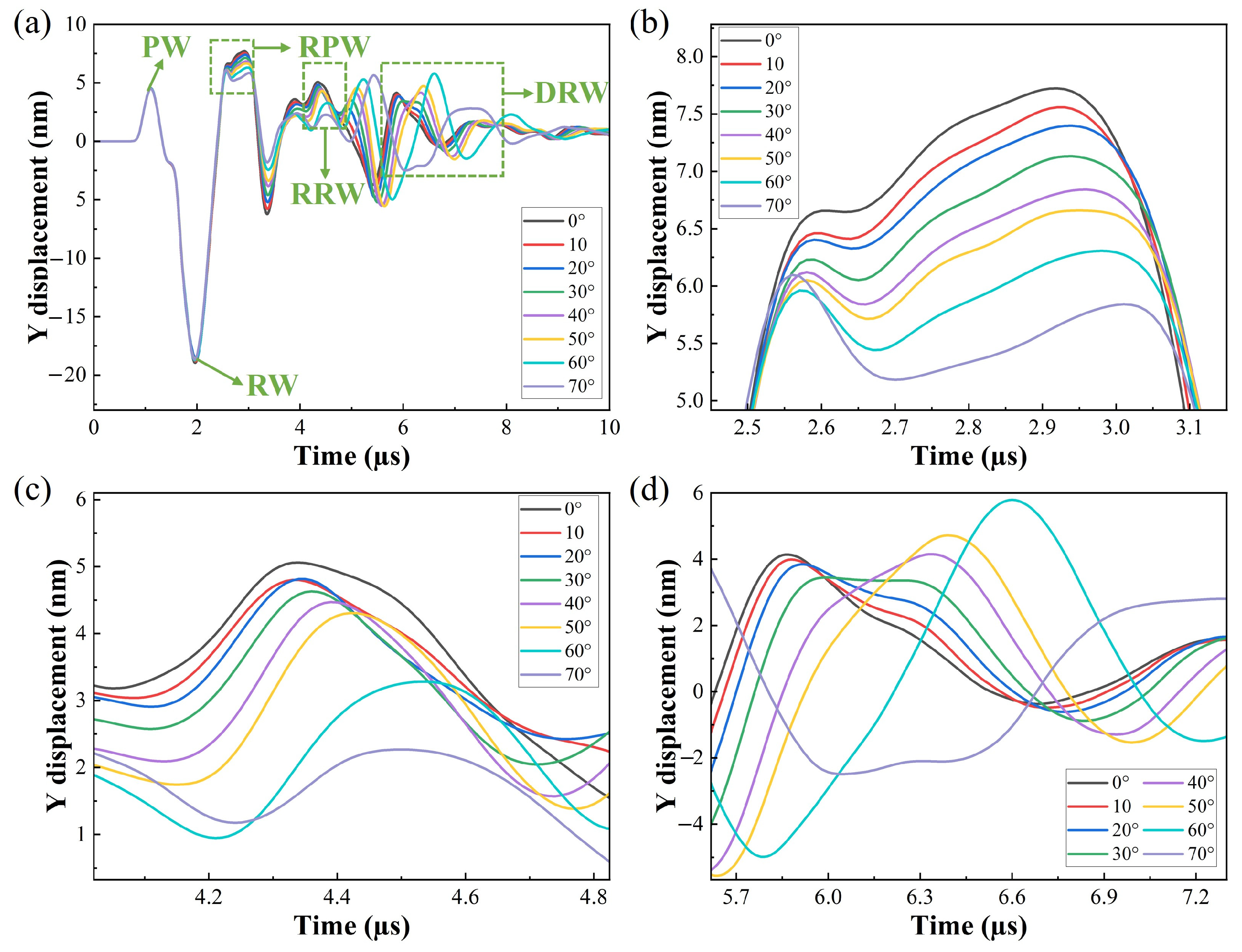
3.2. Crack Angle Detection
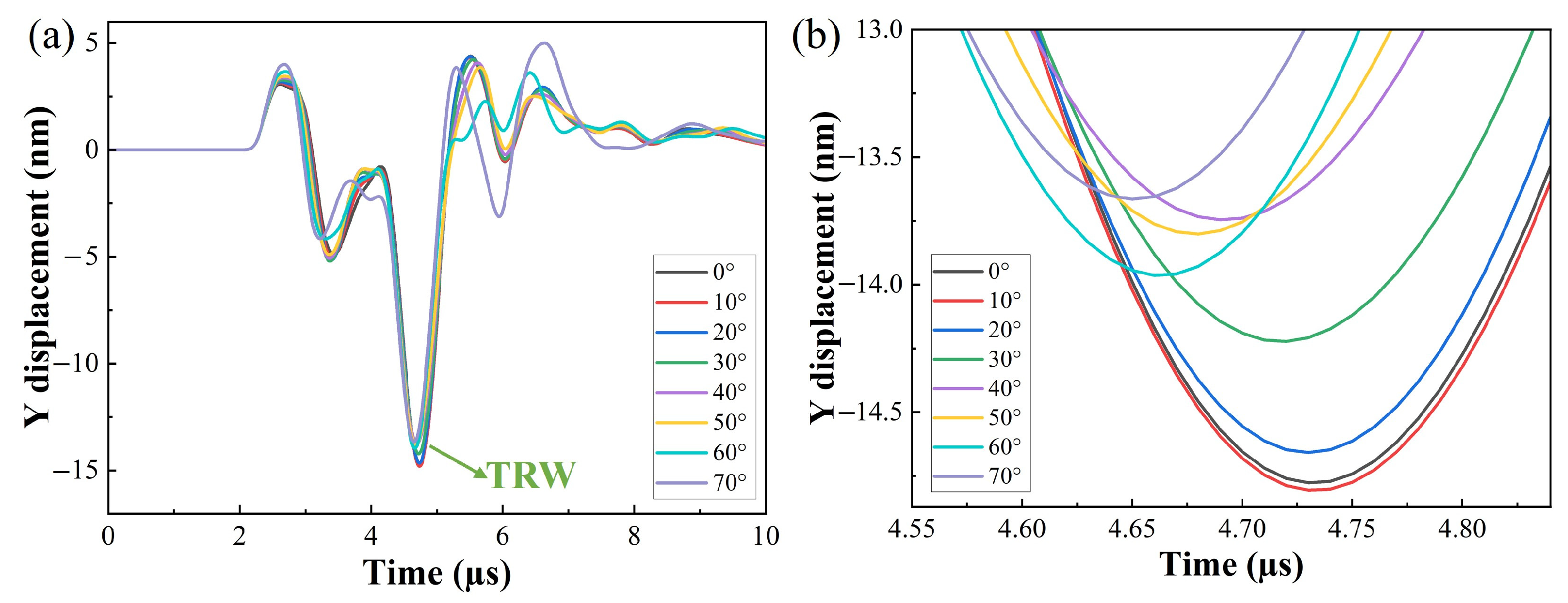
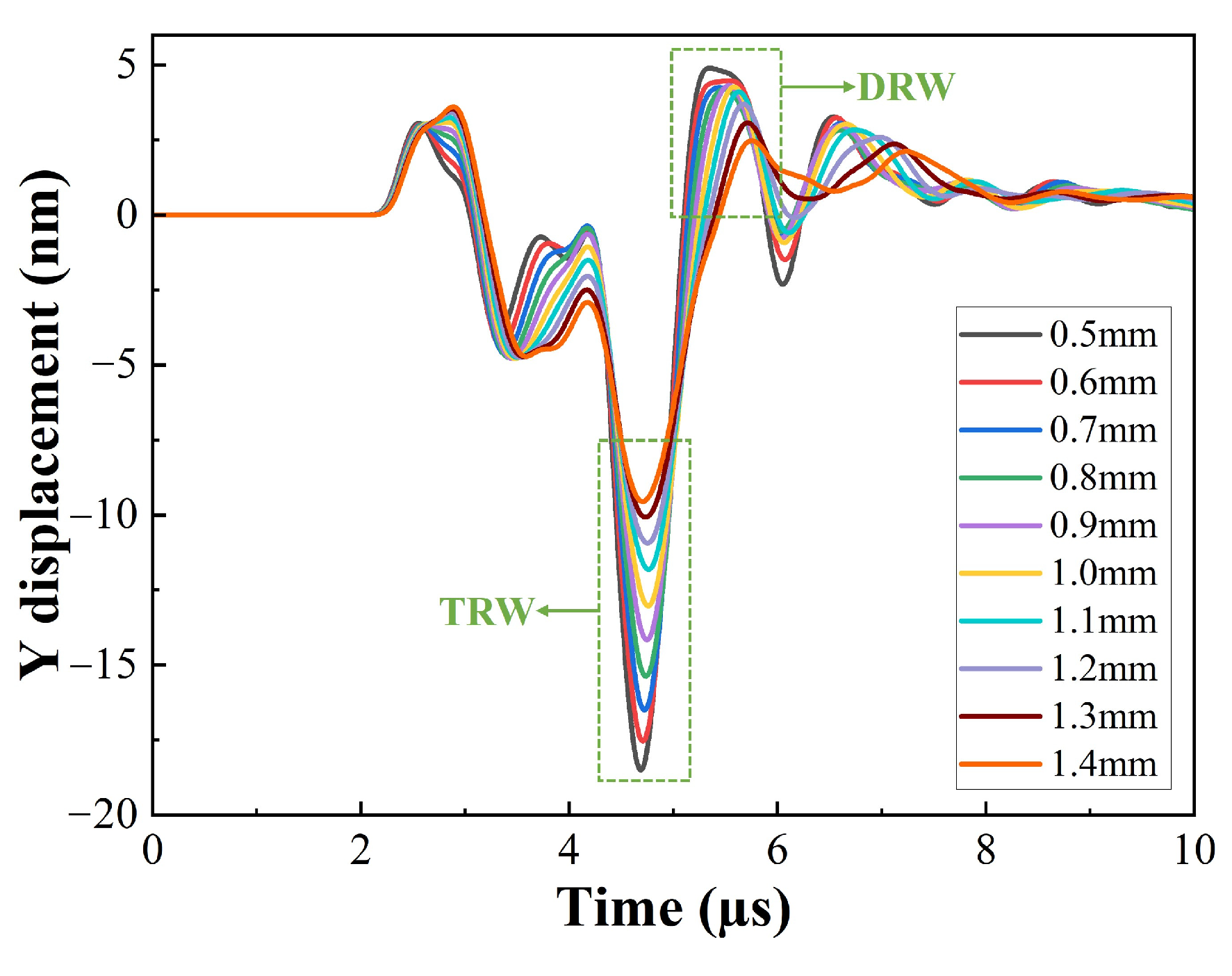
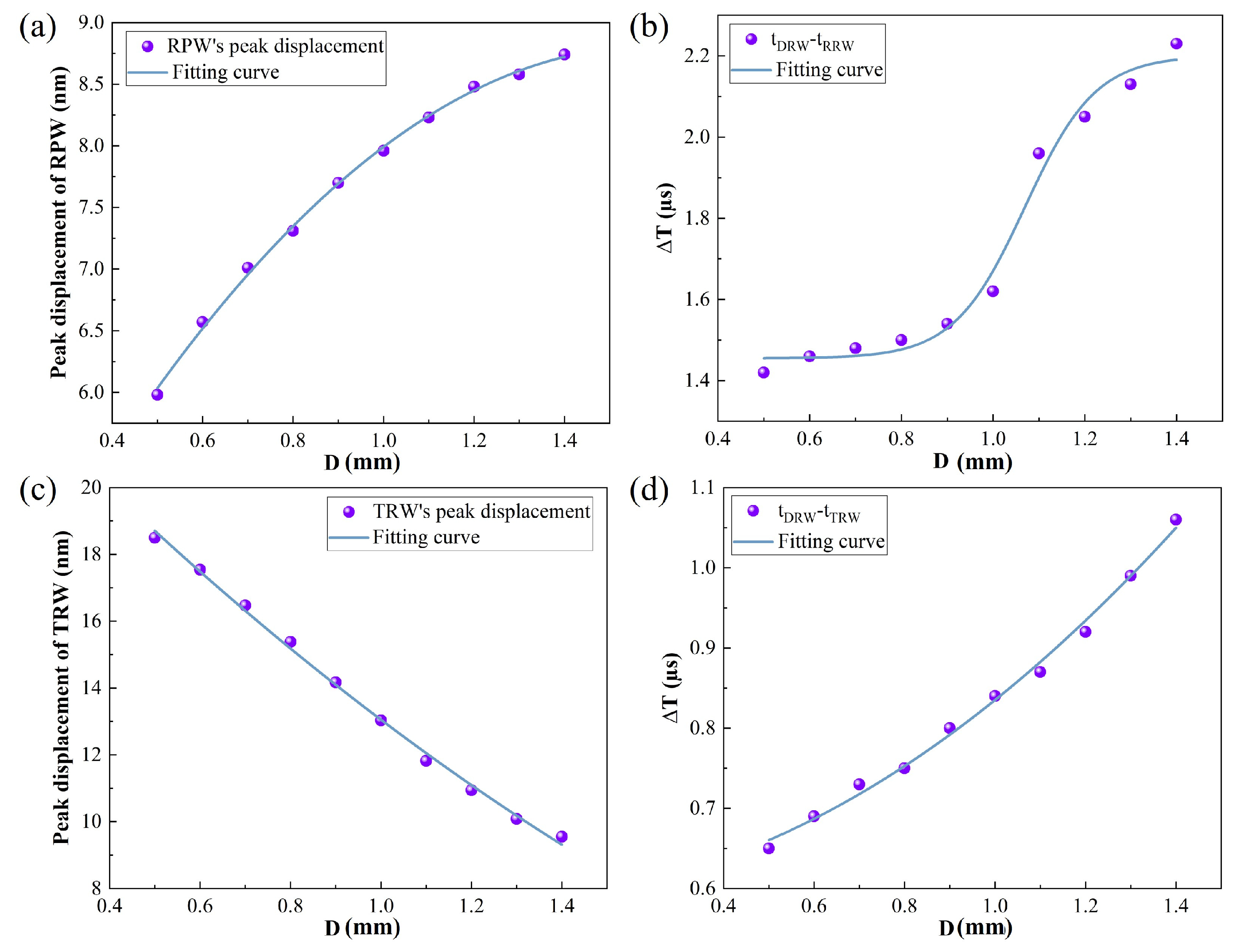
3.3. Crack Depth Detection
3.4. Crack Width Detection
4. Experimental Results
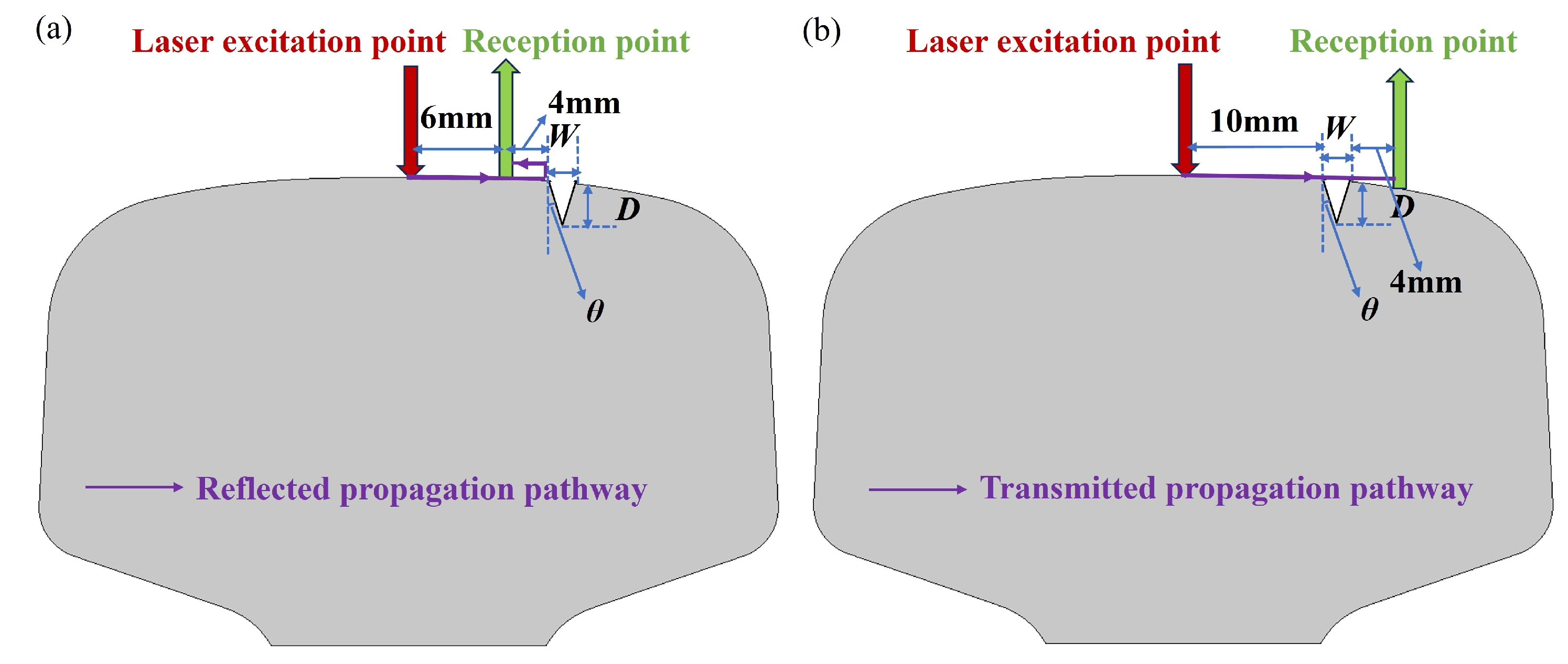
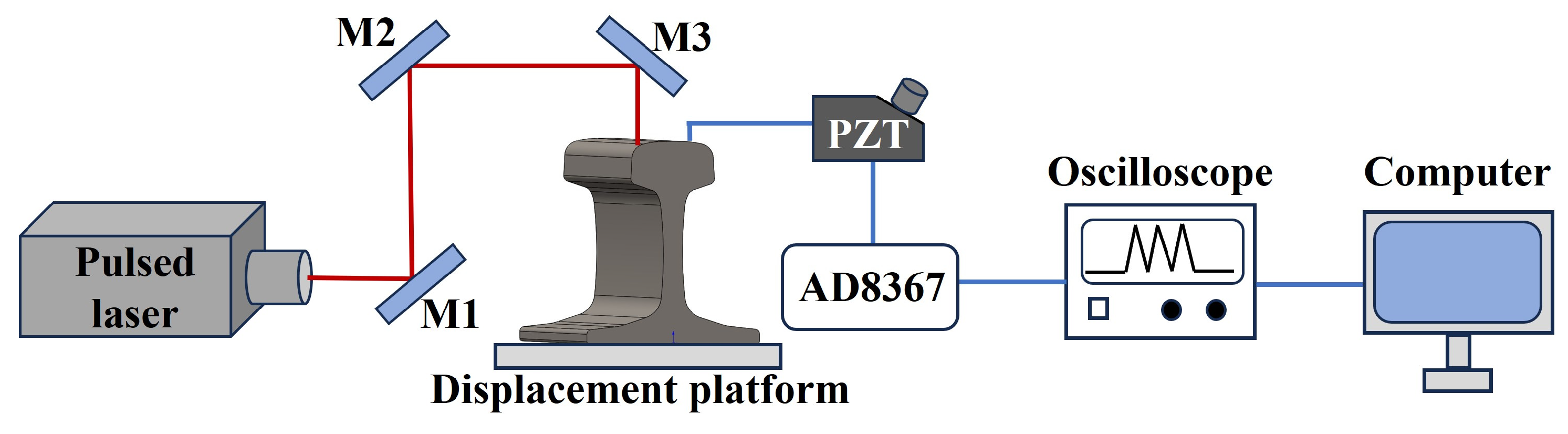
4.1. Experimental Setup and Samples
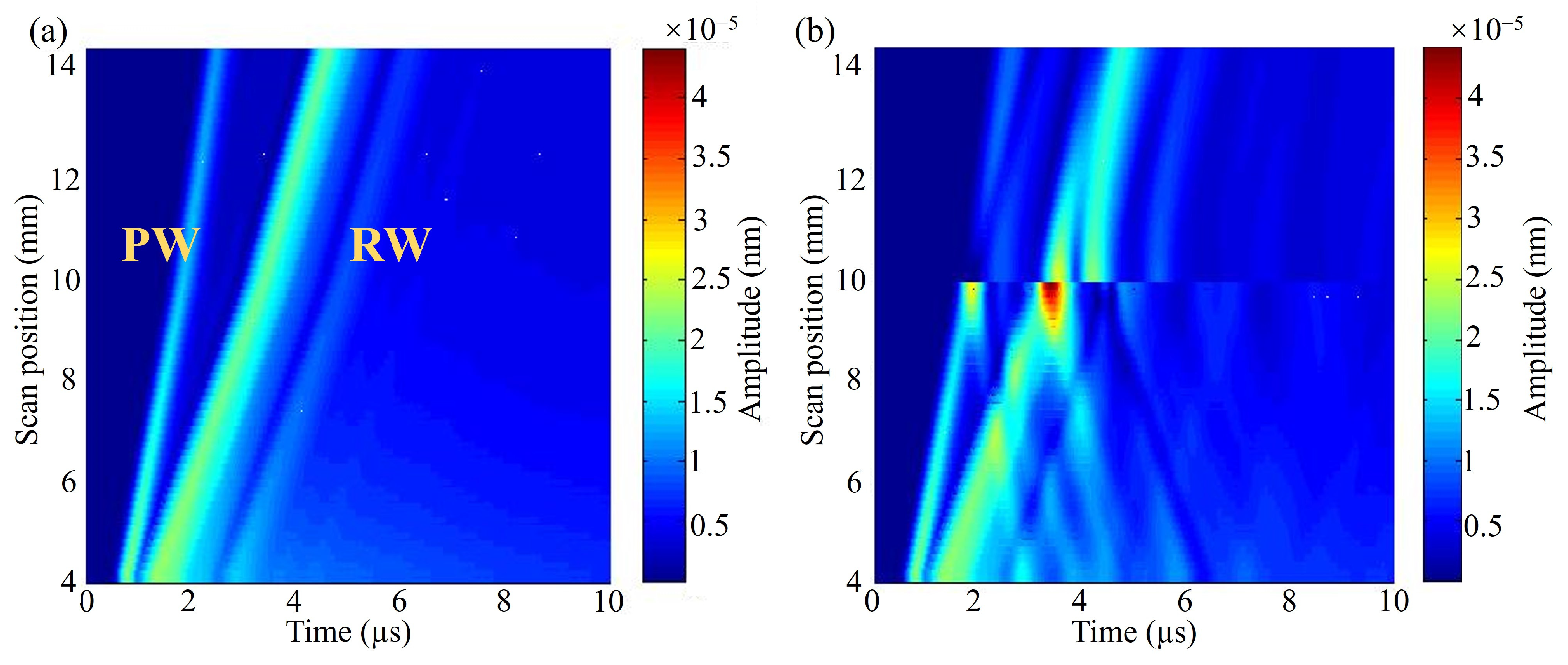
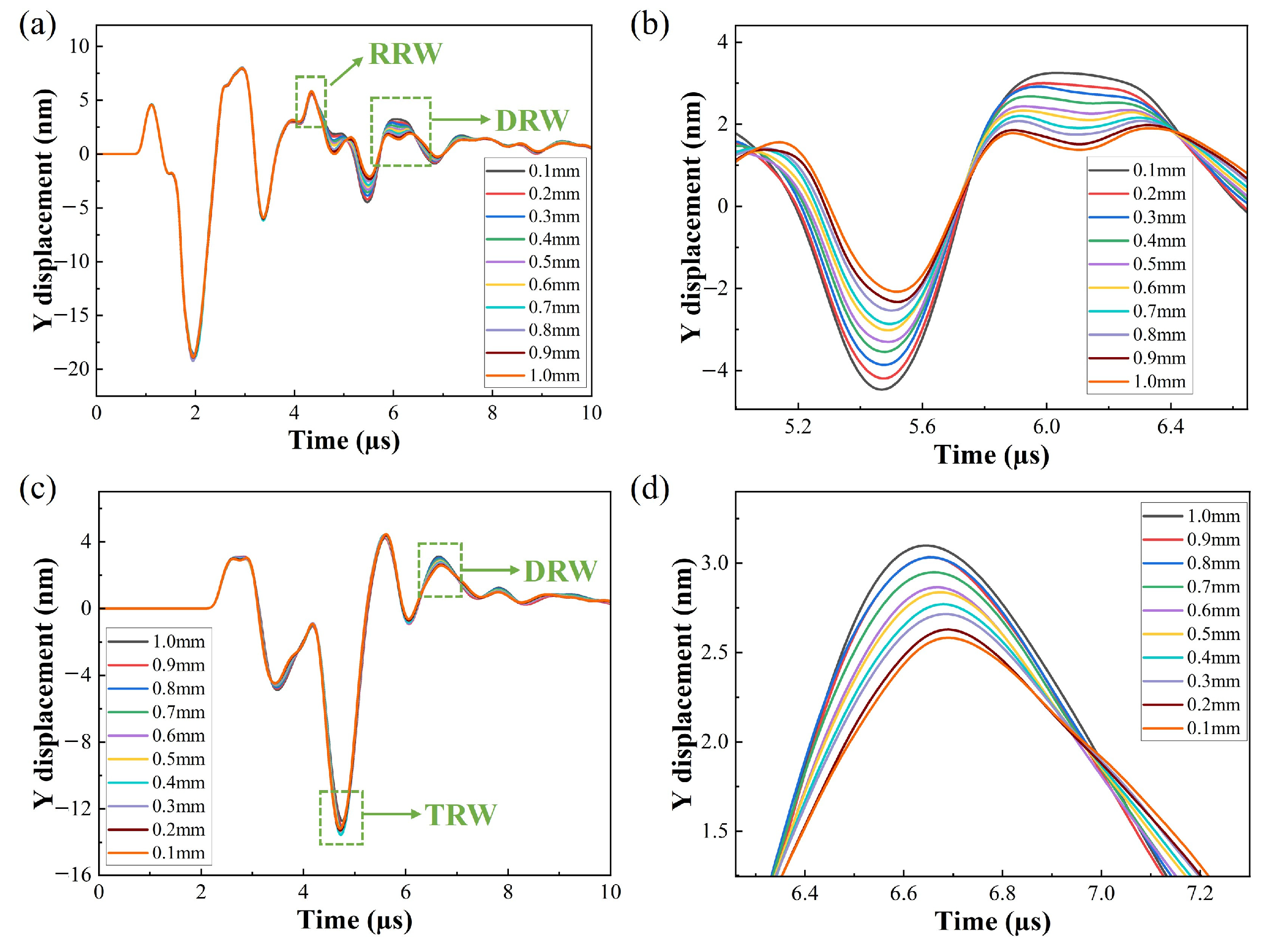
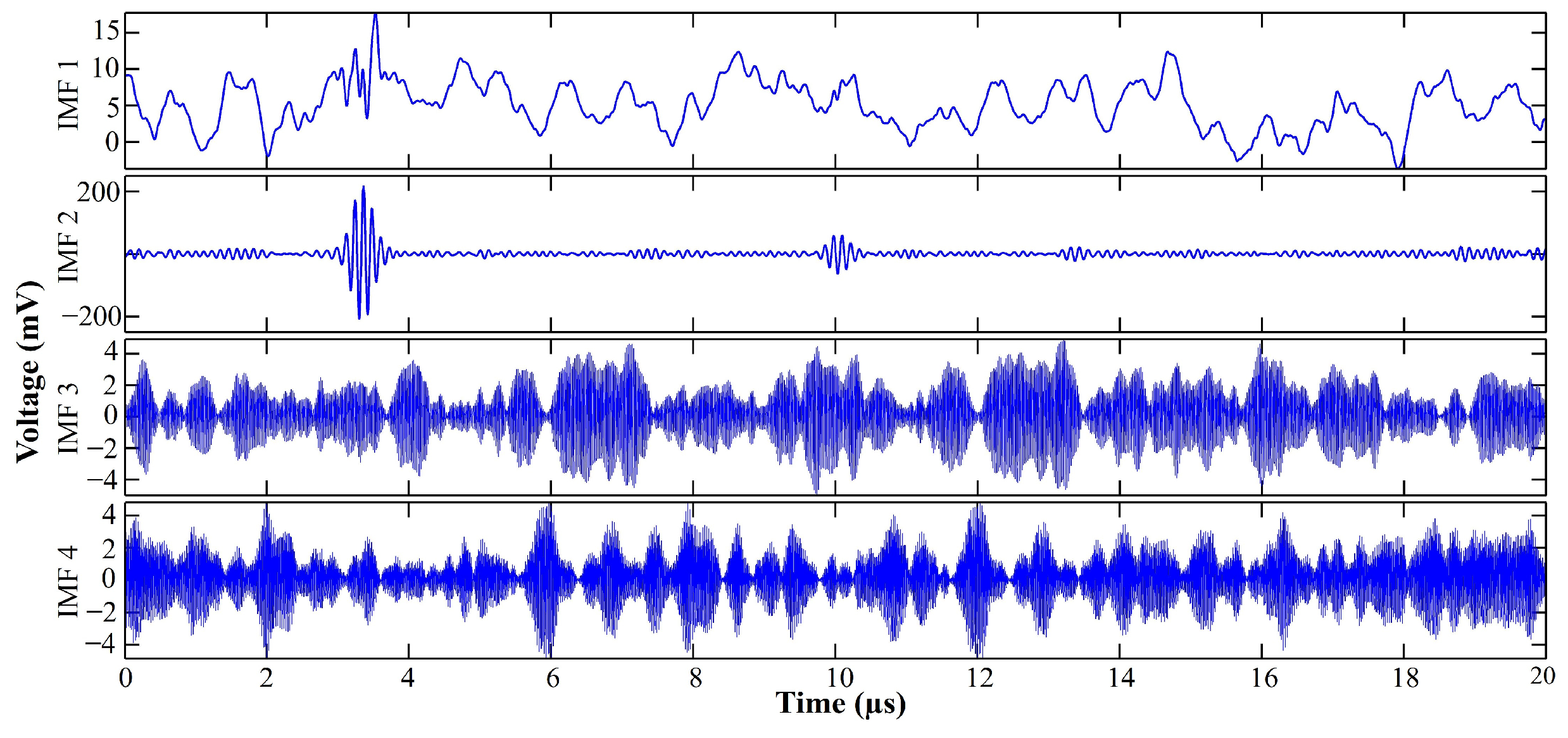
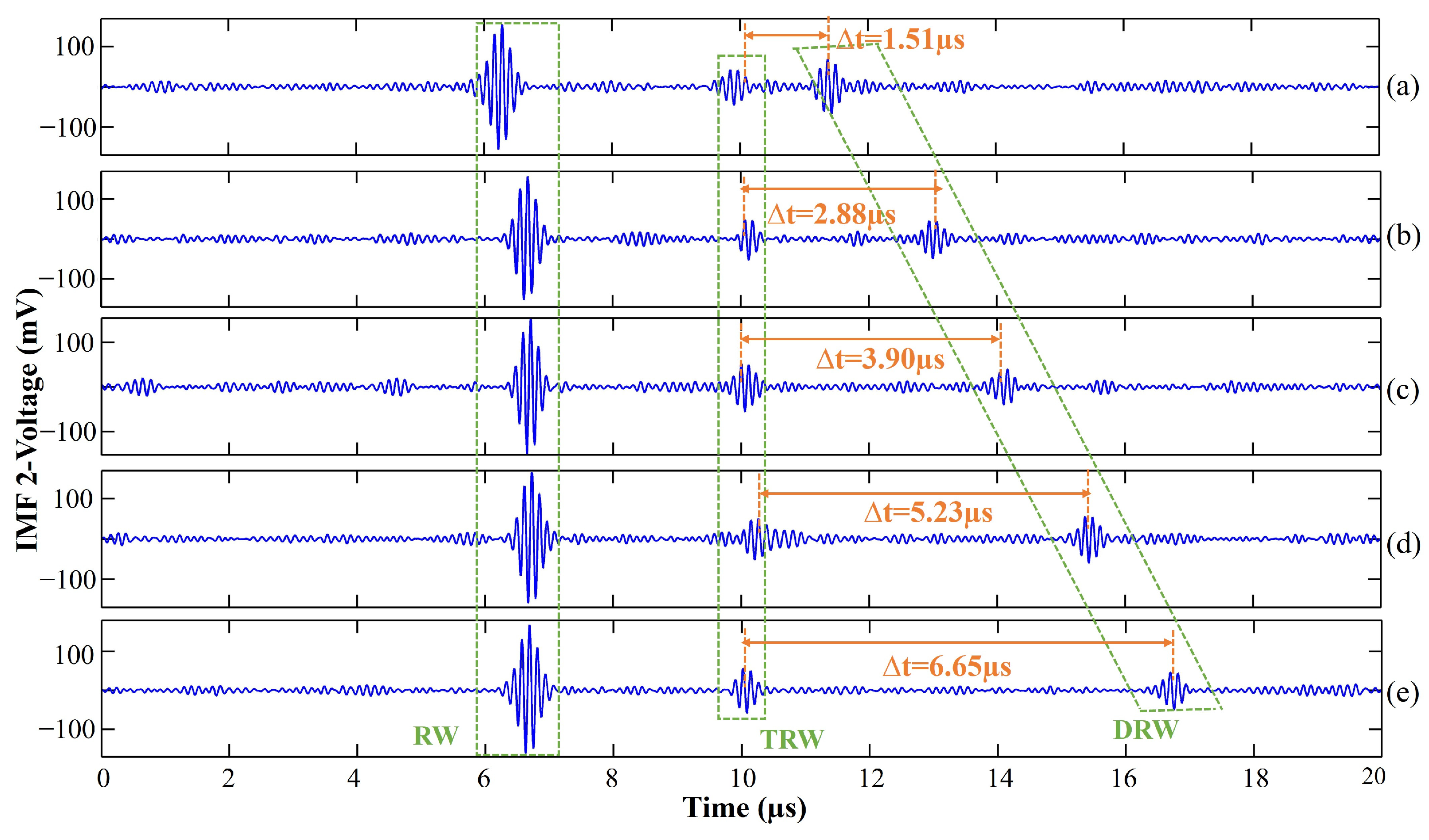
4.2. Crack Location Detection
4.3. Crack Angle Detection
4.4. Crack Depth Detection
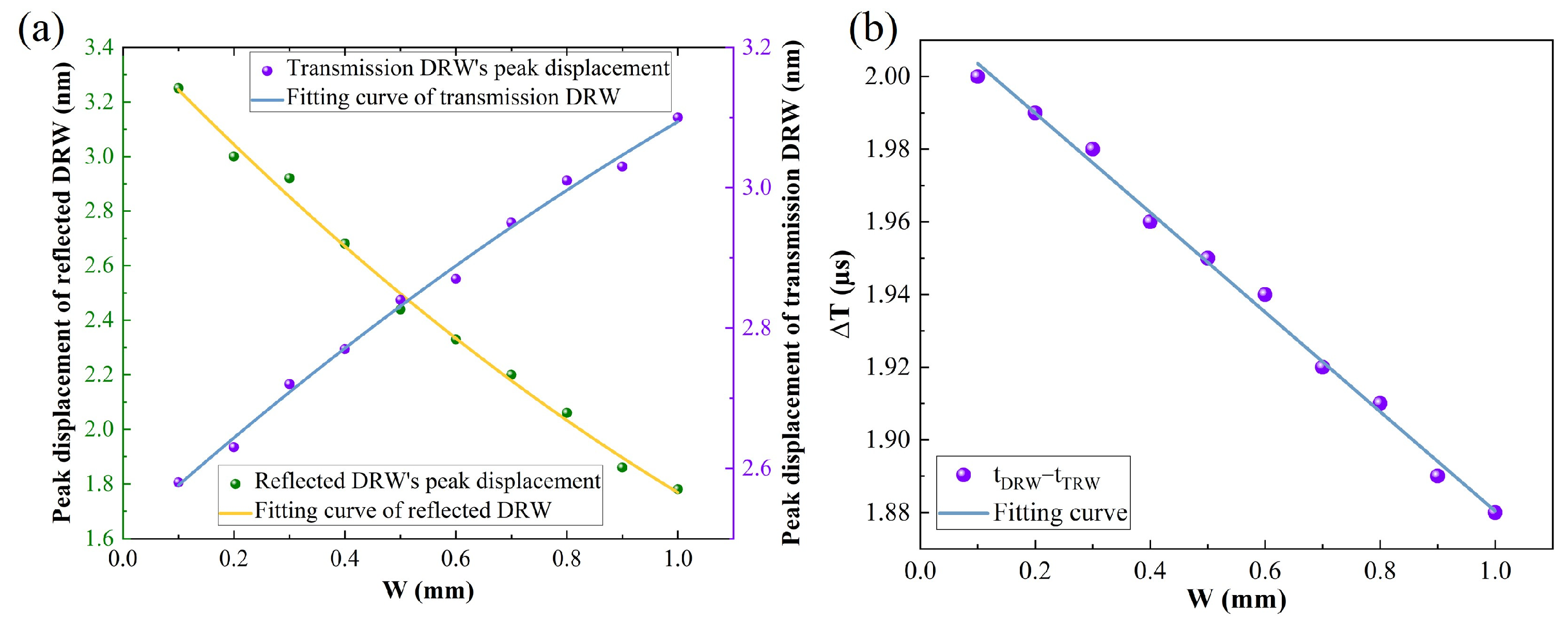
4.5. Crack Width Detection
5. Discussions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, X.; Wang, H.; Guo, J.; Liu, Q.; Zhao, G.; Wang, W. The effect of decarburized layer on rolling contact fatigue of rail materials under dry-wet conditions. Eng. Fail. Anal. 2018, 91, 58–71. [Google Scholar] [CrossRef]
- Steenbergen, M. Rolling contact fatigue: Spalling versus transverse fracture of rails. Wear 2017, 380–381, 96–105. [Google Scholar] [CrossRef]
- Zhang, Y.; Dang, D.; Wang, Y.; Ni, Y. Damage identification for railway tracks using ultrasound guided wave and hybrid probabilistic deep learning. Constr. Build. Mater. 2024, 418, 135466. [Google Scholar] [CrossRef]
- Xu, P.; Chen, Y.; Liu, L.; Liu, B. Study on high-speed rail defect detection methods based on ECT, MFL testing and ACFM. Measurement 2023, 206, 112213. [Google Scholar] [CrossRef]
- Liu, Z.; Li, W.; Xue, F.; Xia, F.; Jun, Y.; Bu, B.; Yi, Z. Electromagnetic Tomography Rail Defect Inspection. IEEE Trans. Magn. 2015, 51, 6201907. [Google Scholar] [CrossRef]
- Li, Y.; Tian, G.; Ward, S. Numerical simulation on magnetic flux leakage evaluation at high speed. NDT E Int. 2005, 39, 367–373. [Google Scholar] [CrossRef]
- Ohara, Y.; Nakajima, H.; Tsuji, T.; Mihara, T. Nonlinear surface-acoustic-wave phased array with fixed-voltage fundamental wave amplitude difference for imaging closed cracks. NDT E Int. 2019, 108, 102170. [Google Scholar] [CrossRef]
- Okuyama, N.; Nomura, K.; Sano, T.; Kadota, K.; Nitta, S.; Era, T.; Asai, S. Study on Detecting Method of Internal Defects by Laser Ultrasonics in Lap Joint Welding of Galvanized Steel Sheet and Finite Element Analysis of Its Detectability. Appl. Sci. 2023, 13, 11515. [Google Scholar] [CrossRef]
- Anandika, R.; Lundberg, J.; Stenström, C. Phased array ultrasonic inspection of near-surface cracks in a railhead and its verification with rail slicing. Insight 2020, 62, 387–395. [Google Scholar] [CrossRef]
- Kim, G.; Seo, M.-K.; Kim, Y.-I.; Kwon, S.; Kim, K.-B. Development of phased array ultrasonic system for detecting rail cracks. Sens. Actuators A Phys. 2020, 311, 112086. [Google Scholar] [CrossRef]
- Gao, F.; Zhou, H.; Huang, C. Defect detection using the phased-array laser ultrasonic crack diffraction enhancement method. Opt. Commun. 2020, 474, 126070. [Google Scholar] [CrossRef]
- Lian, Y.; Du, F.; Xie, L.; Hu, Q.; Jin, P.; Wang, Y.; Lu, Z. Application of laser ultrasonic testing technology in the characterization of material Properties: A review. Measurement 2024, 234, 114855. [Google Scholar] [CrossRef]
- Xie, L.; Lian, Y.; Du, F.; Wang, Y.; Lu, Z. Optical methods of laser ultrasonic testing technology in the industrial and engineering applications: A review. Opt. Laser Technol. 2024, 176, 110876. [Google Scholar] [CrossRef]
- Pathak, M.; Alahakoon, S.; Spiryagin, M.; Cole, C. Rail foot flaw detection based on a laser induced ultrasonic guided wave method. Measurement 2019, 148, 106922. [Google Scholar] [CrossRef]
- Allam, A.; Alfahmi, O.; Patel, H.; Sugino, C.; Harding, M.; Ruzzene, M.; Erturk, A. Ultrasonic testing of thick and thin Inconel 625 alloys manufactured by laser powder bed fusion. Ultrasonics 2022, 125, 106780. [Google Scholar] [CrossRef]
- Zhao, Y.; Jia, Z.Q.; Rui, G.; Ma, J.; Song, J.F.; Sun, J.H.; Liu, S. The Application of Laser-EMAT Technique Used to Testing Defect in Rail. Adv. Mater. Res. 2014, 875–877, 574–577. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, S.; Liu, X. Detection and Quantification of Damage in Metallic Structures by Laser-Generated Ultrasonics. Appl. Sci. 2018, 8, 8050824. [Google Scholar] [CrossRef]
- Huang, Q.; Xie, L.; Yin, G.; Ran, M.; Liu, X.; Zheng, J. Acoustic signal analysis for detecting defects inside an arc magnet using a combination of variational mode decomposition and beetle antennae search. ISA Trans. 2020, 102, 347–364. [Google Scholar] [CrossRef]
- Sun, Y.; Ni, C.; Ying, K.; Xiong, A.; Shuai, T.; Shen, Z. Laser ultrasonic spatially resolved acoustic spectroscopy for grain size study based on Improved Variational Mode Decomposition (IVMD). NDT E Int. 2024, 144, 103090. [Google Scholar] [CrossRef]
- Gschwandl, T.J.; Weniger, T.M.; Antretter, T.; Künstner, D.; Scheriau, S.; Daves, W. Experimental and Numerical Visualisation of Subsurface Rail Deformation in a Full-Scale Wheel–Rail Test Rig. Metals 2023, 13, 1089. [Google Scholar] [CrossRef]
- Zhu, L.; Duan, X.; Yu, Z. On the Identification of Elastic Moduli of In-Service Rail by Ultrasonic Guided Waves. Sensors 2020, 20, 1769. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Han, S.; Yu, Y.; Qi, X.; Zhang, Y.; Lian, Y.; Bai, Z.; Wang, Y.; Lv, Z. Numerical Simulation of Metal Defect Detection Based on Laser Ultrasound. IEEE Photonics J. 2021, 13, 1–9. [Google Scholar] [CrossRef]
- Han, S.; Lian, Y.; Xie, L.; Hu, Q.; Ding, J.; Wang, Y.; Lu, Z. Numerical simulation of angled surface crack detection based on laser ultrasound. Front. Phys. 2022, 10, 982232. [Google Scholar] [CrossRef]
- Xu, Z.; Tian, Q.; Hu, P.; Li, H.; Shen, S. Laser ultrasonic detection of submillimeter artificial holes in laser powder bed fusion manufactured alloys. Opt. Laser Technol. 2024, 169, 110030. [Google Scholar] [CrossRef]











| Characteristic Parameters | A60 Rail |
|---|---|
| Density (kg/m3) | 7840 |
| Thermal expansion coefficient (K−1) | 1.18 × 10−5 |
| Heat capacity (J/(kg∙K)) | 475 |
| Young modulus (Gpa) | 210 |
| Thermal conductivity (W/(m·K)) | 44.5 |
| Poisson’s ratio | 0.29 |
| Spot Radius (mm) | Monopulse-Energy (mJ) | Peak Power Density (W/m2) | Pulse Width (ns) |
|---|---|---|---|
| 1 | 5 | 1.5915 × 1011 | 10 |
| Pulse-Echo | Pitch-Catch | TOF | |
| θ | 9.44% | * | 5.67% |
| D | 0.84% | 1.11% | 1.67% |
| W | 2.27% | 1.72% | 0.76% |
| Spot Radius | Pulse-Energy | Repetition Frequency | Pulse Width | AD8367-Maximum Gain | Sample Rate |
|---|---|---|---|---|---|
| 1 mm | 5 mJ | 1 Hz | 10 ns | 45 dB | 260 MSa/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lian, Y.; Du, F.; Xie, L.; Qi, X.; Jin, P.; Wang, Y.; Lu, Z. Simulation and Experimental Research of V-Crack Testing of Rail Surfaces Based on Laser Ultrasound. Photonics 2024, 11, 920. https://doi.org/10.3390/photonics11100920
Lian Y, Du F, Xie L, Qi X, Jin P, Wang Y, Lu Z. Simulation and Experimental Research of V-Crack Testing of Rail Surfaces Based on Laser Ultrasound. Photonics. 2024; 11(10):920. https://doi.org/10.3390/photonics11100920
Chicago/Turabian StyleLian, Yudong, Fenjiao Du, Luyang Xie, Xuan Qi, Peng Jin, Yulei Wang, and Zhiwei Lu. 2024. "Simulation and Experimental Research of V-Crack Testing of Rail Surfaces Based on Laser Ultrasound" Photonics 11, no. 10: 920. https://doi.org/10.3390/photonics11100920
APA StyleLian, Y., Du, F., Xie, L., Qi, X., Jin, P., Wang, Y., & Lu, Z. (2024). Simulation and Experimental Research of V-Crack Testing of Rail Surfaces Based on Laser Ultrasound. Photonics, 11(10), 920. https://doi.org/10.3390/photonics11100920






