Abstract
In the modern era, the secure transmission and storage of information are among the utmost priorities. Optical security protocols have demonstrated significant advantages over digital counterparts, i.e., a high speed, a complex degree of freedom, physical parameters as keys (i.e., phase, wavelength, polarization, quantum properties of photons, multiplexing, etc.) and multi-dimension processing capabilities. This paper provides a comprehensive overview of optical cryptosystems developed over the years. We have also analyzed the trend in the growth of optical image encryption methods since their inception in 1995 based on the data collected from various literature libraries such as Google Scholar, IEEE Library and Science Direct Database. The security algorithms developed in the literature are focused on two major aspects, i.e., symmetric and asymmetric cryptosystems. A summary of state-of-the-art works is described based on these two aspects. Current challenges and future perspectives of the field are also discussed.
1. Introduction
Due to the advancement in information technology, images and videos are widely used in various applications such as video conferencing, medical imaging, remote sensing, compressive sensing, social media, bank details and various government/corporate documents. These images and videos may be carrying confidential information. The transmission of data takes place over secure/unsecure public networks. The access of sensitive information to unauthorized people may raise national and military security concerns. Thus, the security of the data from unauthorized uses is very crucial. From the literature, it is evident that various data security algorithms have been in play for a long time since World War II, such as the data encryption standard (DES) and advance encryption standard (AES) [1,2]. Digital image encryption algorithms have limitations such as a slow processing speed, complex computation and low efficiency. With time, optical encryption algorithms are developed, which have a high computation power and high efficiency owing to their capability of parallel processing. The optical encryption algorithms have gained a lot of interest recently. The growth in optical image encryption algorithms occurred exponentially. The chart in Figure 1 represents the growth of the number of publications related to optical image encryption algorithms. These data are taken from three major scholarly sources, i.e., Google Scholar, IEEE Library, and Science Direct Database, with the key word “optical image encryption”, and a total 5205 articles were found in the databases. A trend line is drawn, and we found that the optical image encryption algorithm developed exponentially. Image encryption is a method that converts meaningful images into a noisy image which is known as ciphertext. Decryption is a process that converts a ciphertext into an original image with the help of decryption keys. These keys are the backbone of any encryption algorithm. The general block diagram for an image encryption/decryption algorithm is represented in Figure 2.
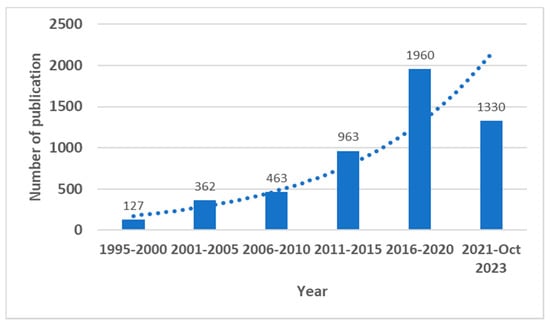
Figure 1.
Publication trends of optical image encryption algorithms based on Google Scholar data.
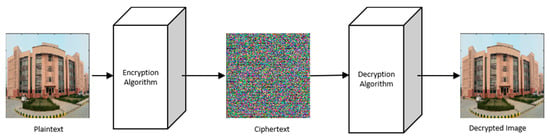
Figure 2.
General algorithm of the image (a) encryption and (b) decryption process.
1.1. Basic Terminology
- Plaintext: In the field of cryptography, plaintext is data that have not undergone any encryption process and can be easily understood by anyone who has access to it—for example, a target image or sensitive text that is being transmitted over the internet and needs to be encrypted.
- Ciphertext or encrypted image: Ciphertext is the encrypted and unreadable output that results from applying an encryption algorithm to plaintext. In the context of cryptography, ciphertext is produced to secure information during transmission or storage. The process of encryption involves converting plaintext (the original, human-readable data) into ciphertext using an algorithm and encryption key.
- Security key: The effectiveness of an encryption algorithm relies on the security of its keys. Encryption and decryption operations rely on the strength and management of these keys. The key length of an encryption algorithm is very important, with longer keys providing enhanced security against evolving computational capabilities. Secure key generation, storage, distribution and exchange are essential components of a robust encryption system. Regular key change and management practices further contribute to maintaining the overall security of encrypted data.
- Symmetric cryptosystem: A symmetric key cryptosystem is a type of algorithm for encryption where a single secret key is shared between communicating parties to encrypt and decrypt data. The efficiency of symmetric key cryptography lies in its simplicity and speed, as the computational processes for encryption and decryption are relatively fast. However, secure key distribution becomes a critical challenge; if the secret key is leaked, the entire communication could be breached. Symmetric key algorithms, such as Advanced Encryption Standard (AES), have been widely used for their robust security and computational efficiency in various applications, including secure data transmission and storage.
- Asymmetric cryptosystem: An asymmetric cryptosystem, which is also known as public-key cryptography, uses a pair of distinct but related keys: a public key and a private key. The public key is openly shared in the public domain and used for encryption, allowing anyone to send encrypted messages to the owner of the paired private key. The private key, kept confidential, is used for decrypting messages received with the corresponding public key. The strength of asymmetric cryptography lies in its ability to facilitate secure communication without requiring a pre-shared secret key. This makes key distribution more straightforward compared to symmetric systems. However, asymmetric encryption tends to be more computationally intensive than symmetric encryption. Common uses of asymmetric cryptography include secure communication over networks, digital signatures for authentication and the establishment of secure communication channels in protocols like SSL/TLS. The combination of symmetric and asymmetric cryptography often provides a robust solution for achieving both efficiency and security in various cryptographic applications.
- Active attack: The purpose of an active attack is to interfere with communication and gain unauthorized access by tampering with or intercepting data. In the context of intercepting general communication, attackers aim to compromise the confidentiality and integrity of the information being transmitted. By gaining access and modifying the text, they can potentially insert malicious content, alter messages or impersonate legitimate users, posing significant security risks. Implementing robust encryption, secure key management and monitoring mechanisms are crucial to thwarting active attacks and safeguarding the confidentiality and integrity of communication channels.
- Passive attack: In passive cryptography attacks, the primary goal is to intercept or eavesdrop on communication without altering the data or communication itself. The attacker seeks to obtain unauthorized access to sensitive information by secretly monitoring and capturing the transmitted data. Unlike active attacks, passive attacks do not involve direct manipulation of the communication content; instead, the focus is on unauthorized information retrieval. Protecting against passive attacks typically involves implementing encryption to secure the confidentiality of the transmitted data, making it more challenging for unauthorized parties to extract meaningful information even if they manage to intercept the communication.
- Known plaintext attack (KPA): A Known Plaintext Attack (KPA) is a type of cryptographic attack where the attacker has knowledge of both the plaintext and its corresponding ciphertext. The attacker’s objective is to deduce the encryption key used in the cryptosystem. By analyzing the known pairs of plaintexts and ciphertext, the attacker aims to uncover patterns or relationships that can lead to the discovery of the encryption key. Once the key is determined, the attacker can then decrypt other ciphertexts encrypted with the same key, compromising the security of the entire system. The key distinction is that the attacker does not necessarily need to implement the key on another ciphertext; the primary goal is to reveal the key for decryption purposes.
- Chosen plaintext attack (CPA): In a Chosen Plaintext Attack (CPA), the attacker could choose arbitrary plaintexts and obtain their corresponding ciphertexts by using the target cryptosystem. The attacker’s goal is to analyze these pairs of chosen plaintext and ciphertext to deduce or estimate the decryption key. Once the attacker successfully estimates the key, they can use it to decrypt other ciphertexts encrypted with the same key. The critical point is that the attacker has the freedom to choose the plaintexts they want to encrypt, allowing for a more flexible and targeted approach to revealing information about the cryptographic key.
- Ciphertext only attack: It is an attacking algorithm in which the attacker has access to the cryptosystem so as to encrypt the data and obtain the corresponding ciphertext. In this method, the attacker has no information regarding the plaintext or keys of the cryptosystem. In this attack process, the intruder tries to recover the input message as much as possible or, preferably, to estimate the encryption key. All encrypted messages that have been encrypted with this key can be recovered once the encryption key has been guessed.
- Chosen ciphertext attack: In this attacking algorithm, the attacks have only information regarding the ciphertexts and try to guess the secret keys of the cryptosystem. In the chosen ciphertext attack, the attacker might have some information regarding the cryptosystem.
- Brute-force attack: A brute-force attack is a hit-and-trial method which is used to estimate encryption keys and find a hidden web page or login info. To estimate correctly, hackers try every possible combination. In the case of long and complex passwords, cracking them can take up to a couple of years. The effectiveness of a brute-force attack also depends on the hardware used by the attacker. This is the old attacking method but is still popular with attackers.
- Specific attack: The same attacks do not work on all cryptosystems, so some specific attacks are designed to test the security of cryptosystems. Specific attacks are designed to test the security of an encryption algorithm based on phase truncation and phase reservation in the Fourier domain (PTFT), equal modulus decomposition (EMD), random modulus decomposition (RMD) and unequal modulus decomposition (UMD)-based cryptosystems, as the decryption keys depend on the plaintext. These attacks are very specific to a particular type of cryptosystem.
- Occlusion attack: A network failure or other reasons may cause some information about the ciphertext to be lost during transmission [3]. Data loss in a ciphertext image is known as an occlusion attack.
- Noise attack: During the transmission of ciphertext over the internet, some unwanted data are to be mixed, which is known as noise [4]. These unwanted data create a problem in the faithful recovery of plaintext. There are some standard noises which are commonly used for contamination, such as Gaussian noise, salt and pepper, speckle, Poisson noise, etc.
1.2. Statistical Measures for Validating Cryptosystems
The quality of an image can be ensured with various statistical measures such as the peak-signal-to-noise ratio (PSNR), correlation coefficient (CC), information entropy, mean squared error (MSE) and visual measures such as histograms and mesh plots. Brief explanations of these parameters are as follows:
- Correlation coefficient: The correlation coefficient (CC) is calculated to evaluate the statistical relationships between pixels in two images. The correlation coefficient is a metric that determines how closely two images are related [5,6]. The correlation coefficient has a value in the range of −1.0 to 1.0. The value of indicates that both images are not related to each other, but a value of indicates that both images are completely related to each other. For a robust cryptosystem, the ideal value of between the plaintext and recovered image is closer to , while the between the plaintext and ciphertext should be far from . The CC between and is given by the expression given in Equation (1).
- Mean squared error (MSE): MSE is a statistical indicator that measures the resistance of a cryptosystem against various attacks. The mean square error between two images is calculated by using the expression given in Equation (2).Here, are two images of size pixels. A robust cryptosystem has a high value of MSE between the plaintext and encrypted image and a low value of MSE between the plaintext and recovered image [7].
- Peak-signal-to-noise ratio: The peak-signal-to-noise ratio (PSNR) is the ratio of the maximum power of the signal to the maximum power of the corrupting noise that impacts its fidelity. The PSNR and MSE are related to each other [8]. The PSNR is calculated using the expression given in Equation (3).Here, MSE is the mean squared error, which can be estimated using Equation (2). A high value of the PSNR between the plaintext and recovered image indicates the good quality of the decrypted image.
- Information entropy: The information entropy measures the randomness inherent in an image, which describes the quality of encryption quality. Information entropy for a grayscale image lies in the range of . If the value of information entropy approaches , it indicates that the image is highly random, and no information about the image is revealed [9,10]. Mathematically, information entropy is expressed in Equation (4).For sourcewhere represent the pixel value, and is the probability of the pixel value .
- Histogram: Histograms represent the number of pixels having the intensity values in an image. The histogram shows how many pixels are present in an image at different intensities. The histogram shows pixels distributed between the 256 different grayscale values in an eight-bit grayscale image. It is also possible to make a histogram of a color image, either as an individual histogram for the red, green and blue channels or as a three-dimensional histogram where each axis represents a channel and the brightness at each point indicates the number of pixels. The histogram plots of the ciphertext and plaintext should be different for a robust cryptosystem, whereas the histogram plots of the plaintext and recovered image should be same.
2. Optical Image Encryption Techniques
There are various methods available in the literature to secure data, such as encryption, watermarking and steganography. In this review, we have studied the security of images using an optical encryption algorithm. The detailed classification of various encryption algorithms is given in Figure 3.
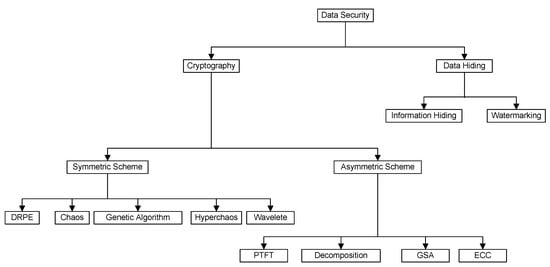
Figure 3.
Different approaches of image encryption algorithms.
Double Random Phase Encoding-Based Cryptosystems
The seminal work in the field of optical image encryption was proposed by Refregier and Javidi in 1995, which is well known as double random phase encoding (DRPE) [11]. It was the first attempt to encode the information using optical methods in which a 4-f setup was employed, as shown in Figure 4. In this, a plaintext image is converted into a white stationary noisy image using two random phase masks: one random phase mask in the spatial domain and a second in the Fourier domain. The encryption and decryption process of the DRPE algorithm is described in Equations (5) and (6). Here, and q are the plaintext and ciphertext, respectively, and are random matrices of the size of the input image.
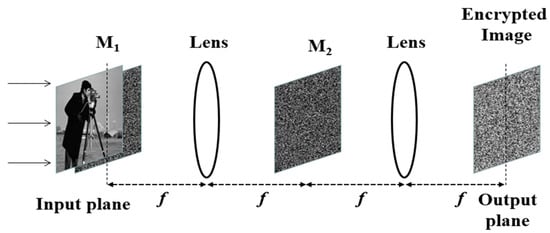
Figure 4.
Optical image encryption process of DRPE proposed by Refregier and Javidi in 1995.
After the inception of DRPE, there was a huge increase in demand for optical cryptosystems, and various algorithms have been developed using the framework of DRPE. In 1996, Javadi et al. proposed the practical demonstration of the DRPE method for image security and authentication [12]. Thereafter, researchers have developed various algorithms to secure the images through different optical aspects [13,14,15] and to encrypt optical memory, binary images and biometrics [13,16,17]. For the numerical simulation of the DRPE method, a MATLAB code is provided in the Supplementary Material.
3. Symmetric Cryptosystems
As we have discussed in the previous sections, in symmetric cryptosystems, encryption and decryption keys are the same and do not depend on the plaintext [16,18,19,20,21,22]. An illustration of this can be seen in the flowchart given in Figure 5. The DRPE architecture falls in the category of symmetrical algorithms. Besides that, various other symmetric methods have also been reported in the literature, which are discussed in the following sections.
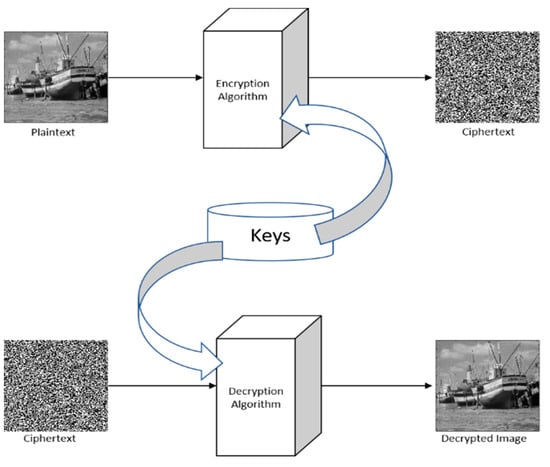
Figure 5.
Diagrammatic flowchart of symmetric key cryptosystems.
3.1. Transform-Based Encryption Algorithm
After the demonstration of DRPE, the optical encryption algorithms have attracted the attention of researchers due to various advantages they have shown over digital counterparts. The DRPE architecture was studied extensively and has been extended in various other transform domains, such as Fractional Fourier, Hartley, Fraction Hartley, Mellin, Fractional Mellin, Gyrator and Fresnel [23,24,25,26,27]. Some optical image encryption algorithms using the wavelet approach, such as discrete wavelet transform, Haar wavelet transform and wavelet fusion [28,29,30,31,32,33], have also been introduced.
3.2. Chaos-Based Symmetric Encryption
In encryption algorithms, decryption keys are the backbone of the cryptosystem. So, the key space should be large enough such that it cannot be breached in real time with existing computation methods and software. To improve the security of symmetric encryption algorithms, chaotic maps seem like good candidates due to their overall stability and local instability and their sensitivity to initial values and parameters. These properties of chaotic maps help to increase the key space and provide an additional layer of security. To apply a chaotic map, an image is divided into multiple blocks of equal lengths and then each block is shuffled according to the sequence generated by the chaotic map. Parameters and initial values act as decryption keys in the cryptosystem. Chaotic maps are highly sensitive to the initial values and parameters, which makes them difficult to predict without knowledge of the correct value of the initial value and parameter. Researchers have proposed optical image encryption algorithms using Logistic, Cosine, Rational, 2-D Lorenz, Baker, Arnold cat, Chen chaotic, Exponential, Umbrella, Tinkerbell, Gauss, Henon map, 3-cell CNN system, Mixed memristive chaotic circuit, Edge map and other chaotic maps [34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49]. For example, to generate the Tinkerbell map, the following equations can be used:
Here, X and Y are the two chaotic Tinkerbell sequences, whereas the constants and are the control parameters which serve as the keys. The initial values (X0, Y0, a, b, c, d) affect the generation of two chaotic sequences [50]. The attractor of the Tinker bell map is shown in Figure 6.
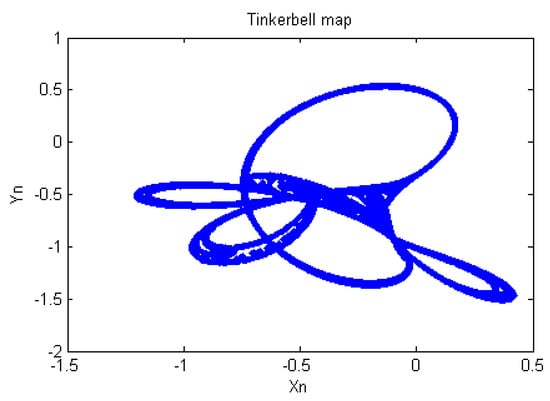
Figure 6.
Attractor of the Tinkerbell chaotic map.
3.3. Pixel Diffusion-Based Symmetric Image Encryption
To further improve the security of symmetric cryptosystems, researchers implementeda pixel diffusion process in the DRPE-based algorithms. Various algorithms are used to diffuse the pixels such as the bit XOR operator, block-level diffusion, bit-level diffusion using Brownian motion, S-box-based diffusion, Cellular automata, chaotic maps, cyclic modulo operators, pixel adaptive and DNA-based diffusion process [29,50,51,52,53,54,55,56]. However, with time, it was found that the linear nature of DRPE architecture makes it vulnerable to cryptographic attacks such as known plaintext and chosen plaintext attacks. This has further prompted the researchers to find an alternative and design more sophisticated optical cryptosystems, i.e., asymmetric cryptosystems.
4. Asymmetric Encryption Algorithm
The vulnerability of symmetric cryptosystems to various cryptographic attacks led to the development of optical asymmetric techniques in which encryption and decryption are different. In these algorithms, decryption keys are generated during the encryption process and depend on the input plaintext. Phase truncation and phase reservation in Fourier transform (PTFT) was the seminal work in this direction [57]. However, the relationship between the ciphertext and private key leads the PTFT-based encryption algorithm to be vulnerable to special iterative attacks [58]. To improve the security of this method, hybrid opto-digital optical cryptosystems have been developed based on mathematical decompositions, such as equal modulus decomposition, random modulus decomposition, unequal modulus decomposition, polar decomposition, QZ decomposition, elliptic curves and many other operators [59,60,61,62,63,64,65,66,67]. This integration of mathematical decomposition with optical techniques is very effective in designing the sophisticated optical cryptosystems which are robust to various attacks. Some of these are discussed in detail in the following sub-sections. A general flowchart of an asymmetric cryptosystem is shown in Figure 7.
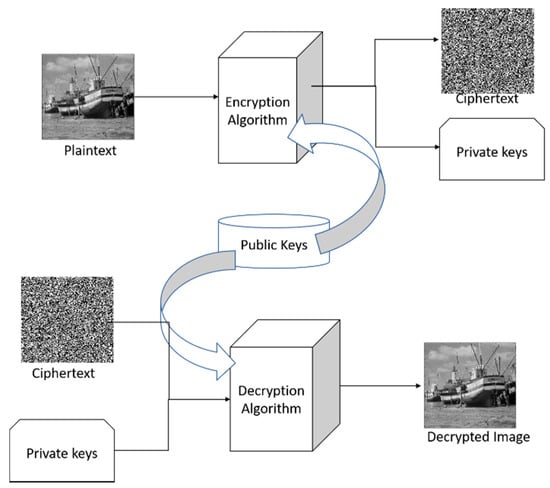
Figure 7.
Schematic flowchart of an asymmetric cryptosystem.
4.1. Phase Truncation and Phase Reservation in Fourier Transform
The phase truncated Fourier transform (PTFT) algorithm was proposed by Qin and Peng [57]. In PTFT, two random phase masks like DRPE are used in the spatial domain and Fourier domain of a 4-f setup. The two decryption keys that are dependent on the plaintext and are different from the public keys are generated using the phase truncation approach. PTFT is further extended in other transform domains as well [60]. The complete PTFT operation can be performed as follows:
- (a)
- Encryption process
Step 1: The plaintext image is modulated with a random phase mask (RPM) and Fourier transformed (FT). Mathematically, it can be represented as:
Step 2: The output of Step 1 is subjected to the phase truncation and phase reservation process. The phase truncated part acts as the ciphertext of the cryptosystem, whereas the phase reserved part acts as the private key of the cryptosystem. Mathematically, Step 2 is discussed in Equations (10) and (11). The schematic flowchart of the encryption process of the PTFT-based cryptosystem is depicted in Figure 8.
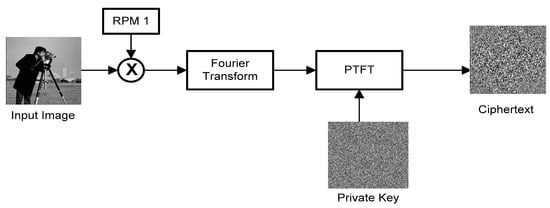
Figure 8.
Schematic flowchart of the encryption process of a PTFT-based cryptosystem.
- (b)
- Decryption process
The decryption process of the PTFT-based cryptosystem is discussed as:
Step 1: The private key and ciphertext are combined and propagated through the Fourier transform. Mathematically, the decryption process is discussed in Equation (12). Figure 9 depicts the schematic flowchart of the decryption process of the PTFT-based cryptosystem.
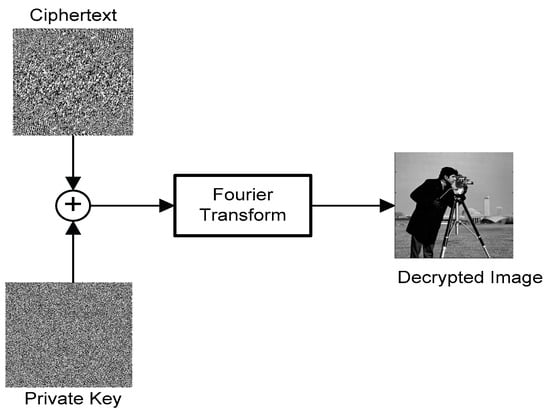
Figure 9.
Schematic flowchart of the decryption process of a PTFT-based cryptosystem.
For a computational demonstration of the PTFT-based encryption, a sample MATLAB code is given in the Supplementary Material.
4.2. Equal Modulus Decomposition
In 2015, Cai et al. proposed equal modulus decomposition (EMD) to solve the silhouette problem [68]. When EMD is applied on an image, it decomposes the signal into two complex masks of equal moduli, i.e., and ; one acts as a private key of the cryptosystem and the other is either further processed in the cryptosystem or acts as a private key [69,70,71]. To discuss the basic principle of equal modulus decomposition, an input image of the Cameraman is bonded with a random phase mask (RPM) and transformed through the Fourier transform. The output obtained after the Fourier transform is decomposed using EMD. The principle of EMD is depicted in Figure 10. The flowchart of a cryptosystem based on EMD is demonstrated in Figure 11 and can be mathematically represented by Equations (13)–(15).
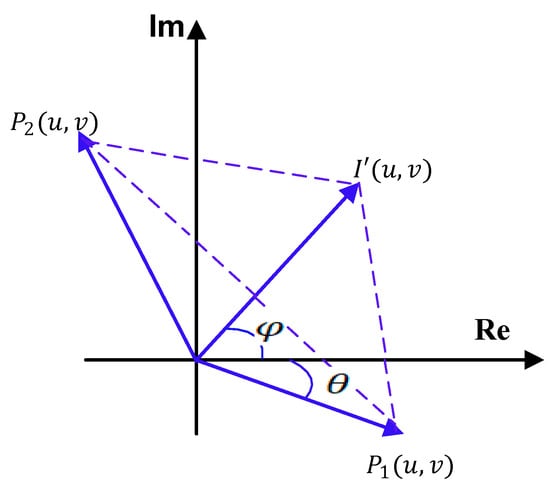
Figure 10.
Graphical representation of the principle of equal modulus decomposition.
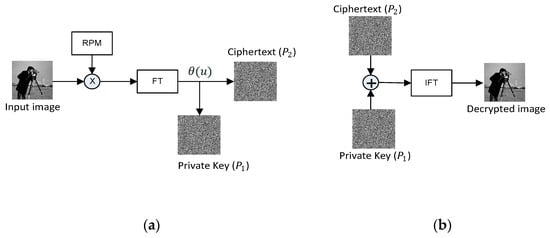
Figure 11.
Basic flow chart of the (a) encryption and (b) decryption process of EMD.
Here, represents the Fourier transform, , and . Choose , a random function which is distributed between to decompose into the equal moduli and given in Equations (14) and (15). The inverse of the equal modulus decomposition is given by Equation (16).
We have provided a MATLAB implementation of equal modulus decomposition in the Supplementary Material.
4.3. Random Modulus Decomposition
In random modulus decomposition (RMD), unlike in the EMD, the input signal is decomposed into two unequal random moduli. Suppose is the input image scrambled with a random phase mask (RPM) and propagated through the Fourier lens. The output obtained in the Fourier transformed signal is decomposed into two parts, and , by virtue of random modulus decomposition, as illustrated in Figure 12. The flowchart of the basic cryptosystem based on RMD is depicted in Figure 13 [72].
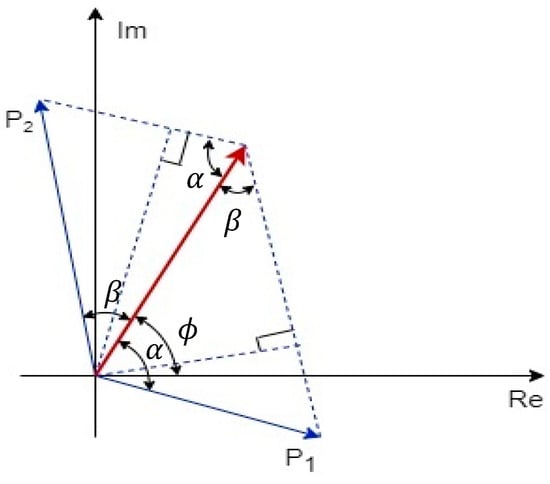
Figure 12.
The geometrical representation of random modulus decomposition.
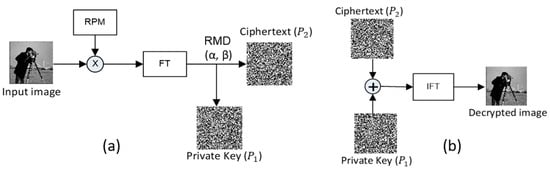
Figure 13.
Basic flow chart of the (a) encryption and (b) decryption process of EMD.
Mathematically,
The input image can be decomposed into two random complex parts, and . Mathematically, the random modulus decomposition is described in Equations (19)–(21).
Here, and are the amplitude and argument of the input image. Let and be random phase masks having values in the interval . The inverse of random modulus decomposition is given by Equation (22).
A simple demonstration of the above-discussed part for random modulation decomposition using MATLAB is given in the Supplementary Material.
4.4. Unequal Modulus Decomposition
This is a decomposition technique that divides a one- or two-dimensional signal into two signals having unequal phases and amplitudes. The unequal modulus decomposition is unlike that of the EMD or RMD and decomposes the input signal into two unequal moduli. Suppose is the input image that is diffused with a random phase mask (RPM) and propagated through the Fourier lens. The output obtained in the Fourier transformed signal is divided into two parts, and , by virtue of unequal modulus decomposition, as discussed in Figure 14. The flowchart of a basic cryptosystem based on UMD is depicted in Figure 15 [62,73,74,75]. Mathematically,
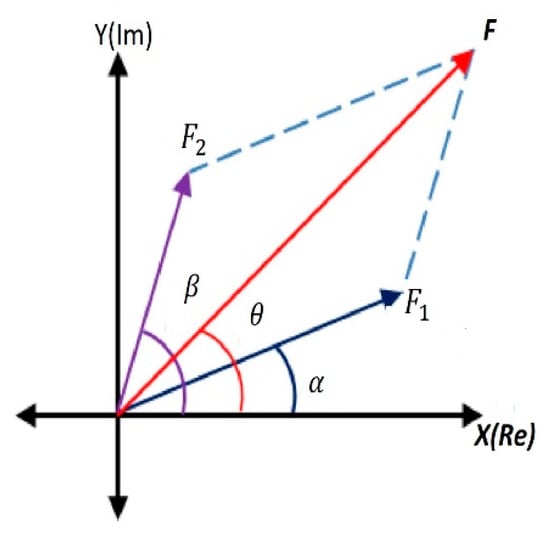
Figure 14.
Geometrical representation of unequal modulus decomposition (UMD).
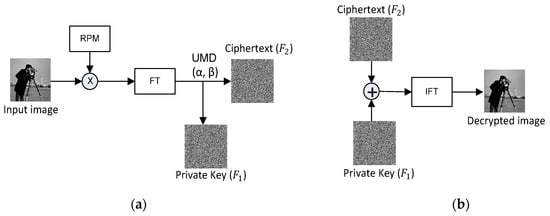
Figure 15.
Basic flow chart of the (a) encryption and (b) decryption process of UMD.
The phase and amplitude of are given by and , repectively. and are two randomly generated functions in the interval Mathematically, the decomposition of the signal is given in Equations (25) and (26).
The notational representation of unequal modulus decomposition is discussed in Equation (27).
where describes the unequal modulus decomposition function with the randomly generated functions and in interval .
The inverse of unequal modulus decomposition is given by Equation (28).
4.5. Polar Decomposition
The polar decomposition (PD) [76,77,78,79] is a process of decomposing a system into linearly independent factors. The PD of an image, of the size is given in Equation (30).
where and are symmetric, positive definite matrices of the size and are known as stretching matrices. is a rotational matrix of the size . A symmetric, positive definite matrix and the rotational matrix can be used to reconstruct the input matrix . Figure 16 demonstrates the geometrical representation of polar decomposition. This kind of decomposition gives the freedom to design multiuser optical encryption and authentication platforms, which can have several real-time applications. The MATLAB implementation of the polar decomposition of an image is given in the Supplementary Material.
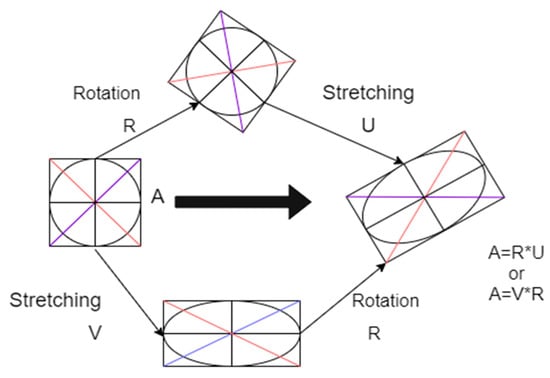
Figure 16.
A geometrical illustration of polar decomposition.
5. Other Optical Encryption Algorithms
Interference- [80,81], ghost imaging- [82,83] and holography [84,85,86]-based encryption algorithms represent innovative approaches to securing digital information, with applications ranging from communication to image protection [87,88,89,90,91,92,93]. Interference-based encryption harnesses the principles of wave interference, exploiting the complexity introduced by superimposing multiple light waves to encode information in a manner that id difficult to decipher without the correct key [94,95,96,97,98,99,100,101,102,103]. A schematic of optical image encryption is given in Figure 17. Here, two phase modulated masks, M1 and M2, are illuminated with a coherent source of light and interfered to obtain the final encrypted image in the output plane.
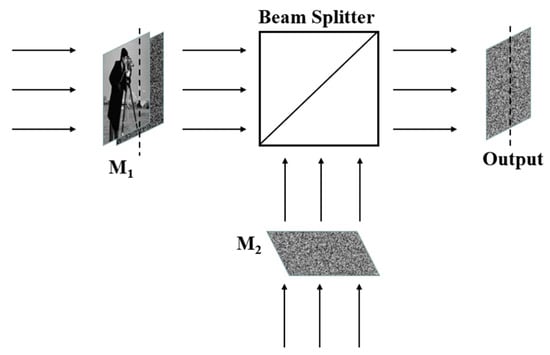
Figure 17.
Optical image encryption using interference.
Ghost imaging, on the other hand, involves capturing information through correlated intensity measurements of entangled photon pairs, providing a novel means of encryption that leverages quantum properties [104,105,106,107,108,109,110,111,112,113]. Holography-based encryption relies on the creation and reconstruction of holograms to encode and decode information [114,115,116,117,118,119,120,121,122,123]. These holographic encryption methods offer unique advantages, such as resistance to certain types of attacks and the ability to secure information in various modalities, contributing to the growing landscape of advanced cryptographic techniques in an era where data security is paramount [124,125,126,127,128,129,130,131]. The polarization properties of light provide another dimension for designing secure optical cryptosystems [132,133,134]. Recently, the physical random patterns or physically unclonable functions, i.e., optical speckles, have also been studied and explored to develop enhanced optical cryptosystems [135,136,137,138].
6. Attacks and Cryptanalysis
The development of new security methods and the attacks on them always go hand in hand. The study of cryptanalysis involves analyzing the operations of cryptosystems to achieve the correct decryption of data without using actual keys. The aim of cryptanalysis is to improve algorithms by identifying their weaknesses. To address the security issues of a cryptosystem, it is necessary to understand Kerckhoff’s principle. It states that a “cryptosystem should be secure even if the attacker has access to everything except the security key”. It was formulated at the end of the nineteenth century by the Dutch cryptographer Auguste Kerckhoff. In the field of optical security, the first attack on DRPE-based architecture was proposed by Peng et al. in 2006 [139]. Gopinathan et al. [87] also proposed a known plaintext attack on DRPE. After that, the inherent linearity of DRPE has been exploited by many to design various attacks for DRPE-based algorithms [140,141,142,143,144,145]. Afterwards, the asymmetric algorithms based on PTFT, EMD, RMD, UMD, polar decomposition, interference and various other methods have been reported. But sooner or later, some weakness of these methods have also been found, and some iterative and special iterative attacks have been designed to break them [6,146,147,148,149,150,151,152,153]. The MATLAB code for a simple chosen plaintext attack on the DRPE method using the Dirac delta function is given in the Supplementary Material.
7. Future Scope
As we know, in the future, more and more data will be generated, and data breaches by unauthorized individuals are inevitable. The current security protocols are not enough to fulfill the demands of the modern world. Thus, more sophisticated secure transmission protocols need to be developed. So, there is a scope for enhancement in the security of image encryption algorithms. Therefore, in the upcoming years, researchers could continue the research by using cutting-edge technology and countering the available challenges. The following are a few directions and potential candidates which can be integrated with optical methods and could provide the necessary solutions to the coming challenges in the field of security:
- Machine learning and AI in encryption: The integration of artificial intelligence (AI) and machine learning (ML) algorithms into an optical encryption system represents a promising avenue for bolstering security. By leveraging these technologies, encryption algorithms can be elevated to a new level of sophistication, dynamically adapting to the characteristics of image data and thereby increasing resilience against decryption attempts. ML’s prowess in pattern recognition is harnessed for anomaly detection, enabling the identification of potential threats or unauthorized access. Furthermore, AI contributes to optimal key management, continuously analyzing usage patterns and recommending adjustments to fortify the encryption system. Real-time threat adaptation and behavioral analysis enhance the system’s ability to respond to evolving risks, while adversarial machine learning techniques can anticipate and counteract specific attacks targeting the security of image data. In addressing quantum computing challenges, AI and ML also play a role in developing quantum-safe encryption methods, ensuring the enduring security of image information. Careful consideration of ethical implications and robust testing accompanies the implementation of these advanced technologies to ensure the reliability and effectiveness of the encrypted systems.
- Multi-modal fusion: Integrating optical image encryption with other modalities, such as infrared or hyper-spectral imaging, offers a promising approach to fortifying the overall security of the encryption process. The synergy of different imaging modalities through multi-modal fusion introduces additional layers of complexity, significantly heightening the challenge for unauthorized entities attempting to decipher encrypted information. By combining optical encryption with diverse imaging techniques, the resulting system becomes more resilient to decryption attempts that rely on understanding a singular mode of information. This multi-modal approach not only enhances security but also broadens the range of potential applications, catering to scenarios where different imaging modalities may provide complementary benefits. As technology evolves, leveraging multi-modal fusion in image encryption underscores a proactive strategy in adapting to emerging threats and ensuring the robustness of secure information transmission.
- Optical communication networks: The increasing prevalence of high-speed optical communication networks is driving a growing demand for efficient and secure optical image encryption methods. This demand is particularly pronounced in critical applications such as secure data transmission within optical communication systems, medical imaging, military communications and various other domains where the confidentiality and integrity of transmitted visual information are paramount. Efficient optical image encryption not only safeguards sensitive data but also ensures the seamless flow of secure information in fast-paced communication environments. The adoption of robust encryption techniques becomes crucial as these technologies play pivotal roles in diverse sectors, ranging from healthcare to defense, underlining the broader societal implications of advancing secure optical image transmission methods.
- Blockchain integration: The integration of optical image encryption with blockchain technology presents a compelling solution for secure image storage and transmission. By leveraging blockchain’s decentralized and tamper-resistant nature, the combination ensures the integrity and authenticity of encrypted images. Blockchain’s distributed ledger technology creates an immutable record of transactions, making it extremely challenging for unauthorized entities to tamper with or alter the encrypted images. This decentralized approach enhances security by eliminating single points of failure and reducing the risk of malicious interference. Moreover, the transparent and traceable nature of blockchain adds an extra layer of trust, providing a verifiable history of image transactions. This innovative fusion of optical image encryption and blockchain technology not only strengthens data security but also aligns with the growing emphasis on decentralized and transparent solutions in various industries.
- Biometric encryption: Integrating optical image encryption with biometric authentication methods offers a potent enhancement to security by introducing a user-specific identification layer. This approach involves incorporating biometric features such as fingerprints, iris scans, or facial recognition to control access to encrypted images. By tying encrypted image access to unique biometric data, the system ensures that only authorized individuals with verified biometric credentials can decrypt and view sensitive visual information. This not only strengthens the overall security posture by adding a personalized layer of authentication but also mitigates risks associated with unauthorized access or data breaches [154]. The combination of optical image encryption and biometric authentication aligns with the trend toward multifactor authentication and provides a robust solution for safeguarding visual data in applications ranging from secure communications to access-controlled image repositories.
8. Conclusions
In conclusion, the security of information stands as a critical imperative in the contemporary era, prompting a continual exploration of advanced encryption methodologies. Optical encryption algorithms emerge as particularly noteworthy in this context due to their high-speed and multi-dimensional processing capabilities. This study presents a comprehensive review of optical image encryption algorithms, as proposed in the literature, analyzing the trends in their growth over time. Drawing upon data collected from reputable sources such as Google Scholar, IEEE Library, and Science Direct, the manuscript provides an in-depth examination of the evolution of optical cryptosystems since their inception. The focus on symmetric and asymmetric cryptosystems in the literature underscores the diverse approaches taken to enhance security. The summary of state-of-the-art works highlights the progress made in this field, while acknowledging the current and future challenges provides valuable insights for ongoing research and development in optical image encryption algorithms. This study contributes to the broader understanding of securing digital information and lays the groundwork for future advancements in optical encryption technology.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/photonics11010099/s1.
Author Contributions
Conceptualization, R.K.; methodology, S. (Sachin) and R.K.; software, S. (Sachin) and R.K.; validation, S. (Sachin), S.(Sakshi), R.Y. and R.K.; formal analysis, S. (Sachin), S. (Sakshi) and R.Y.; investigation, S. (Sachin), S. (Sakshi), R.Y., S.G.R., A.K.Y., P.S. and R.K.; resources, S. (Sachin), A.K.Y., P.S. and R.K.; data curation, S. (Sachin) and R.K.; writing—original draft preparation, S. (Sachin) and R.K.; writing—review and editing, S. (Sachin), S. (Sakshi), R.Y., S.G.R., A.K.Y., P.S. and R.K.; supervision, R.K., P.S. and S.G.R.; project administration, R.K.; funding acquisition, R.K. and S.G.R. All authors have read and agreed to the published version of the manuscript.
Funding
R.K. would like to acknowledge the support from the Science and Engineering Research Board (SERB), the Government of India, under the SERB SURE research grant (File No. SUR/2022/000910) and SRM University—AP for the seed grant SRMAP/URG/SEED/2023-24/044, and S.G.R. would like to acknowledge the support from SRM University—AP for the seed research grants under SRMAP/URG/CG/2022-23/006 and SRMAP/URG/E&PP/2022-23/003.
Data Availability Statement
Not Applicable.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Biryukov, A. The boomerang Attack on 5 and 6-Round Reduced AES. In Advanced Encryption Standard—AES; Dobbertin, H., Rijmen, V., Sowa, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3373, pp. 11–15. [Google Scholar] [CrossRef]
- Al Hasib, A.; Haque, A.A.M.M. A Comparative Study of the Performance and Security Issues of AES and RSA Cryptography. In Proceedings of the 2008 Third International Conference on Convergence and Hybrid Information Technology (ICCIT), Busan, Republic of Korea, 11–13 November 2008; pp. 505–510. [Google Scholar]
- Cai, Z.; Chen, J.; Pedrini, G.; Osten, W.; Liu, X.; Peng, X. Lensless light-field imaging through diffuser encoding. Light. Sci. Appl. 2020, 9, 143. [Google Scholar] [CrossRef]
- Lopez-Caloca, A.; Escalante-Ramirez, B. The Hermite transform: An efficient tool for noise reduction and image fusion in remote-sensing. In Image Processing for Remote Sensing; Chen, C., Ed.; CRC Press: Boca Raton, FL, USA, 2007; pp. 273–291. [Google Scholar] [CrossRef]
- Kumar, R.; Zhong, F.; Quan, C. Optical voice information hiding using enhanced iterative algorithm and computational ghost imaging. J. Opt. 2019, 21, 065704. [Google Scholar] [CrossRef]
- Sachin; Kumar, R.; Singh, P. Modified plaintext attacks in a session for an optical cryptosystem based on DRPE with PFS. Appl. Opt. 2021, 61, 623–628. [Google Scholar] [CrossRef]
- Yadav, R.; Singh, P. Asymmetric image authentication algorithm using double random modulus decomposition and CGI. Comput. Appl. Math. 2023, 42, 305. [Google Scholar] [CrossRef]
- Girija, R.; Singh, H. A robust correlation analysis framework for imbalanced and dichotomous data with uncertainty. 3D Res. 2018, 9, 42. [Google Scholar] [CrossRef]
- Monaghan, D.S.; Gopinathan, U.; Naughton, T.J.; Sheridan, J.T. A Numerical Analysis of Double Random Phase Encryption. In Optical Information Systems IV; SPIE: Bellingham, WA, USA, 2006; pp. 222–230. [Google Scholar]
- Kishk, S.; Javidi, B. Information hiding technique with double phase encoding. Appl. Opt. 2002, 41, 5462. [Google Scholar] [CrossRef]
- Refregier, P.; Javidi, B. Optical image encryption based on input plane and Fourier plane random encoding. Opt. Lett. 1995, 20, 767. [Google Scholar] [CrossRef]
- Javidi, B.; Zhang, G.; Li, J. Experimental demonstration of the random phase encoding technique for image encryption and security verification. Opt. Eng. 1996, 35, 2506–2512. [Google Scholar] [CrossRef]
- Javidi, B.; Zhang, G.; Li, J. Encrypted optical memory using double random phase encoding. In Proceedings of the LEOS’96 9th Annual Meeting IEEE Lasers and Electro-Optics Society, Boston, MA, USA, 18–21 November 1996. [Google Scholar]
- Yang, H.; Kim, E. Practical image encryption scheme by real-valued data. Opt. Eng. 1996, 35, 2473–2478. [Google Scholar] [CrossRef]
- Johnson, E.G.; Brasher, J.D. Phase encryption of biometrics in diffractive optical elements. Opt. Lett. 1996, 21, 1271–1273. [Google Scholar] [CrossRef]
- Javidi, B.; Sergent, A.; Zhang, G.; Guibert, L. Fault tolerance properties of a double phase encoding encryption technique. Opt. Eng. 1997, 36, 992–998. [Google Scholar] [CrossRef]
- Johnson, E.G.; Brasher, J.D. Incoherent optical correlators and phase encoding of identification codes for access control or authentication. Opt. Eng. 1997, 36, 2409–2416. [Google Scholar] [CrossRef]
- Clelland, C.T.; Risca, V.; Bancroft, C. Hiding messages in DNA microdots. Nature 1999, 399, 533–534. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Zhang, Q.; Zhou, C. A multilevel image encryption algorithm based on chaos and DNA coding. In Proceedings of the 2009 Fourth International Conference on Bio-Inspired Computing (BIC-TA), Beijing, China, 16–19 October 2009; pp. 1–5. [Google Scholar]
- Sachin; Archana; Singh, P. Optical image encryption algorithm based on chaotic Tinkerbell map with random phase masks in Fourier domain. In Lecture Notes in Networks and Systems; Ray, K., Roy, K.C., Toshniwal, S.K., Sharma, H., Bandyopadhyay, A., Eds.; Springer: Singapore, 2021; Volume 148, pp. 249–262. [Google Scholar] [CrossRef]
- Krishna, P.R.; Teja, C.V.S.M.S.; Teja, R.D.S. A Chaos Based Image Encryption Using Tinkerbell Map Functions. In Proceedings of the 2018 Second International Conference on Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, 29–31 March 2018; pp. 578–582. [Google Scholar]
- Archana; Sachin; Singh, P. Cryptosystem based on triple random phase encoding with chaotic Henon map. In Lecture Notes in Networks and Systems; Ray, K., Roy, K.C., Toshniwal, S.K., Sharma, H., Bandyopadhyay, A., Eds.; Springer: Singapore, 2021; Volume 148, pp. 73–84. [Google Scholar] [CrossRef]
- Chen, H.; Du, X.; Liu, Z. Optical spectrum encryption in associated fractional Fourier transform and gyrator transform domain. Opt. Quantum Electron. 2015, 48, 12. [Google Scholar] [CrossRef]
- Chen, L.; Zhao, D. Optical image encryption with Hartley transforms. Opt. Lett. 2006, 31, 3438. [Google Scholar] [CrossRef] [PubMed]
- Singh, P.; Yadav, A.K.; Singh, K.; Saini, I. Asymmetric watermarking scheme in fractional Hartley domain using modified equal modulus decomposition. J. Optoelectron. Adv. Mater. 2019, 21, 484–491. [Google Scholar]
- Singh, P.; Yadav, A.K.; Singh, K. Color image encryption using affine transform in fractional Hartley domain. Opt. Appl. 2017, 47, 421–433. [Google Scholar] [CrossRef]
- Kumar, R.; Bhaduri, B. Optical image encryption in Fresnel domain using spiral phase transform. J. Opt. 2017, 19, 095701. [Google Scholar] [CrossRef]
- Agoyi, M.; Çelebi, E.; Anbarjafari, G. A watermarking algorithm based on chirp z-transform, discrete wavelet transform, and singular value decomposition. Signal Image Video Process. 2015, 9, 735–745. [Google Scholar] [CrossRef]
- El-Khamy, S.E.; Mohamed, A.G. An efficient DNA-inspired image encryption algorithm based on hyper-chaotic maps and wavelet fusion. Multimedia Tools Appl. 2021, 80, 23319–23335. [Google Scholar] [CrossRef]
- Fan, P.; Hou, M.; Hu, W.; Xiao, K. Quantum Image Encryption Based on Block Geometric and Haar Wavelet Transform. Int. J. Theor. Phys. 2022, 61, 260. [Google Scholar] [CrossRef]
- Rakheja, P.; Vig, R.; Singh, P. A hybrid multiresolution wavelet transform based encryption scheme. In Proceedings of the Emerging Trends in Mathematical Sciences and Its Applications: Proceedings of the 3rd International Conference on Recent Advances in Mathematical Sciences and its Applications (RAMSA-2019), Noida, India, 17–19 January 2019; p. 020008. [Google Scholar]
- Yuan, S.; Magayane, D.A.; Liu, X.; Zhou, X.; Lu, G.; Wang, Z.; Zhang, H.; Li, Z. A blind watermarking scheme based on computational ghost imaging in wavelet domain. Opt. Commun. 2021, 482, 126568. [Google Scholar] [CrossRef]
- Wu, C.; Chang, J.; Quan, C.; Zhang, X.; Zhang, Y. The optical image compression and encryption method based on Fresnel diffraction and discrete wavelet transform. Results Opt. 2020, 1, 100021. [Google Scholar] [CrossRef]
- Zhu, A.-H.; Li, L. Improving for chaotic image encryption algorithm based on logistic map. In Proceedings of the 2nd Conference on Environmental Science and Information Application Technology (ESIAT), Wuhan, China, 9 September 2010; pp. 211–214. [Google Scholar]
- Jain, A.; Rajpal, N. A robust image encryption algorithm resistant to attacks using DNA and chaotic logistic maps. Multimedia Tools Appl. 2016, 75, 5455–5472. [Google Scholar] [CrossRef]
- Muñoz-Guillermo, M. Image encryption using q-deformed logistic map. Inf. Sci. 2021, 552, 352–364. [Google Scholar] [CrossRef]
- Belokolos, E.; Kharchenko, V.; Kharchenko, D. Chaos in a generalized Lorenz system. Chaos Solitons Fractals 2009, 41, 2595–2605. [Google Scholar] [CrossRef][Green Version]
- Anees, A. An Image Encryption Scheme Based on Lorenz System for Low Profile Applications. 3D Res. 2015, 6, 24. [Google Scholar] [CrossRef]
- Rakheja, P.; Vig, R.; Singh, P. Double image encryption using 3D Lorenz chaotic system, 2D non-separable linear canonical transform and QR decomposition. Opt. Quantum Electron. 2020, 52, 103. [Google Scholar] [CrossRef]
- Elshamy, A.M.; Rashed, A.N.Z.; Mohamed, A.E.-N.A.; Faragalla, O.S.; Mu, Y.; Alshebeili, S.A.; El-Samie, F.E.A. Optical image encryption based on chaotic baker map and double random phase encoding. J. Light. Technol. 2013, 31, 2533–2539. [Google Scholar] [CrossRef]
- Faragallah, O.S.; Afifi, A. Optical color image cryptosystem using chaotic baker mapping based-double random phase encoding. Opt. Quantum Electron. 2017, 49, 89. [Google Scholar] [CrossRef]
- Elshamy, A.M.; El-Samie, F.E.A.; Faragallah, O.S.; Elshamy, E.M.; El-Sayed, H.S.; El-Zoghdy, S.F.; Rashed, A.N.Z.; Mohamed, A.E.-N.A.; Alhamad, A.Q. Optical image cryptosystem using double random phase encoding and Arnold’s Cat map. Opt. Quantum Electron. 2016, 48, 212. [Google Scholar] [CrossRef]
- Guleria, V.; Mishra, D.C. A new multi-layer RGB image encryption algorithm based on Diffie-Hellman cryptography associated with FrDCT and arnold transform. Multimed. Tools Appl. 2020, 79, 33119–33160. [Google Scholar] [CrossRef]
- Jiao, K.; Ye, G.; Dong, Y.; Huang, X.; He, J. Image Encryption Scheme Based on a Generalized Arnold Map and RSA Algorithm. Secur. Commun. Netw. 2020, 2020, 9721675. [Google Scholar] [CrossRef]
- Sachin; Singh, P. A novel chaotic Umbrella map and its application to image encryption. Opt. Quantum Electron. 2022, 54, 266. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Sharma, R.R.; Pachori, R.B. Improved eigenvalue decomposition-based approach for reducing cross-terms in wigner–ville distribution. Circuits Syst. Signal Process. 2018, 37, 3330–3350. [Google Scholar] [CrossRef]
- Anand, V.; Rosen, J.; Ng, S.H.; Katkus, T.; Linklater, D.P.; Ivanova, E.P.; Juodkazis, S. Edge and contrast enhancement using spatially incoherent correlation holography techniques. Photonics 2021, 8, 224. [Google Scholar] [CrossRef]
- Su, Y.; Tang, C.; Chen, X.; Li, B.; Xu, W.; Lei, Z. Cascaded Fresnel holographic image encryption scheme based on a constrained optimization algorithm and Henon map. Opt. Lasers Eng. 2017, 88, 20–27. [Google Scholar] [CrossRef]
- Kumar, R.; Quan, C. Optical colour image encryption using spiral phase transform and chaotic pixel scrambling. J. Mod. Opt. 2019, 66, 776–785. [Google Scholar] [CrossRef]
- Diaconu, A.-V. Circular inter–intra pixels bit-level permutation and chaos-based image encryption. Inf. Sci. 2016, 355–356, 314–327. [Google Scholar] [CrossRef]
- Khan, L.S.; Hazzazi, M.M.; Khan, M.; Jamal, S.S. A novel image encryption based on rossler map diffusion and particle swarm optimization generated highly non-linear substitution boxes. Chin. J. Phys. 2021, 72, 558–574. [Google Scholar] [CrossRef]
- Lin, C.-Y.; Wu, J.-L. Cryptanalysis and improvement of a chaotic map-based image encryption system using both plaintext related permutation and diffusion. Entropy 2020, 22, 589. [Google Scholar] [CrossRef]
- Ben Slimane, N.; Aouf, N.; Bouallegue, K.; Machhout, M. A novel chaotic image cryptosystem based on DNA sequence operations and single neuron model. Multimed. Tools Appl. 2018, 77, 30993–31019. [Google Scholar] [CrossRef]
- Mosso, E.; Suárez, O.; Bolognini, N. Asymmetric multiple-image encryption system based on a chirp z-transform. Appl. Opt. 2019, 58, 5674–5680. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Li, Y. Chaotic image encryption algorithm based on hybrid multi-objective particle swarm optimization and DNA sequence. Opt. Lasers Eng. 2021, 137, 106393. [Google Scholar] [CrossRef]
- Qin, W.; Peng, X. Asymmetric cryptosystem based on phase-truncated Fourier transforms. Opt. Lett. 2010, 35, 118. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, D. A special attack on the asymmetric cryptosystem based on phase-truncated Fourier transforms. Opt. Commun. 2012, 285, 1078–1081. [Google Scholar] [CrossRef]
- Gupta, K.; Silakari, S.; Gupta, R.; Khan, S.A. An Ethical Way of Image Encryption Using ECC. In Proceedings of the 2009 First International Conference on Computational Intelligence, Communication Systems and Networks (CICSYN), Indore, India, 23–25 July 2009; pp. 342–345. [Google Scholar]
- Barfungpa, S.P.; Abuturab, M.R. Asymmetric cryptosystem using coherent superposition and equal modulus decomposition of fractional Fourier spectrum. Opt. Quantum Electron. 2016, 48, 520. [Google Scholar] [CrossRef]
- Deng, X. Asymmetric optical cryptosystem based on coherent superposition and equal modulus decomposition: Comment. Opt. Lett. 2015, 40, 3913. [Google Scholar] [CrossRef]
- Chen, L.; Gao, X.; Chen, X.; He, B.; Liu, J.; Li, D. A new optical image cryptosystem based on two-beam coherent superposition and unequal modulus decomposition. Opt. Laser Technol. 2016, 78, 167–174. [Google Scholar] [CrossRef]
- Rakheja, P.; Vig, R.; Singh, P. An asymmetric hybrid cryptosystem using equal modulus and random decomposition in hybrid transform domain. Opt. Quantum Electron. 2019, 51, 54. [Google Scholar] [CrossRef]
- Chen, H.; Zhu, L.; Liu, Z.; Tanougast, C.; Liu, F.; Blondel, W. Optical single-channel color image asymmetric cryptosystem based on hyperchaotic system and random modulus decomposition in Gyrator domains. Opt. Lasers Eng. 2020, 124, 105809. [Google Scholar] [CrossRef]
- Xiong, Y.; Du, J.; Quan, C. Single-channel optical color image cryptosystem using two-step phase-shifting interferometry and random modulus decomposition. Opt. Laser Technol. 2019, 119, 105580. [Google Scholar] [CrossRef]
- Sachin; Kumar, R.; Singh, P. Multiuser optical image authentication platform based on sparse constraint and polar decomposition in Fresnel domain. Phys. Scr. 2022, 97, 115101. [Google Scholar] [CrossRef]
- Sachin, S.; Kumar, R.; Singh, P. Unequal modulus decomposition and modified Gerchberg Saxton algorithm based asymmetric cryptosystem in Chirp-Z transform domain. Opt. Quantum Electron. 2021, 53, 254–274. [Google Scholar] [CrossRef]
- Cai, J.; Shen, X.; Lei, M.; Lin, C.; Dou, S. Asymmetric optical cryptosystem based on coherent superposition and equal modulus decomposition. Opt. Lett. 2015, 40, 475. [Google Scholar] [CrossRef]
- Rakheja, P.; Vig, R.; Singh, P.; Kumar, R. An iris biometric protection scheme using 4D hyperchaotic system and modified equal modulus decomposition in hybrid multi resolution wavelet domain. Opt. Quantum Electron. 2019, 51, 204. [Google Scholar] [CrossRef]
- Kumar, R.; Bhaduri, B.; Quan, C. Asymmetric optical image encryption using Kolmogorov phase screens and equal modulus decomposition. Opt. Eng. 2017, 56, 113109. [Google Scholar] [CrossRef]
- Kumar, R.; Bhaduri, B.; Nishchal, N.K. Nonlinear QR code based optical image encryption using spiral phase transform, equal modulus decomposition and singular value decomposition. J. Opt. 2018, 20, 015701. [Google Scholar] [CrossRef]
- Cai, J.; Shen, X.; Lin, C. Security-enhanced asymmetric optical cryptosystem based on coherent superposition and equal modulus decomposition. Opt. Commun. 2016, 359, 26–30. [Google Scholar] [CrossRef]
- Abdelfattah, M.; Hegazy, S.F.; Areed, N.F.; Obayya, S.S. Compact optical asymmetric cryptosystem based on unequal modulus decomposition of multiple color images. Opt. Lasers Eng. 2020, 129, 106063. [Google Scholar] [CrossRef]
- Abuturab, M.R. Securing multiple-single-channel color image using unequal spectrum decomposition and 2D-SLIM biometric keys. Opt. Commun. 2021, 493, 127034. [Google Scholar] [CrossRef]
- Archana; Singh, P.; Rakheja, P. Asymmetric watermarking scheme for color images using cascaded unequal modulus decomposition in Fourier domain. J. Mod. Opt. 2021, 68, 1094–1107. [Google Scholar] [CrossRef]
- Higham, N.J. Computing the Polar Decomposition—With Applications. SIAM J. Sci. Stat. Comput. 1986, 7, 1160–1174. [Google Scholar] [CrossRef]
- Kumar, R.; Quan, C. Asymmetric multi-user optical cryptosystem based on polar decomposition and Shearlet transform. Opt. Lasers Eng. 2019, 120, 118–126. [Google Scholar] [CrossRef]
- Oussama, N.; Assia, B.; Lemnouar, N. Secure image encryption scheme based on polar decomposition and chaotic map. Int. J. Inf. Commun. Technol. 2017, 10, 437–453. [Google Scholar] [CrossRef]
- Singh, S.P.; Bhatnagar, G.; Gurjar, D.K. A secure image encryption algorithm based on polar decomposition. In Proceedings of the 2018 IEEE 14th International Colloquium on Signal Processing & Its Applications (CSPA), Penang, Malaysia, 9–10 March 2018; pp. 135–139. [Google Scholar]
- Chen, L.; Liu, J.; Wen, J.; Gao, X.; Mao, H.; Shi, X.; Qu, Q. A new optical image encryption method based on multi-beams interference and vector composition. Opt. Laser Technol. 2015, 69, 80–86. [Google Scholar] [CrossRef]
- He, W.; Peng, X.; Meng, X.; Liu, X. Collision in optical image encryption based on interference and a method for avoiding this security leak. Opt. Laser Technol. 2013, 47, 31–36. [Google Scholar] [CrossRef]
- Chen, Z.; Shi, J.; Zeng, G. Object authentication based on compressive ghost imaging. Appl. Opt. 2016, 55, 8644–8650. [Google Scholar] [CrossRef]
- Li, X.; Meng, X.; Wang, Y.; Yang, X.; Yin, Y.; Peng, X.; He, W.; Dong, G.; Chen, H. Secret shared multiple-image encryption based on row scanning compressive ghost imaging and phase retrieval in the Fresnel domain. Opt. Lasers Eng. 2017, 96, 7–16. [Google Scholar] [CrossRef]
- Kong, D.; Cao, L.; Jin, G.; Javidi, B. Three-dimensional scene encryption and display based on computer-generated holograms. Appl. Opt. 2016, 55, 8296–8300. [Google Scholar] [CrossRef] [PubMed]
- Chang, H.T.; Wang, Y.-T.; Chen, C.-Y. Angle Multiplexing Optical image encryption in the fresnel transform domain using phase-only computer-generated hologram. Photonics 2020, 7, 1. [Google Scholar] [CrossRef]
- Guo, Y.; Huang, Q.; Du, J.; Zhang, Y. Decomposition storage of information based on computer-generated hologram interference and its application in optical image encryption. Appl. Opt. 2001, 40, 2860–2863. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q. Optical image encryption with silhouette removal based on interference and phase blend processing. Opt. Commun. 2012, 285, 4294–4301. [Google Scholar] [CrossRef]
- Shapiro, J.H. Computational ghost imaging. Phys. Rev. A 2008, 78, 061802. [Google Scholar] [CrossRef]
- Nishchal, N.K.; Joseph, J.; Singh, K. Fully phase encryption using digital holography. Opt. Eng. 2004, 43, 2959–2966. [Google Scholar] [CrossRef]
- Xiong, Y.; Gu, J.; Kumar, R. Collision in a phase-only asymmetric cryptosystem based on interference and phase-truncated Fourier transforms. Opt. Quantum Electron. 2023, 55, 667. [Google Scholar] [CrossRef]
- Gopinath, S.; Bleahu, A.; Kahro, T.; Rajeswary, A.S.J.F.; Kumar, R.; Kukli, K.; Tamm, A.; Rosen, J.; Anand, V. Enhanced design of multiplexed coded masks for Fresnel incoherent correlation holography. Sci. Rep. 2023, 13, 7390. [Google Scholar] [CrossRef]
- Huang, J.; Shi, D.; Meng, W.; Zha, L.; Yuan, K.; Hu, S.; Wang, Y. Spectral encoded computational ghost imaging. Opt. Commun. 2020, 474, 126105–126113. [Google Scholar] [CrossRef]
- Zhu, N.; Wang, Y.-T.; Liu, J.; Xie, J.-H.; Zhang, H. Optical image encryption based on interference of polarized light. Opt. Express 2009, 17, 13418–13424. [Google Scholar] [CrossRef]
- Xiong, Y.; Gu, J.; Kumar, R. Security analysis on an interference-based optical image encryption scheme. Appl. Opt. 2022, 61, 9045–9051. [Google Scholar] [CrossRef]
- Deng, X.; Wen, W. Optical multiple-image encryption based on fully phase encoding and interference. Optik 2015, 126, 3210–3214. [Google Scholar] [CrossRef]
- Chen, W.; Chen, X. Security-enhanced interference-based optical image encryption. Opt. Commun. 2013, 286, 123–129. [Google Scholar] [CrossRef]
- Chen, W.; Chen, X. Interference-based optical image encryption using three-dimensional phase retrieval. Appl. Opt. 2012, 51, 6076–6083. [Google Scholar] [CrossRef]
- Gong, Q.; Wang, Z.; Lv, X.; Qin, Y. Interference-based image encryption with silhouette removal by aid of compressive sensing. Opt. Commun. 2016, 359, 290–296. [Google Scholar] [CrossRef]
- Wang, H.; Qin, Y.; Huang, Y.; Wang, Z.; Zhang, Y. Multiple-image encryption and authentication in interference-based scheme by aid of space multiplexing. Opt. Laser Technol. 2017, 95, 63–71. [Google Scholar] [CrossRef]
- Wang, Q.; Guo, Q.; Lei, L.; Zhou, J. Single-beam image encryption using spatially separated ciphertexts based on interference principle in the Fresnel domain. Opt. Commun. 2014, 333, 151–158. [Google Scholar] [CrossRef]
- Liansheng, S.; Bei, Z.; Zhanmin, W.; Qindong, S. Amplitude-phase retrieval attack free image encryption based on two random masks and interference. Opt. Lasers Eng. 2016, 86, 1–10. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, B. Optical image encryption based on interference. Opt. Lett. 2008, 33, 2443–2445. [Google Scholar] [CrossRef]
- Xiong, Y.; Kumar, R. Security analysis on the interference-based optical image cryptosystem with a designed amplitude modulator. Appl. Opt. 2022, 61, 5998–6005. [Google Scholar] [CrossRef]
- Clemente, P.; Durán, V.; Torres-Company, V.; Tajahuerce, E.; Lancis, J. Optical encryption based on computational ghost imaging. Opt. Lett. 2010, 35, 2391–2393. [Google Scholar] [CrossRef]
- Tanha, M.; Kheradmand, R.; Ahmadi-Kandjani, S. Gray-scale and color optical encryption based on computational ghost imaging. Appl. Phys. Lett. 2012, 101, 101108. [Google Scholar] [CrossRef]
- Tao, Y.; Yang, X.; Meng, X.; Wang, Y.; Yin, Y.; Dong, G. Plaintext-related multiple-image encryption based on computational ghost imaging. J. Mod. Opt. 2020, 67, 394–404. [Google Scholar] [CrossRef]
- Yi, C.; Zhengdong, C.; Xiang, F.; Yubao, C.; Zhenyu, L. Compressive sensing ghost imaging based on image gradient. Optik 2019, 182, 1021–1029. [Google Scholar] [CrossRef]
- Zhu, J.; Yang, X.; Meng, X.; Wang, Y.; Yin, Y.; Sun, X.; Dong, G. Computational ghost imaging encryption based on fingerprint phase mask. Opt. Commun. 2018, 420, 34–39. [Google Scholar] [CrossRef]
- Yuan, S.; Han, Y.; Liu, X.; Li, Z.; Bing, P.; Zhou, X. Optical encryption for multi-user based on computational ghost imaging with Hadamard modulation. Optik 2023, 273, 170500. [Google Scholar] [CrossRef]
- Chen, W.; Chen, X. Object authentication in computational ghost imaging with the realizations less than 5% of Nyquist limit. Opt. Lett. 2013, 38, 546–548. [Google Scholar] [CrossRef]
- Liansheng, S.; Yin, C.; Ailing, T.; Asundi, A.K. An optical watermarking scheme with two-layer framework based on computational ghost imaging. Opt. Lasers Eng. 2018, 107, 38–45. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, S.; Cheng, W.; Gong, L.; Chen, H. Optical image hiding based on computational ghost imaging. Opt. Commun. 2016, 366, 314–320. [Google Scholar] [CrossRef]
- Wu, J.; Xie, Z.; Liu, Z.; Liu, W.; Zhang, Y.; Liu, S. Multiple-image encryption based on computational ghost imaging. Opt. Commun. 2016, 359, 38–43. [Google Scholar] [CrossRef]
- Yu, C.; Li, X.; Xu, S.; Li, J. Computer generated hologram-based image cryptosystem with multiple chaotic systems. Wirel. Netw. 2021, 27, 3507–3521. [Google Scholar] [CrossRef]
- Yu, C.; Li, J.; Li, X.; Ren, X.; Gupta, B.B. Four-image encryption scheme based on quaternion Fresnel transform, chaos and computer generated hologram. Multimedia Tools Appl. 2018, 77, 4585–4608. [Google Scholar] [CrossRef]
- Xi, S.; Yu, N.; Wang, X.; Ying, M.; Dong, Z.; Zhu, Q.; Wang, W.; Wang, H. Optical encryption method of multiple-image based on θ modulation and computer generated hologram. Opt. Commun. 2019, 445, 19–23. [Google Scholar] [CrossRef]
- Wang, Y.-Y.; Wang, Y.-R.; Li, H.-J.; Sun, W.-J. Optical image encryption based on binary Fourier transform computer-generated hologram and pixel scrambling technology. Opt. Lasers Eng. 2007, 45, 761–765. [Google Scholar] [CrossRef]
- Liu, J.; Jin, H.; Ma, L.; Li, Y.; Jin, W. Optical color image encryption based on computer generated hologram and chaotic theory. Opt. Commun. 2013, 307, 76–79. [Google Scholar] [CrossRef]
- Kong, D.; Shen, X.; Shen, Y.; Wang, X. Multi-image encryption based on interference of computer generated hologram. Optik 2014, 125, 2365–2368. [Google Scholar] [CrossRef]
- Kong, D.; Cao, L.; Shen, X.; Zhang, H.; Jin, G. Image encryption based on interleaved computer-generated holograms. IEEE Trans. Ind. Inform. 2018, 14, 673–678. [Google Scholar] [CrossRef]
- He, Z.; Liu, K.; Cao, L. Watermarking and encryption for holographic communication. Photonics 2022, 9, 675. [Google Scholar] [CrossRef]
- Kadhim, M.W.; Kafi, D.A.; Abed, E.A.; Jamal, R.K. A novel technique in encryption information based on Chaos–hologram. J. Opt. 2023, 52, 1976–1982. [Google Scholar] [CrossRef]
- Sun, X.; Hu, T.; Ma, L.; Jin, W. The encryption and decryption technology with chaotic iris and compressed sensing based on computer-generated holography. J. Opt. 2022, 51, 124–132. [Google Scholar] [CrossRef]
- Liu, S.; Guo, C.; Sheridan, J.T. A review of optical image encryption techniques. Opt. Laser Technol. 2014, 57, 327–342. [Google Scholar] [CrossRef]
- Pi, D.; Liu, J.; Wang, Y. Review of computer-generated hologram algorithms for color dynamic holographic three-dimensional display. Light. Sci. Appl. 2022, 11, 231. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Li, Z.; Zhao, S.; Wang, L. Encrypting orbital angular momentum holography with ghost imaging. Opt. Express 2023, 31, 11717–11728. [Google Scholar] [CrossRef] [PubMed]
- Clemente, P.; Durán, V.; Tajahuerce, E.; Torres-Company, V.; Lancis, J. Single-pixel digital ghost holography. Phys. Rev. A 2012, 86, 041803. [Google Scholar] [CrossRef]
- Xu, D.; Lu, M.; Jia, C.; Hu, Z. Angular-multiplexing optical multiple-image encryption based on digital holography and random amplitude mask. J. Russ. Laser Res. 2017, 38, 285–293. [Google Scholar] [CrossRef]
- Su, Y.; Xu, W.; Li, T.; Zhao, J.; Liu, S. Optical color image encryption based on fingerprint key and phase-shifting digital holography. Opt. Lasers Eng. 2021, 140, 106550. [Google Scholar] [CrossRef]
- Wei, R.; Li, X.; Wang, Q.-H. Double color image encryption scheme based on off-axis holography and maximum length cellular automata. Optik 2017, 145, 407–417. [Google Scholar] [CrossRef]
- Piao, M.-L.; Wu, H.-Y.; Kim, N. 3D image encryption based on computer-generated hologram. In Proceedings of the Digital Holography and Three-Dimensional Imaging, Bordeaux, France, 19–23 May 2019; p. W3A.21. [Google Scholar]
- Unnikrishnan, G.; Pohit, M.; Singh, K. A polarization encoded optical encryption system using ferroelectric spatial light modulator. Opt. Commun. 2000, 185, 25–31. [Google Scholar] [CrossRef]
- Wang, Q.; Xiong, D.; Alfalou, A.; Brosseau, C. Optical image encryption method based on incoherent imaging and polarized light encoding. Opt. Commun. 2018, 415, 56–63. [Google Scholar] [CrossRef]
- Shikder, A.; Nishchal, N.K. Image encryption using binary polarization states of light beam. Sci. Rep. 2023, 13, 14028. [Google Scholar] [CrossRef]
- Mandapati, V.C.; Vardhan, H.; Prabhakar, S.; Sakshi; Kumar, R.; Reddy, S.G.; Singh, R.P.; Singh, K. Multi-user nonlinear optical cryptosystem based on polar decomposition and fractional vortex speckle patterns. Photonics 2023, 10, 561. [Google Scholar] [CrossRef]
- Gao, Y.; Al-Sarawi, S.F.; Abbott, D. Physical unclonable functions. Nat. Electron. 2020, 3, 81–91. [Google Scholar] [CrossRef]
- Mandapati, V.C.; Prabhakar, S.; Vardhan, H.; Kumar, R.; Reddy, S.G.; Sakshi; Singh, R.P. An asymmetric optical cryptosystem using physically unclonable functions in the fresnel domain. Eng. Proceeding 2023, 34, 1. [Google Scholar]
- Vanitha, P.; Manupati, B.; Muniraj, I.; Anamalamudi, S.; Salla, G.R.; Singh, R.P. Augmenting data security: Physical unclonable functions for linear canonical transform based cryptography. Appl. Phys. B Laser Opt. 2022, 128, 183. [Google Scholar] [CrossRef]
- Peng, X.; Wei, H.; Zhang, P. Chosen-plaintext attack on lensless double-random phase encoding in the Fresnel domain. Opt. Lett. 2006, 31, 3261. [Google Scholar] [CrossRef]
- Wei, H.; Peng, X.; Liu, H.; Feng, S.; Gao, B.Z. Known plain text attack on the double phase encoding and its implementation with parallel hardware. In Information Optics and Photonics Technologies II; SPIE: Bellingham, WA, USA, 2007; pp. 21–27. [Google Scholar]
- Situ, G.; Gopinathan, U.; Monaghan, D.S.; Sheridan, J.T. Cryptanalysis of optical security systems with significant output images. Appl. Opt. 2007, 46, 5257–5262. [Google Scholar] [CrossRef]
- Tashima, H.; Takeda, M.; Suzuki, H.; Obi, T.; Yamaguchi, M.; Ohyama, N. Known plaintext attack on double random phase encoding using fingerprint as key and a method for avoiding the attack. Opt. Express 2010, 18, 13772. [Google Scholar] [CrossRef]
- Qin, W.; He, W.; Meng, X.; Peng, X. Optical cryptanalysis of DRPE-based encryption systems. In Proceedings of the International Conference on Optical Instrumentation and Technology, Shanghai, China, 19–22 October 2009; p. 751203. [Google Scholar]
- Qin, W.; Peng, X. Vulnerability to known-plaintext attack of optical encryption schemes based on two fractional Fourier transform order keys and double random phase keys. J. Opt. A Pure Appl. Opt. 2009, 11, 075402. [Google Scholar] [CrossRef]
- Barrera, J.F.; Vargas, C.; Tebaldi, M.; Torroba, R. Chosen-plaintext attack on a joint transform correlator encrypting system. Opt. Commun. 2010, 283, 3917–3921. [Google Scholar] [CrossRef]
- Xiong, Y.; Kumar, R. Security analysis on asymmetric optical cryptosystem based on interference and equal modulus decomposition. Opt. Quantum Electron. 2022, 54, 507. [Google Scholar] [CrossRef]
- Xiong, Y.; He, A.; Quan, C. Specific attack and security enhancement to optical image cryptosystem based on two random masks and interference. Opt. Lasers Eng. 2018, 107, 142–148. [Google Scholar] [CrossRef]
- Gopinath, S.; Bleahu, A.-I.; Kahro, T.; Rajeswary, A.S.J.F.; Kumar, R.; Kukli, K.; Tamm, A.; Rosen, J.; Anand, V. Enhanced design of pure phase greyscale diffractive optical elements by phase retrieval assisted multiplexing of complex functions. In Proceedings of the Holography: Advances and Modern Trends VIII, Prague, Czech Republic, 24–28 April 2023; pp. 11–15. [Google Scholar]
- Wei, H.; Wang, X. Optical multiple-image authentication and encryption based on phase retrieval and interference with sparsity constraints. Opt. Laser Technol. 2021, 142, 107257. [Google Scholar] [CrossRef]
- Guo, C.; Liu, S.; Sheridan, J.T. Iterative phase retrieval algorithms Part II: Attacking optical encryption systems. Appl. Opt. 2015, 54, 4709. [Google Scholar] [CrossRef]
- Shi, Y.; Han, Y.; Zhang, Q.; Kuang, X. Adaptive iterative attack towards explainable adversarial robustness. Pattern Recognit. 2020, 105, 107309. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, H.; Blondel, W.; Shen, Z.; Liu, S. Image security based on iterative random phase encoding in expanded fractional Fourier transform domains. Opt. Lasers Eng. 2018, 105, 1–5. [Google Scholar] [CrossRef]
- Xiong, Y.; Gu, J.; Kumar, R. Hybrid plaintext attack for cryptosystem based on interference and phase-retrieval technique. Appl. Opt. 2023, 62, 4301–4309. [Google Scholar] [CrossRef]
- Xiong, Y.; Kumar, R.; Quan, C. Security Analysis on an optical encryption and authentication scheme based on phase-truncation and phase-retrieval algorithm. IEEE Photon-J. 2019, 11, 1–14. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).