Influence of Primary Coma on the Tightly Focusing Characteristics of Circular Basis Hybrid Order Poincaré Sphere Beams
Abstract
1. Introduction
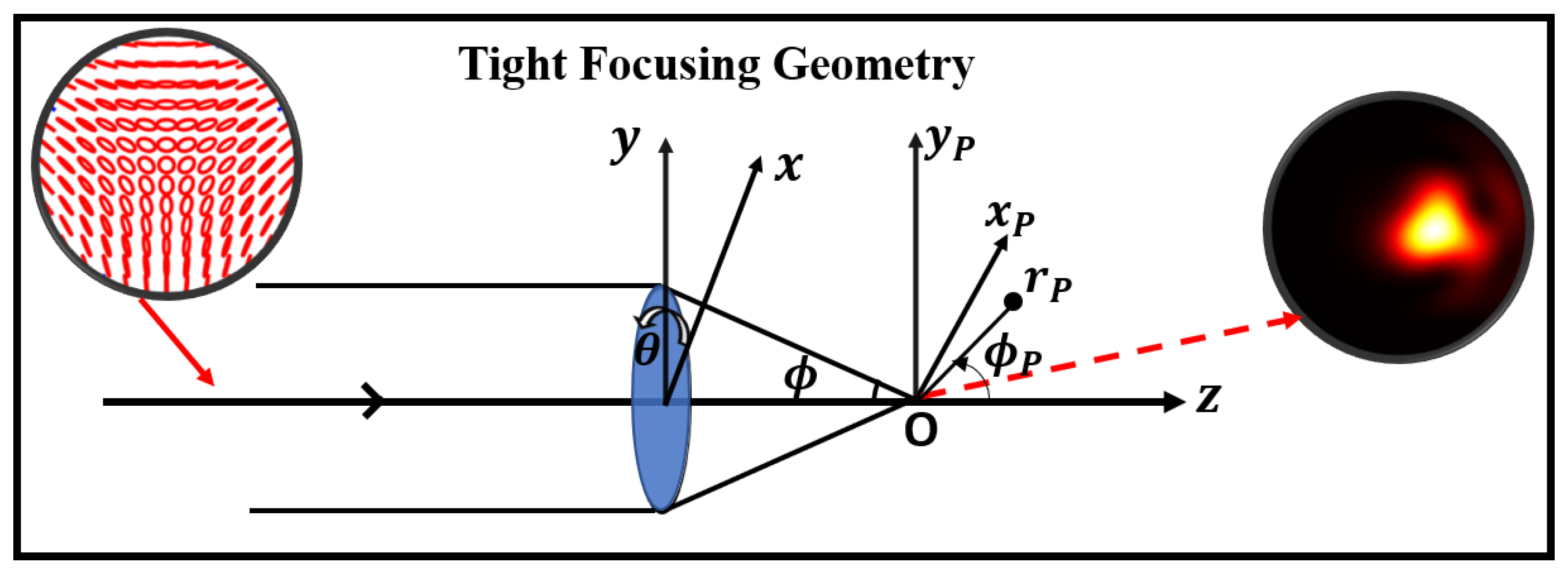
2. Theory of Tight Focusing for Circular Basis HyOPS Beams
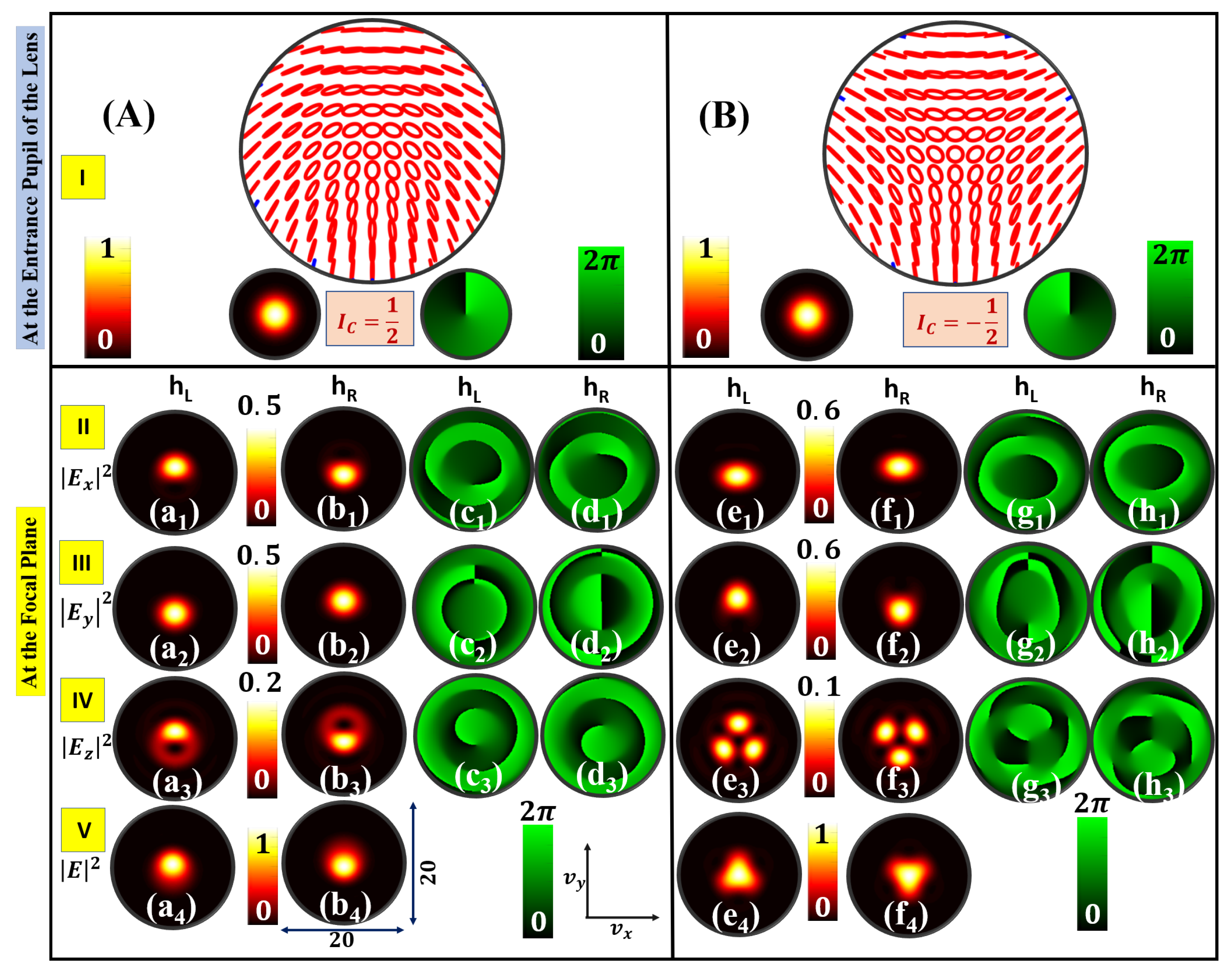
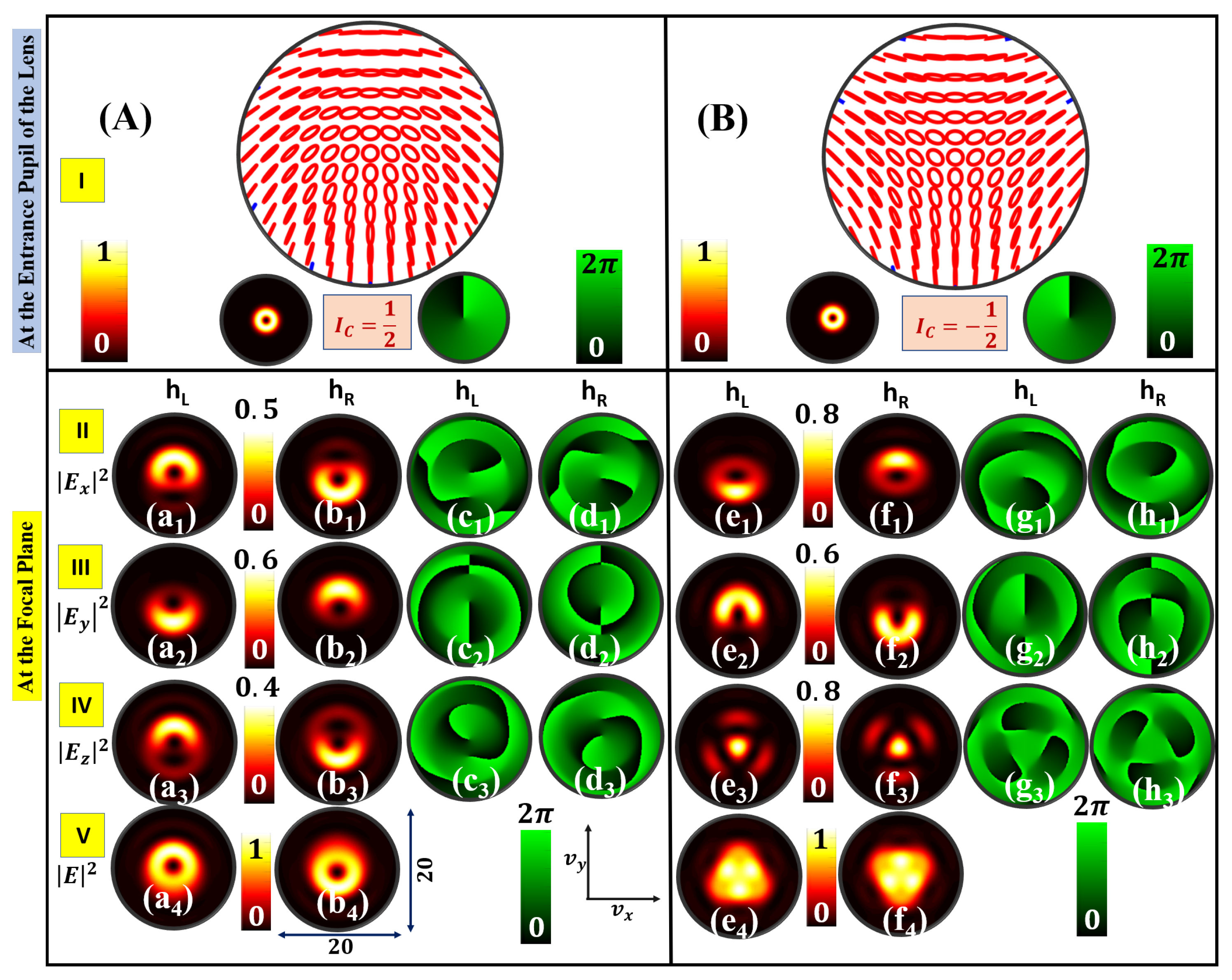
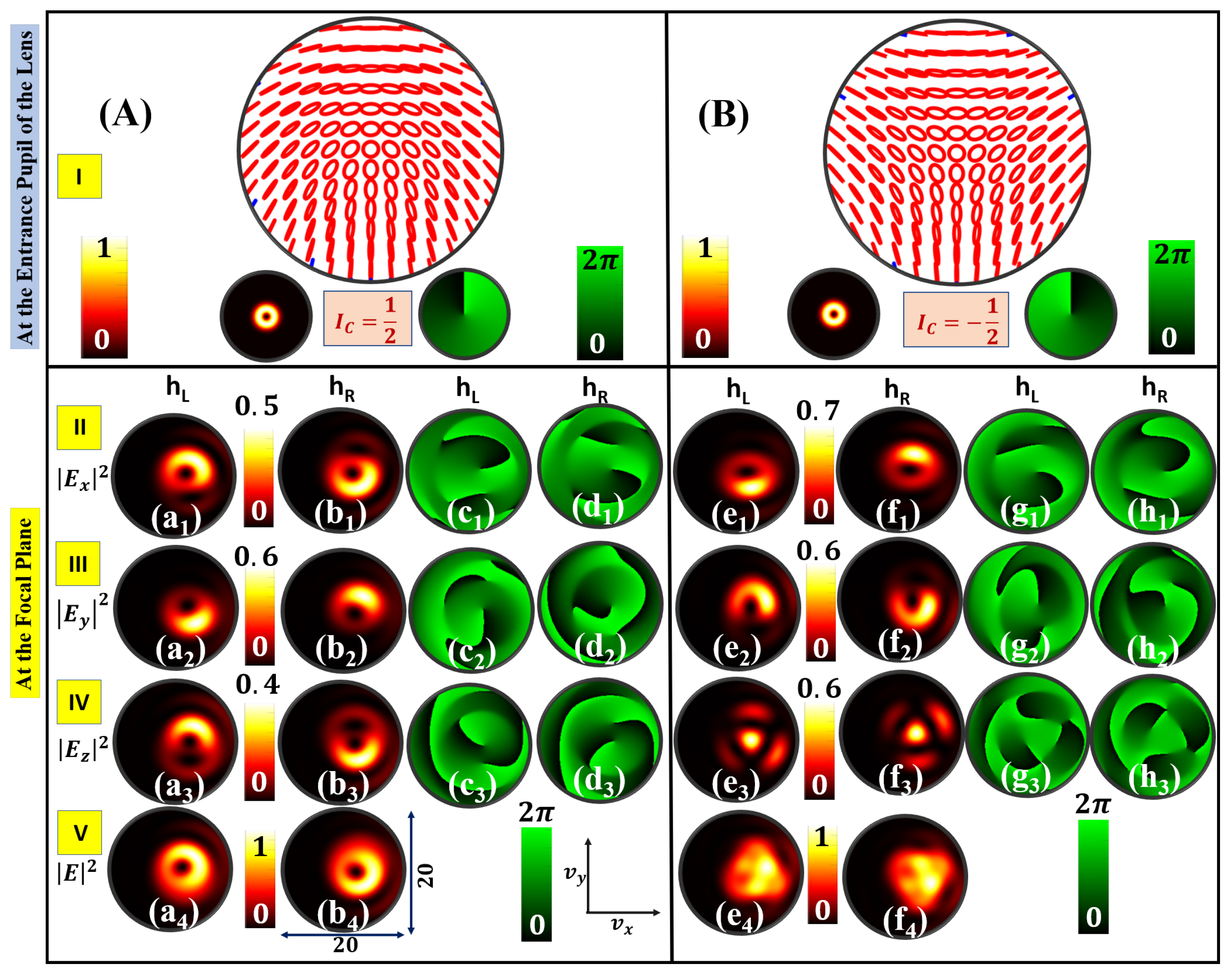
3. Intensity Landscapes of Circular Basis HyOPS Beams
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| NA | numerical aperture |
| PSF | point spread function |
| SOP | state of polarization |
| PS | Poincaré sphere |
| HyOPS | hybrid order Poincaré sphere |
| HOPS | higher order Poincaré sphere |
| OAM | orbital angular momentum |
| RCP | right circular polarization |
| LCP | left circular polarization |
| LG | Laguerre Gaussian |
References
- Linfoot, E.H.; Wolf, E. Diffraction Images in Systems with an Annular Aperture. Proc. Phys. Soc. Lond. B 1953, 66, 145–149. [Google Scholar] [CrossRef]
- Welford, W.T. Use of Annular Apertures to Increase Focal Depth. J. Opt. Soc. Am. 1960, 50, 749–753. [Google Scholar] [CrossRef]
- Singh, K.; Dhillon, H.S. Diffraction of Partially Coherent Light by an Aberration-Free Annular Aperture. J. Opt. Soc. Am. 1969, 59, 395–401. [Google Scholar] [CrossRef]
- Slepian, D. Analytic Solution of Two Apodization Problems. J. Opt. Soc. Am. 1965, 55, 1110–1115. [Google Scholar] [CrossRef]
- Stamnes, J.J. Focusing of two-dimensional waves. J. Opt. Soc. Am. 1981, 71, 15–31. [Google Scholar] [CrossRef]
- Belland, P.; Crenn, J.P. Changes in the characteristics of a Gaussian beam weakly diffracted by a circular aperture. Appl. Opt. 1982, 21, 522–527. [Google Scholar] [CrossRef]
- Duan, K.; Lü, B. Nonparaxial analysis of far-field properties of Gaussian beams diffracted at a circular aperture. Opt. Express 2003, 11, 1474–1480. [Google Scholar] [CrossRef]
- Hao, B.; Burch, J.; Leger, J. Smallest flattop focus by polarization engineering. Appl. Opt. 2008, 47, 2931–2940. [Google Scholar] [CrossRef]
- Wolf, E. Electromagnetic Diffraction in Optical Systems. I. An Integral Representation of the Image Field. Proc. R. Soc. Lond. Ser. A 1959, 253, 349–357. [Google Scholar]
- Richards, B.; Wolf, E. Electromagnetic diffraction in optical systems, II. Structure of the image field in an aplanatic system. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1959, 253, 358–379. [Google Scholar]
- Yoshida, A.; Asakura, T. Electromagnetic field in the focal plane of a coherent beam from a wide-angular annular-aperture system. Optik (Stuttgart) 1974, 40, 322–331. [Google Scholar]
- Yoshida, A.; Asakura, T. Electromagnetic field near the focus of Gaussian beams. Optik (Stuttgart) 1974, 41, 281–292. [Google Scholar]
- Sheppard, C.J.R.; Matthews, H.J. Imaging in high-aperture optical systems. J. Opt. Soc. Am. A 1987, 4, 1354–1360. [Google Scholar] [CrossRef]
- Kant, R. An Analytical Solution of Vector Diffraction for Focusing Optical Systems. J. Mod. Opt. 1993, 40, 337–347. [Google Scholar] [CrossRef]
- Sheppard, C.J.R. High-aperture beams. J. Opt. Soc. Am. A 2001, 18, 1579–1587. [Google Scholar] [CrossRef]
- Chon, J.W.M.; Gan, X.; Gu, M. Splitting of the focal spot of a high numerical-aperture objective in free space. Appl. Phys. Lett. 2002, 81, 1576–1578. [Google Scholar] [CrossRef]
- Niziev, V.G.; Nesterov, A.V. Influence of beam polarization on laser cutting efficiency. J. Phys. D Appl. Phys. 1999, 32, 1455–1461. [Google Scholar] [CrossRef]
- Salamin, Y.I.; Keitel, C.H. Electron Acceleration by a Tightly Focused Laser Beam. Phys. Rev. Lett. 2002, 88, 095005. [Google Scholar] [CrossRef]
- Dorn, R.; Quabis, S.; Leuchs, G. Sharper Focus for a Radially Polarized Light Beam. Phys. Rev. Lett. 2003, 91, 233901. [Google Scholar] [CrossRef] [PubMed]
- Davidson, N.; Bokor, N. High-numerical-aperture focusing of radially polarized doughnut beams with a parabolic mirror and a flat diffractive lens. Opt. Lett. 2004, 29, 1318–1320. [Google Scholar] [CrossRef] [PubMed]
- Quabis, S.; Dorn, R.; Eberler, M.; Glöckl, O.; Leuchs, G. Focusing light to a tighter spot. Opt. Commun. 2000, 179, 1–7. [Google Scholar] [CrossRef]
- Ferrari, J.A.; Dultz, W.; Schmitzer, H.; Frins, E. Achromatic wavefront forming with space-variant polarizers: Application to phase singularities and light focusing. Phys. Rev. A 2007, 76, 053815. [Google Scholar] [CrossRef]
- Gupta, D.N.; Kant, N.; Kim, D.E.; Suk, H. Electron acceleration to GeV energy by a radially polarized laser. Phys. Lett. A 2007, 368, 402–407. [Google Scholar] [CrossRef]
- Youngworth, K.S.; Brown, T.G. Focusing of high numerical aperture cylindrical-vector beams. Opt. Express 2000, 7, 77–87. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, S.; Li, P.; Jiao, X.; Zhao, J. Controlling the polarization singularities of the focused azimuthally polarized beams. Opt. Express 2013, 21, 974–983. [Google Scholar] [CrossRef]
- Schoonover, R.W.; Visser, T.D. Polarization singularities of focused, radially polarized fields. Opt. Express 2006, 14, 5733–5745. [Google Scholar] [CrossRef]
- Dennis, M.R. Fermionic out-of-plane structure of polarization singularities. Opt. Lett. 2011, 36, 3765–3767. [Google Scholar] [CrossRef]
- Freund, I. Cones, spirals, and Möbius strips, in elliptically polarized light. Opt. Commun. 2005, 249, 7–22. [Google Scholar] [CrossRef]
- Bauer, T.; Neugebauer, M.; Leuchs, G.; Banzer, P. Optical Polarization Möbius Strips and Points of Purely Transverse Spin Density. Phys. Rev. Lett. 2016, 117, 013601. [Google Scholar] [CrossRef]
- Bauer, T.; Banzer, P.; Bouchard, F.; Orlov, S.; Marrucci, L.; Santamato, E.; Boyd, R.W.; Karimi, E.; Leuchs, G. Multi-twist polarization ribbon topologies in highly-confined optical fields. New J. Phys. 2019, 21, 053020. [Google Scholar] [CrossRef]
- Bauer, T.; Banzer, P.; Karimi, E.; Orlov, S.; Rubano, A.; Marrucci, L.; Santamato, E.; Boyd, R.W.; Leuchs, G. Observation of optical polarization Möbius strips. Science 2015, 347, 964–966. [Google Scholar] [CrossRef] [PubMed]
- Pal, S.K.; Somers, L.; Singh, R.K.; Senthilkumaran, P.; Arie, A. Focused polarization ellipse field singularities: Interaction of spin-orbital angular momentum and the formation of optical Möbius strips. Phys. Scr. 2023, 98, 055507. [Google Scholar] [CrossRef]
- Goldstein, D.H. Polarized Light; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Born, M.; Wolf, E. Principles of Optics; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Poincaré, H. Mathematical Theory of Light: Mathematical Physics Course; Carre, G., Ed.; Carrè: Paris, France, 1889; Volume 1. [Google Scholar]
- Milione, G.; Sztul, H.I.; Nolan, D.A.; Alfano, R.R. Higher-Order Poincaré Sphere, Stokes Parameters, and the Angular Momentum of Light. Phys. Rev. Lett. 2011, 107, 053601. [Google Scholar] [CrossRef] [PubMed]
- Cardano, F.; Karimi, E.; Slussarenko, S.; Marrucci, L.; de Lisio, C.; Santamato, E. Polarization pattern of vector vortex beams generated by q-plates with different topological charges. Appl. Opt. 2012, 51, C1–C6. [Google Scholar] [CrossRef]
- Holleczek, A.; Aiello, A.; Gabriel, C.; Marquardt, C.; Leuchs, G. Classical and quantum properties of cylindrically polarized states of light. Opt. Express 2011, 19, 9714–9736. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Liu, Y.; Ke, Y.; Liu, Y.; Shu, W.; Luo, H.; Wen, S. Generation of arbitrary vector vortex beams on hybrid-order Poincaré sphere. Photonics Res. 2017, 5, 15–21. [Google Scholar] [CrossRef]
- Yi, X.; Liu, Y.; Ling, X.; Zhou, X.; Ke, Y.; Luo, H.; Wen, S.; Fan, D. Hybrid-order Poincaré sphere. Phys. Rev. A 2015, 91, 023801. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Chen, P.; Ge, S.J.; Wei, T.; Tang, J.; Hu, W.; Lu, Y.Q. Spin-controlled massive channels of hybrid-order Poincaré sphere beams. Appl. Phys. Lett. 2020, 117, 081101. [Google Scholar] [CrossRef]
- Malacara, D. Optical Shop Testing; Wiley Publication: New York, NY, USA, 2007. [Google Scholar]
- Smith, W.J. Modern Optical Engineering; McGraw-Hill Publication: New York, NY, USA, 2000. [Google Scholar]
- Visser, T.D.; Wiersma, S.H. Spherical aberration and the electromagnetic field in high-aperture systems. J. Opt. Soc. Am. A 1991, 8, 1404–1410. [Google Scholar] [CrossRef]
- Visser, T.D.; Wiersma, S.H. Diffraction of converging electromagnetic waves. J. Opt. Soc. Am. A 1992, 9, 2034–2047. [Google Scholar] [CrossRef]
- Kant, R. An Analytical Solution of Vector Diffraction for Focusing Optical Systems with Seidel Aberrations. J. Mod. Opt. 1993, 40, 2293–2310. [Google Scholar] [CrossRef]
- Kant, R. An Analytical Method of Vector Diffraction for Focusing Optical Systems with Seidel Aberrations II: Astigmatism and Coma. J. Mod. Opt. 1995, 42, 299–320. [Google Scholar] [CrossRef]
- Sheppard, C.; Gu, M. Imaging by a High Aperture Optical System. J. Mod. Opt. 1993, 40, 1631–1651. [Google Scholar] [CrossRef]
- Wang, Y.; Yong, K.; Chen, D.; Zhang, R. Influence of spherical aberration on the tightly focusing characteristics of vector vortex beams. Opt. Express 2023, 31, 28229–28240. [Google Scholar] [CrossRef] [PubMed]
- Dai, X.; Li, Y.; Liu, L. Tight focusing properties of hybrid-order Poincaré sphere beams. Opt. Commun. 2018, 426, 46–53. [Google Scholar] [CrossRef]
- Lerman, G.M.; Stern, L.; Levy, U. Generation and tight focusing of hybridly polarized vector beams. Opt. Express 2010, 18, 27650–27657. [Google Scholar] [CrossRef] [PubMed]
- Hu, K.; Chen, Z.; Pu, J. Tight focusing properties of hybridly polarized vector beams. J. Opt. Soc. Am. A 2012, 29, 1099–1104. [Google Scholar] [CrossRef]
- Singh, R.K.; Senthilkumaran, P.; Singh, K. Structure of a tightly focused vortex beam in the presence of primary coma. Opt. Commun. 2009, 282, 1501–1510. [Google Scholar] [CrossRef]
- Dennis, M.R. Polarization singularities in paraxial vector fields: Morphology and statistics. Opt. Commun. 2002, 213, 201–221. [Google Scholar] [CrossRef]
- Berry, M.V. The electric and magnetic polarization singularities of paraxial waves. J. Opt. A Pure Appl. Opt. 2004, 6, 475–481. [Google Scholar] [CrossRef][Green Version]
- Freund, I. Polarization singularity indices in Gaussian laser beams. Opt. Commun. 2002, 201, 251–270. [Google Scholar] [CrossRef]
- Pal, S.K.; Senthilkumaran, P. Index polarity inversion by helicity inversion in Stokes vortices. Appl. Phys. Lett. 2020, 117, 201101. [Google Scholar] [CrossRef]
- Pal, S.K.; Arora, G.; Ruchi; Senthilkumaran, P. Handedness control in polarization lattice fields by using spiral phase filters. Appl. Phys. Lett. 2021, 119, 221106. [Google Scholar] [CrossRef]
- Zhan, Q. Cylindrical vector beams: From mathematical concepts to applications. Adv. Opt. Photon. 2009, 1, 1–57. [Google Scholar] [CrossRef]
- Senthilkumaran, P. Singularities in Physics and Engineering; Number 2053–2563; IOP Publishing: Bristol, UK, 2018. [Google Scholar]
- Freund, I.; Mokhun, A.I.; Soskin, M.S.; Angelsky, O.V.; Mokhun, I.I. Stokes singularity relations. Opt. Lett. 2002, 27, 545–547. [Google Scholar] [CrossRef]
- Samlan, C.T.; Suna, R.R.; Naik, D.N.; Viswanathan, N.K. Spin-orbit beams for optical chirality measurement. Appl. Phys. Lett. 2018, 112, 031101. [Google Scholar] [CrossRef]
- Han, W.; Cheng, W.; Zhan, Q. Flattop focusing with full Poincaré beams under low numerical aperture illumination. Opt. Lett. 2011, 36, 1605–1607. [Google Scholar] [CrossRef]
- Xue, Y.; Wang, Y.; Zhou, S.; Chen, H.; Rui, G.; Gu, B.; Zhan, Q. Focus shaping and optical manipulation using highly focused second-order full Poincaré beam. J. Opt. Soc. Am. A 2018, 35, 953–958. [Google Scholar] [CrossRef]
- Salamin, Y.I. Acceleration in vacuum of bare nuclei by tightly focused radially polarized laser light. Opt. Lett. 2007, 32, 3462–3464. [Google Scholar] [CrossRef]
- Dai, L.; Li, J.X.; Zang, W.P.; Tian, J.G. Vacuum electron acceleration driven by a tightly focused radially polarized Gaussian beam. Opt. Express 2011, 19, 9303–9308. [Google Scholar] [CrossRef]
- Zheng, Y.; Cai, X.; Zhao, X.; Wang, W. Acceleration of electrons by tightly focused azimuthally polarized ultrashort pulses in a vacuum. Opt. Express 2022, 30, 1627–1640. [Google Scholar] [CrossRef] [PubMed]
- Abouraddy, A.F.; Toussaint, K.C. Three-Dimensional Polarization Control in Microscopy. Phys. Rev. Lett. 2006, 96, 153901. [Google Scholar] [CrossRef] [PubMed]
- Cipparrone, G.; Ricardez-Vargas, I.; Pagliusi, P.; Provenzano, C. Polarization gradient: Exploring an original route for optical trapping and manipulation. Opt. Express 2010, 18, 6008–6013. [Google Scholar] [CrossRef] [PubMed]
- Kozawa, Y.; Sato, S. Optical trapping of micrometer-sized dielectric particles by cylindrical vector beams. Opt. Express 2010, 18, 10828–10833. [Google Scholar] [CrossRef]
- Zhan, Q. Trapping metallic Rayleigh particles with radial polarization. Opt. Express 2004, 12, 3377–3382. [Google Scholar] [CrossRef] [PubMed]
- de Sande, J.C.G.; Santarsiero, M.; Piquero, G. Spirally polarized beams for polarimetry measurements of deterministic and homogeneous samples. Opt. Lasers Eng. 2017, 91, 97–105. [Google Scholar] [CrossRef]
- de Sande, J.C.G.; Piquero, G.; Santarsiero, M. Polarimetry with azimuthally polarized light. Opt. Commun. 2018, 410, 961–965. [Google Scholar] [CrossRef]
- Perez-Garcia, B.; Hernández-Aranda, R.I.; López-Mariscal, C.; Gutiérrez-Vega, J.C. Morphological transformation of generalized spirally polarized beams by anisotropic media and its experimental characterization. Opt. Express 2019, 27, 33412–33426. [Google Scholar] [CrossRef]
- Milione, G.; Lavery, M.P.J.; Huang, H.; Ren, Y.; Xie, G.; Nguyen, T.A.; Karimi, E.; Marrucci, L.; Nolan, D.A.; Alfano, R.R.; et al. 4 × 20 Gbit/s mode division multiplexing over free space using vector modes and a q-plate mode (de)multiplexer. Opt. Lett. 2015, 40, 1980–1983. [Google Scholar] [CrossRef]
- Gabriel, C.; Aiello, A.; Zhong, W.; Euser, T.G.; Joly, N.Y.; Banzer, P.; Förtsch, M.; Elser, D.; Andersen, U.L.; Marquardt, C.; et al. Entangling Different Degrees of Freedom by Quadrature Squeezing Cylindrically Polarized Modes. Phys. Rev. Lett. 2011, 106, 060502. [Google Scholar] [CrossRef]
- Davis, J.A.; Nowak, M.D. Selective edge enhancement of images with an acousto-optic light modulator. Appl. Opt. 2002, 41, 4835–4839. [Google Scholar] [CrossRef] [PubMed]
- Pal, S.K.; Gangwar, K.K.; Senthilkumaran, P. Tailoring polarization singularity lattices by phase engineering of three-beam interference. Optik 2022, 255, 168680. [Google Scholar] [CrossRef]
- Pal, S.K.; Manisha; Senthilkumaran, P. Phase engineering in overlapping lattices of polarization singularities. J. Opt. Soc. Am. B 2023, 40, 1830–1836. [Google Scholar] [CrossRef]
- Meier, M.; Romano, V.; Feurer, T. Material processing with pulsed radially and azimuthally polarized laser radiation. Appl. Phys. A 2007, 86, 329–334. [Google Scholar] [CrossRef]
- Shen, Y.; Martínez, E.C.; Rosales-Guzmán, C. Generation of Optical Skyrmions with Tunable Topological Textures. ACS Photonics 2022, 9, 296–303. [Google Scholar] [CrossRef]
- Xu, L.; Zhang, Y.; Lang, S.; Wang, H.; Hu, H.; Wang, J.; Gong, Y. Structured Illumination Microscopy Based on Asymmetric Three-beam Interference. J. Innov. Opt. Health Sci. 2021, 14, 2050027. [Google Scholar] [CrossRef]
- Pal, S.K.; Singh, R.K.; Senthilkumaran, P. Focal intensity landscapes of tightly focused spatially varying bright ellipse fields. J. Opt. 2022, 24, 044013. [Google Scholar] [CrossRef]
- Pal, S.K. Tight focusing of orthogonal C-point polarization states. Optik 2023, 274, 170535. [Google Scholar] [CrossRef]
- Otte, E.; Tekce, K.; Lamping, S.; Ravoo, B.J.; Denz, C. Polarization nano-tomography of tightly focused light landscapes by self-assembled monolayers. Nat. Commun. 2019, 10, 4308. [Google Scholar] [CrossRef]
- Singh, R.K.; Senthilkumaran, P.; Singh, K. Effect of primary coma on the focusing of a Laguerre–Gaussian beam by a high numerical aperture system; vectorial diffraction theory. J. Opt. A Pure Appl. Opt. 2008, 10, 075008. [Google Scholar] [CrossRef]
- Sheppard, C.J.R.; Larkin, K.G. Effect of numerical aperture on interference fringe spacing. Appl. Opt. 1995, 34, 4731–4734. [Google Scholar] [CrossRef]
- Sheppard, C.J.R. Orthogonal aberration functions for high-aperture optical systems. J. Opt. Soc. Am. A 2004, 21, 832–838. [Google Scholar] [CrossRef] [PubMed]
- Matthews, H.J.; Hamilton, D.H.; Sheppard, C. Aberration Measurement by Confocal Interferometry. J. Mod. Opt. 1989, 36, 233–250. [Google Scholar] [CrossRef]
- Kubota, H.; Inoué, S. Diffraction Images in the Polarizing Microscope. J. Opt. Soc. Am. 1959, 49, 191–198. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Gu, M.; Sheppard, C. Investigation of Aberration Measurement in Confocal Microscopy. J. Mod. Opt. 1995, 42, 627–638. [Google Scholar] [CrossRef]
- Mills, J.P.; Thompson, B.J. Effect of aberrations and apodization on the performance of coherent optical systems. I. The amplitude impulse response. J. Opt. Soc. Am. A 1986, 3, 694–703. [Google Scholar] [CrossRef]
- Mills, J.P.; Thompson, B.J. Effect of aberrations and apodization on the performance of coherent optical systems. II. Imaging. J. Opt. Soc. Am. A 1986, 3, 704–716. [Google Scholar] [CrossRef]
- Allred, D.B.; Mills, J.P. Effect of aberrations and apodization on the performance of coherent optical systems. 3: The near field. Appl. Opt. 1989, 28, 673–681. [Google Scholar] [CrossRef]
- Mahajan, V.N. Uniform versus Gaussian beams: A comparison of the effects of diffraction, obscuration, and aberrations. J. Opt. Soc. Am. A 1986, 3, 470–485. [Google Scholar] [CrossRef]
- Bernal-Molina, P.; Castejón-Mochón, J.F.; Bradley, A.; López-Gil, N. Focus correction in an apodized system with spherical aberration. J. Opt. Soc. Am. A 2015, 32, 1556–1563. [Google Scholar] [CrossRef]
- Reddy, A.N.K.; Dev, V.; Pal, V.; Ganeev, R.A. The Effect of a Parabolic Apodizer on Improving the Imaging of Optical Systems with Coma and Astigmatism Aberrations. Photonics 2024, 11, 14. [Google Scholar] [CrossRef]
- Zhang, S.; Bai, Z.; Li, J.; Lyu, Y.; Man, Z.; Xing, F.; Ge, X.; Fu, S. Tunable focal shift induced by polarization and phase shaping. Optik 2019, 199, 162788. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pal, S.K.; Singh, R.K.; Senthilkumaran, P. Influence of Primary Coma on the Tightly Focusing Characteristics of Circular Basis Hybrid Order Poincaré Sphere Beams. Photonics 2024, 11, 98. https://doi.org/10.3390/photonics11010098
Pal SK, Singh RK, Senthilkumaran P. Influence of Primary Coma on the Tightly Focusing Characteristics of Circular Basis Hybrid Order Poincaré Sphere Beams. Photonics. 2024; 11(1):98. https://doi.org/10.3390/photonics11010098
Chicago/Turabian StylePal, Sushanta Kumar, Rakesh Kumar Singh, and Paramasivam Senthilkumaran. 2024. "Influence of Primary Coma on the Tightly Focusing Characteristics of Circular Basis Hybrid Order Poincaré Sphere Beams" Photonics 11, no. 1: 98. https://doi.org/10.3390/photonics11010098
APA StylePal, S. K., Singh, R. K., & Senthilkumaran, P. (2024). Influence of Primary Coma on the Tightly Focusing Characteristics of Circular Basis Hybrid Order Poincaré Sphere Beams. Photonics, 11(1), 98. https://doi.org/10.3390/photonics11010098




