382 mW External-Cavity Frequency Doubling 461 nm Laser Based on Quasi-Phase Matching
Abstract
1. Introduction
2. Theoretical Model and Simulations
2.1. Coupled Wave Equations
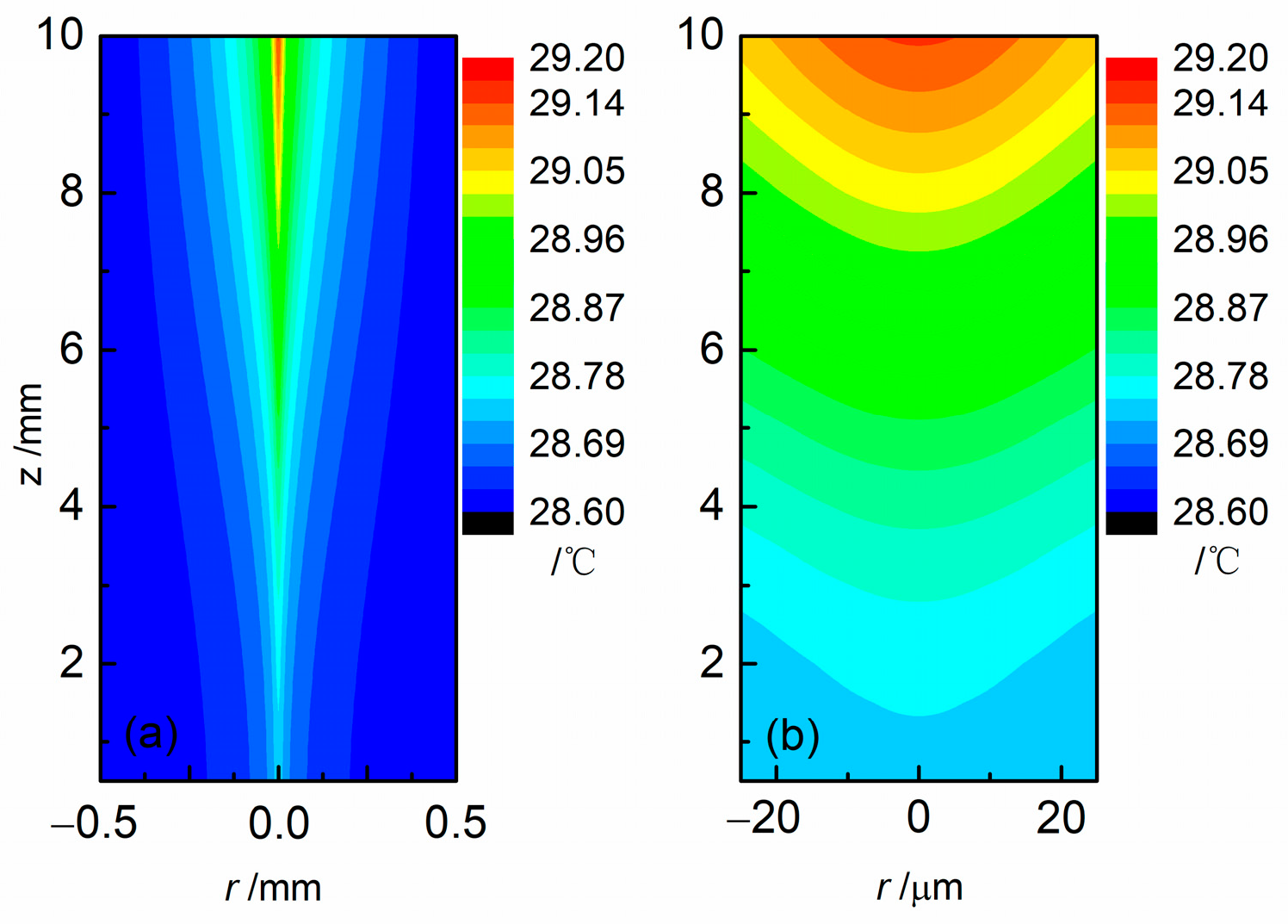
2.2. Optical Absorption and Temperature Distribution in Crystals
2.3. Thermally Induced Phase Mismatching and Thermal Lens
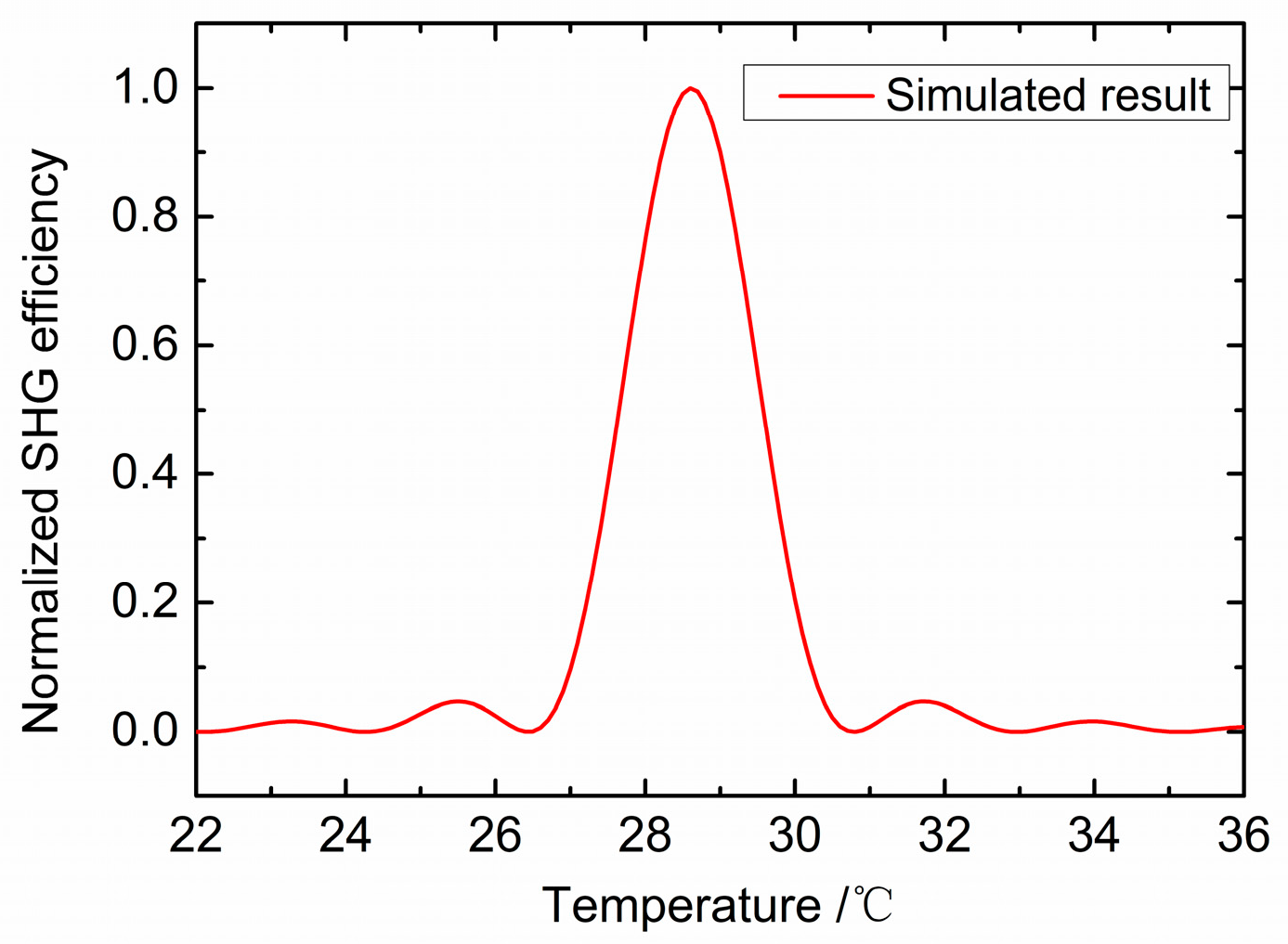
2.4. Simulations of Thermal Effects
2.5. External-Cavity-Enhanced SHG
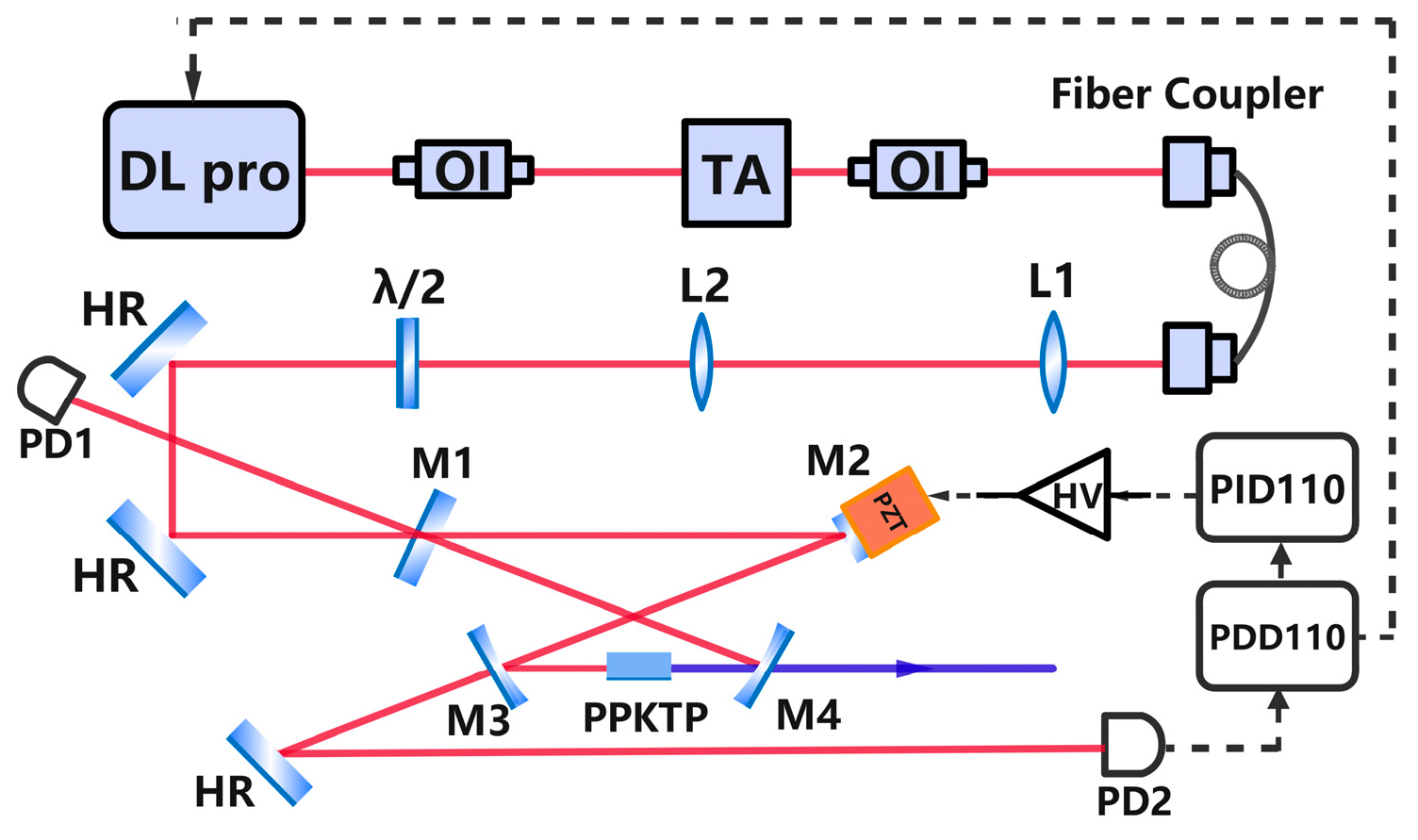
3. Experimental Setup
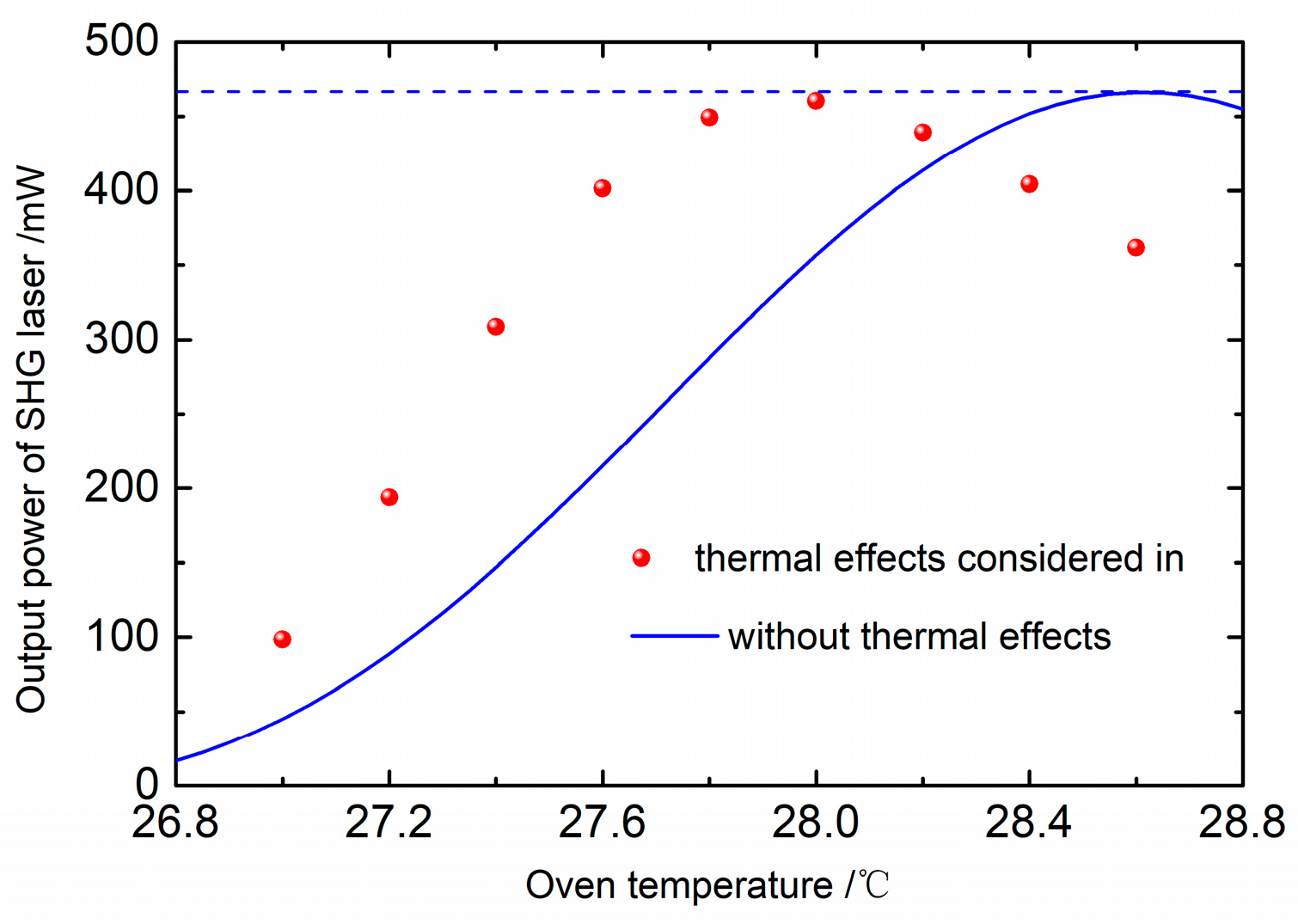
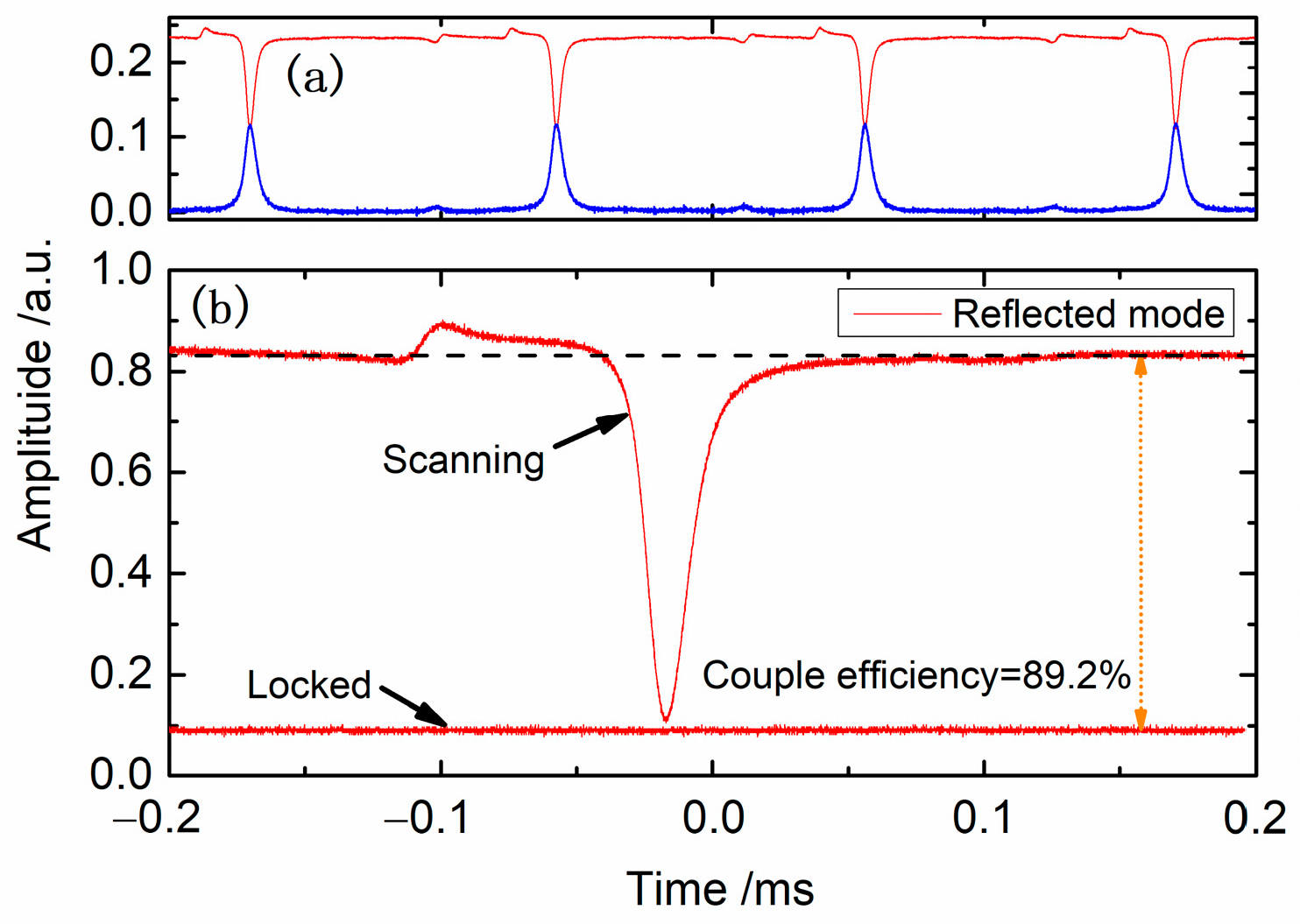
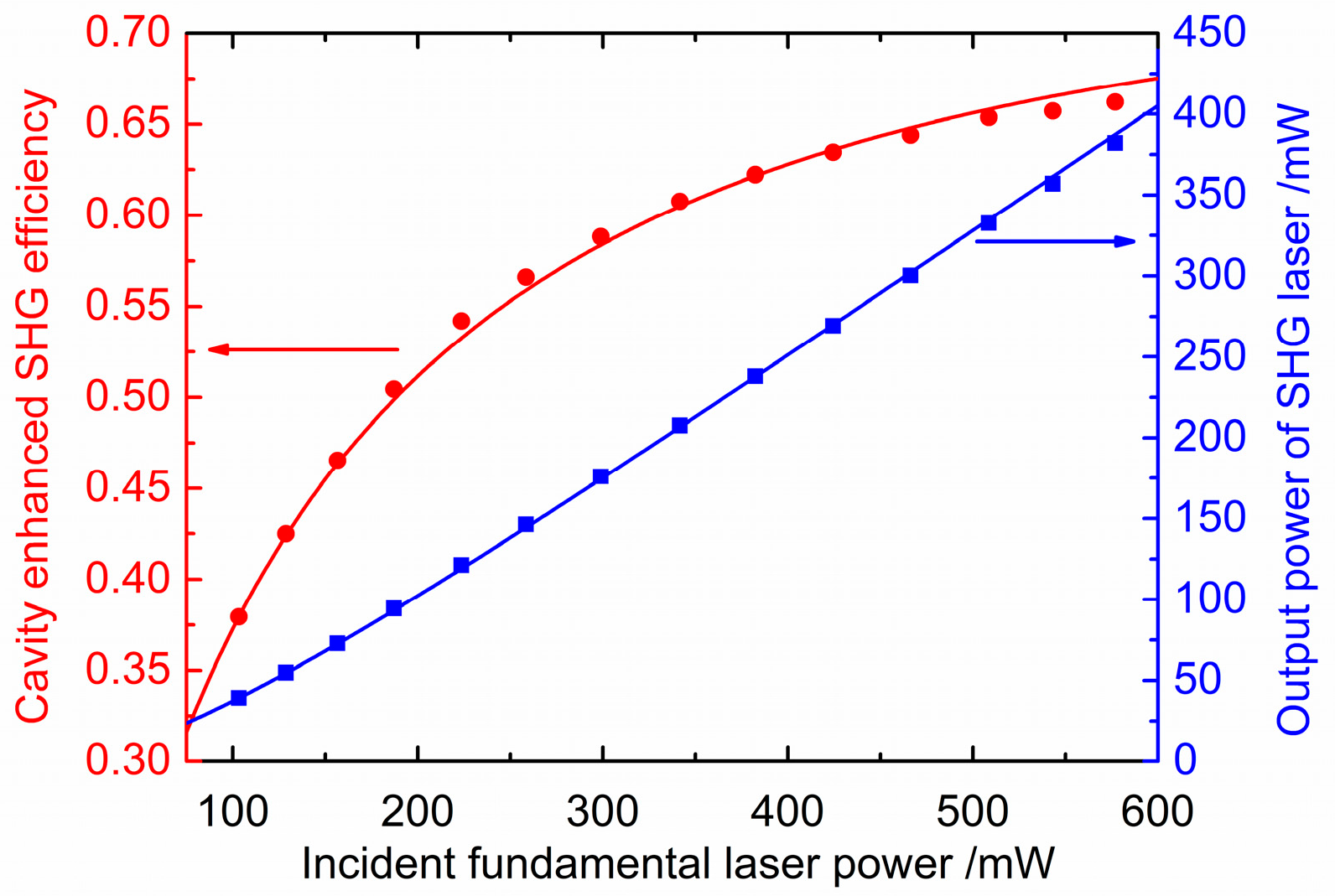
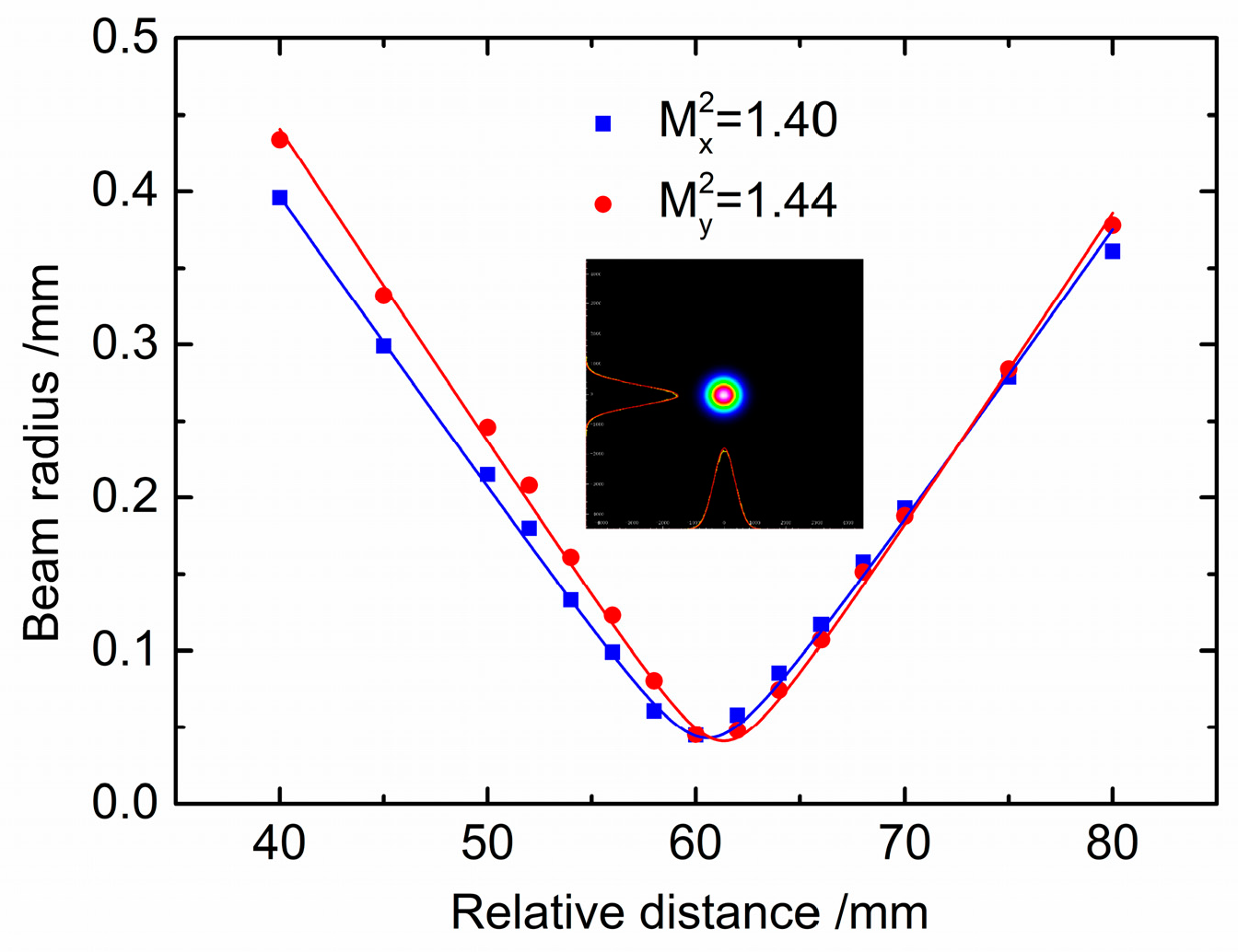
4. Experimental Results and Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sonderhouse, L.; Sanner, C.; Hutson, R.B.; Goban, A.; Bilitewski, T.; Yan, L.; Milner, W.R.; Rey, A.M.; Ye, J. Thermodynamics of a Deeply Degenerate SU(N)-Symmetric Fermi Gas. Nat. Phys. 2020, 16, 1216–1221. [Google Scholar] [CrossRef]
- Burt, E.A.; Prestage, J.D.; Tjoelker, R.L.; Enzer, D.G.; Kuang, D.; Murphy, D.W.; Robison, D.E.; Seubert, J.M.; Wang, R.T.; Ely, T.A. Demonstration of a Trapped-Ion Atomic Clock in Space. Nature 2021, 595, 43–47. [Google Scholar] [CrossRef] [PubMed]
- Wcisło, P.; Morzyński, P.; Bober, M.; Cygan, A.; Lisak, D.; Ciuryło, R.; Zawada, M. Experimental Constraint on Dark Matter Detection with Optical Atomic Clocks. Nat. Astron. 2016, 1, 0009. [Google Scholar] [CrossRef]
- Polzik, E.S.; Carri, J.; Kimble, H.J. Spectroscopy with Squeezed Light. Phys. Rev. Lett. 1992, 68, 3020–3023. [Google Scholar] [CrossRef] [PubMed]
- McGrew, W.F.; Zhang, X.; Fasano, R.J.; Schäffer, S.A.; Beloy, K.; Nicolodi, D.; Brown, R.C.; Hinkley, N.; Milani, G.; Schioppo, M.; et al. Atomic Clock Performance Enabling Geodesy below the Centimetre Level. Nature 2018, 564, 87–90. [Google Scholar] [CrossRef] [PubMed]
- Kolkowitz, S.; Pikovski, I.; Langellier, N.; Lukin, M.D.; Walsworth, R.L.; Ye, J. Gravitational Wave Detection with Optical Lattice Atomic Clocks. Phys. Rev. D 2016, 94, 124043. [Google Scholar] [CrossRef]
- Riehle, F.; Gill, P.; Arias, F.; Robertsson, L. The CIPM List of Recommended Frequency Standard Values: Guidelines and Procedures. Metrologia 2018, 55, 188–200. [Google Scholar] [CrossRef]
- Katori, H.; Takamoto, M.; Pal’chikov, V.G.; Ovsiannikov, V.D. Ultrastable Optical Clock with Neutral Atoms in an Engineered Light Shift Trap. Phys. Rev. Lett. 2003, 91, 173005. [Google Scholar] [CrossRef]
- Bloom, B.; Nicholson, T.; Williams, J.; Campbell, S.; Bishof, M.; Zhang, X.; Zhang, W.; Bromley, S.; Ye, J. An Optical Lattice Clock with Accuracy and Stability at the 10−18 Level. Nature 2014, 506, 71. [Google Scholar] [CrossRef]
- Ludlow, A.D.; Boyd, M.M.; Ye, J.; Peik, E.; Schmidt, P.O. Optical Atomic Clocks. Rev. Mod. Phys. 2015, 87, 637–701. [Google Scholar] [CrossRef]
- Lu, X.; Yin, M.; Li, T.; Wang, Y.; Chang, H. An Evaluation of the Zeeman Shift of the 87Sr Optical Lattice Clock at the National Time Service Center. Appl. Sci. 2020, 10, 1440. [Google Scholar] [CrossRef]
- Origlia, S.; Pramod, M.S.; Schiller, S.; Singh, Y.; Bongs, K.; Schwarz, R.; Al-Masoudi, A.; Dörscher, S.; Herbers, S.; Häfner, S.; et al. Towards an Optical Clock for Space: Compact, High-Performance Optical Lattice Clock Based on Bosonic Atoms. Phys. Rev. A 2018, 98, 053443. [Google Scholar] [CrossRef]
- Takamoto, M.; Ushijima, I.; Ohmae, N.; Yahagi, T.; Kokado, K.; Shinkai, H.; Katori, H. Test of General Relativity by a Pair of Transportable Optical Lattice Clocks. Nat. Photonics 2020, 14, 411–415. [Google Scholar] [CrossRef]
- Kong, D.-H.; Wang, Z.-H.; Guo, F.; Zhang, Q.; Lu, X.-T.; Wang, Y.-B.; Chang, H. A Transportable Optical Lattice Clock at the National Time Service Center. Chin. Phys. B 2020, 29, 070602. [Google Scholar] [CrossRef]
- Poli, N.; Schioppo, M.; Vogt, S.; Falke, S.; Sterr, U.; Lisdat, C.; Tino, G.M. A Transportable Strontium Optical Lattice Clock. Appl. Phys. B 2014, 117, 1107–1116. [Google Scholar] [CrossRef]
- Kale, Y.B.; Singh, A.; Gellesch, M.; Jones, J.M.; Morris, D.; Aldous, M.; Bongs, K.; Singh, Y. Field Deployable Atomics Package for an Optical Lattice Clock. Quantum Sci. Technol. 2022, 7, 045004. [Google Scholar] [CrossRef]
- Pagett, C.J.H.; Moriya, P.H.; Celistrino Teixeira, R.; Shiozaki, R.F.; Hemmerling, M.; Courteille, P.W. Injection Locking of a Low Cost High Power Laser Diode at 461 nm. Rev. Sci. Instrum. 2016, 87, 053105. [Google Scholar] [CrossRef]
- Verma, G.; Wang, E.; Assendelft, J.; Poli, N.; Rosi, G.; Tino, G.M.; Salvi, L. A Scalable Laser System at 461 nm for Laser Cooling and Trapping of Sr Atoms. Appl. Phys. B 2022, 128, 100. [Google Scholar] [CrossRef]
- Peng, Y.; Zhao, Y.; Li, Y.; Cao, J.P.; Fang, Z.J.; Zang, E.J. Three Methods to Lock the Second Harmonic Generation for 461 nm. Chin. J. Laser 2010, 37, 345–350. [Google Scholar] [CrossRef]
- Chen, L.; Huang, C.-J.; Xu, X.-B.; Lu, Z.-T.; Wang, Z.-B.; Chen, G.-J.; Zhang, J.-Z.; Tang, H.X.; Dong, C.-H.; Liu, W.; et al. Planar Integrated Magneto Optical Trap. Phys. Rev. A 2022, 17, 034031. [Google Scholar] [CrossRef]
- Han, J.; Zhang, J.; Shan, X.; Peng, H.; Zhang, Y.; Qin, L.; Wang, L. High-Power Narrow-Linewidth Blue External Cavity Diode Laser. Opt. Laser Technol. 2023, 159, 10897. [Google Scholar] [CrossRef]
- Ruhnke, N.; Müller, A.; Eppich, B.; Maiwald, M.; Sumpf, B.; Erbert, G.; Tränkle, G. 400 mW External Cavity Diode Laser with Narrowband Emission at 445 nm. Opt. Lett. 2014, 39, 3794. [Google Scholar] [CrossRef]
- Chi, M.; Jensen, O.B.; Petersen, P.M. Tuning Range and Output Power Optimization of an External-Cavity GaN Diode Laser at 455 nm. Appl. Opt. 2016, 55, 2263. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Torabi-Goudarzi, F.; Riis, E. Efficient cw High-Power Frequency Doubling in Periodically Poled KTP. Opt. Commun. 2003, 227, 389–403. [Google Scholar] [CrossRef]
- Hemmerich, A.; McIntyre, D.H.; Zimmermann, C.; Hänsen, T.W. Second-Harmonic Generation and Optical Stabilization of a Diode Laser in an External Ring Resonator. Opt. Lett. 1990, 15, 372. [Google Scholar] [CrossRef] [PubMed]
- Polzik, E.S.; Kimble, H.J. Frequency Doubling with KNbO3 in an External Cavity. Opt. Lett. 1991, 16, 1400. [Google Scholar] [CrossRef]
- Adams, C.S.; Ferguson, A.I. Tunable Narrow Linewidth Ultra-Violet Light Generation by Frequency Doubling of a Ring Ti:Sapphire Laser Using Lithium Tri-Borate in an External Enhancement Cavity. Opt. Commun. 1992, 90, 89–94. [Google Scholar] [CrossRef]
- Arie, A.; Rosenman, G.; Korenfeld, A.; Skliar, A.; Oron, M.; Katz, M.; Eger, D. Efficient Resonant Frequency Doubling of a cw Nd:YAG Laser in Bulk Periodically Poled KTiOPO4. Opt. Lett. 1998, 23, 28. [Google Scholar] [CrossRef]
- Hashemi, S.S.; Sabouri, S.G.; Khorsandi, A. The Effect of Thermal De-Phasing on the Beam Quality of a High-Power Single-Pass Second Harmonic Generation. J. Opt. 2018, 20, 045502. [Google Scholar] [CrossRef]
- Feng, C.-H.; Vidal, S.; Robert, P.; Bouyer, P.; Desruelle, B.; Prevedelli, M.; Boullet, J.; Santarelli, G.; Bertoldi, A. High Power Continuous Laser at 461 nm Based on a Compact and High-Efficiency Frequency-Doubling Linear Cavity. Opt. Express 2021, 29, 27760. [Google Scholar] [CrossRef]
- Tian, L.; Wang, Q.W.; Yao, W.X.; Li, Q.H.; Wang, Y.J.; Zheng, Y.H. Experimental realization of high-efficiency blue light at 426 nm by external frequency doubling resonator. Acta Phys. Sin. 2020, 69, 044201. [Google Scholar] [CrossRef]
- Wang, Q.; Tian, L.; Yao, W.; Wang, Y.; Zheng, Y. Realizing a High-Efficiency 426nm Laser with PPKTP by Reducing Mode-Mismatch Caused by the Thermal Effect. Opt. Express 2019, 27, 28534. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.-Z.; Shen, Y.; Liu, Q.; Zou, H.-X. Generation of 266 nm continuous-wave with elliptical Gaussian beams. Acta Phys. Sin. 2014, 63, 054204. [Google Scholar] [CrossRef]
- Deng, X.; Zhang, J.; Zhang, Y.; Li, G.; Zhang, T. Generation of Blue Light at 426 nm by Frequency Doubling with a Monolithic Periodically Poled KTiOPO4. Opt. Express 2013, 21, 25907. [Google Scholar] [CrossRef] [PubMed]
- Paschotta, R.; Kürz, P.; Henking, R.; Schiller, S.; Mlynek, J. 82% Efficient Continuous-Wave Frequency Doubling of 1.06 μm with a Monolithic MgO:LiNbO3 Resonator. Opt. Lett. 1994, 19, 1325. [Google Scholar] [CrossRef] [PubMed]
- Tinsley, J.N.; Bandarupally, S.; Penttinen, J.-P.; Manzoor, S.; Ranta, S.; Salvi, L.; Guina, M.; Poli, N. Watt-Level Blue Light for Precision Spectroscopy, Laser Cooling and Trapping of Strontium and Cadmium Atoms. Opt. Express 2021, 29, 25462. [Google Scholar] [CrossRef] [PubMed]
- Wen, X.; Han, Y.; Wang, J. Comparison and Characterization of Efficient Frequency Doubling at 397.5 nm with PPKTP, LBO and BiBO Crystals. Laser Phys. 2016, 26, 045401. [Google Scholar] [CrossRef]
- Zuo, X.; Yan, Z.; Jia, X. High-Efficiency Generation of a Low-Noise Laser at 447 nm. Appl. Phys. Express 2019, 12, 032010. [Google Scholar] [CrossRef]
- Mamrashev, A.; Nikolaev, N.; Antsygin, V.; Andreev, Y.; Lanskii, G.; Meshalkin, A. Optical Properties of KTP Crystals and Their Potential for Terahertz Generation. Crystals 2018, 8, 310. [Google Scholar] [CrossRef]
- Fengqin, L.; Huijuan, L.; Huadong, L.; Kunchi, P. High-Power Tunable Single-Frequency 461 nm Generation from an Intracavity Doubled Ti:Sapphire Laser with PPKTP. Laser Phys 2016, 26, 025802. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, J.; Wu, J.; Ma, R.; Wang, D.; Zhang, J. Single-Frequency Tunable 447.3 nm Laser by Frequency Doubling of Tapered Amplified Diode Laser at Cesium D1 Line. Opt. Express 2016, 24, 19769. [Google Scholar] [CrossRef] [PubMed]
- Ast, S.; Nia, R.M.; Schönbeck, A.; Lastzka, N.; Steinlechner, J.; Eberle, T.; Mehmet, M.; Steinlechner, S.; Schnabel, R. High-Efficiency Frequency Doubling of Continuous-Wave Laser Light. Opt. Lett. 2011, 36, 346. [Google Scholar] [CrossRef] [PubMed]
- Schwedes, C.; Peik, E.; Von Zanthier, J.; Nevsky, A.Y.; Walther, H. Narrow-Bandwidth Diode-Laser-Based Blue and Ultraviolet Light Source. Appl. Phys. B Lasers Opt. 2003, 76, 143–147. [Google Scholar] [CrossRef]
- Le Targat, R.; Zondy, J.-J.; Lemonde, P. 75%-Efficiency Blue Generation from an Intracavity PPKTP Frequency Doubler. Opt. Commun. 2005, 247, 471–481. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, Y.; Peng, Y.; Cao, J.P.; Fang, Z.J.; Zang, E.J. Stable Second Harmonic Generation 461 nm Blue Radiation by PPKTP Crystal. Acta Opt. Sin. 2009, 29, 2473. [Google Scholar] [CrossRef]
- Zhang, Y.T.; Qu, Q.Z.; Qian, J.; Ren, W.; Xiang, J.F.; Lü, D.S.; Liu, L. Thermal Effect Analysis of 1560 nm Laser Frequency Doubling in a PPLN. Chin. J. Laser 2015, 42, 0708002. [Google Scholar] [CrossRef]
- Yao, J.; Wang, Y. Nonlinear Optics and Solid-State Lasers: Advanced Concepts, Tuning-Fundamentals and Applications; Springer Series in Optical Sciences; Springer: Berlin/Heidelberg, Germany, 2012; Volume 164, pp. 130–131. [Google Scholar]
- Innocenzi, M.E.; Yura, H.T.; Fincher, C.L.; Fields, R.A. Thermal Modeling of Continuous-Wave End-Pumped Solid-State Lasers. Appl. Phys. Lett. 1990, 56, 1831–1833. [Google Scholar] [CrossRef]
- Kato, K. Temperature Insensitive SHG at 0.5321 μm in KTP. IEEE J. Quantum Electron. 1992, 28, 1974–1976. [Google Scholar] [CrossRef]
- Boyd, G.; Kleinman, D. Parametric Interaction of Focused Gaussian Light Beams. IEEE J. Quantum Electron. 1968, 4, 353. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Zhao, G.; Tan, W.; Chang, H. 382 mW External-Cavity Frequency Doubling 461 nm Laser Based on Quasi-Phase Matching. Photonics 2024, 11, 40. https://doi.org/10.3390/photonics11010040
Chen Y, Zhao G, Tan W, Chang H. 382 mW External-Cavity Frequency Doubling 461 nm Laser Based on Quasi-Phase Matching. Photonics. 2024; 11(1):40. https://doi.org/10.3390/photonics11010040
Chicago/Turabian StyleChen, Yingxin, Guodong Zhao, Wei Tan, and Hong Chang. 2024. "382 mW External-Cavity Frequency Doubling 461 nm Laser Based on Quasi-Phase Matching" Photonics 11, no. 1: 40. https://doi.org/10.3390/photonics11010040
APA StyleChen, Y., Zhao, G., Tan, W., & Chang, H. (2024). 382 mW External-Cavity Frequency Doubling 461 nm Laser Based on Quasi-Phase Matching. Photonics, 11(1), 40. https://doi.org/10.3390/photonics11010040




