Nonlinear Scattering of 248 nm Wavelength Light in High-Pressure SF₆ and CH₄ Gases for the Temporal Compression of a 20 ns KrF Laser Pulse

Abstract

The nonlinear compression of narrowband (Δν ≈ 0.2 cm⁻¹) 20 ns KrF laser pulses in SF₆ at 10 atm and in CH₄ at 50 atm pressure was studied. Both SBS and SRS optically phase-conjugated backward-reflected radiation was registered with an energy reflectivity of 10–14% in SF₆ and CH₄. In SF₆, the SBS pulses gradually shortened from 10 ns to 2–3 ns with a decrease in pumping to the SBS threshold of ~10 mJ, while the SRS pulse had the shortest length of 30–60 ps for the maximal pumping of 120 mJ and broadened near the SRS threshold of ~30 mJ. For the SRS pulse energy, the ~2 mJ peak power 5 × 10⁷ W was tenfold higher than the pump power. The theoretical model predicted a soliton-like SRS pulse compression to a temporal length of the order of the vibrational relaxation time. There was no pulse compression of backward SBS and SRS radiation in CH₄, while, in the forward direction, SRS pulses shortened to 3–4 ns at reduced pumping.

1. Introduction

In the most energetically efficient inertial confinement fusion (ICF) scheme with a “shock ignition” (SI), the processes of the capsule implosion with deuterium–tritium (DT) fuel and its subsequent “ignition” are separated in time [1,2]. After a uniform, close-to-adiabatic, compression of the capsule for several tens of nanoseconds, a thermonuclear fusion begins in the hottest and densest central region of the compressed target. This region is additionally heated by converging to the central strong shock wave. The latter is generated by an even more powerful laser pulse spike with a duration of several hundreds of picoseconds. During this time, the compressed fuel does not have time to expand. The escape of neutrons and their absorption in a fusion reactor blanket provide useful energy to the power cycle of the inertial fusion energy (IFE) plant, whereas α-particles absorbed nearby in the dense DT fuel provide additional heating and thus support thermonuclear fusion in the rest of the fuel. The described scheme of the SI ICF can be implemented with laser pulses having a complex time shape with a short final spike, whose power exceeds the main driving pulse by one or two orders of magnitude.

After a recent demonstration of the ignition in indirect compression experiments at the NIF 3ω Nd glass facility [3], the undoubted advantage of which is the homogeneity of target compression, the focus of ICF research is shifting to the implementation of advanced direct compression schemes, e.g., SI ICF with more efficient laser drivers. The laser driver for the IFE power station must meet a number of challenges. First of all, it must have the highest overall efficiency and a short radiation wavelength λ for efficient absorption in plasma and higher ablation pressure, and it must allow temporal profiling of laser pulses for the SI ICF. Most of these requirements could be satisfied with e-beam-pumped KrF drivers [4,5].

Compared to solid-state lasers, a KrF laser possesses (i) a short lifetime of the excited B state of KrF molecule τ_c ≈ 2 ns (taking into account a radiation decay time and quenching collisions); (ii) low gain saturation parameters—the saturation intensity I_s ≈ 2 MW/cm² for a quasi-stationary amplification of “long” nanosecond pulses with τ ≥ τ_c, for which an instant intensity manages the gain saturation, as well as saturation energy density ε_s ≈ 2 mJ/cm² for “short” sub-nanosecond and picosecond pulses with τ ≤ τ_c. The three-orders-of-magnitude-lower I_s and ε_s are well compensated by a larger gain volume of KrF lasers effectively pumped by e-beams. As a small τ_c does not allow storage of the population inversion in the gain medium during the pumping time τ_p >> τ_c (usually of a few hundred nanoseconds), an angular multiplexing scheme is conventionally used to effectively extract the pump energy from amplifiers in a train of time-separated and angularly separated pulses obtained by splitting the initial laser beam into multiple beamlets (see, e.g., [5]). But a direct amplification of the entire SI ICF pulse shape meets difficulties as a steep high-intensity final spike strongly saturates the gain medium compared with a pulse foot. A precise precompensation of the saturation is required before pulse amplification, which increases the spike-to-foot ratio of the initial pulse shape even more [6]. An alternative approach is a simultaneous-in-time amplification of both long and short pulses in separate beamlets, in which the rest gain remains in a course of a quasi-continuous amplification of long pulses in addition to amplifying short pulses [7,8]. A combining of long and short pulses on a target after their demultiplexation makes it possible to produce a temporal shape required for the SI ICF.

The feasibility of the simultaneous amplification of high-energy long pulses (~50 J, 100 ns) on par with a train of sub-ps pulses with a sub-TW peak power has already been demonstrated [9]. Short pulses were generated using a Ti: Sapphire front end, which was frequency-tripled into the KrF amplification band [8]. Unfortunately, a local growth of energy density in the evolving filaments significantly reduced the amplifier gain while three-photon absorption in the CaF₂ windows (material of the choice) produced window degradation [9]. Also, the filamentation of powerful UV pulses in atmospheric air strongly distorted the laser beam distribution [10].

In the present study, we deal with a nonlinear UV pulse compression when focusing radiation into a nonlinear medium. It differs favorably from other methods of generating short pulses using a mode-locking technique, dye lasers, or frequency tripling of a Ti: Sapphire laser by means of its simplicity, availability in terms of the cost, and high contrast (the ratio of the peak power of the short pulse to the pre-pulse) determined by the threshold nature of nonlinear processes. A nonlinear temporal compression of discharge-pumped KrF laser pulses was investigated over decades in high-pressure SF₆ and CH₄ gases, which are promising nonlinear medium [11,12,13,14,15,16,17,18,19,20,21]. It was shown that an effective pulse compression with an appropriate increase in peak power can be obtained via a backward stimulated Brillouin scattering (SBS) [12,13,14,15,17,18,21], backward stimulated Raman scattering (SRS) [11,16], and their combination in a four-wave mixing (FWM) scheme [19,20]. An advantage of the SBS is the small frequency shift in the Stokes components (Δλ_B~10⁻³ nm) compared to the width of the KrF laser gain bandwidth (Δλ~2 nm), which allows one further amplification of the compressed pulses in KrF amplifiers. However, a large dephasing time T₂ determined by a lifetime of hypersonic phonons in the medium, namely, 100–600 ps in gases compressed up to 10 atm and 30–150 ps in various SBS-active liquids, generally sets lower limits for the achievable pulse duration. The length of the nonlinear interaction L_nl for SBS generated from a spontaneously scattered light is typically selected to be g_B × I × L_nl ≥ 25 for one pass just to exceed the SBS threshold. Some advantages in pulse shortening below T₂ and the higher reflection give a so-called self-seeding SBS configuration implemented with a Nd: YAG laser in CCl₄ [22] and C₈F₁₈ [23], in which a part of the transmitted pump radiation was reflected back into the nonlinear interaction region by means of an additional mirror. Unfortunately, the choice of transparent liquids for the UV KrF laser wavelength is very limited; the best ones are the fluorocarbons C₆F₁₄ and C₈F₁₈ (g_B ≈ 0.5 × 10⁻² cm/MW). Among gases, SF₆ has the largest SBS gain (g_B ≈ 0.9 × 10⁻² cm/MW).

The advantage of the SRS compression is a shorter phase dephasing time: in CH₄ compressed up to 7.5 atm, T₂~25ps, this makes it possible to obtain shorter picosecond pulses in a backward reflection. The disadvantage of the SRS is a significant shift in the wavelength of the Stokes components out of the KrF gain bandwidth Δλ_R >> Δλ. To overcome this wavelength misalignment, the FWM of Stokes and anti-Stokes components was additionally used, wherein the original frequency of the KrF laser wavelength was restored in temporally compressed pulses, which could be further amplified in the chain of KrF amplifiers [19,20].

The present experiments were conceived to elucidate the competition between nonlinear SBS and SRS processes in compressed SF₆ and CH₄ gases in the case of backscattering and forward scattering. Such competition has commonly been observed in experiments with various types of lasers, including excimer lasers, while the results obtained often contradicted each other. In the present experiments, we used both narrowband and broadband pumping radiation with a final goal to select an effective scheme for the temporary compression of UV pulses generated using a discharge-pumped KrF laser with a 20 ns pulse length. The obtained sub-ns pulses will be further implemented for combining the SI ICF pulse shape at a multistage e-beam-pumped GARPUN KrF laser facility [8].

2. A Layout of Experiments

A discharge-pumped KrF laser EMG 150 TMSC 150 (Lambda Physik, GmbH) was used in the experiments on the nonlinear scattering of λ = 248 nm radiation in high-pressure SF₆ and CH₄ gases. This is a two-chamber laser (oscillator and amplifier) with a common power supply operating in an injection-controlled scheme. When a narrowband seed radiation from the oscillator was injected into an unstable resonator cavity of the amplifier, the output radiation had an energy of up to 200 mJ in pulses of τ ≈ 20 ns FWHM, a beam divergence of ~0.3 mrad, and a narrow bandwidth of Δλ ≈ 1.2 × 10⁻³ nm (Δν ≈ 0.2 cm⁻¹). Alternatively, with a blocked narrowband oscillator, the bandwidth of the output radiation was Δλ ≈ 0.25 nm (Δν ≈ 40 cm⁻¹), while other laser parameters changed slightly. The experiments were performed with a repetition rate of 1 Hz, although the laser could operate with 80 Hz.

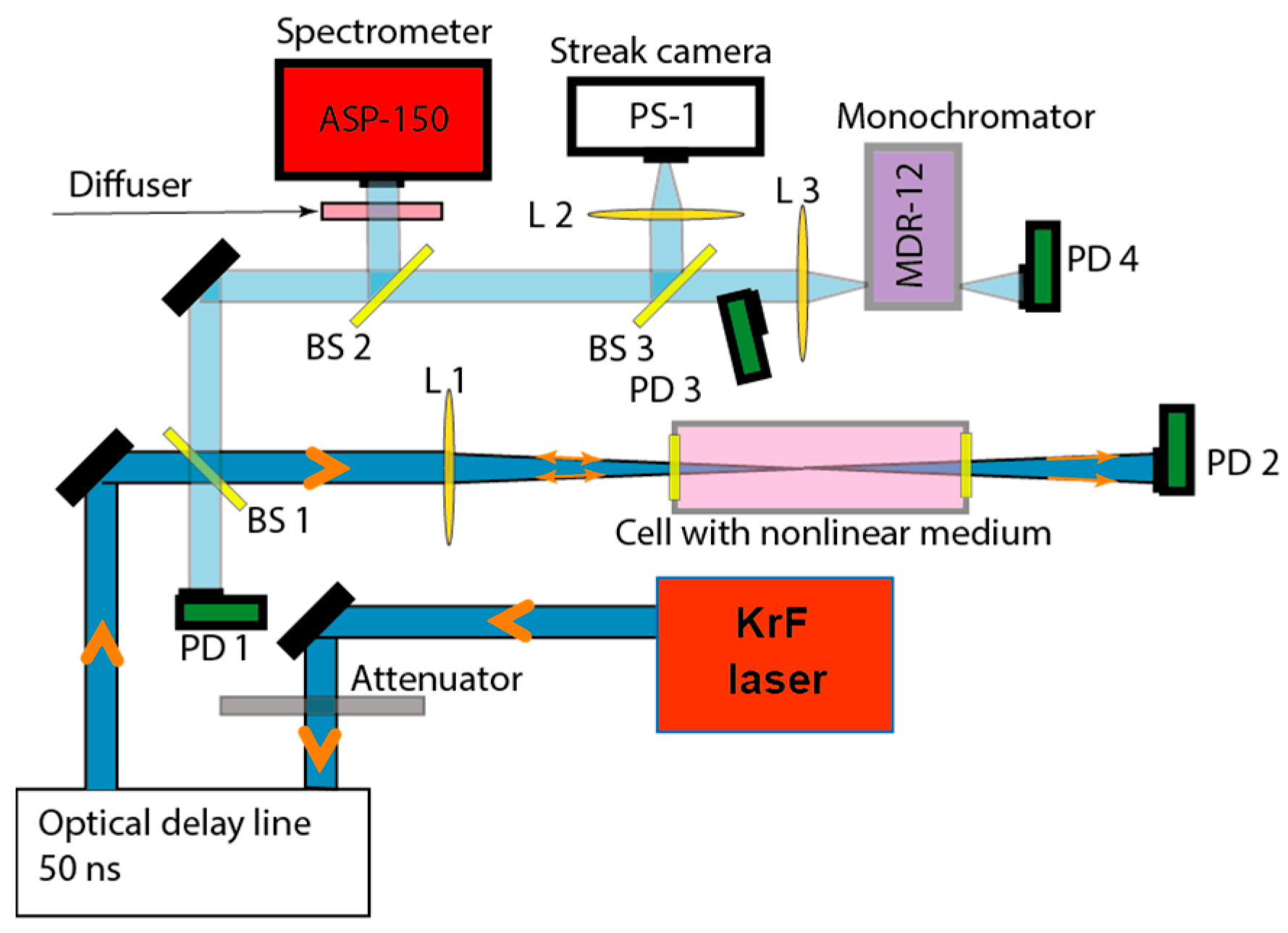
The backscattered radiation was monitored in the layout shown in Figure 1. The laser energy, before being focused in a gas cell, was step-wise attenuated in the dynamic range 0.01–0.94 from the initial value E using a nine-stage diffraction attenuator DVA-22-250 (Inst. of Automation and Electrometry SB RAS, Novosibirsk, Russia). The energy was measured using a PESO-SH-V2 calorimeter with a NOVA II display (Ophir Photonics, Jerusalem, Israel). To monitor the radiation time behavior, high-speed photodiodes (Thorlabs DET10A) were used. The pulse shapes of the incident radiation that passed through the cell with the nonlinear medium and that reflected back were recorded using photodiodes PD 1, PD 2, and PD 3, respectively, with a TDS 3054C 500 MHz oscilloscope (Tektronix Inc., Beaverton, OR, USA) with a time resolution of ~1 ns. Even shorter UV pulses obtained through nonlinear compression were measured using a streak camera PS-1/S1 (Institute of General Physics of the RAS, Moscow, Russia) with a picosecond time resolution. The images on the screen of the streak camera were registered with an Anima-PX reader (Optronics Gmbh, Kehl, Germany). The time-integrated spectra of the scattered radiation were recorded using an ASP-150 T (Avesta Project Ltd., Moscow, Russia) spectrometer with a spectral resolution of ~0.3 nm. To illuminate the entrance slit of the spectrometer uniformly, a scattering diffuser was set in front of it. The temporal dynamics of scattered spectral components was studied using an MDR-12 grating monochromator (LOMO, St. Petersburg, Russia) tuned to the required wavelength range with a registration of the selected radiation by the PD 4 photodiode.

Due to a small spectral shift, the radiation reflected by the SBS stays inside the laser bandwidth. Therefore, there was a potential danger of damage to the output meniscus coupler of the laser and its output window due to the radiation back reflected from the nonlinear medium when it was focused in an inverse converging wave of the unstable telescopic resonator. In this regard, a polarization decoupling of the incident radiation and that reflected back from the cell was foreseen with a help of a quarter-wave phase plate and a polarizer. However, in the experiments described below, an optical delay line of about 15 m length was used between the laser and the cell, thanks to which the reflected pulse returned after 100 ns, i.e., to the moment when the gain in the laser decayed after a termination of the pumping discharge.

The cell with the SF₆ had an inner diameter of 26 mm and a length of 250 cm; it was filled at a pressure of 10 atm. It was chosen based on previous experiments [12,13,16,17]. Plane-parallel windows made of fused silica glass KU-1 with a diameter of 40 mm and a thickness of 10 mm were used. The pump radiation was focused into the cell using lenses with focal lengths of F = 0.8 or 2 m. The first lens was set close to the cell entrance, and the second one was 70 cm in front of the cell. The Fresnel reflection from the windows was excluded from the registration of backward radiation by means of a slight inclination of the cell axis relative to the axis of the incident radiation. The cell with CH₄ at a pressure of 50 atm had an inner diameter of 20 mm and a length of 70 cm. It was closed from both sides with thick, wedge-shaped windows of 30 mm diameter, which excluded the Fresnel reflection of the pump radiation being focused into the cell using a lens with F = 0.5 m set at 15 cm in front of the cell.

The radiation distribution in the focal plane was measured using a Spiricon SP620U profiler (Ophir Photonics), while a K8 glass plate was used to convert the UV laser light into green fluorescence [10]. The focal distribution had a Gaussian-like symmetric central part and broad, low-intensity wings, originating from a temporal evolution of laser light in the unstable resonator cavity of the laser [24]. The distribution of pump radiation in the focal spot for all lenses used in the experiments remained similar and scaled proportionally to the focal length F, while the peak intensity in the spot I varied as $I\propto E/\tau F^2$. For a given pulse duration τ ≈ 20 ns, the peak intensity in the center of the focal spot could be expressed via other variables as $I\left[\mathrm{W}/{\mathrm{c}\mathrm{m}}^2\right]={9\times 10}^{10}\times E\left[\mathrm{J}\right]∕{\left(F\left[\mathrm{m}\right]\right)}^2$. Note that, for the highest pump energy E_max ≈ 120 mJ and the shortest focal length F = 0.5 m, the maximal peak intensity was 4.3 × 10¹⁰ W/cm², which was still less than the breakdown thresholds for the gases under investigation.

3. Experimental Results

The radiation reflected exactly backward was recorded in the experiments with a narrowband pumping of SF₆ and CH₄ gases, thus evidencing that an optical phase conjugation (OPC) was realized via the SBS and SRS mechanisms. A quite different temporal behavior of the backscattered radiation, that is, pulse compression dependent on the pump energy E_p, was observed in these two gases. Note that, for broadband pumping, no backward reflection was detected at all in both gases. On the contrary, the SRS in the forward direction was more pronounced for broadband pumping in CH₄.

3.1. Backscattering in SF₆

The time-integrated spectrum of the reflected radiation is shown in Figure 2a. The spectral line widths were broadened due to the ASP spectral resolution, while a broad pedestal arose due to scattered light inside the spectrometer. The most intensive peak at the wavelength λ = 248.4 nm corresponded to SBS, which had a small shift relative to the pump radiation bandwidth Δλ_B ≤ Δλ, being unresolved at the spectrometer. In addition to this practically “unshifted” SBS peak, the spectrum contained significantly weaker SRS peaks at λ = 253.3 and 258.3 nm. The frequency shift for these first- and second-order SRS components being a multiple of the 775 cm⁻¹ quantum, which corresponded to the strongest SRS line associated with completely symmetrical vibrations of the SF₆ molecule [25]. A ratio of the first SRS to the SBS peaks found from the time-integrated spectrum gives the approximate ratio of the corresponding SRS and SBS energies, which was E_SRS/E_SBS ≈ 1/6.5 for E_p ≈ 120 mJ and decreased drastically on decreasing the pump energy.

A study of the temporal dynamics of reflected radiation was carried out with an F = 2 m focusing lens. It shows a reduction in the leading edge of reflected pulses, with the most significant being for the SRS components (Figure 3). As some small variations were observed for registered pulse forms dependent on the occasional fluctuation of pump energy or its spectral width, we provide the most typical of them, which were repeated in a series of at least ten shots. Note that, due to a difference in the optical paths to the PDs and the lengths of their cables, the signals on the oscilloscope have different delays relative to the beginning of the time scan. For example, relative to the pump radiation (PD 1), the signal of reflected radiation in the entire spectral range including all scattered components (PD 3) was delayed by 33 ns, and the reflected radiation of the selected spectral components SBS or SRS (PD 4) was delayed by 46 ns. The pulse length of the SBS component at the maximal pump energy of ~120 mJ was ~10 ns at the FWHM, i.e., twice less than the pump length of ~20 ns. The reflected SBS pulse length decreased down to 2–3 ns at the FWHM when the pump energy approached the SBS threshold of ~10 mJ (Figure 3c). The pulse length of the reflected SRS radiation, on the contrary, decreased with an increase in the pump energy above the threshold of ~30 mJ; at E_p ≈ 120 mJ, it was 1–2 ns (Figure 3b), which was about the temporal resolution of the PD. Therefore, a fast streak camera was used to resolve the components of the backscattered radiation. A possible explanation for SRS pulse shortening with pump intensity is discussed in Section 4.

The streak camera images obtained with various scanning speeds are shown in Figure 4a–c together with the temporal pulse profiles. The presence of two components with different time widths is evident in streak image (a) with a 100 ns scanning time. The long time component of ~50 ns corresponds to the SBS signal on the oscilloscope traces (Figure 3a). The second, a short time component, which is time integrated and looks like a leading peak in the temporal profile of streak image (a) is well resolved with a shorter sweeping time of 0.5 ns in streak images (b,c). Its length variation in the range 30–60 ps corresponds to the unresolved SRS signals in Figure 3b. The doubled structure of images separated across time (horizontal axis) and space (vertical axis) originates from a difference in the course of light reflected from two faces of the beam splitter plate that diverted radiation from the cell (BS 3 in Figure 1). The single-humped and double-humped temporal profiles in case (b) were obtained with different integration regions of the streak images in a perpendicular (space) direction, which accounted for one or two spots.

3.2. Backscattering in CH₄

In experiments with the CH₄ cell, in which a narrowband pump radiation (focused with F = 0.5 m lens) was also reflected strictly backward, the time-integral spectrum in addition to the main SBS peak at λ = 248.4 nm contained a peak at λ = 267.8 nm with a comparable amplitude (Figure 2b). The frequency shift for the Stokes component 2917 cm⁻¹ corresponded to the strongest line in the SRS spectrum of CH₄ [13]. The reflected signals for both the SBS and the SRS components gradually shortened with decreasing pump energy; however, the shortest pulses were ~4 ns (Figure 5). The thresholds for SBS ~6 mJ and for SRS −30 mJ were close to the values in SF₆. Note that, for broadband pump radiation, no backward reflection was registered in the experiments.

3.3. Backscattering Efficiencies

Energies of the total (both SBS and SRS) backscattered radiation E_refl and pump radiation E_p were measured using calorimeters, and the efficiency of a backward nonlinear reflection was calculated as R_refl = E_refl/E_p × 100%. It is represented in Figure 6 for SF₆ (a) and CH₄ (b). All experimental dots in the graphs represent averaging over 10 successive measurements. In both gases, the R_refl grew rapidly with increasing pump energy above the threshold of nonlinear reflection, gradually saturating at high E_p. In SF₆, the maximum efficiency amounted to (R_refl)_max ≈ 10% and was approximately equal for different focal lengths of the focusing lenses F = 0.8 m and F = 2 m. An additional mirror installed behind the cell increased the R_refl especially at low pump energy (curve “F = 1 m + mirror”), thus indicating that the radiation reflected by the mirror highly contributed to the nonlinear scattering process additively to a spontaneous scattering in the gas similar to that obtained with a Nd: YAG laser in [22,23]. At the highest pump energy, the maximum efficiency increased by 30% up to (R_refl)_max ≈ 14%. The maximum efficiency in CH₄ for the lens with F = 0.5 m amounted to (R_refl)_max ≈ 14% without any additional mirror. It should be noted once again that a ratio of the SRS to SBS radiation gradually decreased for lower pump energies.

3.4. Forward Scattering in CH₄

The forward radiation passed through a CH₄ cell was measured in a scheme similar to that shown in Figure 1 with a F = 50 cm lens being set behind the cell confocal with the focusing lens. This additional lens collimated both the transmitted pump radiation and the forward-scattered one, which were analyzed with the spectrometer and monochromator placed at ~7.5 m behind the cell. Similar to Figure 1, photodiode PD 3 measured the total radiation reflected by the lens L3 at the monochromator entrance, while PD 4 measured the total radiation output at specific wavelengths of various spectral components.

The spectra of a forward radiation through the CH₄ cell are presented in Figure 7 for both narrowband (a) and broadband pump radiation (b). It is seen that, for narrowband pumping, besides the “wavelength-unshifted” main line at λ = 248.4 nm, the spectrum contained the first- and second-order Stokes SRS peaks at λ = 267.8 and 290.5 nm, respectively. For broadband pumping, an additional third-order Stokes SRS peak at λ = 317.4 nm and a weak first-order anti-Stokes SRS peak at λ = 231.6 nm appeared in the spectrum, which means that a cascade nonlinear process of high-order forward SRS component generation is more effective for broadband pump radiation.

As no backscattered light was registered for broadband pumping, the oscilloscope signals for both forward radiation at λ ≈ 248.4 nm (passed through the monochromator) and total transmitted radiation including pumping and all scattered SRS components increased at the expense of suppressed back-reflected radiation compared with a narrowband pumping.

The pulse shapes for a narrowband pump radiation measured in front of the cell, backscattered SBS and SRS components, and transmitted radiation at specific wavelengths selected by the monochromator are shown in Figure 8. At a high pump energy of E_p ≈ 120 mJ, a pulse of transmitted radiation at λ = 248.4 nm had a slowly rising leading front and a steep trailing front compared with the pump pulse (a). It might be explained by a depletion of pump radiation being converted into backscattered SBS and SRS, as well as forward-scattered SRS. Oppositely, a pulse form at λ = 267.8 nm for a forward first-order SRS component had a steep leading front (b). However, the pulse widths for the pump, reflected back, total transmitted, and forward-scattered SRS radiation were all comparable. The difference in transmitted pulse lengths became clear at a reduced pump energy of E_p ≈ 25 mJ (c). The forward SRS pulses shortened down to 3–4 ns, while the transmitted radiation at λ = 248.4 nm did not change noticeably.

4. Discussion

The above-described results demonstrate a strong competition between two nonlinear scattering processes, SBS and SRS. Firstly, it was observed in compressed gases with a ruby laser [26,27], and then it was reported for shorter laser wavelengths (see e.g., [12,28]). Both the SBS and SRS, each having different dependencies on gas pressure, could occur simultaneously even if one of them had higher gain coefficient in some region of parameters. Their interaction originates mainly from the change in the spatial distribution of optical fields altered (depleted) by an intense level of scattering. Backward SRS pulse compressors for KrF ICF were also discussed in [16,29,30], wherein limitations from the other scattering processes were considered, e.g., SBS and forward SRS. The latter was shown to be asymmetric relative to the backward SRS and was able to proceed with a broadband pumping, similar to present experiments.

Among other things, there is a discrepancy between our results on backscattering in SF₆ and in the experiments [17], wherein, in similar conditions, no backscattered SRS radiation was measured at all. On the other hand, in accordance with present experiments, Tomov et al. [12] observed a short backward Raman scattering with a pulse duration in the range of 120–400 ps preceding the Brillouin backscattered signal. However, after the development of the SBS, the SRS was suppressed because of the higher gain for the Brillouin mode.

Conventionally, the shortest scattered laser pulses are obtained near the threshold of corresponding stimulated scattering process. After exceeding the threshold, the rapidly growing Stokes signal results in a depletion of the pump wave, so that the pump intensity drops below the threshold and the stimulated amplification is ended. With an increase in the pump peak intensity, the threshold for stimulated scattering is exceeded for a longer part of the pump pulse, which is why pulse width of the scattered signal should increase proportionally. In our experiments, this natural behavior held for the backward SBS and forward SRS, while, in the case of backward SRS in SF₆, the Stokes pulse width was found to decrease with an increase in pump pulse intensity. Below, we provide a simple theoretical consideration that allows us to explain this anomalous dependency.

The conventional model of backward SRS is based on the following set of equations [31,32,33]:

$$\begin{array}{l}\frac{\partial E_p}{\partial t}+v_p\frac{\partial E_p}{\partial x}+\frac{{\gamma }_p}{2}{E}_p=-{\beta }_p{E}_{s}Q,\\ \frac{\partial E_s}{\partial t}-v_s\frac{\partial E_s}{\partial x}+\frac{{\gamma }_s}{2}{E}_s={\beta }_s{E}_{p}Q,\\ \frac{\partial Q}{\partial t}+\Gamma Q={\beta }_a{E}_s{E}_p\end{array}$$

(1)

Here, $E_p$ and $E_s$ are the slow-varying amplitudes of the forward pump and the backward Stokes waves, $E_p\mathit{exp}(i[k_{p}x-{\omega }_{p}t])$ and $E_s\mathit{exp}(i[k_{s}x-{\omega }_{s}t])$, having the wavenumbers $k_{p,s}$, the frequencies ${\omega }_{p,s}$, and the group velocities $v_{p,s}$, respectively. The constants ${\gamma }_p$ and ${\gamma }_s$ describe linear attenuation at the pump and the Stokes waves, while $\Gamma$ is the relaxation rate of the specific normal vibrational coordinate $q=Q(x,t)\mathit{exp}(i[k_{a}x-{\omega }_{0}t])$, where $Q(x,t)$ is its slow-varying amplitude and ${\omega }_0={\omega }_p-{\omega }_s$ is the resonant vibrational frequency, $k_a=k_p+k_s$. The light–matter coupling coefficients are ${\beta }_{p,s}=(\pi N{\omega }_{p,s}/n_{p,s}c)(\partial \alpha /\partial q)$ and ${\beta }_a=(1/4M{\omega }_0)(\partial \alpha /\partial q)$, where $n_{p,s}=k_{p,s}/{\omega }_{p,s}$ are the refractive indices at the pump and the Stokes frequencies, and $N,M,(\partial \alpha /\partial q)$ are, respectively, the number density of Raman-active molecules, their effective mass, and the derivative of the molecular polarizability with respect to the normal coordinate.

Introducing the new amplitude functions according to the following substitution $(E_p,E_s,Q)=(A_p,A_s,R)\mathit{exp}(-{\gamma }_{p}t/2)$, one can rewrite (1) as follows:

$$\begin{array}{l}\frac{\partial A_p}{\partial t}+v_p\frac{\partial A_p}{\partial x}=-{\beta }_p{A}_{s}R{e}^{-\frac{{\gamma }_{p}t}{2}},\\ \frac{\partial A_s}{\partial t}-v_s\frac{\partial A_s}{\partial x}+{\kappa }_s{A}_s={\beta }_s{A}_{p}R{e}^{-\frac{{\gamma }_{p}t}{2}},\\ \frac{\partial R}{\partial t}+{\kappa }_{a}R={\beta }_a{A}_s{A}_p{e}^{-{\gamma }_{p}t/2}\end{array}$$

(2)

where ${\kappa }_s=({\gamma }_s-{\gamma }_p)/2$ and ${\kappa }_a=\Gamma -{\gamma }_p/2\approx \Gamma$ are the new attenuation coefficients. In view of the fact that the attenuation coefficient ${\gamma }_p$ is rather small so that ${\gamma }_{p}t<<1$ during the entire interaction process, one can solve Equation (2) within the perturbation theory. To the lowest order of the perturbation theory [34], we insert the exponents in the right-hand side of (2) being equal to unity and seek transient solutions of the following shape:

$$A_s=C_s/\mathit{cos}h(\xi ),R=C_a/\mathit{cos}h(\xi )$$

(3)

where the transient coordinate $\xi =(x+ut)/\Delta$, and $\Delta$ characterizes the pulse width $\tau \propto \Delta /u$. One can easily find that both the soliton-like solutions (3) satisfy the second and the third part of Equation (2) under the following conditions:

$$u=\frac{v_s}{1-{\kappa }_s/{\kappa }_a},{\left(\frac{C_s}{C_a}\right)}^2=\frac{{\beta }_s{\kappa }_a}{{\beta }_a{\kappa }_s}$$

(4)

The pump wave amplitude is then described as follows:

$$A_p={\left(\frac{{\kappa }_s{\kappa }_a}{{\beta }_s{\beta }_a}\right)}^{1/2}\left(1-\frac{u}{{\kappa }_a\Delta }\mathit{tan}h(\xi )\right)$$

(5)

Substituting (5) in the first of Equation (2), we find the following:

$$C_s^2=\frac{1}{{\beta }_s{\beta }_a}\frac{u(u+v_p)}{{\Delta }^2}$$

(6)

Note that, when ${\gamma }_s>{\gamma }_p$, we have the coefficient ${\kappa }_s>0$, the velocity of the transients exceeds the group velocity of the Stokes signal $u>v_s$ and all the amplitudes $C_s,C_a,A_p$ have the same phase. Vice versa, when ${\gamma }_s<{\gamma }_p$, we have ${\kappa }_s<0$, the amplitudes $C_a,A_p$ differ from $C_s$ by $\pi /2$ in phase, and the transient velocity becomes less than the group velocity $u<v_s$.

The above transient solutions describe the backward SRS process in which the Stokes characteristic pulse width decreases with an increase in pump intensity. Really, the initial intensity of the pump laser pulse $I_0$ corresponds to the limiting value of (5) at $\xi \to -\infty$, i.e.,

$$\tau \propto \frac{\Delta }{u}=\frac{{\kappa }_a^{-1}}{\sqrt{I_0/I_{th}}-1}$$

(7)

Here, the characteristic threshold intensity $I_{th}=(c/8\pi )|{\kappa }_s{\kappa }_a{\beta }_a/{\beta }_s|$. According to (7), the pulse width of the Stokes pulse is large near the threshold intensity and gradually decreases with an increase in $I_0/I_{th}$, being of the order of ${\kappa }_a^{-1}\approx {\Gamma }^{-1}$, i.e., of the order of the characteristic vibrational relaxation time of the Raman-active medium. This dependency qualitatively agrees with the experimental data in Section 3.1.

5. Conclusions

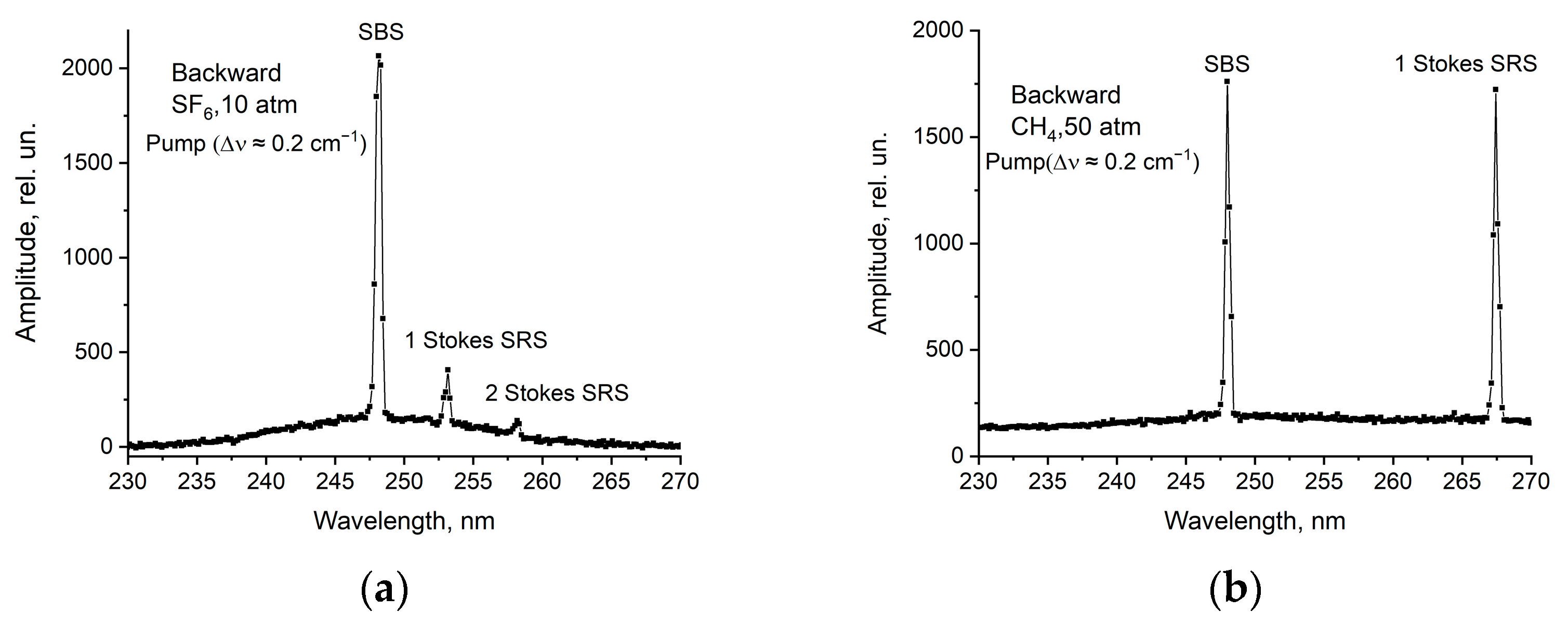
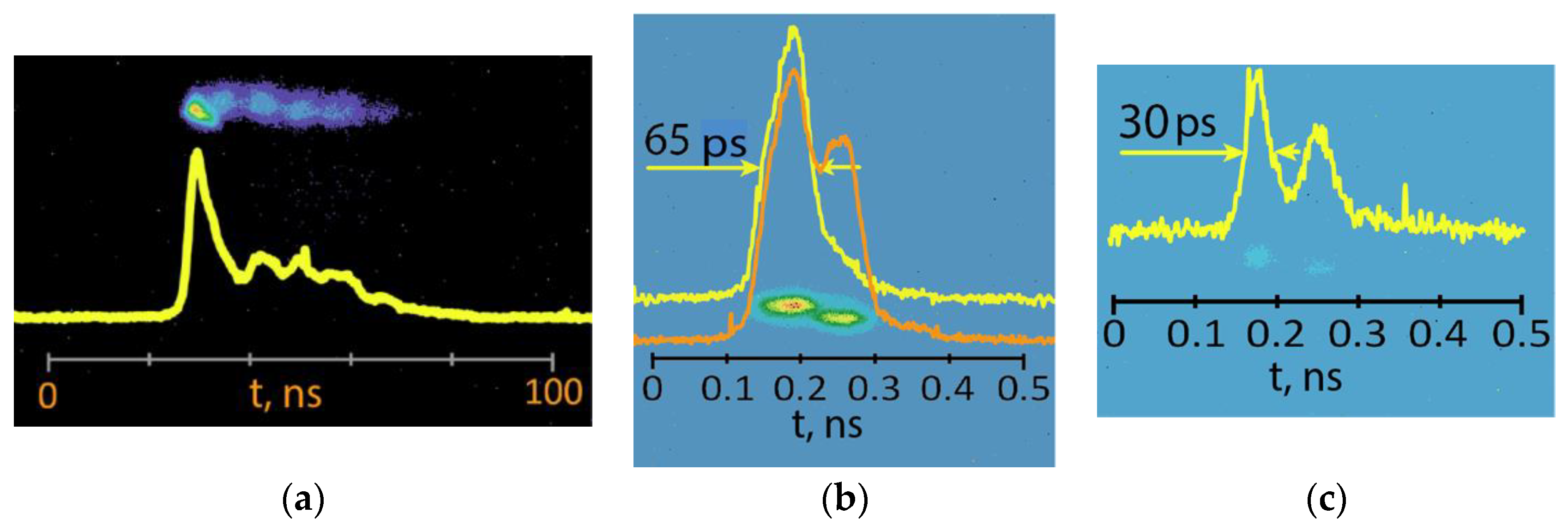
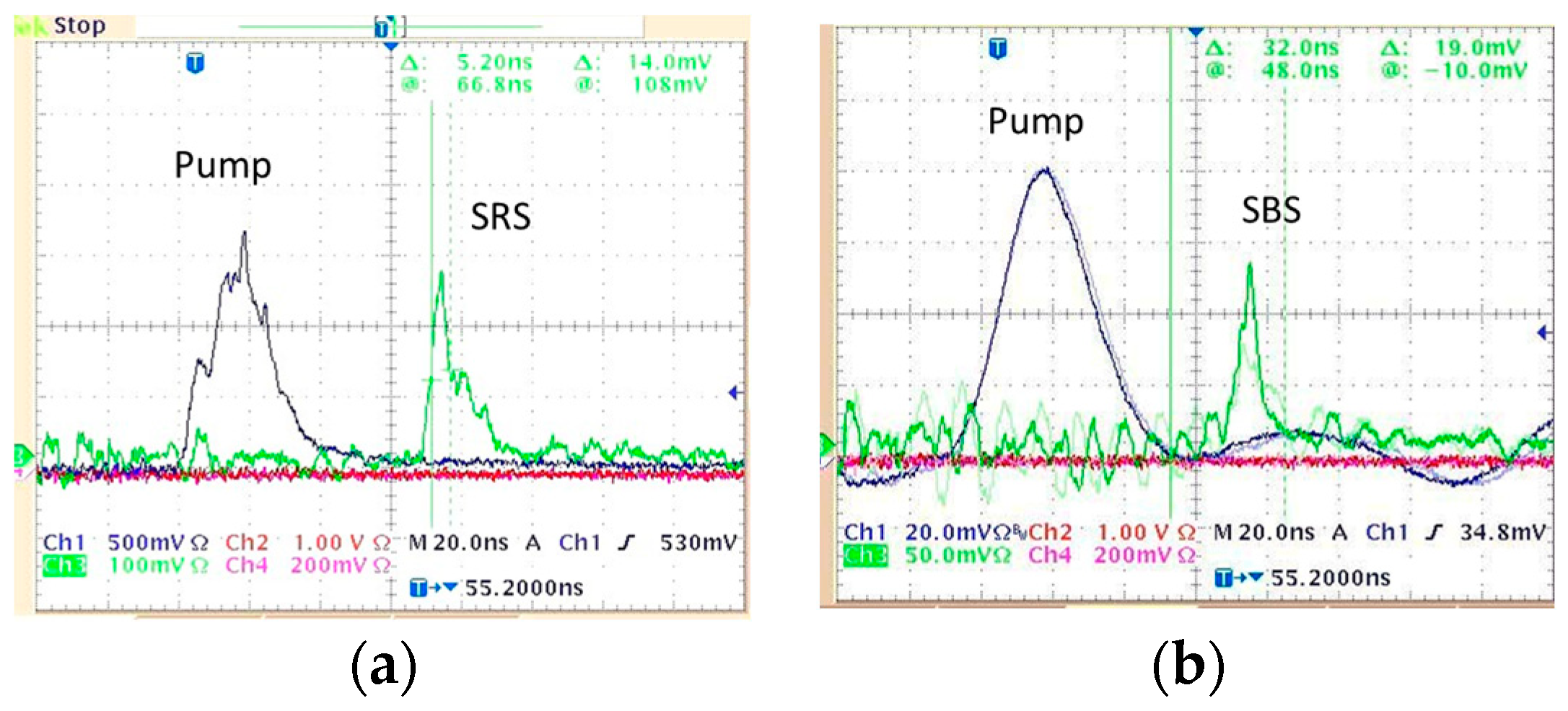
A nonlinear pulse compression was obtained for a narrowband KrF laser radiation in compressed gases. When KrF laser pulses with a 20 ns temporal width were focused into a SF₆ cell at 10 atm pressure both SBS and SRS optically phase-conjugated backward reflection was registered with an energy reflectivity of 10–14%. While the SBS pulse gradually shortened from 10 ns for a high pump energy of 100 mJ to 2–3 ns when approaching the SBS threshold of ~10 mJ, the SRS pulse exhibited an abnormal behavior. It had the shortest width of 30–60 ps for the maximal pumping of 120 mJ and broadened near the SRS threshold of ~30 mJ. The SRS pulse energy was about 2 mJ, which corresponded to the peak power of 5 × 10⁷ W, and this was tenfold higher than the pump power (120 mJ and 20 ns). The theoretical model predicted a soliton-like SRS pulse compression to a temporal width of the order of the vibrational relaxation time.

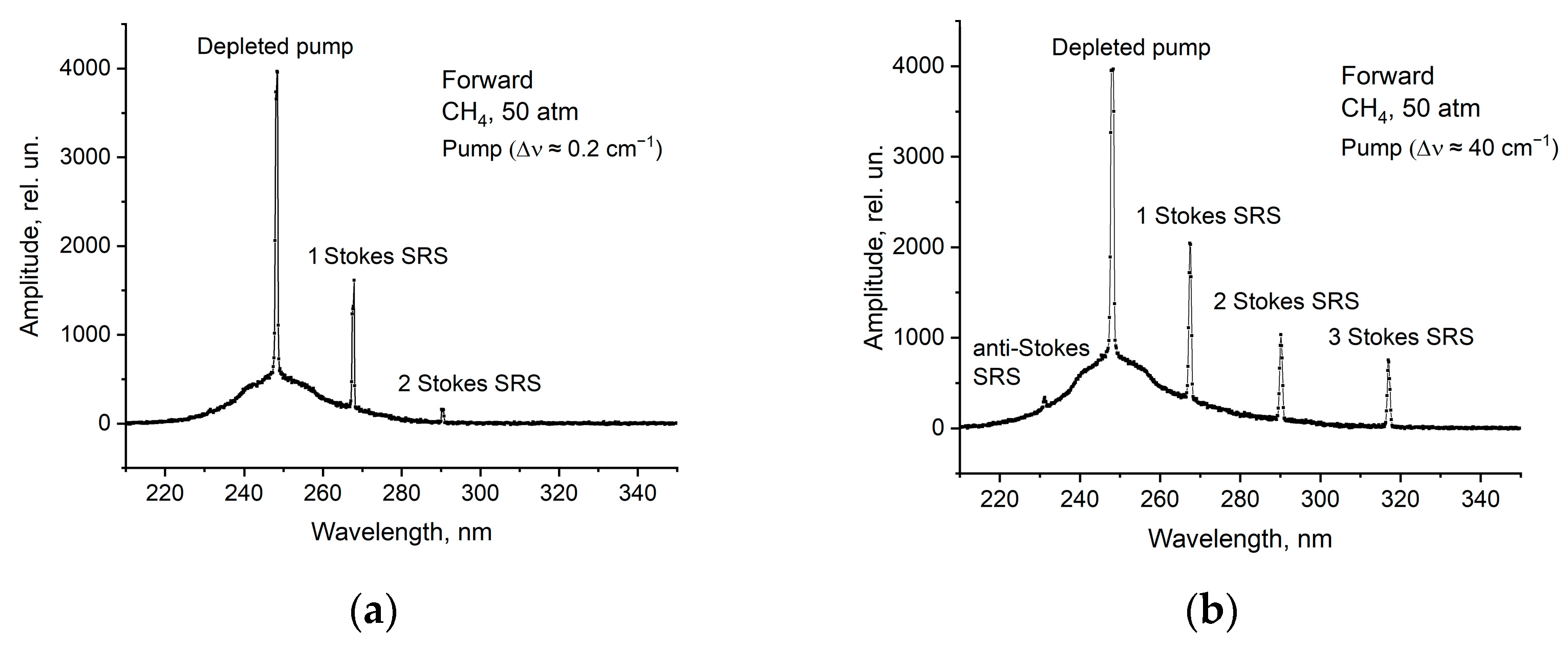
In a CH₄ gas cell at 50 atm pressure, both SBS and SRS optically phase conjugated backward reflection was observed for narrowband pumping with an energy reflectivity of 14%. There was no pulse compression of backward radiation, while, in the forward direction, SRS pulses shortened to 3–4 ns at reduced pumping. For broadband pumping (Δν ≈ 40 cm⁻¹), a strong asymmetry was observed: a backward SRS and SBS reflection was completely absent, while, in the forward direction, the spectra were enriched by high-order Stokes SRS components as well as by the first anti-Stokes component.

Further experiments are underway to implement the best backward nonlinear reflection scheme for pulse compression and sequential amplification in a multistage GARPUN KrF laser installation [8]. First, to increase the efficiency, we are going to use capillaries, which will increase the length of the nonlinear interaction over the Rayleigh length, while maintaining the high intensity of the focused laser beam [35]. Secondly, the preliminary wrapping of the pump pulse by the Pockels cell will be implemented in a similar way to the experiments [20].