Investigation of an Improved Angular Spectrum Method Based on Holography

Abstract

Digital holography (DH) is a novel, real-time, non-destructive, and quantitative phase-contrast imaging method that is particularly suitable for label-free live biological cell imaging and real-time dynamic monitoring. It is currently a research hotspot in the interdisciplinary field of optics and biomedical sciences, both domestically and internationally. This article proposes an improved angle spectrum algorithm based on holographic technology, which reconstructs a cellular hologram based on phase information. Optical images and chromosome cell images, reconstructed using holographic technology at different diffraction distances under the improved angle spectrum algorithm, were analyzed and compared. The optimal diffraction distance for reconstructing chromosome cell images was selected, and chromosome cell images reproduced using traditional angle spectrum algorithms, angle spectrum algorithms combined with GS, and improved angle spectrum algorithms were compared. Comparative experiments with the different models show that the proposed algorithm is superior to traditional angle spectrum algorithms in reconstructing cell images based on phase information. Furthermore, experiments have shown that images reconstructed using the improved algorithm can resolve high signal-to-noise ratio information. This algorithmic improvement provides new applications for cellular detection in clinical diagnostics and is more suitable for cell phase reconstruction in practical applications.

1. Introduction

In digital holography, the most commonly used methods for numerical reconstruction are Fresnel diffraction, convolution, and angular spectrum theory. Fresnel diffraction is an approximate algorithm based on Kirchhoff’s diffraction theory. It requires that the reconstruction distance satisfies the Fresnel approximation condition. Convolution and angular spectrum methods, on the other hand, represent the Rayleigh-Sommerfeld diffraction theory in the form of convolution and angular spectrum, respectively, to achieve numerical reconstruction. The Fresnel method is suitable for numerical reconstruction when the reconstruction distance is greater than the reference distance. Conversely, the convolution and angular spectrum methods are suitable for numerical reconstruction when the reconstruction distance is smaller than the reference distance [1]. The only difference between the transfer function of the impulse response and the transfer function of the convolution response is that they are represented in different domains—the transfer function of the convolution response is represented in the zero domain, while the transfer function of the impulse response is represented in the frequency domain. In the continuously evolving field of biomedical research, there are certain limitations to the application of traditional optical microscopy. Digital holographic microscopy has been widely used for micro-particle imaging and tracking [2], polymer growth monitoring [3,4], and biological cell observation [5,6,7,8,9], as it is capable of simultaneously recording and reproducing three-dimensional information about an object and measuring samples in a non-invasive and non-contact manner. A fluorescence microscope was proposed to improve the contrast of cell imaging [10,11]. However, prior to using such a microscope, biological cells need to be stained with rhodamine, acridine orange, or green fluorescent protein [12]. This pre-processing makes the operation more complex, and unavoidably impacts the physiological properties of biological cells. To perform non-invasive, dynamic, and quantitative analysis on biological cells and subcellular samples there is a pressing need in life science research for new imaging and analysis techniques [13,14,15,16]. Digital holography replaces the use of photographic plates with optical sensors such as CCD or CMOS to record holograms, which are then stored in a computer. The computer performs computational simulations using optical diffraction to reconstruct and analyze the recorded holograms of objects. Existing optical devices easily capture the intensity information of the light waves due to their high frequency, however, obtaining phase information can be challenging and this information is frequently lost during the acquisition process. The phase of the light wave carries a considerable amount of information about the object being imaged, potentially up to 80% of the information needed. Phase retrieval algorithms have been developed to recover lost phase information, enabling the reconstruction of the complete information about the imaged object.

The Spatial Light Modulator (SLM) plays a key role; the role of converting digital information into light wave modulation signals, and realizing the recording and display of holographic images through the modulation and reconstruction of light waves. It provides a precise light wave control capability for digital holography and expands the application fields of optical imaging and information processing; SLM digital holography can be used to realize high-resolution, high-contrast digital holographic microscopy, for the imaging of cells, tissues, and organs, and it can be used for cell manipulation, optical capture, and the manipulation of individual biomolecules. SLM digital holography can be used to realize photorealistic three-dimensional images [17], providing a more realistic and immersive experience by generating visual 3D images in light field, large-size three-dimensional video via electronic holography using multiple spatial light modulators [18]. In biomedicine, this technique can be used to visualize anatomical structures, pathological changes, and biological processes [19].

Digital holography has been successfully applied in various fields [20,21,22]. Measurements of object shape and deformation analysis, biomedical research, and 3D dynamic measurements are some of the advanced applications that make use of the phase information of light waves [23,24,25]. Although detailed descriptions of the process of the digital holographic reconstruction of biological cells are relatively scarce at present, researchers are constantly exploring and improving relevant algorithms and technologies to achieve more accurate and efficient biological cell reconstruction and analysis [26,27,28,29,30,31,32].

An improved angular spectrum method is used to encode the phase information in complex amplitudes, thus obtaining a suitable transfer function for phase reconstruction. Experimental results show with a high signal-to-noise ratio; the algorithm effectively reconstructs the phase information while preserving details about the image edges and overall structure. Furthermore, it can be applied in the detection of chromosome cells. By leveraging the advantages of angular spectroscopy, the algorithm enhances the quality of phase reconstruction, enabling the generation of chromosome cell images with distinct edges and facilitating precise cell detection.

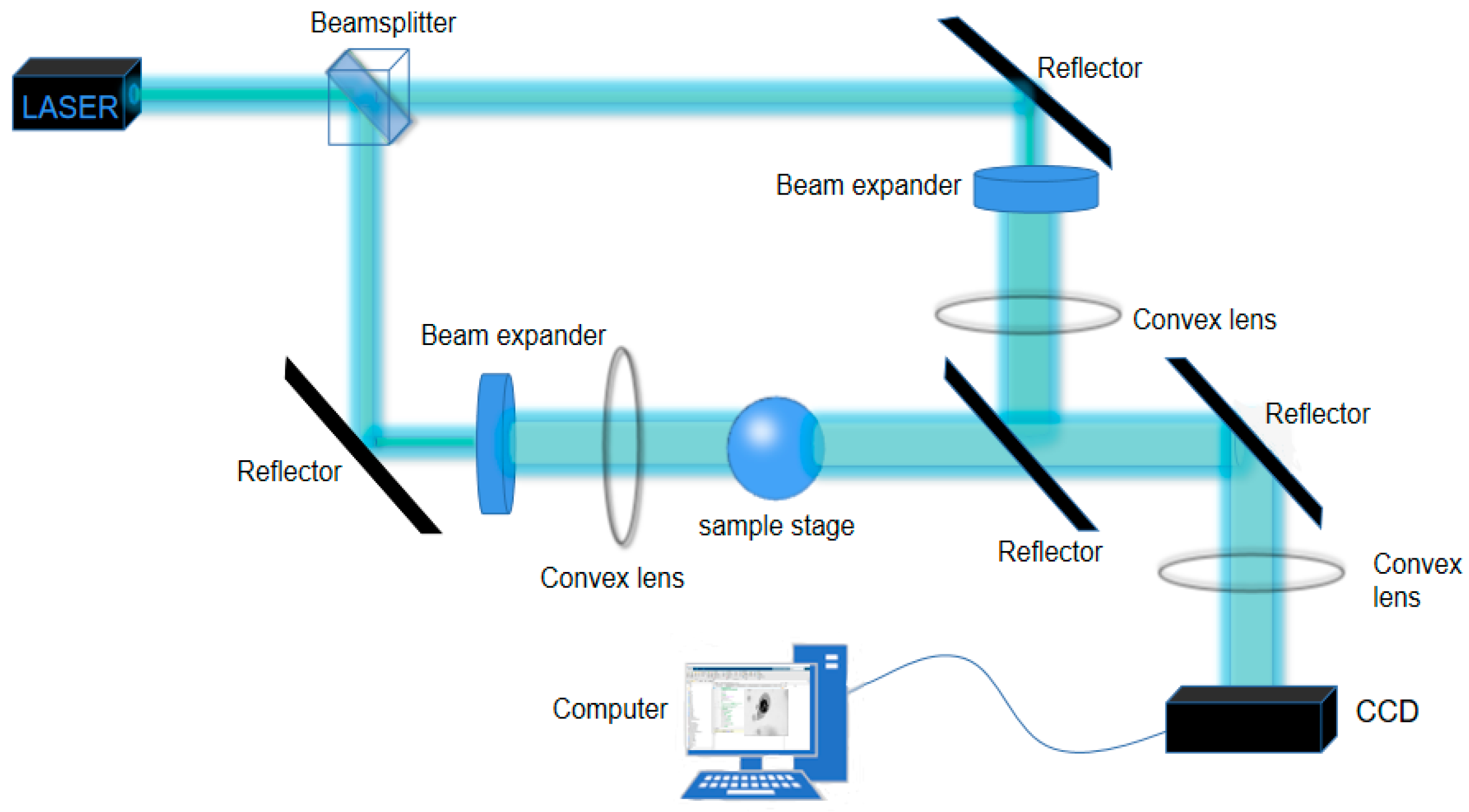
2. Holographic Principle

Optical holography employs the principles of light interference and diffraction to create a composite optical path, enabling the recording and reproduction of holograms of objects. Figure 1 provides the schematic of digital holographic imaging.

A laser light source is used to emit a parallel beam of light, which is split by a beam splitter into two beams: a reference beam and an object beam. One beam passes through a beam expander and lens and is directed toward an object as an object wave. The object light passes through the object, picks up the reflection or transmission information of the object, and then irradiates onto a photosensitive material, where the interference pattern formed is the superposition of the reference wave and the object wave, which contains the amplitude and phase information of the object. The other beam is used as the reference wave, which is directed to the object after passing through the beam expander and lens, such that beams of different frequencies are transmitted to the beam splitter. The object and reference waves converge to illuminate the CCD recording plane. Two beams of light from the same source propagate through different paths and simultaneously interfere with the CCD plane, converting the interference pattern into an electrical signal. The electrical signals are digitized, analyzed, and reconstructed via computer algorithms. Through the computer algorithm, the reference wave and the object wave in the interference pattern are separated, and by determining the complex amplitude distribution of the light wave, encoding its phase or amplitude, and depicting the encoding function, the hologram plane can be used to diffract the object wave to either the object plane or the image plane. It can be realized in order to reconstruct the image in the optical hologram. The hologram is eventually documented by visualizing the reconstructed image of the object through a display device (e.g., a monitor) [33].

Figure 2 illustrates the phase extraction and reconstruction process of digital holography, which consists of four essential steps: filtering, diffraction propagation, unwrapping, and aberration compensation. It is worth noting that filtering methods can be divided into two categories: spatial domain filtering and frequency domain filtering. The figure shows the traditional Fourier spectrum with the window filtering method, which includes the following steps: First, perform a Fourier transform on the hologram. Next, shift the first-order spectrum to the center and eliminate other interference terms. Finally, retrieve the complex amplitude distribution of the object field on the CCD surface through an inverse Fourier transform.

From a spectral perspective, when analyzing the propagation of light, we find that if we perform a Fourier analysis on the complex field distribution of a monochromatic disturbance on any plane, the Fourier components which are in different spatial frequencies can be regarded as plane waves propagating from this plane in different directions. The complex amplitude of the light field at any other point in space (or on any other plane in space) can be calculated by summing the contributions of the plane waves propagating to that point, taking into account the phase shift of these plane waves during propagation [34].

Suppose a light wave is incident on the medium parallel to the $(\mathrm{x},\mathrm{y})$ plane, and one of its components propagates along the positive $\mathrm{z}$ direction. We want to calculate the distribution of the light field on another parallel plane at a distance $\mathrm{z}$. First, we perform a Fourier transform on the light field in the plane, obtaining its spectral expression as:

$$A\left(f_X,f_Y;0\right)=\iint U\left(x,y,0\right)\exp \left[-i2\pi \left(f_{X}x+f_{Y}y\right)\right]dxdy$$

(1)

The Fourier transform operation can be viewed as a decomposition of a complex function into a set of exponential functions:

$$U(x,y;0)={\displaystyle \iint A(f_X,f_Y;0)\exp \left[i2\pi \left(f_X+f_Y\right)\right]}d{f}_{X}d{f}_Y$$

(2)

Thus in the $z=0$ plane, the complex exponential function $\exp \left[i2\pi (f_{X}x+f_{Y}y)\right]$ can be viewed as a plane wave whose propagation direction is determined by $\left(f_X,f_Y\right)$. Then, the distribution of the light field in this plane can be seen as being generated by the superposition of plane waves propagating along different directions, and the complex amplitude of the plane wave component is $A\left(f_X,f_Y;0\right)$, and we call $A\left(f_X,f_Y;0\right)$ the angular spectrum of $U\left(x,y,0\right)$.

Now we look at the angular spectrum of the distribution in $U\left(x,y,z\right)$, the plane of distance $\mathrm{z}$. $A\left(f_X,f_Y;z\right)$, the relationship between the angular spectra of the two planes, can be obtained by solving the Helmholtz differential equation, as

$$A(f_X,f_Y;0)=A(f_X,f_Y;0)\exp \left(i2\pi z\sqrt{\frac{1}{{\lambda }^2}-f_x{}^2-f_y{}^2}\right)$$

(3)

Projecting a result shows that the effect of propagating a distance z only changes the relative phase of the individual angular spectral components. This is because each plane wave component propagates at different angles and passes between two parallel planes at different distances, thus introducing a relative phase delay. Then, after we know the angular spectrum in the plane at distance $\mathrm{z}$, we perform an inverse Fourier transform on it and obtain the light field distribution in the plane.

$$U\left(x,y;z\right)={\displaystyle \iint A(f_X,f_Y;0)\exp \left(i2\pi z\sqrt{\frac{1}{{\lambda }^2}-f_x{}^2-f_y{}^2}\right)}\exp \left[i2\pi \left(f_{X}x+f_{Y}y\right)\right]d{f}_{X}d{f}_Y$$

(4)

The angular spectrum method provides an alternative approach and method for calculating the diffraction of light in space by describing the propagation of light between two parallel planes from another perspective, i.e., the Fourier spectrum of the light field distribution in each plane is connected by a transfer function. Based on the above theory, the initial phase is used as the initial value of the angular spectrum iterative algorithm and is used for iterative recovery by setting iterations and repeating the above steps to obtain the final phase, thereby improving the angular spectrum theory. The basic process is shown in Figure 3.

This is an alternative algorithmic procedure for phase recovery. The basic idea is to iteratively solve for the phase information of an input optical field in order to achieve phase retrieval. The specific steps include selecting an initial phase, combining it with amplitude information to obtain the distribution of the input optical field, performing angular spectrum diffraction to obtain the distribution of the output optical field, extracting the phase information of the output field, replacing the amplitude using an amplitude variable parameter to obtain a new output optical field, performing inverse angular spectrum diffraction to obtain a new input optical field, calculating the phase information for the current iteration and preserving the phase information of the input optical field, replacing the amplitude based on the input field amplitude, using gradient direction calculations to accelerate the convergence speed, and repeating the process iteratively until the specified criteria are met.

3. Method

An improved angular spectrum method based on holographic technology was used to extract the wavefront phase maps of chromosome cells, based on the comparative analysis of light word images with different diffraction distances, and reconstruct the wavefront phase maps of chromosome cells using the optimal diffraction distance for correlation analysis. Meanwhile, the comparison experiments, using the angular spectrum method, the combined angular spectrum method with the GS algorithm, and the improved angular spectrum method, show that this cell image reconstruction algorithm based on the improved angular spectrum method has better reconstruction quality than the first two algorithms, and that the algorithm is highly suitable for practical applications involving reconstructing the phase of cells.

Optical character images and chromosome cell images were used as experimental subjects, and the experiments were modeled and analyzed, using Matlab 2022b for the relevant modeling. The fundamental procedure of modeling is outlined below. Firstly, the data are inputted, and then the correlation-processed images with different diffraction distances are processed separately through the correlation formula of angular spectrum theory, as follows:

(1)

The modeling process begins with input data, where an RGB cell image with M × N pixels is preprocessed and processed. The original image is then resized to 256 × 256 pixels, subjected to grayscale processing, and the object data are then generated by sampling the 256 × 256 pixel image.

(2)

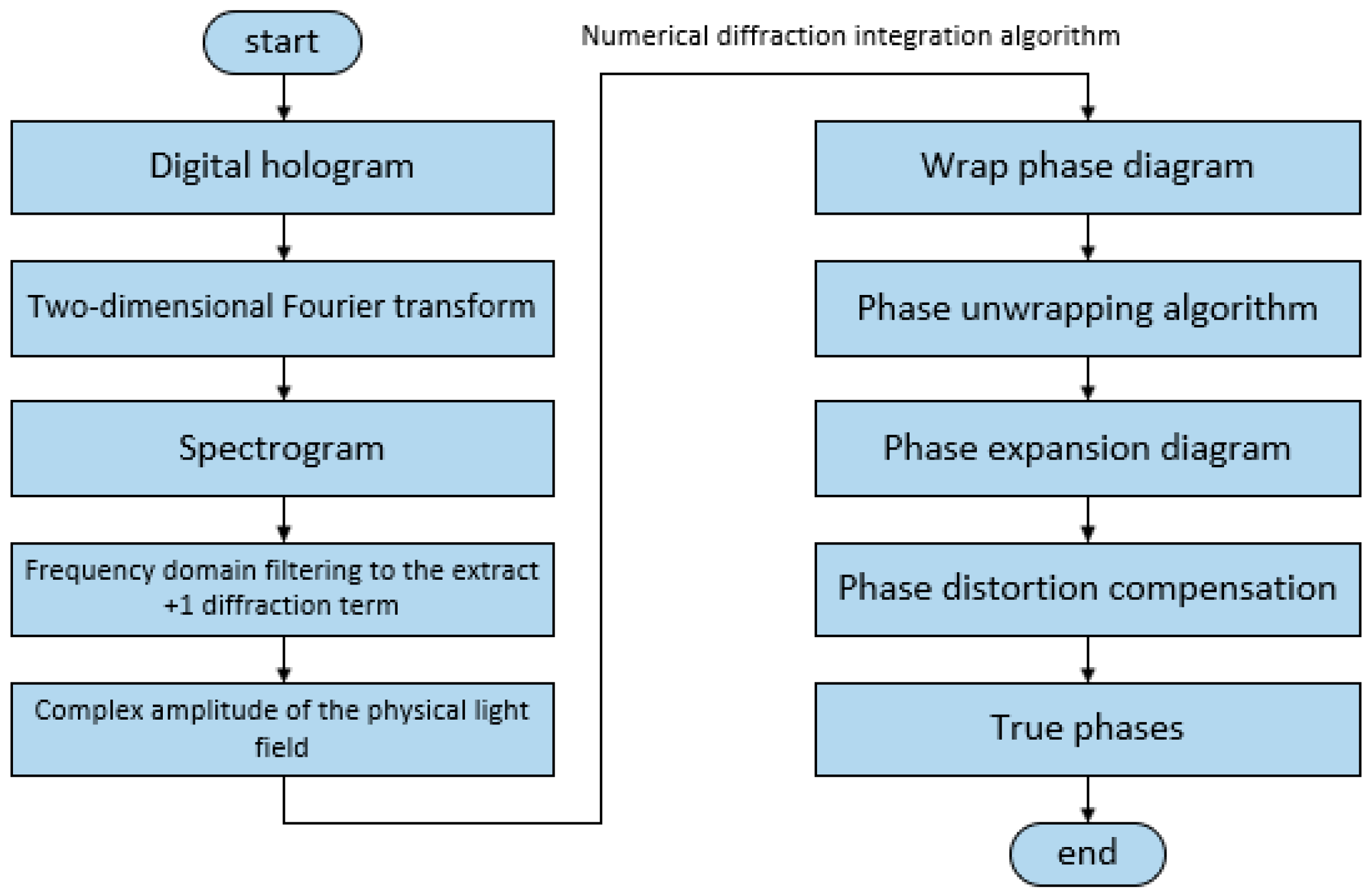
Suppose we have a two-dimensional image f(x,y), in which the two dimensions x and y represent the horizontal and vertical directions of the image; its corresponding complex function can then be defined as F(u,v). When we perform the Fourier transform of the function F(u,v), we can obtain its frequency domain information G(u,v), and finally, we can obtain the spatial domain information of the original image via the inverse Fourier transform of G(u,v), which is the basic formula behind the reasoning of angular spectral theory.

(3)

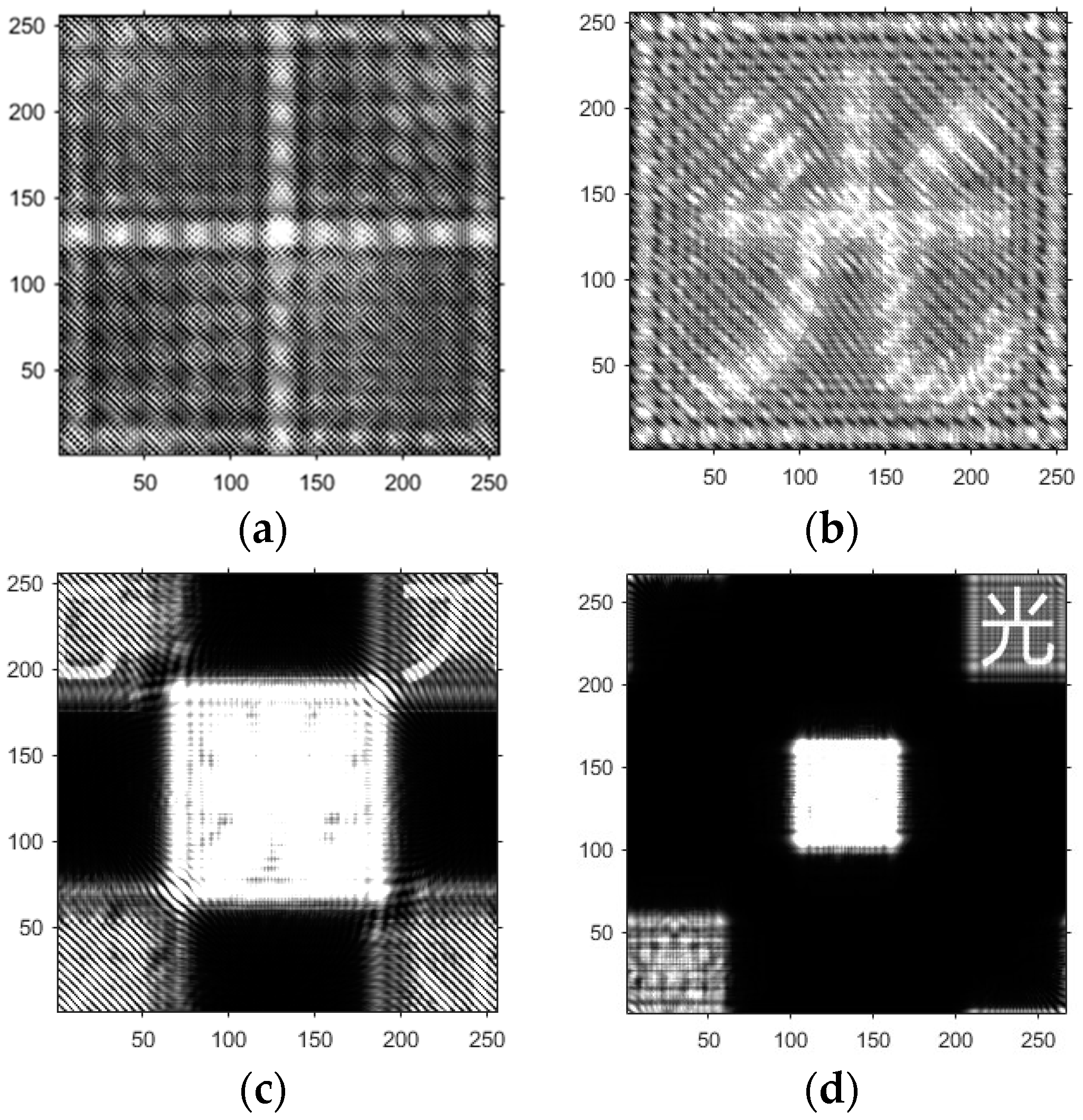
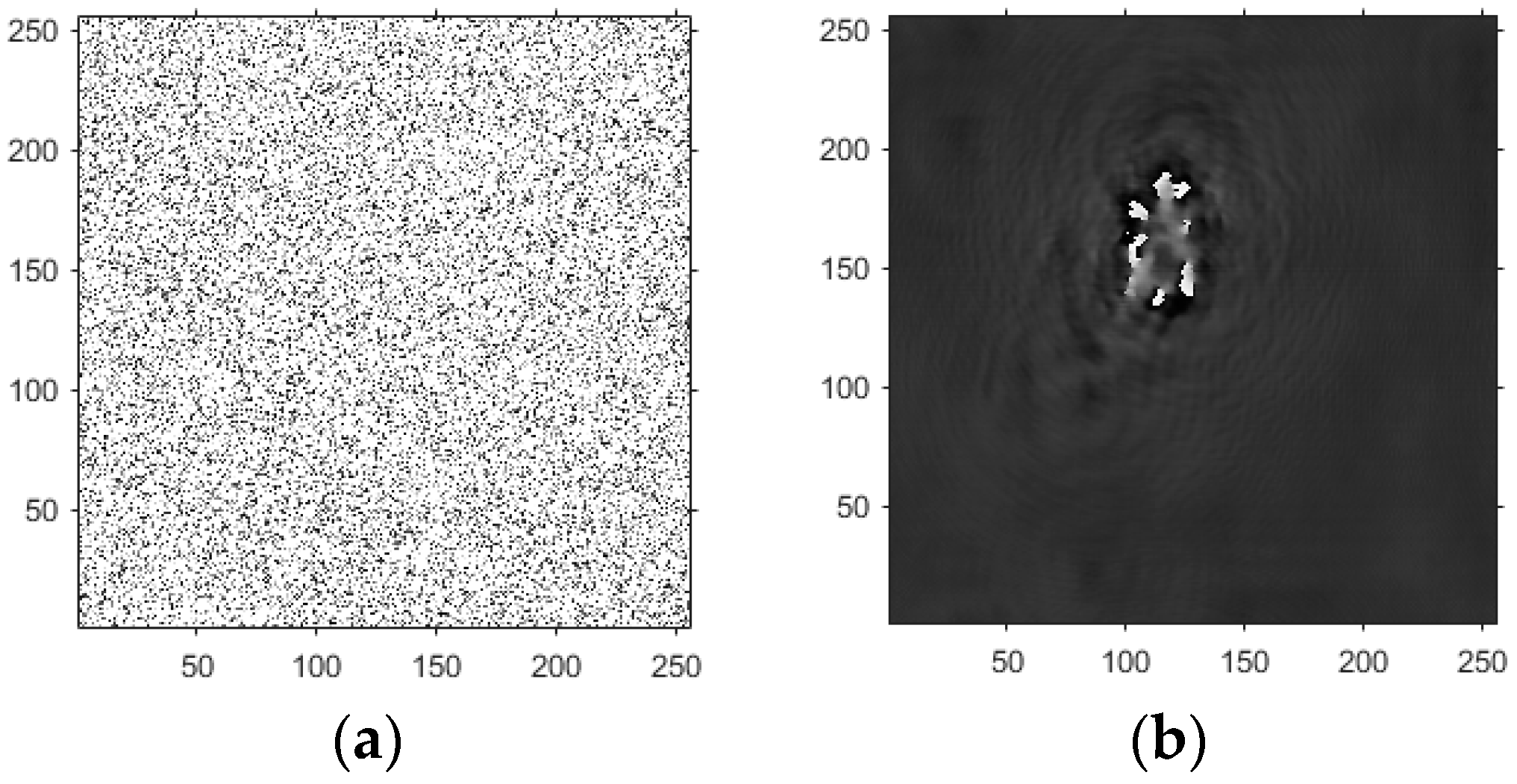
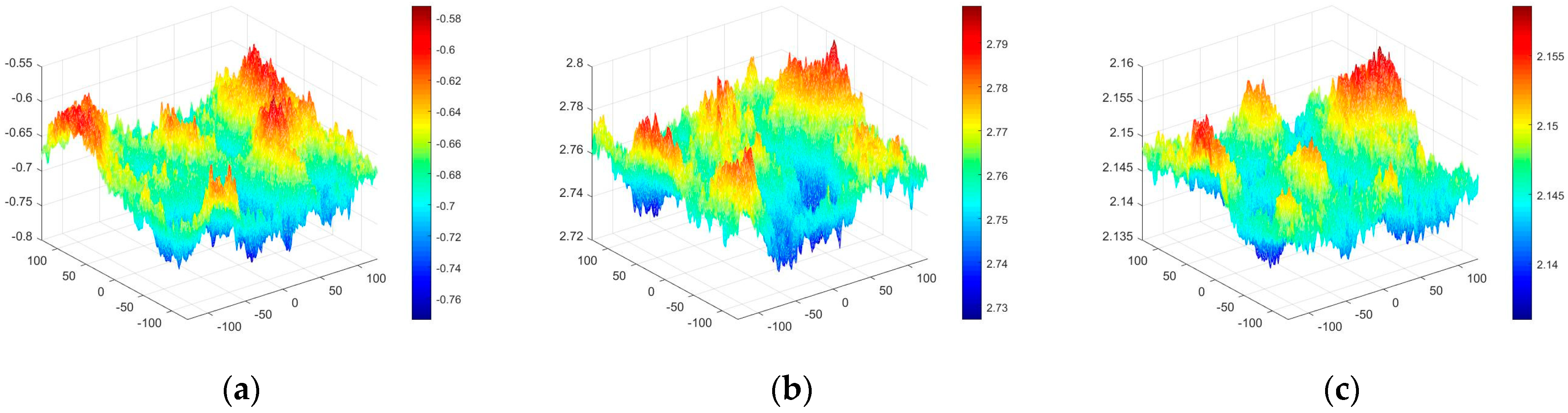
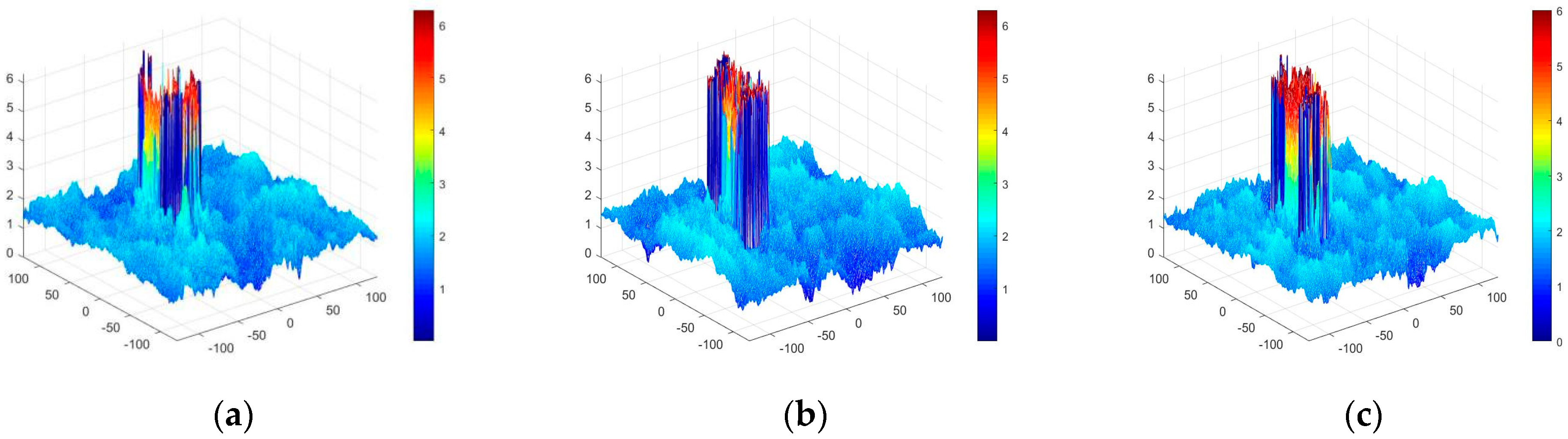
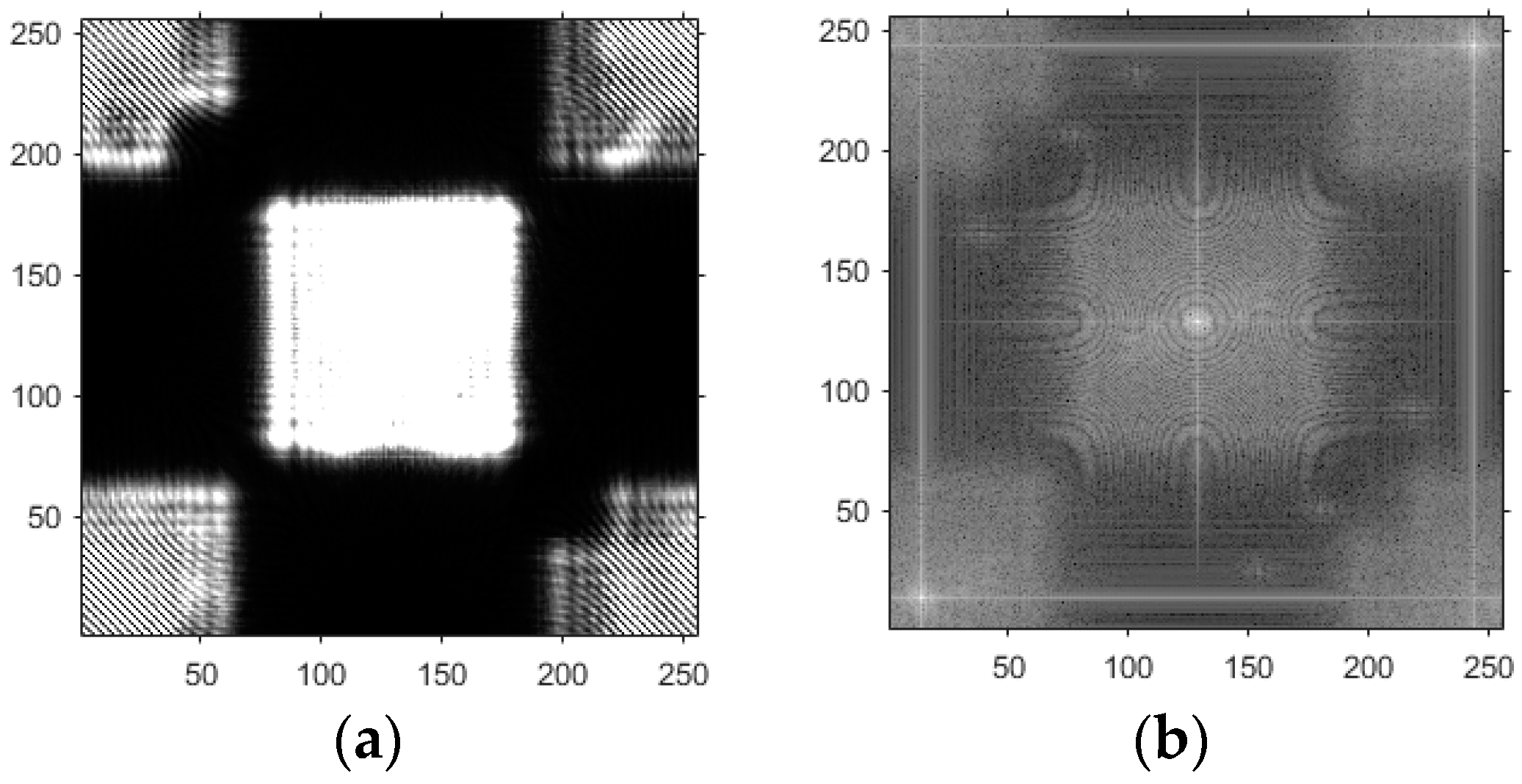
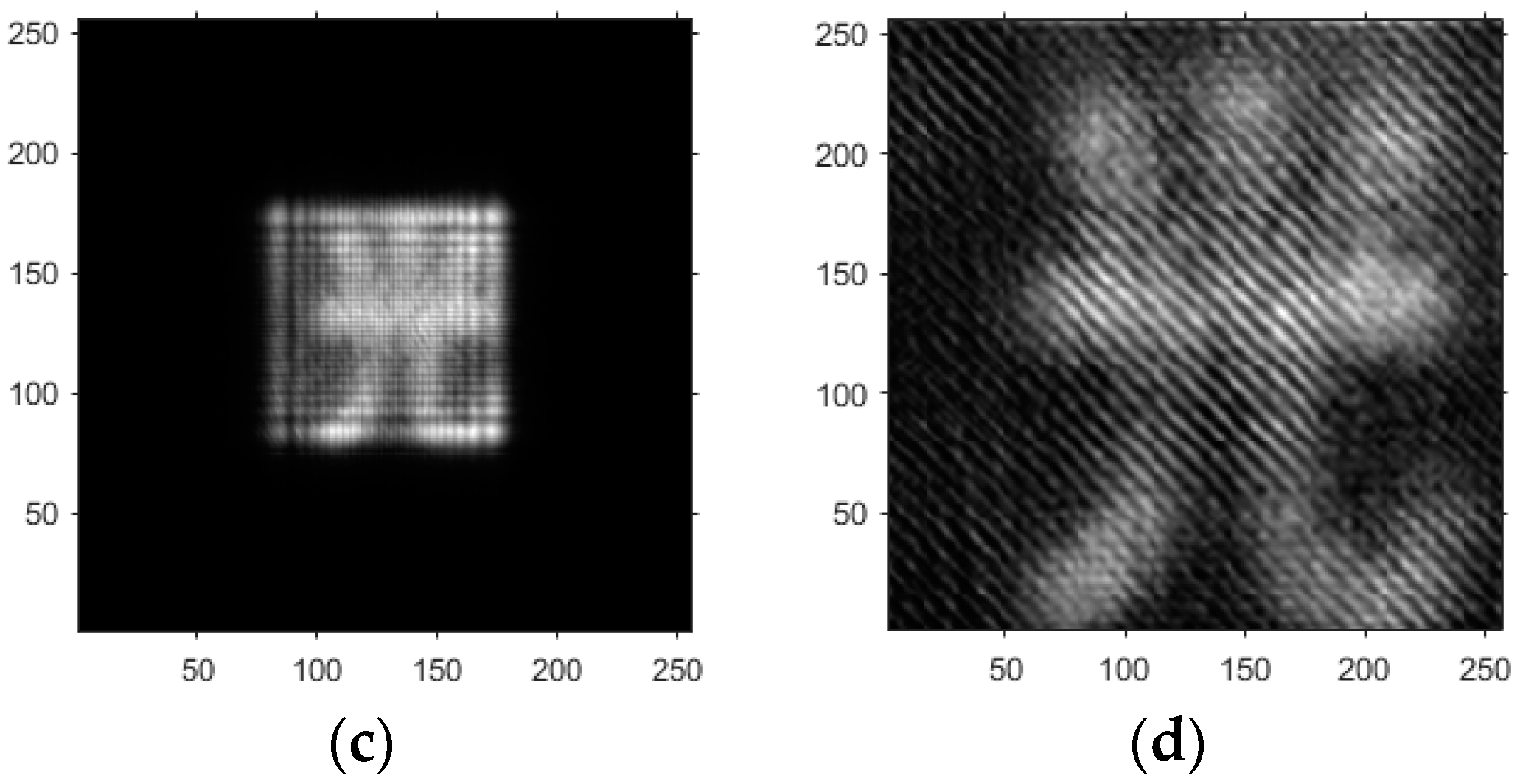
Based on the above principles, five models were established and the superiority of the improved angular spectrum algorithm for the phase reconstruction of cell images was experimentally verified. Model 1, in digital holography experiments, based on the reproduction method of the improved angular spectrum method, created diffraction images of the object reference 1: 1 light field with diffraction distances of 10, 20, 30, and 40 cm; Model 2, in digital holography experiments, based on the reproduction method of the improved angular spectrum method, set up the zero-level image, the original image, and the conjugate image with the diffraction distances of 10, 20, 30, and 40 cm, respectively; Model 3, in the digital holography experiment, set up holographic spectral images with diffraction distances of 10, 20, 30, and 40 cm, based on the improved angular spectrum reproduction method; Model 4, in the digital holography experiment, set up CCD screen interference patterns with diffraction distances of 10, 20, 30, and 40 cm, based on the improved angular spectrum reproduction method; Model 5, in the digital holography experiment, set up diffraction distances of 10, 20, 30, and 40 cm for the restored image according to the improved angular spectrum reproduction method. The five models were processed accordingly using light word images and chromosome cell images, respectively, and the results are shown in Models 1–9, respectively.

(4)

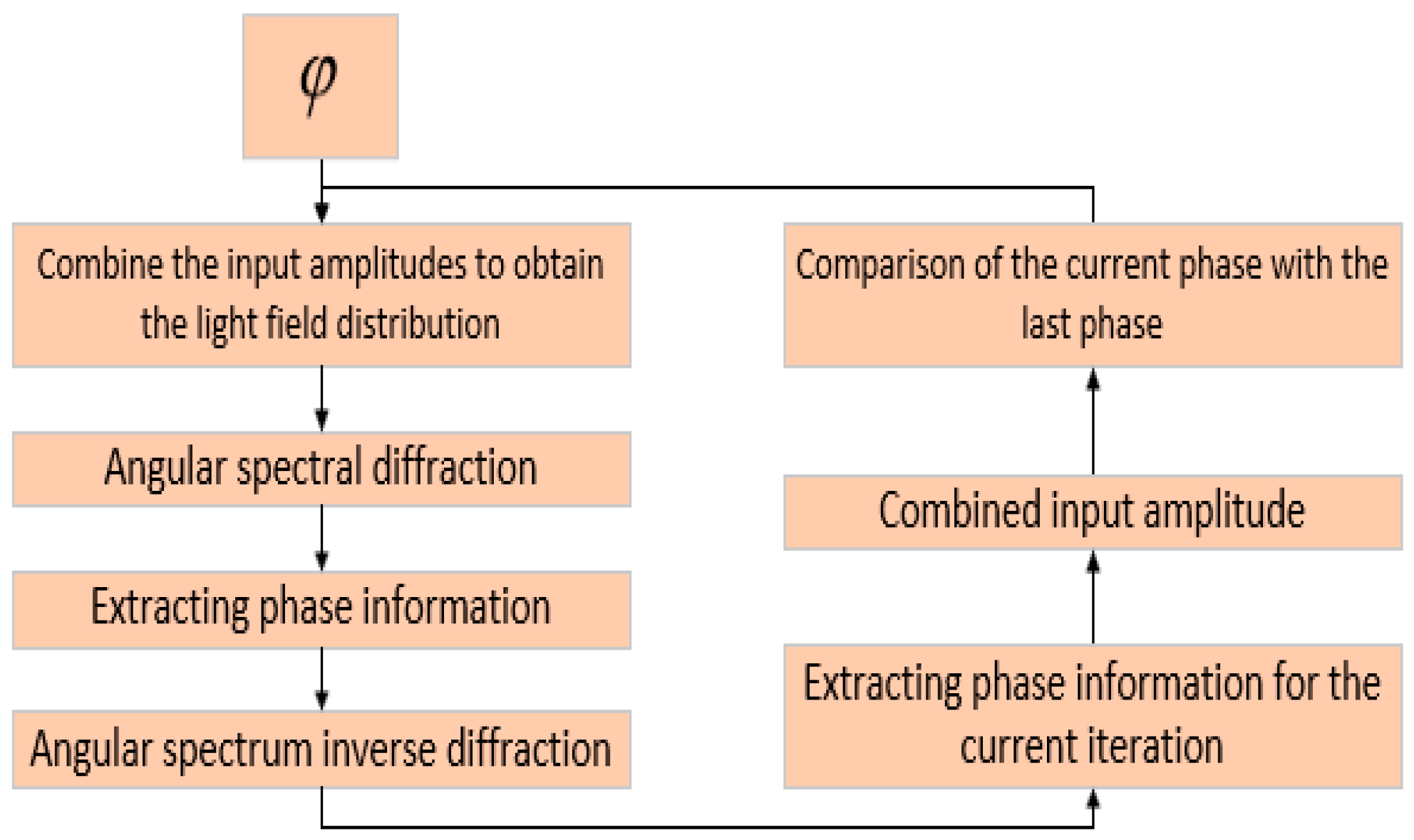
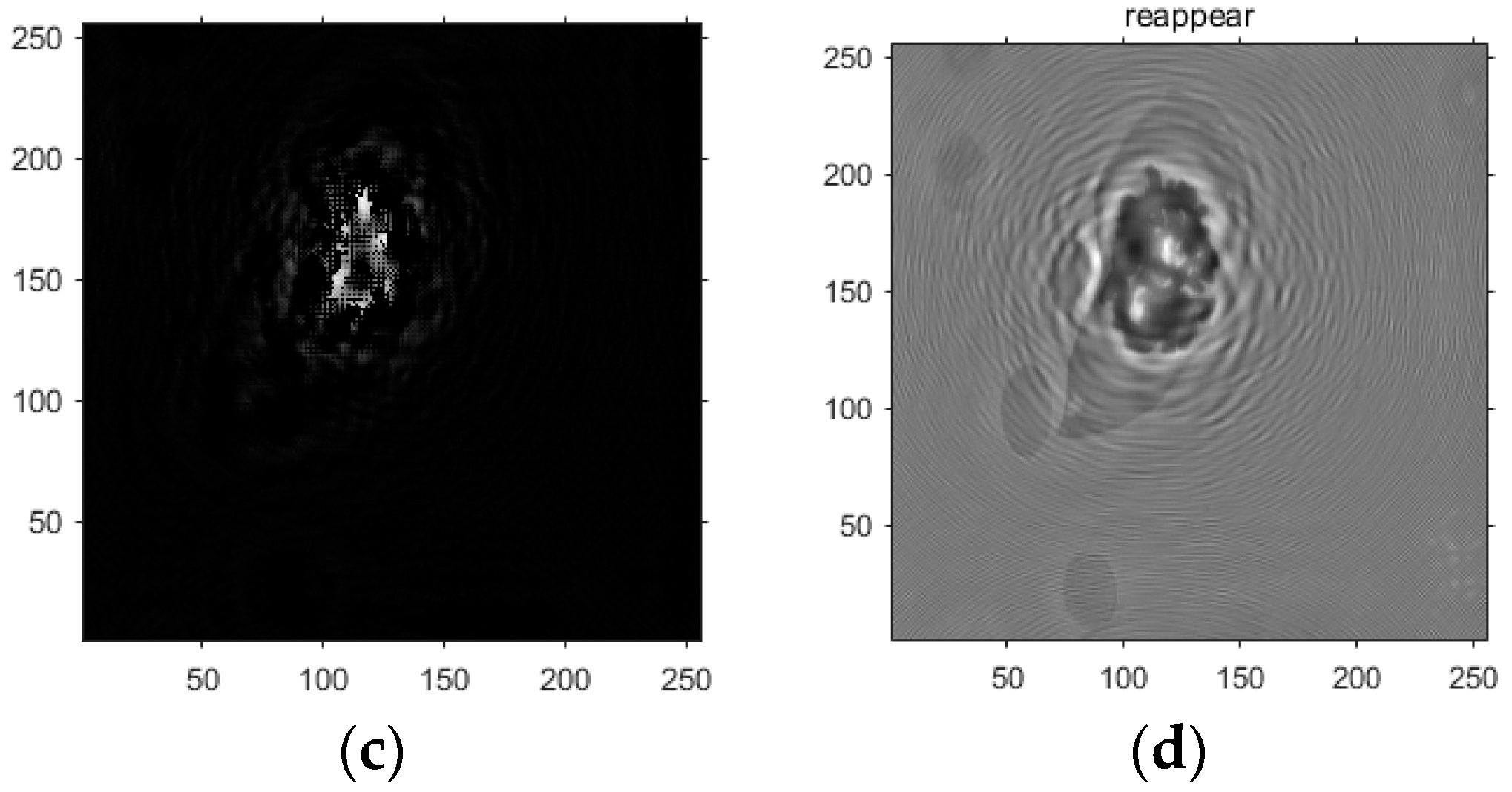
Based on this model, the GS algorithm is combined with the improved angular spectrum method to accomplish the following steps. First, the extracted phase image is displayed. Perform normalization of the extracted phase image. Perform an inverse Fourier transform and phase extraction to display the phase from the extracted phase image. Finally, diffraction compensation is performed using the diffraction compensation function to obtain the reconstructed phase image. The results are displayed in Model 10.

4. Light Word and Chromosome Cell Computational Holography Experiments

4.1. Optical Character Computational Holography Experiment

Figure 4a shows the homemade original optical character image. The original image type is a PNG color image of 298 × 267 pixels. After pre-processing the PNG image, a grayscale image of 256 × 256 matrix size is obtained. This is shown in Figure 4b.

Model 1: Using Figure 4b as the target image, and the improved reproduced angular spectrum method, the diffraction images of the light word image are created at diffraction distances of 10, 20, 30, and 40 cm, as shown in Figure 5a–d.

Through comparison, it can be concluded that when the diffraction distance is 10 cm, the diffraction image cannot be imaged or has no general imaging contour because of the close distance, with only some diffraction streaks carrying information, while, when the diffraction distance is 40 cm, the image contour starts to become blurred, and only the contour information of the time characters is relatively clear at 20 or 30 cm.

Model 2: with Figure 4b as the target image, and based on digital holography, the improved angular spectrum method reproduces zero-level images with diffraction distances of 10, 20, 30, and 40 cm, and the phase reconstruction images obtained using the original and conjugate images are shown in Figure 6a–d.

Through comparison, it can be concluded that when the diffraction distance is too small, the zero-level image, the original image, and the conjugate image are not separated, and as the diffraction distance increases, the image starts to become clear, but when the diffraction distance is too large, it again leads to three images that are too small to be imaged.

Model 3: the spectrograms for diffraction distances of 10, 20, 30, and 40 cm are shown in Figure 7a–d.

All spectral components are clearly shown in logarithmic form, including zero, positive, and negative levels. A comparison of the results shows that the intermediate spectral range increases with an increasing diffraction distance from 10–30 cm but becomes smaller at a distance of 40 cm.

Model 4: the CCD screen interference images obtained from diffraction distances of 10, 20, 30, and 40 cm are shown in Figure 8a–d, based on the digital holography technique, with Figure 4b as the target image and a modified angular spectrum method.

Model 5: with Figure 4b as the target image, the light word reduction images obtained from diffraction distances of 10, 20, 30, and 40 cm, based on digital holography with a modified angular spectrum method, are shown in Figure 9a–d.

4.2. Chromosome Cell Image Computational Holography Experiment

The flow of the holographic improved angular spectroscopy method based on light words reproduces the image, as shown above. Next, chromosomal cell pictures have the above correlation analysis applied to them, and the chromosomal cell-based model is built according to the model for processing light words, Models 6–10.

Figure 10a shows the observed chromosome cell images. The original image type was a JPG color image of 940 × 615 pixels. After pre-processing the JPG image, a grayscale image with a matrix size of 256 × 256 was obtained. This is shown in Figure 10b.

Model 6: using Figure 10b as the target image, the modified reproduced angular spectrum method is used to establish the diffraction images of chromosome cells with diffraction distances of 10, 20, 30, and 40 cm, as shown in Figure 11a–d.

Through comparative analysis, it can be seen that, similar to the results obtained from the light word images described above, the diffraction images of the chromosome cells obtained are progressively clearer with an increasing diffraction distance.

Model 7: with Figure 10b as the target image, and based on digital holography, the improved angular spectrum method reproduces zero-level images with diffraction distances of 10, 20, 30, and 40 cm, and the phase reconstruction images obtained using the original and conjugate images are shown in Figure 12a–d.

Model 8: the spectrogram images obtained from diffraction distances of 10, 20, 30, and 40 cm are shown in Figure 13a–d, based on the digital holography technique, with Figure 10b as the target image and using the improved angular spectrum method.

Model 9: the CCD screen interference images obtained from diffraction distances of 10, 20, 30, and 40 cm are shown in Figure 14a–d and based on the digital holography technique, with Figure 10b as the target image and a modified angular spectrum method.

Model 10: Using Figure 10b as the target image, the combined GS algorithm and the angular spectrum method was applied to process it, and the resulting image is shown in Figure 15a–d. Image a shows the random phase added into the processing algorithm. Image 15b shows the phase image extracted from the chromosome cell image in the processing algorithm. Image 15c shows the reconstructed phase image of the chromosome cell image using this algorithm. Image 15d shows the final recovered image using this algorithm.

Model 11: using Figure 10b as the target image, the holography-based angular spectrum method, the improved holography-based angular spectrum method, and the combined GS algorithm and the angular spectrum method were used to reproduce the chromosome cell image, as shown in Figure 16a–c.

The holography-based algorithm is reproduced via the angular spectrum technique, which firstly compares the differences in the reproduced images at different diffraction distances using analysis of the light character and then carries out the same analysis as above with the chromosome cells as the research object to set a diffraction distance with a better initial value for the subsequent iteration of the angular spectrum. The above results illustrate that the processing effect is better when the recovered phase and amplitude information is at a suitable distance. Finally, the current optimal diffraction distance is determined based on the previous preparations.

According to the above correlation analysis, when the diffraction distance is 30 cm, the chromosome cell images are processed and restored via the angular spectrum method, the angular spectrum method combined with GS, and the improved angular spectrum method, respectively, as shown in Figure 16. The results show that when the chromosome cells are restored using the angle spectrum method, the restored image still has a large amount of phase information, resulting in a blurred image; the angle spectrum method combined with the GS algorithm becomes relatively clearer, due to the angle spectrum method, but part of the interfering phase information still exists; and when the image is restored using the improved angle spectrum method, the image in (c) becomes clearer after the image is processed, compared to (a) and (b).

4.3. Experimental Discussion of Improved Angular Spectrum Method for Calculating Holography

In digital holography, common metrics for evaluating the quality of reconstructed images include the Peak Signal-to-Noise Ratio (PSNR), Root Mean Squared Error (RMSE), Structural Similarity Index (SSIM), and the Combined Evaluation of Peak Signal-to-Noise Ratio and Structural Similarity Index (CPSNRSSIM). These metrics allow for the quantitative assessment of reconstructed image quality and the comparison of different reconstruction parameters or algorithms. Different evaluation metrics may have varying relevance for different types of images or applications, and thus, in this article, RMSE was chosen as the evaluation metric.

In general, a smaller RMSE value indicates a smaller difference between the reconstructed image and the original image, which implies a better quality of the reconstructed image. However, since the RMSE value is related to the dynamic range and the degree of difference between the images, it cannot be interpreted solely based on its value. Therefore, in this article, the RMSE values of three algorithms, namely the contrast spectral method, the improved contrast spectral method, and the GS-based modified-contrast spectral method, are compared to each other for relative evaluation.

The metrics of the different algorithms are shown in

Table 1. RMSE values based on different models.

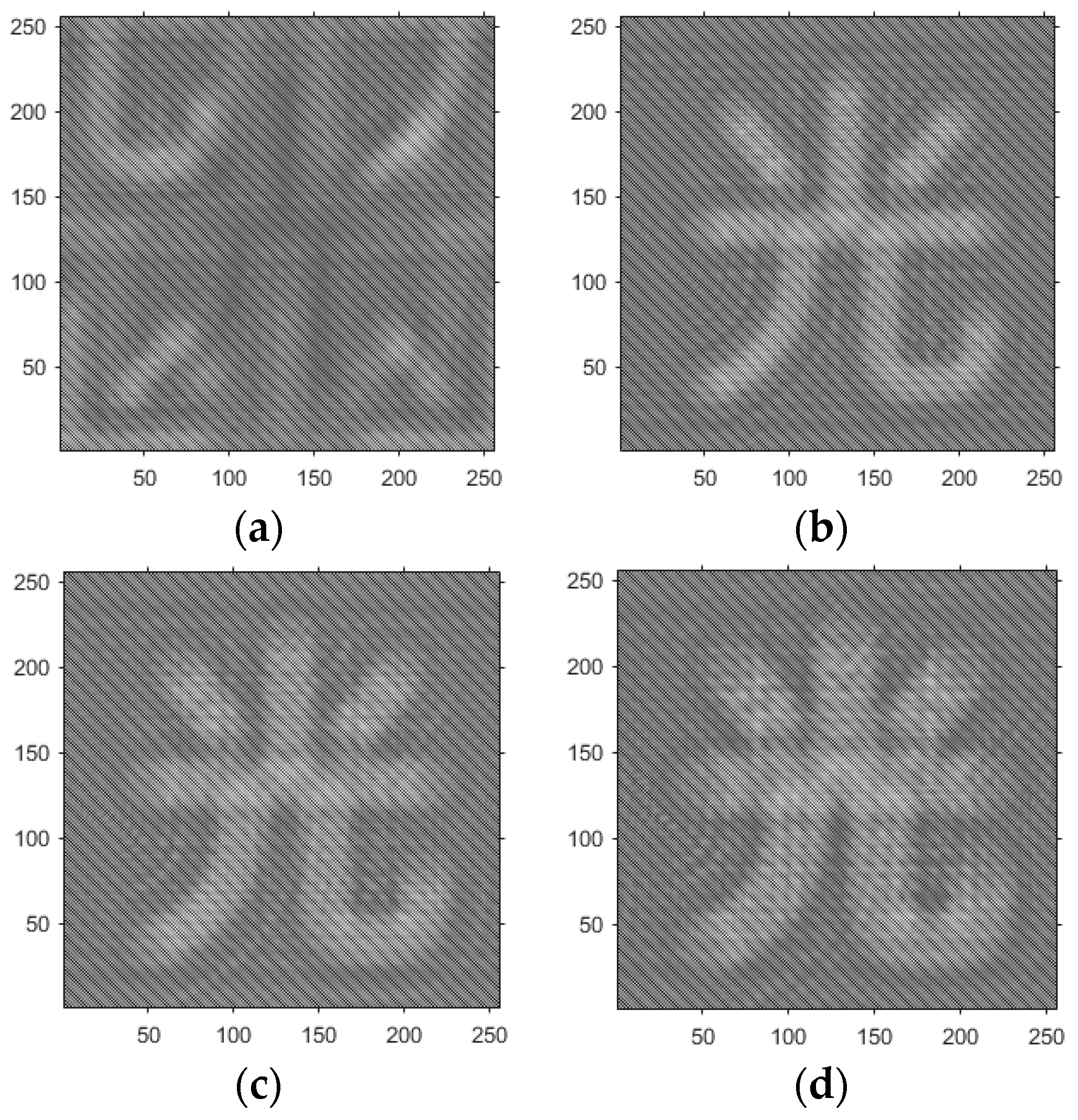
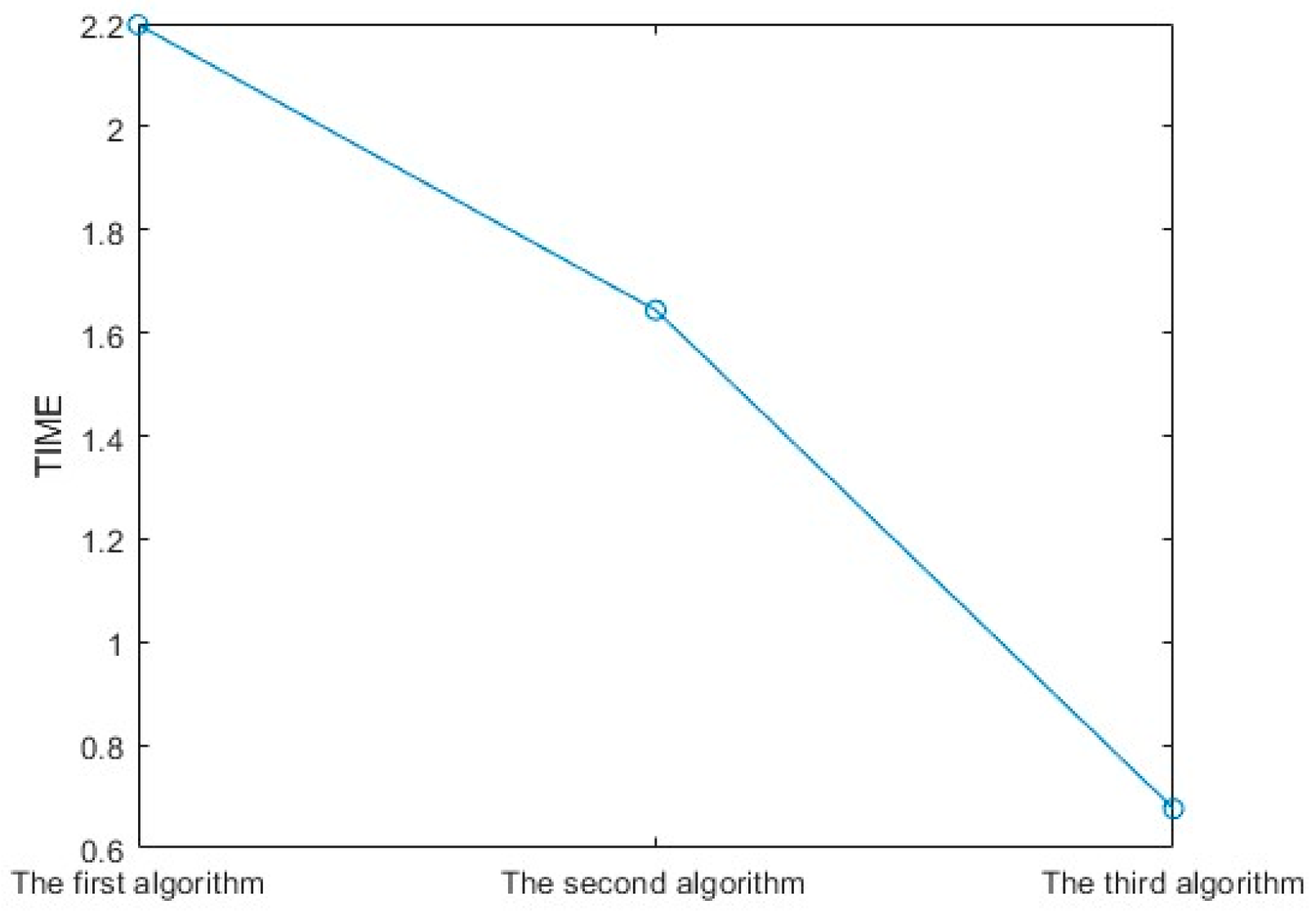
RMSE of the Angular Spectrum Method	RMSE of the Angular Spectrum Method Combined with the GS Algorithm	RMSE of the Improved Angular Spectrum Method
0.4610	0.2836	0.1361

, with the RMSE applied to the angular spectrum method, the angular spectrum method combined with the GS algorithm, and the improved angular spectrum method, respectively. From the table, it can be seen that the logarithmic value of the peak signal-to-noise ratio of the improved angular spectrum method is significantly lower than that of the angular spectrum method and the angular spectrum method combined with the GS algorithm, which once again demonstrates the superiority of the improved angular spectrum method.

The runtime values of the reconstructed chromosome cell images via the three algorithms, using a NVIDIA GeForce GT 730 GPU, are plotted in Figure 17. From Figure 17 it can be seen more intuitively that the runtime values of the angular spectrum method, the GS algorithm combined with the improved angular spectrum method, and the improved angular spectrum method are decreasing in order, which indicates that the improved algorithm is not only superior in terms of its RMSE value but also in that the runtime of processing the cellular image using this algorithm is relatively reduced.

The first method refers to the angular spectrum theory method, the second method refers to the GS algorithm combined with the angular spectrum theory method, and the third method refers to the improved angular spectrum theory method.

Comparison of the processed information is not possible because the imaging is not clear at a diffraction distance of 10 cm. After processing the optical characters via the holography-based angular spectrum method, the GS algorithm combined with the angular spectrum method, and the improved angular spectrum method, the phases are expressed in the form of energy, and it can be seen that the information on the optical characters is relatively simple and the phase peaks are not very obvious. However, the energy phase diagram of the improved angular spectrum method is still relatively more prominent, as shown in Figure 18. After processing the chromosome cell images using the holography-based angular spectrum method, the GS algorithm combined with the angular spectrum method, and the improved angular spectrum method, it can be seen that the phase peaks in (c) are slightly higher compared to the phase peaks in (b) and (a), and the phase imaging quality is slightly improved. As shown in Figure 19. The comparison of these two sets of energy phase maps shows that the improved angular spectrum method optimizes the phase reconstruction to some extent, which is very helpful in the reproduction of images.

In order to further investigate the imaging properties of the improved angular spectrum method in the experiment, the reconstruction results of digital holographic imaging using light word images are shown in Figure 20a.

After the study of the above improved angular spectrum method, we established a digital holography experimental light path, with optical experimental equipment calibrated to the wavelength of a 632.8 nm laser, a S1TC05C-C/M scientific research-grade camera, an attenuating sheet, reflector, 10× microscope objective, CCD camera, PC-20210710RFIS computer, etc., to carry out the relevant experiments. The corresponding experimental validation was carried out with the light character as the research object.

The wavelength of the experimental setup laser is generated by a He-Ne laser (He-Ne laser), and the wavelength is defined as lambda = 632.8 × 10⁻⁶ in meters. The light corresponding to this wavelength is red light, which is a part of visible light. Red laser light is often used to record holograms of objects in holography experiments because the longer wavelength of red light reduces the effects of diffraction and interference fringes during recording and reconstruction to obtain a better quality of the reconstructed image. The hologram on the holographic plate is obtained as shown in Figure 20a, which is then grayscaled and resized to 256 × 256 using the resize function, as shown in Figure 20b, respectively.

The hologram recorded on the holographic plate is recorded directly via holographic photo technology without digital algorithm processing. Hologram technology records all the information about an object by interfering with the light waves of the object to form a hologram of the object. This technique is an optical recording technique with high resolution and a large volume of data, but it is not a digital technique, so the hologram itself is not a digital image. Holograms require the use of a reconstruction device to recombine the light beams in order to obtain three-dimensional information about the object. In the reconstruction process, the hologram of Figure 20b can be processed by improving the angular spectrum method algorithm, which can improve the resolution and clarity of the reconstructed image; the resulting image is shown in Figure 21a–d.

Through the comparison of Figure 20b and Figure 21d, it is obvious that the resolution and clarity of the image are improved after processing using the improved angular spectrum method and because the feasibility of the improved angular spectrum method was also verified from the experiment.

This paper focuses on analyzing and comparing the improved angular spectral phase reconstruction methods based on digital holography at different diffraction distances, which are set to 10, 20, 30, and 40 cm, respectively, and analyzes the process of reproducing the images of light characters and chromosome cells via the improved angular spectrum method at different distances. The demonstration of the energy-phase maps and the peak signal-to-noise ratios highlights the superiority of the improved angular spectrum method, which is suitable for the practical application of the phase reconstruction of the cells.

During the course of this study, comparative analysis was used separately. This analysis was accomplished via longitudinal comparison. By setting different diffraction distances, the experiments within each model were compared to make the results clearer.

By comparing Model 1 and Model 5, these results show that the improved angular spectrum method, under digital holography conditions with different diffraction distances, does not fully contain the extracted phase information when the distance is too close to be imaged, while the phase information that can be extracted when the imaging distance is too large is limited, which suggests that recovering phase information is crucial for accurately restoring image information. Normalization techniques can be used to restrict the data to a specific range necessary for processing. Normalization can simplify subsequent data processing by making the data more consistent and easier to analyze; additionally, the normalization procedure converges faster. Since the grayscale image has a certain range of values, while the resulting values of the Fourier transform (the real part, imaginary part, amplitude, or phase) can be influenced by the normalization technique applied to the data, these are arbitrary and unrestricted, this means that when writing the two matrices into the image, the data should be transformed to meet the specific requirements of the image analysis task.

By adding the improved angular spectrum method to the model, the actual output light field amplitude is combined with the output light field amplitude obtained via angular spectrum diffraction to replace the traditional angular spectrum method, and the diffraction results of each iteration are superimposed on the output surface light field information, which is fed back to the input light field via the process of inverse diffraction, thus forming a feedback loop and accelerating the speed of iteration. The rationality and superiority of the improved angular spectrum method are verified in various areas by later comparing the different methods, and then the confirmation of the proposed method is accomplished again through experiments.

With digital holographic imaging, three-dimensional information on the internal [35] and external structures of cells can be obtained [36], which is very helpful for analyzing the morphology, movement, and change processes of cells. Digital holography can provide high-resolution imaging, which can effectively observe and analyze the microscopic features and details of cells that are useful for detecting and tracking cytoplasmic abnormalities and changes in living cells [37]. In addition, digital holography can be combined with other analytical methods, such as computer vision and machine learning, to further improve the accuracy and speed of detecting and analyzing cytoplasmic abnormalities [38]. This combination can utilize the rich information of digital holograms for more comprehensive cellular analysis [39] and automate and efficiently assess cellular states and abnormalities through the application of algorithms and models.

Both two-photon excitation microscopy technique and computational holography are more advanced techniques in modern optical imaging. The two-photon excitation microscopy technique is a technique that utilizes a nonlinear process for microscopic imaging. It uses a high energy density beam to scan the sample and excite the two-photon absorption inside the sample. By controlling the position and power of the laser beam, high-resolution, deep, three-dimensional imaging of the sample’s structural information can be obtained [40].

Theoretically, computational holography can be used in combination with two-photon excitation microscopy techniques. Specifically, multiple 2D images acquired via two-photon excitation microscopy can be converted into 3D data and then reconstructed using computational holography algorithms [41,42]. This allows for more accurate 3D structural information, which leads to a better understanding of the morphology and structure of the sample. However, since the two-photon excitation microscopy technique itself still has some limitations [43], such as depth limitation and imaging speed, it needs to be continuously improved and refined by researchers [44] in order to better apply computational holography.

Laser speckle imaging (LSI) is a technique for surface reconstruction and the imaging of scattering media with the following advantages and disadvantages. Advantages: 1. Anti-scattering: by capturing and analyzing the propagation path of the laser speckles, the LSI technique can inhibit and eliminate the effects of scattering on the sample surface and improve the imaging quality [45,46]. 2. Large-depth imaging: by adjusting the focusing depth of the laser speckle, LSI technology can realize the imaging of large-depth samples [47,48]. 3. Fast imaging speed: since LSI technology is based on the imaging mode of point scanning, it has a faster imaging speed than the imaging method of full field scanning [49]. 4. Suitable for opaque samples: the LSI technique can image non-transparent samples, such as semiconductor chips, biological tissues, etc. [50]. Disadvantages: 1. Limited by light source power: LSI technology has high requirements for light source power, and if the light source power is insufficient, the imaging quality and depth may be affected. 2. Limited resolution: the resolution of LSI technology is limited by the size and propagation path of the laser spot, which is relatively low compared to other high-resolution imaging techniques, such as electron microscopy [51].

Computational holographic angular spectrum algorithms are more suitable for imaging 3D samples which are in transmission or reflection modes, while laser speckle imaging (LSI) is a technique used to overcome surface scattering [52]. Although both computational holographic angular spectrum algorithms and LSI techniques are methods of optical imaging, their application scenarios and principles are different, so computational holographic angular spectrum algorithms are generally not directly applied to laser speckle imaging (LSI).

5. Conclusions

In traditional optical microscopy, only the amplitude information of cells, such as their brightness and color, can be obtained. However, the phase information of cells can provide more detailed structural and morphological information, including the position of the cell nucleus, the hierarchical structure within the cell, and the shape of the cell membrane. The phase information is crucial for understanding the biological function and pathological changes of cells.

Advanced phase imaging techniques, such as digital holography, can be used to acquire the phase information of cells and reconstruct their three-dimensional shapes. The improved angular spectrum method, based on digital holography, in this study effectively describes the phase information of the reconstructed image, making it more suitable for practical applications in cell phase reconstruction. In this study, the features of the improved angular spectrum method can be applied to the detection of abnormal chromosomal cells, aiding in the correct diagnosis of significant diseases through the analysis of the number and shape of abnormal cells in clinical settings. This technique can accurately detect live cells and diagnose cytoplasmic lesions, holding great promise for applications in the biomedical field. Future research will focus on recording various transients. This approach to modeling involves capturing images of moving cells, which helps to enhance the speed and accuracy of processing the image information and recovering the phase.

In cell reconstruction, phase information has the following advantages: it provides more comprehensive structural information, it can effectively identify cell changes, and it assists in disease diagnosis and treatment. By analyzing the phase information, abnormal cell changes such as cancer cells and pathological cells can be detected and diagnosed, providing strong support for early disease diagnosis and treatment. Phase information is of great significance in cell reconstruction as it provides more detailed and accurate cell morphology and structural information, offering new methods and approaches for cell biology research and clinical diagnosis.

For millimeter- to micrometer-level fine 3D distance measurements, the difficulties faced by existing technologies include the following: 1. Limitations in resolution; In order to achieve high-precision measurements, high-resolution equipment and images are required. However, high-resolution images often require longer shooting times or higher gray depths, all of which make the acquisition of images more costly. 2. The Data Alignment Problem; Existing technology acquires data from multiple viewpoints via various means to realize three-dimensional measurements, but these data are different, so they need to be aligned. However, the process of data alignment takes up a lot of computing resources and time, and it is difficult to ensure the accuracy of the alignment. 3. Poor operability; Existing technologies require complex equipment and specialized operating skills, which makes them difficult to popularize and apply. In addition, data post-processing and analysis are often required, requiring further specialized knowledge and skills. 4. Limitations of the sample being tests; Different samples have different characteristics and limitations. For example, some samples may not be suitable for laser scanning techniques or require special pre-processing before measurements can be made. 5. A high instrumentation cost; The instrumentation and technology required for millimeter- to micrometer-fine 3D distance measurements are high-end and relatively costly, not all laboratories or organizations are capable of performing such measurements. The difficulty of the prior art is the next problem to be solved.