Abstract
In the field of X-ray phase-contrast imaging, a time-saving approach and preservation of details are crucial factors for obtaining phase-contrast images. In this manuscript, a single grating imaging system is proposed to perform the X-ray phase-contrast imaging. Instead of the time-consuming phase-stepping method, this system uses a single-shot algorithm to retrieve the distribution of samples’ attenuation and phase gradient. Unlike the single-shot Fourier transform algorithm, which truncates the high-frequency component of the image and reduces the spatial resolution, our method can retrieve the attenuation and phase information images with the same spatial resolution as the images acquired directly by the X-ray detector used. Furthermore, by using a large-size X-ray detector (29 cm × 23 cm), the imaging system can be configured as either a microscopic instrument or a normal large field-of-view imaging system. Finally, a series of experiments were performed to validate the feasibility of the proposed method.
1. Introduction
The use of a grating interferometer (GI) has enabled the implementation of X-ray phase-contrast imaging in traditional X-ray tube laboratories [1,2,3,4,5]. This technology, based on GI, allows the simultaneous acquisition of differential phase-contrast and dark-field signals along with absorption images, thus, providing superior capabilities in fields such as biological imaging, materials science, and non-destructive testing [6,7,8,9]. Conventional X-ray GI comprises three gratings, the source, phase, and analyzer gratings, each of which has a different function. The source grating provides an arrayed coherent X-ray beam, the phase grating generates interferograms, and the analyzer grating reduces the requirement on the detector’s resolution. By using the phase-stepping algorithm, the absorption, phase gradient, and dark-field information can be retrieved from a few images captured with different grating positions. Theoretically, a minimum of three X-ray exposures are required to extract these signals. In practice, however, the number of exposures required often exceeds three, resulting in an increased X-ray dose absorbed by the sample and more rigorous mechanical stability requirements that hinder the widespread use of the technique. In addition, the inclusion of two absorption gratings (source and analyzer gratings) reduces the signal-to-noise ratio of the system and halves the utilization efficiency of the X-ray photons.
Since 2007, A. Momose et al. have proposed a method using only one phase grating to retrieve phase signals [10,11,12,13,14]. However, their reconstruction of phase gradient distribution still relies on the time-consuming fringe scanning method. In the visible light field, M. Takeda et al. introduced a Fourier transform algorithm in 1982 that could extract phase information from a single fringe-distributed image recorded by a high-resolution detector [15]. In the last decade, researchers have introduced a Fourier transform algorithm into X-ray imaging [16,17,18], but this approach filters out high spatial frequency information. In 2010, F. Krejci et al. presented a new approach using only one absorption grating in their imaging system. Although it requires only a single exposure image, it results in a loss of half the spatial resolution of the detector used [19]. With the development of deep learning technology, this approach has been applied to single-shot X-ray phase-contrast imaging [20,21]. In the field of visible light imaging, it is relatively straightforward to collect the necessary dataset for the algorithm; however, X-ray imaging poses challenges. Changing conditions, such as X-ray tube voltage, tube current, or imaging distance, can render the algorithm ineffective because the neural network parameters are trained under specific conditions.
In this work, we construct an X-ray phase-contrast imaging setup with a single grating and propose a fast algorithm to retrieve attenuation and phase-contrast signals from a single-shot image. Compared with the previous methods mentioned above, our algorithm not only maintains a time-saving process, but also preserves the full spatial resolution of the X-ray detector used in our phase-contrast images.
2. Methods
In this section, we first establish the data model of the X-ray detector with and without samples in the imaging system. The data model incorporates three grating background signals that need to be measured before reconstructing the sample attenuation and phase information. In Section 2.2, we measure the background signals using the four-step phase shift algorithm. Then, in Section 2.3, we present the method for extracting the sample attenuation and phase information from the single-shot intensity image of the sample.
2.1. Data Model
With respect to a commonly used Talbot-like X-ray imaging system, the fringe pattern downstream the grating can approximately be written as [6]
where T is the fringe period, and are the direct component (DC), intensity modulation, and initial phase shift of the grating, respectively. When a sample is inserted into the beam path, it causes attenuation and phase shift of the X-ray, which affects the fringe pattern. Therefore, the intensity expression can be modified as [22]
where and are related to the attenuation and phase gradient rendered by the sample and are
where are the attenuation and phase distribution, L is the distance from the sample to the detector, λ is the X-ray wavelength, and the weak scattering signals are neglected [23]. As shown in Figure 1, we adjust the magnification of the imaging system so that two adjacent pixels can measure the fringe’s intensity of one period.
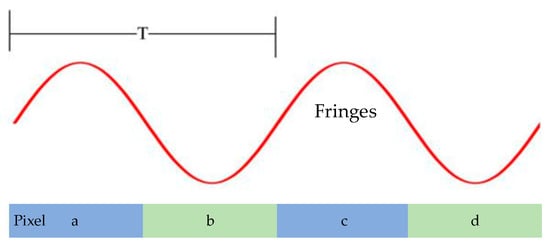
Figure 1.
The sizes of fringes of the grating and detector pixels. T is the period of fringes.
When the sample size is much larger than the detector pixel size and in the range of one pixel, the sample’s attenuation and phase distribution () are assumed as constants. With these assumptions, the pixel’s signal value can be obtained by integrating the fringe’s intensity. In Figure 1, the integral ranges of pixels a and b are and , respectively, and the results are
where the ‘0’ or ‘1’ in the subscript denotes the absence or presence of a sample in the beam path, and the subscript ‘a’ or ‘b’ represents the intensity value in pixel a or b, and , . What we deliberately plan is to retrieve the sample-contributed attenuation and phase gradient and (x = a, b), which requires that α, β, and be known first.
2.2. Background Signals
When there are no samples in the beam path, the intensity signals with the grating positioned at each different position can be expressed by introducing a series of phase shift as an additional item in Equation (5):
In case of N = 4 and at specific position corresponding to = 1, 2, 3, 4, = 0, π/2, π, 3π/2, , , and can be solved as:
For the same grating, the parameters of , , and are constants that can be used for any experiment with the same imaging system.
2.3. Attenuation and Phase Information Reconstruction
According to Equation (4), the unknown variables are , and . In the range of two pixels, if the attenuation and phase distribution of the sample are slow variables, in other words, and , the attenuation and phase signals can be solved from Equations (4) and (6) as:
Besides pixel a, pixel b has another adjacent pixel c, as shown in Figure 1; thus, from and , pixel b can obtain new attenuation and phase gradient values and with the same algorithm used for pixel a.
3. Experiments
The imaging setup shown in Figure 2 comprises a microfocus X-ray source, a grating, and an X-ray flat panel detector. Prior to measuring a sample, it is essential to acquire the background signal , the local visibility , and the initial phase shift information of the grating without any sample in the imaging system. In Section 3.2, we acquire four intensity images corresponding to four different positions of the grating. Then, we calculate the three constants , and from the four images using a four-step phase-shift algorithm (Equation (6)). In Section 3.3 and Section 3.4, the samples are positioned near the grating and exposed to an X-ray beam only once. The image of the sample is used to reconstruct the attenuation () and phase gradient distributions () using Equation (7).
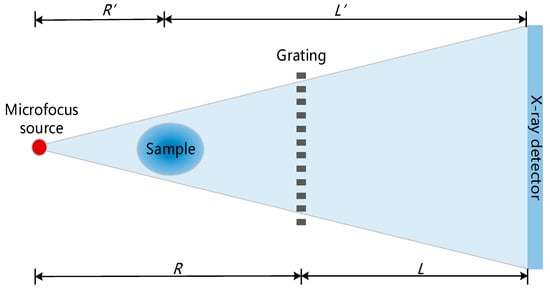
Figure 2.
Imaging configuration with a single absorption grating. The magnification of the grating is , the magnification of the sample is .
3.1. Grating
Both phase and absorption gratings can produce fringe patterns. For a π-shift phase grating, the distance between the grating and the detector must satisfy the following condition:
where R is the distance from the source to the phase grating, T is the period of the phase grating, and is the Talbot distance. The X-ray flat panel detector has a higher photosensitivity per pixel than CCD-based X-ray detectors, making it more sensitive to X-rays. However, due to the larger pixel size of the detector, a larger fringe period is required in such imaging systems, unless an absorption grating is placed in front of the detector to produce Moiré fringes.
Two methods can be employed to create a large fringe period. (i) Decreasing the distance between the X-ray source and phase grating and increasing the distance between the grating and imaging plane creates a large fringe period, as demonstrated in reference [15]. However, this method requires high mechanical stability in the imaging system due to the significant magnification; (ii) utilizing a grating with a large period results in a long imaging distance, as indicated by Equation (8). For example, if the grating period is 42 µm and the X-ray energy is 20 keV, the imaging distance L and the total length from the source to the detector must be at least 3.4 m and 6.4 m, respectively. Alternatively, the limitations mentioned above can be overcome by replacing the phase grating with an absorption grating. In this study, we use a tungsten particle-based absorption grating with a 42 µm period and a 150 µm depth that was reported in reference [24].
3.2. Background Signals
Limited by fabrication techniques, the grating is inevitably non-uniform, resulting in the parameters α, β, and becoming spatial variables (). This non-uniformity can create background signals that would interfere with the reconstruction of attenuation and phase information. Fortunately, Equation (6) can be used to eliminate this disturbance.
In our experiments, we used a microfocus X-ray source (HAMAMATSU PHOTONICS, L9421-02) with a nominal focal spot of 7 µm, and set the voltage to 40 kV and the tube current to 100 µA to obtain each image with an exposure time of 10 s. An X-ray flat panel detector (PerkinElmer, Waltham, MA, USA, Dexela 2923NDT) with a pixel size of 74.8 µm × 74.8 µm and a total active area of 29 cm × 23 cm was used to record all images. We set two imaging distances, R and L (Figure 2), to be 393 mm and 1007 mm, respectively, resulting in a magnification of M = (R + L)/R = 3.56. The Hybrid Hexapod (PI H-824) was used to adjust the grating position. We aligned one fringe period with the size of two detector pixels.
First, we moved the grating three times and acquired four images without the sample in the beam path, and then calculated the distributions of , , and , as shown in Figure 3e–g. The pixel profile shown in Figure 3i indicates that the fringe period is equal to two pixels. It is worth noting that various factors affect the actual fringe period in different parts of the same image on the detecting plane. These factors include different magnification M from the image center to the edge and grating distortion from the grating holder and non-uniformity of the grating. Therefore, the appearance of non-uniform Moiré fringes in Figure 3a–d is inevitable.

Figure 3.
Measurement of background signals. (a–d) are the intensity distributions with gratings at different positions, and the relative positions are 0, T/4, 2T/4, 3T/4, respectively. (e–g) are the distribution of , and . (h) is the enlarged image marked by the red rectangle in (d). (i): the profile marked by the red line in (h) shows that the period of the projection fringes is the size of two pixels. Each exposure time is 10 s.
3.3. Micrography
We tested two samples, chicken feet and an insect with a complex structure under the same conditions as in Figure 3. Both samples were placed near and in front of the grating. Using the data measured in Section 3.2 and Equation (7), attenuation and differential phase-contrast information were extracted from the radiography images of the single-shot samples, as shown in Figure 4. The figure includes the obtained multimodal images of the chicken feet: the attenuation and phase-contrast images. Figure 4b,c are both phase-contrast images retrieved using the Fourier transform algorithm [25] and our proposed method, respectively. Since the Fourier transform algorithm requires the use of a window function, some information loss is inevitable. Therefore, Figure 4b appears smooth and blurred, while Figure 4c shows more details. The more complex insect was also used to demonstrate the advantages of phase-contrast images over attenuation images, as shown in Figure 5. Figure 5a,b are the obtained full attenuation and phase-contrast images, respectively; Figure 5c,d are zoomed-in images corresponding to the regions marked by red rectangles in Figure 5a,b. Obviously, the phase-contrast image in Figure 5d shows more structure than the conventional attenuation image in Figure 5c. Especially for the parts with the red arrows, those tissues are clearly visible in Figure 5d but not in Figure 5c.

Figure 4.
The obtained attenuation and phase-contrast images of chicken feet. (a) is the attenuation image. (b,c) are the phase-contrast images retrieved using Fourier transform and our proposed methods, respectively. The imaging area of each image is 29 cm × 23 cm.
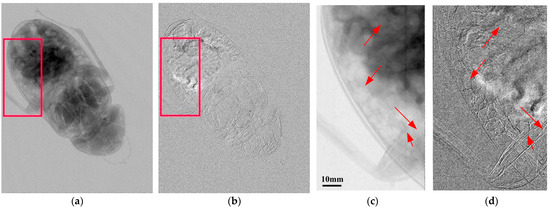
Figure 5.
X-ray attenuation and phase-contrast imaging of an insect. (a,b) are attenuation and phase-contrast images, respectively. The imaging areas of (a,b) are 29 cm × 23 cm. (c,d) are zoomed-in images corresponding to (a,b), respectively, marked with red rectangles. The red arrows show some structural features that are clear in the phase-contrast image (d) but not in the attenuation image (c).
3.4. Large Field of View
Since the grating we used has a diameter of 20 cm and the detector has an active area of 29 cm × 23 cm, our imaging system provides a field of view as large as 14.5 cm × 11.5 cm. To demonstrate this feature, a biological sample (Branchiostegus argentatus) with a size of 16 cm × 4.5 cm was tested behind the grating. The distance from the source to the detector is 1.4 m, and the sample was located in the middle of the source and the detector. The background information (, , and ) was remeasured without any sample. Then, the sample was exposed to the X-ray beam only once, and the obtained image of the sample and the background distribution were employed to reconstruct attenuation and phase-contrast images. Undoubtedly, the phase-contrast image (Figure 6c) shows more details than the attenuation image (Figure 6b). In particular, the zoomed-in images in Figure 6g–i contain more structural information than those in Figure 6d–f, as indicated by the red arrows. In fact, there is no major restriction on where the sample is located, either in front of or behind the grating.

Figure 6.
(a) is a photograph of the sample used (Branchiostegus argentatus). (b,c) are conventional attenuation and differential phase-contrast images. (d–f) are the enlarged image of (b) marked by red rectangles, and (g–i) correspond to the blue rectangles in (c). The areas indicated by the red arrows represent the features that are not visible in the attenuation images (d–f) and are more clear in the phase-contrast images (g–i).
4. Discussion and Conclusions
The phase retrieval algorithm used in this study is the phase-stepping method, which is a well-known technique in the field of visible light for reconstructing the phase of a wavefront by introducing a time-varying phase shift [26]. To avoid the need for multiple exposures of the sample, we used a space-varying phase shift method to compute the phase information. The main difference between these two methods is that the former samples the intensity in the time domain, while the latter samples it in the spatial domain.
Typically, the intensity at each point varies sinusoidally with the introduced phase shift, and three sampling points are required to reconstruct the sinusoidal signal in one period. In the time-varying method, the sample is exposed to the X-ray beam at least three times, so each pixel has three intensity signals that are used to retrieve the attenuation and phase gradient information. For the sample whose attenuation and phase distribution are slowly varying, in other words, the adjacent pixels of the detector have the same attenuation and phase information, the signal values of the two pixels come from the same sinusoidal function. We can then build two equations for the sinusoidal function from the values of the two pixels. The initial phase shift of the sinusoidal function can be retrieved before exposing the sample to X-rays, so the unknown variations (attenuation and phase information) can be reconstructed from the two equations.
In terms of our algorithm, the attenuation and phase-contrast values of a pixel (denoted by a) can be calculated from the intensity of the two adjacent pixels (denoted by a and b), and the b pixel’s values can be reconstructed from the next two adjacent pixels (b and c). Thus, from M pixels, there are M-1 values that can be reconstructed. Unlike the filtering effect of the window function in the Fourier transform method, the whole processing method demonstrates no information loss occurs during reconstruction. From this point of view, there is no loss of spatial resolution in our configuration. According to the algorithm, only the pixels in the last two pixels columns have the same retrieval values, and only the pixels in the last column cannot provide phase information. In practice, the pixels in the last column of detectors are generally not used to provide important information, so it is acceptable to omit the last column.
In this manuscript, we propose a new method for retrieving phase-contrast information in X-ray phase-contrast imaging that allows the use of a single shot, which means a low exposure dose, and preserves the high-frequency information by keeping the image resolution the same as that directly acquired by the detector used. This method is verified by our constructed imaging system, where a microfocus source is used to perform micrography. Furthermore, this method can also be extended to the imaging system using a synchrotron radiation source. Because of the time-saving advantages and lack of spatial resolution loss, our method can be applied to the inspection of biological soft tissues and the non-destructive testing of organic materials and their devices.
Author Contributions
Conceptualization, X.L. and Y.L.; methodology, X.L.; software, Y.L.; validation, J.H.; formal analysis, X.L.; investigation, J.H.; writing—original draft preparation, L.L.; writing—review and editing, Y.L.; visualization, L.L.; supervision, X.L. and J.L.; project administration, Y.L.; funding acquisition, Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Special Foundation of Shenzhen Science and Technology Bureau (20200812122925001), Natural Science Foundation of Guangdong Province (2021A1515010051), and the National Natural Science Foundation of China (grant numbers 62075141 and 61571305).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data underlying the results presented in this study are not currently publicly available but may be obtained from the authors upon request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pil-Ali, A.; Adnani, S.; Karim, K.S. Self-aligned multi-layer X-ray absorption grating using large-area fabrication methods for X-ray phase-contrast imaging. Sci. Rep. 2023, 13, 2508. [Google Scholar] [CrossRef] [PubMed]
- Andrejewski, J.; De Marco, F.; Willer, K.; Noichl, W.; Gustschin, A.; Koehler, T.; Meyer, P.; Kriner, F.; Fischer, F.; Braun, C.; et al. Whole-body X-ray dark-field radiography of a human cadaver. Eur. Radiol. Exp. 2021, 5, 6. [Google Scholar] [CrossRef]
- Momose, A.; Yashiro, W.; Kuwabara, H.; Kawabata, K. Grating-based X-ray phase imaging using multiline X-ray source. Jpn. J. Appl. Phys. 2009, 48, 076512. [Google Scholar] [CrossRef]
- Arboleda, C.; Wang, Z.; Stampanoni, M. Tilted-grating approach for scanning-mode X-ray phase contrast imaging. Opt. Express 2014, 22, 15447–15458. [Google Scholar] [CrossRef]
- Liu, H.; Liu, M.; Jiang, X.; Luo, J.; Song, Y.; Chu, X.; Zan, G. Multimodal Image Fusion for X-ray Grating Interferometry. Sensors 2023, 23, 3115. [Google Scholar] [CrossRef]
- Pfeiffer, F.; Bech, M.; Bunk, O.; Kraft, P.; Eikenberry, E.F.; Bronnimann, C.; Grunzweig, C.; David, C. Hard-X-ray dark-field imaging using a grating interferometer. Nature Mater. 2008, 7, 134–137. [Google Scholar] [CrossRef] [PubMed]
- Pinkert-Leetsch, D.; Frohn, J.; Ströbel, P.; Alves, F.; Salditt, T.; Missbach-Guentner, J. Three-dimensional analysis of human pancreatic cancer specimens by phase-contrast based X-ray tomography–the next dimension of diagnosis. Cancer Imaging 2023, 23, 43. [Google Scholar] [CrossRef]
- Momose, A.; Yashiro, W.; Harasse, S.; Kuwabara, H. Four-dimensional X-ray phase tomography with talbot interferometry and white synchrotron radiation: Dynamic observation of a living worm. Opt. Express 2011, 19, 8423–8432. [Google Scholar] [CrossRef] [PubMed]
- Miki, H.; Yoneyama, A.; Hirano, K. Visualizing morphological structures of rice grains in precooked products using synchrotron radiation X-ray phase-contrast computed tomography. Food Funct. 2023, 14, 87–93. [Google Scholar] [CrossRef]
- Takeda, Y.; Yashiro, W.; Suzuki, Y.; Aoki, S.; Hattori, T.; Momose, A. X-ray phase imaging with single phase grating. Jpn. J. Appl. Phys. 2007, 46, L89–L91. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, Z.; Zhang, L.; Kang, K.; Zhu, P. Fast X-ray phase-contrast imaging using high resolution detector. IEEE Trans. Nucl. Sci. 2009, 56, 1383–1388. [Google Scholar] [CrossRef]
- Morimoto, N.; Fujino, S.; Ohshima, K.; Harada, J.; Hosoi, T.; Watanabe, H.; Shimura, T. Two dimensional X-ray phase imaging using single grating interferometer with embedded X-ray targets. Opt. Express 2015, 23, 16582–16588. [Google Scholar] [CrossRef] [PubMed]
- Morimoto, N.; Fujino, S.; Ito, Y.; Yamazaki, A.; Sano, I.; Hosoi, T.; Watanabe, H.; Shimura, T. Design and demonstration of phase gratings for 2d single grating interferometer. Opt. Express 2015, 23, 29399–29412. [Google Scholar] [CrossRef] [PubMed]
- Morimoto, N.; Fujino, S.; Ohshima, K.; Harad, J.; Hosoi, T.; Watanabe, H.; Shimura, T. X-ray phase contrast imaging by compact Talbot-Lau interferometer with a single transmission grating. Opt. Lett. 2014, 39, 4297–4300. [Google Scholar] [CrossRef] [PubMed]
- Takeda, M.; Ina, H.; Kobayashi, S. Fourier-transform method of fringe pattern analysis for computer-based topography and interferometry. J. Opt. Soc. Am. 1982, 72, 156–160. [Google Scholar] [CrossRef]
- Itoh, H.; Nagai, K.; Sato, G.; Yamaguchi, K.; Nakamura, T.; Kondoh, T.; Ouchi, C.; Teshima, T.; Setomoto, Y.; Den, T. Two-dimensional grating-based X-ray phase-contrast imaging using fourier transform phase retrieval. Opt. Express 2011, 19, 3339–3346. [Google Scholar] [CrossRef]
- Wen, H.H.; Bennett, E.E.; Kopace, R.; Stein, A.F.; Pai, V. Single-shot X-ray differential phase-contrast and diffraction imaging using two-dimensional transmission gratings. Opt. Lett. 2010, 35, 1932–1934. [Google Scholar] [CrossRef]
- Lim, H.; Lee, J.; Lee, S.; Cho, H.; Lee, H.; Jeon, D. Low-density foreign body detection in food products using single-shot grid-based dark-field X-ray imaging. J. Food Eng. 2022, 335, 111189. [Google Scholar] [CrossRef]
- Krejci, F.; Jakubek, J.; Kroupa, M. Hard X-ray phase contrast imaging using single absorption grating and hybrid semiconductor pixel detector. Rev. Sci. Instrum. 2010, 81, 113702. [Google Scholar] [CrossRef]
- Xu, Y.; Tao, S.; Bian, Y.; Bai, L.; Tian, Z.; Hao, X.; Kuang, C.; Liu, X. Single-shot grating-based X-ray phase contrast imaging via generative adversarial network. Opt. Laser. Eng. 2022, 152, 106960. [Google Scholar] [CrossRef]
- Shi, S.Q.Z.; Shapira, N.; Noël, P.B.; Meyer, S. Convolutional neural network-based single-shot speckle tracking for X-ray phase-contrast imaging. arXiv 2023, arXiv:2305.01871. [Google Scholar] [CrossRef]
- Liu, X.; Guo, J.; Lei, Y.; Du, Y.; Niu, H. Two-step phase retrieval method with unknown phase shift on non-absorption grating X-ray differential phase contrast imaging system. Nucl. Instrum. Methods Phys. Res. 2012, 691, 86–89. [Google Scholar] [CrossRef]
- Zhu, P.; Zhang, K.; Wang, Z.; Liu, X.; Liu, Y.; Wu, Z.; McDonald, S.A.; Marone, F.; Stampanoni, M. Low-dose, simple, and fast grating-based X-ray phase-contrast imaging. Proc. Natl. Acad. Sci. USA 2010, 107, 13576–13581. [Google Scholar] [CrossRef] [PubMed]
- Lei, Y.; Xu, G.; Wali, F.; Li, Q.; Liu, X.; Huang, J.; Li, J. An 8-inch absorption grating used in cascaded Talbot-Lau interferometers for X-ray phase-contrast imaging. Appl. Phys. Express 2019, 12, 126504. [Google Scholar] [CrossRef]
- Huang, J.; Wali, F.; Lei, Y.; Liu, X.; Li, J. Fourier transform phase retrieval for X-ray phase-contrast imaging based on cascaded Talbot-Lau interferometers. Opt. Eng. 2020, 59, 033101. [Google Scholar]
- Zuo, C.; Feng, S.; Huang, L.; Tao, T.; Yin, W.; Chen, Q. Phase shifting algorithms for fringe projection profilometry: A review. Opt. Laser. Eng. 2018, 109, 23–59. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).