Abstract
Spectral imaging plays a crucial role in various fields, including remote sensing, medical imaging, and material analysis, but it often requires specialized and expensive equipment, making it inaccessible to many. Its application is also limited by the interdependent constraints of temporal, spatial, and spectral resolutions. In order to address these issues, and thus, obtain high-quality spectral images in a time-efficient and affordable manner, we proposed one two-step method for spectral image reconstruction from easily available RGB images under the down-sampling schemes. Specifically, we investigated how RGB values characterize spectral reflectance and found that, compared to the intuitive and straightforward RGB images themselves, their corresponding basis vector coefficients can represent the prior information of spectral images more explicitly and are better suited for spectral image reconstruction tasks. Thus, we derived one data-driven algebraic method to recover the corresponding basis vector coefficients from RGB images in an analytical form and then employed one CNN-based neural network to learn the patch-level mapping from the recovered basis vector coefficients to spectral images. To evaluate the effect of introducing the basis vector coefficient recovery step, several CNNs which typically perform well in spectral image reconstruction are chosen as benchmarks to compare the variation in reconstruction performance. Experimental results on a large public spectral image dataset and our real-world dataset demonstrate that compared to the unaltered version, those CNNs guided by the recovered basis vector coefficients can achieve significant performance improvement in the reconstruction accuracy. Furthermore, this method is plug-and-play, with very little computational performance consumption, thus maintaining a high speed of calculation.
1. Introduction
Spectral imaging technology is a non-invasive imaging modality that obtains simultaneous spectral reflectance and spatial information, providing the physical features inherent to the surfaces of objects composed of different materials and having vital significance in visual tasks. Spectral images encompass more detailed narrow-band spectral information compared to the standard RGB images, which essentially represent down-sampled versions of spectral images attained through integration with specific wide-band spectral sensitivity functions [1] (the details are provided in Equation (1)). Due to this unique property, spectral imaging technology has been widely used in remote sensing [2,3], camouflage target recognition [4,5,6], medical diagnostics [7,8,9,10], and many other fields [11]. Studies in spectral imaging systems are, therefore, extremely important and have been broadly conducted for decades.
Persistent challenges in the design of spectral imaging systems are mainly centered on improving the resolutions of different dimensions of the spectral data (e.g., the spectral, spatial, and temporal dimensions) [12]. According to the sampling strategy of hardware systems, methods in this area can be roughly divided into two groups: the conventional full-sampling schemes [13,14,15,16] and the recent down-sampling schemes [17,18,19].
Since realistic sensors can often only obtain data in up to two dimensions at once, the initial generation of spectral imaging systems is based on time-domain imaging, using mechanical path-length scanning to supplement the information of the missing dimension [20] (e.g., the whiskbroom, pushbroom [13,14,15], sequential filter wheels [16], and acousto-optic tunable filter (AOTF) [21,22] spectral imaging systems). Under the full-sampling schemes, these conventional scanning-based methods can gather all available three-dimensional data and then plausibly reconstruct the corresponding spectral images. These methods allow a high spatial or spectral resolution but also bring the drawbacks of poor time efficiency and restricted application scenarios.
To expand the applicability of spectral imaging systems in dynamic circumstances, several techniques using down-sampling schemes have been presented to produce spectral images in a time-efficient way. These methods all capture fewer measurements than full-sampling schemes and reconstruct spectral images from incomplete data, thereby enhancing the temporal resolution and preventing data overload in a short period [23]. For instance, by replacing the mechanical path-length scanning section with computational elements (e.g., spatial light modulators (SLM) and digital micromirror devices (DMD)), the acquisition of spectral images at video rate can be accomplished [12]. In addition to this, capitalizing on recent breakthroughs in compressive sensing theory [24], computed tomography imaging spectrometry (CTIS) [25] and coded aperture snapshot imaging (CASSI) have also been developed. Especially, the introduction of coded aperture enables CASSI-like methods [26,27,28,29,30] to implement snapshot imaging, which means the ability to capture spectral data within a single exposure. However, while the above systems can move beyond the problem of poor temporal resolution, they are hindered by diminished spectral and spatial resolutions instead. Other than this, the precision optical components required by some methods are not only prohibitively expensive but also reduce the luminous flux of the whole spectral image system. In such a system, when the light source is weak, the absolute number of collected photons can be quite modest, resulting in a low signal-to-noise ratio.
To obtain spectral images more conveniently and affordably, the popular recent focus is to reconstruct spectral images from readily available data without overly specialized equipment, such as the multi-channel images obtained by one or more than one commercial cameras [31,32], or under different shooting conditions (e.g., dynamic illumination or changing angles [33,34,35]). Spectral images capture light distribution across numerous narrow spectral bands within a scene, while multi-channel images are confined to several broad or narrow spectral bands. Consequently, the reconstruction of spectral images from multi-channel images can be perceived as achieving super-resolution within the spectral domain. Due to the lack of optical components to encode spectral and spatial information, such methods can readily achieve high luminous fluxes. Common reconstruction methods encompass pseudo-inverse methods [36], Wiener estimation methods [37], and kernel methods [38,39]. These methods heavily rely on certain prior knowledge (e.g., the sparsity, the similarity in spatial or spectral dimensions, and the statistical characteristics embedded in the prior datasets) or constraints imposed on the spectral reflectance distribution. Additionally, machine-learning techniques offer promising alternatives for integrating prior knowledge into the spectral reconstruction process [40]. A prevalent strategy involves addressing the mapping from a multi-channel image to its corresponding spectral image by training an end-to-end neural network, achieving implicit transformation. This phenomenon is evident in the recent new trends in image restoration and enhancement (NTIRE) challenges [41,42]. Under this paradigm, the acquisition of multi-channel images is a crucial step in accurately reconstructing full spectral information. While the plain three-channel RGB image is the most convenient, it is inadequate for accurate spectral reconstruction. Increasing the number of channels can improve accuracy, but compromises convenience. Thus, a balance must be struck between accuracy and convenience in multi-channel image acquisition. Conversely, the meticulous selection of camera response filters has the potential to elevate hyperspectral estimation accuracy by more than 33%, even when restricting the number of channels in the input image (e.g., in the context of RGB images) [43]. This revelation prompts us to explore the possibility of enhancing reconstruction performance without the need to increase the channel count. This can be achieved by transforming the RGB image to create inputs enriched with implicit information. While this perspective offers significant value, it has received comparatively less attention in current discussions.
In summary, there are currently mutual constraints between several important attributes of spectral imaging technology that limit its widespread application. In order to facilitate the application of spectral imaging technology in more general dynamic scenarios, we intend to develop a time-efficient algorithm that can simultaneously balance convenience, and affordability. Through the analysis of the above development status, our path to that goal was formulated as an improvement to the multi-channel-image-based down-sampling schemes. In this paper, on the foundation of those common end-to-end neural network methods with no hand-crafted features (i.e., the multi-channel images are directly used as input to the network), we propose an additional basis vector coefficient recovery step to exploit the prior knowledge embedded in spectral images explicitly. Specifically, through the pairs of RGB tri-stimulus values and related spectral reflectance in the prior training spectral datasets, we estimate the spectral weight function by one data-driven algebraic method and from this, the method for calculating the basis vector coefficients is derived. Then, we employed one convolutional neural network (CNN) to learn the patch-level mapping from recovered basis vector coefficients to spectral images, utilizing its excellent fitting ability and effective use of spatial contextual information.
The innovation and contributions of this work are summarized as follows:
- We investigated the characterization of spectral reflectance by RGB values and demonstrated the superiority of their corresponding basis vector coefficients for the reconstruction of spectral images.
- Accordingly, we developed one data-driven algebraic method for recovering these coefficients and used them as inputs for the employed CNN networks.
- To ensure the convenience of the spectral imaging systems, we validated the algorithm on a large spectral dataset and our real-world dataset with RGB images as input.
- To strike a balance between accuracy and convenience, we also conducted further research to investigate the effect of channels on the reconstruction performance and offered recommendations for optimal channel selection.
2. Methodology
2.1. RGB Digital Camera Imaging Principle
The RGB digital cameras sense the reflective scene through a tri-stimulus mechanism, causing three channels to respond differently to the same target [31]. Specifically, the tri-stimulus values are formed by conflating the spectral reflectance with the incoming illumination and spectral sensitivity function of the sensors [44]. Let denote the spectral reflectance of a specific scene with wavelength . The incoming illumination and the spectral sensitivity function of the color channel are indicated by and . In this way, the response of each color channel can be presented as an integral over all the range of visible wavelengths as:
where is the range of visible wavelengths.
For mathematical simplicity, we set and sample the visible wavelength at intervals between 400~700 nm, resulting in the spectral image of 31 channels to be reconstructed. Equation (1) can, therefore, be discretized across wavelengths and represented in vector-matrix form as Equation (2):
where is written as
and and are both column vectors.
According to Equation (2), we can consider that the essence of spectral reconstruction is to solve for the spectral reflectance of 31 channels when only the tri-stimulus values of the RGB camera are known, leading to the ill-posed inverse process of this equation. Directly solving such an ill-posed equation cannot lead to a unique solution.
2.2. Basis Vector Coefficients
Utilizing certain prior knowledge or constraints imposed on the distribution of spectral reflectance, Equation (2) can be solved more stably. As the spectral reflectance curve of a natural scene is smooth, the spectral information with similar wavelengths is correlated and can be represented in a lower-dimensional space [45]. In other words, the spectral reflectance can be adequately approximated by the linear combination of a small number of basis vectors:
where the columns in and , respectively, denote the basis vectors and their corresponding linear combination coefficients, and is the amount of employed basis vectors.
The decomposition process of basis vectors is a planning problem that allows basis vectors to be the best approximation to the target under the defined error function. Additionally, extracted from the prior training spectral datasets, those basis vectors implicitly characterize the spectral reflectance of natural scenes, especially the statistical distribution properties that have a greater impact on the reconstruction quality, adding a solid and practical constraint to this reconstruction. There are many well-established methods that can be used to perform the extraction of basis vectors, including singular value decomposition (SVD) [46], principal component analysis (PCA) [47], t-SNE [48], and autoencoder (AE) [49], to name a few. They can provide basis vectors that minimize reconstruction errors under different defined error function senses. For instance, the basis vectors produced by the SVD method are orthogonal, devoid of redundant information, and the error in the reconstructed result concerning the targets is minimized under the Euclidean distance definition which is consistent with the mean squared error (MSE) metric commonly used to evaluate the accuracy of spectral reconstruction. Current studies have shown that the spectral reflectance of a natural scene can be reconstructed with high accuracy using a linear combination of basis vectors [50]. That is, this constraint is indeed practical.
The numerous properties of the basis vectors mentioned above are also inherited by their coefficients. By transforming Equation (3) as follows, we can obtain some properties of the basis vector coefficients:
where the symbol represents the pseudo-inverse operation. Notice that the dimensions of the basis vector coefficients and the spectral reflectance are and , respectively, so that in the case of , the basis vector coefficients serve as a kind of reduced dimensional representation of the spectral reflectance.
It is not difficult to find that Equations (2) and (4) have the same form (i.e., both are the fork multiplication of one matrix to the spectral reflectance vector), which indicates that the tri-stimulus values and basis vector coefficients are formed by a similar computational process and are essentially a kind of encoding of spectral reflectance. The difference is that the former is encoded using the spectral sensitivity function of RGB cameras, while the latter is encoded using basis vectors. The spectral sensitivity function of RGB cameras is initially designed to mimic the visual characteristics of human eyes, showing that they are intrinsically unsuited for spectral reconstruction tasks. Conversely, the principle of basis vector extraction algorithms guarantees that those extracted basis vectors are the best approximation to the target under the defined error function. Furthermore, these defined error functions are generally consistent with metrics for evaluating the spectral reconstruction quality (e.g., the previously mentioned SVD method’s error function conforms to the MSE metric). That is to say, compared with the intuitive and straightforward RGB images, the recovered basis vector coefficients can represent the prior information of spectral images more explicitly and are more suitable for spectral reconstruction.
2.3. Spectral Reconstruction
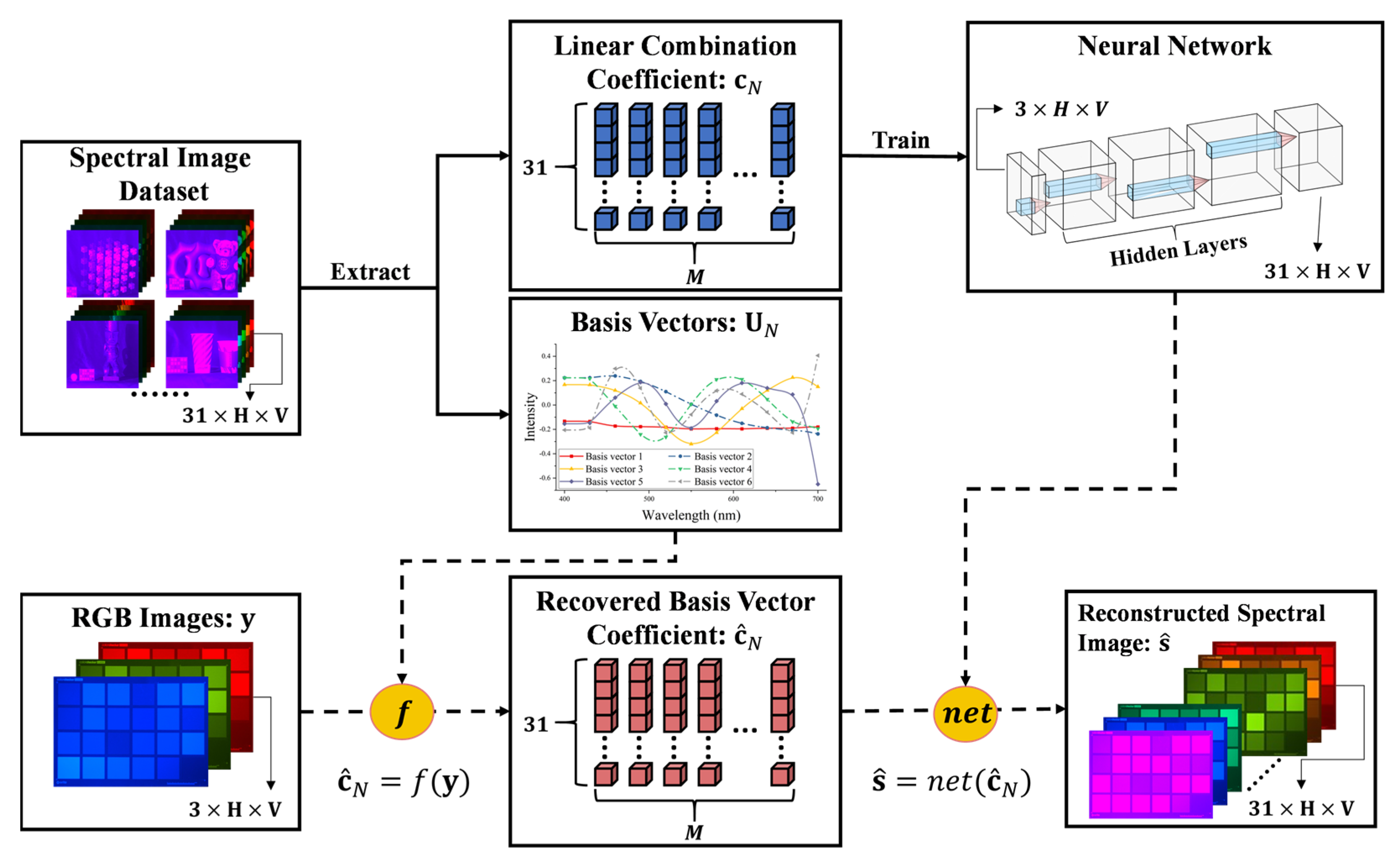
The specific implementation of our proposed method consists of two main steps. Firstly, it is required to calculate the corresponding basis vector coefficients from the tri-stimulus values of input RGB images. After that, under the prior spectral datasets, we need to solve the mapping from the recovered basis vector coefficients to the related spectral reflectance. Once the computational methods for recovering the basis vector coefficients and the mapping function are derived and obtained, respectively, during the inference process, we can calculate the basis vector coefficients from the input RGB images, and then map them into the spectral images. In the following content, the specific details of these two steps will be elaborated. The flowchart of the entire calculation process is shown in Figure 1, and the symbols involved are described later.
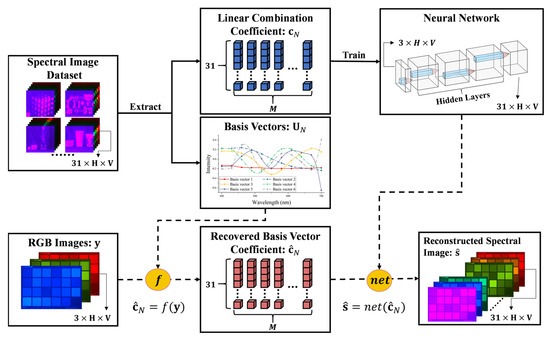
Figure 1.
Flowchart of spectral image reconstruction using recovered basis vector coefficients.
Let us first identify a specific basis vector extraction algorithm and derive how to calculate its basis vector coefficients. The basis vectors extracted from the prior spectral datasets vary with the basis vector extraction algorithm, as does the basis vector coefficients recovery algorithm. In this article, the SVD algorithm, which performs a linear representation of the spectral reflectance, is employed to extract the orthogonal basis vectors without redundant information.
By combining Equations (2) and (3), we can obtain one general method for estimating the linear combination coefficients , which is also the in Figure 1:
This method is straightforward and applicable to all linear basis vector extraction algorithms, but suffers from some systematic errors and shortcomings. On the one hand, from a mathematical point of view, the inverse matrix of this singular matrix will introduce unavoidable errors since we cannot obtain a unique solution from an ill-posed equation. To solve this problem, we can set the number of employed basis vectors and imaging sensors to be equal (for RGB cameras, this means setting to 3). Then, the matrix would be singular, thus avoiding the systematic errors in the pseudo-inverse process. On the other hand, in general, the spectral weight function requires some sophisticated and expensive instruments to measure, which is inconvenient and unacceptable for some application scenarios. However, for a defined scenario, the spectral weight function can be estimated using pairs of tri-stimulus values and related spectral reflectance in the prior training spectral datasets. In a spectral dataset with a huge number of spectral images, let there be a total of data pairs. Then, Equation (2) can be expanded as follows:
where and represent the set of tri-stimulus values and spectral reflectance in the whole training spectral dataset, respectively. Since there are typically far more data pairs than 31 (i.e., ), this equation is over-determined. Transformed into the following optimization problem of minimizing the sum of squared errors, such a system of those over-determined equations can be solved using the linear least squares method:
To solve this optimization problem, firstly, let denote the transposed objective function to be minimized:
Then, find the partial derivative of the objective function with respect to :
Assign it to zero to minimize it:
Obviously, the is a full-rank matrix, whose inverse matrix can be found directly. In this case, the spectral weight function can be obtained:
Once the spectral weight function is solved, the estimated linear combination coefficients can be recovered according to Equation (5).
Then, although we can calculate the spectral reflectance of individual pixels using Equation (3) and then rearrange it to form the corresponding spectral images, this linear mathematical approach is straightforward and inaccurate because it does not take the optoelectronics of the device into account. When we consider a real digital image capture device, with noise, these estimations are unpredictable [51]. In addition, this pixel-based approach fails to utilize the spatial correlation information implied in the spectral images, which limits the reconstruction accuracy. Coincidentally, the neural networks, especially those based on patch-level mapping, not only have an excellent fitting ability but also can exploit spatial contextual information, which just forms a complement. Therefore, we can employ a neural network as the reconstruction algorithm module. What distinguishes different neural network methods is the network architecture. There are a number of traditional architectures, including ResNet [52,53], UNet [54], and DenseNet [55], etc. Usually, these architectures will be modified to suit the specific needs of different scenarios. In the following content, several neural network architectures that perform well in spectral reconstruction will be briefly introduced and used as benchmarks. The first benchmark we used in this work was a deep dense network, called the HSCNN-D model [56]. It consists of several dense blocks, and plays an essential role in the research of spectral image reconstruction, for it was the best performing model in the NTIRE 2018 challenge [41]. The second benchmark is a modified UNet proposed by Zhao [57] (hereinafter referred to as the ZYYNet model). In addition to down-sampling and up-sampling in the spectral dimension like the first model, the ZYYNet model also performs those sampling works in the spatial dimension to further exploit the correlation among pixels over receptive fields of different scales, precisely the characteristic of UNet.
3. Experiments on a Public Dataset
3.1. Settings
To demonstrate the effectiveness of our proposed method, we analyze the performance of those two benchmark networks before and after introducing the suggested additional basis vector recovery phase step. The specific settings of our experiments are described below.
Spectral dataset. The experiments of our proposed method and benchmarks are conducted on one new natural spectral image dataset provided by the NTIRE 2020 challenge [42]. Containing two tracks and consisting of 510 high-quality natural spectral images in total, this dataset is one of the most comprehensive datasets available. The “clean” track aims to recover spectral images from the noise-free RGB images, while the “real world” track requires participants to rebuild the spectral images from noisy JPEG-compression RGB images created by an unknown camera response function [58]. The original spectral images have a uniform spatial resolution of , and the visible wavelength range of 400–700 nm is sampled at intervals.
Evaluation metrics. In order to adequately perform the quantitative evaluation of our proposed method, several metrics are used, including the root mean squared error (RMSE), mean relative absolute error (MRAE), structural similarity index (SSIM) [59], and peak signal-to-noise ratio (PSNR). Among them, MRAE is the metric recommended by the NTIRE challenges for the ability to avoid over-weighting errors in higher luminance areas of the test images [58]. In addition, compared to the other metrics, that can only evaluate the spectral reflectance reconstruction accuracy of the individual pixels, the SSIM metric is used to assess the similarity of the whole spectral image to the ground truth. For the metrics mentioned above, including RMSE, MRAE, and SSIM, all values fall within the range of 0 to 1. Higher values of SSIM and PSNR indicate superior reconstruction performance, while the converse holds true for RMSE and MRAE.
Implementation details. With reference to the employed benchmarks in this work, the metric RMSE is used as the loss function and minimized with the well-known adaptive moment estimation method (Adam) [60] by setting , , and . All neural networks are trained for 35 epochs while the learning rate is initialized as and scaled to one-tenth of the previous one every 10 epochs. During the training process, RGB patches of size and their corresponding spectral data cubes are fed into the models. Data augmentation is performed by means of random horizontal and vertical flipping. All networks are implemented within the PyTorch framework and trained on an NVIDIA RTX 2080Ti hardware platform.
3.2. Results
Experiments are conducted on the official validation set to assess the effectiveness of our proposed method. The average results of the employed benchmarks with vanilla input-end (i.e., the RGB image, denoted as “direct”) and modified input-end (i.e., the recovered basis vector coefficients, denoted as “coeff”) for each metric in the two tracks are presented in Table 1. It can be clearly seen that after modifying the input-end of the networks to the recovered basis vector coefficients, the overall reconstruction accuracy is significantly improved with all the selected metrics.

Table 1.
Quantitative results of spectral reconstruction on the public dataset. The better result is shown in bold.
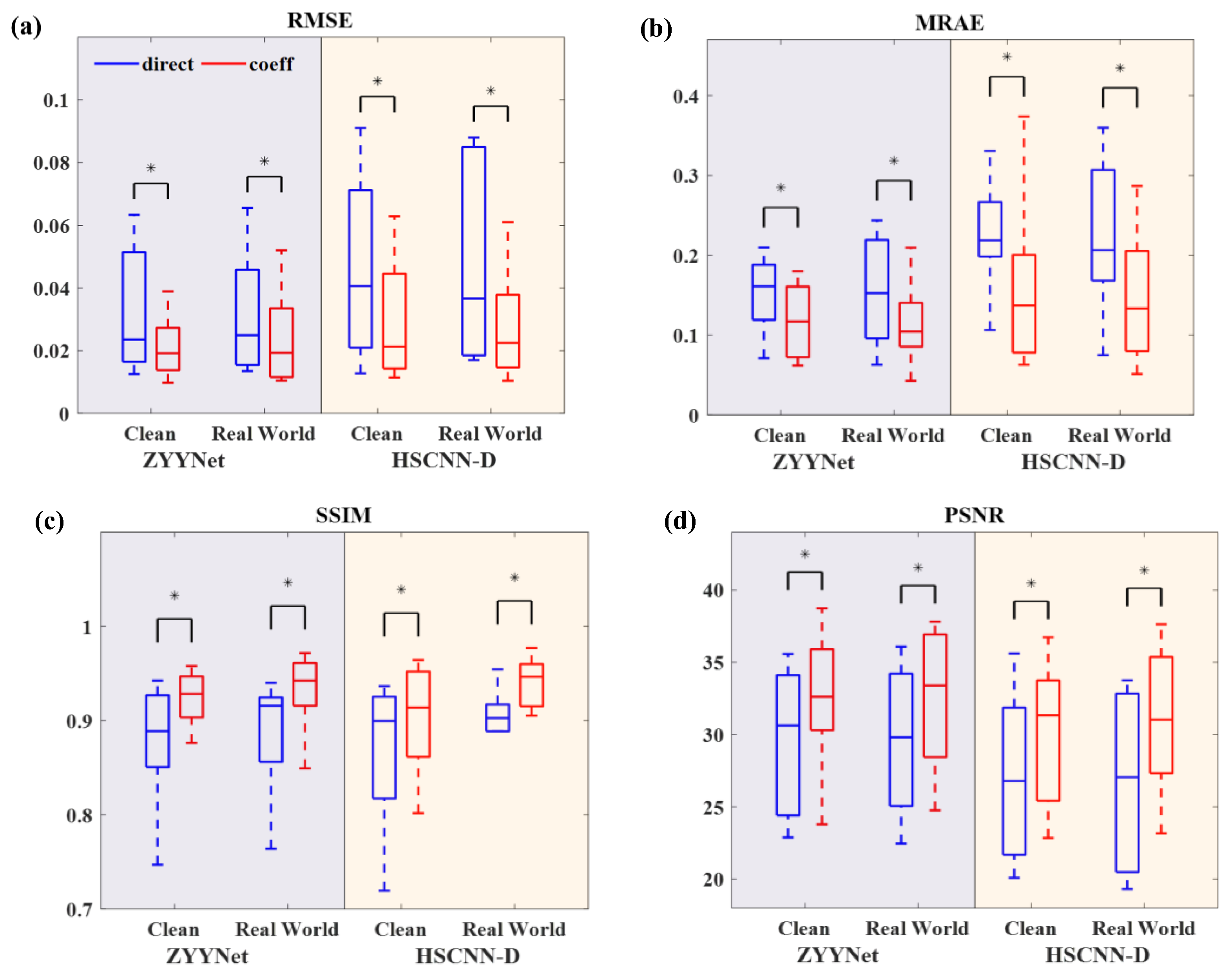
As a further analysis, we also performed a statistical analysis based on the paired t-test using a series of boxplots (shown in Figure 2). The asterisk above each pair of data indicates that there is a statistically significant difference between these paired data (* p < 0.05). The spacings in each subsection of boxplots visually show the distribution of numerical data and skewness by displaying their data quartiles, which is also referred to as the five-number summary (i.e., the minimum, maximum, median, lower quartile, and upper quartile). In contrast to the mean values in Table 1, the results of the paired t-tests show that the proposed method not only improves the performance of the benchmarks on the validation set as a whole but also achieves a statistically significant improvement in the reconstruction accuracy of each sample. Except for the oddity of the HSCNN-D network on the MARE metric (Figure 2b, the part with a light-yellow background), the two benchmark networks with modified input-end demonstrated an improvement in each data quartile and in the median values on the various metrics and tracks. In addition, the decreased interquartile range (IQR) of almost all of the boxplots (except for the HSCNN-D network’s performance on the MRAE and SSIM metric under partial tracks), indicates that the variance of each metric has also decreased, thus further ensuring the reliability and consistency of the spectral image reconstruction.
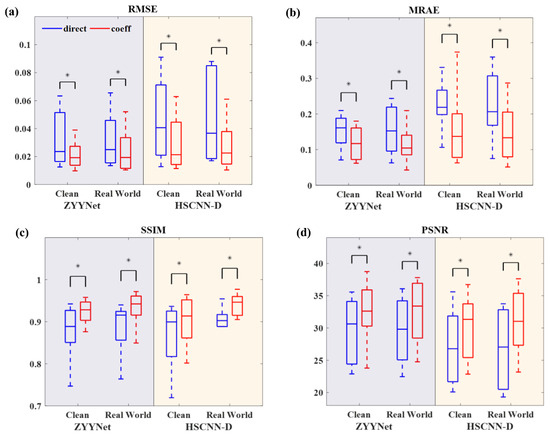
Figure 2.
Results of statistical analysis based on the paired t-test (* p < 0.05). (a–d) the statistical analysis of RMSE, MRAE, SSIM and PSNR. The blue and red boxplots represent the results for the benchmarks with vanilla input-end (denoted as “direct”) and modified input-end (denoted as “coeff”), respectively.
3.3. Visualization
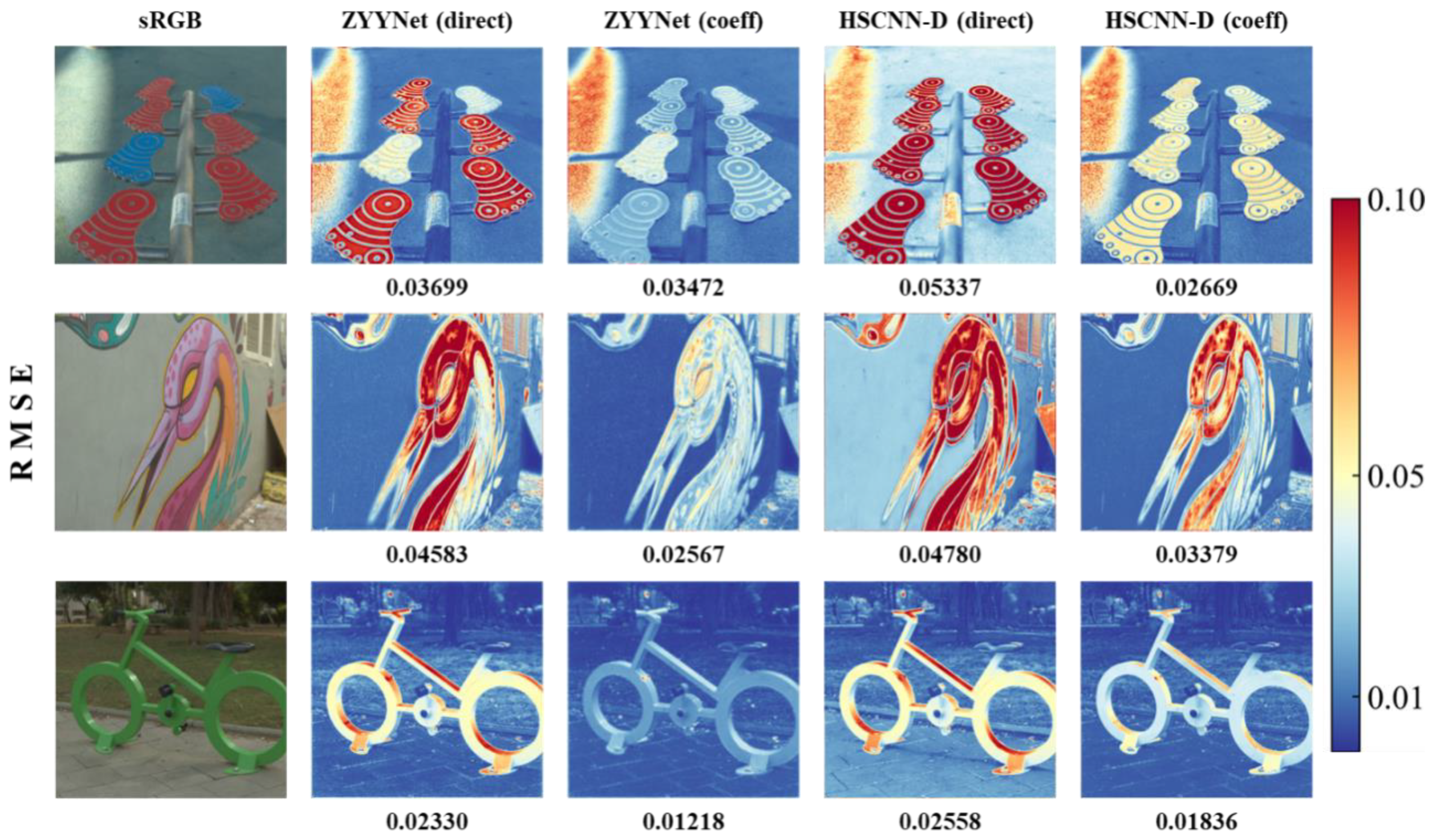
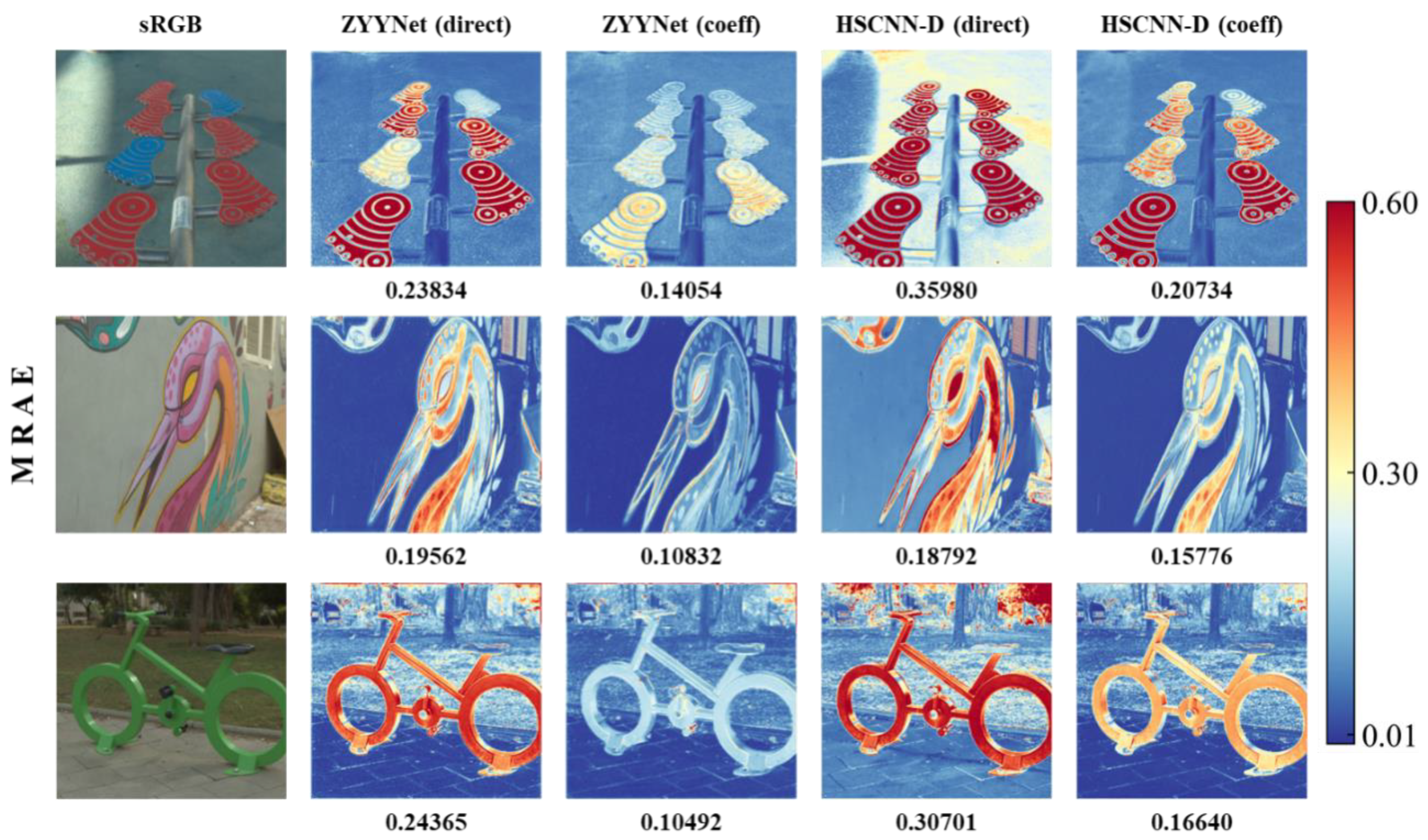
To evaluate the perceptual quality of the spectral reconstruction results, two metrics, RMSE and MRAE, are selected to draw the error maps between several recovered spectral images and their corresponding ground truths (see Figure 3 and Figure 4). The values of those two metrics all range from 0 to 1, and smaller values represent better reconstruction results (i.e., the blue parts in the error maps mean better reconstruction results). Obviously, the error maps of the “coeff” series are bluer than those of the “direct” series, no matter from the perspective of the overall or local texture. These figures demonstrate that our proposed method outperforms those benchmarks in terms of recovery results and reconstruction fidelity.
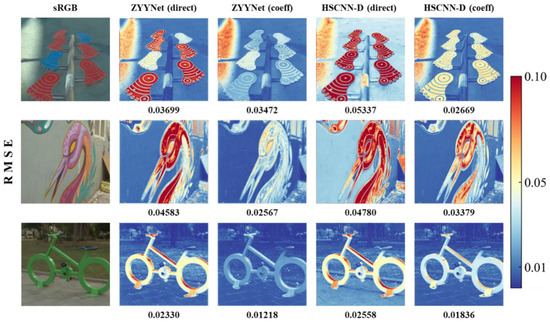
Figure 3.
Visual comparison of the metric RMSE between the ground truth and the corresponding reconstructed spectral image under the employed benchmarks with vanilla input-end and modified input-end.
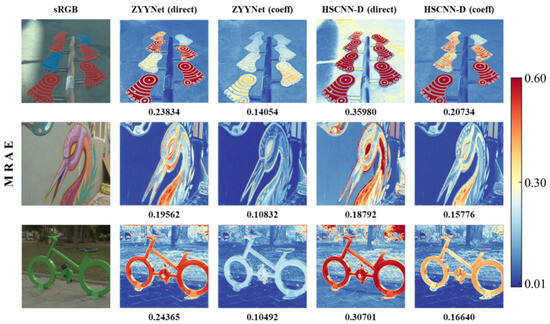
Figure 4.
Visual comparison of the metric MRAE between the ground truth and the corresponding reconstructed spectral image under the employed benchmarks with vanilla input-end and modified input-end.
4. Experiments on the Real-World Dataset
4.1. Settings
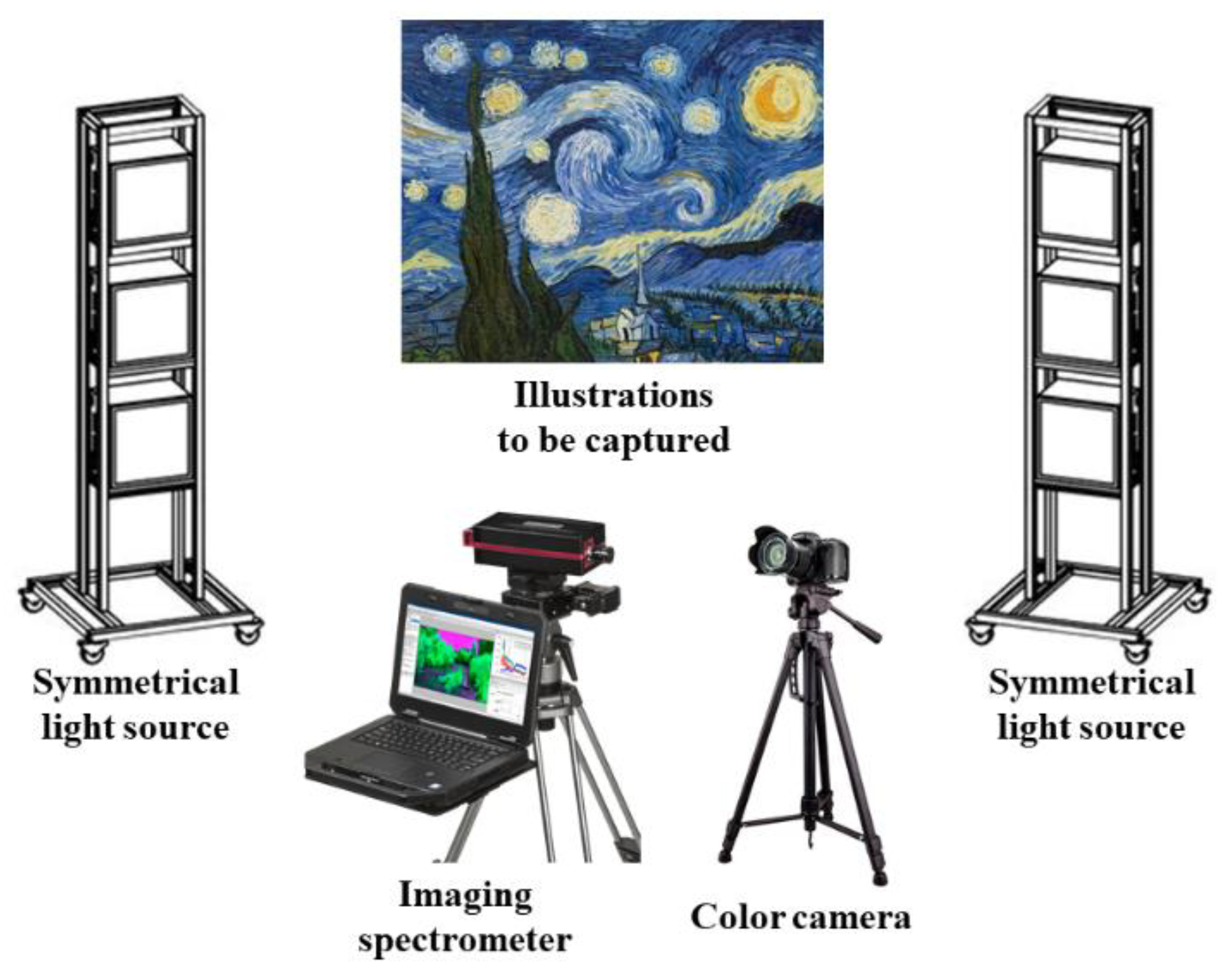
In practice, we construct a hybrid-resolution imaging system for capturing real-world spectral images along with their corresponding RGB images. Figure 5 illustrates the configuration of the imaging spectrometer (Pika L, Resonon Inc., Bozeman, MT, USA), commercial color camera (EOS 6D Mark II, Canon Inc., Kyoto, Japan), and the arrangement of the light sources employed in this system. To account for the disparity in physical location and view field between the imaging spectrometer and the commercial color camera, the SIFI algorithm is utilized to detect and match feature points, thereby achieving image registration. An illustration set is utilized as the object to be captured, and some of the registered RGB images are shown in Figure 6.
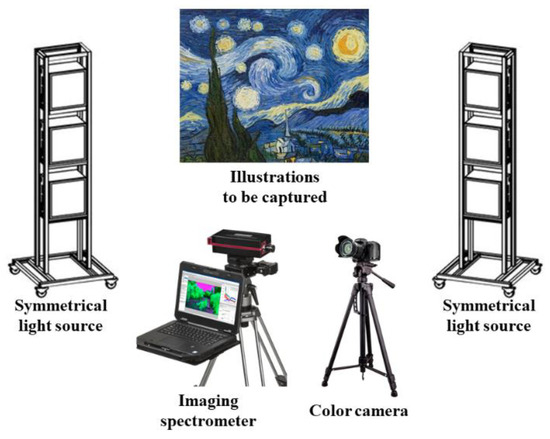
Figure 5.
The diagram of the hybrid-resolution imaging system.

Figure 6.
Some registered RGB images of our real-world dataset.
Implementation details. In order to achieve improved reconstruction results, adjustments were made to various hyperparameters and learning rate strategies of the neural network, considering the differences in the intrinsic properties of the real-world dataset. Specifically, all neural networks were trained for 60 epochs while the learning rate was initialized as and the cosine annealing scheme was adopted.
4.2. Results
The average results of the employed benchmarks with vanilla input-end and modified input-end for each metric on the real-world dataset are presented in Table 2. Due to the degradation of the dataset quality caused by image registration, there has been an overall decline in the accuracy of the reconstruction. However, with the incorporation of our proposed basis vector coefficient recovery step, the neural network can still maintain a favorable level of reconstruction accuracy.

Table 2.
Quantitative results of spectral reconstruction on the real-world dataset. The better result is shown in bold.
5. Discussion
5.1. Computational Efficiency and Flexibility
Essentially, our proposed method is formed by modifying the input-end of common end-to-end neural networks from RGB images to corresponding basis vector coefficients. Compared to the original benchmark, the difference is the addition of a module for recovering the basis vector coefficients. This module can be applied to any neural-network-based systems which reconstruct spectral images directly from RGB images, demonstrating the flexibility of our proposed method. In addition, this module is performed by a linear matrix operation with negligible computational effort, thus having the advantage of high computational efficiency.
5.2. The Effect of Channels
In this work, we set the quantity of employed basis vectors to three to match the number of channels of RGB cameras, for those conventional commercial cameras can only acquire up to three channels of images. However, for a broader range of cases, the multi-channel images used as model inputs may have a larger number of channels. In fixed industrial application scenarios, for example, a certain level of convenience can be sacrificed to obtain images with more channels. Intuitively, more channels of input multi-channel images can lead to a higher reconstruction accuracy. However, due to the high redundancy of spectral reflectance, the unlimited addition of channels does not effectively improve reconstruction accuracy. Instead, it increases the difficulty and cost of sampling. Here, we will discuss the effect of channels on reconstruction accuracy to guide the design of high-precision spectral imaging systems.
Firstly, the multi-channel images are synthesized as inputs to models by imitating the setup of the “clean” track. When the number of channels is greater than three, RGB cameras no longer apply. Thus, without using RGB cameras as the image capture device, there is no need to take the visual properties of the human eyes into consideration anymore, and there is more freedom in choosing the spectral sensitivity function of the imaging sensors. Filters, which have any required number of evenly spaced peaks, can be yielded by the concept of equivalent indices and the theory of the Fabry–Perot etalon [61]. Thus, Gaussian functions with evenly distributed peaks are used to synthesize the response of imaging sensors from the given spectral dataset in the hope of obtaining more fully unduplicated spectral information. In addition, a D65 light source was used for the incoming illumination, and the ZYYNet was employed as the reconstruction algorithm module with similar settings as described in Section 3.1.
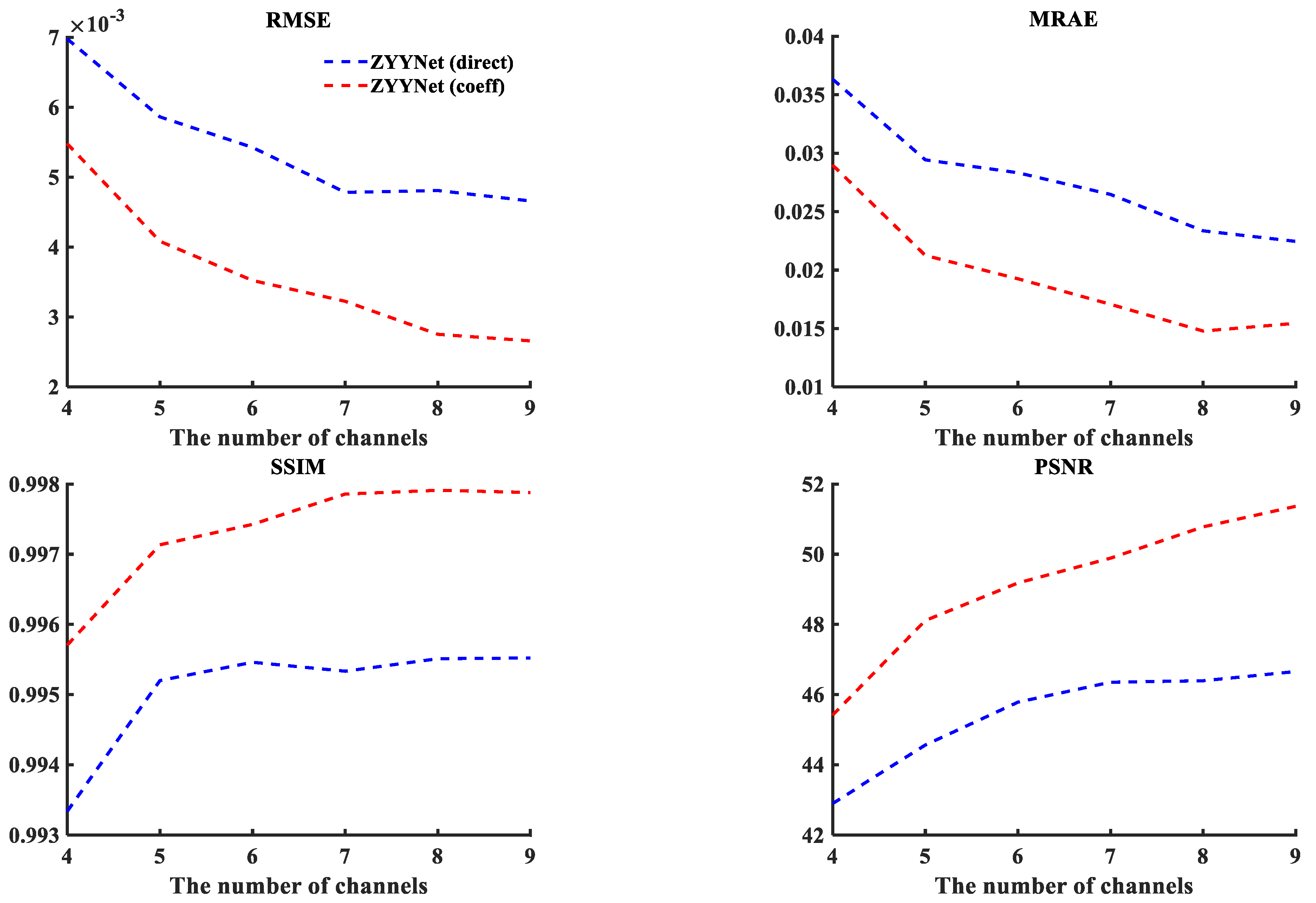
The trend in spectral reconstruction accuracy under each metric as the number of channels grows is shown in Figure 7. Not surprisingly, as the number of channels grows, the performance of spectral reconstruction in each metric improves. This growth becomes slower when the number of channels is larger than six, which corresponds to the current studies [50].
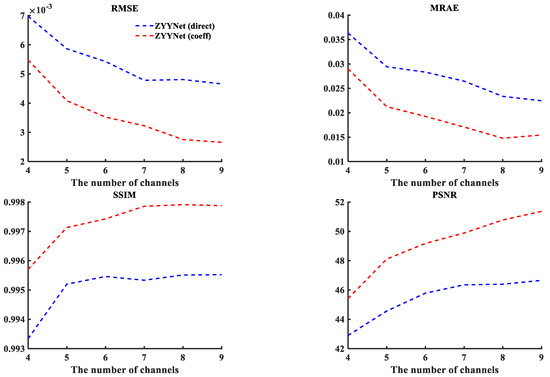
Figure 7.
Reconstruction metrics for different numbers of channels (taking ZYYNet as an example).
In terms of the design of image capture devices, suppose a color camera is used to acquire the multi-channel image. In that case, the number of channels of the acquired images is a multiple of three, whether multiple cameras or dynamic illumination are used. In addition, modifying the Bayer filter in the camera to a or array also makes it convenient to obtain images with six or nine channels in one snapshot at an acceptable cost of spatial resolution. Considering the above reasons, in follow-up studies, we recommend that both the channels of multi-channel images and the number of employed basis vectors are set to six or nine to meet the physical constraint from basis vector theories and balance the convenience and reconstruction accuracy. However, in some application scenarios, where convenience is sought over accuracy, the direct use of RGB cameras to acquire images for spectral image reconstruction is still an excellent option.
6. Conclusions
In this work, we proposed an improved method for spectral image reconstruction from easily available RGB images. We observed that compared with the intuitive and straightforward RGB images, the recovered basis vector coefficients can represent the prior information of spectral images more explicitly and are more suitable for spectral reconstruction. Specifically, through pairs of tri-stimulus values and related spectral reflectance in the prior training spectral datasets, we can estimate the spectral weight function, and, from this the method for calculating the basis vector coefficients is derived. Then, to exploit the spatial contextual information of spectral images, and thus improve the reconstruction accuracy, we employed a CNN-based neural network to learn the patch-level mapping from the basis vector coefficients to the corresponding spectral image. As the experiment results demonstrated in one large dataset, modifying the input-end of common end-to-end neural networks from RGB images to corresponding basis vector coefficients can effectively improve the reconstruction performance.
Additionally, we have discussed the effect of channels on the reconstruction performance and recommend that both the channels of multi-channel images and the number of employed basis vectors should be set to six or nine to meet the physical constraint from basis vector theories and balance the convenience and reconstruction accuracy. Future work would be to develop a high-precision spectral imaging system based on multi-channel images and explore whether the overall performance can be further improved when other more sophisticated nonlinear methods are used to calculate the basis vector coefficients.
Author Contributions
Funding acquisition, Y.L.; investigation, W.X.; methodology, W.X.; supervision, Y.L.; writing—original draft, W.X.; writing—review and editing, W.X., L.W. and X.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Shanghai 2022 “Science and Technology Innovation Action Plan”, grant number 22dz1202402.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
The data underlying the results presented in this paper are available in Ref. [33].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Arad, B.; Timofte, R.; Yahel, R.; Morag, N.; Bernat, A.; Cai, Y.; Lin, J.; Lin, Z.; Wang, H.; Zhang, Y.; et al. NTIRE 2022 Spectral Recovery Challenge and Data Set. In Proceedings of the 2022 IEEE CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), New Orleans, LA, USA, 18–24 June 2022; pp. 862–880. [Google Scholar] [CrossRef]
- Zhou, D.K.; Larar, A.M.; Liu, X.; Reisse, R.A.; Smith, W.L.; Revercomb, H.E.; Bingham, G.E.; Zollinger, L.J.; Tansock, J.J.; Huppi, R.J. Geosynchronous imaging Fourier transform spectrometer (GIFTS): Imaging and tracking capability. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007; pp. 3855–3857. [Google Scholar] [CrossRef]
- Hamlin, L.; Green, R.O.; Mouroulis, P.; Eastwood, M.; Wilson, D.; Dudik, M.; Paine, C. Imaging spectrometer science measurements for Terrestrial Ecology: AVIRIS and new developments. In Proceedings of the 2011 Aerospace Conference, Big Sky, MT, USA, 5–12 March 2011; pp. 1–7. [Google Scholar] [CrossRef]
- Yan, Q.; Li, H.; Wu, Y.; Zhang, X.; Wang, S.; Zhang, Q. Camouflage target detection based on short-wave infrared hyperspectral images. In Proceedings of the Fifth Symposium on Novel Optoelectronic Detection Technology and Application, Xi’an, China, 12 March 2019; SPIE: Bellingham, WC, USA, 2019; pp. 655–661. [Google Scholar] [CrossRef]
- Zavvartorbati, A.; Dehghani, H.; Rashidi, A.J. Evaluation of camouflage effectiveness using hyperspectral images. J. Appl. Remote Sens. 2017, 11, 045008. [Google Scholar] [CrossRef]
- Yan, Y.; Hua, W.; Zhang, Y.; Cui, Z.; Wu, X.; Liu, X. Hyperspectral camouflage target characteristic analysis. In Proceedings of the 9th International Symposium on Advanced Optical Manufacturing and Testing Technologies: Optoelectronic Materials and Devices for Sensing and Imaging, Chengdu, China, 8 February 2019; SPIE: Bellingham, WC, USA, 2019; pp. 95–100. [Google Scholar] [CrossRef]
- Greenberg, J.A.; Lakshmanan, M.N.; Brady, D.J.; Kapadia, A.J. Optimization of a coded aperture coherent scatter spectral imaging system for medical imaging. In Medical Imaging 2015: Physics of Medical Imaging; Orlando, FL, USA, 18 March; SPIE: Bellingham, WC, USA, 2015; pp. 1325–1330. [Google Scholar] [CrossRef]
- Kendall, C.A.; Hugh Barr, M.D.; Shepherd, N.; Stone, N. Optimum procedure for construction of spectral classification algorithms for medical diagnosis. In Biomedical Vibrational Spectroscopy II; San Jose, CA, USA, 27 March 2002; SPIE: Bellingham, WC, USA, 2002; pp. 152–158. [Google Scholar] [CrossRef]
- Liu, P.; Liu, D. Periodically gapped data spectral velocity estimation in medical ultrasound using spatial and temporal dimensions. In Proceedings of the 2009 IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan, 19–24 April 2009; pp. 437–440. [Google Scholar] [CrossRef]
- Mill, J.; Li, L. Recent Advances in Understanding of Alzheimer’s Disease Progression Through Mass Spectrometry-Based Metabolomics. Phenomics 2022, 2, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Gill, T.; Gill, S.K.; Saini, D.K.; Chopra, Y.; de Koff, J.P.; Sandhu, K.S. A Comprehensive Review of High Throughput Phenotyping and Machine Learning for Plant Stress Phenotyping. Phenomics 2022, 2, 156–183. [Google Scholar] [CrossRef] [PubMed]
- Cao, X.; Yue, T.; Lin, X.; Lin, S.; Yuan, X.; Dai, Q.; Carin, L.; Brady, D.J. Computational Snapshot Multispectral Cameras: Toward dynamic capture of the spectral world. IEEE Signal Process. Mag. 2016, 33, 95–108. [Google Scholar] [CrossRef]
- Jiang, Z.; Yu, Z.; Yu, Y.; Huang, Z.; Ren, Q.; Li, C. Spatial resolution enhancement for pushbroom-based microscopic hyperspectral imaging. Appl. Opt. 2019, 58, 850–862. [Google Scholar] [CrossRef]
- Gehm, M.E.; Kim, M.S.; Fernandez, C.; Brady, D.J. High-throughput, multiplexed pushbroom hyperspectral microscopy. Opt. Express 2008, 16, 11032–11043. [Google Scholar] [CrossRef]
- Portnoy, A.D.; Gehm, M.E.; Brady, D.J. Pushbroom Hyperspectral Imaging With a Coded Aperture. Front. Opt. 2006, 2006, FMB2. [Google Scholar] [CrossRef]
- Eichenholz, J.M.; Barnett, N.; Fish, D. Sequential Filter Wheel Multispectral Imaging Systems. Imaging Appl. Opt. Congr. 2010, 2010, ATuB2. [Google Scholar] [CrossRef]
- Diaz, N.; Hinojosa, C.; Arguello, H. Adaptive grayscale compressive spectral imaging using optimal blue noise coding patterns. Opt. Laser Technol. 2019, 117, 147–157. [Google Scholar] [CrossRef]
- Zhu, J.; Zhao, J.; Yu, J.; Cui, G. Adaptive local sparse representation for compressive hyperspectral imaging. Opt. Laser Technol. 2022, 156, 108467. [Google Scholar] [CrossRef]
- Jiang, H.; Xu, C.; Liu, L. Joint spatial structural sparsity constraint and spectral low-rank approximation for snapshot compressive spectral imaging reconstruction. Opt. Lasers Eng. 2023, 162, 107413. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, T.; Singh, M.; Çetintaş, E.; Luo, Y.; Rivenson, Y.; Larin, K.V.; Ozcan, A. Neural network-based image reconstruction in swept-source optical coherence tomography using undersampled spectral data. Light Sci. Appl. 2021, 10, 155. [Google Scholar] [CrossRef] [PubMed]
- Bürmen, M.; Pernuš, F.; Likar, B. Spectral Characterization of Near-Infrared Acousto-optic Tunable Filter (AOTF) Hyperspectral Imaging Systems Using Standard Calibration Materials. Appl. Spectrosc. 2011, 65, 393–401. [Google Scholar] [CrossRef]
- Krauz, L.; Páta, P.; Bednář, J.; Klíma, M. Quasi-collinear IR AOTF based on mercurous halide single crystals for spatio-spectral hyperspectral imaging. Opt. Express 2021, 29, 12813–12832. [Google Scholar] [CrossRef] [PubMed]
- Hagen, N.A.; Kudenov, M.W. Review of snapshot spectral imaging technologies. Opt. Eng. 2013, 52, 090901. [Google Scholar] [CrossRef]
- Candes, E.J.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Descour, M.; Dereniak, E. Computed-tomography imaging spectrometer: Experimental calibration and reconstruction results. Appl. Opt. 1995, 34, 4817–4826. [Google Scholar] [CrossRef]
- Lin, X.; Liu, Y.; Wu, J.; Dai, Q. Spatial-spectral Encoded Compressive Hyperspectral Imaging. ACM Trans. Graph. 2014, 33, 233. [Google Scholar] [CrossRef]
- Choi, I.; Jeon, D.S.; Nam, G.; Gutierrez, D.; Kim, M.H. High-quality hyperspectral reconstruction using a spectral prior. ACM Trans. Graph. 2017, 36, 218. [Google Scholar] [CrossRef]
- Chen, X.-D.; Liu, Q.; Wang, J.; Wang, Q.-H. Asymmetric encryption of multi-image based on compressed sensing and feature fusion with high quality image reconstruction. Opt. Laser Technol. 2018, 107, 302–312. [Google Scholar] [CrossRef]
- Zhu, Q.; Wang, L.; Sun, Y.; Yang, T.; Xie, H.; Yang, L. Improved collection efficiency for spectrally encoded imaging using 4f configuration. Opt. Laser Technol. 2021, 135, 106611. [Google Scholar] [CrossRef]
- Sun, R.; Long, J.; Ding, Y.; Kuang, J.; Xi, J. Hadamard Single-Pixel Imaging Based on Positive Patterns. Photonics 2023, 10, 395. [Google Scholar] [CrossRef]
- Oh, S.W.; Brown, M.S.; Pollefeys, M.; Kim, S.J. Do It Yourself Hyperspectral Imaging with Everyday Digital Cameras. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 2461–2469. [Google Scholar] [CrossRef]
- Nguyen, R.M.H.; Prasad, D.K.; Brown, M.S. Training-Based Spectral Reconstruction from a Single RGB Image. In Proceedings of the Computer Vision–ECCV 2014: 13th European Conference, Zurich, Switzerland, 6–12 September 2014; Fleet, D., Pajdla, T., Schiele, B., Tuytelaars, T., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 186–201. [Google Scholar] [CrossRef]
- Fu, Y.; Zou, Y.; Zheng, Y.; Huang, H. Spectral reflectance recovery using optimal illuminations. Opt. Express 2019, 27, 30502–30516. [Google Scholar] [CrossRef]
- Han, S.; Sato, I.; Okabe, T.; Sato, Y. Fast Spectral Reflectance Recovery Using DLP Projector. Int. J. Comput. Vis. 2014, 110, 172–184. [Google Scholar] [CrossRef]
- Park, J.-I.; Lee, M.-H.; Grossberg, M.D.; Nayar, S.K. Multispectral Imaging Using Multiplexed Illumination. In Proceedings of the 2007 IEEE 11th International Conference on Computer Vision, Rio de Janeiro, Brazil, 14–20 October 2007; pp. 1–8. [Google Scholar] [CrossRef]
- Shen, H.-L.; Xin, J.H. Spectral characterization of a color scanner based on optimized adaptive estimation. JOSA A. 2006, 23, 1566–1569. [Google Scholar] [CrossRef]
- Shen, H.-L.; Cai, P.-Q.; Shao, S.-J.; Xin, J.H. Reflectance reconstruction for multispectral imaging by adaptive Wiener estimation. Opt. Express 2007, 15, 15545–15554. [Google Scholar] [CrossRef]
- Akhtar, N.; Mian, A. Hyperspectral Recovery from RGB Images using Gaussian Processes. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 100–113. [Google Scholar] [CrossRef]
- Wei, L.; Xu, W.; Weng, Z.; Sun, Y.; Lin, Y. Spectral reflectance estimation based on two-step k-nearest neighbors locally weighted linear regression. Opt. Eng. 2022, 61, 063102. [Google Scholar] [CrossRef]
- Yang, Z.; Albrow-Owen, T.; Cai, W.; Hasan, T. Miniaturization of optical spectrometers. Science 2021, 371, eabe0722. [Google Scholar] [CrossRef]
- Arad, B.; Liu, D.; Wu, F.; Lanaras, C.; Galliani, S.; Schindler, K.; Stiebel, T.; Koppers, S.; Seltsam, P.; Zhou, R.; et al. NTIRE 2018 Challenge on Spectral Reconstruction from RGB Images. In Proceedings of the 2018 IEEE CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar] [CrossRef]
- Arad, B.; Timofte, R.; Ben-Shahar, O.; Lin, Y.-T.; Finlayson, G.; Givati, S.; Li, J.; Wu, C.; Song, R.; Li, Y.; et al. NTIRE 2020 Challenge on Spectral Reconstruction from an RGB Image. In Proceedings of the 2020 IEEE CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Seattle, DC, USA, 14–19 June 2020; pp. 1806–1822. [Google Scholar] [CrossRef]
- Arad, B.; Ben-Shahar, O. Filter Selection for Hyperspectral Estimation. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 3172–3180. [Google Scholar] [CrossRef]
- Gardner, M.-A.; Hold-Geoffroy, Y.; Sunkavalli, K.; Gagné, C.; Lalonde, J.-F. Deep Parametric Indoor Lighting Estimation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 7174–7182. [Google Scholar] [CrossRef]
- Chang, Y.; Bailey, D.; Le Moan, S. A new coefficient estimation method when using PCA for spectral super-resolution. In Proceedings of the 2021 36th International Conference on Image and Vision Computing New Zealand (IVCNZ), Tauranga, New Zealand, 9–10 December 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Smithies, F. The Eigen-Values and Singular Values of Integral Equations. Proc. Lond. Math. Soc. 1938, s2–s43, 255–279. [Google Scholar] [CrossRef]
- Vrhel, M.J.; Gershon, R.; Iwan, L.S. Measurement and Analysis of Object Reflectance Spectra. Color Res. Appl. 1994, 19, 4–9. [Google Scholar] [CrossRef]
- van der Maaten, L.; Hinton, G. Visualizing Data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Masci, J.; Meier, U.; Cireşan, D.; Schmidhuber, J. Stacked Convolutional Auto-Encoders for Hierarchical Feature Extraction. In Proceedings of the Artificial Neural Networks and Machine Learning–ICANN 2011: 21st International Conference on Artificial Neural Networks, Espoo, Finland, 14–17 June 2011; Honkela, T., Duch, W., Girolami, M., Kaski, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 52–59. [Google Scholar] [CrossRef]
- Connah, D.; Westland, S.; Thomson, M.G.A. Recovering spectral information using digital camera systems. Color. Technol. 2001, 117, 309–312. [Google Scholar] [CrossRef]
- Martínez-Verdú, F.; Pujol, J.; Capilla, P. Calculation of the Color-Matching Functions of Digital Cameras from their Complete Spectral Responsitivities. J. Imaging Sci. Technol. 2000, 46, 211–216. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Identity Mappings in Deep Residual Networks. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; pp. 630–645. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015 Conference Proceedings, Munich, Germany, 5–9 October 2015; pp; pp. 234–241. [Google Scholar]
- Huang, G.; Liu, Z.; Maaten, L.V.D.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2261–2269. [Google Scholar] [CrossRef]
- Shi, Z.; Chen, C.; Xiong, Z.; Liu, D.; Wu, F. HSCNN+: Advanced CNN-Based Hyperspectral Recovery from RGB Images. In Proceedings of the 2018 IEEE CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Salt Lake City, Utah, 18–22 June 2018. [Google Scholar] [CrossRef]
- Zhao, Y.; Guo, H.; Ma, Z.; Cao, X.; Yue, T.; Hu, X. Hyperspectral Imaging With Random Printed Mask. In Proceedings of the 2019 IEEE CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 10149–10157. [Google Scholar] [CrossRef]
- Li, J.; Wu, C.; Song, R.; Li, Y.; Liu, F. Adaptive Weighted Attention Network with Camera Spectral Sensitivity Prior for Spectral Reconstruction from RGB Images. In Proceedings of the IEEE CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Seattle, DC, USA, 14–19 June 2020; pp. 1894–1903. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar] [CrossRef]
- Pelletier, E.; Macleod, H.A. Interference filters with multiple peaks. J. Opt. Soc. Am. 1982, 72, 683–687. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).