An Insight to the Outage Performance of Multi-Hop Mixed RF/FSO/UWOC System
Abstract
:1. Introduction
Contributions
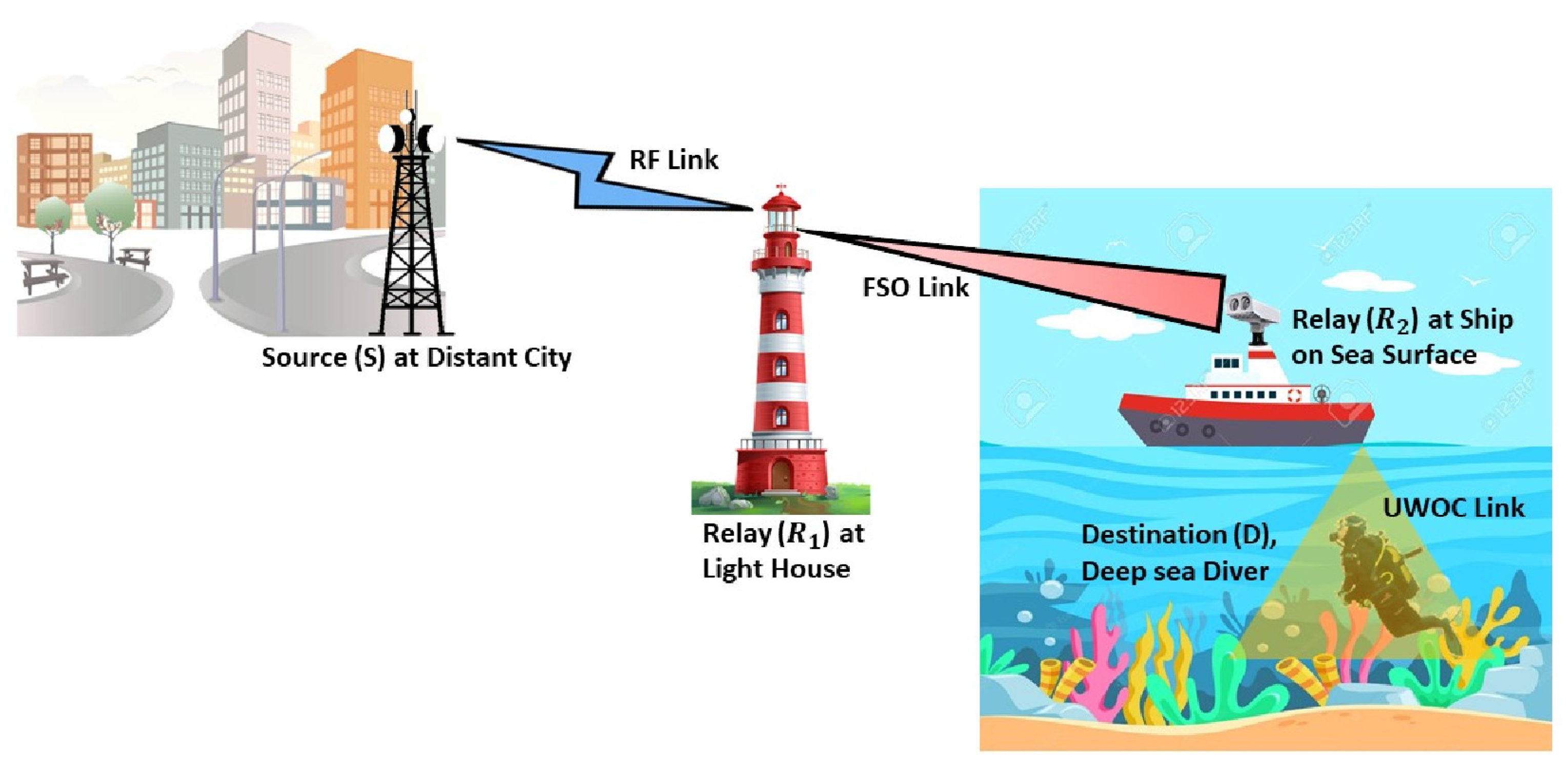
2. System Modeling
2.1. RF Link Modeling
2.2. FSO Link
2.3. UWOC Link Modeling
3. Outage Probability Analysis
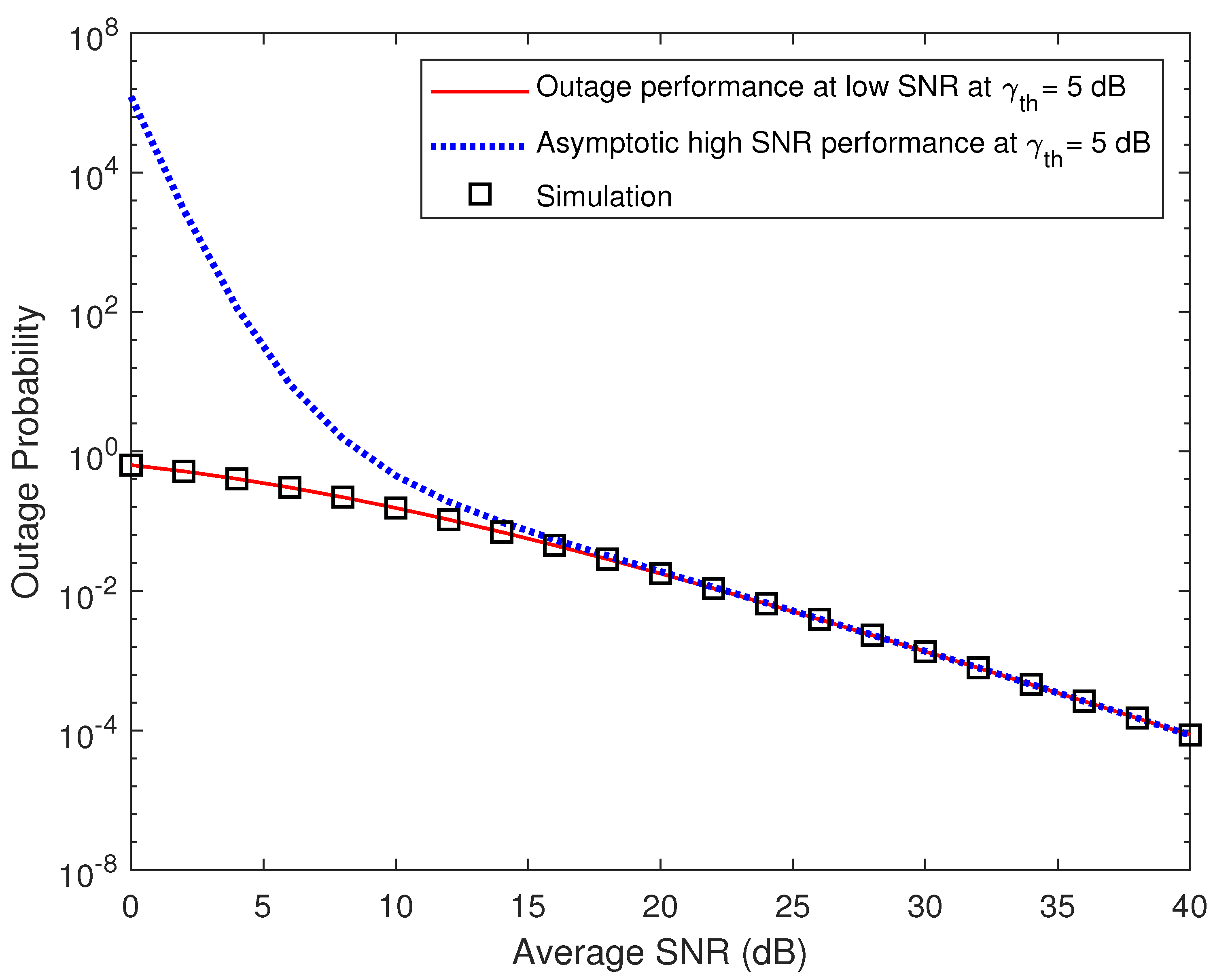
4. Asymptotic Analysis
4.1. RF Link
4.2. FSO Link
- to 6,
- .
4.3. UWOC Link
- Case 1: Among three links, when only one link is dominating, the coding gain can be written as
- Case 2: When two links are dominating out of three links, the coding gain can be written as
- Case 3: When all three links are dominating, then the coding gain can be written as
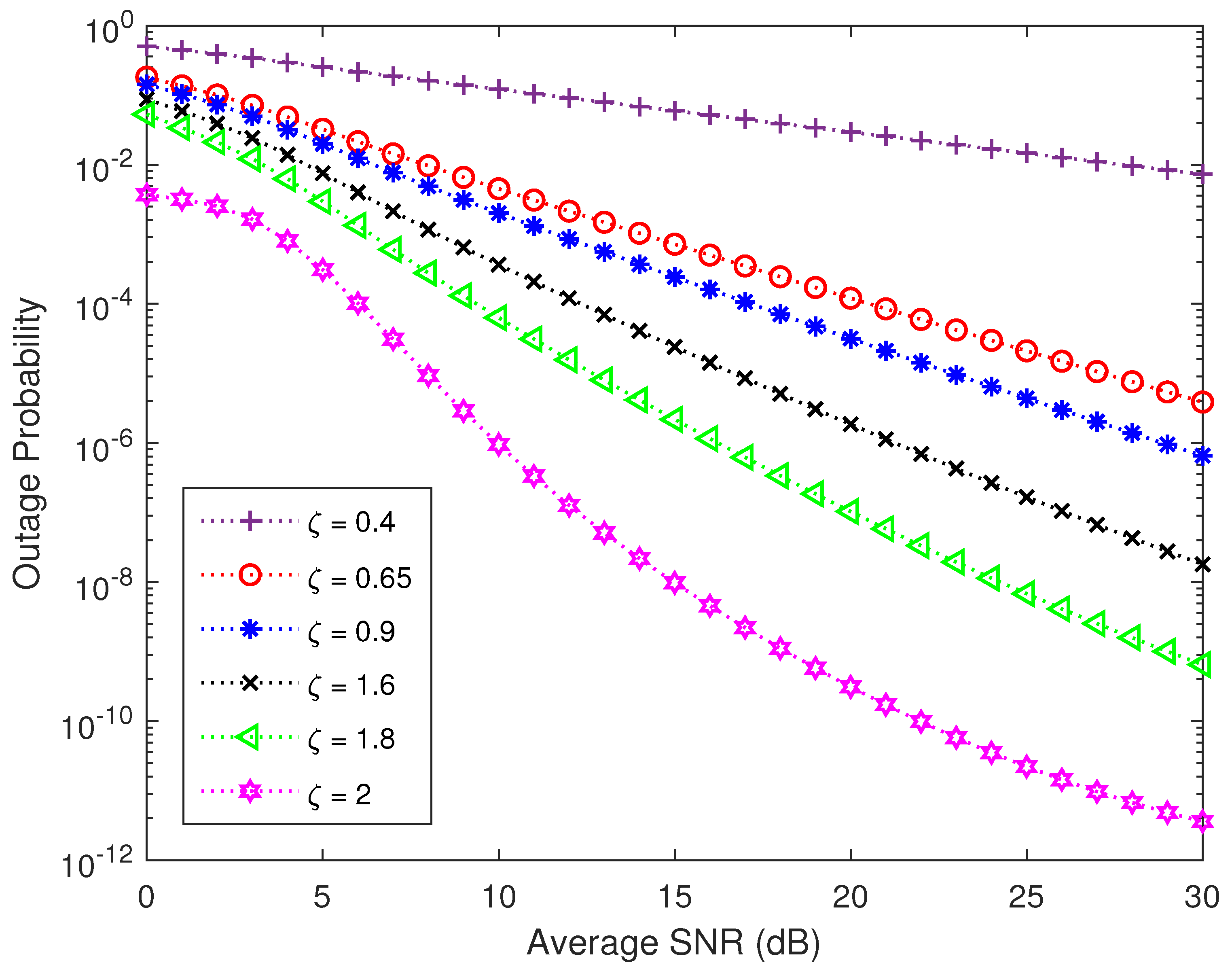
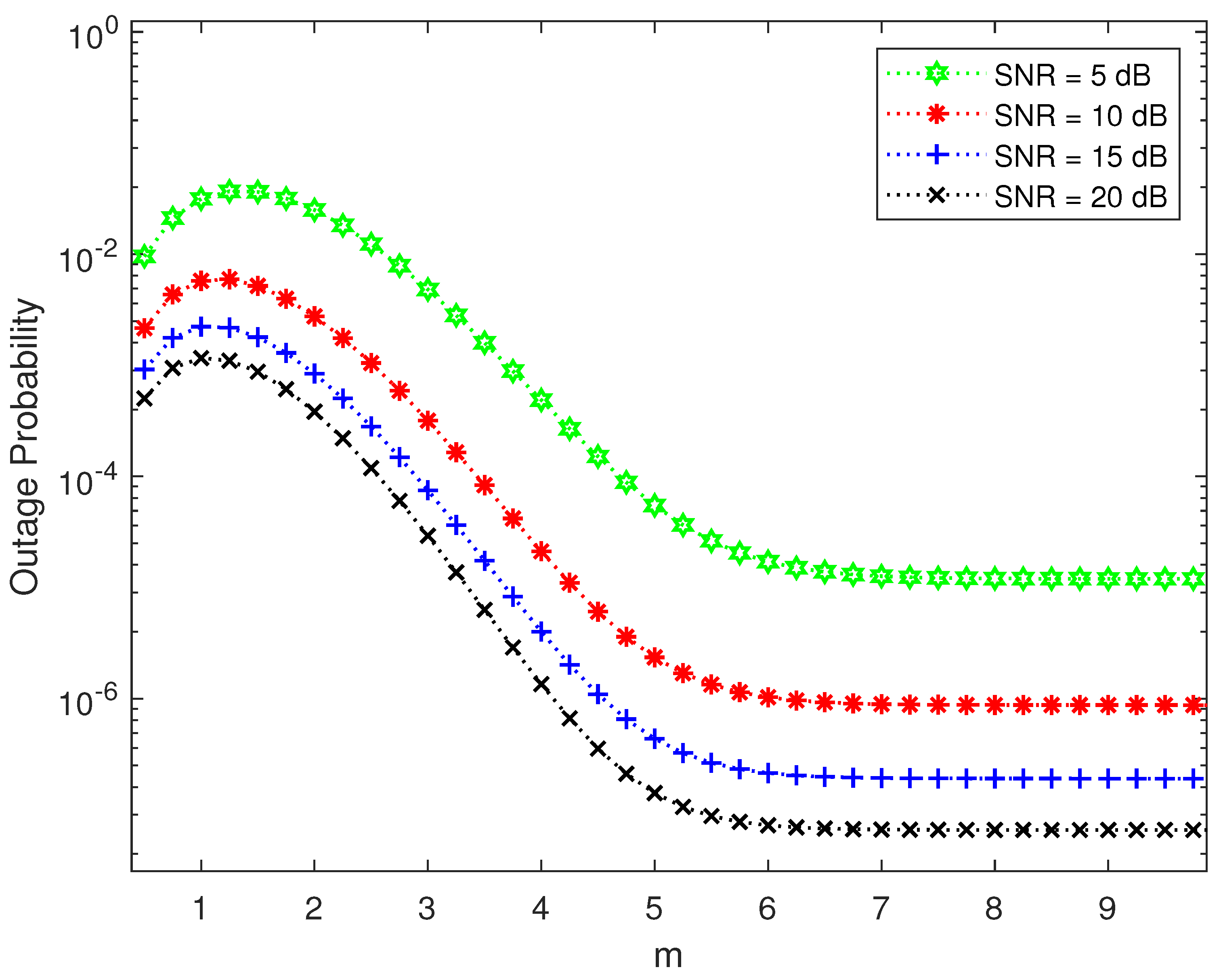
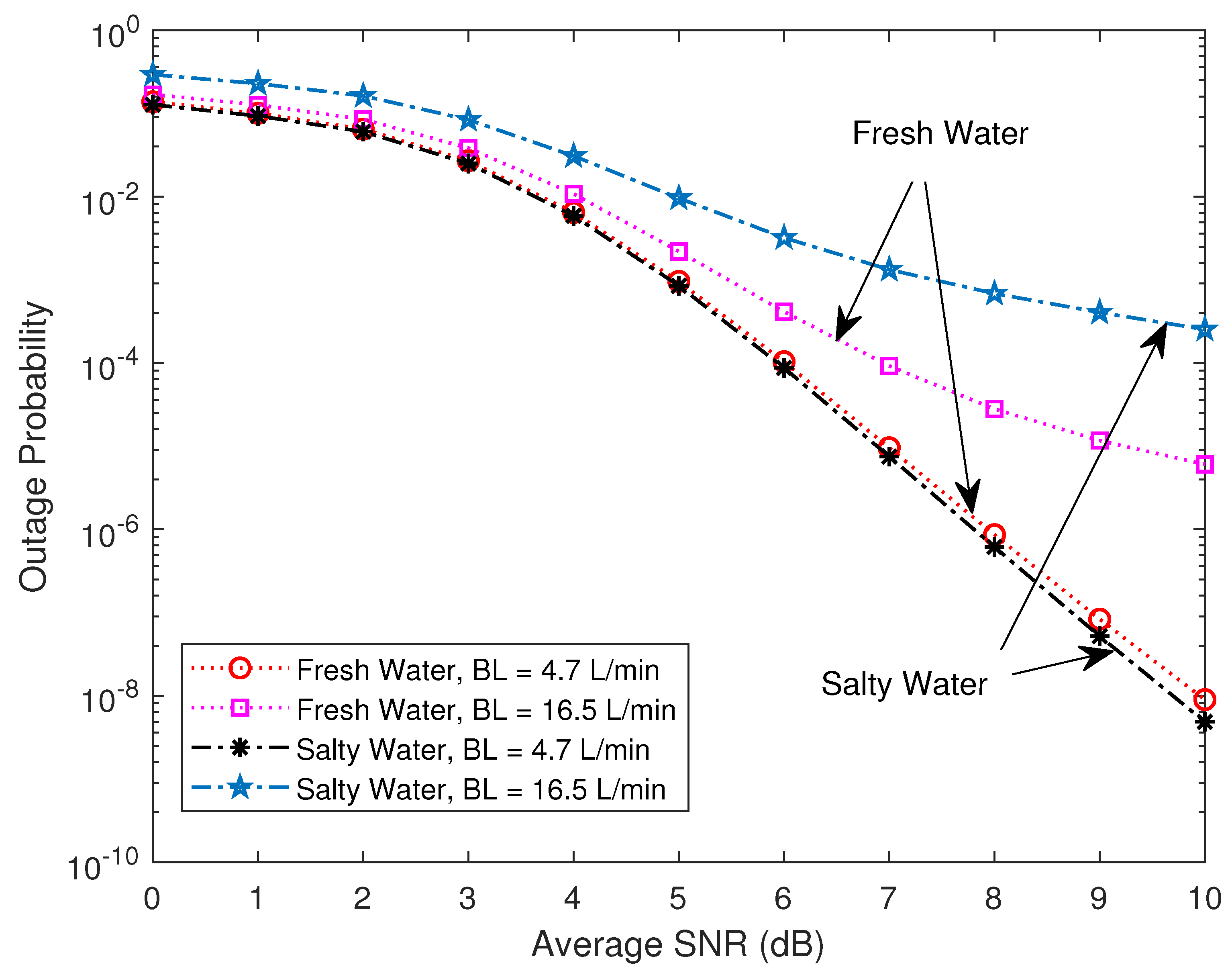
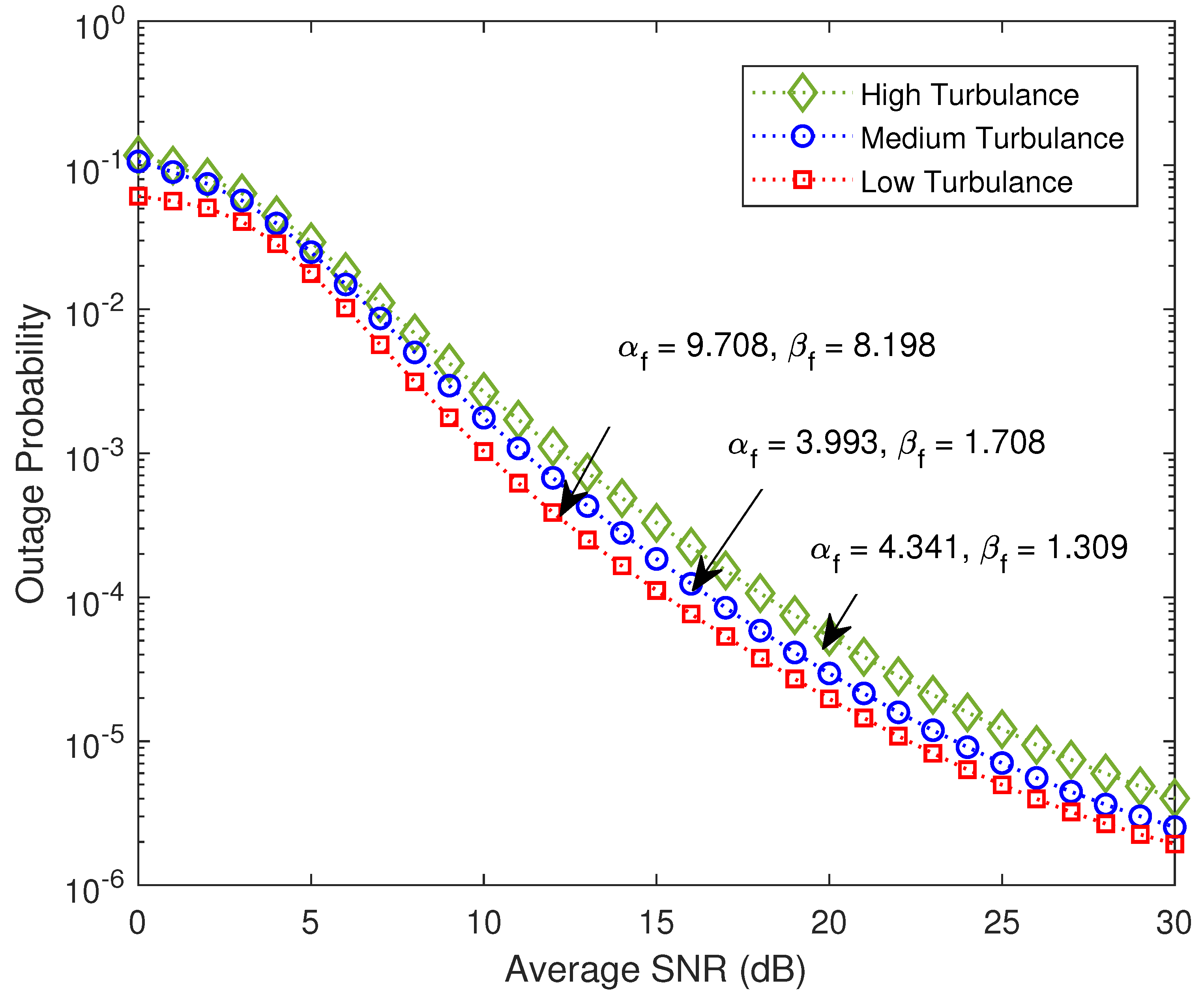
5. Numerical Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Soleimani-Nasab, E.; Uysal, M. Generalized Performance Analysis of Mixed RF/FSO Cooperative Systems. IEEE Trans. Wirel. Commun. 2016, 15, 714–727. [Google Scholar] [CrossRef]
- Al-Habash, A.; Andrews, L.C.; Philips, R.L. Mathematical model for the irradiance PDF of a laser beam propagating through turbulent media. Opt. Eng. J. 2001, 40, 1554–1562. [Google Scholar] [CrossRef]
- Khalighi, M.A.; Uysal, M. Survey on Free Space Optical Communication: A Communication Theory Perspective. IEEE Commun. Surv. Tutorials 2014, 16, 2231–2258. [Google Scholar] [CrossRef]
- Aggarwal, M.; Garg, P.; Puri, P. Analysis of subcarrier intensity modulation-based optical wireless DF relaying over turbulence channels with path loss and pointing error impairments. IET Commun. 2014, 8, 3170–3178. [Google Scholar] [CrossRef]
- Vats, A.; Aggarwal, M.; Ahuja, S. End-to-End Performance Analysis of Hybrid VLC-RF System using Decode and Forward Relay in E-Health Medical Applications. Opt.-Int. J. Electron Opt. 2019, 187, 297–310. [Google Scholar] [CrossRef]
- Khanna, H.; Aggarwal, M.; Ahuja, S. Performance analysis of a variable-gain amplify-and-forward relayed mixed RF-FSO system. Int. J. Commun. Syst. 2018, 31, e3400. [Google Scholar]
- Puri, P.; Garg, P.; Aggarwal, M.; Sharma, P.K. Multiple user pair scheduling in bi-directional single relay assisted FSO systems. In Proceedings of the 2014 IEEE International Conference on Communications (ICC), Sydney, Australia, 10–14 June 2014; pp. 3401–3405. [Google Scholar]
- Bag, B.; Das, A.; Ansari, I.S.; Prokes, A.; Bose, C.; Chandra, A. Performance Analysis of Hybrid FSO Systems Using FSO/RF-FSO Link Adaptation. IEEE Photonics J. 2018, 10, 7904417. [Google Scholar] [CrossRef]
- Lee, E.; Park, J.; Han, D.; Yoon, G. Performance Analysis of the Asymmetric Dual-Hop Relay Transmission With Mixed RF/FSO Links. IEEE Photonics Technol. Lett. 2011, 23, 1642–1644. [Google Scholar] [CrossRef]
- Shukla, N.K.; Mayet, A.M.; Vats, A.; Aggarwal, M.; Raja, R.K.; Verma, R.; Muqeet, M.A. High speed integrated RF–VLC data communication system: Performance constraints and capacity considerations. Phys. Commun. 2022, 50, 101492. [Google Scholar] [CrossRef]
- Zedini, E.; Ansari, I.; Alouini, M.-S. Performance analysis of mixed Nakagami-m and gamma–gamma dual-hop FSO transmission systems. IEEE Photonics J. 2015, 7, 1–20. [Google Scholar] [CrossRef]
- Ansari, I.S.; Yilmaz, F.; Alouini, M. Impact of Pointing Errors on the Performance of Mixed RF/FSO Dual-Hop Transmission Systems. IEEE Wirel. Commun. Lett. 2013, 2, 351–354. [Google Scholar] [CrossRef]
- Zedini, E.; Ansari, I.S.; Alouini, M. Unified performance analysis of mixed line of sight RF-FSO fixed gain dual-hop transmission systems. In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), New Orleans, LA, USA, 9–12 March 2015; pp. 46–51. [Google Scholar]
- Miridakis, N.I.; Matthaiou, M.; Karagiannidis, G.K. Multiuser Relaying over Mixed RF/FSO Links. IEEE Trans. Commun. 2014, 62, 1634–1645. [Google Scholar] [CrossRef]
- Anees, S.; Bhatnagar, M.R. Performance evaluation of decode-and-forward dual-hop asymmetric radio frequency free space optical communication system. IET Optoelectron. 2015, 9, 232–240. [Google Scholar] [CrossRef]
- Miridakis, N.I.; Matthaiou, M.; Karagiannidis, G.K. Multiuser dual-hop relaying over mixed RF/FSO links. In Proceedings of the IEEE International Conference on Communications (ICC), Sydney, NSW, Australia, 10–14 June 2014; pp. 3389–3394. [Google Scholar]
- Yang, L.; Yuan, J.; Liu, X.; Hasna, M.O. On the Performance of LAP-Based Multiple-Hop RF/FSO Systems. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 499–505. [Google Scholar] [CrossRef]
- Mamaghani, M.T.; Hong, Y. On the Performance of Low-Altitude UAV-Enabled Secure AF Relaying With Cooperative Jamming and SWIPT. IEEE Access 2019, 7, 153060–153073. [Google Scholar] [CrossRef]
- Hanson, F.; Radic, S. High bandwidth underwater optical communication. Appl. Opt. 2008, 47, 277–283. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Yang, L.; Costa, D. Performance Analysis of UAV-based Mixed RF/UWOC Transmission Systems. arXiv 2020, arXiv:2011.09062. [Google Scholar] [CrossRef]
- Anees, S.; Deka, R. On the Performance of DF Based Dual-Hop Mixed RF/UWOC System. In Proceedings of the IEEE 89th Vehicular Technology Conference (VTC2019-Spring), Kuala Lumpur, Malaysia, 28 April–1 May 2019; pp. 1–5. [Google Scholar]
- Yadav, S.; Vats, A.; Aggarwal, M.; Ahuja, S. Performance Analysis and Altitude Optimization of UAV-Enabled Dual-Hop Mixed RF-UWOC System. IEEE Trans. Veh. Technol. 2021, 70, 12651–12661. [Google Scholar] [CrossRef]
- Anees, S.; Bhatnagar, M.R. Performance of an Amplify-and-Forward Dual-Hop Asymmetric RF-FSO Communication System. IEEE Osa J. Opt. Commun. Netw. 2015, 7, 124–135. [Google Scholar] [CrossRef]
- Lei, H.; Zhang, Y.; Park, K.; Ansari, I.S.; Pan, G.; Alouini, M. On the Performance of Dual-Hop RF-UWOC System. In Proceedings of the IEEE International Conference on Communications Workshops (ICC Workshops), Dublin, Ireland, 7–11 June 2020; pp. 1–6. [Google Scholar]
- Illi, E.; El Bouanani, F.; da Costa, D.B.; Sofotasios, P.C.; Ayoub, F.; Mezher, K.; Muhaidat, S. Physical Layer Security of a Dual-Hop Regenerative Mixed RF/UOW System. IEEE Trans. Sustain. Comput. 2021, 6, 90–104. [Google Scholar] [CrossRef]
- Sarma, P.; Deka, R.; Anees, S. Performance Analysis of DF based Mixed Triple Hop RF-FSO-UWOC Cooperative System. In Proceedings of the IEEE 92nd Vehicular Technology Conference (VTC2020-Fall), Victoria, BC, Canada, 18 November–16 December 2020; pp. 1–5. [Google Scholar]
- Alouini, M.; Simon, M.K. Performance of coherent receivers with hybrid SC/MRC over Nakagami-m fading channels. IEEE Trans. Veh. Technol. 1999, 48, 1155–1164. [Google Scholar] [CrossRef]
- Shen, T.; Ochiai, H. A UAV-Enabled Wireless Powered Sensor Network Based on NOMA and Cooperative Relaying with Altitude Optimization. IEEE Open J. Commun. Soc. 2021, 2, 21–34. [Google Scholar] [CrossRef]
- Aggarwal, M.; Garg, P.; Puri, P. Exact MGF-Based Performance Analysis of Dual-Hop AF-Relayed Optical Wireless Communication Systems. J. Light. Technol. 2015, 33, 1913–1919. [Google Scholar] [CrossRef]
- Vaiopoulos, N.; Vavoulas, A.; Sandalidis, H.G. An assessment of a unmanned aerial vehicle-based broadcast scenario assuming random terrestrial user locations. IET Optoelectron. 2021, 15, 121–130. [Google Scholar] [CrossRef]
- Safi, H.; Dargahi, A.; Cheng, J.; Safari, M. Analytical Channel Model and Link Design Optimization for Ground-to-HAP Free-Space Optical Communications. J. Light. Technol. 2020, 38, 5036–5047. [Google Scholar] [CrossRef]
- The Mathematical Functions Site. Available online: http://functions.wolfram.com (accessed on 5 June 2022).
- Zedini, E.; Oubei, H.M.; Kammoun, A.; Hamdi, M.; Ooi, B.S.; Alouini, M. Unified Statistical Channel Model for Turbulence-Induced Fading in Underwater Wireless Optical Communication Systems. IEEE Trans. Commun. 2019, 67, 2893–2907. [Google Scholar] [CrossRef]
- Laneman, J.N.; Tse, D.N.C.; Wornell, G.W. Cooperative diversity in wireless networks: Efficient protocols and outage behavior. IEEE Trans. Inf. Theory 2004, 50, 3062–3080. [Google Scholar] [CrossRef]
- Ikki, S.S.; Aissa, S. A Study of Optimization Problem for Amplify-and-Forward Relaying over Weibull Fading Channels with Multiple Antennas. IEEE Commun. Lett. 2011, 15, 1148–1151. [Google Scholar] [CrossRef]
- Vats, A.; Aggarwal, M.; Ahuja, S. Outage and error analysis of three hop hybrid VLC/FSO/VLC–based relayed optical wireless communication system. Trans. Emerg. Telecommun. Tech. 2019, 30, e3544. [Google Scholar] [CrossRef]
- Zhong, C.; Wong, K.; Jin, S.; Alouini, M.; Ratnarajah, T. Asymptotic Analysis for Nakagami-m Fading Channels with Relay Selection. In Proceedings of the IEEE International Conference on Communications (ICC), Kyoto, Japan, 5–9 June 2011; pp. 1–5. [Google Scholar]
- Dale, M. The Algebra of Random Variables; Wiley: New York, NY, USA, 1979; Volume 1. [Google Scholar]
- Amer, M.; Al-Eryani, Y. Underwater optical communication system relayed by α − μ fading channel: Outage, capacity and asymptotic analysis. arXiv 2019, arXiv:1911.04243. [Google Scholar]

| 1. | RF | Radio frequency |
| 2. | FSO | Free space optics |
| 3. | UWOC | Underwater optical communication |
| 4. | EGG | Exponential generalized gamma |
| 5. | DF | Decode and forward |
| 6. | AF | Amplify and forward |
| 7. | LOS | Line-of-sight |
| 8. | IM/DD | Intensity modulation/direct detection |
| 9. | UAV | Unmanned aerial vehicle |
| 10. | AUV | Autonomous underwater vehicle |
| 11. | ABER | Average bit error rate |
| 12. | OP | Outage probability |
| 13. | CDF | Cumulative distribution function |
| 14. | Probability density function | |
| 15. | SNR | Signal-to-noise ratio |
| 16. | AOA | Angle-of-arrival |
| 1. | Relay 1, Relay 2 | |
| 2. | Angle-of-arrival fluctuations | |
| 3. | CDF of SNR of RF link | |
| 4. | PDF of SNR of RF link | |
| 5. | Average SNR of RF link | |
| 6. | Instantaneous SNR of the RF/FSO/UWOC link | |
| 7. | Upper incomplete Gamma function | |
| 8. | RF channel path loss | |
| 9. | Path loss exponent | |
| 10. | A | Constant related to the transmission environment and frequency of the RF information signal |
| 11. | Distance between source and relay 1 | |
| 12. | m | Nakagami-m fading parameter |
| 13. | K | Rician factor |
| 14. | Average SNR of FSO link | |
| 15. | Optical-to-electrical efficiency | |
| 16. | Source transmitted optical power | |
| 17. | Standard deviation of Gaussian noise | |
| 18. | Variance of Tx–Rx misalignment orientations | |
| 19. | Pointing error in FSO link | |
| 20. | Standard deviation of the pointing error displacement | |
| 21. | Equivalent beam width at the receiver | |
| 22. | Atmospheric turbulence parameters | |
| 23. | Standard Gamma function | |
| 24. | Error function | |
| 25. | Atmospheric path loss | |
| 26. | CDF of SNR of FSO link | |
| 27. | PDF of SNR of FSO link | |
| 28. | CDF of SNR of UWOC link | |
| 29. | PDF of SNR of UWOC link | |
| 30. | r | Constant for modulation and detection technique |
| 31. | Average SNR of the UWOC link | |
| 32. | Parameters associated with the EGG distribution of the UWOC link | |
| 32. | SNR of the received signal at destination node | |
| 33. | Instantaneous SNR of the RF, FSO and UWOC links resp. | |
| 34. | CDF of the end-to-end source to destination link | |
| 35. | Threshold SNR | |
| 36. | Outage probability of the system | |
| 37. | Outage probability of the system at high-SNR region | |
| 38. | Coding gain | |
| 39. | Diversity gain | |
| 40. | FSO link distance |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alhashim, H.H.; Mayet, A.M.; Shukla, N.K.; Birla, S.; Aggarwal, M.; Vats, A.; Kaushal, H.; Kuchhal, P.; Qaisi, R.M.A.; Sabherwal, P.; et al. An Insight to the Outage Performance of Multi-Hop Mixed RF/FSO/UWOC System. Photonics 2023, 10, 1010. https://doi.org/10.3390/photonics10091010
Alhashim HH, Mayet AM, Shukla NK, Birla S, Aggarwal M, Vats A, Kaushal H, Kuchhal P, Qaisi RMA, Sabherwal P, et al. An Insight to the Outage Performance of Multi-Hop Mixed RF/FSO/UWOC System. Photonics. 2023; 10(9):1010. https://doi.org/10.3390/photonics10091010
Chicago/Turabian StyleAlhashim, Hala H., Abdulilah Mohammad Mayet, Neeraj Kumar Shukla, Shilpi Birla, Mona Aggarwal, Anshul Vats, Hemani Kaushal, Piyush Kuchhal, Ramy Mohammed Aiesh Qaisi, Pooja Sabherwal, and et al. 2023. "An Insight to the Outage Performance of Multi-Hop Mixed RF/FSO/UWOC System" Photonics 10, no. 9: 1010. https://doi.org/10.3390/photonics10091010
APA StyleAlhashim, H. H., Mayet, A. M., Shukla, N. K., Birla, S., Aggarwal, M., Vats, A., Kaushal, H., Kuchhal, P., Qaisi, R. M. A., Sabherwal, P., & Muqeet, M. A. (2023). An Insight to the Outage Performance of Multi-Hop Mixed RF/FSO/UWOC System. Photonics, 10(9), 1010. https://doi.org/10.3390/photonics10091010






