Machine Learning for Self-Coherent Detection Short-Reach Optical Communications
Abstract
:1. Introduction
2. SCD Systems
2.1. VSB System
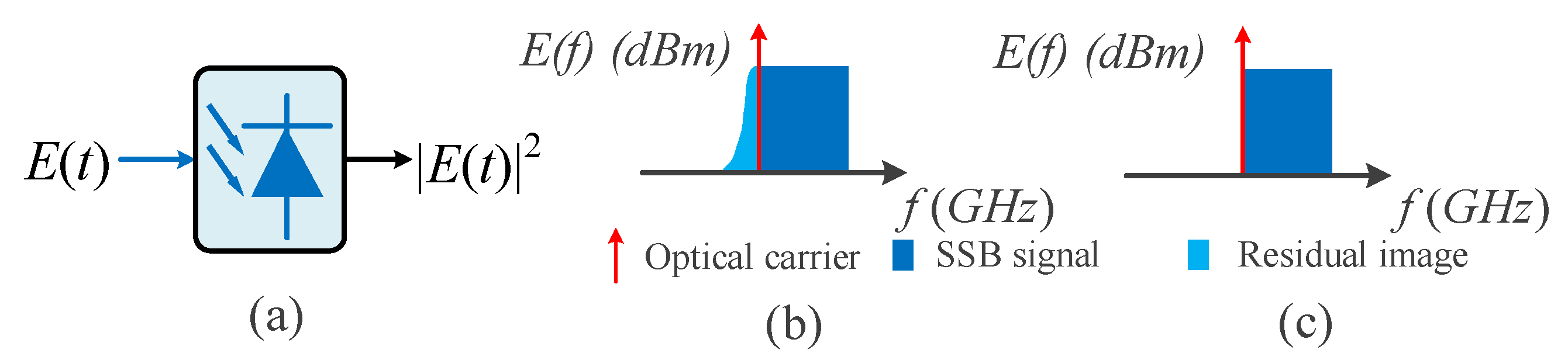
2.2. SSB System
2.3. PR Receiver
2.4. CADD
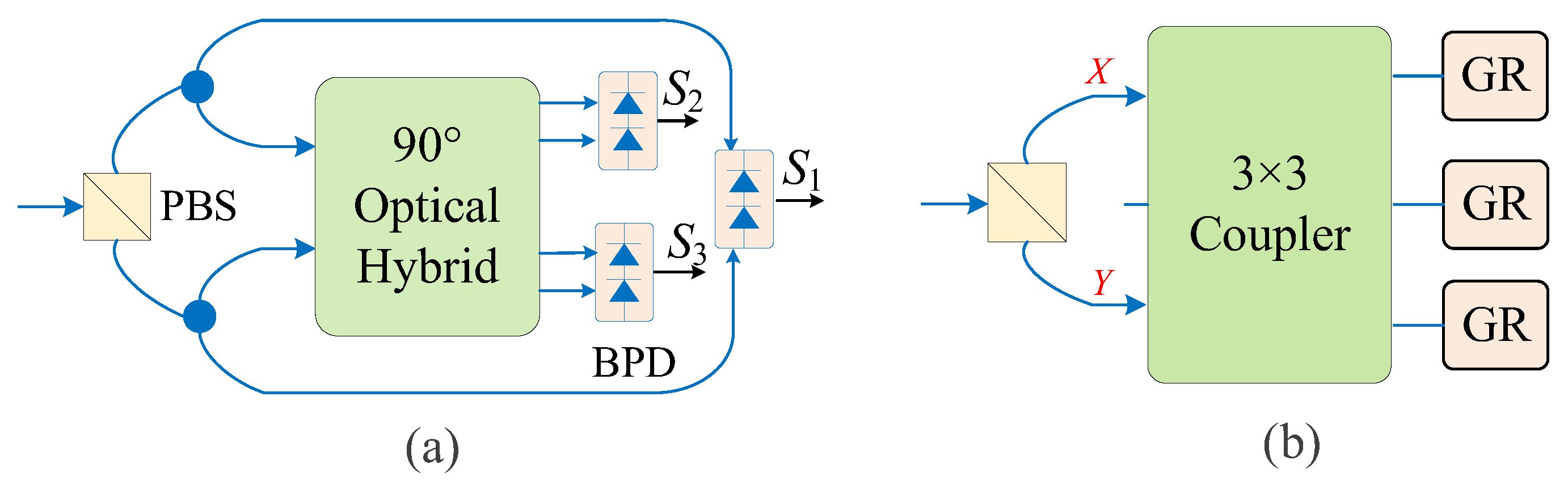
2.5. SVR
2.6. JSFR
3. ML Techniques in SCD System
3.1. Nonlinear Compensation
3.1.1. Fiber Nonlinearity
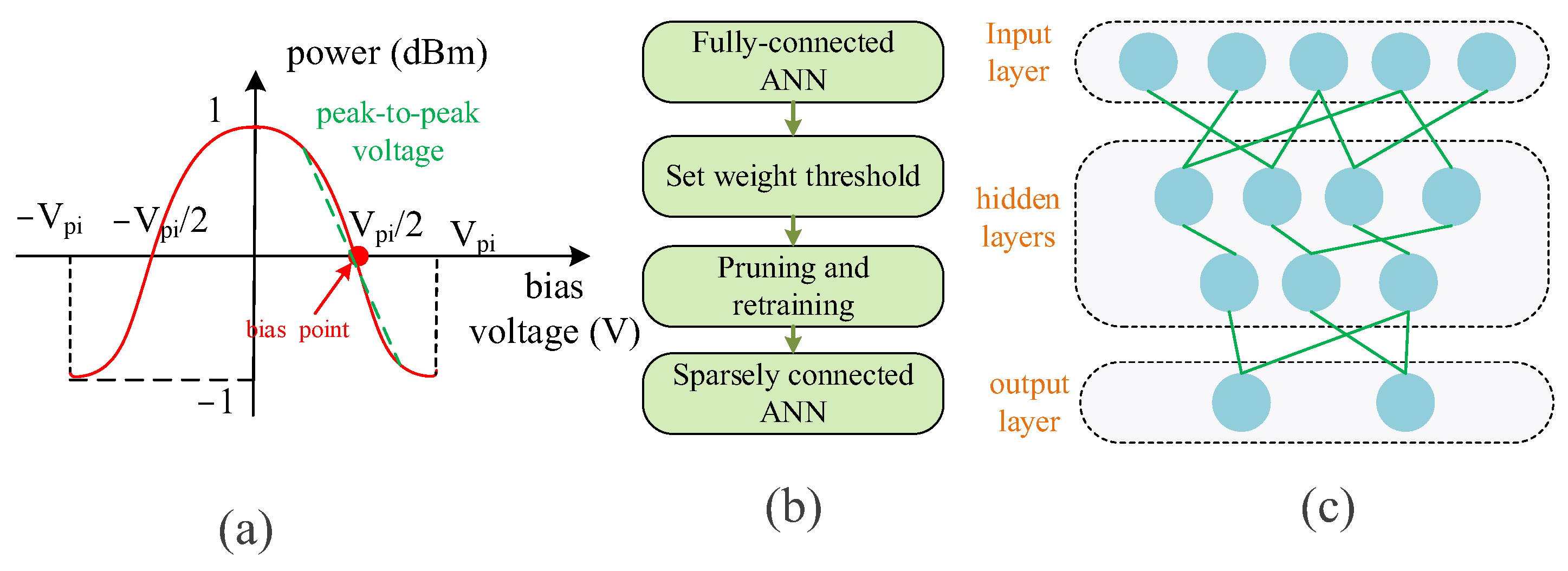
3.1.2. Device Nonlinearity
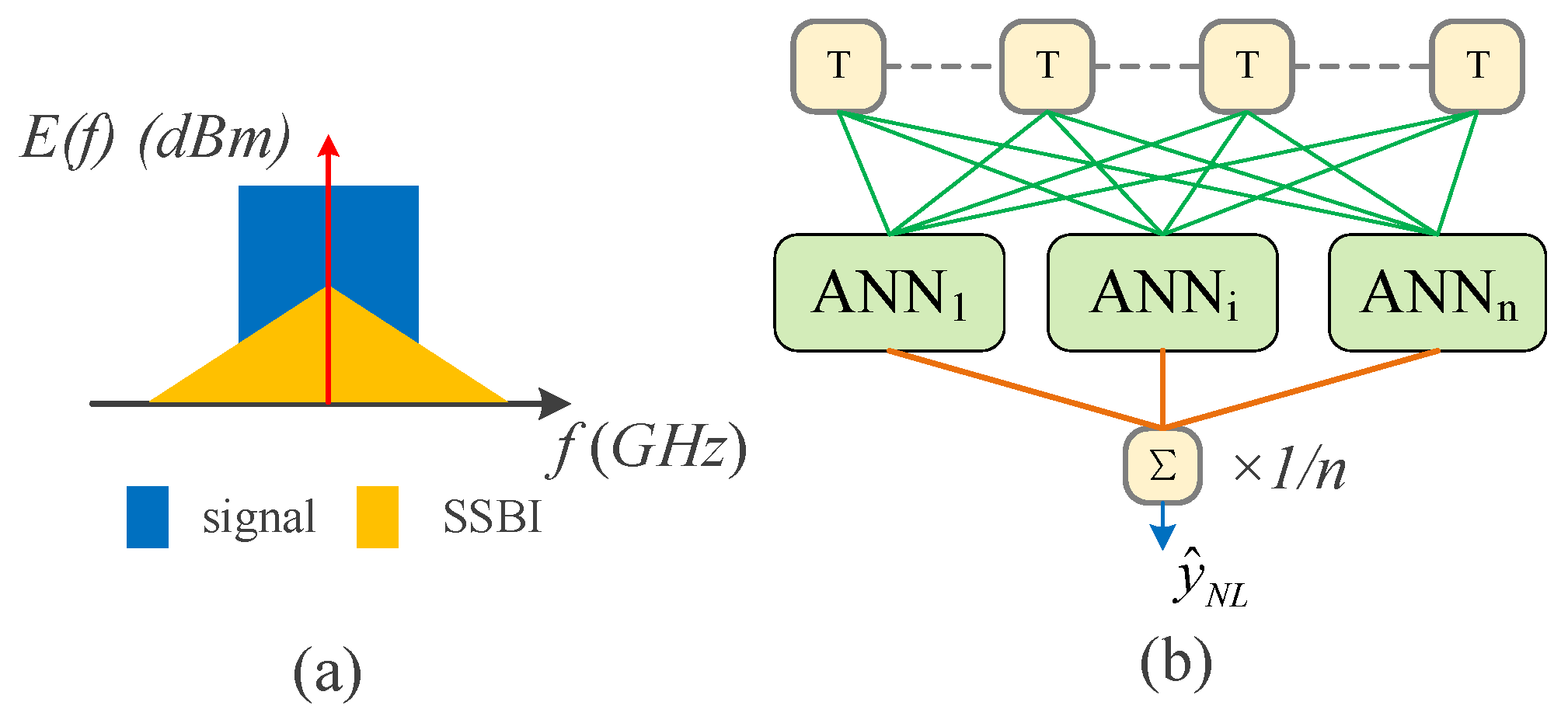
3.1.3. SSBI Cancellation
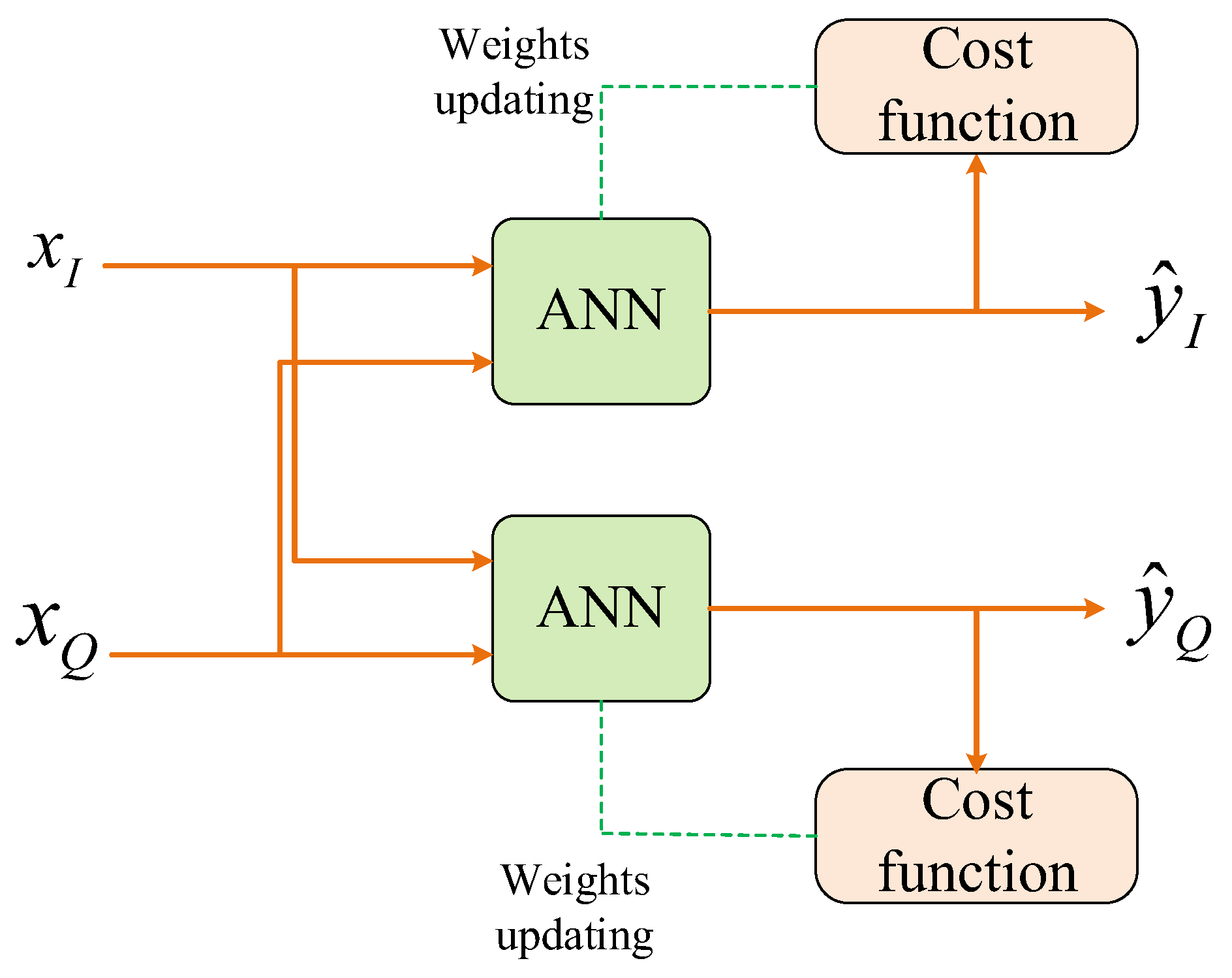
3.2. IQ Imbalance Correction
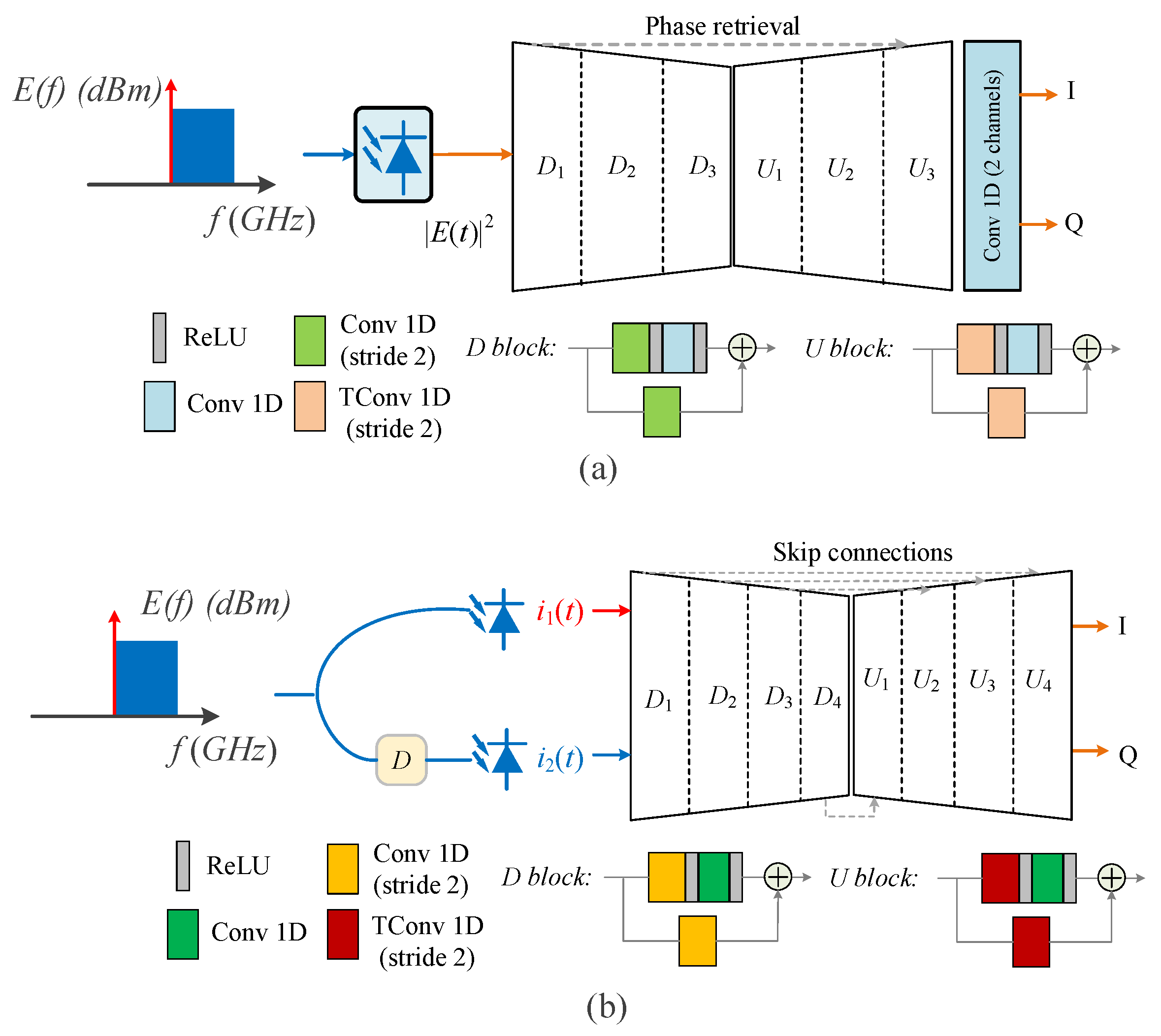
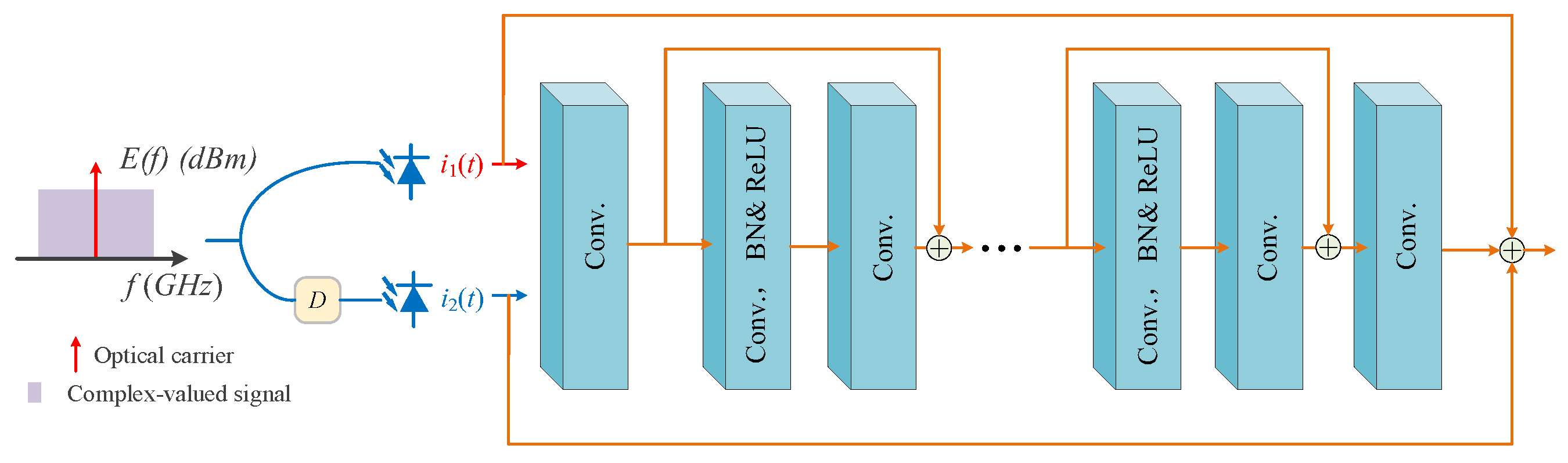
3.3. PR and Optical Field Recovery
3.4. Polarization Demultiplexing
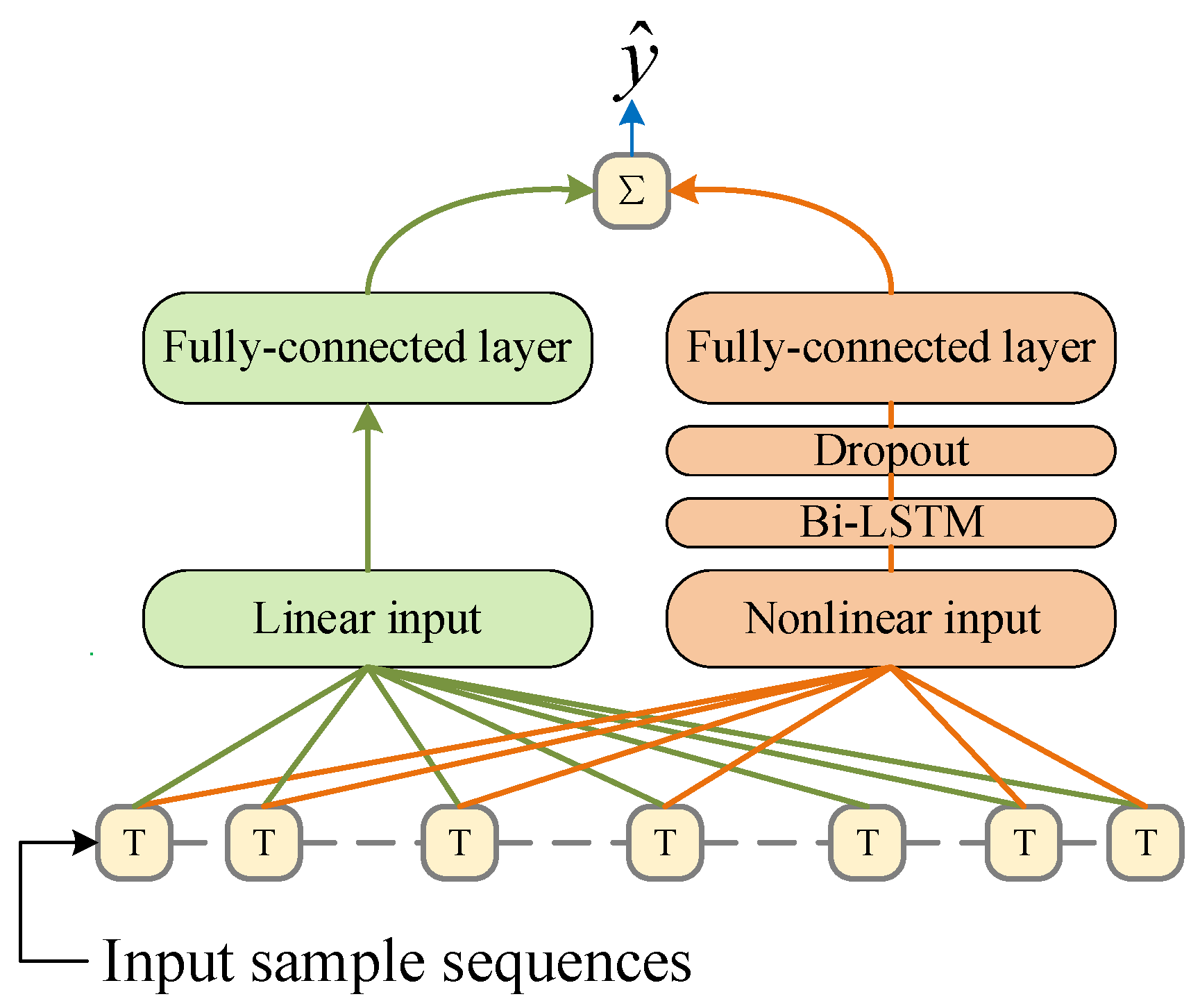
3.5. Fast Remodeling
3.6. Optical Signal Processing
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Abbreviation | Definition | Abbreviation | Definition |
|---|---|---|---|
| LO | Local oscillator | CD | Chromatic dispersion |
| DSP | Digital signal processing | IM-DD | Intensity modulation and direct detection |
| SE | Spectral efficiency | PD | Photodetector |
| VSB | Vestigial sideband | DSB | Double-sideband |
| PR | Phase retrieval | SSB | Single-sideband |
| CADD | Carrier-assisted differential detection | ASCD | Asymmetric self-coherent detection |
| SVR | Stokes-vector receiver | JSFR | Jones-space field recovery |
| SCD | Self-coherent detection | SSBI | Signal-to-signal beating interference |
| ML | Machine learning | ADC | Analog-to-digital converter |
| MZM | Mach–Zehnder modulator | NN | Neural network |
| CNN | Convolutional neural network | BPD | Balanced photodetector |
| CSPR | Carrier-to-signal power ratio | PBS | Polarization beam splitter |
| MIMO | Multi-input multi-output | GR | Generalized receiver |
| QAM | Quadrature amplitude modulation | NLSE | Nonlinear Schrödinger equation |
| ANN | Artificial neural network | LSTM | Long short-term memory network |
| RNN | Recurrent neural network | WDM | Wavelength-division-multiplexing |
| BER | Bit-error-rate | KK | Kramers–Kronig |
| ReLU | Rectified Linear Unit | TL | Transfer learning |
| RC | Reservoir computing | ROSS | Recurrent optical spectrum slicing |
| MZDI | Mach–Zehnder delay interferometer |
References
- Kikuchi, K. Fundamentals of Coherent Optical Fiber Communications. J. Light. Technol. 2016, 34, 157–179. [Google Scholar] [CrossRef]
- Cvijetic, M. Coherent and Nonlinear Lightwave Communications; Artech House: Boston, MA, USA, 2016; ISBN 13-978-0890065907. [Google Scholar]
- Batagelj, B.; Janyani, V.; Tomazic, S. Research challenges in optical communications towards 2020 and beyond. Inf. MIDEM 2014, 44, 177–184. [Google Scholar]
- Ip, E.M.; Kahn, J.M. Fiber Impairment Compensation Using Coherent Detection and Digital Signal Processing. J. Light. Technol. 2009, 28, 502–519. [Google Scholar] [CrossRef]
- Uzunidis, D.; Logothetis, M.; Stavdas, A.; Hillerkuss, D.; Tomkos, I. Fifty Years of Fixed Optical Networks Evolution: A Survey of Architectural and Technological Developments in a Layered Approach. Telecom 2022, 3, 619–674. [Google Scholar] [CrossRef]
- Savory, S.J.; Gavioli, G.; Killey, R.I.; Bayvel, P. Electronic compensation of chromatic dispersion using a digital coherent receiver. Opt. Express 2007, 15, 2120–2126. [Google Scholar] [CrossRef]
- Winzer, J.; Essiambr, R. Advanced Optical Modulation Formats. Proc. IEEE 2006, 94, 952–985. [Google Scholar] [CrossRef]
- Zhong, K.; Zhou, X.; Huo, J.; Yu, C.; Lu, C.; Lau, A.P.T. Digital Signal Processing for Short-Reach Optical Communications: A Review of Current Technologies and Future Trends. J. Light. Technol. 2018, 36, 377–400. [Google Scholar] [CrossRef]
- Wu, Q.; Zhu, Y.; Cheng, Z.; Yin, L.; Hu, W. Spectrally sliced heterodyne coherent receiver with halved electrical bandwidth. Chin. Opt. Lett. 2022, 20, 090601-1-090601-6. [Google Scholar] [CrossRef]
- Shieh, W.; Sun, C.; Ji, H. Carrier-assisted differential detection. Light. Sci. Appl. 2020, 9, 1–9. [Google Scholar] [CrossRef]
- Che, D.; Sun, C.; Shieh, W. Maximizing the spectral efficiency of Stokes vector receiver with optical field recovery. Opt. Express 2018, 26, 28976–28981. [Google Scholar] [CrossRef]
- Che, D.; Hu, Q.; Shieh, W. Linearization of Direct Detection Optical Channels Using Self-Coherent Subsystems. J. Light. Technol. 2016, 34, 516–524. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, J.; Li, X.; Wei, Y.; Wang, K.; Zhao, L.; Zhou, W.; Kong, M.; Pan, X.; Liu, B.; et al. 100 Gbit/s VSB-PAM-n IM/DD transmission system based on 10 GHz DML with optical filtering and joint nonlinear equalization. Opt. Express 2019, 27, 6098–6105. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Erkilinc, M.S.; Shi, K.; Sillekens, E.; Galdino, L.; Thomsen, B.C.; Bayvel, P.; Killey, R.I. SSBI Mitigation and the Kramers–Kronig Scheme in Single-Sideband Direct-Detection Transmission with Receiver-Based Electronic Dispersion Compensation. J. Light Technol. 2017, 35, 1887–1893. [Google Scholar] [CrossRef]
- Wu, Q.; Zhu, Y.; Hu, W. Low-complexity and Non-iterative SSBI Decomposition and Cancellation Algorithm for SSB Direct Detection System. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 6–10 March 2022; p. M2H.6. [Google Scholar]
- Bo, T.; Kim, B.; Yu, Y.; Kim, D.; Kim, H. Generation of Broadband Optical SSB Signal Using Dual Modulation of DML and EAM. J. Light Technol. 2021, 39, 3064–3071. [Google Scholar] [CrossRef]
- Bo, T.; Kim, H. Generalized model of optical single sideband generation using dual modulation of DML and EAM. Opt. Express 2020, 28, 28491–28501. [Google Scholar] [CrossRef]
- Chen, H.; Fontaine, N.K.; Gene, J.M.; Ryf, R.; Neilson, D.T.; Raybon, G. Dual Polarization Full-Field Signal Waveform Reconstruction Using Intensity Only Measurements for Coherent Communications. J. Light. Technol. 2020, 38, 2587–2597. [Google Scholar] [CrossRef]
- Gerchberg, R. A practical algorithm for the determination of phase from image and diffraction plane pictures. Optik 1972, 35, 237–246. [Google Scholar]
- Karar, A.; Falou, A.; Barakat, J.; Gürkan, Z.; Zhong, K. Recent Advances in Coherent Optical Communications for Short-Reach: Phase Retrieval Methods. Photonics 2023, 10, 308. [Google Scholar] [CrossRef]
- Wu, Q.; Zhu, Y.; Zhuge, Q.; Hu, W. Carrier-Assisted Phase Retrieval with Multiple Projections. J. Light. Technol. 2022, 36, 465–468. [Google Scholar] [CrossRef]
- Qin, P.; Bai, C.; Wang, Z.; Xu, H.; Yang, L.; Zhang, Y.; Ge, P.; Luo, X. Offset double sideband carrier assisted differential de-tection with field recovery at low carrier-to-signal power ratio. Opt. Express 2022, 30, 48112–48132. [Google Scholar] [CrossRef]
- Qin, P.; Bai, C.; Xu, H.; Yang, L.; Zhang, Y.; Luo, X.; Chi, X.; Zhang, R.; Li, P.; Wu, Y. Offset double-sideband signal field re-covery at low CSPR using filter-assisted direct detection. Opt. Express 2022, 30, 48112–48132. [Google Scholar] [CrossRef]
- Li, X.; O’sullivan, M.; Xing, Z.; Alam, S.; Mousa-Pasandi, M.E.; Plant, D.V. Asymmetric self-coherent detection. Opt. Express 2021, 29, 25412–25427. [Google Scholar] [CrossRef] [PubMed]
- Che, D.; Li, A.; Chen, X.; Hu, Q.; Wang, Y.; Shieh, W. Stokes Vector Direct Detection for Linear Complex Optical Channels. J. Light. Technol. 2015, 33, 678–684. [Google Scholar] [CrossRef]
- Kikuchi, K. Quantum Theory of Noise in Stokes Vector Receivers and Application to Bit Error Rate Analysis. J. Light. Technol. 2020, 38, 3164–3172. [Google Scholar] [CrossRef]
- Qian, D.; Cvijetic, N.; Hu, J.; Wang, T. 108 Gb/s OFDMA-PON with Polarization Multiplexing and Direct Detection. J. Light. Technol. 2009, 28, 484–493. [Google Scholar] [CrossRef]
- Ji, H.; Li, J.; Li, X.; Dong, S.; Xu, Z.; Su, Y.; Shieh, W. Complementary Polarization-Diversity Coherent Receiver for Self-Coherent Homodyne Detection with Rapid Polarization Tracking. J. Light. Technol. 2022, 40, 2773–2779. [Google Scholar] [CrossRef]
- Wu, Q.; Zhu, Y.; Zhuge, Q.; Hu, W. Dual-Carrier-Assisted Phase Retrieval for Polarization Division Multiplexing. J. Light. Technol. 2022, 40, 7297–7306. [Google Scholar] [CrossRef]
- Wu, Q.; Zhu, Y.; Jiang, H.; Zhuge, Q.; Hu, W. Optical Field Recovery in Jones Space. J. Light. Technol. 2022, 41, 66–74. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–16 December 2012; pp. 1097–1105. [Google Scholar]
- Otter, D.W.; Medina, J.R.; Kalita, J.K. A Survey of the Usages of Deep Learning for Natural Language Processing. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 604–624. [Google Scholar] [CrossRef]
- Richens, J.; Lee, C.; Johri, S. Improving the accuracy of medical diagnosis with causal machine learning. Nat. Commun. 2022, 11, 3923. [Google Scholar] [CrossRef]
- Musumeci, F.; Rottondi, C.; Nag, A.; Macaluso, I.; Zibar, D.; Ruffini, M.; Tornatore, M. An Overview on Application of Machine Learning Techniques in Optical Networks. IEEE Commun. Surv. Tutor. 2018, 21, 1383–1408. [Google Scholar] [CrossRef]
- Rottondi, C.; Barletta, L.; Giusti, A.; Tornatore, M. Machine-learning method for quality of transmission prediction of unes-tablished lightpaths. J. Opt. Commun. Netw. 2018, 10, A286. [Google Scholar] [CrossRef]
- Khan, F.N.; Zhou, Y.; Lau, A.P.T.; Lu, C. Modulation format identification in heterogeneous fiber-optic networks using artificial neural networks. Opt. Express 2012, 20, 12422–12431. [Google Scholar] [CrossRef] [PubMed]
- Saif, W.S.; Esmail, M.A.; Ragheb, A.M.; Alshawi, T.A.; Alshebeili, S.A. Machine Learning Techniques for Optical Performance Monitoring and Modulation Format Identification: A Survey. IEEE Commun. Surv. Tutor. 2020, 22, 2839–2882. [Google Scholar] [CrossRef]
- Eriksson, T.A.; Bulow, H.; Leven, A. Applying Neural Networks in Optical Communication Systems: Possible Pitfalls. IEEE Photon-Technol. Lett. 2017, 29, 2091–2094. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, W.; Zou, D.; Ni, W.; Luo, D.; Li, F. Real-Valued Neural Network Nonlinear Equalization for Long-Reach PONs Based on SSB Modulation. IEEE Photon-Technol. Lett. 2022, 35, 167–170. [Google Scholar] [CrossRef]
- Xu, Z.; Ji, H.; Yang, Y.; Qiao, G.; Wu, Q.; Li, J.; Lu, W.; Liu, L.; Wang, S.; Wei, J.; et al. Mixed-Precision Integer-Arithmetic-Only Neural Network-Based Equalizers for DML-Based Short-Reach IM/DD Systems. In Proceedings of the 2023 European Conference on Optical Communication (ECOC), Glasgow, Scotland, 1–5 October 2023; p. Th.A.3.4. [Google Scholar]
- Xu, Z.; Dong, S.; Manton, J.H.; Shieh, W. Low-Complexity Multi-Task Learning Aided Neural Networks for Equalization in Short-Reach Optical Interconnects. J. Light. Technol. 2021, 40, 45–54. [Google Scholar] [CrossRef]
- Giacoumidis, E. Blind Nonlinearity Equalization by Machine Learning based Clustering for Single-and Multi-Channel Coherent Optical OFDM. J. Light. Technol. 2018, 36, 721–727. [Google Scholar] [CrossRef]
- Zibar, D.; Piels, M.; Jones, R.; Schaeffer, C.G. Machine Learning Techniques in Optical Communication. J. Light. Technol. 2016, 34, 1442–1452. [Google Scholar] [CrossRef]
- Lu, X.; Qiao, L.; Zhou, Y.; Yu, W.; Chi, N. An I-Q-Time 3-dimensional post-equalization algorithm based on DBSCAN of machine learning in CAP VLC system. Opt. Commun. 2019, 430, 299–303. [Google Scholar] [CrossRef]
- Nguyen, T.; Mhatli, S.; Giacoumidis, E.; Van Compernolle, L.; Wuilpart, M.; Mégret, P. Fiber Nonlinearity Equalizer Based on Support Vector Classification for Coherent Optical OFDM. IEEE Photon-J. 2016, 8, 2. [Google Scholar] [CrossRef]
- Giacoumidis, E.; Mhatli, S.; Stephens, M.F.; Tsokanos, A.; Wei, J.; McCarthy, M.E.; Doran, N.J.; Ellis, A.D. Reduction of Non-linear Inter-Subcarrier Intermixing in Coherent Optical OFDM by a Fast Newton-based Support Vector Machine Nonlinear Equalizer. J. Light. Technol. 2017, 35, 2391–2397. [Google Scholar] [CrossRef]
- Chagnon, M.; Karanov, B.; Schmalen, L. Experimental demonstration of a dispersion tolerant end-to-end deep learning-based im-dd transmission system. In Proceedings of the European Conference on Optical Communication (ECOC), Roma, Italy, 23–27 September 2018; pp. 1–3. [Google Scholar]
- Katumba, A.; Yin, X.; Dambre, J.; Bienstman, P. A Neuromorphic Silicon Photonics Nonlinear Equalizer for Optical Com-Munications with Intensity Modulation and Direct Detection. J. Light. Technol. 2019, 37, 2232–2239. [Google Scholar] [CrossRef]
- Haigh, P.A.; Ghassemlooy, Z.; Rajbhandari, S.; Papakonstantinou, I.; Popoola, W. Visible Light Communications: 170 Mb/s Using an Artificial Neural Network Equalizer in a Low Bandwidth White Light Configuration. J. Light. Technol. 2014, 32, 1807–1813. [Google Scholar] [CrossRef]
- Tanimura, T.; Hoshida, T.; Kato, T.; Watanabe, S.; Morikawa, H. Data-analytics-based optical performance monitoring technique for optical transport networks. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 11–15 March 2018; p. Tu3E.3. [Google Scholar]
- Xu, Z.; Sun, C.; Manton, J.H.; Shieh, W. Joint Equalization of Linear and Nonlinear Impairments for PAM4 Short-Reach Direct Detection Systems. IEEE Photon-Technol. Lett. 2021, 33, 425–428. [Google Scholar] [CrossRef]
- You, Y.; Jiang, Z.; Janz, C. Machine Learning-Based EDFA Gain Model. In Proceedings of the 2018 European Conference on Optical Communication (ECOC), Rome, Italy, 23–27 September 2018; pp. 1–3. [Google Scholar]
- Morais, R.M.; Pedro, J. Machine Learning Models for Estimating Quality of Transmission in DWDM Networks. J. Opt. Commun. Netw. 2018, 10, D84–D99. [Google Scholar] [CrossRef]
- Yankov, M.; Ros, F.; Moura, U.; Carena, A.; Zibar, D. Flexible Raman Amplifier Optimization Based on Machine Learn-ing-Aided Physical Stimulated Raman Scattering Model. J. Light. Technol. 2017, 35, 1887–1893. [Google Scholar]
- Panayiotou, T.; Savva, G.; Shariati, B.; Tomkos, I.; Ellinas, G. Machine learning for QoT estimation of unseen optical network states. In Proceedings of the Optical Fiber Communication Conference 2019, San Diego, CA, USA, 3–7 March 2019; p. Tu2E.2. [Google Scholar]
- Jimenez, T.; Aguado, J.C.; de Miguel, I.; Duran, R.J.; Angelou, M.; Merayo, N.; Fernandez, P.; Lorenzo, R.M.; Tomkos, I.; Abril, E.J. A Cognitive Quality of Transmission Estimator for Core Optical Networks. J. Light. Technol. 2013, 31, 942–951. [Google Scholar] [CrossRef]
- Xu, Z.; Sun, C.; Ji, T.; Ji, H.; Manton, J.; Shieh, W. Cascade Recurrent Neural Network Enabled 100-Gb/s PAM4 Short-Reach Optical Link Based on DML. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 8–12 March 2020; p. W2A.45. [Google Scholar]
- Sambo, N.; Pointurier, Y.; Cugini, F.; Valcarenghi, L.; Castoldi, P.; Tomkos, I. Light path Establishment Assisted by Offline QoT Estimation in Transparent Optical Networks. J. Opt. Commun. Netw. 2010, 2, 928–937. [Google Scholar] [CrossRef]
- Seve, E.; Pesic, J.; Delezoide, C.; Bigo, S.; Pointurier, Y. Learning process for reducing uncertainties on network parameters and design margins. J. Opt. Commun. Netw. 2018, 10, A298–A306. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, M.; Li, J.; Li, Z.; Li, J.; Song, C.; Chen, X. Intelligent constellation diagram analyzer using convolutional neural network-based deep learning. Opt. Express 2017, 25, 17150–17166. [Google Scholar] [CrossRef] [PubMed]
- Musumeci, F.; Rottondi, C.E.M.; Corani, G.; Shahkarami, S.; Cugini, F.; Tornatore, M. A Tutorial on Machine Learning for Failure Management in Optical Networks. J. Light. Technol. 2019, 37, 4125–4139. [Google Scholar] [CrossRef]
- Varughese, S.; Lippiatt, D.; Richter, T.; Tibuleac, S.; Ralph, S.E. Identification of Soft Failures in Optical Links Using Low Complexity Anomaly Detection. In Proceedings of the Optical Fiber Communication Conference (OFC) 2019, San Diego, CA, USA, 3–7 March 2019; p. W2A.46. [Google Scholar]
- Shahkarami, S.; Musumeci, F.; Cugini, F.; Tornatore, M. Machine-Learning-Based Soft-Failure Detection and Identification in Optical Networks. In Proceedings of the Optical Fiber Communications Conference and Exposition (OFC 2018), San Diego, CA, USA, 11–15 March 2018; pp. 1–3. [Google Scholar] [CrossRef]
- Khan, F.N.; Fan, Q.; Lu, C.; Lau, A.P.T. An Optical Communication’s Perspective on Machine Learning and Its Applications. J. Light. Technol. 2019, 37, 493–516. [Google Scholar] [CrossRef]
- Vela, A.P.; Ruiz, M.; Fresi, F.; Sambo, N.; Cugini, F.; Meloni, G.; Poti, L.; Velasco, L.; Castoldi, P. BER Degradation Detection and Failure Identification in Elastic Optical Networks. J. Light. Technol. 2017, 35, 4595–4604. [Google Scholar] [CrossRef]
- Qin, P.; Bai, C.; Qi, Q.; Xu, H.; Yang, F.; Li, P.; Zhang, Y. Analytical Study and Noise Mitigation for Complex-Valued Optical DSB Transmission with Carrier-Assisted Differential Detection Receiver. IEEE Access 2023, 11, 31443–31455. [Google Scholar] [CrossRef]
- Zhang, K.; Fan, Y.; Ye, T.; Tao, Z.; Oda, S.; Tanimura, T.; Akiyama, Y.; Hoshida, T. Fiber nonlinear noise-to-signal ratio esti-mation by machine learning. In Proceedings of the Optical Fiber Communication Conference (OFC) 2019, San Diego, CA, USA, 3–7 March 2019; p. Th2A.45. [Google Scholar]
- Schaedler, M.; Kuschnerov, M.; Pachnicke, S.; Bluemm, C.; Pittala, F.; Changsong, X. Subcarrier Power Loading for Coherent Optical OFDM optiMized by Machine Learning. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 3–7 March 2019. [Google Scholar]
- Wang, C.; Fu, S.; Xiao, Z.; Tang, M.; Liu, D. Long Short-Term Memory Neural Network (LSTM-NN) Enabled Accurate Optical Signal-to-Noise Ratio (OSNR) Monitoring. J. Light. Technol. 2019, 37, 4140–4146. [Google Scholar] [CrossRef]
- Kamalov, V.; Jovanovski, L.; Vusirikala, V.; Zhang, S.; Yaman, F.; Nakamura, K.; Inoue, T.; Mateo, E.; Inada, Y. Evolution from 8QAM live Traffic to PS 64-QAM with Neural-Network Based Nonlinearity Compensation on 11000 km Open Subsea Cable. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 11–15 March 2018. [Google Scholar]
- Wang, Z.; Yang, A.; Guo, P.; He, P. OSNR and nonlinear noise power estimation for optical fiber communication systems using LSTM based deep learning technique. Opt. Express 2018, 26, 21346–21357. [Google Scholar] [CrossRef]
- Jones, R.; Eriksson, T.; Yankov, M.; Zibar, D. Deep Learning of Geometric Constellation Shaping Including Fiber Nonlinearities. In Proceedings of the 2018 European Conference on Optical Communication (ECOC), Rome, Italy, 23–27 September 2018; pp. 1–3. [Google Scholar]
- Jones, R.; Yankov, M.; Zibar, D. End-to-end learning for GMI optimized geometric constellation shape. In Proceedings of the 2018 European Conference on Optical Communication (ECOC), Dublin, Ireland, 22–26 September 2019; pp. 1–3. [Google Scholar]
- Khan, F.N.; Zhong, K.; Zhou, X.; Al-Arashi, W.H.; Yu, C.; Lu, C.; Lau, A.P.T. Joint OSNR monitoring and modulation format identification in digital coherent receivers using deep neural networks. Opt. Express 2017, 25, 17767–17776. [Google Scholar] [CrossRef]
- Jarajreh, M.A.; Giacoumidis, E.; Aldaya, I.; Le, S.T.; Tsokanos, A.; Ghassemlooy, Z.; Doran, N.J. Artificial Neural Network Nonlinear Equalizer for Coherent Optical OFDM. IEEE Photon-Technol. Lett. 2015, 27, 387–390. [Google Scholar] [CrossRef]
- Khan, F.N.; Yu, Y.; Tan, M.C.; Yu, C.; Lau, A.P.T.; Lu, C. Simultaneous OSNR monitoring and modulation format identification using asynchronous single channel sampling. In Proceedings of the Asia Communications and Photonics Conference 2015, Hong Kong, China, 19–23 November 2015; p. AS4F.6. [Google Scholar]
- Tanimura, T.; Hoshida, T.; Kato, T.; Watanabe, S.; Morikawa, H. Convolutional Neural Network-Based Optical Performance Monitoring for Optical Transport Networks. J. Opt. Commun. Netw. 2019, 11, A52–A59. [Google Scholar] [CrossRef]
- Antonelli, C.; Mecozzi, A.; Shtaif, M.; Chen, X.; Chandrasekhar, S.; Winzer, P.J. Kramers-Kronig coherent receiver. Optica 2016, 3, 1220–1227. [Google Scholar] [CrossRef]
- Bo, T.; Kim, H. Kramers-Kronig receiver operable without digital upsampling. Opt. Express 2018, 26, 13810–13818. [Google Scholar] [CrossRef] [PubMed]
- Bo, T.; Kim, H. Toward Practical Kramers-Kronig Receiver: Resampling, Performance, and Implementation. J. Light. Technol. 2018, 37, 461–469. [Google Scholar] [CrossRef]
- Ming, H.; Zhang, L.; Yang, F.; Ruan, X.; Zhang, F. High-speed SSB transmission with a silicon MZM and a soft combined artificial neural network-based equalization. Opt. Lett. 2020, 45, 2066–2069. [Google Scholar] [CrossRef] [PubMed]
- Wu, Q.; Li, X.; Zhu, Y.; Chen, C.; Xu, Z.; Li, J.; He, Z.; Hu, W. Single-Wavelength Net 1 Tb/s Transmission in SMF and 6.4 Tb/s in Weakly-Coupled 7-Core MCF Using a Phase-and Polarization-Diverse Direct Detection Receiver in Jones spacey. In Proceedings of the 2023 OptoElectronics and Communications Conference (OECC), Shanghai, China, 2–6 July 2023. [Google Scholar]
- Li, X.; An, S.; Ji, H.; Li, J.; Shieh, W.; Su, Y. Deep-learning-enabled high-performance full-field direct detection with dispersion diversity. Opt. Express 2022, 30, 11767–11788. [Google Scholar] [CrossRef]
- Li, X.; Li, J.; An, S.; Liu, H.; Shieh, W.; Su, Y. Deep-learning-enabled Direct Detection with Reduced Computational Complexity and High Electrical-spectral-efficiency. J. Light. Technol. 2023, 41, 5495–5502. [Google Scholar] [CrossRef]
- Wu, Q.; Zhu, Y.; Jiang, H.; Fu, M.; Zhang, Y.; Zhuge, Q.; Hu, W. Four-dimensional direct detection with Jones space optical full field recovery. arXiv 2022, arXiv:2212.14587. [Google Scholar]
- Wan, Z.; Li, J.; Shu, L.; Luo, M.; Li, X.; Fu, S.; Xu, K. Nonlinear equalization based on pruned artificial neural networks for 112-Gb/s SSB-PAM4 transmission over 80-km SSMF. Opt. Express 2018, 26, 10631–10642. [Google Scholar] [CrossRef]
- Fang, X.; Chen, X.; Yang, F.; Zhang, L.; Zhang, F. 6.4Tb/s SSB WDM Transmission Over 320km SSMF with Linear Network-Assisted LSTM. Photonic. Tech. Lett. 2021, 33, 1407–1410. [Google Scholar] [CrossRef]
- An, S.; Zhu, Q.; Li, J.; Ling, Y.; Su, Y. 112-Gb/s SSB 16-QAM signal transmission over 120-km SMF with direct detection using a MIMO-ANN nonlinear equalizer. Opt. Express 2019, 27, 12794–12805. [Google Scholar] [CrossRef]
- Orsuti, D.; Antonelli, C.; Chiuso, A.; Santagiustina, M.; Mecozzi, A.; Galtarossa, A.; Palmieri, L. Phase Retrieval Receiver Based on Deep Learning for Minimum-Phase Signal Recovery. In Proceedings of the 2018 European Conference on Optical Com-munication (ECOC), Basel, Switzerland, 18–22 September 2022; pp. 1–3. [Google Scholar]
- Orsuti, D.; Antonelli, C.; Chiuso, A.; Santagiustina, M.; Mecozzi, A.; Galtarossa, A.; Palmieri, L. Deep Learning-Based Phase Retrieval Scheme for Minimum-Phase Signal Recovery. J. Light. Technol. 2023, 41, 578–592. [Google Scholar] [CrossRef]
- Orsuti, D.; Cappelletti, M.; Santagiustina, M.; Galtarossa, A.; Palmieri, L. Edge-carrier-assisted Phase-Retrieval Based on Deep Learning Enabling low CSPR and low Applied Dispersion Values. In Proceedings of the Optical Fiber Communication Con-ference, San Diego, CA, USA, 5–9 March 2023; p. M2F.3. [Google Scholar]
- Zhu, Y.; Li, L.; Fu, Y.; Hu, W. Symmetric carrier assisted differential detection receiver with low-complexity signal-signal beating interference mitigation. Opt. Express 2020, 28, 19008–19022. [Google Scholar] [CrossRef] [PubMed]
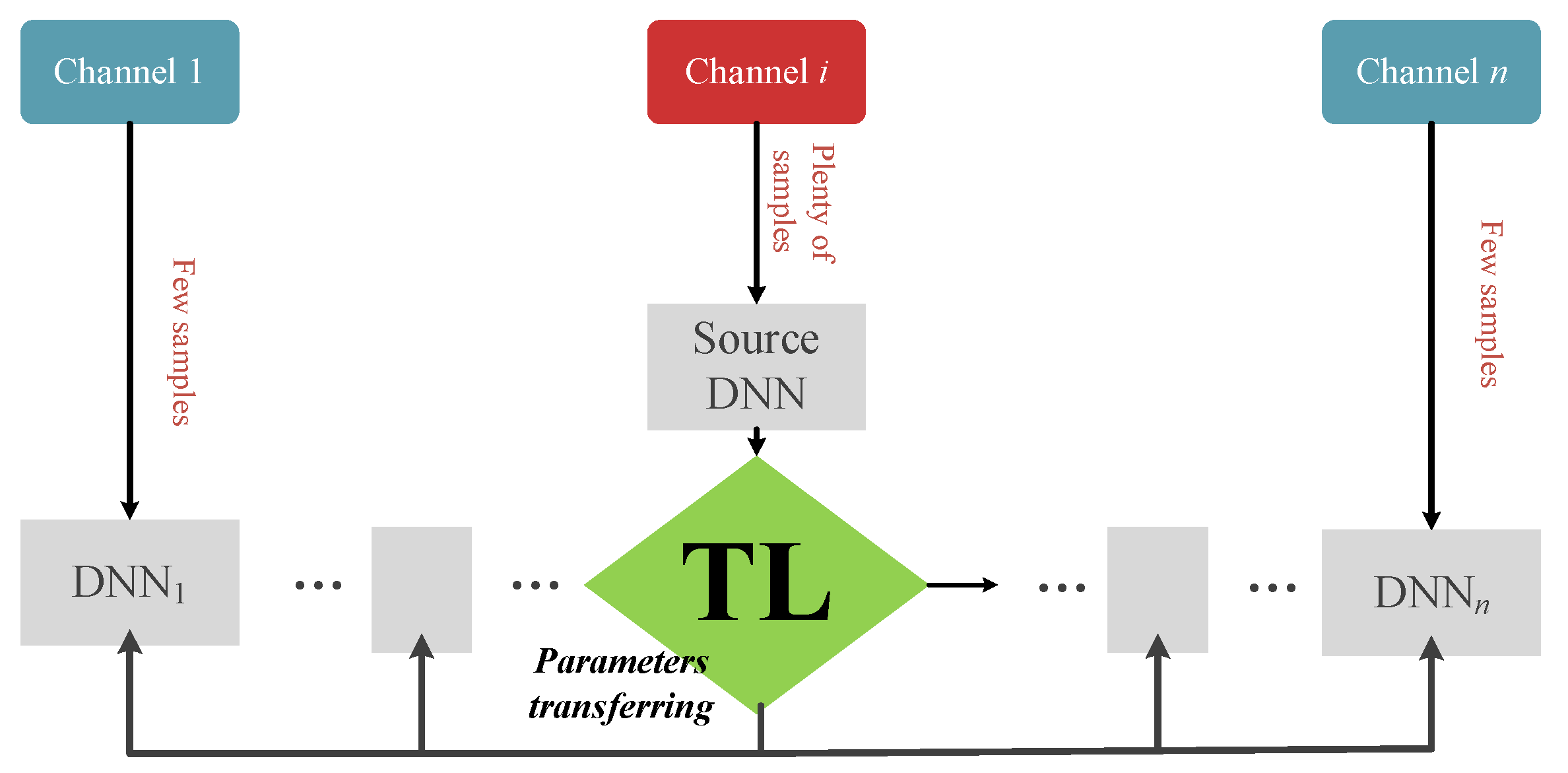
- Zhang, J.; Xia, L.; Zhu, M.; Hu, S.; Xu, B.; Qiu, K. Fast remodeling for nonlinear distortion mitigation based on transfer learning. Opt. Lett. 2019, 44, 4243–4246. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Sun, C.; Ji, T.; Ji, H.; Manton, J.; Shieh, W. Transfer learning aided neural networks for nonlinear equalization in short-reach direct detection systems. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 8–12 March 2020; p. T4D.4. [Google Scholar]
- Xia, L.; Zhang, J.; Hu, S.; Zhu, M.; Song, Y.; Qiu, K. Transfer learning assisted deep neural network for OSNR estimation. Opt. Express 2019, 27, 19398–19406. [Google Scholar] [CrossRef]
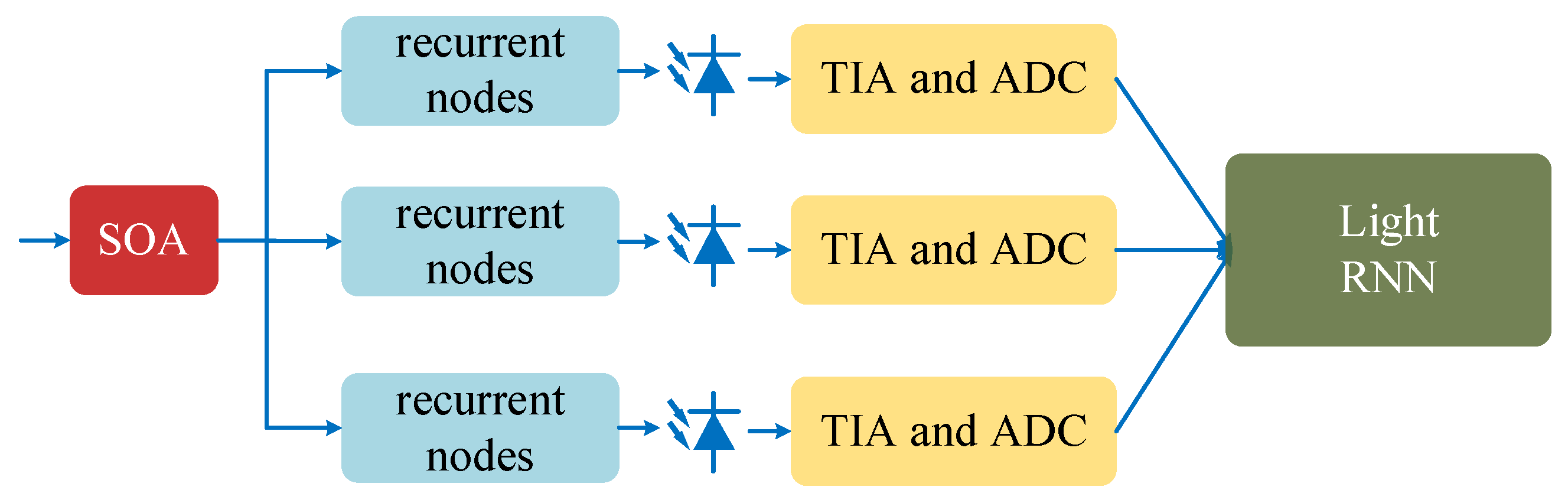
- Sozos, K.; Deligiannidis, S.; Mesaritakis, C.; Bogris, A. Self-Coherent Receiver Based on a Recurrent Optical Spectrum Slicing Neuromorphic Accelerator. J. Light. Technol. 2023, 41, 2666–2674. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Q.; Xu, Z.; Zhu, Y.; Zhang, Y.; Ji, H.; Yang, Y.; Qiao, G.; Liu, L.; Wang, S.; Liang, J.; et al. Machine Learning for Self-Coherent Detection Short-Reach Optical Communications. Photonics 2023, 10, 1001. https://doi.org/10.3390/photonics10091001
Wu Q, Xu Z, Zhu Y, Zhang Y, Ji H, Yang Y, Qiao G, Liu L, Wang S, Liang J, et al. Machine Learning for Self-Coherent Detection Short-Reach Optical Communications. Photonics. 2023; 10(9):1001. https://doi.org/10.3390/photonics10091001
Chicago/Turabian StyleWu, Qi, Zhaopeng Xu, Yixiao Zhu, Yikun Zhang, Honglin Ji, Yu Yang, Gang Qiao, Lulu Liu, Shangcheng Wang, Junpeng Liang, and et al. 2023. "Machine Learning for Self-Coherent Detection Short-Reach Optical Communications" Photonics 10, no. 9: 1001. https://doi.org/10.3390/photonics10091001
APA StyleWu, Q., Xu, Z., Zhu, Y., Zhang, Y., Ji, H., Yang, Y., Qiao, G., Liu, L., Wang, S., Liang, J., Wei, J., Li, J., He, Z., Zhuge, Q., & Hu, W. (2023). Machine Learning for Self-Coherent Detection Short-Reach Optical Communications. Photonics, 10(9), 1001. https://doi.org/10.3390/photonics10091001









