The Role of Stepwise Photoionization in Measurements of the Ionization Potentials in Dense Plasma

Abstract

The interaction of high-contrast high-intensity laser radiation with solids allows us to create hot or warm plasma of solid or even over-solid density, such as in the case of inertial fusion particularly. The multicharged ions contained in it can no longer be considered isolated. As a result, this leads to a decrease in the ionization potentials and to the disappearance of a number of bound ionic states. To describe the ionization potential depression, two major approaches are now used predominantly, where the key parameter is either average interelectronic or interionic distance. Since neither of the approaches can be substantiated purely theoretically, their applicability can only be established by comparison with experimental results. In recent experiments with X-ray free-electron lasers, it was concluded that the ionization potential depression rather depends on the interelectronic distance. However, when measuring ionization potentials, it was assumed that the main role in ionization processes is played by the direct photoionization of the ion ground state. In the present paper, we show that stepwise photoionization processes should play a significant role in dense plasma, disrupting a straight correspondence between the threshold in direct photoionization by X-ray laser photons and the actual ionization potential of multicharged ions. It means that the measurement results mentioned above are not correct, and the main conclusion about the importance of the interelectronic distance for depression of the ionization potential is not correct.

1. Introduction

When considering the properties of a high-temperature plasma, it is usually thought to be ideal, and the ions are isolated or free. However, when the plasma density increases to values characteristic of solids, this approach may no longer be justified. First, when the ion density becomes so high that the distance between the ions is of the order of the orbital radius of the optical electron, the ion can no longer be considered isolated. Second, when the Debye radius becomes comparable to the orbital radius of the optical electron due to the increase in electron density, this electron no longer moves in a pure Coulomb field of the ion nucleus, but in a field weakened by Debye shielding. These effects can drastically change the properties of ions. First, they lower the ionization potential of the ion and cause a number of bound states to cease to exist. And second, they decrease the energies of the remaining bound states. All of this should lead to a significant change in all the binding energies in the plasma; the statistical sum and hence the equation of the state; the ionization balance; and the transport properties of such a superdense plasma.

Two approaches are most commonly used today to describe the effect of lowering of ionization potential (LPI) in plasmas: EK [1] and SP [2], where the key parameters are the mean distances between electrons and between ions, respectively. They are versatile and give qualitatively similar results, but with significantly different values of plasma density. Since neither approach can be justified purely theoretically, their applicability can only be determined by comparison with experimental results.

Recently, these approaches have been used to interpret experimental results obtained in plasma generation by radiation from X-ray free-electron lasers [3,4] and powerful optical lasers [5,6]. It was found that in the first case the observational results agree with the EK model, while in the second case the SP model is suitable for the experiment, and the difference between the results obtained by the above methods is significant. Since the density effects are of paramount importance for studying the state of matter at high-energy densities—which are widely used both in astrophysical objects and in laboratory objects created within inertial thermonuclear fusion projects—the importance of eliminating the discovered contradiction can hardly be overestimated.

In the present work, it is shown that the methods used in [3,4] to measure the ionization potentials of ions can lead to results that depend on the atomic kinetic models used to calculate the ionization composition of the plasma. Namely, they rely on the completeness of accounting for excited ion configurations and, consequently, on the consideration of stepwise ionization transitions. The methods for determining ionization potentials by direct observation of the photorecombination continuum boundary are free from this drawback. Therefore, we can conclude that the measurements performed in [5,6] provide more reliable data on the lowering of ionization potentials in dense plasmas and the Stewart–Pyatt (SP) model [2] describes this phenomenon more adequately.

It should be noted that stepwise processes of a different nature can play an important role in plasma physics and in its kinetics. In this case, of course, the efficiency of a multistage process depends on the probability of passing through each stage. Until recently, it was thought that stepwise processes must be important for ultrahigh-density plasmas because each “step” is caused by a collisional transition whose probability is proportional to the plasma density. However, with the advent of powerful X-ray free-electron lasers (XFELs), it became clear that stepwise processes can indeed occur with the participation of laser photons, since the probabilities of photoabsorption or photoionization under these conditions are on the order of, or even higher than, the probabilities of spontaneous transitions in highly charged ions. If in a dense plasma the chain of transitions was formed by collision processes, then in a plasma irradiated by X-ray laser the chain of transitions is formed by photoprocesses.

In the pioneering work [7], it was found that when a single strong femtosecond X-ray pulse from LCLS (Linac Coherent Light Source, Stanford Linear Accelerator Center of National Accelerator Laboratory, USA) interacts with isolated neon atoms, a chain of photoionization processes takes place, leading to the ionization of the atoms into bare nuclei. During photoionization, the electrons of the inner shell are knocked out. As a result, so-called hollow ions are produced, and the effect of induced X-ray transparency occurs.

Later, the multiple multi-photon ionization of Xe atoms by SACLA (SPring-8 Angstrom Compact free electron Laser, Harima Science Garden City, Japan) pulse was studied. It was found that Xe^q+ ions with q up to 26 are generated when the energy of the laser photons is 5.5 keV. Moreover, highly charged (q > 24) ions are produced due to a five-step process involving the inner shells of the ions [8].

In studying the interaction of X-ray laser radiation with clusters leading to nanoplasma generation, it was also found that various stepwise and cascade transitions play an important role in this process [9,10]. For example, on tuning the X-ray laser to the lowest resonant transition the system becomes multiply excited, and more efficient; indirect ionization pathways become operative. These mechanisms are now known as interatomic Coulombic decay (ICD), where one of the species de-excites to its ground state, transferring its energy to ionize another excited species. In Ref. [9] it is shown that on tuning to a higher resonant transition, a previously unknown type of interatomic Coulombic decay, intra-Rydberg ICD, occurs. In it, the de-excitation of an atom to a close-lying Rydberg state leads to electron emission from another neighboring Rydberg atom. Moreover, systems multiply excited to higher Rydberg states will decay by a cascade of such processes, producing even more ions.

In Ref. [10] it was shown that highly excited states of atomic fragments are generated in the process of XFEL-induced nanoplasma formation, and the inelastic scattering of Auger electrons and interatomic Coulombic decay are the mechanisms populating and depopulating these excited states.

In cases where the radiation of an X-ray laser interacts with a high-density or even solid plasma, it is expected that a stepwise process may involve both photo- and collisional processes. Such a case is considered in this work.

2. Ionization in Dense Plasma Exposed to Strong Shortwave Radiation

The method for measuring the ionization potentials used in [3,4] is based on the threshold character of the photoionization process.

In general, ionization processes in plasmas of multicharged ions can occur both by radiation (photoionization) and by collisions, i.e., collisions of ions with electrons. In the vast majority of cases, collisional ionization dominates in dense plasmas. However, situations are possible in which the plasma is subjected to very intense photon fluxes generated by lasers. When the energy of the laser photons is in the IR or in the optical range, laser photoionization is possible only for the outer shells of ions with low charge, while the ionization of multicharged ions occurs by collision processes.

When a plasma is exposed to or generated by strong X-ray radiation, photoionization processes can play an important role, even for inner shells of multicharged ions. In this case, the ionization process itself may occur in a stepwise manner. For example, photoionization of an inner-shell electron can produce an autoionization state, which then decays following the process of autoionization. A chain of processes such as “photoexcitation–photoionization” or “photoexcitation–collision ionization” is also possible. Obviously, the excited states of the ions are involved in the step processes, and the simulation results depend crucially on which excited configurations are taken into account in the calculation of the ion kinetics.

Let us consider the simplest case, in which there are only H-like ions and the bare nuclei of the chemical element (for example aluminum) in the plasma. Let us denote by N_H the concentration of H-like ions Al XIII, by H_N the concentration of nuclei Al XIV, and calculate the dependence of the relative concentration of nuclei α = N_N/(H_H + N_N) on various plasma parameters.

Let us first assume that excited H-like states do not exist at all. In this case, the dependence of N_N/(N_H + N_N) on the photon energy of the radiation pump is described by the yellow curve (No) in Figure 1.

As long as the photon energy is less than the ionization potential of the 1s level of the Al XIII ion, photoionization processes in the system are impossible. Above the threshold value corresponding to the ionization potential of the Al XIII ion, the number of Al XIV nuclei starts to increase sharply. The increase of the nuclei concentration can be determined, for example, by time-of-flight techniques, and the energy of the pump photon corresponding to the jump position on the curve α(E_ph) seems to provide the value of the ionization potential.

If the calculations take into account the effect of the lowering of the ionization potential in dense plasma, then depending on the model used, the jump position will be shifted by a certain value, which depends quite strongly on the model (see blue and light green curves in Figure 1).

Such measurements, performed in [3,4] for aluminum ions of different multiplicities, have shown that when scanning the pump photon energy, the appearance moments of certain ions agree well with the Ecker–Kroll model [1] for lowering of the ionization potential and are not described by the Stewart–Pyatt model [2].

However, the occurrence times of ions of the next multiplicity may not correspond to the equality of the pump photons’ energy with the corresponding ionization potential value. This is a consequence of the step channels of the ionization process. We show this by considering a fairly simple system consisting of H-like ions and nuclei as above, but now we will consider the excited levels of the H-like ion up to the value of the principal quantum number n = 10. The calculations were performed using the radiation-collisional code IPRAX [11]. IPRAX is the radiation-collisional kinetic code for non-stationary and stationary calculations. The following atomic processes (direct and reverse) are included in IPRAX: Collisional ionization, recombination, excitation and de-excitation, photorecombination, radiative decay, dielectronic recombination, autoionization, photoexcitation, and photoionization. Stark and Doppler broadening are considered. In the atomic model all levels with a principal quantum number n < 10 are included. Fine splitting is taken into account for all the levels.

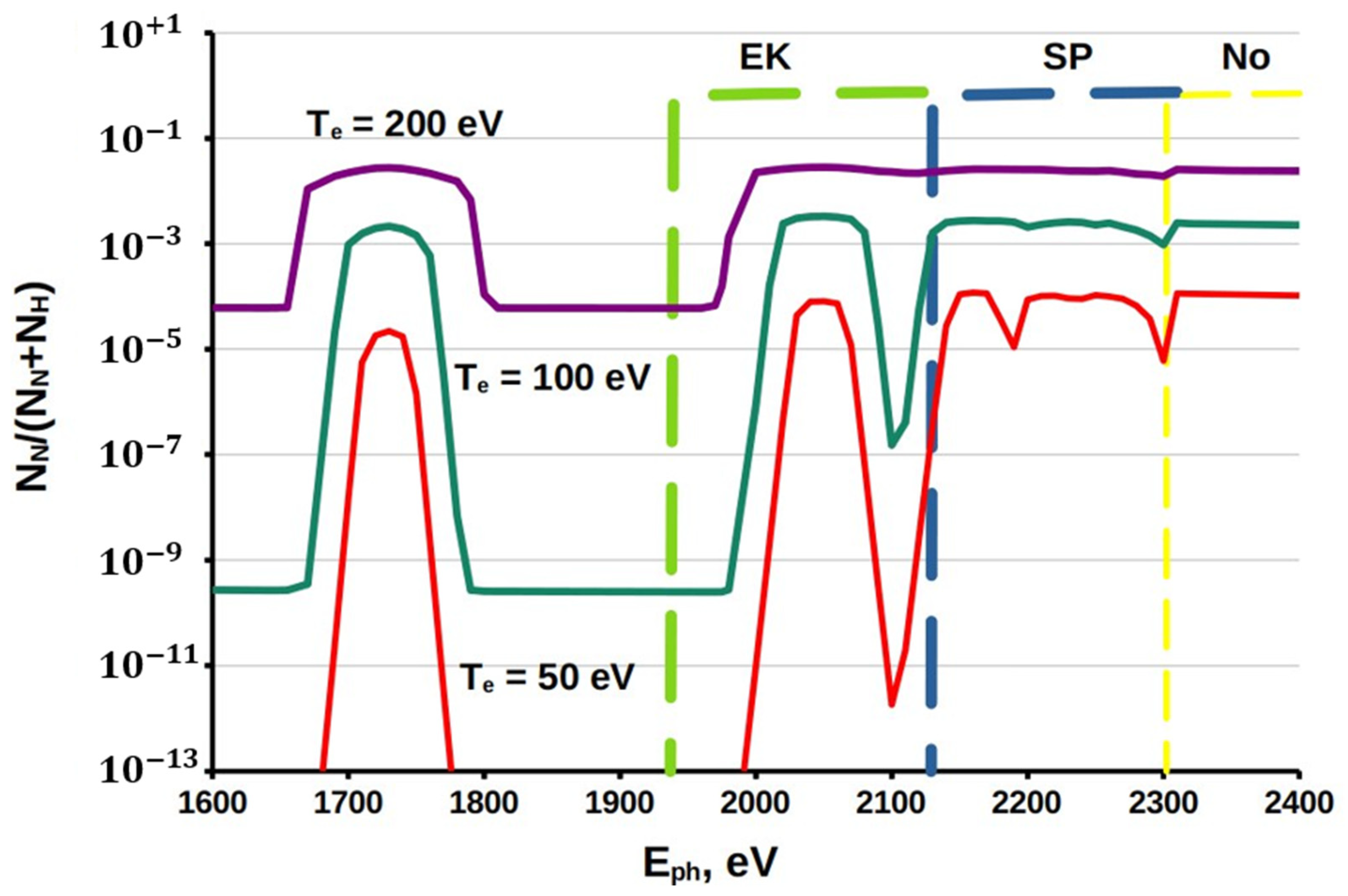
We first consider the case of solid aluminum plasma with N_i = 6 × 10²² cm⁻³. The results of the calculations performed without taking into account the effect of decreasing the ionization potential are shown in Figure 1 for different T_e values.

This figure shows the results obtained for a fixed pump intensity I_ph = 10¹⁷ W/cm² in the spectral bandwidth of 6 eV. These values correspond approximately to the conditions of the experiments [3,4] performed with the X-ray free-electron laser LCLS. It is well seen that the dependence of the concentration of nuclei on the energy of the pump photons now has a completely different character—there are maxima on the curves, the width of which increases with increasing electronic temperature. The reason for the occurrence of such maxima are the processes of stepwise ionization. For example, the maximum in the range of 1730 eV is due to a step process, the first stage of which is the photoexcitation of Al XIII(1s) + ħω_ph → Al XIII (2p) and the second stage of which is the photoionization of Al XIII (2p) + ħω_ph → Al XIV + e or the collisional ionization of Al XIII (2p) + e → Al XIV + 2e. The other maxima are due to similar causes, but the first step here is 1s → np photoexcitations. As np levels become closer with the increasing of n, the maxima also get closer together and then begin to overlap when the width of the absorption line is on the order of the distance between the levels. Since the width of the absorption lines increases with increasing temperature and plasma density, the overlap occurs in the low photon energy region. For example, Figure 1 shows that at T_e = 200 eV, the complete ionization of Al XIII ions already occurs at energies ħω_ph~2000 eV, although their ionization potential is 2304 eV. If the role of the excited states were not taken into account, this could be attributed to the effect of lowering the ionization potential, although in this case this has absolutely nothing to do with the lowering of the ionization potential.

Figure 2 shows the results of calculations performed for the same conditions as in Figure 1, but for ion densities 10²⁰ cm⁻³. Note that this density corresponds approximately to the critical density of laser plasma produced by radiation with a wavelength of about 1 μm. From Figure 1 and Figure 2 it is well seen that in a dense plasma the threshold for the ionization of ions by external X-rays with photon energy E_ph does not usually correspond to the condition E_ph = IP (IP is the ionization potential of the ion), but is determined by the threshold of step ionization coinciding with the photoexcitation energy of one or more levels of the ionizing ion. In the case of H-like ions, these are nl states, and the value of n depends on temperature and plasma density. As can be seen in Figure 1, n is greater than 2 even in a solid-state plasma.

3. Discussion

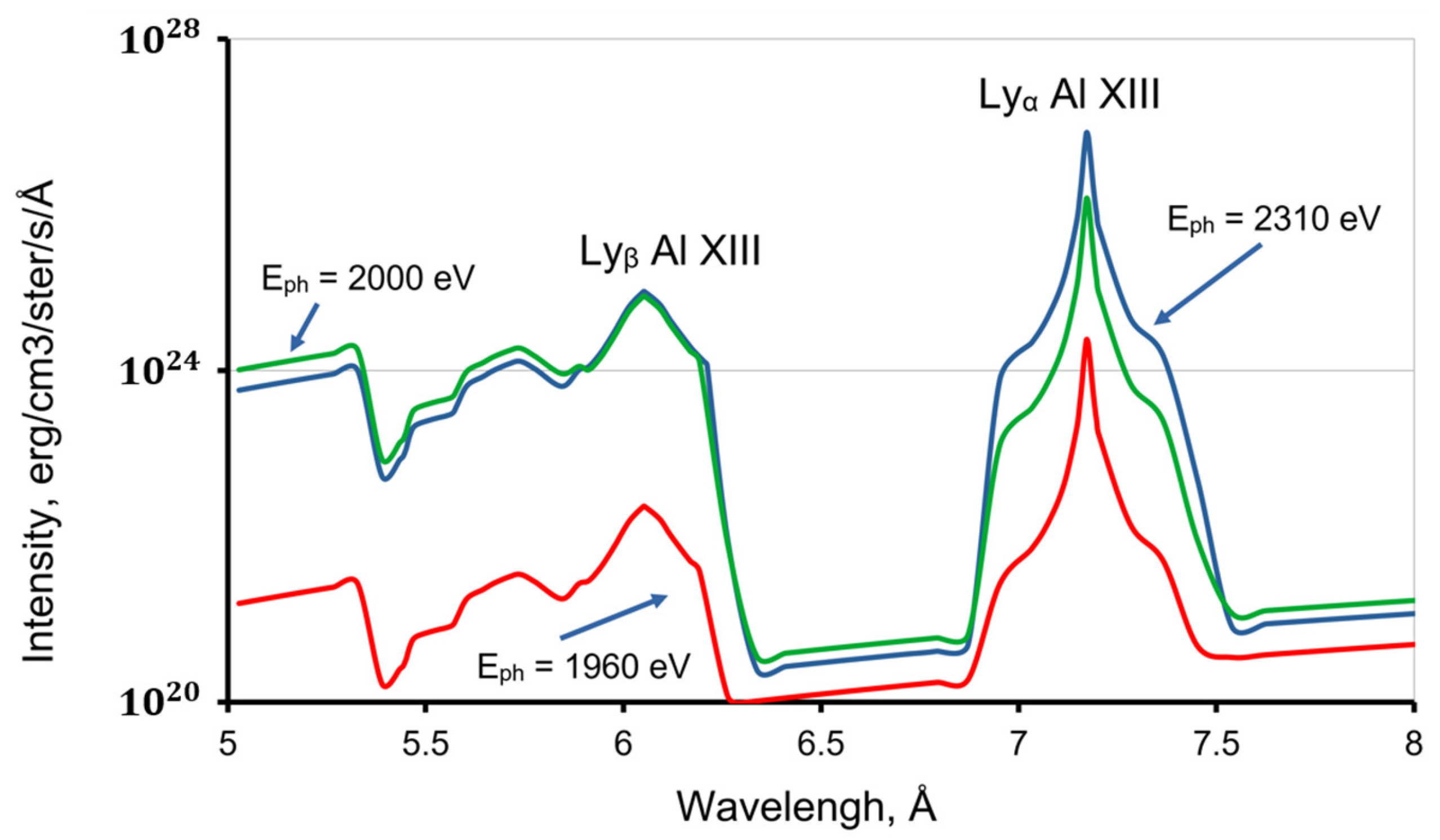
As can be seen from the calculations, the step ionization processes strongly affect the charge state of the photoionizing plasma. Obviously, they should also affect the emission spectrum of such a plasma. An example of the calculation of the emission spectrum for the 5–8 Å region containing H-like aluminum lines is shown in Figure 3. The energies of the pump photons were chosen to be in the range where photoionization is impossible (1st case, E_ph = 1960 eV), photoionization occurs in a stepwise manner (2nd case, E_ph = 2000 eV), and photoionization can occur directly from the ground state (3rd case, E_ph = 2310 eV > IP = 2304 eV). Note that the emission spectra for the 2nd and 3rd cases are extremely similar to each other and differ strongly in intensity from the 1st case.

It means that by scanning the frequency of the heating radiation and recording the emission spectrum of the plasma, we can, generally speaking, determine the appearance moment of the corresponding ion spectrum by the sharp increase in the intensities of its spectral lines, but this moment may not correspond to the equality of the incident photon energy with the ionization potential and the threshold of step ionization, which is much lower. It should be noted, that in a relatively cold photoionized plasma, the main contribution to the Al XIII Ly_α spectral line intensity is caused by the recombination of Al XIV nuclei. So, the sharp increasing of Al XIII spectra corresponds to the intensification of Al XIII–Al XIV ionization, and the corresponding rising of nuclei in the plasma.

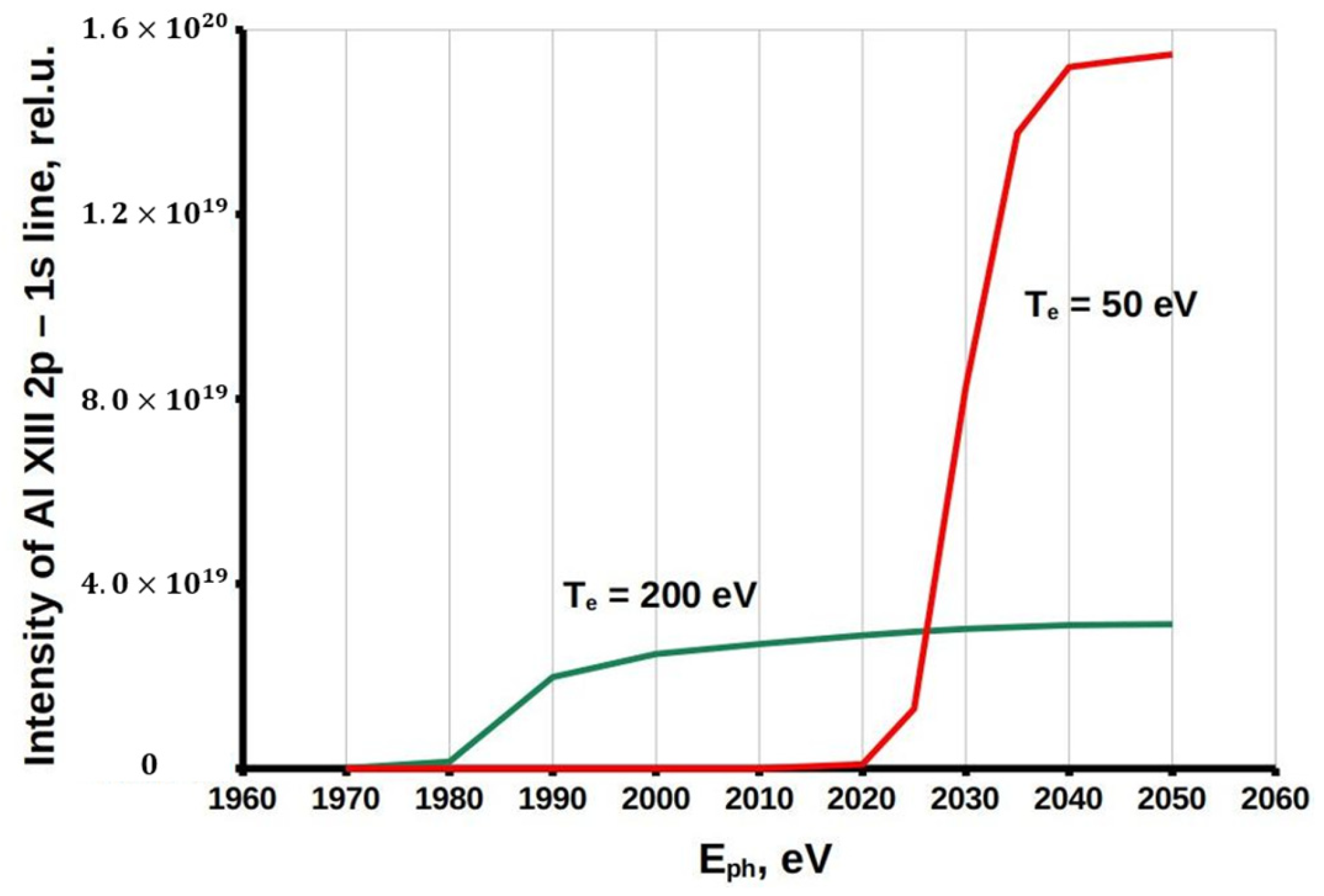
In Figure 4, the dependences of intensity of the Ly_α line on the photon pump energy are presented for solid-state plasma with temperatures of 50 eV and 200 eV. By comparing these data with the data of Figure 1 it may be concluded that positions of high intensity gradients correspond to the stepwise photoionization and are not ionization potentials.

This allows us to make a suggestion as to why the experiments with X-ray free-electron lasers [3,4] obtained results that contradict the models of SP (and HM [12]), and the results of the experiment [5,6]—measuring the lowering of the ionization potential in the plasma generated by optical lasers. Although in all cases the measurements of the LPI were based on the analysis of the X-ray emission spectra of the plasma, the methods used were fundamentally different.

In Refs. [5,6], the effects of LPI were measured by the shift of the photocombination continuum (SPC) boundary to the long-wavelength region of the spectrum and estimated by the disappearance of spectral lines with large values of the principal quantum number, n. In this case, it is necessary, first, to invest the energy of the optical laser pulse directly into the solid matter and, second, to ensure the registration of the emission spectra only up to the moment of plasma separation. While the first problem can be solved with short laser pulses of ultrahigh contrast, the second problem is much more difficult to solve, since X-ray detectors with the required temporal resolution do not currently exist. Obviously, the only currently applicable approach should not be based on reducing the time of spectrum registration, but on increasing the time of existence of the plasma in the solid-density state. This can be done, for example, by limiting the dispersion with a solid envelope, which can be realized most easily by using layered targets (see, e.g., [13,14,15,16,17]). Nevertheless, dispersion of the high-temperature plasma will almost always occur to one extent or another, and the mean ion density of the plasma will not be fixed but can be measured. On the one hand, this is a drawback of the approach, but on the other hand, it is an advantage because it allows us to study the effects of LPI at different densities.

In the approach used in [3,4], the heating X-ray pulse deliberately penetrates deep into the solid target, and the scattering of the formed plasma with solid density is not so important due to the much lower initial temperature, which is certainly an advantage. However, as we have shown above using the example of ions with a very simple energy structure, the experimental results obtained may not be sufficient to provide data on ionization potentials due to the contribution of stepwise ionization processes. For the formation of multi-electron ions, there are similar alternative ionization channels, and much more diverse ones, because in these cases the states of ions with one or more (hollow ion) vacancies in the inner shells should play a major role. In our opinion, it is the insufficient consideration of hollow-ion states that has led to the overestimation of the LPI effects in [3,4].

4. Conclusions

In conclusion, we would like to emphasize that the use of high-power X-ray free-electron lasers is generally a very promising approach for the study of photoionization and photoexcitation processes in multicharged ions. For solid-density plasma only XFELs can practically provide an intensity of X-rays at which the probabilities of photo-stimulated processes are higher than that of collisional processes. This is particularly promising when the plasma is relatively cold (low-temperature plasma, warm dense matter) and the self-emission of the plasma is suppressed. Note that the use of XFELs in this case allows the study of plasmas under conditions where the ions are ordered, and the free-electron gas is degenerate.

However, care must be taken when interpreting the experimental results obtained. A different type of stepwise processes must be considered in collisional-radiation modelling. This means that the measurement results [3,4] are probably not correct and the conclusion about the importance of the interelectronic distance for depression of the ionization potential is most likely not correct.