Temporal Dynamics of an Asymmetrical Dielectric Nanodimer Wrapped with Graphene
Abstract
1. Introduction
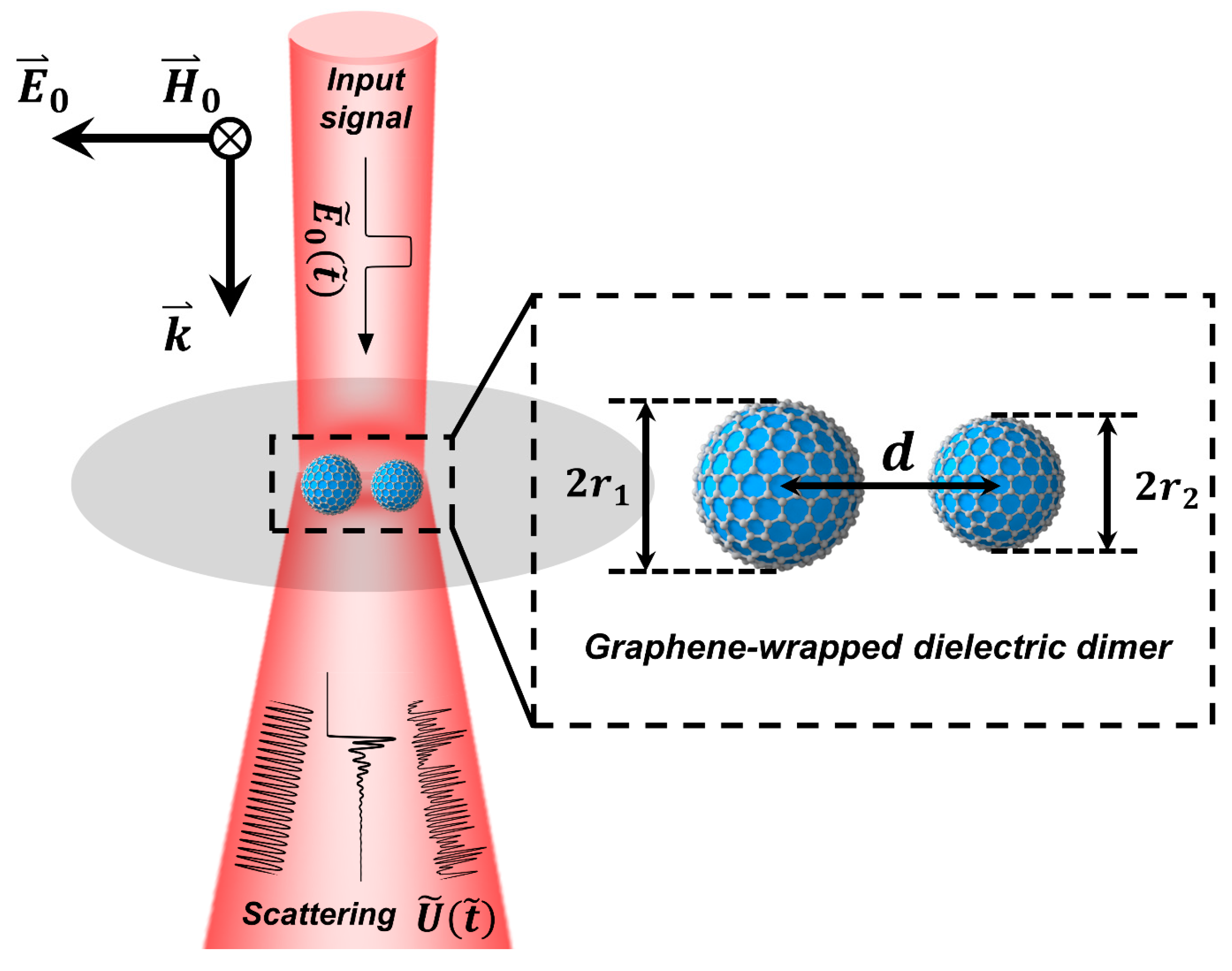
2. Materials and Methods
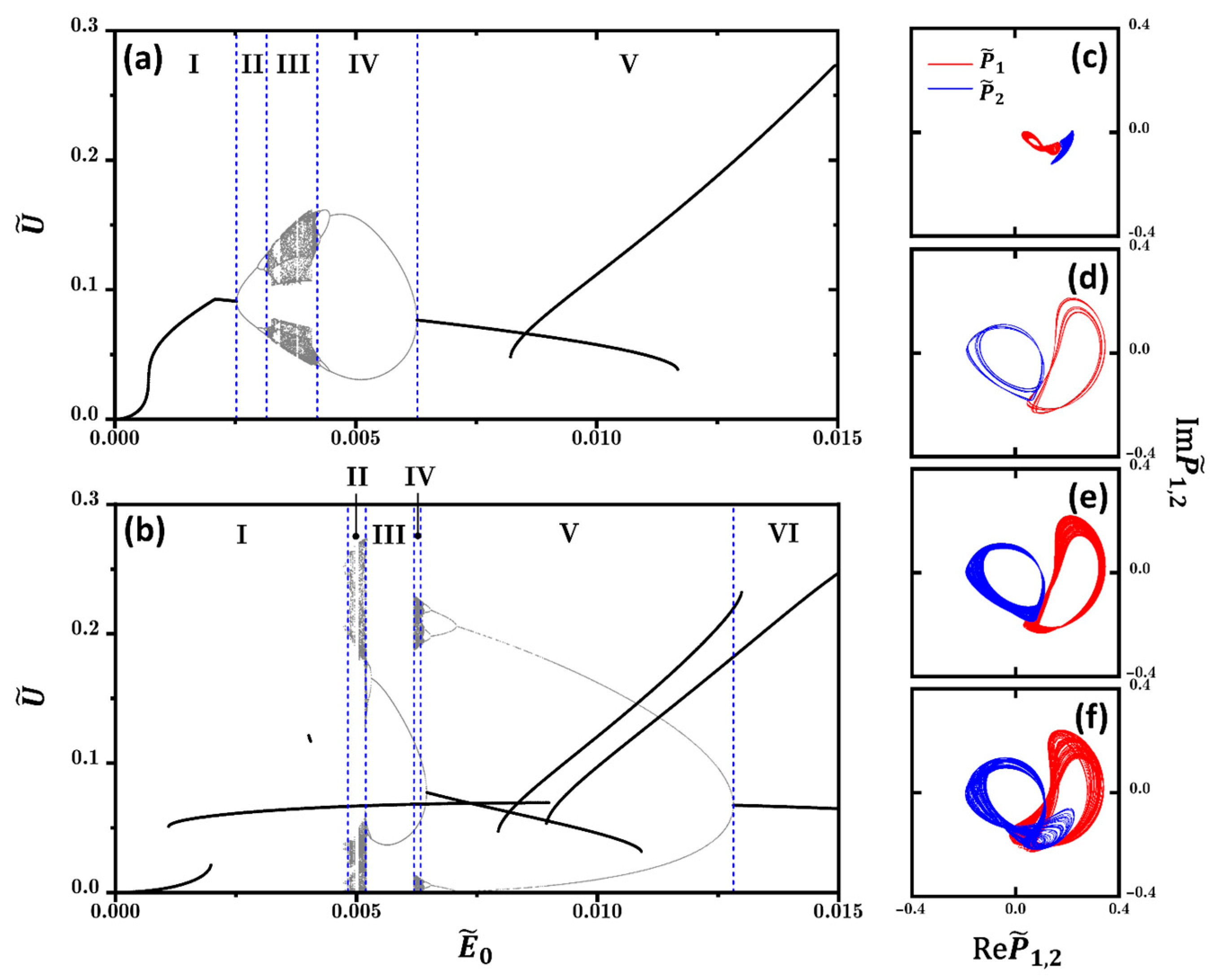
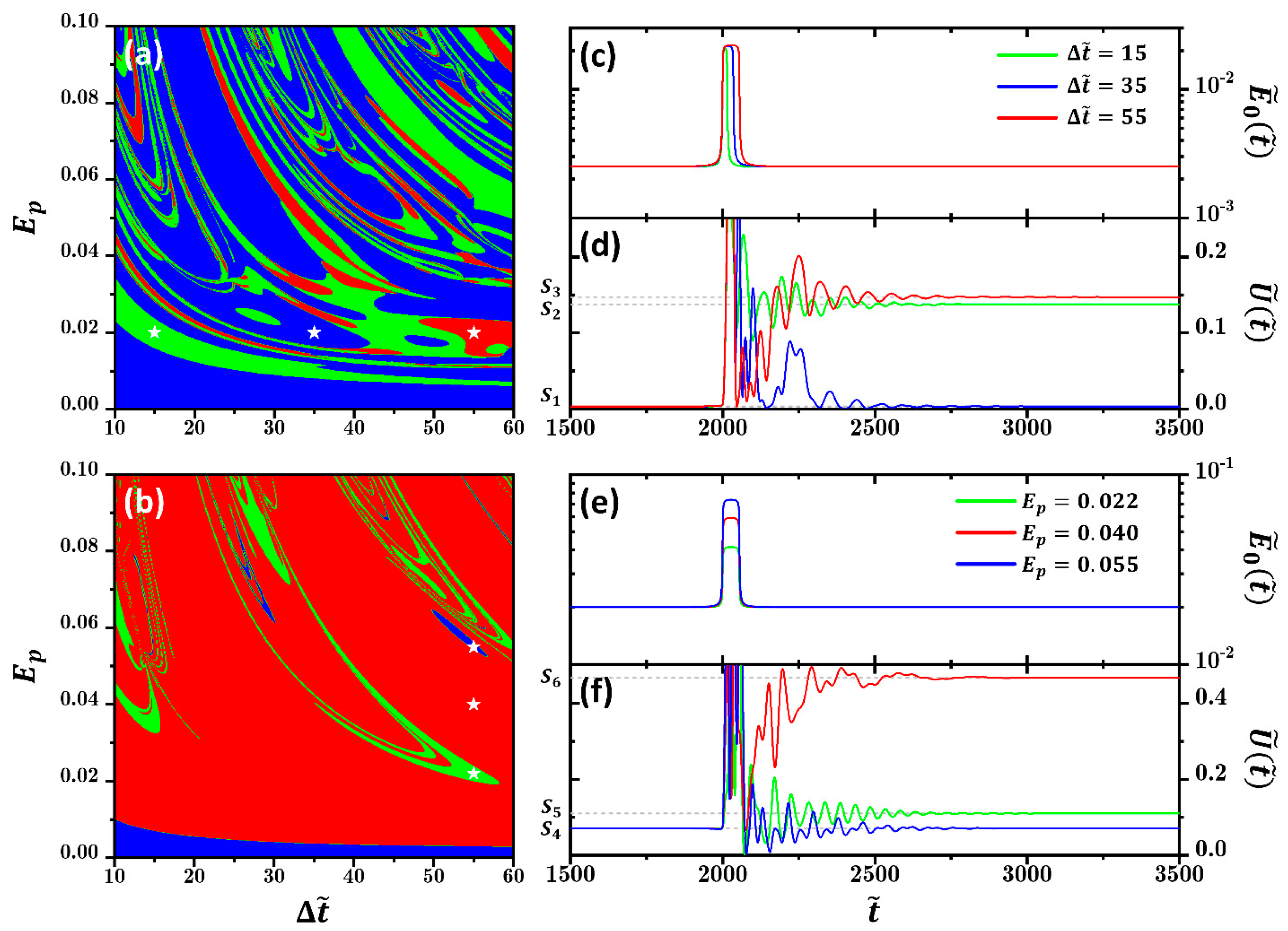
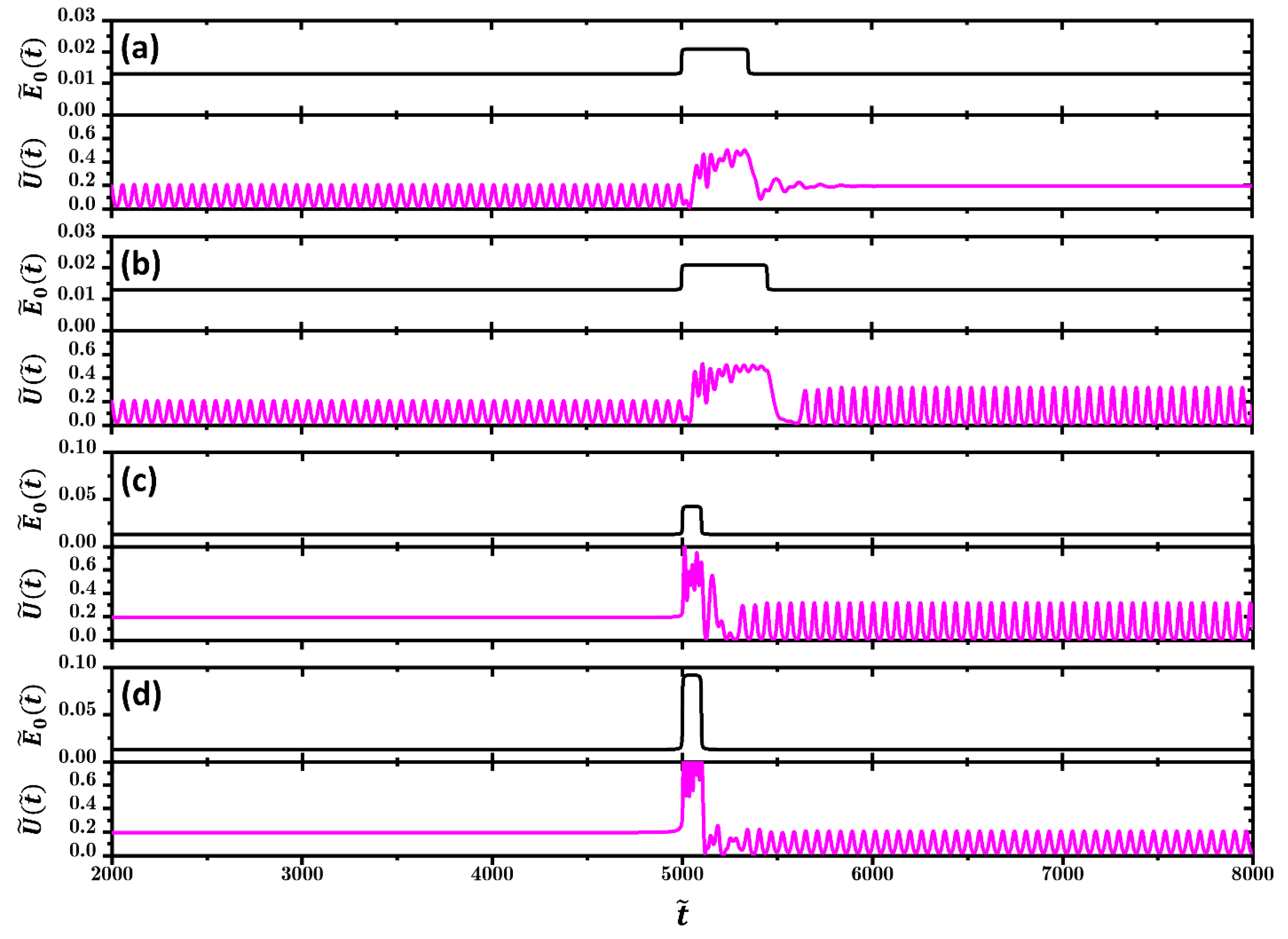
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Horowitz, P. The Art of Electronics, 3rd ed.; Cambridge University Press: New York, NY, USA, 2015; ISBN 978-0-521-80926-9. [Google Scholar]
- Kılıç, R. A Practical Guide for Studying Chua’s Circuits; World Scientific Series on Nonlinear Science Series A; World Scientific Publishing Company: Singapore, 2010; Volume 71, ISBN 978-981-4291-13-2. [Google Scholar]
- Yang, Y.; Wang, D.; Tan, Z.J.; Xiong, X.; Wang, M.; Peng, R.; Fang, N.X. Ultrathin Platelet Antennas Mediated Light-Matter Interaction in Monolayer MoS2. Opt. Express 2017, 25, 10261–10269. [Google Scholar] [CrossRef]
- Tyagi, D.; Chen, T.-Y.; Huang, C.-B. Polarization-Enabled Steering of Surface Plasmons Using Crossed Reciprocal Nanoantennas. Laser Photonics Rev. 2020, 14, 2000076. [Google Scholar] [CrossRef]
- Zhan, Y.; Zhang, L.; Rahmani, M.; Giannini, V.; Miroshnichenko, A.E.; Hong, M.; Li, X.; Maier, S.A.; Lei, D. Synthetic Plasmonic Nanocircuits and the Evolution of Their Correlated Spatial Arrangement and Resonance Spectrum. ACS Photonics 2021, 8, 166–174. [Google Scholar] [CrossRef]
- Kuznetsov, A.V.; Valero, A.C.; Tarkhov, M.; Bobrovs, V.; Redka, D.; Shalin, A.S. Transparent Hybrid Anapole Metasurfaces with Negligible Electromagnetic Coupling for Phase Engineering. Nanophotonics 2021, 10, 4385–4398. [Google Scholar] [CrossRef]
- Canós Valero, A.; Gurvitz, E.A.; Benimetskiy, F.A.; Pidgayko, D.A.; Samusev, A.; Evlyukhin, A.B.; Bobrovs, V.; Redka, D.; Tribelsky, M.I.; Rahmani, M.; et al. Theory, Observation, and Ultrafast Response of the Hybrid Anapole Regime in Light Scattering. Laser Photonics Rev. 2021, 15, 2100114. [Google Scholar] [CrossRef]
- Chen, Y.; Qian, S.; Wang, K.; Xing, X.; Wee, A.; Loh, K.P.; Wang, B.; Wu, D.; Chu, J.; Alu, A.; et al. Chirality-Dependent Unidirectional Routing of WS2 Valley Photons in a Nanocircuit. Nat. Nanotechnol. 2022, 17, 1178–1182. [Google Scholar] [CrossRef] [PubMed]
- Kuznetsov, A.V.; Canós Valero, A.; Shamkhi, H.K.; Terekhov, P.; Ni, X.; Bobrovs, V.; Rybin, M.V.; Shalin, A.S. Special Scattering Regimes for Conical All-Dielectric Nanoparticles. Sci. Rep. 2022, 12, 21904. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.; Huang, Y.; Ma, P.; Shalin, A.S.; Gao, L. The Temporal Dynamics of Nonlocal Plasmonic Nanoparticle under the Ultrashort Pulses. Results Phys. 2023, 48, 106437. [Google Scholar] [CrossRef]
- Xiong, X.; Zeng, Z.-Y.; Peng, R.; Wang, M. Directional Chiral Optical Emission by Electron-Beam-Excited Nano-Antenna. Chin. Phys. Lett. 2023, 40, 017801. [Google Scholar] [CrossRef]
- Wu, P.-Y.; Chang, Y.-C.; Huang, C.-B. Broadband Plasmonic Half-Subtractor and Digital Demultiplexer in Pure Parallel Connections. Nanophotonics 2022, 11, 3623–3629. [Google Scholar] [CrossRef]
- Xie, J.; Niu, X.; Hu, X.; Wang, F.; Chai, Z.; Yang, H.; Gong, Q. Ultracompact All-Optical Full-Adder and Half-Adder Based on Nonlinear Plasmonic Nanocavities. Nanophotonics 2017, 6, 1161–1173. [Google Scholar] [CrossRef]
- Li, Y.; An, N.; Lu, Z.; Wang, Y.; Chang, B.; Tan, T.; Guo, X.; Xu, X.; He, J.; Xia, H.; et al. Nonlinear Co-Generation of Graphene Plasmons for Optoelectronic Logic Operations. Nat. Commun. 2022, 13, 3138. [Google Scholar] [CrossRef]
- Zharov, A.A.; Noskov, R.E.; Tsarev, M.V. Plasmon-Induced Terahertz Radiation Generation Due to Symmetry Breaking in a Nonlinear Metallic Nanodimer. J. Appl. Phys. 2009, 106, 073104. [Google Scholar] [CrossRef]
- Lapshina, N.S.; Noskov, R.E.; Kivshar, Y.S. Nonlinear Nanoantenna with Self-Tunable Scattering Pattern. JETP Lett. 2013, 96, 759–764. [Google Scholar] [CrossRef]
- Yu, W.; Ma, P.; Sun, H.; Gao, L.; Noskov, R.E. Optical Tristability and Ultrafast Fano Switching in Nonlinear Magnetoplasmonic Nanoparticles. Phys. Rev. B 2018, 97, 075436. [Google Scholar] [CrossRef]
- Ma, P.; Gao, L.; Ginzburg, P.; Noskov, R.E. Nonlinear Nanophotonic Circuitry: Tristable and Astable Multivibrators and Chaos Generator. Laser Photonics Rev. 2020, 14, 1900304. [Google Scholar] [CrossRef]
- Ziani, Z.; Lévêque, G.; Coulibaly, S.; Taki, A.; Akjouj, A. Investigating Route to Chaos in Nonlinear Plasmonic Dimer. Ann. Phys. 2020, 532, 2000240. [Google Scholar] [CrossRef]
- Noskov, R.E.; Belov, P.A.; Kivshar, Y.S. Subwavelength Modulational Instability and Plasmon Oscillons in Nanoparticle Arrays. Phys. Rev. Lett. 2012, 108, 093901. [Google Scholar] [CrossRef] [PubMed]
- Noskov, R.; Belov, P.; Kivshar, Y. Oscillons, Solitons, and Domain Walls in Arrays of Nonlinear Plasmonic Nanoparticles. Sci. Rep. 2012, 2, 873. [Google Scholar] [CrossRef]
- Smirnova, D.A.; Noskov, R.E.; Smirnov, L.A.; Kivshar, Y.S. Dissipative Plasmon Solitons in Graphene Nanodisk Arrays. Phys. Rev. B 2015, 91, 075409. [Google Scholar] [CrossRef]
- Savelev, R.S.; Yulin, A.V.; Krasnok, A.E.; Kivshar, Y.S. Solitary Waves in Chains of High-Index Dielectric Nanoparticles. ACS Photonics 2016, 3, 1869–1876. [Google Scholar] [CrossRef]
- Noskov, R.E.; Smirnova, D.A.; Kivshar, Y.S. Subwavelength Solitons and Faraday Waves in Two-Dimensional Lattices of Metal Nanoparticles. Opt. Lett. 2013, 38, 2554–2556. [Google Scholar] [CrossRef]
- Ziani, Z.; Lévêque, G.; Akjouj, A.; Coulibaly, S.; Taki, A. Characterization of Spatiotemporal Chaos in Arrays of Nonlinear Plasmonic Nanoparticles. Phys. Rev. B 2019, 100, 165423. [Google Scholar] [CrossRef]
- Halas, N.J.; Lal, S.; Chang, W.-S.; Link, S.; Nordlander, P. Plasmons in Strongly Coupled Metallic Nanostructures. Chem. Rev. 2011, 111, 3913–3961. [Google Scholar] [CrossRef] [PubMed]
- Zohar, N.; Chuntonov, L.; Haran, G. The Simplest Plasmonic Molecules: Metal Nanoparticle Dimers and Trimers. J. Photochem. Photobiol. C Photochem. Rev. 2014, 21, 26–39. [Google Scholar] [CrossRef]
- Grigorenko, A.N.; Roberts, N.W.; Dickinson, M.R.; Zhang, Y. Nanometric Optical Tweezers Based on Nanostructured Substrates. Nat. Photon. 2008, 2, 365–370. [Google Scholar] [CrossRef]
- Sukhov, S.; Shalin, A.; Haefner, D.; Dogariu, A. Actio et Reactio in Optical Binding. Opt. Express OE 2015, 23, 247–252. [Google Scholar] [CrossRef]
- Kostina, N.A.; Kislov, D.A.; Ivinskaya, A.N.; Proskurin, A.; Redka, D.N.; Novitsky, A.; Ginzburg, P.; Shalin, A.S. Nanoscale Tunable Optical Binding Mediated by Hyperbolic Metamaterials. ACS Photonics 2020, 7, 425–433. [Google Scholar] [CrossRef]
- Large, N.; Abb, M.; Aizpurua, J.; Muskens, O.L. Photoconductively Loaded Plasmonic Nanoantenna as Building Block for Ultracompact Optical Switches. Nano Lett. 2010, 10, 1741–1746. [Google Scholar] [CrossRef]
- El Barghouti, M.; Akjouj, A.; Mir, A. Design of Silver Nanoparticles with Graphene Coatings Layers Used for LSPR Biosensor Applications. Vacuum 2020, 180, 109497. [Google Scholar] [CrossRef]
- Shegai, T.; Chen, S.; Miljković, V.D.; Zengin, G.; Johansson, P.; Käll, M. A Bimetallic Nanoantenna for Directional Colour Routing. Nat. Commun. 2011, 2, 481. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Ma, P.; Wu, Y.M. Abnormal Fano Profile in Graphene-Wrapped Dielectric Particle Dimer. Photonics 2020, 7, 124. [Google Scholar] [CrossRef]
- Ma, P.; Gao, L.; Ginzburg, P.; Noskov, R.E. Ultrafast Cryptography with Indefinitely Switchable Optical Nanoantennas. Light Sci. Appl. 2018, 7, 77. [Google Scholar] [CrossRef]
- Ávalos-Ovando, O.; Besteiro, L.V.; Wang, Z.; Govorov, A.O. Temporal Plasmonics: Fano and Rabi Regimes in the Time Domain in Metal Nanostructures. Nanophotonics 2020, 9, 3587–3595. [Google Scholar] [CrossRef]
- Yelo-Sarrión, J.; Leo, F.; Gorza, S.-P.; Parra-Rivas, P. Neuronlike Spiking Dynamics in Asymmetrically Driven Dissipative Nonlinear Photonic Dimers. Phys. Rev. A 2022, 106, 013512. [Google Scholar] [CrossRef]
- Dana, B.D.; Koya, A.N.; Song, X.; Lin, J. Ultrafast Plasmon Dynamics in Asymmetric Gold Nanodimers. Chin. Phys. B 2022, 31, 064208. [Google Scholar] [CrossRef]
- Yelo-Sarrión, J.; Leo, F.; Gorza, S.-P.; Parra-Rivas, P. Self-Pulsing and Chaos in the Asymmetrically Driven Dissipative Photonic Bose–Hubbard Dimer: A Bifurcation Analysis. Chaos 2022, 32, 083103. [Google Scholar] [CrossRef]
- Skokos, C. The lyapunov characteristic exponents and their computation. In Dynamics of Small Solar System Bodies and Exoplanets; Souchay, J.J., Dvorak, R., Eds.; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2010; Volume 790, pp. 63–135. ISBN 978-3-642-04457-1. [Google Scholar]
- Ramasubramanian, K.; Sriram, M.S. A Comparative Study of Computation of Lyapunov Spectra with Different Algorithms. Phys. D Nonlinear Phenom. 2000, 139, 72–86. [Google Scholar] [CrossRef]
- Naseri, T.; Daneshfar, N.; Moradi-Dangi, M.; Eynipour-Malaee, F. Terahertz Optical Bistability of Graphene-Coated Cylindrical Core–Shell Nanoparticles. J. Theor. Appl. Phys. 2018, 12, 257–263. [Google Scholar] [CrossRef]
- Christensen, T.; Yan, W.; Jauho, A.-P.; Wubs, M.; Mortensen, N.A. Kerr Nonlinearity and Plasmonic Bistability in Graphene Nanoribbons. Phys. Rev. B 2015, 92, 121407. [Google Scholar] [CrossRef]
- Huang, Y.; Miroshnichenko, A.E.; Gao, L. Low-Threshold Optical Bistability of Graphene-Wrapped Dielectric Composite. Sci. Rep. 2016, 6, 23354. [Google Scholar] [CrossRef]
- Mai, Z.; Lin, F.; Pang, W.; Xu, H.; Tan, S.; Fu, S.; Li, Y. Anderson Localization in Metallic Nanoparticle Arrays. Opt. Express OE 2016, 24, 13210–13219. [Google Scholar] [CrossRef]
- Bergman, D.J.; Levy, O.; Stroud, D. Theory of Optical Bistability in a Weakly Nonlinear Composite Medium. Phys. Rev. B 1994, 49, 129–134. [Google Scholar] [CrossRef]
- Gao, L. Optical Bistability in Composite Media with Nonlinear Coated Inclusions. Phys. Lett. A 2003, 318, 119–125. [Google Scholar] [CrossRef]
- Noskov, R.E.; Krasnok, A.E.; Kivshar, Y.S. Nonlinear Metal–Dielectric Nanoantennas for Light Switching and Routing. New J. Phys. 2012, 14, 093005. [Google Scholar] [CrossRef]
- Lapshina, N.; Noskov, R.; Kivshar, Y. Nanoradar Based on Nonlinear Dimer Nanoantenna. Opt. Lett. 2012, 37, 3921–3923. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Gao, L.; Ma, P.; Jiang, X.; Fan, W.; Shalin, A.S. Nonlinear Chaotic Dynamics in Nonlocal Plasmonic Core-Shell Nanoparticle Dimer. Opt. Express 2023, 31, 19646–19656. [Google Scholar] [CrossRef]
- Li, H.H. Refractive Index of Alkaline Earth Halides and Its Wavelength and Temperature Derivatives. J. Phys. Chem. Ref. Data 1980, 9, 161–290. [Google Scholar] [CrossRef]
- Kaplan, J.L.; Yorke, J.A. Chaotic behavior of multidimensional difference equations. In Functional Differential Equations and Approximation of Fixed Points; Peitgen, H.-O., Walther, H.-O., Eds.; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1979; Volume 730, pp. 204–227. ISBN 978-3-540-09518-7. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, X.; Huang, Y.; Ma, P.; Shalin, A.S.; Gao, L. Temporal Dynamics of an Asymmetrical Dielectric Nanodimer Wrapped with Graphene. Photonics 2023, 10, 914. https://doi.org/10.3390/photonics10080914
Jiang X, Huang Y, Ma P, Shalin AS, Gao L. Temporal Dynamics of an Asymmetrical Dielectric Nanodimer Wrapped with Graphene. Photonics. 2023; 10(8):914. https://doi.org/10.3390/photonics10080914
Chicago/Turabian StyleJiang, Xinchen, Yang Huang, Pujuan Ma, Alexander S. Shalin, and Lei Gao. 2023. "Temporal Dynamics of an Asymmetrical Dielectric Nanodimer Wrapped with Graphene" Photonics 10, no. 8: 914. https://doi.org/10.3390/photonics10080914
APA StyleJiang, X., Huang, Y., Ma, P., Shalin, A. S., & Gao, L. (2023). Temporal Dynamics of an Asymmetrical Dielectric Nanodimer Wrapped with Graphene. Photonics, 10(8), 914. https://doi.org/10.3390/photonics10080914





