A New Quantum Sealed-Bid Auction Protocol with a Set of Local Indistinguishable Orthogonal Product States

Abstract

Quantum sealed-bid auction (QSA) is a special form of transaction with significant applications in the economic and financial fields. Using a unique set of locally indistinguishable orthogonal product (LIOP) states, we propose a new QSA protocol in this paper. In the protocol, the bid message is encoded as a quantum sequence of LIOP states, and the different particles of LIOP states are transmitted separately. Even though an attacker obtains a portion of the particles, they cannot recover the entire bid message because of the local indistinguishability of LIOP states. Once the auctioneer announces the winner’s bid, all bidders are able to confirm the authenticity of their bid. With the help of a semi-honest third party, collusion between the auctioneer and a malicious bidder can be discovered. Finally, our protocol is capable of meeting all requirements for secure sealed-bid auctions through security and completeness analysis. Additionally, the proposed protocol does not require any entangled resources and complicated operations, so it can be easily implemented in practice.

1. Introduction

With the rapid development of communications and Internet technologies, the public demand for information security is increasing. Compared with classical systems, quantum systems show more advantages. The security of information is guaranteed by the basic properties of quantum mechanics. In particular, after quantum electrodynamics was established, it was confirmed that photons are medium particles for the transmission of electromagnetic information. Photons are often used for quantum information transmission [1,2,3,4] because of their excellent properties of easy generation and manipulation and their ability to transmit over long distances through free-space or fiber channels [5]. Therefore, It is very important and meaningful to study various applications in electronic commerce based on quantum mechanics using photons as information carriers.

Auctions, as one of the most important businesses of electronic commerce transactions, are gaining increasing societal attention. Generally, public auctions and sealed-bid auctions are the two primary categories of auctions [6]. With the former, every step of the auction process is open to the participants, every legitimate bidder is able to see the bids of other bidders, and the highest bidder ultimately prevails. The primary distinction between public auctions and sealed-bid auctions is that sealed-bid auctions must guarantee the privacy of each bidder’s bid. A secret bid is submitted before the limit deadline to the auctioneer by a legitimate bidder. In other words, no bidder will be aware of other bidders’ bids except for their own, and no outside eavesdropper will be able to wiretap the bids. In addition, the auctioneer cannot legally help a malicious bidder win the auction. Consequently, sealed-bid auctions offer the highest level of bidder privacy protection. Moreover, there are some requirements for a safe sealed-bid auction, which are anonymity, public verifiability, fairness, and so on.

The advancement of quantum computing poses a significant threat to conventional auction security schemes. The quantum sealed-bid auction (QSA) is proposed to preserve auction security in the context of quantum computing. The first QSA protocol based on GHZ states was proposed by Naseri [7] in 2009, and used multiparty quantum secure direct communication. However, Qin et al. [8], and Yang et al. [9] pointed out separately that malicious bidders could obtain the secret bids of others in the same year. The problem of collusion between a dishonest auctioneer and malicious bidders was not resolved, despite the fact that they solved this problem by adding decoy photons. Furthermore, to address the problem of auctioneer and bidder collusion, Zhao et al. [10] first proposed a secure quantum QSA protocol with a post-confirmation mechanism. The most important feature of this protocol is that bidders prepare particles in a secret order to encode their bids in the post-confirmation phase, and in the public verification phase, other bidders can recover the winner’s bid to determine whether there is a collusive attack. Nevertheless, Xu et al. [11] and He et al. [12] found that the scheme cannot resist a collusive attack by a group of malicious bidders. Later, Wang et al. [13] proposed a QSA protocol based on a set of ordered EPR pairs. This protocol is only used for three parties, i.e., the participants consisting of only one auctioneer and two bidders. In this protocol, the two bidders perform unitary operations on one sequence of the EPR pairs to encrypt their secret bids and deduce the other party’s bid after the auctioneer has received all the particles and finished the measurement. However, Liu et al. [14] found a leak in Wang’s protocol, i.e., a dishonest auctioneer could collude with a bidder to help him win the auction by changing his bid. In Ref. [14], having each bidder send the hash of his bid price to the other bidders guarantees that the bid cannot be changed.

In 2016, Liu et al. [15] designed a multiparty QSA scheme using single photons as message carriers to reduce the complexity of quantum resources. The protocol introduces an improved post-confirmation mechanism using EPR pairs and permutation operators to guarantee the fairness of the auction. Subsequently, Zhang et al. [16] pointed out that Liu et al.’s QSA model cannot be prevented from collusion attacks either. There is no unconditionally safe post-confirmation mechanism in the current QSA model if a dishonest participant can control multi-particle entanglement. They proposed two potential approaches to design the post-confirmation mechanism when the bidders are semi-quantum. In 2020, Han et al. [17] proposed a new protocol based on GHZ states that involve a trusted third party and may thus ensure the bidder’s anonymity and the accuracy of the bidder’s message. With the help of the third party, using quantum sequences as the information carrier of bidding, the auction center and bidders can conduct quantum teleportation to obtain bids. In 2022, Gao et al. [18] proposed a protocol in which two auctioneers are employed to convey bids with EPR pairs from the bidder to the auctioneer. In addition, a hash function and a bulletin board are used to implement the post-confirmation mechanism. Until now, collusive attacks have continued to be a major consideration in the quantum sealed-bid auction process. Many experts and scholars have been devoted to studying post-confirmation mechanisms to resist collusion attacks. Even now, the post-confirmation mechanism has been researched and modified by several academics [19,20,21,22,23,24].

In summary, most QSA protocols are achieved by entangled states. It is essential to design a QSA protocol that does not utilize entangled states due to the difficulty of preparing entangled states practically. In 2015, Yu et al. [25] constructed a set of orthogonal product states that are not perfectly distinguishable by local operations and classical communication (LOCC). In fact, the local indistinguishable orthogonal product (LIOP) states are easier to prepare compared with the entangled states. Nowadays, LIOP states have been used in many applications. For example, in 2001, Guo et al. [26] proposed a quantum key distribution (QKD) protocol based on LIOP states. In 2019, Jiang et al. [27] proposed a quantum voting protocol based on LIOP states. In 2019, Jiang et al. [28] proposed a trusted third-party e-payment protocol with LIOP states. In 2022, Fu et al. [29] implemented a quantum secret sharing (QSS) protocol using LIOP states. In the proposed protocol, we solve the QSA problem based on the LIOP states. The bidder’s bidding message is encoded as a quantum sequence of LIOP states, and these quantum sequences are described in a unique method. Thereafter, the different particles of LIOP states are transmitted separately to prevent information leakage. Finally, by comparing the measurements, the auctioneer announces the highest bid. According to the property of LIOP states, even if an attacker obtains $n-1$ particles of orthogonal product states, it is impossible to determine the secret message. The transmission of quantum states between participants uses photons as carriers in this scheme. Moreover, compared with previous protocols, our protocol does not require sharing keys in advance. Since the indistinguishability of the LIOP states ensures the security of the protocol.

The rest of the paper is arranged as follows. In Section 2, we present some necessary preliminary of the sealed-bid auction and LIOP states. In Section 3, a new QSA protocol is presented. In Section 4, the correctness, security, and completeness of this protocol are analyzed. Finally, the conclusions are summarized in Section 5.

2. Preliminary Information

In this section, some necessary preliminary about the sealed-bid auction and LIOP states required in the protocol is introduced.

2.1. Sealed-Bid Auction

The winner of a sealed-bid auction will be decided by the auctioneer after the bidders have submitted their bids anonymously and discreetly by a predetermined deadline. With this kind of auction, the time consideration is eliminated, allowing participants can make less impulsive, more deliberate decisions [30]. To be specific, there are some important requirements of a secure auction as follows [22]:

(1)

Anonymity: Each bidder who participates in an auction can keep anonymity. In a secure auction, no one can obtain any bidder’s identity information except the auctioneer.

(2)

Public verifiability: The winning bid can be validated by any bidder. Every bidder is able to confirm the winning bid, which is determined by the auctioneer during the verification step. This implies that the attack may be immediately detected if there is collusion between a malicious bidder and a dishonest auctioneer.

(3)

Accountability of bidder: Any malicious bidder with a fake bid cannot interrupt the auction without being detected.

(4)

Fairness: Each bidder performs the same operations in the auction. The auctioneer cannot help a dishonest bidder to win the auction illegally without being found by other bidders.

(5)

Traceability: The winning bidder and the highest bid can be verified even after the auction has finished.

(6)

Non-repudiation: The bidder cannot deny that he has cast his bid, and accordingly, the auctioneer cannot deny that he has received the bid from the bidder.

The first-price sealed-bid auction, in which the bidder who bids the highest price wins and is obligated to pay it, is the most popular kind of sealed-bid auction. The second-price sealed-bid auction means the bidder who offers the highest price wins but only needs to pay the second-highest amount. We will only focus on the first-price sealed-bid auction in this study because there are no notable distinctions between the two types of auctions.

2.2. LIOP States

In 1999, Bennett et al. [31] proposed a unique set of LIOP states, and also demonstrated its local indistinguishability. In a $2\otimes 2\otimes 2$ quantum system, the product basis that contains the 8 orthogonal product states are as follows:

$$\begin{array}{cc}\hfill & |{\phi }_1{\rangle =|0\rangle }_1{|0\rangle }_2{|0\rangle }_3\hfill \\ \hfill & |{\phi }_2{\rangle =|1\rangle }_1{|1\rangle }_2{|1\rangle }_3\hfill \\ \hfill & |{\phi }_3{\rangle =|+\rangle }_1{|0\rangle }_2{|1\rangle }_3\hfill \\ \hfill & |{\phi }_4{\rangle =|-\rangle }_1{|0\rangle }_2{|1\rangle }_3\hfill \\ \hfill & |{\phi }_5{\rangle =|1\rangle }_1{|+\rangle }_2{|0\rangle }_3\hfill \\ \hfill & |{\phi }_6{\rangle =|1\rangle }_1{|-\rangle }_2{|0\rangle }_3\hfill \\ \hfill & |{\phi }_7{\rangle =|0\rangle }_1{|1\rangle }_2{|+\rangle }_3\hfill \\ \hfill & |{\phi }_8{\rangle =|0\rangle }_1{|1\rangle }_2{|-\rangle }_3\hfill \end{array}$$

(1)

LIOP states cannot be perfectly distinguished by LOCC. In this case, an attacker cannot capture the entire state if he only obtains a few particles. By encoding secret messages in this format, we can protect the privacy of participants. As a result, it has a wide range of uses in cryptographic protocols. The non-locality of the LIOP states will not be explained in detail here. In our protocol, the sealed-bid auction protocol is designed using corresponding LIOP states.

3. The Proposed Protocol

In this section, the specific process of the protocol is described. There are several participants in this protocol: (1) $Alice$ is the auctioneer who compares the bids of the bidders and announces the highest bid and the winner; (2) $Bo{b}_i$ is one of the bidders, there are n bidders in our protocol; (3) $Trent$ is a semi-honest auction center for checking the identity of bidders and verifying their honesty.

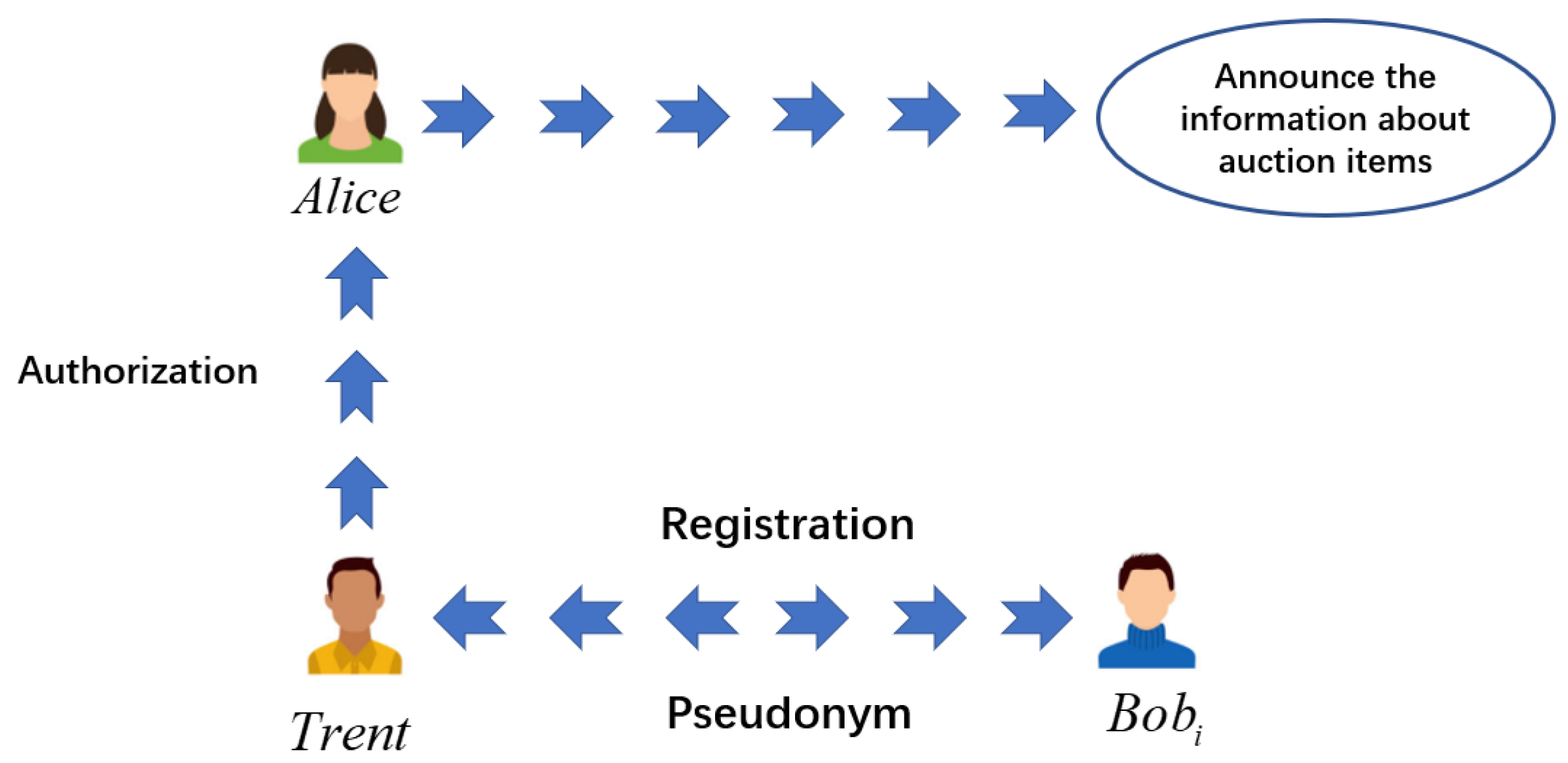
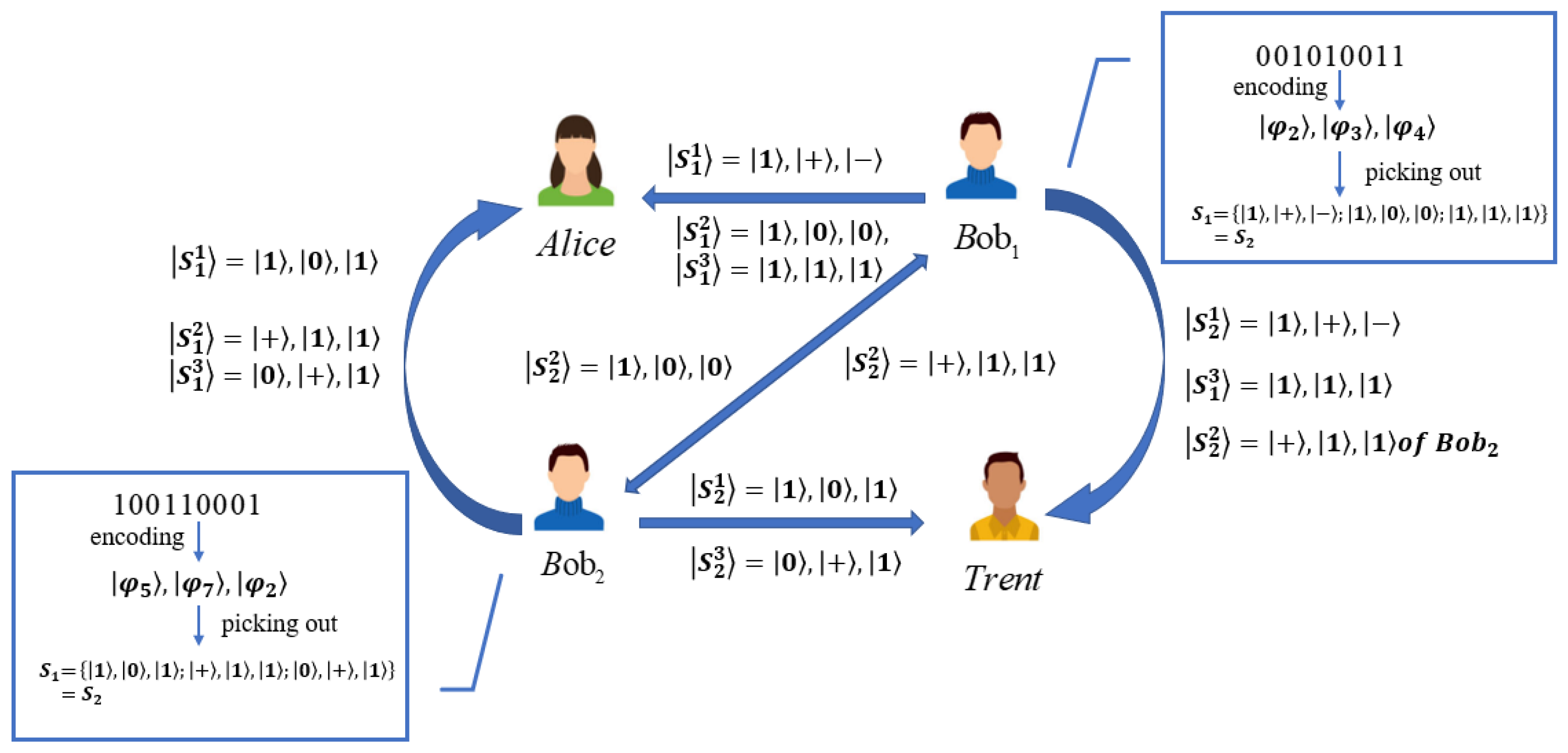
3.1. Stage of Preparation

Step 1: $Alice$ announces the items in the auction.

Step 2: Bidders who want to participate in the auction require to register with $Trent$. $Trent$ checks their status to see if they are eligible to participate in the auction. There is a collection containing eligible bidders who have credit certificates, authorization letters, and assets, etc. $Trent$ determines whether the bidder applying for registration belongs to the collection. If so, the bidder is qualified to participate in the auction. $Trent$ will send him a unique pseudonym representing his identity. In addition, he will also record the relationship between the pseudonym and each bidder’s true identity. Otherwise, $Trent$ will reject him.

Step 3: After all bidders have registered, $Trent$ authorizes the auctioneer $Alice$ to announce the information about the items to be auctioned. (The sketch is shown in Figure 1).

3.2. Stage of Auction

Step 1: $Bo{b}_i$ converts the bid message $M_i$ into a $3l$-long binary classical sequence and divides $M_i$ into l groups. $M_i=M_{i1}\parallel M_{i2}\parallel \cdots \parallel M_{it}\parallel \cdots \parallel M_{il},M_{it}\in \{000,001,010,100,101,011,110,111\},i=1,2,\cdots ,n.$

Step 2: $Bo{b}_i$ encodes the secret bid message into a quantum sequence according to the

Table 1. Coding rule of bid message $M_i$.

${\mathit{M}}_{\mathbf{it}}$	The Quantum Sequence of Encoding
000	$|{\phi }_1{\rangle =|0\rangle }_1{|0\rangle }_2{|0\rangle }_3$
001	$|{\phi }_2{\rangle =|1\rangle }_1{|1\rangle }_2{|1\rangle }_3$
010	$|{\phi }_3{\rangle =|+\rangle }_1{|0\rangle }_2{|1\rangle }_3$
011	$|{\phi }_4{\rangle =|-\rangle }_1{|0\rangle }_2{|1\rangle }_3$
100	$|{\phi }_5{\rangle =|1\rangle }_1{|+\rangle }_2{|0\rangle }_3$
101	$|{\phi }_6{\rangle =|1\rangle }_1{|-\rangle }_2{|0\rangle }_3$
110	$|{\phi }_7{\rangle =|0\rangle }_1{|1\rangle }_2{|+\rangle }_3$
111	$|{\phi }_8{\rangle =|0\rangle }_1{|1\rangle }_2{|-\rangle }_3$

.

Step 3: $Bo{b}_i$ generates n identical sequences denoted as $S_1,S_2,\cdots ,S_k\cdots ,S_n$. By picking out each particle in the sequences above, the corresponding quantum sequences represent as $S_k=\left\{\right|S_k^1\rangle ,|S_k^2\rangle ,|S_k^3\rangle \}$, where $k=1,2,\cdots ,n$.

To facilitate understanding of how the sequence is generated, $Bo{b}_i$’s bid message is encoded as $|{\phi }_2\rangle ,|{\phi }_3\rangle ,|{\phi }_5\rangle$. Then, the unique forms of $|S_k^1\rangle ,|S_k^2\rangle$, and $|S_k^3\rangle (k=1,2,\cdots ,n)$ are described as follows:

$$\begin{array}{cc}\hfill & |S_k^1\rangle =\left\{\right|1\rangle ,|+\rangle ,|1\rangle \},\hfill \\ \hfill & |S_k^2\rangle =\left\{\right|1\rangle ,|0\rangle ,|+\rangle \},\hfill \\ \hfill & |S_k^3\rangle =\left\{\right|1\rangle ,|1\rangle ,|0\rangle \}.\hfill \end{array}$$

(2)

And,

$$\begin{array}{cc}\hfill S_k& =\left\{\right|1\rangle ,|+\rangle ,|1\rangle ;|1\rangle ,|0\rangle ,|+\rangle ;|1\rangle ,|1\rangle ,|0\rangle \}\hfill \end{array}$$

(3)

Step 4: $Bo{b}_i$ inserts N decoy photons for eavesdropping detection into the quantum sequence $|S_1^1\rangle$ to form $|S_1^1{\rangle }^{\prime }$, all decoy photons are selected randomly in one of the states $\left\{\right|0\rangle ,|1\rangle ,|+\rangle ,|-\rangle \}$. At the same time, he records the original forms and positions of these decoy photons. Finally, $Bo{b}_i$ sends $|S_1^1{\rangle }^{\prime }$ to auctioneer $Alice$.

Step 5: After confirming that $Alice$ has received $|S_1^1{\rangle }^{\prime }$, $Bo{b}_i$ announces the original forms and positions of the decoy photons. $Alice$ measures each of the decoy photons with the corresponding bases. Then, $Alice$ compares whether the measurement results and the original forms are the same to check for eavesdropping. If the error rate is below a certain threshold, $Alice$ drops the decoy photons and recovers the sequence $|S_1^1\rangle$. The protocol continues to the next step. Otherwise, the protocol terminates.

Step 6: $Bo{b}_i$ sends the sequence $|S_k^1\rangle$ ($k=2,3,\cdots ,n$) in $S_k$ to $Trent$ perform the eavesdropping detection as Step 5. After successfully passing the security test, $Trent$ gets the sequence $|S_k^1\rangle$.

Step 7: Similarly, $Bo{b}_i$ sends the sequence $|S_k^2\rangle$ to $Bo{b}_j(j\ne i)$ randomly. In other words, he sends $n-1$ sequences to $n-1$ bidders in case these bidders conspire with the auctioneer to change the particles in their hands.

Step 8: Subsequently, $Bo{b}_i$ sends the sequence $|S_k^3\rangle$ to $Trent$. Finally, $Bo{b}_i$ sends the sequence $|S_1^2\rangle ,|S_1^3\rangle$ to $Alice$. The transmission process uses decoy photons to ensure secure communication.

Step 9: After successfully passing the eavesdropping detection, $Trent$ recovers the quantum sequence to obtain $|S_k^3\rangle$, $Alice$ gets $|S_1^2\rangle ,|S_1^3\rangle$. In Step 5, $Bo{b}_i$ has sent $|S_1^1\rangle$ to $Alice$, at which point she gets $S_1=\left\{\right|S_1^1\rangle ,|S_1^2\rangle ,|S_1^3\rangle \}$. According to Table 1, $Alice$ uses the corresponding bases to measure the sequence $S_1$ and records the measurement results.

Step 10: By comparing the measurement results, the auctioneer announces the highest price and the pseudonym of the winner, who is recorded as $Bo{b}_i^{\ast }$. (The sketch is shown in Figure 2).

3.3. Stage of Verification

Step 1: After $Alice$ announces the highest price and the winner, $Bo{b}_j$ sends $|S_k^2\rangle$ of $Bo{b}_i^{\ast }$ to $Trent$ in order to verify whether the bid has been changed.

Step 2: $Trent$ receives these quantum sequences and measures them. If all of the measurement results are the same and equal to the open highest price, the auction is reasonable. Otherwise, the auction is invalid.

Step 3: After verifying that the auction is reasonable, all participants follow the above steps for the next item until all items are auctioned off.

4. Analysis of the Protocol

In this section, we first explain the correctness of the presented protocol. Furthermore, we analyze the security of this protocol against various quantum attacks. Finally, we demonstrate that our protocol satisfies all of the conditions for a secure auction and successfully completes the task of a secure auction.

4.1. Analysis of Correctness

In order to understand the correctness of the protocol more intuitively, we take an example (the eavesdropping detection is ignored). For two bidders, $Bo{b}_1$ and $Bo{b}_2$, $Bo{b}_1$’s auction message is 001010011, encoded as $|{\phi }_2\rangle ,|{\phi }_3\rangle ,|{\phi }_4\rangle$; $Bo{b}_2$’s auction message is 100110001, encoded as $|{\phi }_5\rangle ,|{\phi }_7\rangle ,|{\phi }_2\rangle$.

For $Bo{b}_1$

$$\begin{array}{cc}\hfill S_1& =\left\{\right|S_1^1\rangle ,|S_1^2\rangle ,|S_1^3\rangle \}\hfill \\ & =\left\{\right|1\rangle ,|+\rangle ,|-\rangle ;|1\rangle ,|0\rangle ,|0\rangle ;|1\rangle ,|1\rangle ,|1\rangle \}\hfill \\ & =S_2;\hfill \end{array}$$

(4)

For $Bo{b}_2$

$$\begin{array}{cc}\hfill S_1& =\left\{\right|S_1^1\rangle ,|S_1^2\rangle ,|S_1^3\rangle \}\hfill \\ & =\left\{\right|1\rangle ,|0\rangle ,|1\rangle ;|+\rangle ,|1\rangle ,|1\rangle ;|0\rangle ,|+\rangle ,|1\rangle \}\hfill \\ & =S_2.\hfill \end{array}$$

(5)

After that, $Bo{b}_1\left(Bo{b}_2\right)$ sends $|1\rangle ,|+\rangle ,|-\rangle (|1\rangle ,|0\rangle ,|1\rangle$) of $S_1$ to $Alice$. Similarly, he sends $|1\rangle ,|+\rangle ,|-\rangle (|1\rangle ,|0\rangle ,|1\rangle$) of $S_2$ to $Trent$. Next, $Bo{b}_1\left(Bo{b}_2\right)$ sends $|1\rangle ,|0\rangle ,|0\rangle (|+\rangle ,|1\rangle ,|1\rangle$) of $S_2$ to $Bo{b}_2\left(Bo{b}_1\right)$. $Bo{b}_1\left(Bo{b}_2\right)$ sends $|1\rangle ,|1\rangle ,|1\rangle (|0\rangle ,|+\rangle ,|1\rangle$) of $S_2$ to $Trent$. Then, $Bo{b}_1\left(Bo{b}_2\right)$ sends $|1\rangle ,|0\rangle ,|0\rangle ;|1\rangle ,|1\rangle ,|1\rangle \left(\right|+\rangle ,|1\rangle ,|1\rangle ;|0\rangle ,|+\rangle ,|1\rangle$) of $S_1$ to $Alice$. At this moment, $Alice$ holds the sequences of all particles in $S_1$. After the measurement, $Alice$ recovers the secret bid messages and announces $Bo{b}_2$ as the winner. Afterwards, $Bo{b}_1$ sends $Bo{b}_2$’s $|S_2^2\rangle =|+\rangle ,|1\rangle ,|1\rangle$ to $Trent$ so as to verify the authenticity of $Bo{b}_2$’s message. (The sketch is shown in Figure 3).

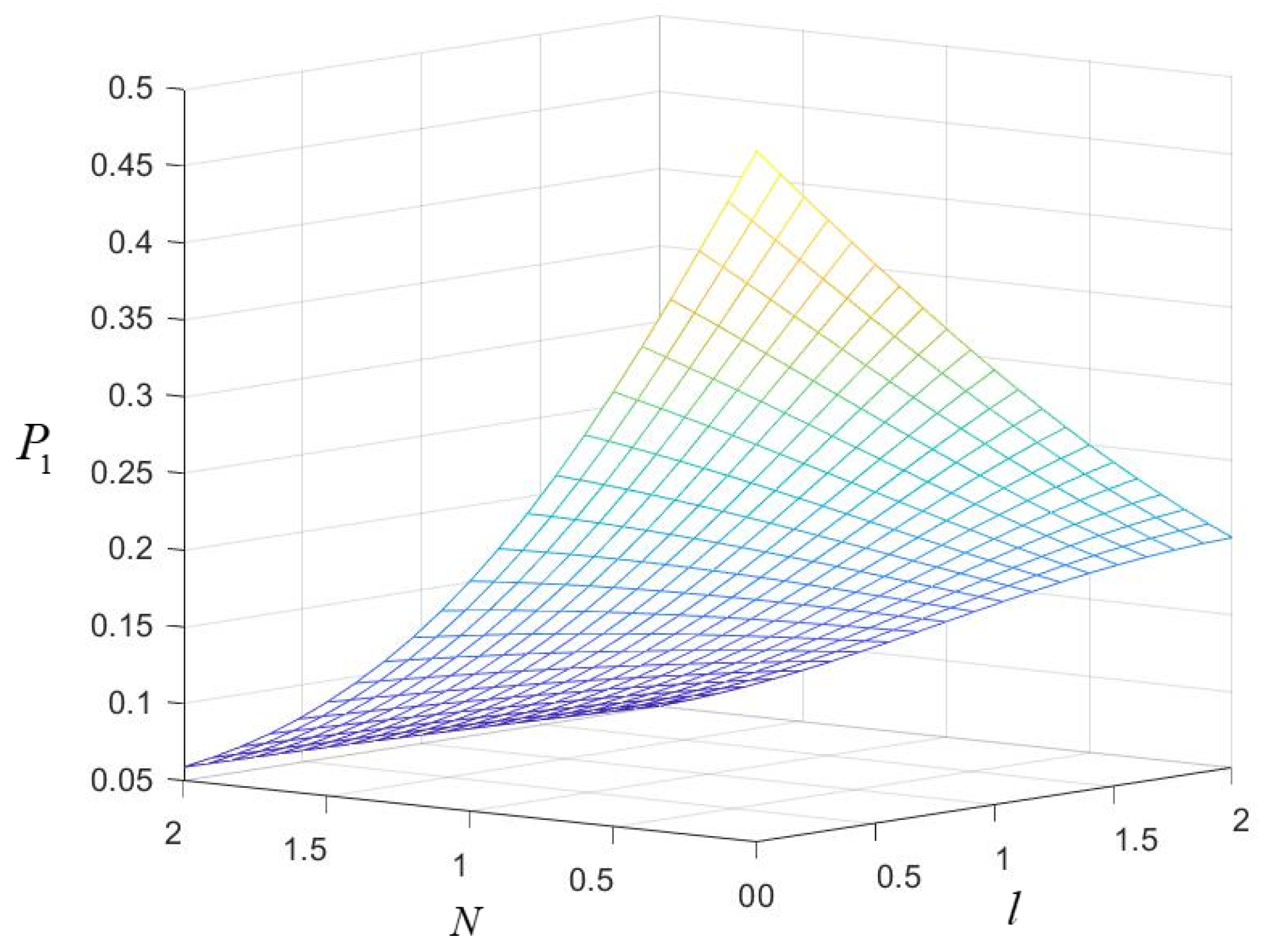
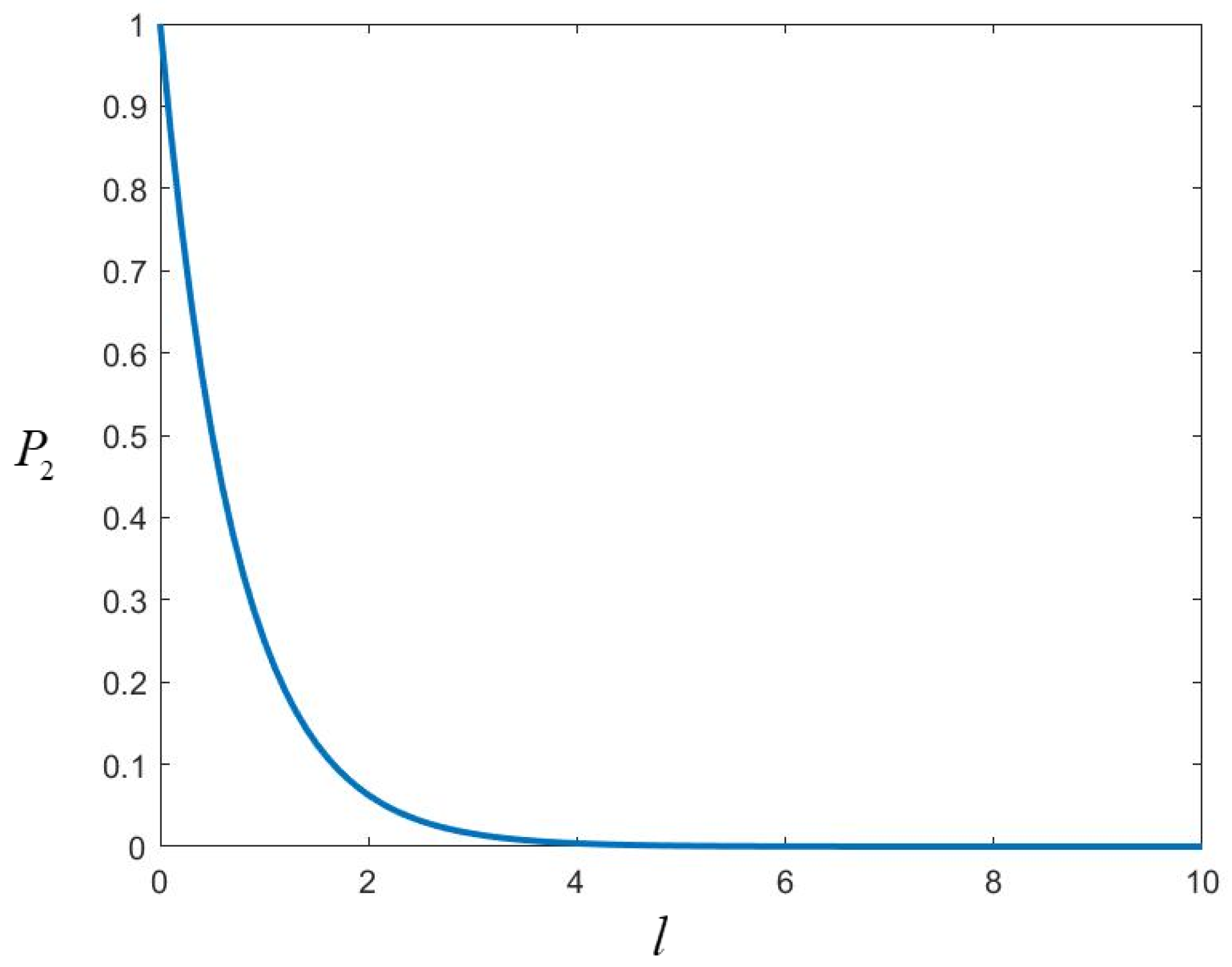
4.2. Analysis of Security

To protect the privacy of bidders and the fairness of the auction process, the issue of security in the QSA requires following the rules [32]: (1) The outer eavesdroppers cannot obtain any messages about bids; (2) Any bidder or a group of bidders cannot obtain the secret bid messages of other bidders; (3) A malicious bidder or a group of malicious bidders can collude with the dishonest auctioneer, but they cannot escape detection by the auction center during the verification stage.

4.2.1. Intercept-Resend Attack

$Eve$ is an eavesdropper who wishes to intercept the sequence during the quantum sequence transmission process and tries to recover the secret message. In comparison, it is optimal to intercept the sequence at Step 8 of the auction stage. During the transmission from $Bo{b}_i$ to $Alice,Eve$ intercepts $|S_1^2\rangle ,|S_1^3\rangle$ and replaces them with $|S_1^2{\rangle }^{″},{|S_1^3\rangle }^{″}$ at the same time. However, since $Eve$ does not know the locations of all the decoy photons and the corresponding measurement bases, $Alice$ will receive the wrong measurement results after performing eavesdropping detection. Of course, $Bo{b}_i$ will find out that he is being eavesdropped on instantly, and then this transmission will be interrupted. Consequently, the malicious eavesdropper will not receive any secret messages.

Actually, the decoy photons can prevent the outer eavesdroppers from gaining the bids of bidders efficiently. Even if $Eve$ is lucky enough not to be discovered, the probability of choosing the correct bases will be $\frac{1}{2^N}$. She can only know at most two of the three quantum sequences. If he tries to guess $|S_1^1\rangle$, the probability of being correct is $\frac{1}{4^l}$. Finally, the probability $P_1$=$\frac{1}{2^N}·\frac{1}{4^l}$ of $Eve$’s attack being found tends to be 0 in Figure 4. When $l,N$ is sufficiently large, it is almost impossible for $Eve$ to succeed in his guess.

In short, $Eve$ does not have access to the secret messages of bidders in any way.

4.2.2. TP’s Attack

It is assumed that the third party $Trent$ intentionally steals the bid message from the bidder $Bo{b}_i$. In the proposed protocol, $Trent$ has complete access to obtaining $|S_k^1\rangle ,|S_k^3\rangle$ of $Bo{b}_i$ after Step 6 and Step 8 in the auction stage. Then, since $Trent$ is supposed to be semi-honest, he cannot collude with other participants. If $Trent$ intercepts $|S_k^2\rangle$ sent by $Bo{b}_i$ to $Bo{b}_j$ in Step 7, $Bo{b}_i$ will realize that he is being eavesdropped because of the presence of the decoy photons. The protocol will be terminated at once. In fact, $Trent$ will not obtain $|S_k^2\rangle$. Thus, if $Trent$ wants to obtain complete the message about the bid, he must infer the true $|S_k^2\rangle$. According to the special properties of LIOP states, $Trent$ guesses that the probability of success is $P_2$=$\frac{1}{4^l}$ in Figure 5. When l is large enough, the probability of being correct is negligible. Therefore, without colluding with any party, $Trent$ cannot obtain the private bid messages of the participants.

4.2.3. Collusion Attack

There are two types of collusion attacks: (1) A group of bidders collude with each other to obtain the bid of the honest bidder; (2) A malicious bidder colludes with the dishonest auctioneer to win the auction illegally.

Case 1: Here, some bidders conspired as dishonest participants to steal $Bo{b}_i$’s secret message. No matter how many bidders collude, they can only obtain $|S_k^2\rangle$. In fact, even $n-1$ dishonest bidders cannot collusively obtain any secret messages about the bid $M_i$. Based on the previous analysis of the external interception of retransmission attack, obviously, it is not feasible for a group of malicious bidders to intercept messages from other steps due to the presence of decoy photons. Accordingly, their collusion is feasible only if they guess $|S_k^1\rangle$ and $|S_k^3\rangle$, and the probability of guessing correctly is $P_3$=$\frac{1}{4^{2l}}$ in Figure 6.

Case 2: The issue of malicious bidders colluding with the auctioneer in a QSA protocol is very noteworthy. As an auctioneer, he will finally collect the secret messages of all the bidders and compare the highest price to come up with the winner. Accordingly, a malicious bidder who conspires with the auctioneer must know the bids of other bidders, and he wants to change his bid to win the auction at the most appropriate price.

In Step 9 of our protocol, $Alice$ measures and gets the bids of all bidders, at which point he conspires with a malicious bidder to make him change his bid. Then, $Alice$ will announce that the bidder with the changed price is the winner, and the auction center $Trent$ will verify whether the winner’s bid has changed. In fact, all bidders have sent some of their messages to other bidders in Step 7. If the malicious bidder changes his particles, the final verification result will be different from the price announced by $Alice$. Therefore, the presence of the auction center in our protocol is particularly important. With the verification of the auction center, he is able to quickly detect whether the winner’s bid message has been altered.

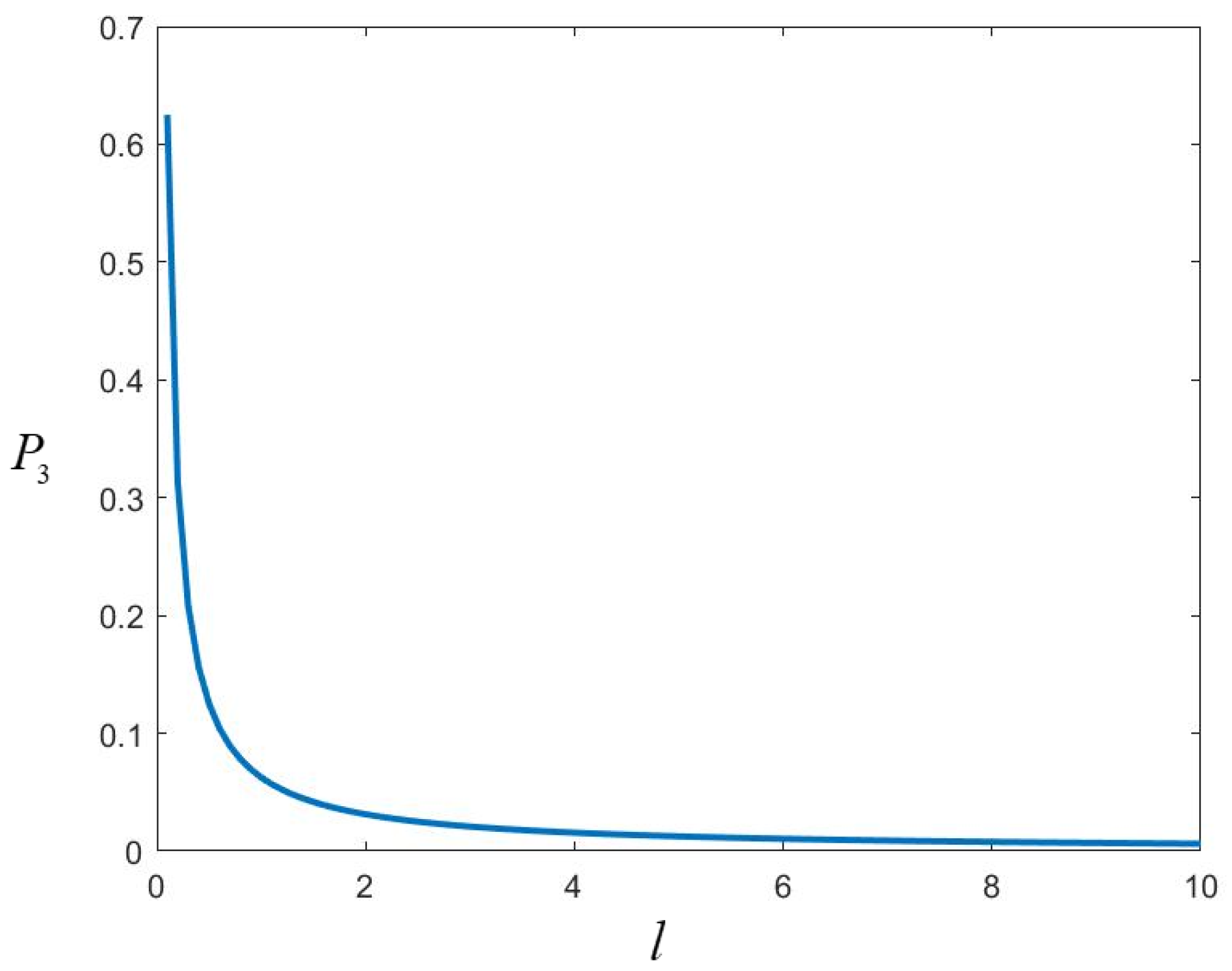
4.2.4. Entangle-Measure Attack

Next, we consider the entangle-measure attack. Supposing that an outsider $Eve$ wants to obtain the bid of the bidder $Bo{b}_i$ by performing an entangle-measure attack. We suppose $Eve$ prepares an additional photon $|e\rangle$ when the qubits are sent from $Bo{b}_i$ to $Alice$ and performs operation U on the system composed of decoy photons {$|0\rangle ,|1\rangle ,|+\rangle ,|-\rangle$} and the additional photon. We can obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill U|0\rangle |e\rangle & ={\alpha }_0|0\rangle |e_{00}\rangle +{\beta }_0|1\rangle |e_{01}\rangle \hfill \\ \hfill U|1\rangle |e\rangle & ={\alpha }_1|0\rangle |e_{10}\rangle +{\beta }_1|1\rangle |e_{11}\rangle \hfill \end{array}\end{array}$$

(6)

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill U|+\rangle |e\rangle & =\frac{1}{\sqrt{2}}\left({\alpha }_0\right|0\rangle |e_{00}\rangle +{\beta }_0|1\rangle |e_{01}\rangle )\hfill \\ \hfill & +\frac{1}{\sqrt{2}}\left({\alpha }_1\right|0\rangle |e_{10}\rangle +{\beta }_1|1\rangle |e_{11}\rangle )\hfill \\ \hfill & =\frac{1}{2}\left(\right|+\rangle \left({\alpha }_0\right|e_{00}\rangle +{\beta }_0|e_{01}\rangle \left)\right)\hfill \\ \hfill & +\frac{1}{2}\left(\right|+\rangle \left({\alpha }_1\right|e_{10}\rangle +{\beta }_1|e_{11}\rangle \left)\right)\hfill \\ \hfill & +\frac{1}{2}\left(\right|-\rangle \left({\alpha }_0\right|e_{00}\rangle -{\beta }_0|e_{01}\rangle \left)\right)\hfill \\ \hfill & +\frac{1}{2}\left(\right|-\rangle \left({\alpha }_1\right|e_{10}\rangle -{\beta }_1|e_{11}\rangle \left)\right)\hfill \end{array}\end{array}$$

(7)

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill U|-\rangle |e\rangle & =\frac{1}{\sqrt{2}}\left({\alpha }_0\right|0\rangle |e_{00}\rangle +{\beta }_0|1\rangle |e_{01}\rangle )\hfill \\ \hfill & -\frac{1}{\sqrt{2}}\left({\alpha }_1\right|0\rangle |e_{10}\rangle +{\beta }_1|1\rangle |e_{11}\rangle )\hfill \\ \hfill & =\frac{1}{2}\left(\right|+\rangle \left({\alpha }_0\right|e_{00}\rangle +{\beta }_0|e_{01}\rangle \left)\right)\hfill \\ \hfill & -\frac{1}{2}\left(\right|+\rangle \left({\alpha }_1\right|e_{10}\rangle +{\beta }_1|e_{11}\rangle \left)\right)\hfill \\ \hfill & +\frac{1}{2}\left(\right|-\rangle \left({\alpha }_0\right|e_{00}\rangle -{\beta }_0|e_{01}\rangle \left)\right)\hfill \\ \hfill & -\frac{1}{2}\left(\right|-\rangle \left({\alpha }_1\right|e_{10}\rangle -{\beta }_1|e_{11}\rangle \left)\right)\hfill \end{array}\end{array}$$

(8)

In order not to change the state of the original particle, it is necessary to satisfy

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \left\{\begin{array}{c}{\beta }_0|e_{01}\rangle =0,\hfill \\ {\alpha }_1|e_{10}\rangle =0,\hfill \\ {\alpha }_0|e_{00}\rangle +{\beta }_0|e_{01}\rangle -{\alpha }_1|e_{10}\rangle -{\beta }_1|e_{11}\rangle =0\hfill \end{array}\right.\end{array}\end{array}$$

(9)

Obviously, ${\alpha }_0|e_{00}\rangle ={\beta }_1|e_{11}\rangle$. It means that $Eve$ cannot distinguish between ${\alpha }_0|e_{00}\rangle$ and ${\beta }_1|e_{11}\rangle$. Consequently, the proposed protocol can resist the entangle-measure attack.

4.3. Analysis of Completeness

Next, we will continue to demonstrate that our proposed protocol meets the requirements for a secure auction, including Anonymity, Public verifiability, Accountability of bidder, Fairness, Traceability, and Non-repudiation.

(1)

Anonymity

In our protocol, the bidder applies and registers with the auction center before the auction starts, and bidders use pseudonyms to participate in the entire auction process. As a result, except for the auction center, no one can obtain any information about the bidder’s identity.

(2)

Public verifiability

Our proposed protocol incorporates a semi-honest auction center for verifying that a bidder has legitimately won the auction, and any bidder can participate in the verification process of the winner. In Step 7 of the auction stage, each bidder is required to send the same sequence to all other $n-1$ bidders. Finally, they assist the auction center during the verification process, confirming that the winning bidder’s price has not changed in the verification stage. Thus, our protocol is able to satisfy public verifiability.

(3)

Accountability of bidder

By analyzing the security of the collusion attack, where the semi-honest third party and other bidders serve as monitors, it is clear that any malicious fake bidders cannot interrupt the auction without being detected. That is, it meets accountability of bidder.

(4)

Fairness

All bidders perform the same auction procedure before the bid opening, so there is no bias. In addition, under case 2 of the collusive attack analysis, the auctioneer cannot collude with any malicious bidders to help him win the auction legally.

(5)

Traceability

Since the auction center records the correspondence between the pseudonym and the real identity of the bidder, $Trent$ can verify the identity of the winner during the verification phase.

(6)

Non-repudiation

In our protocol, the post-confirmation mechanism ensures that the bidder cannot deny having placed a bid on $Alice$. Concurrently, auctioneer $Alice$ cannot deny having received bids from bidders. Whether a group of bidders conspires or a dishonest bidder and a dishonest auctioneer conspire, the non-repudiation of the participants is satisfied.

5. Conclusions and Perspectives

In this paper, a new QSA protocol based on LIOP states is proposed. In this protocol, bid messages are encoded as a sequence of LIOP states, and different particles of LIOP states containing bid messages are transmitted separately. The indistinguishability of LIOP states guarantees the security of secret messages. The analysis of security shows that neither an external attacker nor a group of bidders colluding can obtain any secret messages. In addition, the auctioneer’s collusion with the bidders is immediately detected. Compared with previous protocols, our protocol is easier to implement because it does not introduce entanglement. Finally, due to the high privacy protection and availability, it is hoped that the proposed scheme has a wider application prospect. The properties of LIOP states provide new perspectives for the design of future quantum cryptography protocols.