Author Contributions
Conceptualization, L.Z.; Methodology, L.Z.; Validation, L.Z., M.A., X.L. and W.W.; Analysis, L.Z., M.A., X.L. and W.W.; Investigation, L.Z.; Resources, L.Z.; Data Curation, L.Z.; Writing—Original Draft Preparation, L.Z.; Writing—Review & Editing, L.Z. All authors have read and agreed to the published version of the manuscript.
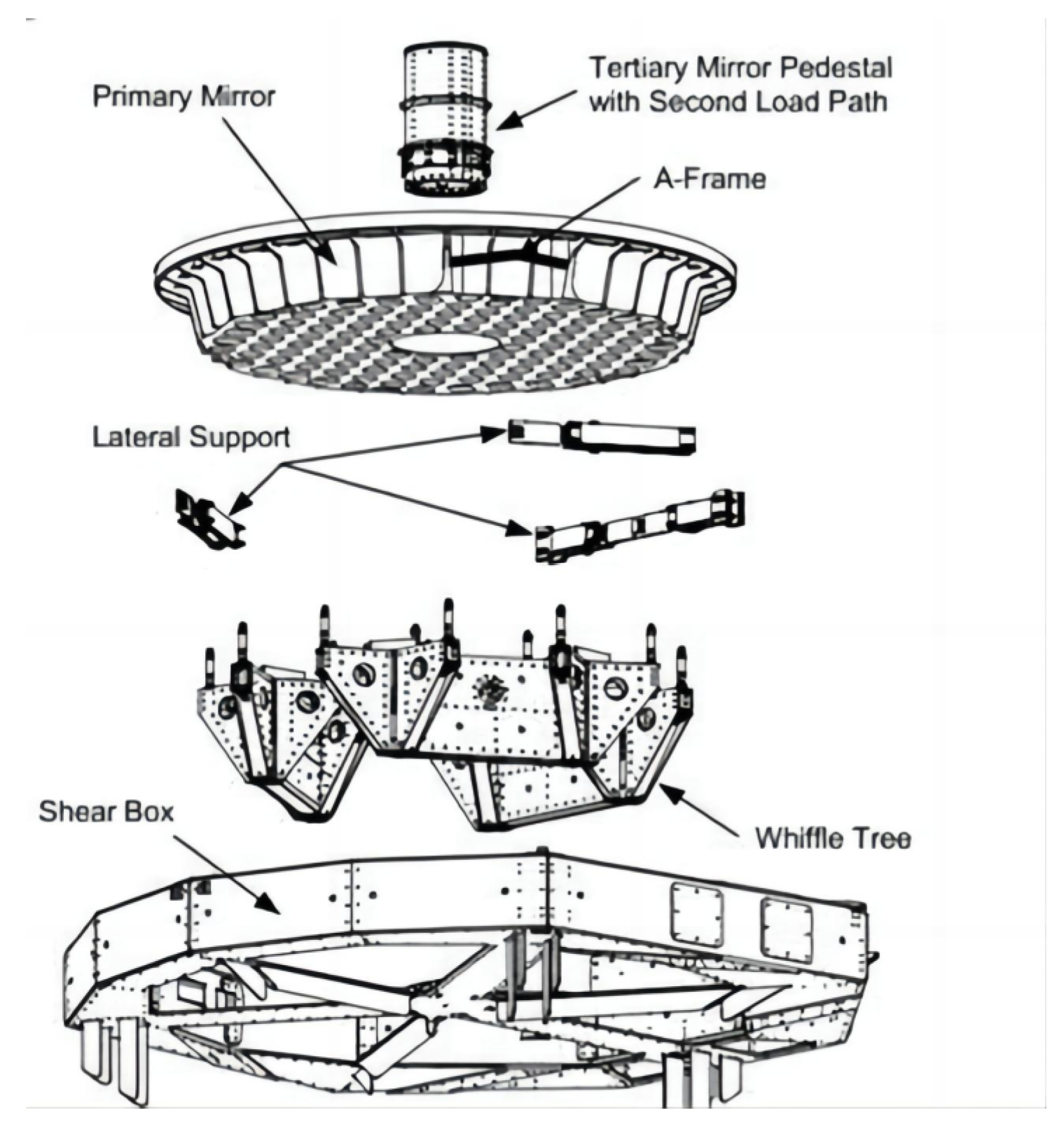
Figure 1.
The whiffletree support structure of the SOFIA telescope.
Figure 1.
The whiffletree support structure of the SOFIA telescope.
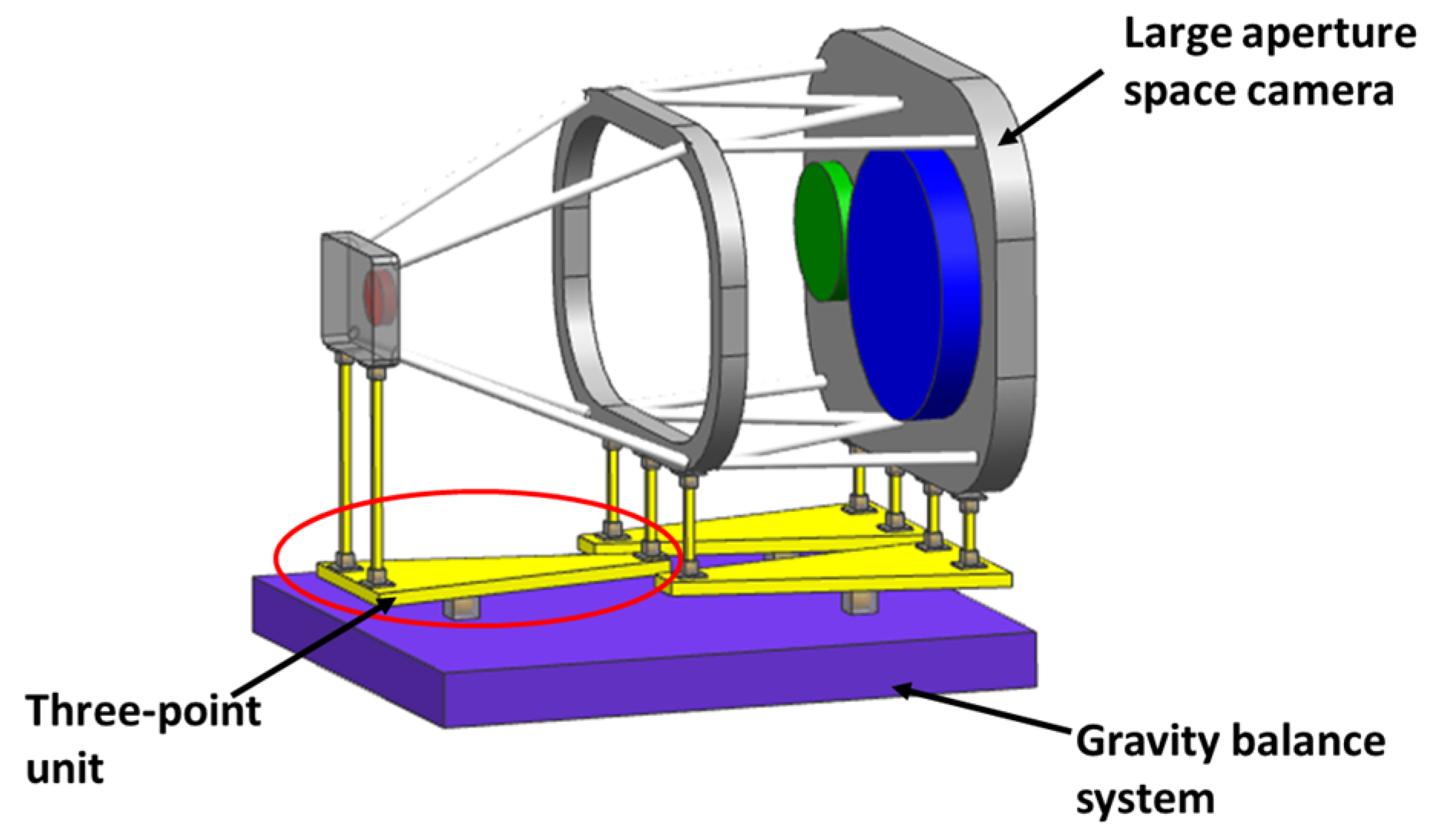
Figure 2.
Schematic diagram of the gravity balance system of a large-aperture space camera.
Figure 2.
Schematic diagram of the gravity balance system of a large-aperture space camera.
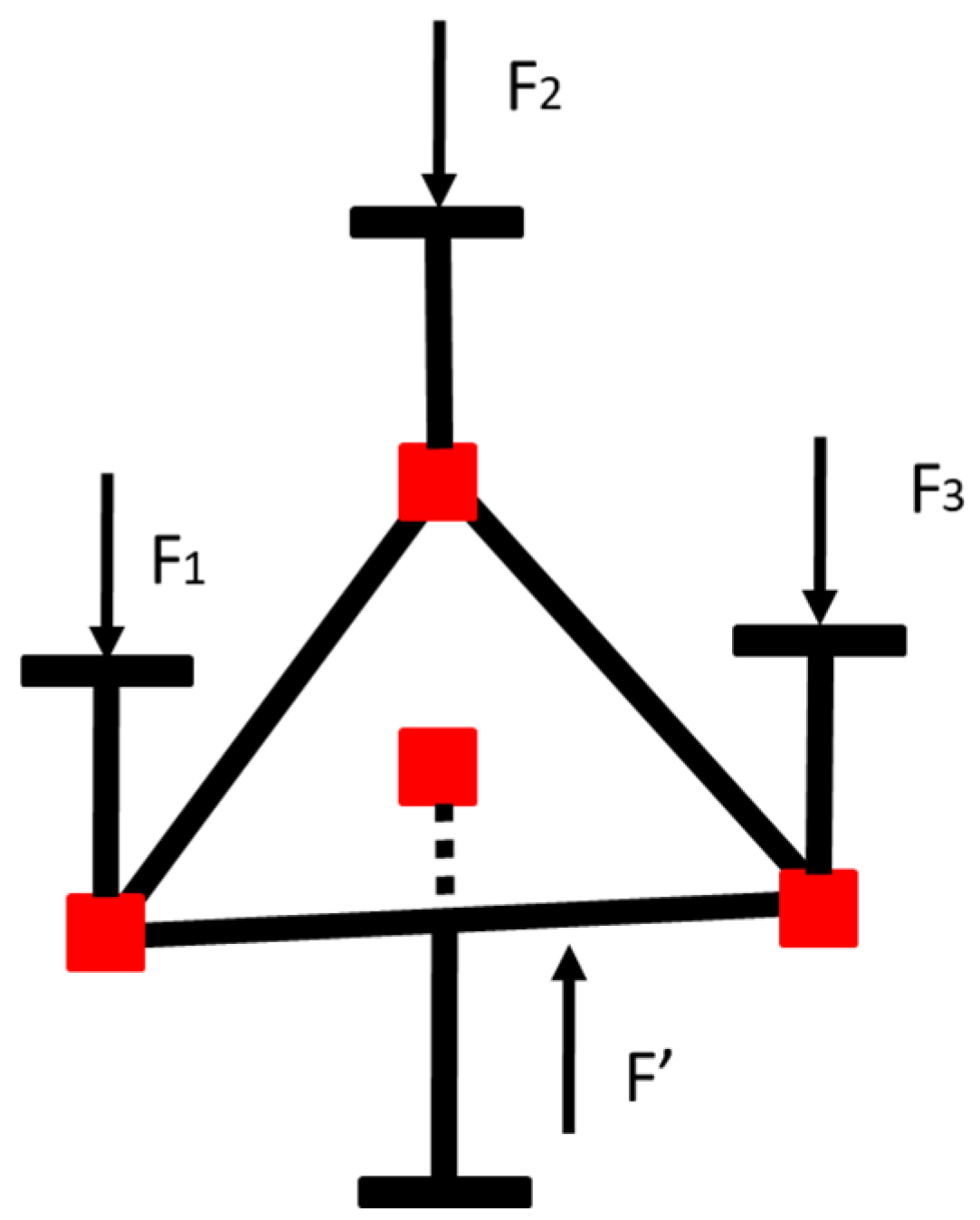
Figure 3.
Schematic diagram of three-point unit.
Figure 3.
Schematic diagram of three-point unit.
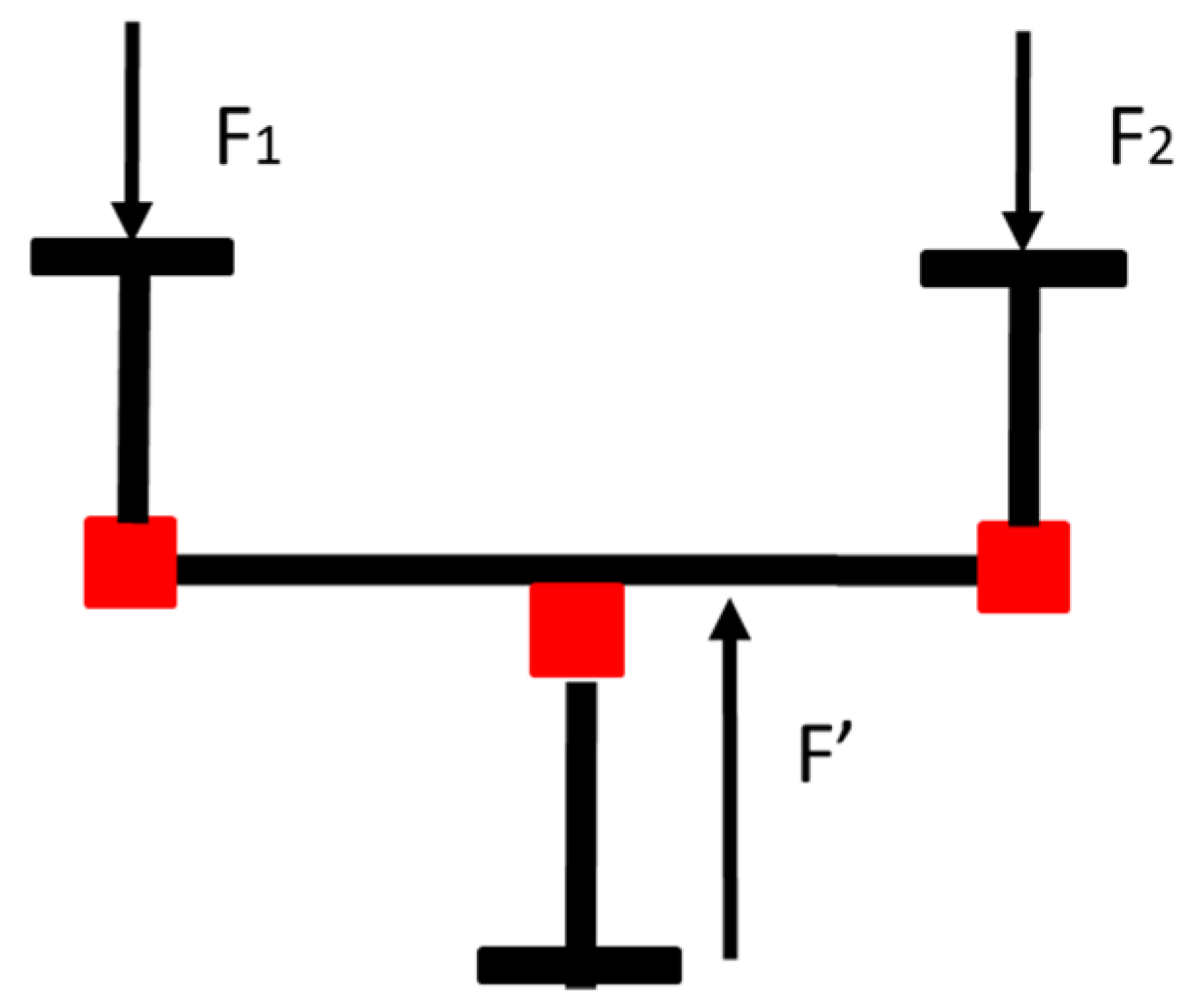
Figure 4.
Schematic diagram of two-point unit.
Figure 4.
Schematic diagram of two-point unit.
Figure 5.
Single-stage schematic diagram.
Figure 5.
Single-stage schematic diagram.
Figure 6.
Large-aperture space camera.
Figure 6.
Large-aperture space camera.
Figure 7.
The distribution of gravity balance point of a large-aperture space camera. Point 1, 2, 3, 4 on the front frame; Point 5, 6, 7 on the first middle frame; Point 8,9,10 on the second middle frame; Point 11, 12, 13, 14, 15 on the main frame.
Figure 7.
The distribution of gravity balance point of a large-aperture space camera. Point 1, 2, 3, 4 on the front frame; Point 5, 6, 7 on the first middle frame; Point 8,9,10 on the second middle frame; Point 11, 12, 13, 14, 15 on the main frame.
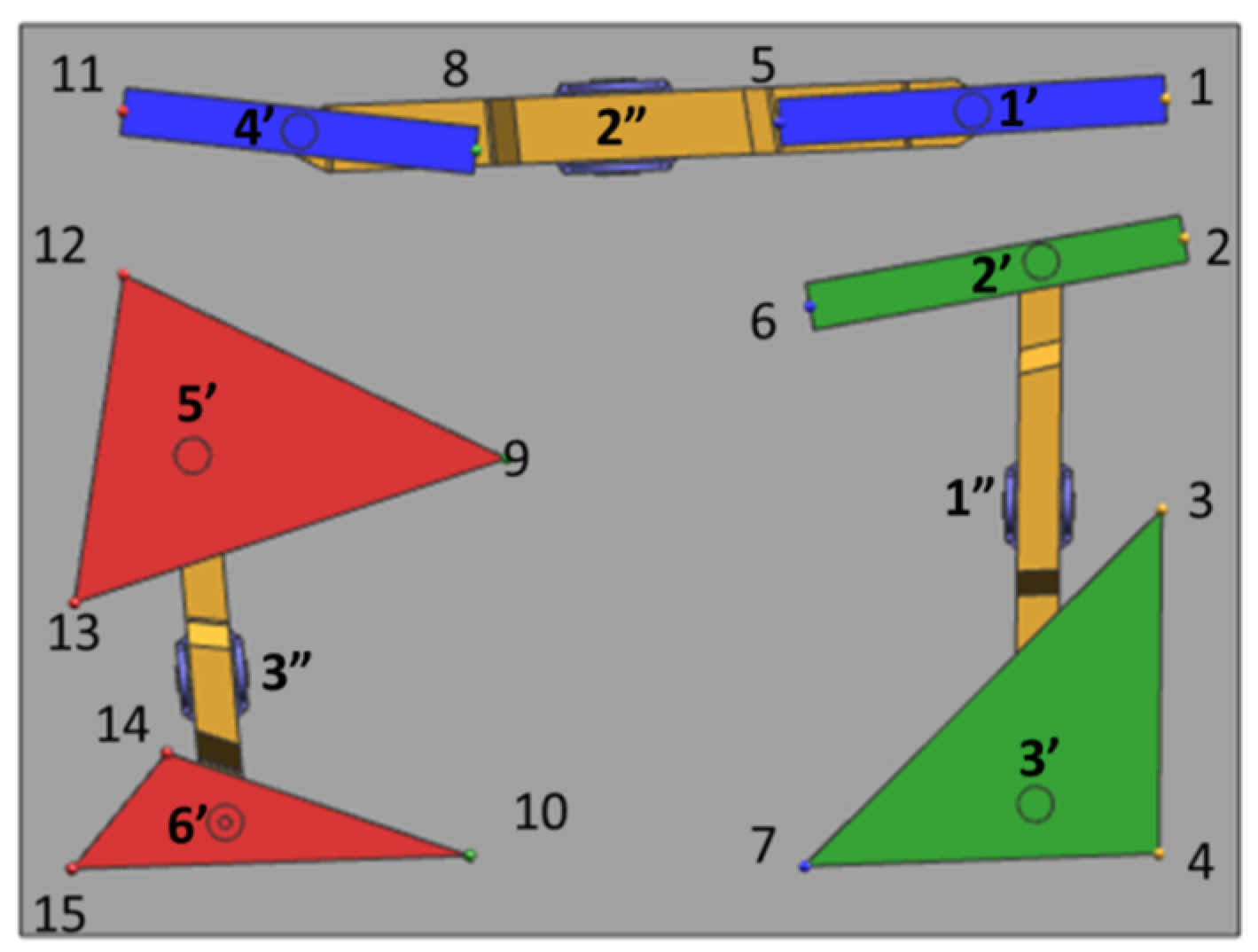
Figure 8.
The multi-point gravity balance system. Point 1, 2, 3, 4 on the front frame; Point 5, 6, 7 on the first middle frame; Point 8, 9, 10 on the second middle frame; Point 11, 12, 13, 14, 15 on the main frame.
Figure 8.
The multi-point gravity balance system. Point 1, 2, 3, 4 on the front frame; Point 5, 6, 7 on the first middle frame; Point 8, 9, 10 on the second middle frame; Point 11, 12, 13, 14, 15 on the main frame.
Figure 9.
The finite element model of the large-aperture space camera and the gravity balance system.
Figure 9.
The finite element model of the large-aperture space camera and the gravity balance system.
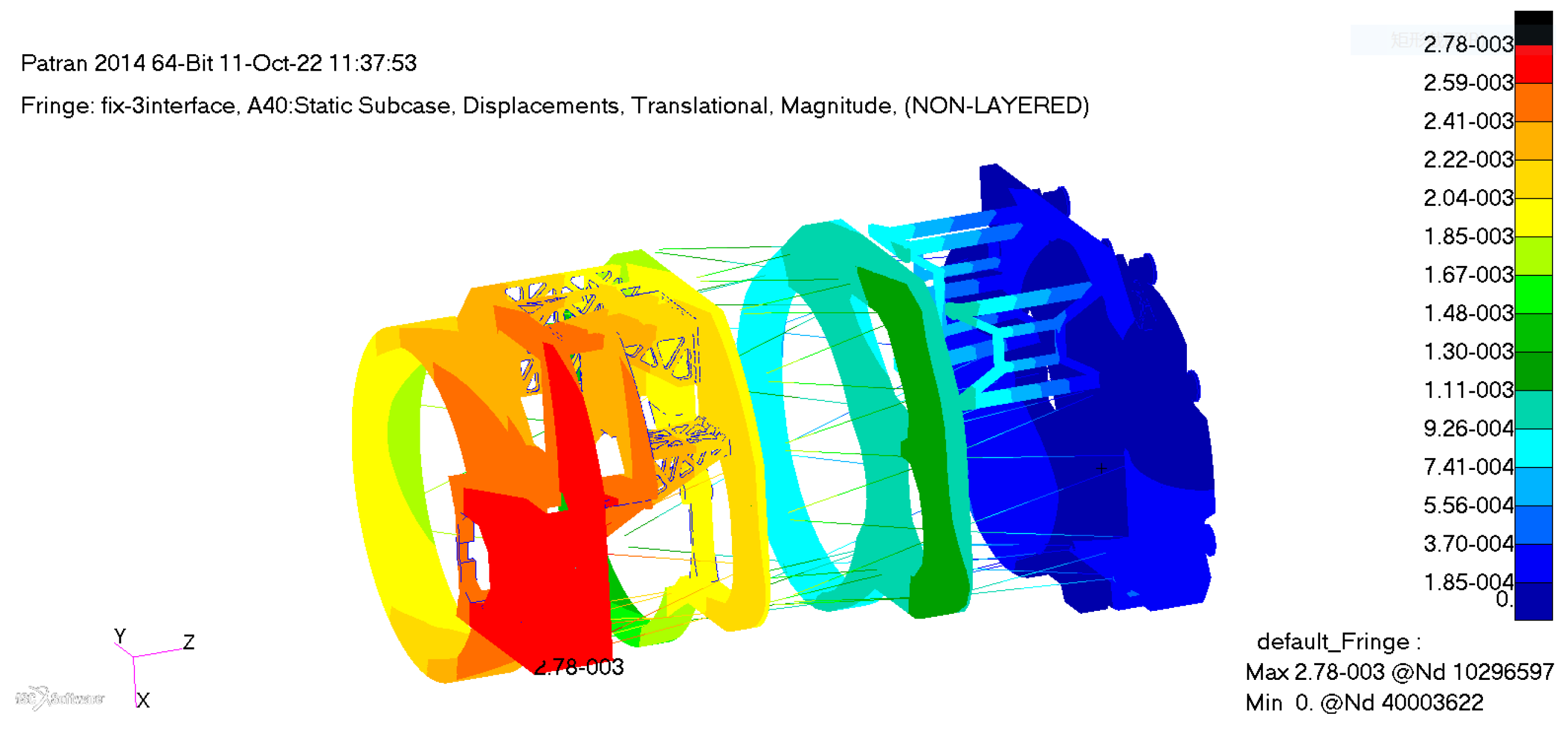
Figure 10.
The displacement of the large-aperture space camera under the traditional support.
Figure 10.
The displacement of the large-aperture space camera under the traditional support.
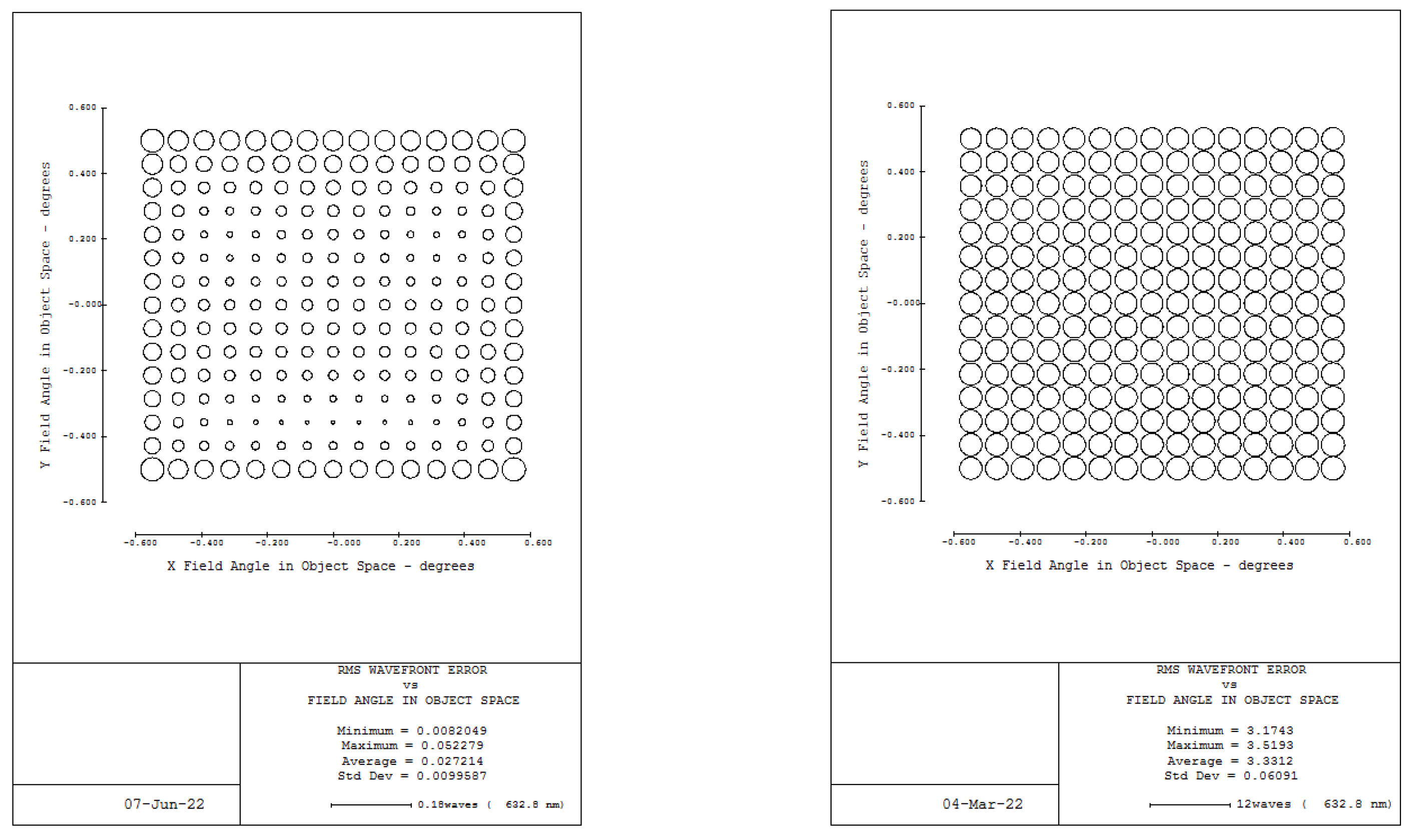
Figure 11.
The WFE of the large-aperture space camera under the traditional support.
Figure 11.
The WFE of the large-aperture space camera under the traditional support.
Figure 12.
The displacement of the large-aperture space camera under the gravity balance system.
Figure 12.
The displacement of the large-aperture space camera under the gravity balance system.
Figure 13.
The WFE of the large-aperture space camera under the gravity balance system.
Figure 13.
The WFE of the large-aperture space camera under the gravity balance system.
Table 1.
The location coordinates of 15 unloading points.
Table 1.
The location coordinates of 15 unloading points.
| Unloading Point | X (m) | Y (m) | Z (m) |
|---|
| 1 | 0.490 | −0.701 | −4.220 |
| 2 | 0.490 | −0.061 | −4.220 |
| 3 | 0.693 | 0.590 | −4.154 |
| 4 | 0.381 | 2.775 | −4.154 |
| 5 | 0.308 | −0.780 | −2.862 |
| 6 | 0.550 | 0.278 | −2.868 |
| 7 | 0.256 | 2.793 | −2.861 |
| 8 | 0.673 | −0.508 | −1.416 |
| 9 | 0.705 | 0.392 | −1.416 |
| 10 | 0.755 | 2.560 | −1.412 |
| 11 | 0.809 | −0.611 | 0.300 |
| 12 | 0.888 | −0.050 | 0.300 |
| 13 | 1.080 | 0.597 | 0.300 |
| 14 | 1.185 | 1.706 | 0.251 |
| 15 | 0.521 | 2.688 | 0.161 |
Table 2.
The main coefficients and the coupling coefficients.
Table 2.
The main coefficients and the coupling coefficients.
| 1 | 2 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 13 | 14 |
|---|
| 1 | 5.40 × 10−8 | 3.03 × 10−8 | −1.12 × 10−8 | 3.71 × 10−8 | 2.07 × 10−8 | −9.63 × 10−9 | 1.90 × 10−8 | 1.19 × 10−8 | −5.09 × 10−9 | 2.92 × 10−11 | −8.00 × 10−11 | −2.32 × 10−10 |
| 2 | 3.03 × 10−8 | 2.21 × 10−8 | −2.76 × 10−9 | 2.11 × 10−8 | 1.32 × 10−8 | −2.70 × 10−9 | 1.09 × 10−8 | 7.24 × 10−9 | −1.49 × 10−0 | −9.00 × 10−12 | −8.80 × 10−11 | −1.70 × 10−10 |
| 4 | −1.12 × 10−8 | −2.76 × 10−9 | 1.13 × 10−7 | −1.02 × 10−8 | 1.10 × 10−8 | 7.38 × 10−8 | −3.68 × 10−9 | 7.88 × 10−9 | 3.74 × 10−8 | −4.64 × 10−10 | −7.99 × 10−10 | −4.92 × 10−10 |
| 5 | 3.71 × 10−8 | 2.11 × 10−8 | −1.02 × 10−8 | 5.49 × 10−8 | 2.96 × 10−8 | −7.79 × 10−9 | 2.64 × 10−8 | 1.71 × 10−8 | −2.94 × 10−9 | 2.67 × 10−10 | 2.65 × 10−10 | −2.20 × 10−11 |
| 6 | 2.07 × 10−8 | 1.32 × 10−8 | 1.10 × 10−8 | 2.96 × 10−8 | 4.48 × 10−8 | 9.46 × 10−9 | 1.68 × 10−8 | 1.44 × 10−8 | 6.65 × 10−9 | 1.51 × 10−10 | 1.29 × 10−10 | −6.20 × 10−11 |
| 7 | −9.63 × 10−9 | −2.70 × 10−9 | 7.38 × 10−8 | −7.79 × 10−9 | 9.46 × 10−9 | 7.42 × 10−8 | −1.52 × 10−9 | 9.08 × 10−0 | 3.75 × 10−8 | −2.28 × 10−10 | −3.78 × 10−10 | −2.39 × 10−10 |
| 8 | 1.90 × 10−8 | 1.09 × 10−8 | −3.68 × 10−9 | 2.64 × 10−8 | 1.68 × 10−8 | −1.52 × 10−9 | 3.30 × 10−8 | 2.21 × 10−8 | 2.02 × 10−9 | 5.01 × 10−10 | 6.13 × 10−10 | 1.93 × 10−10 |
| 9 | 1.19 × 10−8 | 7.24 × 10−9 | 7.88 × 10−9 | 1.71 × 10−8 | 1.44 × 10−8 | 9.08 × 10−9 | 2.21 × 10−8 | 2.41 × 10−8 | 9.33 × 10−9 | 4.88 × 10−10 | 6.57 × 10−10 | 2.41 × 10−10 |
| 10 | −5.09 × 10−9 | −1.49 × 10−9 | 3.74 × 10−8 | −2.94 × 10−9 | 6.65 × 10−9 | 3.75 × 10−8 | 2.02 × 10−9 | 9.33 × 10−9 | 3.93 × 10−8 | 2.04 × 10−11 | 6.28 × 10−11 | 1.40 × 10−10 |
| 12 | 2.92 × 10−11 | −9.00 × 10−12 | −4.64 × 10−10 | 2.67 × 10−10 | 1.51 × 10−10 | −2.28 × 10−10 | 5.01 × 10−10 | 4.88 × 10−10 | 2.04 × 10−11 | 2.68 × 10−9 | 1.86 × 10−9 | 6.18 × 10−10 |
| 13 | −8.00 × 10−11 | −8.80 × 10−11 | −7.99 × 10−10 | 2.65 × 10−10 | 1.29 × 10−10 | −3.78 × 10−10 | 6.13 × 10−10 | 6.57 × 10−10 | 6.28 × 10−11 | 1.86 × 10−9 | 3.52 × 10−9 | 1.33 × 10−9 |
| 14 | −2.32 × 10−10 | −1.70 × 10−10 | −4.92 × 10−10 | −2.20 × 10−11 | −6.20 × 10−11 | −2.39 × 10−10 | 1.93 × 10−10 | 2.41 × 10−10 | 1.40 × 10−10 | 6.18 × 10−10 | 1.33 × 10−9 | 4.22 × 10−9 |
Table 3.
The free terms.
| | 1 | 2 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 13 | 14 |
|---|
| −3.04 × 10−4 | −3.30 × 10−4 | −6.81 × 10−4 | −4.03 × 10−4 | −5.79 × 10−4 | −4.99 × 10−4 | −4.28 × 10−4 | −5.15 × 10−4 | −2.54 × 10−4 | −1.56 × 10−5 | −4.40 × 10−5 | −1.50 × 10−5 |
Table 4.
Fifteen points input loads of the first stage.
Table 4.
Fifteen points input loads of the first stage.
| Load | F (N) | Load | F (N) |
|---|
| F1 | −3270.36 | F9 | −4575.70 |
| F2 | −4906.32 | F10 | −1985.09 |
| F3 | −1768.35 | F11 | −3243.11 |
| F4 | −3035.01 | F12 | −2657.57 |
| F5 | −3131.87 | F13 | −6133.72 |
| F6 | −3965.12 | F14 | −2611.90 |
| F7 | −2610.04 | F15 | −6017.92 |
| F8 | −3992.43 | - | - |
Table 5.
The first stage of the gravity balance system.
Table 5.
The first stage of the gravity balance system.
| First Stage | Load Point | F′ (N) | X (m) | Y (m) | Z (m) |
|---|
| 1′ | 1, 5 | −6402.23 | 1.3 | −0.740 | −3.556 |
| 2′ | 2, 6 | −8871.44 | 1.3 | 0.091 | −3.616 |
| 3′ | 3, 4, 7 | −7413.4 | 1.3 | 2.260 | −3.698 |
| 4′ | 8, 11 | −7235.54 | 1.3 | −0.554 | −0.647 |
| 5′ | 9, 12, 13 | −13,367 | 1.3 | 0.398 | −0.287 |
| 6′ | 10, 14, 15 | −10,614.9 | 1.3 | 2.422 | −0.111 |
Table 6.
The second stage of the gravity balance system.
Table 6.
The second stage of the gravity balance system.
| Second Stage | First Stage | F″ (N) | X (m) | Y (m) | Z (m) |
|---|
| 1″ | 2′ | −16,284.8 | 1.4 | 1.078 | −3.654 |
| 3′ |
| 2″ | 1′ | −13,637.8 | 1.4 | −0.641 | −2.012 |
| 4′ |
| 3″ | 5′ | −23,981.9 | 1.4 | 1.294 | −0.209 |
| 6′ |
Table 7.
The displacement of each mirror under the traditional support.
Table 7.
The displacement of each mirror under the traditional support.
| Mirror | Tx (μm) | Ty (μm) | Tz (μm) |
|---|
| Primary mirror | −50.58 | −1.85 | −121.26 |
| Secondary mirror | −2650.87 | −151.58 | −171.41 |
| Tertiary mirror | −38.88 | −2.99 | −154.84 |
Table 8.
The displacement of each mirror under the gravity balance system.
Table 8.
The displacement of each mirror under the gravity balance system.
| Mirror | Tx (μm) | Ty (μm) | Tz (μm) |
|---|
| Primary mirror | −7.32 | −20.48 | 1.30 |
| Secondary mirror | −16.85 | 57.23 | −9.88 |
| Tertiary mirror | −4.55 | −17.89 | −25.90 |