Quantum Secure Multi-Party Summation with Identity Authentication Based on Commutative Encryption
Abstract
1. Introduction
2. Quantum Commutative Encryption
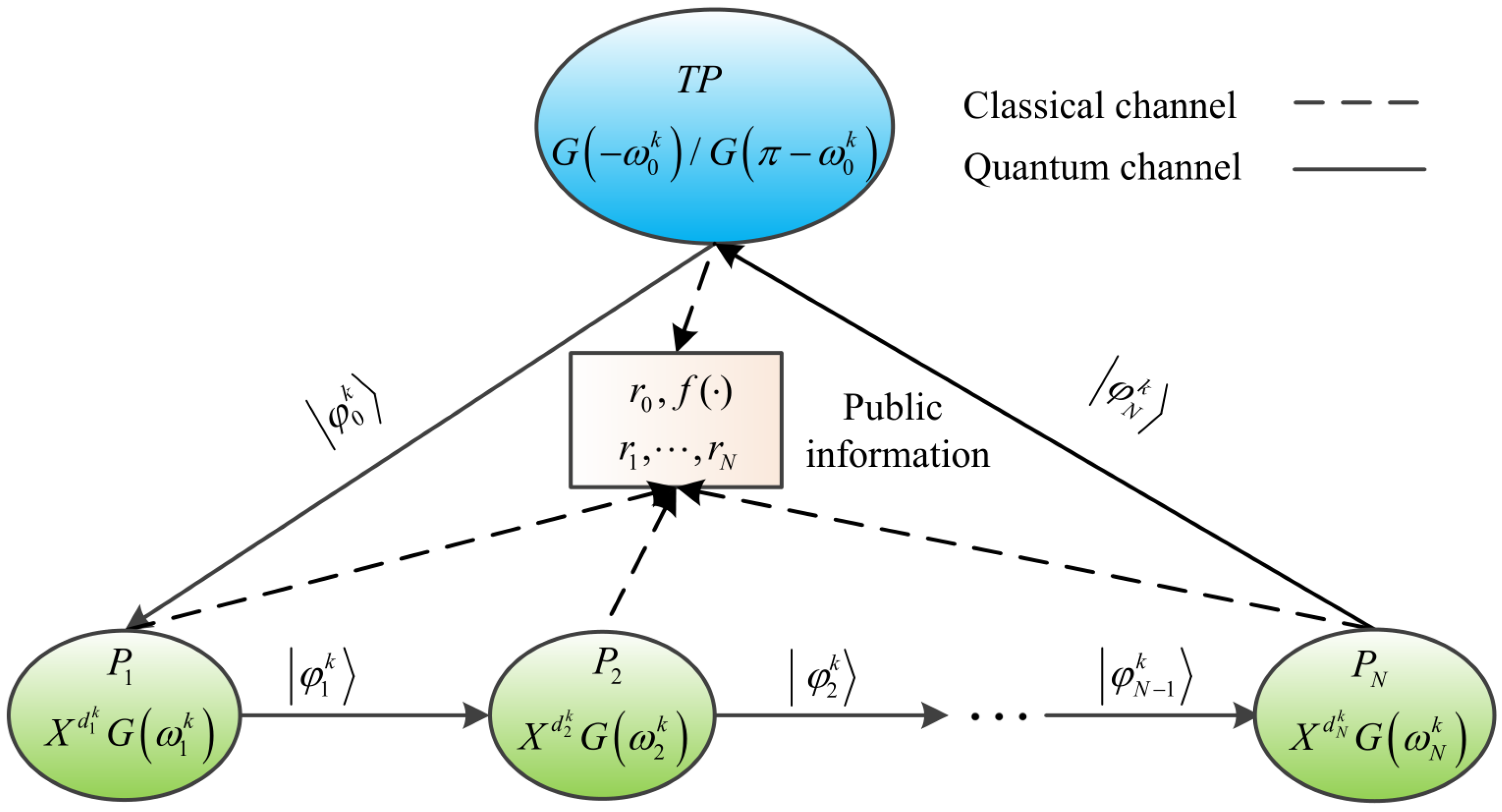
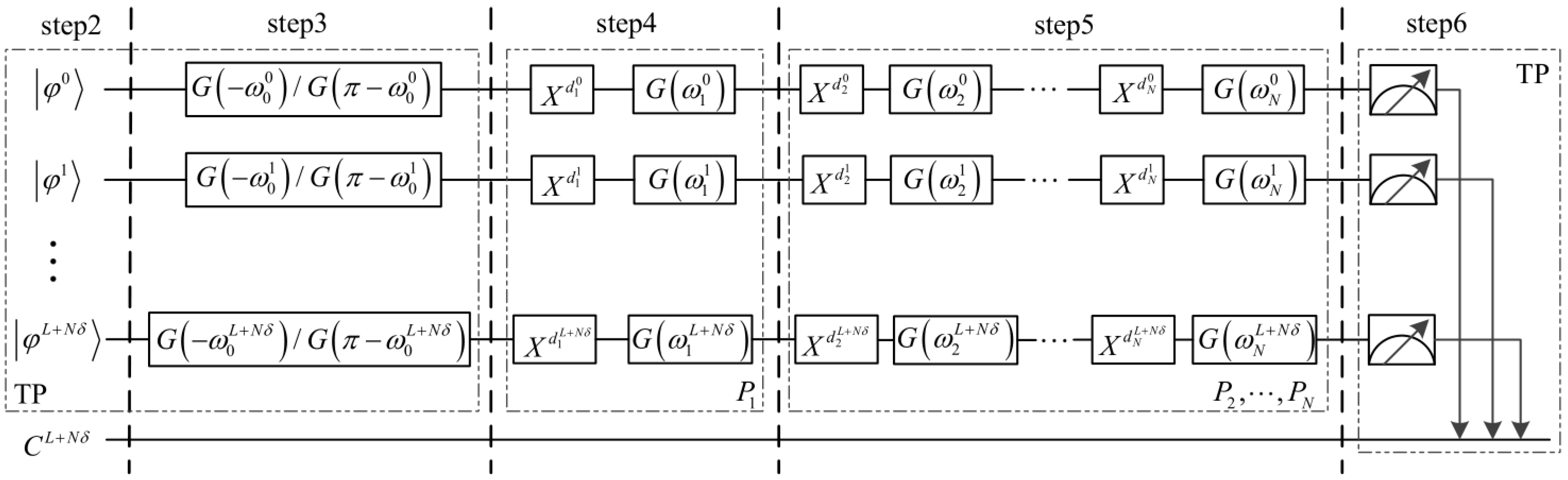
3. Quantum Secure Multi-Party Summation Protocol
4. Protocol Analysis
4.1. Correctness
4.2. Security
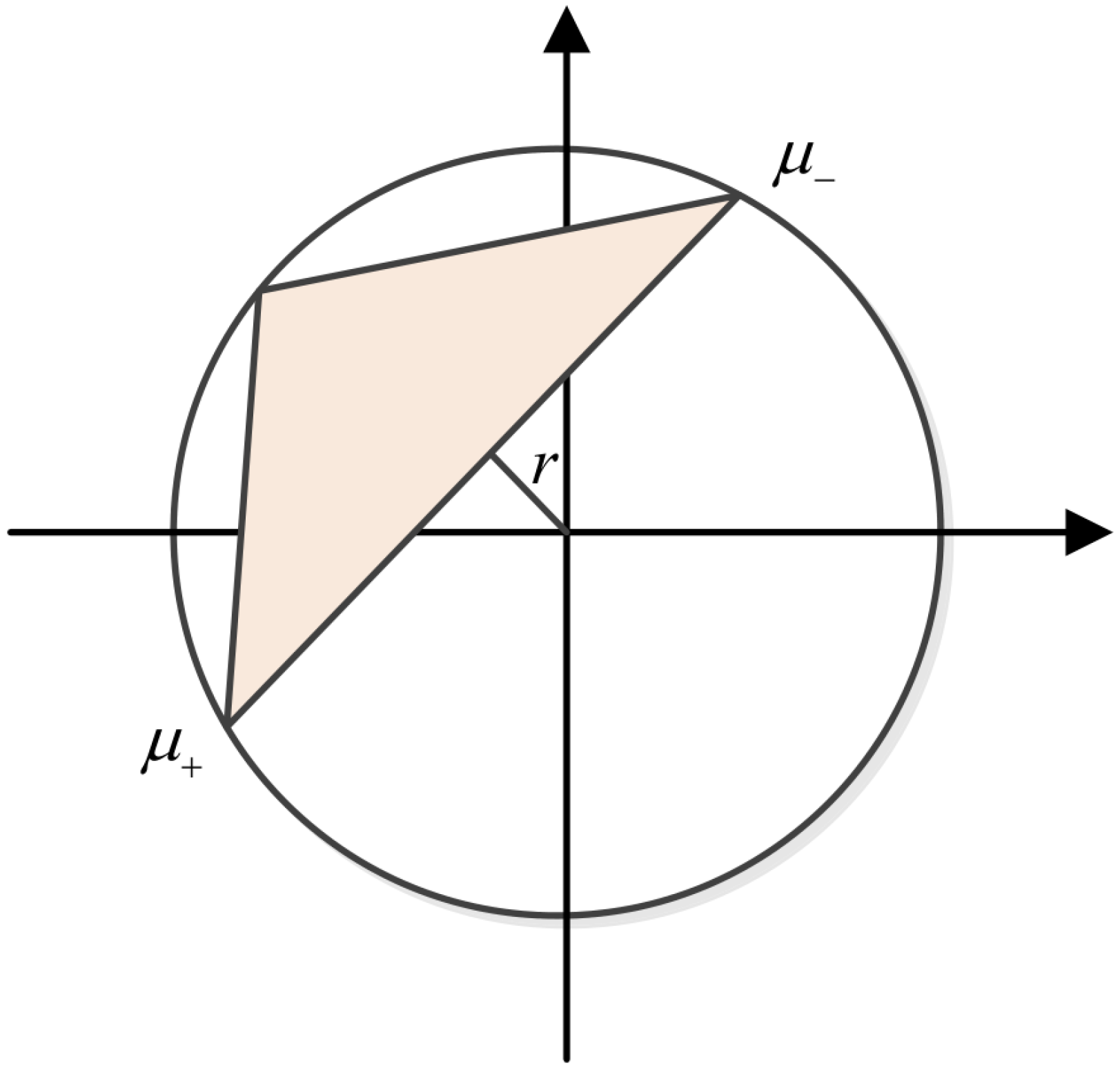
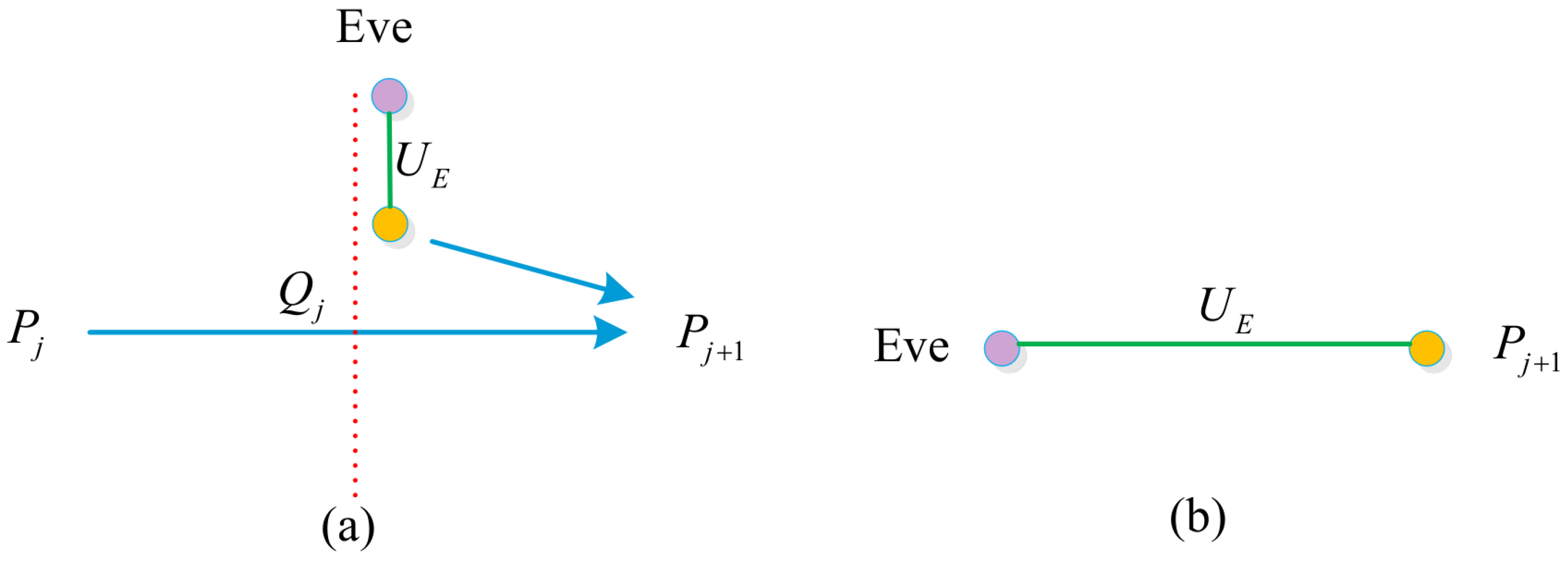
4.2.1. External Attack
- (1)
- Intercept resend attack
- (2)
- Entangle measure attack
- (3)
- Trojan Horse attacks
4.2.2. Internal Attack
- (1)
- A dishonest participant’s attack
- (2)
- Dishonest participants’ collusion attack
- (3)
- A semi-trusted third party’s attack
- (4)
- Impersonation attack
4.3. Comparison
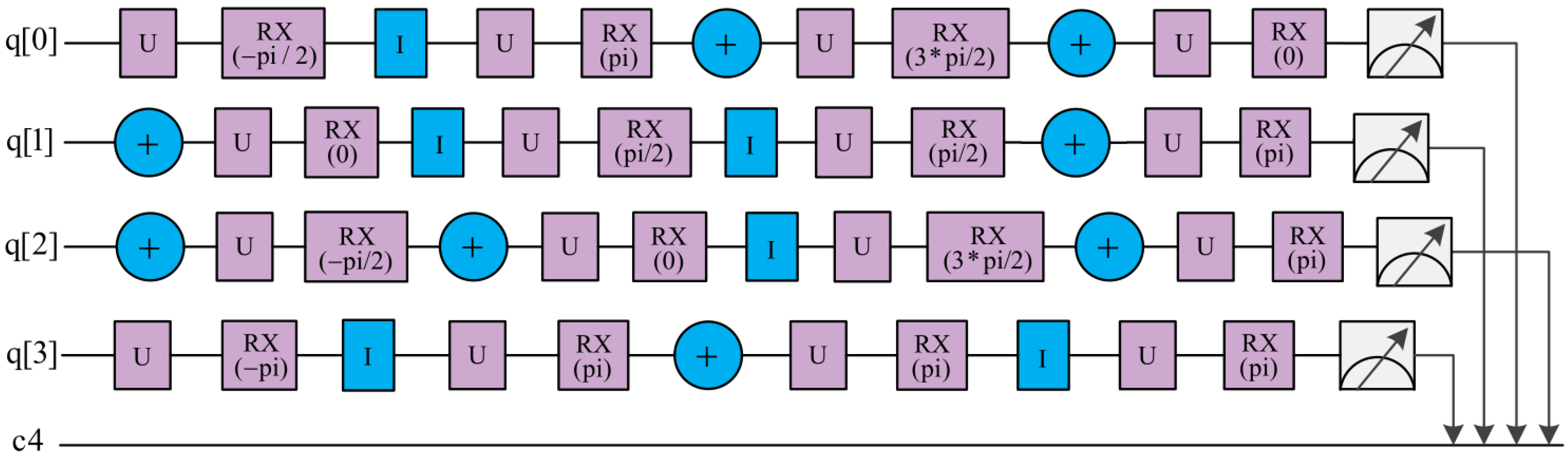
5. Experiments on the IBM Q Experience
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Paraiso, T.K.; Woodward, R.I.; Marangon, D.G.; Lovic, V.; Yuan, Z.; Shields, A.J. Advanced laser technology for quantum communications (tutorial review). Adv. Quantum Tech. 2021, 4, 2100062. [Google Scholar] [CrossRef]
- Ekert, A.K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661. [Google Scholar] [CrossRef] [PubMed]
- Gisin, N.; Ribordy, G.; Tittel, W.; Zbinden, H. Quantum cryptography. Rev. Modern Phys. 2002, 74, 145. [Google Scholar] [CrossRef]
- Cao, Y.; Zhao, Y.; Wang, Q.; Zhang, J.; Ng, S.X.; Hanzo, L. The evolution of quantum key distribution networks: On the road to the qinternet. IEEE Comm. Surv. Tutor. 2022, 24, 839–894. [Google Scholar] [CrossRef]
- Sidhu, J.S.; Brougham, T.; McArthur, D.; Pousa, R.G.; Oi, D.K.L. Finite key effects in satellite quantum key distribution. npj Quantum Inf. 2022, 8, 18. [Google Scholar] [CrossRef]
- Bloom, Y.; Fields, I.; Maslennikov, A.; Rozenman, G.G. Quantum cryptography—A simplified undergraduate experiment and simulation. Physics 2022, 4, 104–123. [Google Scholar] [CrossRef]
- Liu, R.; Rozenman, G.G.; Kundu, N.K.; Chandra, D.; De, D. Towards the industrialisation of quantum key distribution in communication networks: A short survey. IET Quantum Comm. 2022, 3, 151–163. [Google Scholar] [CrossRef]
- Zhong, Z.Q.; Wang, S.; Zhan, X.H.; Yin, Z.-Q.; Chen, W.; Guo, G.-C.; Han, Z.-F. Realistic and general model for quantum key distribution with entangled-photon sources. Phys. Rev. A 2022, 106, 052606. [Google Scholar] [CrossRef]
- Shirko, O.; Askar, S. A novel security survival model for quantum key distribution networks enabled by software-defined networking. IEEE Access 2023, 11, 21641–21654. [Google Scholar] [CrossRef]
- Li, D.D.; Tang, Y.L.; Zhao, Y.K.; Zhou, L.; Zhao, Y.; Tang, S.-B. Security of optical beam splitter in quantum key distribution. Photonics 2022, 9, 527. [Google Scholar] [CrossRef]
- Mafu, M.; Sekga, C.; Senekane, M. Security of Bennett–Brassard 1984 quantum-key distribution under a collective-rotation noise channel. Photonics 2022, 9, 941. [Google Scholar] [CrossRef]
- Jiang, X.L.; Deng, X.Q.; Wang, Y.; Lu, Y.F.; Li, J.-J.; Zhou, C.; Bao, W.-S. Weak randomness analysis of measurement-device-independent quantum key distribution with finite resources. Photonics 2022, 9, 356. [Google Scholar] [CrossRef]
- Hillery, M.; Bužek, V.; Berthiaume, A. Quantum secret sharing. Phys. Rev. A 1999, 59, 1829–1834. [Google Scholar] [CrossRef]
- Karlsson, A.; Koashi, M.; Imoto, N. Quantum entanglement for secret sharing and secret splitting. Phys. Rev. A 1999, 59, 162–168. [Google Scholar] [CrossRef]
- Xiao, L.; Long, G.L.; Deng, F.G.; Pan, J.W. Efficient multiparty quantum-secret-sharing schemes. Phys. Rev. A 2004, 69, 052307. [Google Scholar] [CrossRef]
- Liu, B.; Gao, F.; Huang, W.; Wen, Q.Y. Multiparty quantum key agreement with single particles. Quantum Inf. Process. 2013, 12, 1797–1805. [Google Scholar] [CrossRef]
- Sun, Z.W.; Cheng, R.; Wu, C.H.; Zhang, C. New fair multiparty quantum key agreement secure against collusive attacks. Sci. Rep. 2019, 9, 17177. [Google Scholar] [CrossRef]
- Lin, S.; Zhang, X.; Guo, G.D.; Wang, L.L.; Liu, X.F. Multiparty quantum key agreement. Phys. Rev. A 2021, 104, 042421. [Google Scholar] [CrossRef]
- Liu, B.; Gao, Z.F.; Xiao, D.; Huang, W.; Zhang, Z.-Q.; Li, Y.; Xu, B.-J. QKD-based quantum private query protocol in the single-photon interference communication system. IEEE Access. 2019, 7, 104749–104758. [Google Scholar] [CrossRef]
- Liu, B.; Gao, F.; Huang, W.; Wen, Q.Y. QKD-based quantum private query without a failure probability. Sci. China Phys. Mech. Astr. 2015, 58, 100301. [Google Scholar] [CrossRef]
- Gao, F.; Liu, B.; Wen, Q.Y.; Chen, H. Flexible quantum private queries based on quantum key distribution. Opt. Exp. 2012, 20, 17411–17420. [Google Scholar] [CrossRef] [PubMed]
- Lo, H.K. Insecurity of quantum secure computations. Phys. Rev. A 1997, 56, 1154. [Google Scholar] [CrossRef]
- Chau, H.F. Quantum-classical complexity-security trade off in secure multiparty computations. Phys. Rev. A 2000, 61, 032308. [Google Scholar] [CrossRef]
- Ben-Or, M.; Crépeau, C.; Gottesman, D.; Hassidim, A.; Smith, A. Secure multiparty quantum computation with (only) a strict honest majority. In Proceedings of the 2006 47th Annual IEEE Symposium on Foundations of Computer Science (FOCS’06), Berkeley, CA, USA, 21–24 October 2006; IEEE: New York, NY, USA, 2006; pp. 249–260. [Google Scholar]
- Smith, A. Multi-party Quantum Computation. arXiv 2010, arXiv:quant-ph/0111030. [Google Scholar]
- Shi, R.H.; Li, Y.F. Quantum protocol for secure multiparty logical AND with application to multiparty private set intersection cardinality. IEEE Trans. Circuits Syst. I Reg. Pap. 2022, 69, 5206–5218. [Google Scholar] [CrossRef]
- Goldreich, O.; Micali, S.; Wigderson, A. How to play any mental game. In Proceedings of the Nineteenth Annual ACM Symposium on Theory of Computing; ACM: New York, NY, USA, 1987; p. 218. [Google Scholar]
- Heinrich, S. Quantum summation with an application to integration. J. Complex. 2002, 18, 1. [Google Scholar] [CrossRef]
- Heinrich, S.; Novak, E. On a problem in quantum summation. J. Complex. 2003, 19, 1. [Google Scholar] [CrossRef]
- Heinrich, S.; Kwas, H.; Wozniakowski, M. Quantum Boolean summation with repetitions in the worst-average setting. arXiv 2003, arXiv:quant-ph/0311036. [Google Scholar]
- Hillery, M.; Ziman, M.; Buzĕ˘k, V.; Bielikova, M. Towards quantum-based privacy and voting. Phys. Lett. A 2006, 349, 75. [Google Scholar] [CrossRef]
- Chen, X.B.; Xu, G.; Yang, Y.X.; Wen, Q.Y. An efficient protocol for the secure multi-party quantum summation. Int. J. Theor. Phys. 2010, 49, 2793. [Google Scholar] [CrossRef]
- Zhang, C.; Sun, Z.; Huang, Y.; Long, D. High-capacity quantum summation with single photons in both polarization and spatial-mode degrees of freedom. Int. J. Theor. Phys. 2014, 53, 933–941. [Google Scholar] [CrossRef]
- Shi, R.H.; Mu, Y.; Zhong, H.; Cui, J.; Zhang, S. Secure multiparty quantum computation for summation and multiplication. Sci. Rep. 2016, 6, 19655. [Google Scholar] [CrossRef] [PubMed]
- Shi, R.H.; Zhang, S. Quantum solution to a class of two-party private summation problems. Quantum Inf. Process. 2017, 16, 225. [Google Scholar] [CrossRef]
- Zhang, C.; Situ, H.; Huang, Q.; Yang, P. Multi-party quantum summation without a trusted third party based on single particles. Int. J. Quantum Inf. 2017, 15, 1750010. [Google Scholar] [CrossRef]
- Liu, W.; Wang, Y.B.; Fan, W.Q. An novel protocol for the quantum secure multi-party summation based on two-particle bell states. Int. J. Theor. Phys. 2017, 56, 2783. [Google Scholar] [CrossRef]
- Liu, W.; Ma, M.Y. An dynamic protocol for the quantum secure multi-party summation based on commutative encryption. In Proceedings of the International Conference on Artificial Intelligence and Security; Springer: Cham, Switzerland, 2019; pp. 537–547. [Google Scholar]
- Yang, H.Y.; Ye, T.Y. Secure multi-party quantum summation based on quantum Fourier transform. Quantum Inf. Process. 2018, 17, 129. [Google Scholar] [CrossRef]
- Sutradhar, K.; Om, H. Hybrid quantum protocols for secure multiparty summation and multiplication. Sci. Rep. 2020, 10, 9097. [Google Scholar] [CrossRef]
- Zhang, C.; Razavi, M.; Sun, Z.W.; Situ, H.Z. Improvementn “Secure multi-party quantum summation based on quantum Fourier transform”. Quantum Inf. Process. 2019, 18, 336. [Google Scholar] [CrossRef]
- Zhang, C.; Long, Y.X.; Li, Q. Quantum summation using d-level entanglement swapping. Quantum Inf. Process. 2021, 20, 137. [Google Scholar] [CrossRef]
- Wu, W.Q.; Ma, X.X. Multi-party quantum summation without a third party based on d-dimensional bell states. Quantum Inf. Process. 2021, 20, 200. [Google Scholar] [CrossRef]
- Wang, Y.L.; Hu, P.C.; Xu, Q.L. Quantum secure multi-party summation based on entanglement swapping. Quantum Inf. Process. 2021, 20, 319. [Google Scholar] [CrossRef]
- Zhang, X.; Lin, S.; Guo, G.D. Quantum secure multi-party summation based on Grover’s search algorithm. Int. J. Theor. Phys. 2021, 60, 3711–3721. [Google Scholar] [CrossRef]
- Sutradhar, K.; Om, H. A generalized quantum protocol for secure multiparty summation. IEEE Trans. Circuits Syst. II Exp. Briefs. 2020, 67, 2978–2982. [Google Scholar] [CrossRef]
- Goldreich, O. Secure multi-party computation. Manuscript. Prelim. Vers. 1998, 78, 110. [Google Scholar]
- Brandt, N.; Maier, S.; Müller, T.; Müller-Quade, J. Constructing Secure Multi-Party Computation with Identifiable Abort. Cryptology ePrint Archive. 2020. Available online: https://eprint.iacr.org/2020/153 (accessed on 30 April 2023).
- Kanamori, Y. Quantum Encryption and Authentication Protocols. Ph.D. Thesis, University of Alabama in Huntsville, Huntsville, AL, USA, 2006. [Google Scholar]
- Cai, B.B.; Guo, G.D.; Lin, S. Multi-party Quantum Key Agreement without Entanglement. Int. J. Theor. Phys. 2017, 56, 1039–1051. [Google Scholar] [CrossRef]
- D’Ariano, G.M.; Presti, P.L.; Paris, M.G.A. Improved discrimination of unitary transformations by entangled probes. J. Opt. B Quantum Semiclass. Opt. 2002, 4, 273. [Google Scholar]
- Helstrom, C.W. Quantum Detection and Estimation Theory; Academic Press: Cambridge, MA, USA, 1976. [Google Scholar]
- Huang, S.L.; Hwang, T.; Gope, P. Multi-party quantum private comparison with an almost-dishonest third party. Quantum Inf. Process 2015, 14, 4225–4235. [Google Scholar] [CrossRef]
- Chefles, A.; Barnett, S.M. Optimum unambiguous discrimination between linearly independent symmetric states. Phys. Lett. A 1998, 250, 223–229. [Google Scholar] [CrossRef]
- Deng, F.; Li, X.; Zhou, H.; Zhang, Z.-J. Improving the security of multiparty quantum secret sharing against Trojan horse attack. Phys. Rev. A 2005, 72, 044302. [Google Scholar] [CrossRef]
- Li, X.H.; Deng, F.G. Improving the security of secure direct communication based on the secret transmitting order of particles. Phys. Rev. A 2006, 74, 054302. [Google Scholar] [CrossRef]
- Lu, C.B.; Miao, F.Y.; Hou, J.P.; Su, Z.F.; Xiong, Y. Quantum multiparty cryptosystems based on ahomomorphic random basis encryption. Quantum Inf. Process. 2020, 19, 293. [Google Scholar] [CrossRef]
- Raynal, P. Unambiguous State Discrimination of two density matrices in Quantum Information Theory. arXiv 2006, arXiv:quant-ph/0611133. [Google Scholar]
- Zyczkowski, K.; Sommers, H.J. Average fidelity between random quantum states. Phys. Rev. A 2005, 71, 032313. [Google Scholar] [CrossRef]


| TP | ||||
|---|---|---|---|---|
| - | 01101011 | 10101101 | 11010010 | |
| 0101 | 1100 | 1111 | 0010 | |
| 01000110 | 10010010 | 11011110 | 00101010 | |
| 0110 | 0010 | 1001 | 1110 | |
| - | 1100 | 1010 | 0010 | |
| - | 1110 | 0011 | 1100 |
| Secret Data | Encoded Quantum State | |
|---|---|---|
| 00 | ||
| 01 | ||
| 10 | ||
| 11 |
| Secret Data | Encoded Quantum State | |
|---|---|---|
| 00 | ||
| 01 | ||
| 10 | ||
| 11 |
| Protocols | Quantum Resource | TP | Authentication | Quantum Efficiency |
|---|---|---|---|---|
| Zhang et al. [33] | Single-particle state | Yes | No | |
| Zhang et al. [36] | Single-particle state | No | No | |
| Liu et al. [37] | 2-particle Bell state | Yes | No | |
| Liu et al. [38] | single-particle state | Yes | No | |
| Zhang et al. [45] | 2-particle entangled state | Yes | No | |
| Our protocol | Single-particle state | Yes | Yes |
| Final Quantum State | Measurement Probability | Expected Probability | Fidelity |
|---|---|---|---|
| 1.00 | |||
| 1.00 | |||
| 1.00 | |||
| 1.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, N.; Tian, X.; Zhang, X.; Lin, S. Quantum Secure Multi-Party Summation with Identity Authentication Based on Commutative Encryption. Photonics 2023, 10, 558. https://doi.org/10.3390/photonics10050558
Wang N, Tian X, Zhang X, Lin S. Quantum Secure Multi-Party Summation with Identity Authentication Based on Commutative Encryption. Photonics. 2023; 10(5):558. https://doi.org/10.3390/photonics10050558
Chicago/Turabian StyleWang, Ning, Xinying Tian, Xiaodong Zhang, and Song Lin. 2023. "Quantum Secure Multi-Party Summation with Identity Authentication Based on Commutative Encryption" Photonics 10, no. 5: 558. https://doi.org/10.3390/photonics10050558
APA StyleWang, N., Tian, X., Zhang, X., & Lin, S. (2023). Quantum Secure Multi-Party Summation with Identity Authentication Based on Commutative Encryption. Photonics, 10(5), 558. https://doi.org/10.3390/photonics10050558





