High-Sensitivity Quantum-Enhanced Interferometers
Abstract
1. Introduction
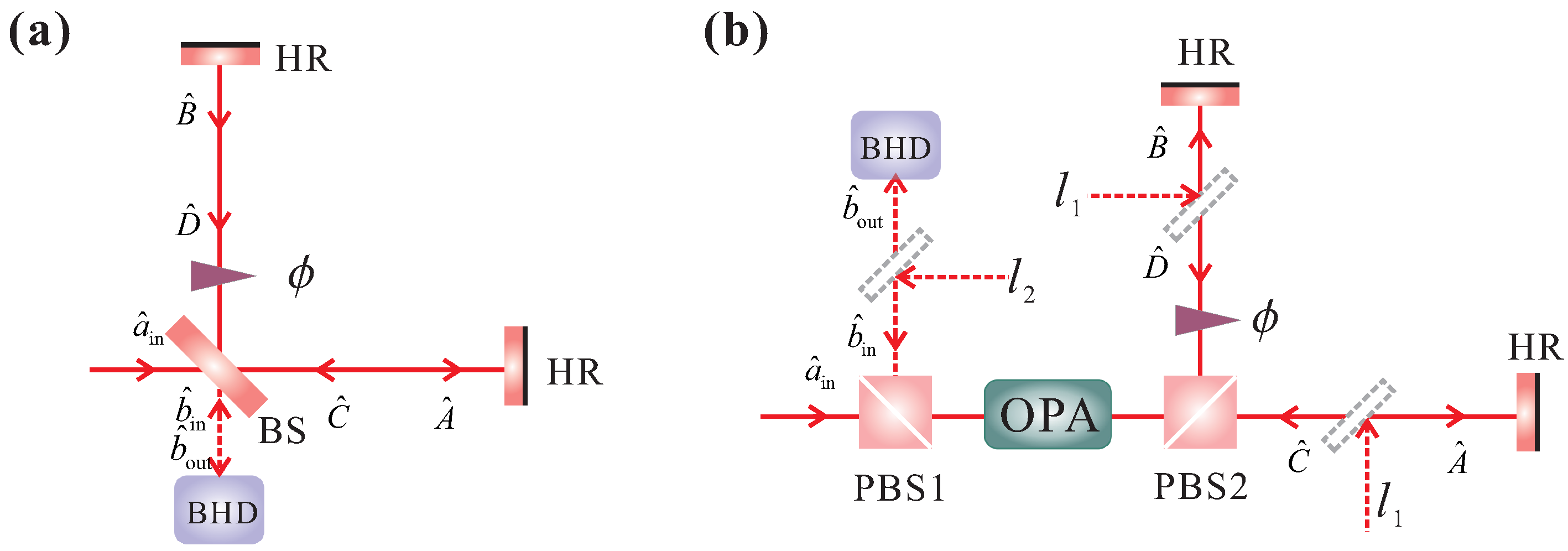
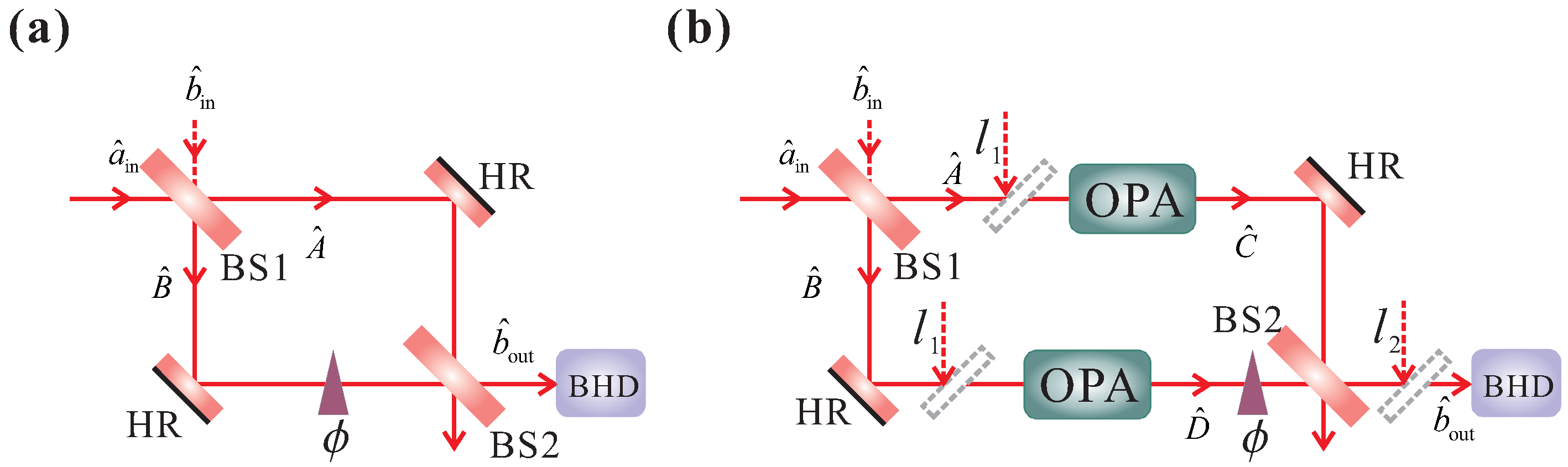
2. Quantum Interferometers
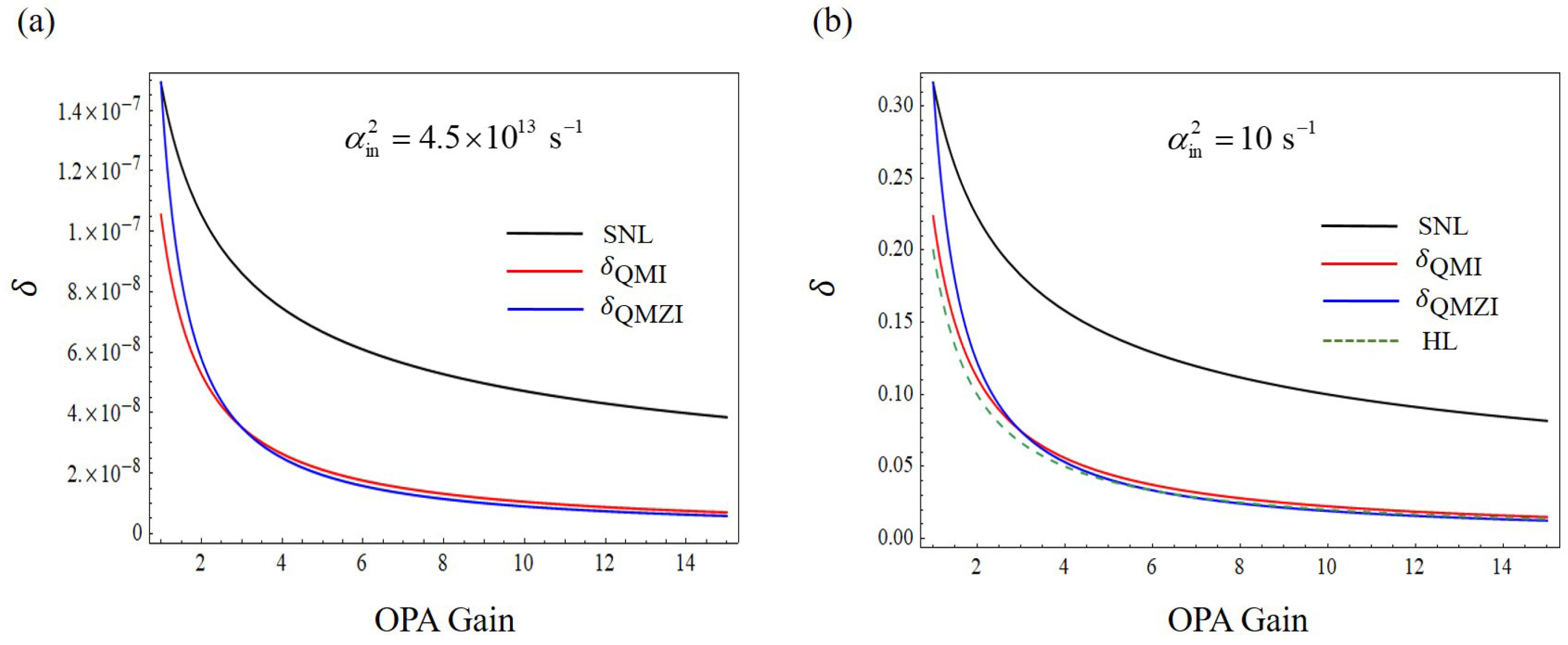
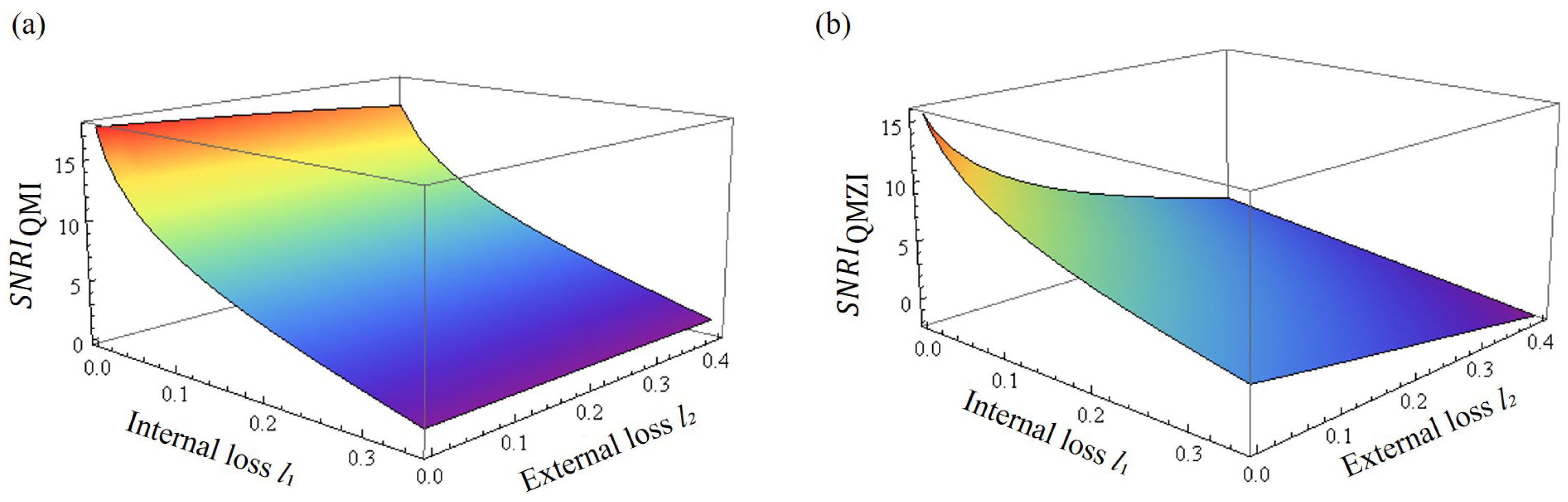
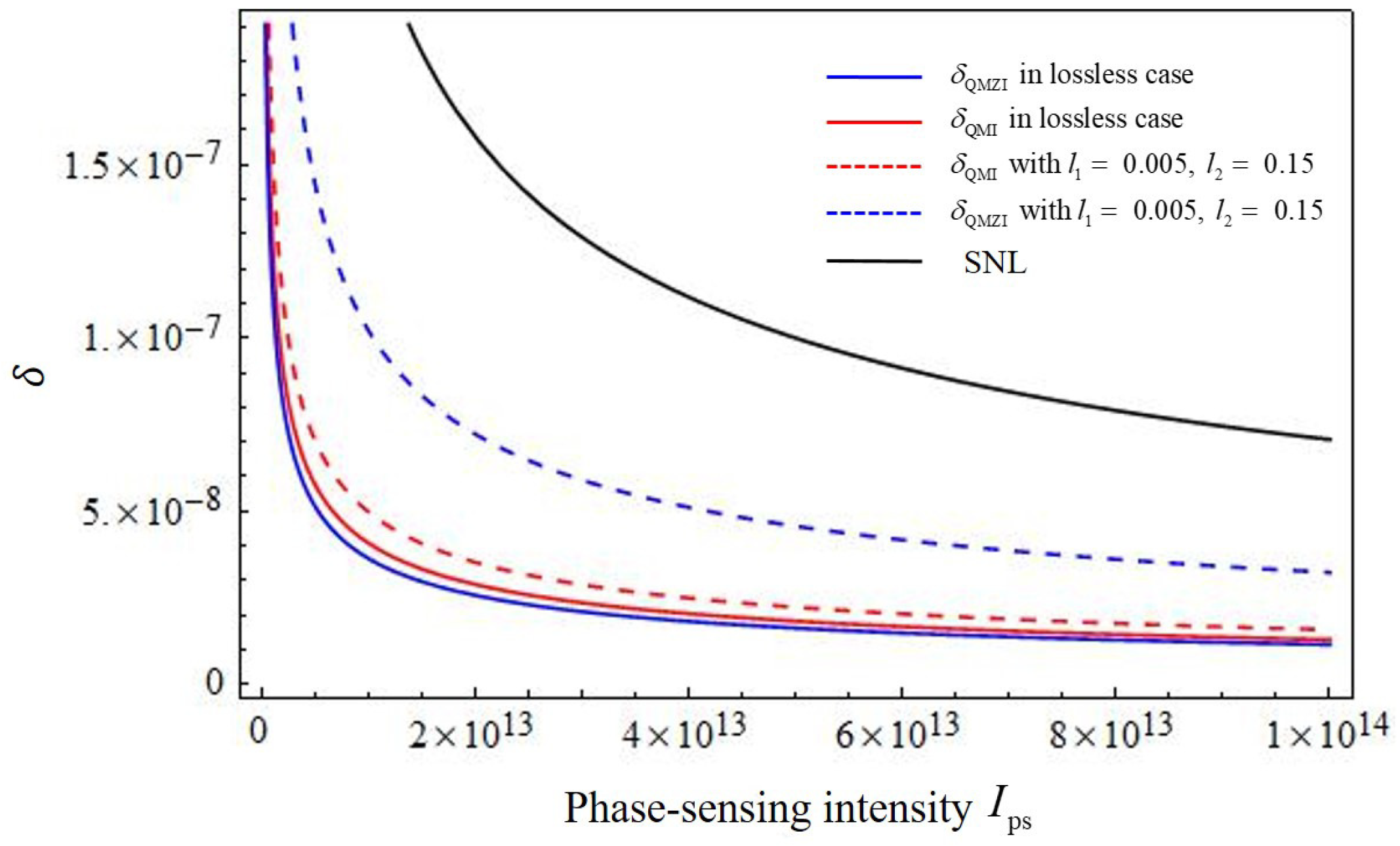
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Taylor, M.A.; Janousek, J.; Daria, V.; Knittel, J.; Hage, B.; Bachor, H.-A.; Bowen, W.P. Sub diffraction-Limited Quantum Imaging within a Living Cell. Phys. Rev. X 2014, 4, 011017. [Google Scholar]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Advances in quantum metrology. Nat. Photonics 2011, 5, 222–229. [Google Scholar] [CrossRef]
- Tse, M.; Yu, H.; Kijbunchoo, N.; Fernandez-Galiana, A.; Dupej, P.; Barsotti, L.; Blair, C.D.; Brown, D.D.; Dwyer, S.E.; Effler, A.; et al. Quantum-Enhanced Advanced LIGO Detectors in the Era of Gravitational-Wave Astronomy. Phys. Rev. Lett. 2019, 123, 231107. [Google Scholar] [CrossRef]
- Acernese, F.; Agathos, M.; Aiello, L.; Allocca, A.; Amato, A.; Ansoldi, S.; Antier, S.; Arene, M.; Arnaud, N.; Ascenzi, S.; et al. Increasing the Astrophysical Reach of the Advanced Virgo Detector via the Application of Squeezed Vacuum States of Light. Phys. Rev. Lett. 2019, 123, 231108. [Google Scholar] [CrossRef]
- Kimble, H.J.; Levin, Y.; Matsko, A.B.; Thorne, K.S.; Vyatchanin, S.P. Conversion of conventional gravitational-wave interferometers into quantum nondemolition interferometers by modifying their input and/or output optics. Phys. Rev. D 2001, 65, 022002. [Google Scholar] [CrossRef]
- Peters, A.; Chung, K.Y.; Chu, S. High-precision gravity measurements using atom interferometry. Metrologia 2001, 38, 25. [Google Scholar] [CrossRef]
- Rosi, G.; Sorrentino, F.; Cacciapuoti, L.; Prevedelli, M.; Tino, G. Precision measurement of the Newtonian gravitational constant using cold atoms. Nature 2014, 510, 518–521. [Google Scholar] [CrossRef] [PubMed]
- Gault, W.; Shepherd, G. WAMDII—A wide angle Michelson Doppler imaging interferometer for spacelab. Adv. Space Res. 1982, 2, 111–114. [Google Scholar] [CrossRef]
- Boixo, S.; Davis, M.J.; Shaji, A. Quantum Metrology: Dynamics versus Entanglement. Phys. Rev. Lett. 2008, 101, 040403. [Google Scholar] [CrossRef]
- Holland, M.J.; Burnett, K. Interferometric detection of optical phase shifts at the Heisenberg limit. Phys. Rev. Lett. 1993, 71, 1355. [Google Scholar] [CrossRef]
- Xiao, M.; Wu, L.A.; Kimble, H.J. Precision Measurement beyond the Shot-Noise Limit. Phys. Rev. Lett. 1987, 59, 278. [Google Scholar] [CrossRef]
- Grangier, P.; Slusher, R.E.; Yurke, B.; LaPorta, A. Squeezed-Light-Enhanced Polarization Interferometer. Phys. Rev. Lett. 1987, 59, 19. [Google Scholar] [CrossRef]
- Degen, C.L.; Reinhard, F.; Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 2017, 89, 035002. [Google Scholar] [CrossRef]
- Ma, Y.; Miao, H.; Pang, B.H.; Evans, M.; Zhao, C.; Harms, J.; Schnabel, R.; Chen, Y. Proposal for gravitational-wave detection beyond the standard quantum limit through EPR entanglement. Nat. Photonics 2017, 13, 776–780. [Google Scholar] [CrossRef]
- Ou, Z.Y. Enhancement of the phase-measurement sensitivity beyond the standard quantum limit by a nonlinear interferometer. Phys. Rev. A 2012, 85, 023815. [Google Scholar] [CrossRef]
- Caves, C.M. Quantum mechanical noise in an interferometer. Phys. Rev. D 1981, 23, 1693. [Google Scholar] [CrossRef]
- Huang, Z.X.; Motes, K.R.; Anisimov, P.M.; Dowling, J.P.; Berry, D.W. Adaptive phase estimation with two-mode squeezed vacuum and parity measurement. Phys. Rev. A 2017, 95, 053837. [Google Scholar] [CrossRef]
- Liu, F.; Zhou, Y.Y.; Yu, J.; Guo, J.L.; Wu, Y.; Xiao, S.X.; Wei, D.; Zhang, Y.; Jia, X.J.; Xiao, M. Squeezingenhanced fiber Mach-Zehnder interferometer for lowfrequency phase measurement. Appl. Phys. Lett. 2017, 110, 021106. [Google Scholar] [CrossRef]
- Higgins, B.L.; Berry, D.W.; Bartlett, S.D.; Wiseman, H.M.; Pryde, G.J. Entanglement-free Heisenberg-limited phase estimation. Nature 2007, 450, 393–396. [Google Scholar] [CrossRef] [PubMed]
- Xiang, G.Y.; Higgins, B.L.; Berry, D.W.; Wiseman, H.M.; Pryde, G.J. Entanglement-enhanced measurement of a completely unknown optical phase. Nat. Photonics 2010, 5, 43–47. [Google Scholar] [CrossRef]
- Yonezawa, H.; Nakane, D.; Wheatley, T.A.; Iwasawa, K.; Takeda, S.; Arao, H.; Ohki, K.; Tsumura, K.; Berry, D.W.; Ralph, T.C.; et al. Quantum-enhanced optical phase tracking. Science 2012, 337, 1514–1517. [Google Scholar] [CrossRef]
- Yu, J.; Qin, Y.; Qin, J.L.; Wang, H.; Yan, Z.H.; Jia, X.J.; Peng, K.C. Quantum Enhanced Optical Phase Estimation With a Squeezed Thermal State. Phys. Rev. Appl. 2020, 13, 024037. [Google Scholar] [CrossRef]
- Guo, X.S.; Breum, C.R.; Borregaard, J.; Izumi, S.; Larsen, M.V.; Gehring, T.; Christandl, M.; Neergaard-Nielsen, J.S.; Andersen, U.L. Distributed quantum sensing in a continuous variable entangled network. Nat. Phys. 2020, 16, 281–284. [Google Scholar] [CrossRef]
- Dinani, H.T.; Berry, D.W. Adaptive estimation of a time-varying phase with a power-law spectrum via continuous squeezed states. Phys. Rev. A 2017, 95, 063821. [Google Scholar] [CrossRef]
- Nagata, T.; Okamoto, R.; O’Brien, J.L.; Sasaki, K.; Takeuchi, S. Beating the Standard Quantum Limit with Four-Entangled Photons. Science 2007, 316, 726–729. [Google Scholar] [CrossRef]
- Huo, M.R.; Qin, J.L.; Cheng, J.L.; Yan, Z.H.; Qin, Z.Z.; Su, X.L.; Jia, X.J.; Xie, C.D.; Peng, K.C. Deterministic quantum teleportation through fiber channels. Sci. Adv. 2018, 4, eaas9401. [Google Scholar] [CrossRef]
- Zhou, Y.Y.; Yu, J.; Yan, Z.H.; Jia, X.J.; Zhang, J.; Xie, C.D.; Peng, K.C. Quantum Secret Sharing among Four Players Using Multipartite Bound Entanglement of an Optical Field. Phys. Rev. Lett. 2018, 121, 150502. [Google Scholar] [CrossRef] [PubMed]
- Yan, Z.H.; Qin, J.; Qin, Z.Z.; Su, X.L.; Jia, X.J.; Xie, C.D.; Peng, K.C. Generation of non-classical states of light and their application in deterministic quantum teleportation. Fundam. Res. 2021, 1, 43–49. [Google Scholar] [CrossRef]
- Ma, L.X.; Lei, X.; Yan, J.L.; Li, R.Y.; Chai, T.; Yan, Z.H.; Jia, X.J.; Xie, C.D.; Peng, K.C. High-performance cavity-enhanced quantum memory with warm atomic cell. Nat. Commun. 2022, 13, 2368. [Google Scholar] [CrossRef] [PubMed]
- Nichols, R.; Bromley, T.R.; Correa, L.A.; Adesso, G. Practical quantum metrology in noisy environments. Phys. Rev. A 2016, 94, 042101. [Google Scholar] [CrossRef]
- Yurke, B.; McCall, S.L.; Klauder, J.R. SU(2) and SU(1,1) interferometers. Phys. Rev. A 1986, 33, 4033. [Google Scholar] [CrossRef] [PubMed]
- Hudelist, F.; Kong, J.; Liu, C.; Jing, J.; Ou, Z.Y.; Zhang, W. Quantum metrology with parametric amplifier-based photon correlation interferometers. Nat. Commun. 2014, 5, 3049. [Google Scholar] [CrossRef]
- Zheng, K.M.; Mi, M.H.; Wang, B.; Xu, L.Y.; Hu, L.; Liu, S.S.; Lou, Y.B.; Jing, J.T.; Zhang, L.J. Quantum-enhanced stochastic phase estimation with SU(1,1) interferometer. Photonics Res. 2020, 8, 1653–1661. [Google Scholar] [CrossRef]
- Li, J.M.; Liu, Y.H.; Cui, L.; Huo, N.; Assad, S.M.; Li, X.Y.; Ou, Z.Y. Joint measurement of multiple noncommuting parameters. Phys. Rev. A 2018, 97, 052127. [Google Scholar] [CrossRef]
- Zuo, X.J.; Yan, Z.H.; Feng, Y.N.; Ma, J.X.; Jia, X.J.; Xie, C.D.; Peng, K.C. Quantum interferometer combining squeezing and parametric amplification. Phys. Rev. Lett. 2020, 124, 173602. [Google Scholar] [CrossRef]
- Pooser, R.C.; Savino, N.; Batson, E.; Beckey, J.L.; Garcia, J.; Lawrie, B.J. Truncated nonlinear interferometry for quantum-enhanced atomic force microscopy. Phys. Rev. Lett. 2020, 124, 230504. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Liang, X.; Zhu, B.; Yan, Y.; Yuan, C.; Zhang, W.; Chen, L.Q. Protection of Noise Squeezing in a Quantum Interferometer with Optimal Resource Allocation. Phys. Rev. Lett. 2023, 130, 073601. [Google Scholar] [CrossRef] [PubMed]
- Heinze, J.; Danzmann, K.; Willke, B.; Vahlbruch, H. 10 dB Quantum-Enhanced Michelson Interferometer with Balanced Homodyne Detection. Phys. Rev. Lett. 2022, 129, 031101. [Google Scholar] [CrossRef]
- Zander, J.; Rembe, C.; Schnabel, R. 10 dB interferometer enhancement by squeezing of photon shot noise with sub-femtometer resolution and eye-safe optical power. Quantum Sci. Technol. 2023, 8, 01LT01. [Google Scholar] [CrossRef]
- Kalinin, N.; Dirmeier, T.; Sorokin, A.A.; Anashkina, E.A.; Sáchez-Soto, L.L. Quantum-enhanced interferometer using Kerr squeezing. Nanophotonics 2023, 00323. [Google Scholar] [CrossRef]
- Zuo, X.; Sun, Y.; Yan, Z.; Jia, X. High sensitivity quantum Michelson interferometer. Acta Phys. Sin. 2018, 67, 134202. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, J.; Wu, Y.; Nie, L.; Zuo, X. High-Sensitivity Quantum-Enhanced Interferometers. Photonics 2023, 10, 749. https://doi.org/10.3390/photonics10070749
Yu J, Wu Y, Nie L, Zuo X. High-Sensitivity Quantum-Enhanced Interferometers. Photonics. 2023; 10(7):749. https://doi.org/10.3390/photonics10070749
Chicago/Turabian StyleYu, Juan, Yinhua Wu, Liang Nie, and Xiaojie Zuo. 2023. "High-Sensitivity Quantum-Enhanced Interferometers" Photonics 10, no. 7: 749. https://doi.org/10.3390/photonics10070749
APA StyleYu, J., Wu, Y., Nie, L., & Zuo, X. (2023). High-Sensitivity Quantum-Enhanced Interferometers. Photonics, 10(7), 749. https://doi.org/10.3390/photonics10070749




