First Experimental Demonstration of the Wide-Field Amplitude Surface Plasmon Resonance Microscopy in the Terahertz Range
Abstract
1. Introduction
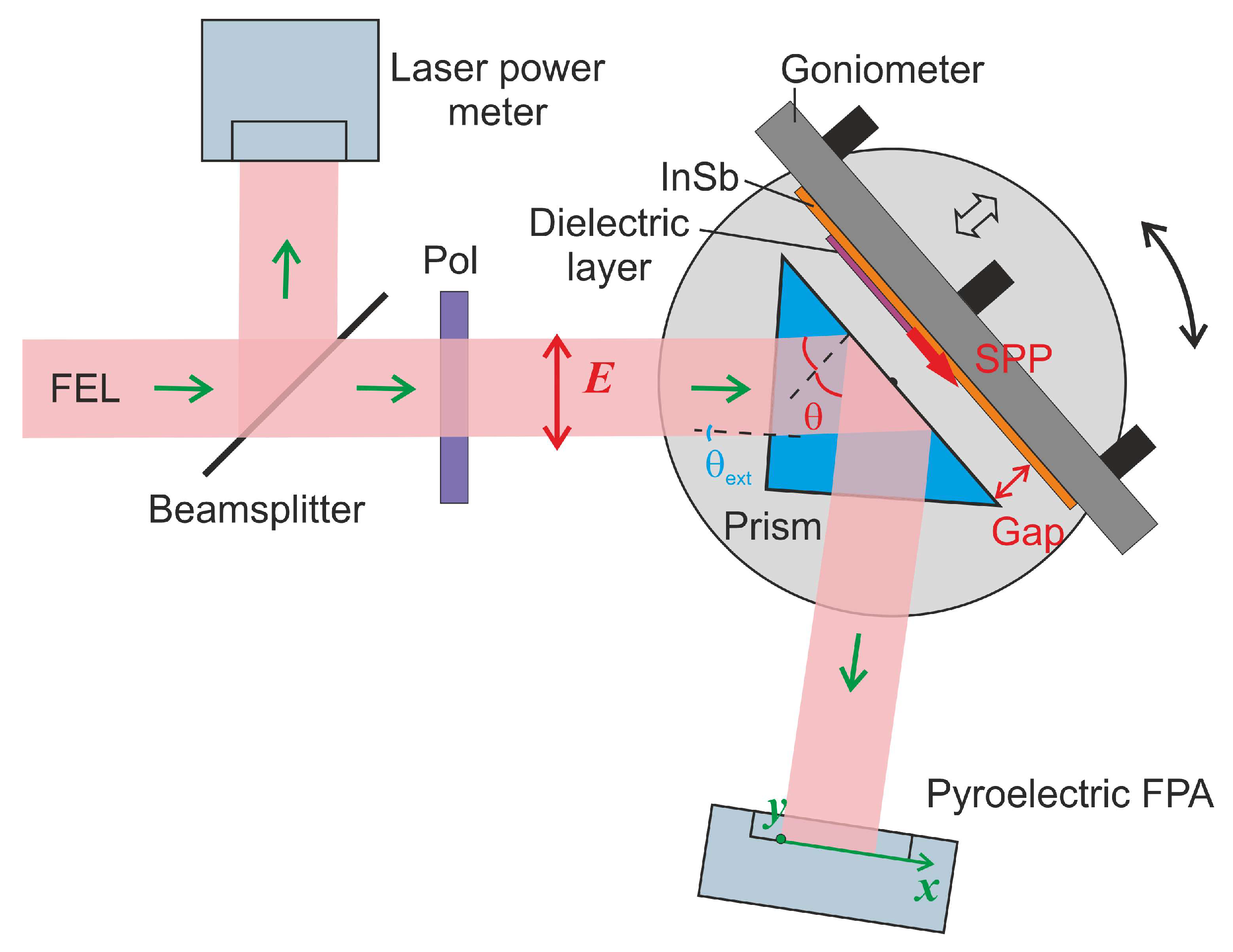
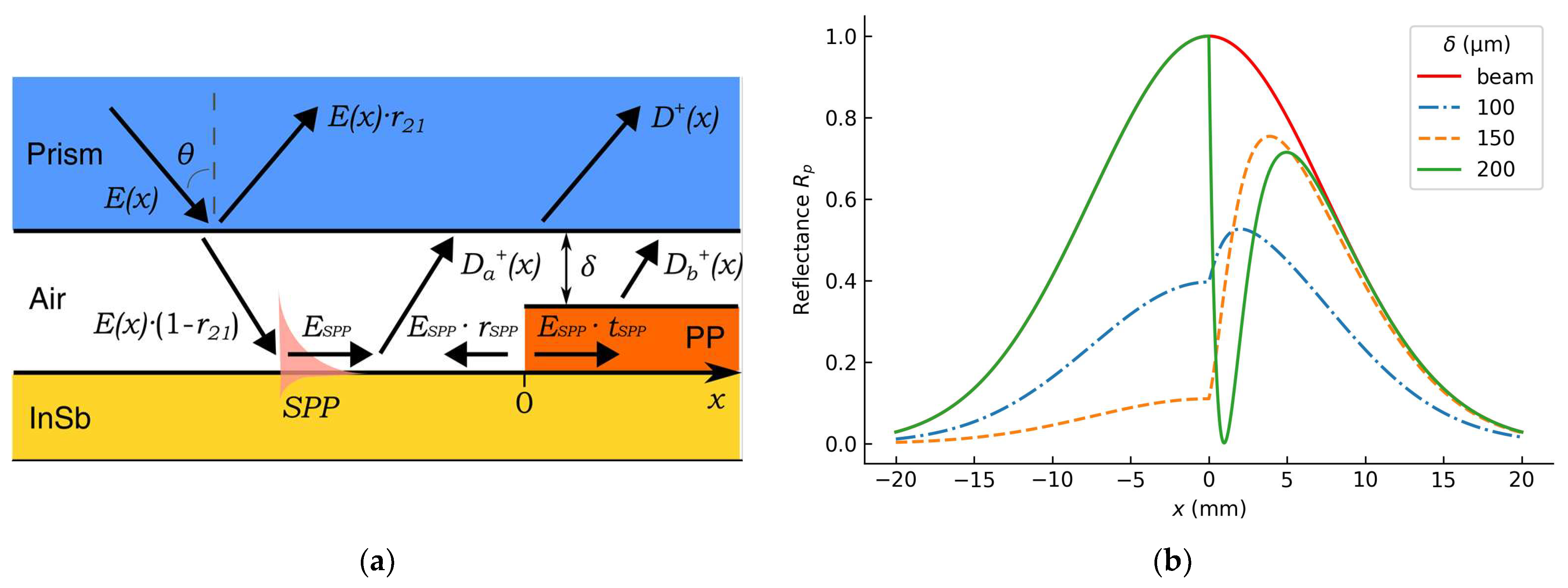
2. Materials and Methods
3. Results and Discussion
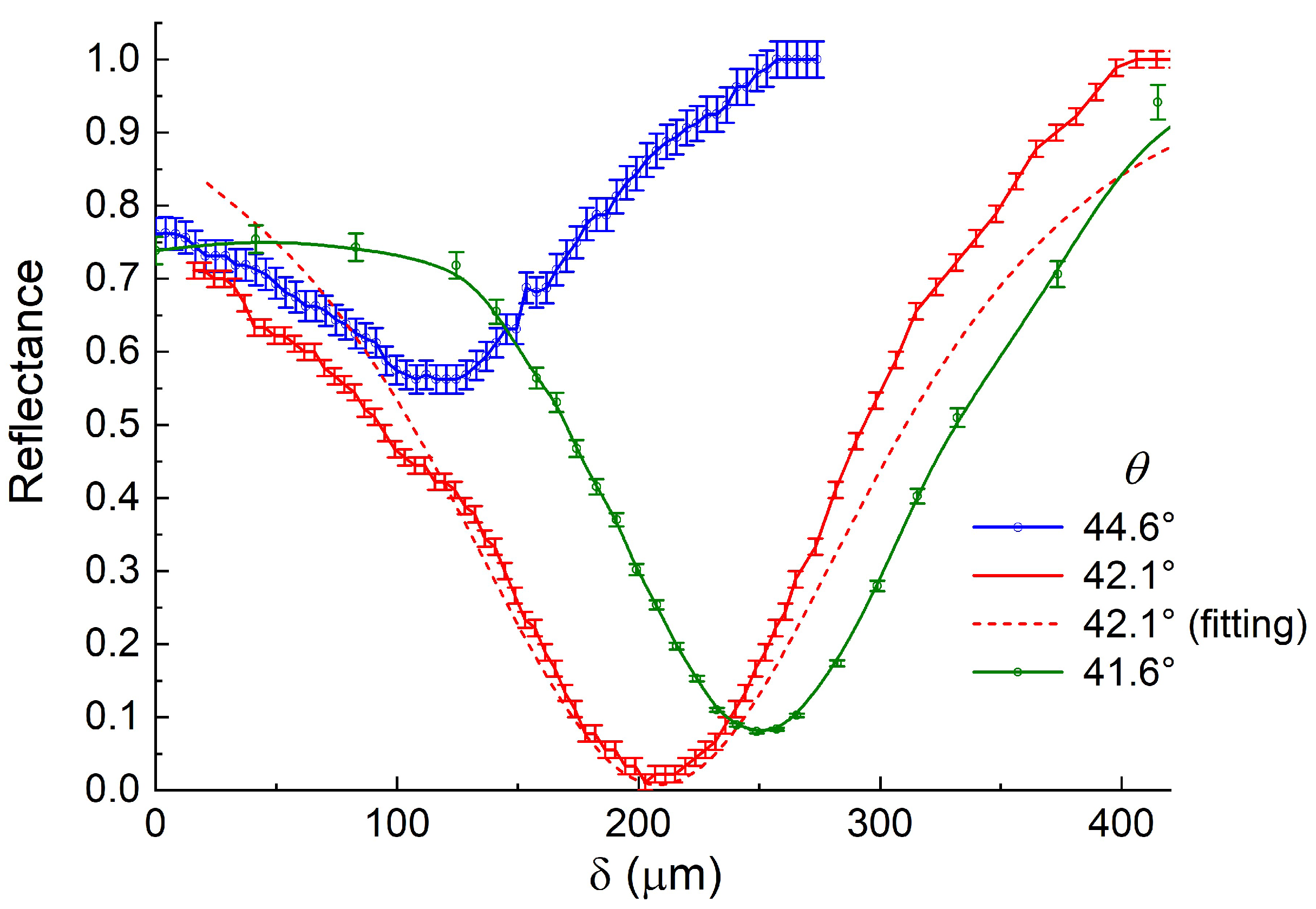
3.1. Experiments with Free Surface of InSb
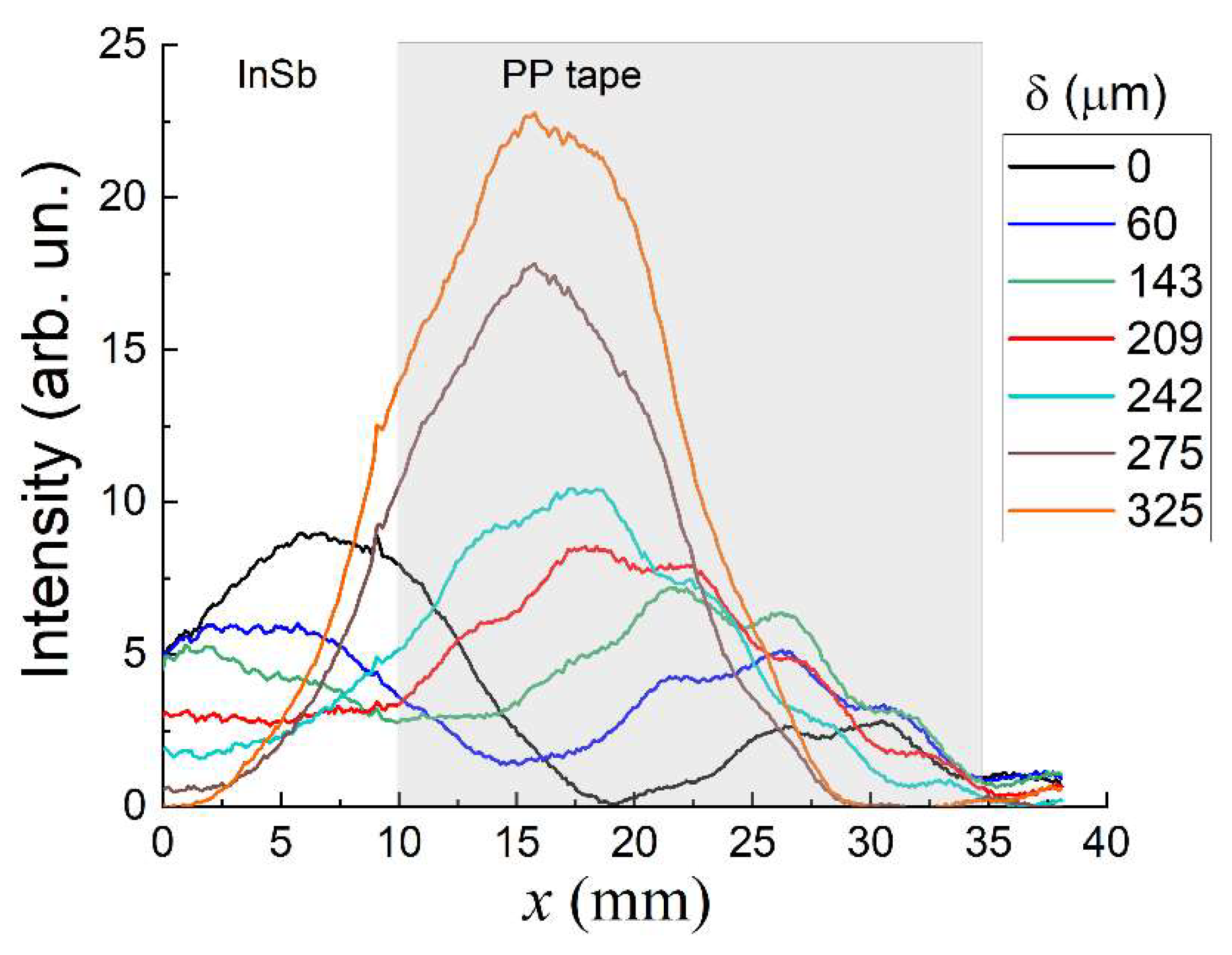
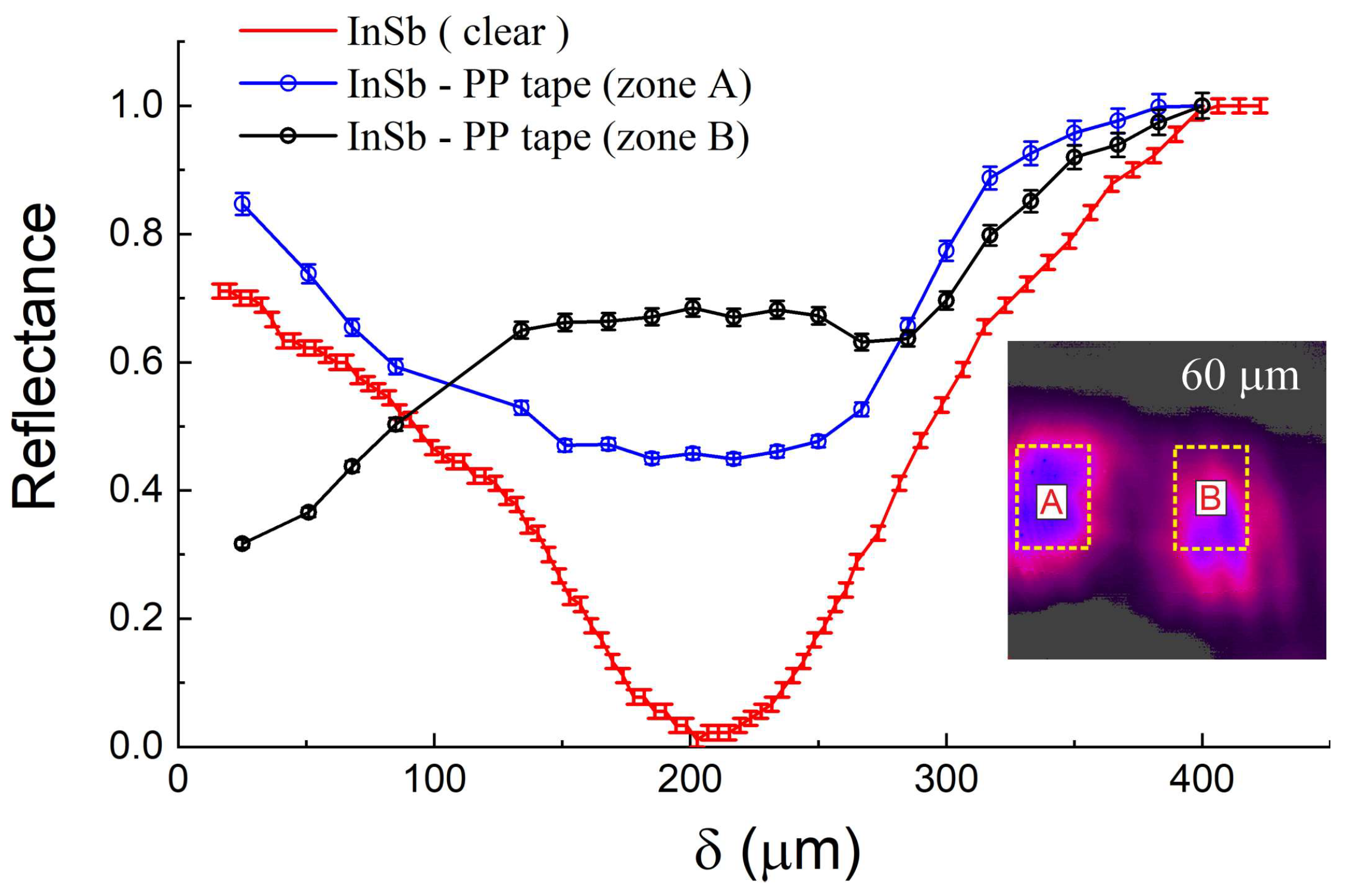
3.2. Localization of Polypropylene Film on the InSb Surface
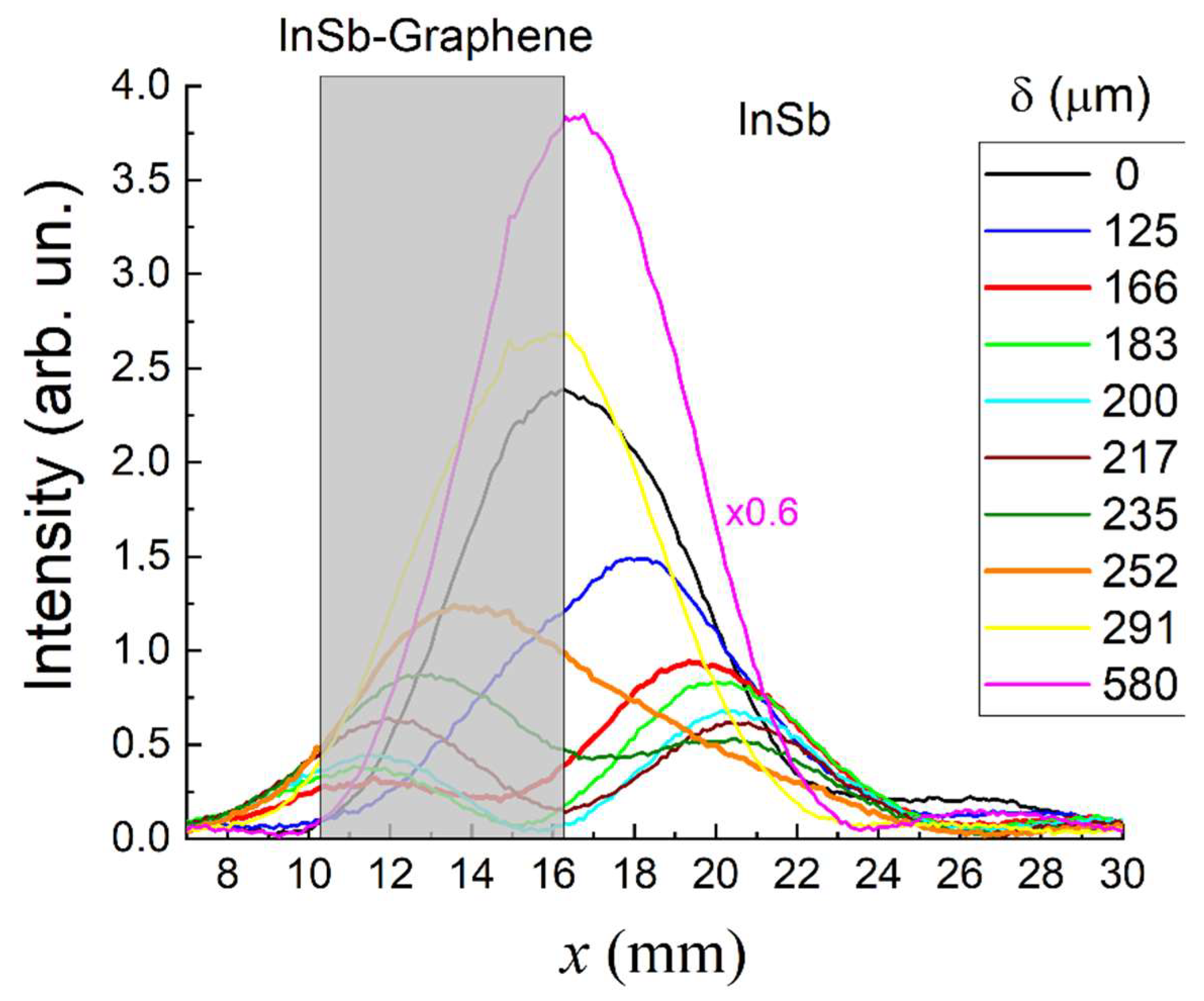
3.3. Localization of Graphene Coating on the InSb Surface
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Peiponen, K.-E.; Zeitler, J.A.; Kuwata-Gonokami, M. Terahertz Spectroscopy and Imaging; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2013; ISBN 978-3-642-29563-8. [Google Scholar]
- Cherkasova, O.P.; Serdyukov, D.S.; Ratushnyak, A.S.; Nemova, E.F.; Kozlov, E.N.; Shidlovskii, Y.V.; Zaytsev, K.I.; Tuchin, V.V. Effects of Terahertz Radiation on Living Cells: A Review. Opt. Spectrosc. 2020, 128, 855–866. [Google Scholar] [CrossRef]
- Chernomyrdin, N.V.; Musina, G.R.; Nikitin, P.V.; Dolganova, I.N.; Kucheryavenko, A.S.; Alekseeva, A.I.; Wang, Y.; Xu, D.; Shi, Q.; Tuchin, V.V.; et al. Terahertz Technology in Intraoperative Neurodiagnostics: A Review. Opto Electron. Adv. 2022, 6, 220071. [Google Scholar] [CrossRef]
- Costa, F.B.; Machado, M.A.; Bonfait, G.J.; Vieira, P.; Santos, T.G. Continuous Wave Terahertz Imaging for NDT: Fundamentals and Experimental Validation. Measurement 2021, 172, 108904. [Google Scholar] [CrossRef]
- Cosentino, A. Terahertz and Cultural Heritage Science: Examination of Art and Archaeology. Technologies 2016, 4, 6. [Google Scholar] [CrossRef]
- Wang, J.; Ando, M.; Nagata, H.; Yoshida, S.; Sakai, K.; Kiwa, T. Multifunctional Terahertz Microscopy for Biochemical and Chemical Imaging and Sensing. Biosens. Bioelectron. 2023, 220, 114901. [Google Scholar] [CrossRef]
- Moon, K.; Do, Y.; Park, H.; Kim, J.; Kang, H.; Lee, G.; Lim, J.-H.; Kim, J.-W.; Han, H. Computed Terahertz Near-Field Mapping of Molecular Resonances of Lactose Stereo-Isomer Impurities with Sub-Attomole Sensitivity. Sci. Rep. 2019, 9, 16915. [Google Scholar] [CrossRef]
- Chen, S.; Bylinkin, A.; Wang, Z.; Schnell, M.; Chandan, G.; Li, P.; Nikitin, A.Y.; Law, S.; Hillenbrand, R. Real-Space Nanoimaging of THz Polaritons in the Topological Insulator Bi2Se3. Nat. Commun. 2022, 13, 1374. [Google Scholar] [CrossRef] [PubMed]
- Chernomyrdin, N.V.; Skorobogatiy, M.; Ponomarev, D.S.; Bukin, V.V.; Tuchin, V.V.; Zaytsev, K.I. Terahertz Solid Immersion Microscopy: Recent Achievements and Challenges. Appl. Phys. Lett. 2022, 120, 110501. [Google Scholar] [CrossRef]
- Ning, W.; Hu, N.; Xu, P.; Song, Y.; Li, Y. Performance Comparison of Different Deconvolution Methods on 2D Terahertz Imaging. Microw. Opt. Technol. Lett. 2023, 1–6. [Google Scholar] [CrossRef]
- Guerboukha, H.; Cao, Y.; Nallappan, K.; Skorobogatiy, M. Super-Resolution Orthogonal Deterministic Imaging Technique for Terahertz Subwavelength Microscopy. ACS Photonics 2020, 7, 1866–1875. [Google Scholar] [CrossRef]
- Khasanov, I.S.; Zykova, L.A. Terahertz Ghost Imaging and Surface Plasmon Resonance Microscopy: Analysis of Factors Affecting the Image Quality. In Proceedings of the Fourth International Conference on Terahertz and Microwave Radiation: Generation, Detection, and Applications, Tomsk, Russian, 24–26 August 2020; Romanovskii, O.A., Kistenev, Y.V., Eds.; SPIE: Tomsk, Russian, 2020; p. 54. [Google Scholar]
- Ma, D.; Zhao, J.; Wang, D.; Lin, H.; Rong, L.; Wang, Y.; Lin, S. Full-Field Super-Resolution Terahertz Imaging Based on Rotating Coherent Scattering Microscopy. Appl. Sci. 2023, 13, 982. [Google Scholar] [CrossRef]
- Yeatman, E.; Ash, E.A. Surface Plasmon Microscopy. Electron. Lett. 1987, 23, 1091. [Google Scholar] [CrossRef]
- Rothenhäusler, B.; Knoll, W. Surface–Plasmon Microscopy. Nature 1988, 332, 615–617. [Google Scholar] [CrossRef]
- Gerasimov, V.V.; Knyazev, B.A.; Kotelnikov, I.A.; Nikitin, A.K.; Cherkassky, V.S.; Kulipanov, G.N.; Zhizhin, G.N. Surface Plasmon Polaritons Launched Using a Terahertz Free-Electron Laser: Propagation along a Gold–ZnS–Air Interface and Decoupling to Free Waves at the Surface Edge. J. Opt. Soc. Am. B 2013, 30, 2182–2190. [Google Scholar] [CrossRef]
- Liu, Z. (Ed.) Plasmonics and Super-Resolution Imaging; Pan Stanford Publishing: Singapore, 2017; ISBN 978-981-4669-91-7. [Google Scholar]
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer: New York, NY, USA, 2007; ISBN 978-0-387-33150-8. [Google Scholar]
- Teng, Y.-Y.; Stern, E.A. Plasma Radiation from Metal Grating Surfaces. Phys. Rev. Lett. 1967, 19, 511–514. [Google Scholar] [CrossRef]
- Raether, H. Surface Plasmons on Smooth and Rough Surfaces and on Gratings; Springer Tracts in Modern Physics; Springer: Berlin/Heidelberg, Germany, 1988; Volume 111, ISBN 978-3-540-17363-2. [Google Scholar]
- Harris, R.D.; Wilkinson, J.S. Waveguide Surface Plasmon Resonance Sensors. Sens. Actuators B Chem. 1995, 29, 261–267. [Google Scholar] [CrossRef]
- Otto, A. Excitation of Nonradiative Surface Plasma Waves in Silver by the Method of Frustrated Total Reflection. Z. Phys. A Hadron. Nucl. 1968, 216, 398–410. [Google Scholar] [CrossRef]
- Kretschmann, E.; Raether, H. Notizen: Radiative Decay of Non Radiative Surface Plasmons Excited by Light. Z. Nat. A 1968, 23, 2135–2136. [Google Scholar] [CrossRef]
- Shibayama, J.; Mitsutake, K.; Yamauchi, J.; Nakano, H. Kretschmann- and Otto-Type Surface Plasmon Resonance Waveguide Sensors in the Terahertz Regime. Microw. Opt. Technol. Lett. 2021, 63, 103–106. [Google Scholar] [CrossRef]
- Yang, Y.; Zhai, C.; Zeng, Q.; Khan, A.L.; Yu, H. Quantitative Amplitude and Phase Imaging with Interferometric Plasmonic Microscopy. ACS Nano 2019, 13, 13595–13601. [Google Scholar] [CrossRef]
- Nikitin, A.K.; Gerasimov, V.V.; Knyazev, B.A.; Lien, N.T.H.; Trang, T.T. Control of the Conducting Surface by Terahertz Surface Electromagnetic Waves. J. Phys. Conf. Ser. 2020, 1636, 012036. [Google Scholar] [CrossRef]
- Vinokurov, N.A.; Shevchenko, O.A. Free electron lasers and their development at the Budker Institute of Nuclear Physics, SB RAS. Physics-Uspekhi 2018, 61, 435–448. [Google Scholar] [CrossRef]
- Anisimov, A.V.; Khasanov, I.S. Algorithm for Optical Characterization of Dielectric Gradient Index Nanofilm by Surface Plasmon Resonance Spectroscopy. J. Phys. Conf. Ser. 2021, 2091, 012067. [Google Scholar] [CrossRef]
- Yeatman, E.M. Resolution and Sensitivity in Surface Plasmon Microscopy and Sensing. Biosens. Bioelectron. 1996, 11, 635–649. [Google Scholar] [CrossRef]
- Bell, R.J.; Alexander, R.W.; Ward, C.A.; Tyler, I.L. Introductory theory for surface electromagnetic wave spectroscopy. Surf. Sci. 1975, 48, 253–287. [Google Scholar] [CrossRef]
- Raether, H. Surface plasma oscillations and their applications. Phys. Thin Film. 1977, 9, 145–261. [Google Scholar]
- Pockrand, I. Surface plasma oscillations at silver surfaces with transparent and absorbing coatings. Surf. Sci. 1978, 72, 577–588. [Google Scholar] [CrossRef]
- Yakimchuk, E.A.; Soots, R.A.; Kotin, I.A.; Antonova, I.V. 2D printed graphene conductive layers with high carrier mobility. Curr. Appl. Phys. 2017, 17, 1655–1661. [Google Scholar] [CrossRef]
- Antonova, I.V.; Shavelkina, M.B.; Ivanov, A.I.; Poteryaev, D.A.; Nebogatikova, N.A.; Buzmakova, A.A.; Soots, R.A.; Katarzhis, V.A. Graphene: Hexagonal Boron Nitride Composite Films with Low-Resistance for Flexible Electronics. Nanomaterials 2022, 12, 1703. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gerasimov, V.V.; Kameshkov, O.E.; Nikitin, A.K.; Khasanov, I.S.; Lemzyakov, A.G.; Antonova, I.V.; Ivanov, A.I.; Lien, N.T.H.; Nghia, N.T.; Anh, L.T.; et al. First Experimental Demonstration of the Wide-Field Amplitude Surface Plasmon Resonance Microscopy in the Terahertz Range. Photonics 2023, 10, 723. https://doi.org/10.3390/photonics10070723
Gerasimov VV, Kameshkov OE, Nikitin AK, Khasanov IS, Lemzyakov AG, Antonova IV, Ivanov AI, Lien NTH, Nghia NT, Anh LT, et al. First Experimental Demonstration of the Wide-Field Amplitude Surface Plasmon Resonance Microscopy in the Terahertz Range. Photonics. 2023; 10(7):723. https://doi.org/10.3390/photonics10070723
Chicago/Turabian StyleGerasimov, Vasiliy Valerievich, Oleg Eduardovich Kameshkov, Alexey Konstantinovich Nikitin, Ildus Shevketovich Khasanov, Alexey Georgievich Lemzyakov, Irina Veniaminovna Antonova, Artem Ilyich Ivanov, Nghiem Thi Ha Lien, Nguyen Trong Nghia, Le Tu Anh, and et al. 2023. "First Experimental Demonstration of the Wide-Field Amplitude Surface Plasmon Resonance Microscopy in the Terahertz Range" Photonics 10, no. 7: 723. https://doi.org/10.3390/photonics10070723
APA StyleGerasimov, V. V., Kameshkov, O. E., Nikitin, A. K., Khasanov, I. S., Lemzyakov, A. G., Antonova, I. V., Ivanov, A. I., Lien, N. T. H., Nghia, N. T., Anh, L. T., Hung, N. Q., & Trang, T. T. (2023). First Experimental Demonstration of the Wide-Field Amplitude Surface Plasmon Resonance Microscopy in the Terahertz Range. Photonics, 10(7), 723. https://doi.org/10.3390/photonics10070723






