Advanced Numerical Methods for Graphene Simulation with Equivalent Boundary Conditions: A Review
Abstract
1. Introduction
2. Advanced Numerical Methods
2.1. Mathematical Model
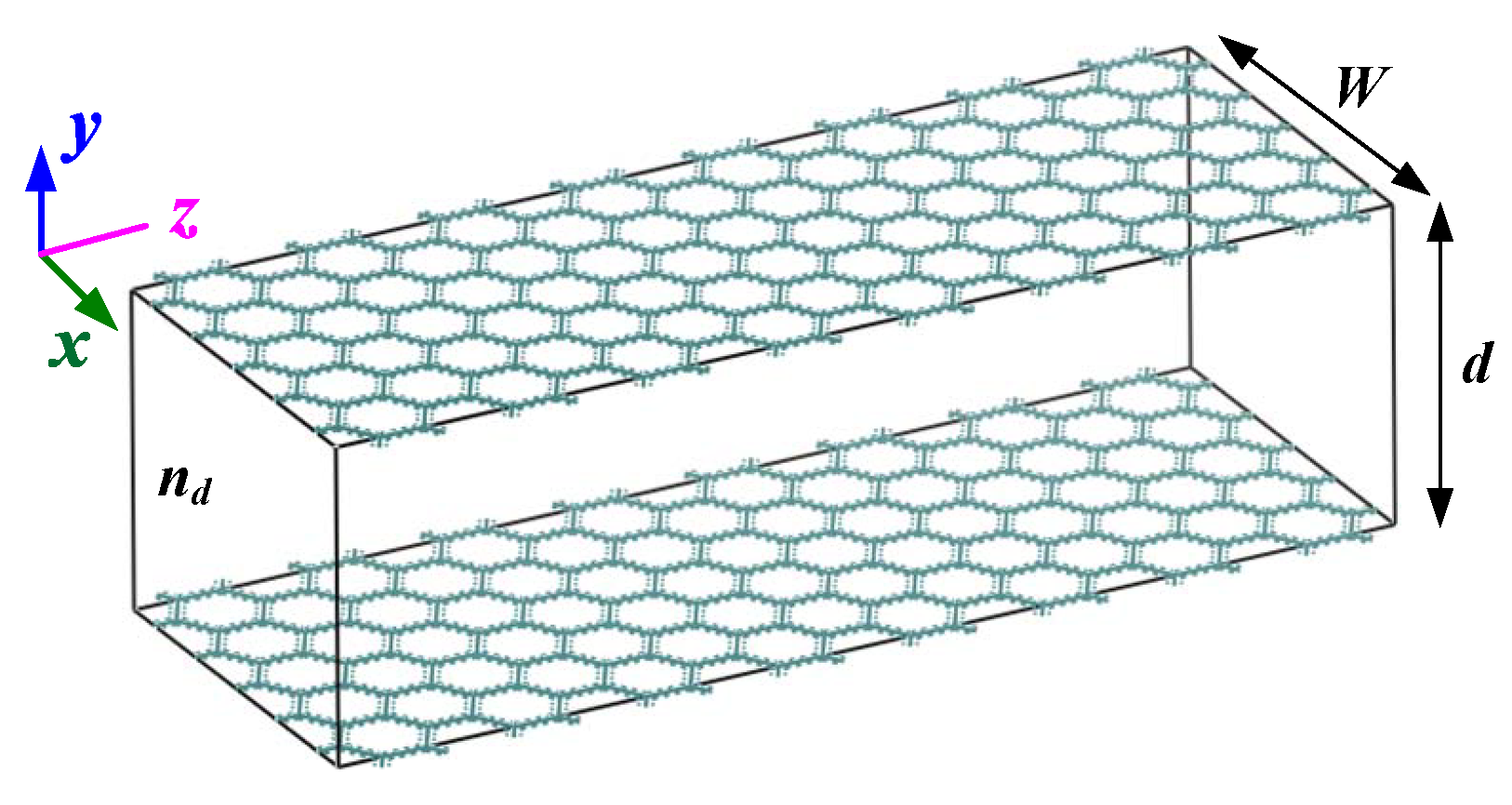
2.2. Mixed Finite Element Method
2.2.1. Impedance Transmission Boundary Condition
2.2.2. Surface Current Boundary Condition
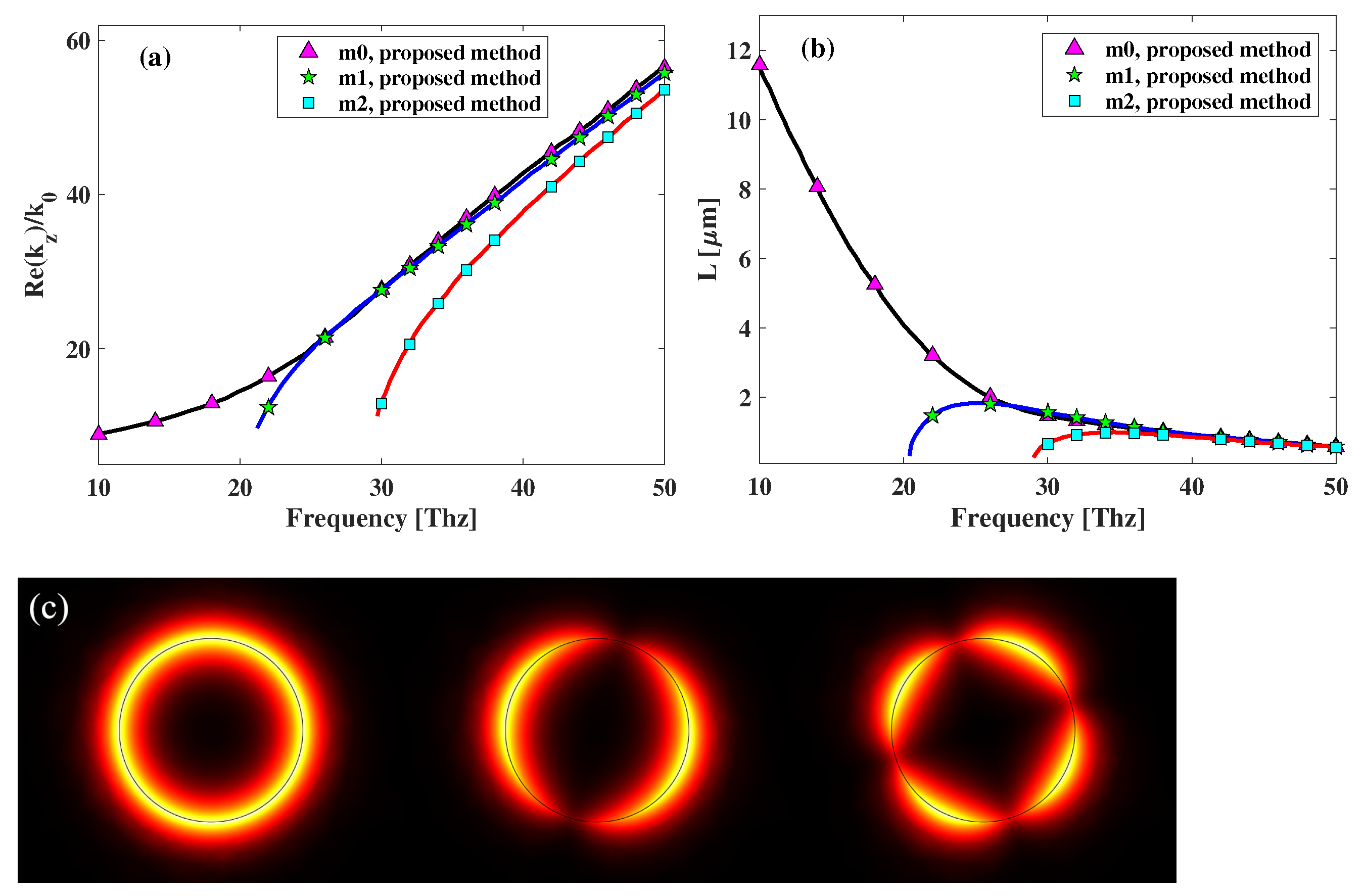
2.3. Mixed Spectral Element Method with SCBC
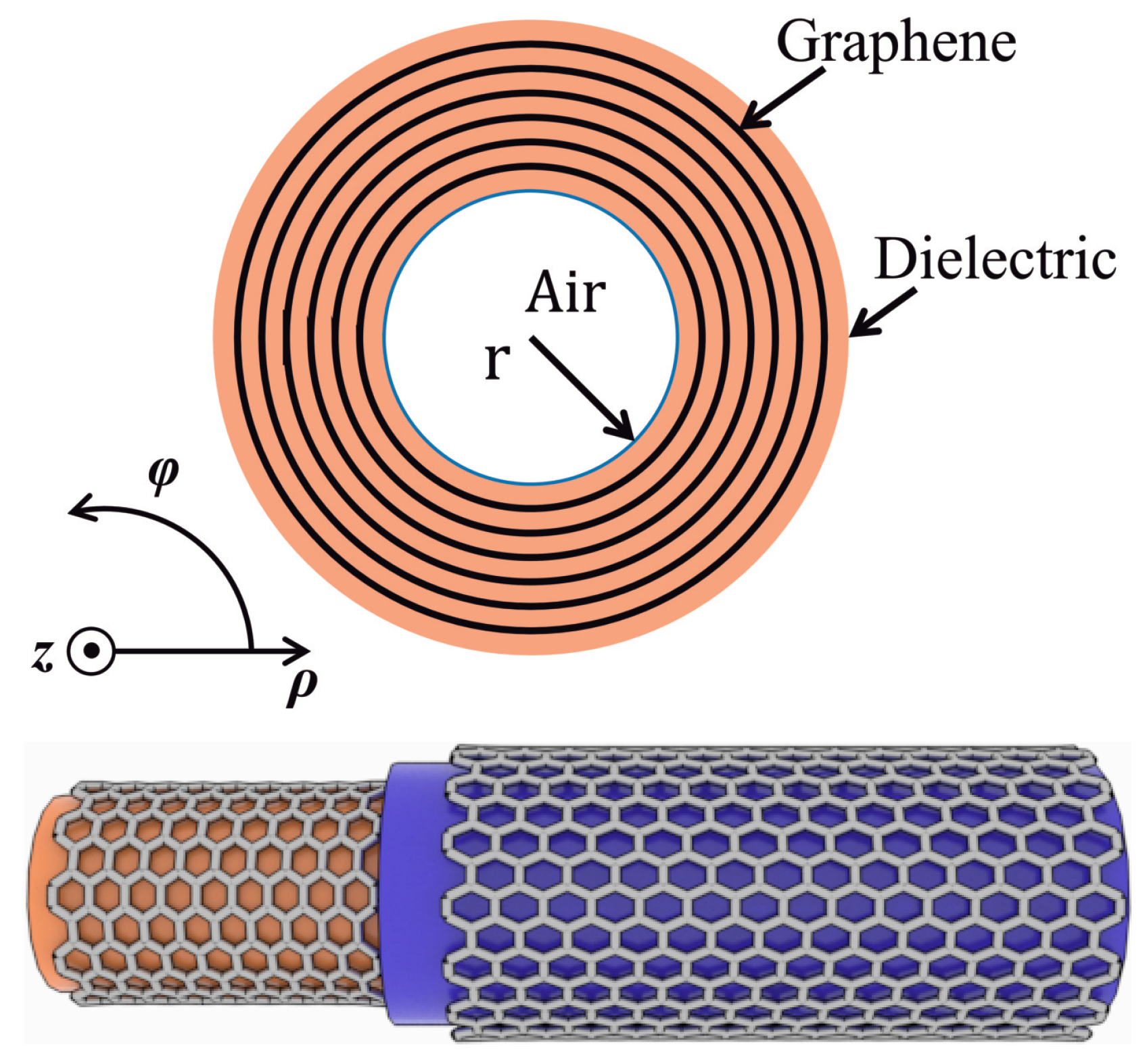
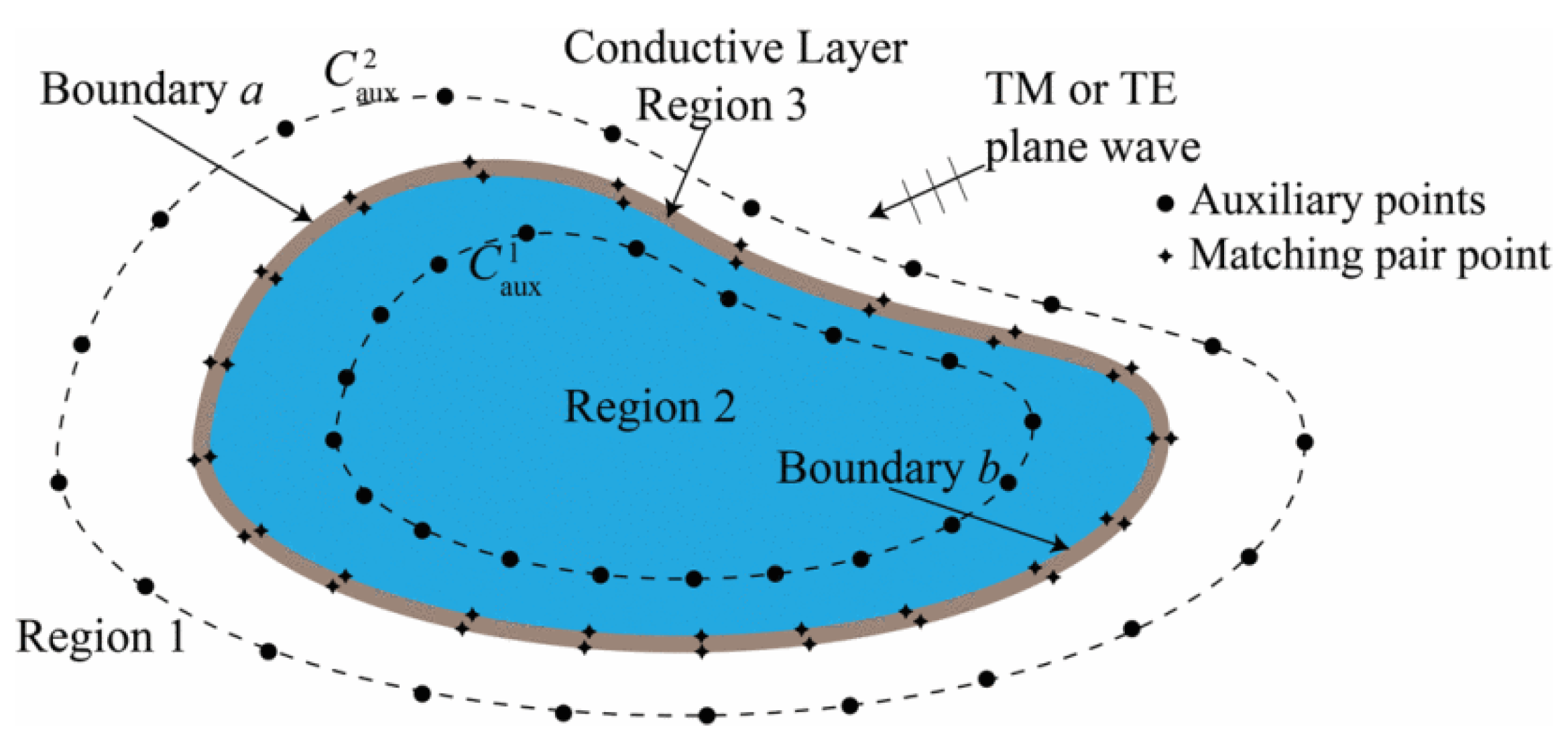
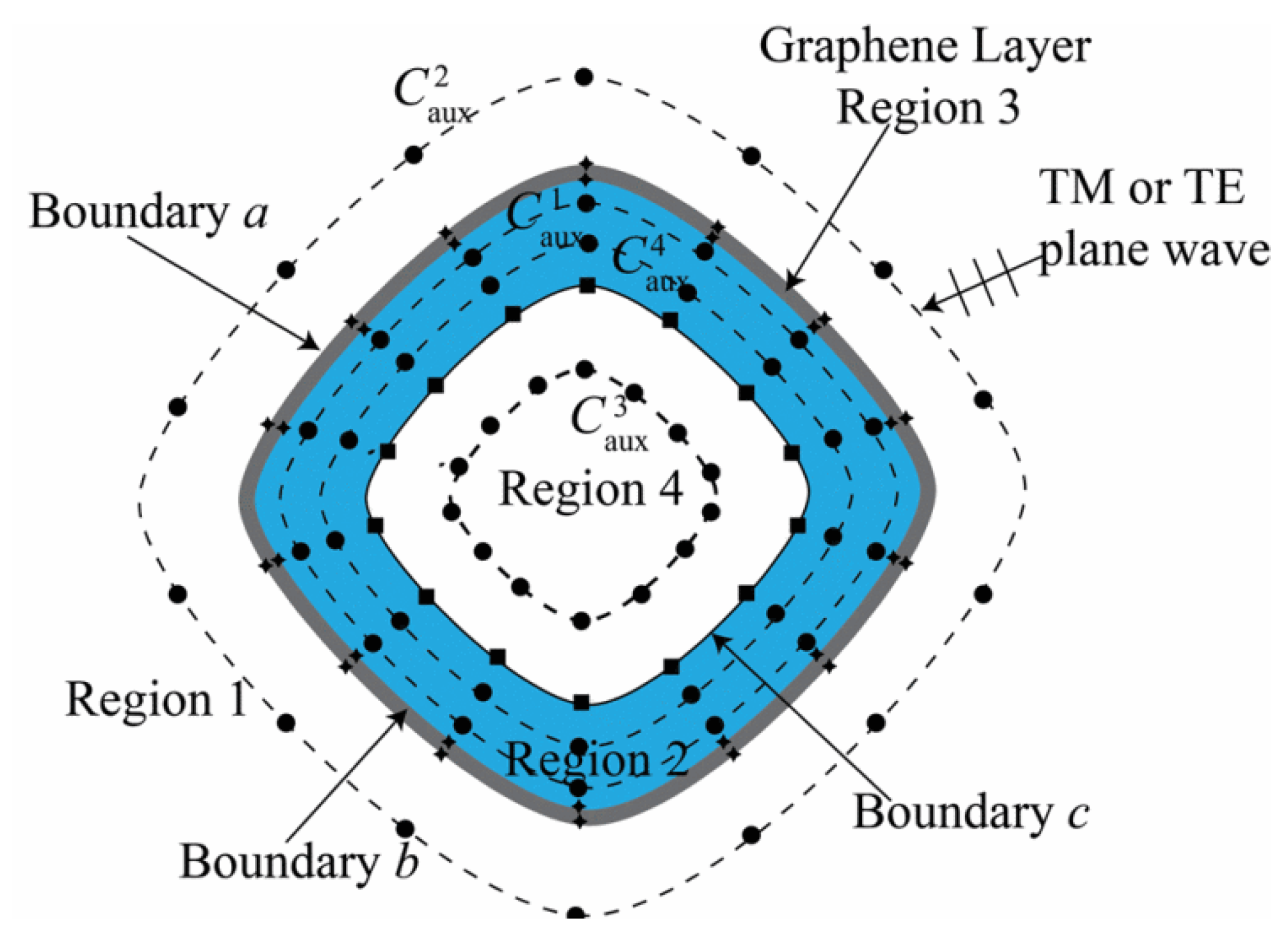
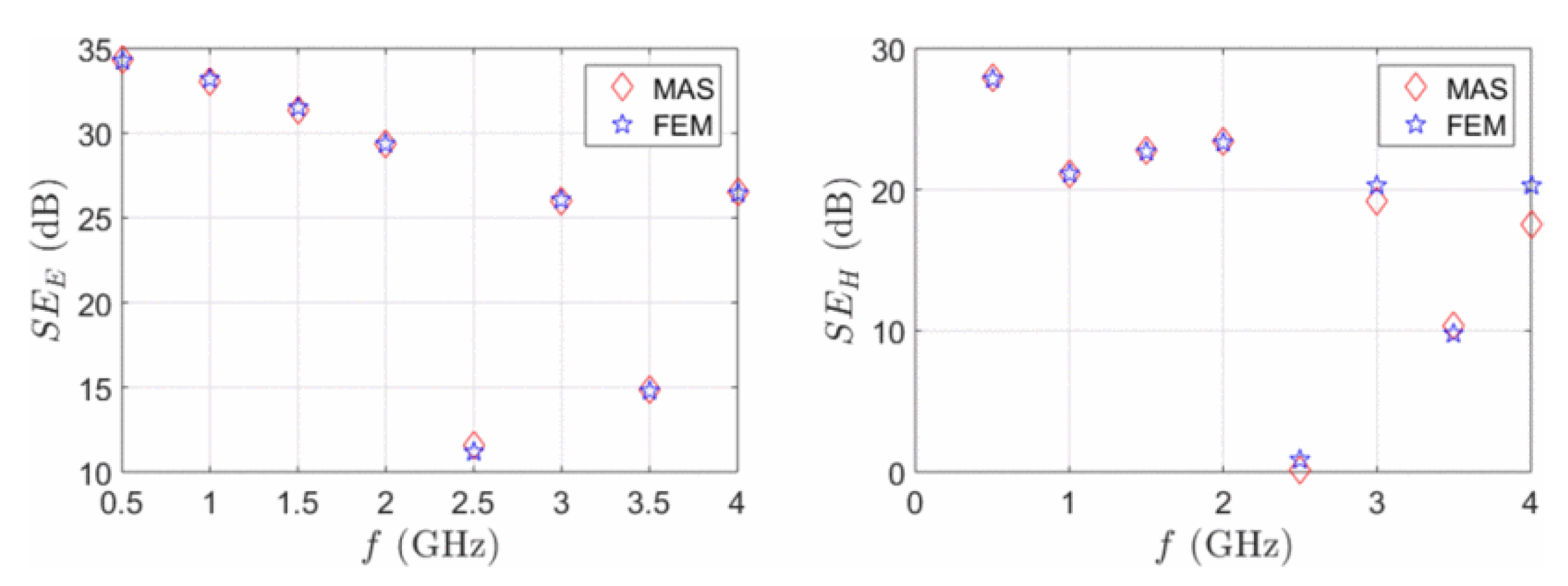
2.4. The Method of Auxiliary Sources with IMBC
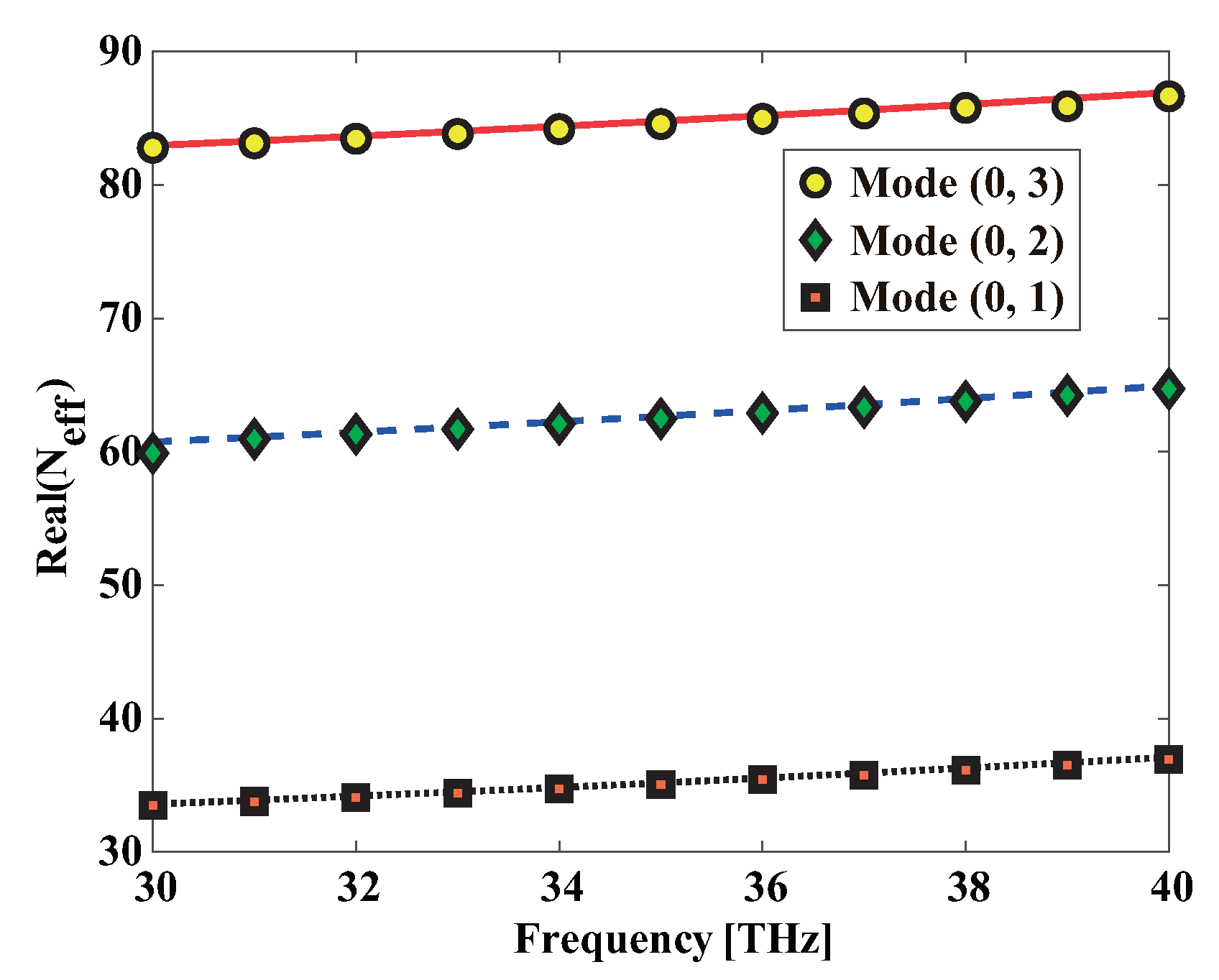
2.5. Discontinuous Galerkin Time-Domain Method with SIBC
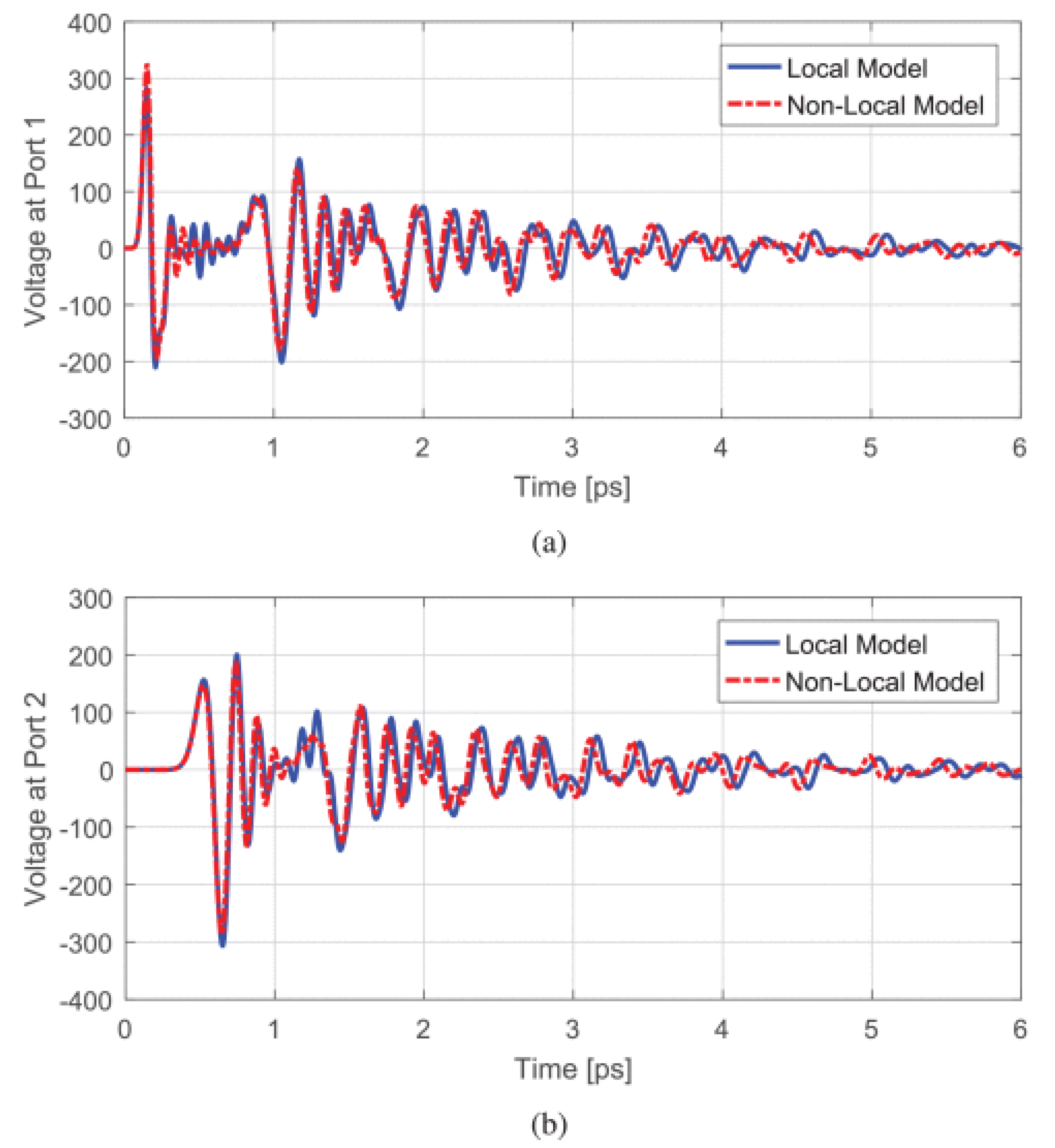
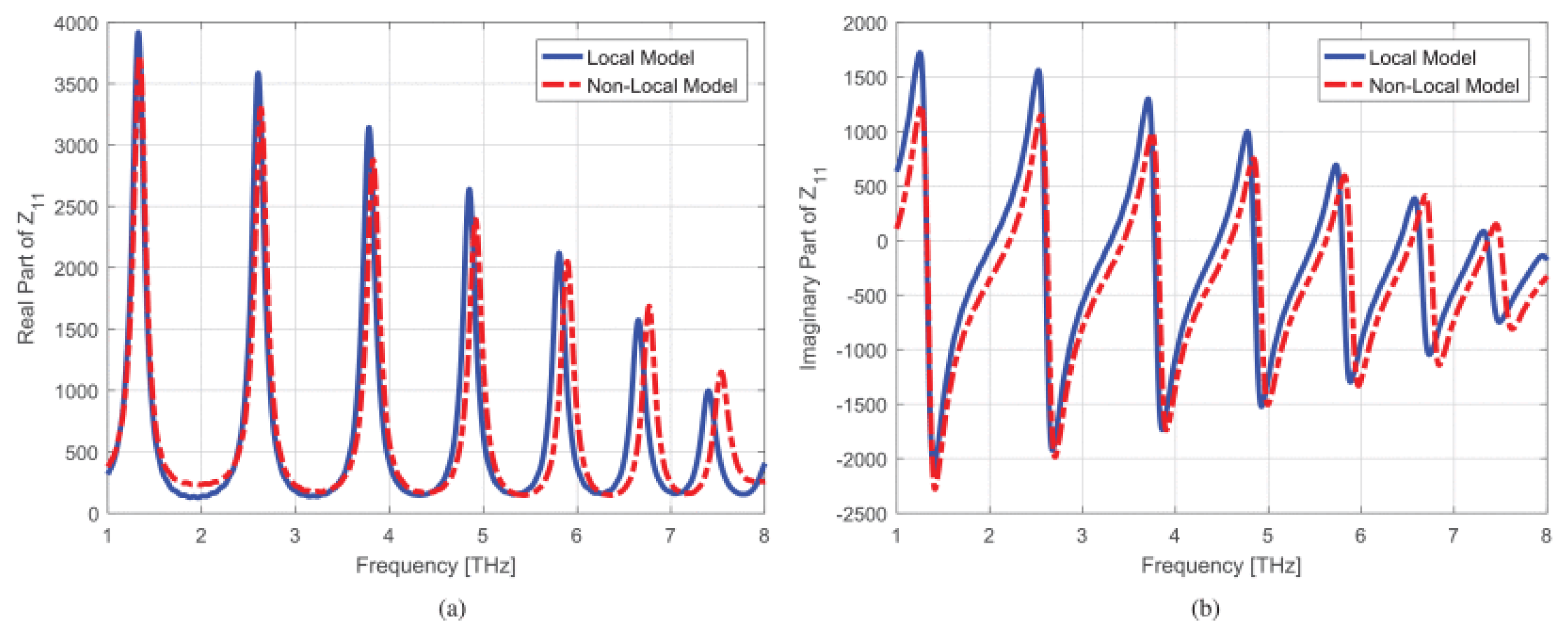
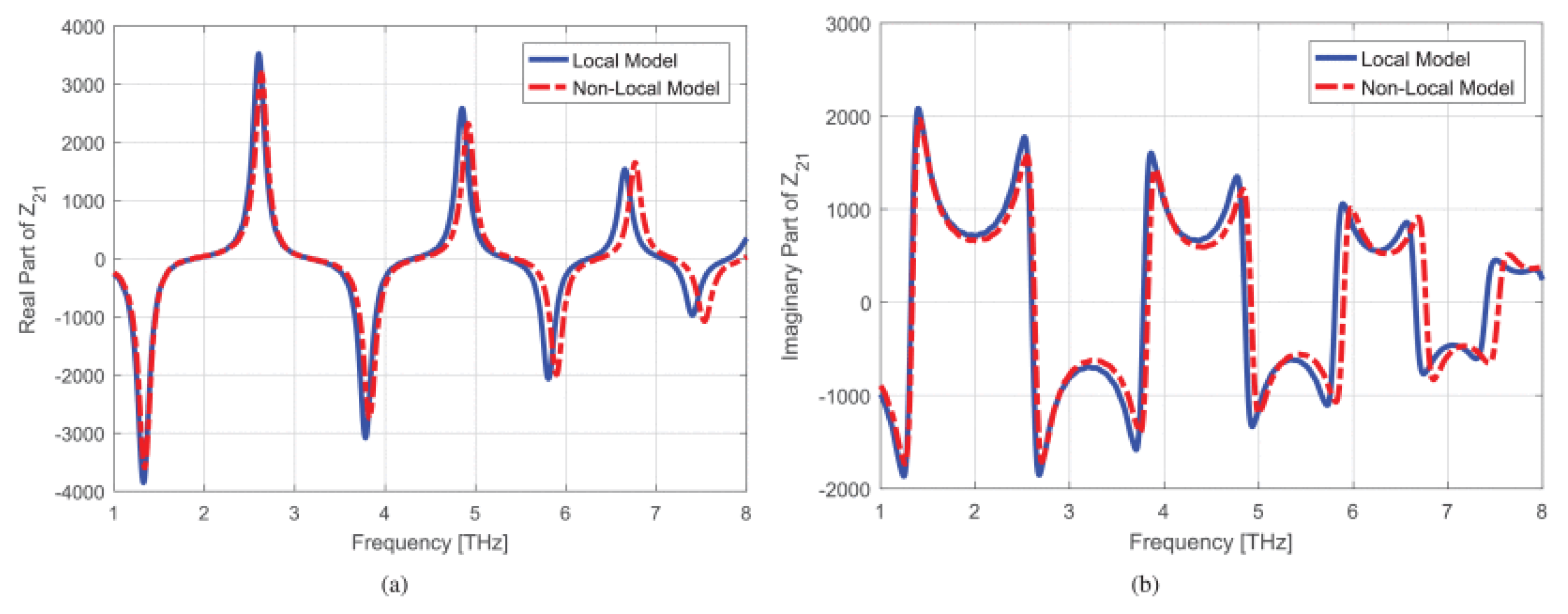
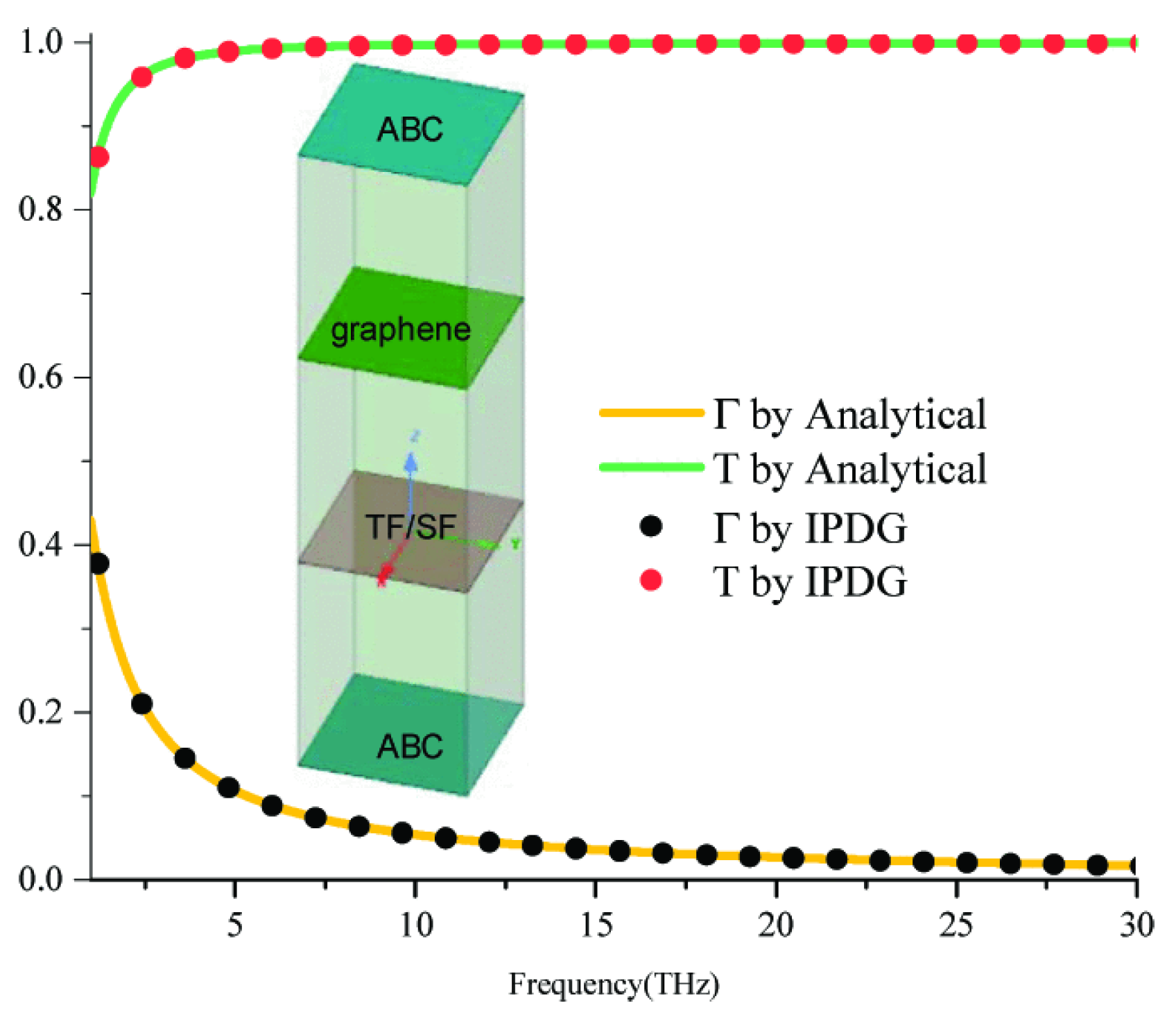
2.6. Interior Penalty Discontinuous Galerkin-Time Domain Method with ITBC
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Mixed FEM | Mixed Finite Element Method |
| Mixed SEM | Mixed Spectral Element Method |
| MAS | Method of Auxiliary Sources |
| DGTD | Discontinuous Galerkin Time-domain |
| IPDG | Interior Penalty Discontinuous Galerkin |
| ITBC | Impedance Transmission Boundary Condition |
| SCBC | Surface Current Boundary Condition |
| IMBC | Impedance Matrix Boundary Condition |
| SIBC | Surface Impedance Boundary Condition |
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.E.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Fal’ ko, V.I.; Colombo, L.; Gellert, P.R.; Schwab, M.G.; Kim, K. A roadmap for graphene. Nature 2012, 490, 192–200. [Google Scholar] [CrossRef] [PubMed]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Lai, R.; Shi, P.; Yi, Z.; Li, H.; Yi, Y. Triple-Band Surface Plasmon Resonance Metamaterial Absorber Based on Open-Ended Prohibited Sign Type Monolayer Graphene. Micromachines 2023, 14, 953. [Google Scholar] [CrossRef]
- Tang, B.; Jia, Z.; Huang, L.; Su, J.; Jiang, C. Polarization-Controlled Dynamically Tunable Electromagnetically Induced Transparency-Like Effect Based on Graphene Metasurfaces. IEEE J. Sel. Top. Quantum Electron. 2021, 27, 4700406. [Google Scholar] [CrossRef]
- Neto, A.C.; Guinea, F.; Peres, N.M.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109. [Google Scholar] [CrossRef]
- Bonaccorso, F.; Sun, Z.; Hasan, T.; Ferrari, A.C. Graphene photonics and optoelectronics. Nat. Photonics 2010, 4, 611–622. [Google Scholar] [CrossRef]
- Blake, P.; Brimicombe, P.D.; Nair, R.R.; Booth, T.J.; Jiang, D.; Schedin, F.; Ponomarenko, L.A.; Morozov, S.V.; Gleeson, H.F.; Hill, E.W.; et al. Graphene-based liquid crystal device. Nano Lett. 2008, 8, 1704–1708. [Google Scholar] [CrossRef]
- Meric, I.; Han, M.Y.; Young, A.F.; Ozyilmaz, B.; Kim, P.; Shepard, K.L. Current saturation in zero-bandgap, top-gated graphene field-effect transistors. Nat. Nanotechnol. 2008, 3, 654–659. [Google Scholar] [CrossRef]
- Shih, C.J.; Wang, Q.H.; Son, Y.; Jin, Z.; Blankschtein, D.; Strano, M.S. Tuning on–off current ratio and field-effect mobility in a MoS2–graphene heterostructure via Schottky barrier modulation. ACS Nano 2014, 8, 5790–5798. [Google Scholar] [CrossRef]
- Tang, G.P.; Zhou, J.C.; Zhang, Z.H.; Deng, X.Q.; Fan, Z.Q. A theoretical investigation on the possible improvement of spin-filter effects by an electric field for a zigzag graphene nanoribbon with a line defect. Carbon 2013, 60, 94–101. [Google Scholar] [CrossRef]
- Tang, B.; Ren, Y. Tunable and switchable multi-functional terahertz metamaterials based on a hybrid vanadium dioxide-graphene integrated configuration. Phys. Chem. Chem. Phys. 2022, 24, 8408–8414. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Jiang, D.; Schedin, F.; Booth, T.J.; Khotkevich, V.V.; Morozov, S.V.; Geim, A.K. Two-dimensional atomic crystals. Proc. Natl. Acad. Sci. USA 2005, 102, 10451–10453. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Magnuson, C.W.; Venugopal, A.; An, J.; Suk, J.W.; Han, B.; Borysiak, M.; Cai, W.; Velamakanni, A.; Zhu, Y.; et al. Graphene films with large domain size by a two-step chemical vapor deposition process. Nano Lett. 2010, 10, 4328–4334. [Google Scholar] [CrossRef] [PubMed]
- Khan, U.; O’Neill, A.; Lotya, M.; De, S.; Coleman, J.N. High-concentration solvent exfoliation of graphene. Small 2010, 6, 864–871. [Google Scholar] [CrossRef]
- Coleman, J.N. Liquid exfoliation of defect-free graphene. Accounts Chem. Res. 2013, 46, 14–22. [Google Scholar] [CrossRef]
- Sasikala, S.P.; Poulin, P.; Aymonier, C. Advances in subcritical hydro-/solvothermal processing of graphene materials. Adv. Mater. 2017, 46, 1605473. [Google Scholar] [CrossRef]
- Peng, Z.; Chen, X.; Fan, Y.; Srolovitz, D.J.; Lei, D. Strain engineering of 2D semiconductors and graphene: From strain fields to band-structure tuning and photonic applications. Light. Sci. Appl. 2021, 9, 190. [Google Scholar] [CrossRef]
- Bafekry, A.; Gogova, D.; Fadlallah, M.M.; Chuong, N.V.; Ghergherehchi, M.; Faraji, M.; Feghhi, S.A.H.; Oskoeian, M. Electronic and optical properties of two-dimensional heterostructures and heterojunctions between doped-graphene and C-and N-containing materials. Phys. Chem. Chem. Phys. 2021, 23, 4865–4873. [Google Scholar] [CrossRef]
- Tang, B.; Guo, Z.; Jin, G. Polarization and symmetry-dependent multiple plasmon-induced transparency in graphene-based metasurfaces. Optics Express 2022, 30, 35554–35566. [Google Scholar] [CrossRef]
- Koppens, F.H.; Chang, D.E.; Abajo, F.J.G.D. Graphene plasmonics: A platform for strong light–matter interactions. Nano Lett. 2011, 11, 3370–3377. [Google Scholar] [CrossRef] [PubMed]
- Grigorenko, A.N.; Polini, M.; Novoselov, K.S. Graphene plasmonics. Nat. Photonics 2012, 6, 749–758. [Google Scholar] [CrossRef]
- Rodrigo, D.; Limaj, O.; Janner, D.; Etezadi, D.; García, F.J.A.D.; Pruneri, V.; Altug, H. Mid-infrared plasmonic biosensing with graphene. Science 349 2015, 165–168. [Google Scholar] [CrossRef]
- Emani, N.K.; Kildishev, A.V.; Shalaev, V.M.; Boltasseva, A. Graphene: A dynamic platform for electrical control of plasmonic resonance. Nanophotonics 2015, 4, 214–223. [Google Scholar] [CrossRef]
- Nikitin, A.Y.; Guinea, F.; Garcia-Vidal, F.J.; Martin-Moreno, L. Fields radiated by a nanoemitter in a graphene sheet. Phys. Rev. B 2011, 84, 195446. [Google Scholar] [CrossRef]
- Francescato, Y.; Giannini, V.; Aier, S.A. Strongly confined gap plasmon modes in graphene sandwiches and graphene-on-silicon. New J. Phys. 2013, 15, 063020. [Google Scholar] [CrossRef]
- Hanson, G.W. Dyadic Green’s functions and guided surface waves for a surface conductivity model of graphene. J. Appl. Phys. 2008, 103, 064302. [Google Scholar] [CrossRef]
- Hanson, G.W. Dyadic Green’s functions for an anisotropic, non-local model of biased graphene. IEEE Trans. Antennas Propag. 2008, 56, 747–757. [Google Scholar] [CrossRef]
- Obayya, S.S.A.; Rahman, B.A.; El-Mikati, H.A. New full-vectorial numerically efficient propagation algorithm based on the finite element method. J. Light. Technol. 2000, 18, 409. [Google Scholar] [CrossRef]
- Saitoh, K.; Koshiba, M. Full-vectorial finite element beam propagation method with perfectly matched layers for anisotropic optical waveguides. J. Light. Technol. 2001, 19, 405–413. [Google Scholar] [CrossRef]
- Ishizaka, Y.; Kawaguchi, Y.; Saitoh, K.; Koshiba, M. Three-dimensional finite-element solutions for crossing slot-waveguides with finite core-height. J. Light. Technol. 2012, 30, 3394–3400. [Google Scholar] [CrossRef]
- Yu, C.P.; Chang, H.C. Yee-mesh-based finite difference eigenmode solver with PML absorbing boundary conditions for optical waveguides and photonic crystal fibers. Opt. Express 2004, 12, 6165–6177. [Google Scholar] [CrossRef] [PubMed]
- Shao, Y.; Yang, J.J.; Huang, M. A review of computational electromagnetic methods for graphene modeling. Int. J. Antennas Propag. 2016, 2016, 7478621. [Google Scholar] [CrossRef]
- Niu, K.; Li, P.; Huang, Z.; Jiang, L.J.; Bagci, H. Numerical methods for electromagnetic modeling of graphene: A review. IEEE J. Multiscale Multiphys. Comput. Tech. 2020, 5, 44–58. [Google Scholar] [CrossRef]
- Li, P.; Shi, Y.; Jiang, L.J.; Bagci, H. DGTD analysis of electromagnetic scattering from penetrable conductive objects with IBC. IEEE Trans. Antennas Propag. 2015, 63, 5686–5697. [Google Scholar]
- Li, P.; Jiang, L.J.; Bağci, H. Transient analysis of dispersive power-ground plate pairs with arbitrarily shaped antipads by the DGTD method with wave port excitation. IEEE Trans. Electromagn. Compat. 2016, 59, 172–183. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, S.; Chen, S.; Luo, H.; Wen, S. Examining the optical model of graphene via the photonic spin Hall effect. Opt. Lett. 2022, 47, 846–849. [Google Scholar] [CrossRef]
- Kaliberda, M.E.; Lytvynenko, L.M.; Pogarsky, S.A.; Sauleau, R. Excitation of guided waves of grounded dielectric slab by a THz plane wave scattered from finite number of embedded graphene strips: Singular integral equation analysis. IET Microw. Antennas Propag. 2021, 15, 1171–1180. [Google Scholar] [CrossRef]
- Nayyeri, V.; Soleimani, M.; Ramahi, O.M. Modeling graphene in the finite-difference time-domain method using a surface boundary condition. IEEE Trans. Antennas Propag. 2013, 61, 4176–4182. [Google Scholar] [CrossRef]
- Vakil, A.; Engheta, N. Transformation optics using graphene. Science 2011, 332, 1291–1294. [Google Scholar] [CrossRef]
- Gao, W.; Shu, J.; Qiu, C.; Xu, Q. Excitation of plasmonic waves in graphene by guided-mode resonances. ACS Nano 2012, 6, 7806–7813. [Google Scholar] [CrossRef] [PubMed]
- Rickhaus, P.; Liu, M.H.; Kurpas, M.; Kurzmann, A.; Lee, Y.; Overweg, H.; Eich, M.; Pisoni, R.; Taniguchi, T.; Watanabe, K.; et al. The electronic thickness of graphene. Sci. Adv. 2020, 6, eaay8409. [Google Scholar] [CrossRef] [PubMed]
- Echtermeyer, T.J.; Milana, S.; Sassi, U.; Eiden, A.; Wu, M.; Lidorikis, E.; Ferrari, A.C. Surface plasmon polariton graphene photodetectors. Nano Lett. 2016, 16, 8–20. [Google Scholar] [CrossRef]
- Wang, P.; Shi, Y.; Li, L. An impedance transmission boundary condition-based interior penalty discontinuous Galerkin time domain method for analysis of graphene. In Proceedings of the 2019 IEEE International Conference on Computational Electromagnetics (ICCEM), Shanghai, China, 20–22 March 2019; Volume 16, pp. 1–3. [Google Scholar]
- Mao, Y.; Zhan, Q.; Sun, Q.; Wang, D.; Liu, Q.H. Mesh-splitting impedance transition boundary condition for accurate modeling of thin structures. IEEE Trans. Antennas Propag. 2023, 71, 4612–4617. [Google Scholar] [CrossRef]
- Hou, X.; Liu, N.; Chen, K.; Zhuang, M.; Liu, Q.H. The efficient hybrid mixed spectral element method with surface current boundary condition for modeling 2.5-D fractures and faults. IEEE Access 2020, 8, 135339–135346. [Google Scholar] [CrossRef]
- Qian, Z.G.; Chew, W.C.; Suaya, R. Generalized impedance boundary condition for conductor modeling in surface integral equation. IEEE Trans. Microw. Theory Tech. 2007, 55, 2354–2364. [Google Scholar] [CrossRef]
- Feliziani, M.; Cruciani, S. FDTD modeling of impedance boundary conditions by equivalent LTI circuits. IEEE Trans. Microw. Theory Tech. 2012, 60, 3656–3666. [Google Scholar] [CrossRef]
- Feliziani, M.; Cruciani, S.; Maradei, F. Circuit-oriented FEM modeling of finite extension graphene sheet by impedance network boundary conditions (INBCs). IEEE Trans. Terahertz Sci. Technol. 2014, 4, 734–740. [Google Scholar] [CrossRef]
- Crépieux, A.; Bruno, P. Theory of the anomalous Hall effect from the Kubo formula and the Dirac equation. Phys. Rev. B 2001, 64, 014416. [Google Scholar] [CrossRef]
- Zhao, Z.; Sun, C.; Zhou, R. Thermal conductivity of confined-water in graphene nanochannels. Int. J. Heat Mass Transf. 2020, 152, 119502. [Google Scholar] [CrossRef]
- Zare, S.; Tajani, B.Z.; Edalatpour, S. Effect of nonlocal electrical conductivity on near-field radiative heat transfer between graphene sheets. Phys. Rev. B 2022, 105, 125416. [Google Scholar] [CrossRef]
- Sun, D.; Manges, J.; Yuan, X.; Cendes, Z. Spurious modes in finite-element methods. IEEE Antennas Propag. Mag. 1995, 37, 12–24. [Google Scholar] [CrossRef]
- Vardapetyan, L.; Demkowicz, L. Full-wave analysis of dielectric waveguides at a given frequency. Math. Comput. 2003, 72, 105–129. [Google Scholar] [CrossRef]
- Vardapetyan, L.; Demkowicz, L. HP-vector finite element method for the full-wave analysis of waveguides with no spurious modes. Electromagnetics 2002, 22, 419–428. [Google Scholar] [CrossRef]
- Liu, N.; Tobón, L.E.; Zhao, Y.; Tang, Y.; Liu, Q.H. Mixed spectral-element method for 3-D Maxwell’s eigenvalue problem. IEEE Trans. Microw. Theory Tech. 2015, 63, 317–325. [Google Scholar] [CrossRef]
- Liu, N.; Cai, G.; Ye, L.; Liu, Q.H. The efficient mixed FEM with the impedance transmission boundary condition for graphene plasmonic waveguides. J. Light. Technol. 2016, 34, 5363–5370. [Google Scholar] [CrossRef]
- Woyna, I.; Gjonaj, E.; Weiland, T. Broadband surface impedance boundary conditions for higher order time domain discontinuous Galerkin method. COMPEL 2014, 33, 1082–1096. [Google Scholar] [CrossRef]
- Liu, N.; Cai, G.; Zhu, C.; Huang, Y.; Liu, Q.H. The mixed finite-element method with mass lumping for computing optical waveguide modes. IEEE J. Sel. Top. Quantum Electron. 2015, 22, 187–195. [Google Scholar] [CrossRef]
- Nayyeri, V.; Soleimani, M.; Ramahi, O.M. Wideband modeling of graphene using the finite-difference time-domain method. IEEE Trans. Antennas Propag. 2013, 61, 6107–6114. [Google Scholar] [CrossRef]
- Gao, Y.; Ren, G.; Zhu, B.; Liu, H.; Lian, Y.; Jian, S. Analytical model for plasmon modes in graphene-coated nanowire. Opt. Express 2014, 22, 24322–24331. [Google Scholar] [CrossRef]
- Emani, N.K.; Wang, D.; Chung, T.F. Prokopeva, L.J.; Kildishev, A.V.; Shalaev, V.M.; Chen, Y.P.; Boltasseva, A. Plasmon resonance in multilayer graphene nanoribbons. Laser Photonics Rev. 2015, 9, 650–655. [Google Scholar] [CrossRef]
- Liu, N.; Chen, X.; Cao, Y.; Cai, G.; Zhuang, M.; Liu, N.; Liu, Q.H. Modeling graphene-based plasmonic waveguides by mixed FEM with surface current boundary condition. IEEE Photonics Technol. Lett. 2021, 33, 735–738. [Google Scholar] [CrossRef]
- Patera, A.T. A spectral element method for fluid dynamics: Laminar flow in a channel expansion. J. Comput. Phys. 1984, 54, 468–488. [Google Scholar] [CrossRef]
- Liu, Q.H. A pseudospectral frequency-domain (PSFD) method for computational electromagnetics. IEEE Antennas Wirel. Propag. Lett. 2002, 1, 131–134. [Google Scholar] [CrossRef]
- Liu, N.; Cai, G.; Zhu, C.; Tang, Y.; Liu, Q.H. The mixed spectral-element method for anisotropic, lossy, and open waveguides. IEEE Trans. Microw. Theory Tech. 2015, 63, 3094–3102. [Google Scholar] [CrossRef]
- Xing, R.; Engheta, N. Numerical analysis on tunable multilayer nanoring waveguide. IEEE Photonics Technol. Lett. 2017, 29, 967–970. [Google Scholar] [CrossRef]
- Lin, X.; Cai, G.; Chen, H.; Liu, N.; Liu, Q.H. Modal analysis of 2-D material-based plasmonic waveguides by mixed spectral element method with equivalent boundary condition. J. Light. Technol. 2020, 38, 3677–3686. [Google Scholar] [CrossRef]
- Kaklamani, D.I.; Anastassiu, H.T. Aspects of the method of auxiliary sources (MAS) in computational electromagnetics. IEEE Antennas Propag. Mag. 2002, 44, 48–64. [Google Scholar] [CrossRef]
- Kouroublakis, M.; Tsitsas, N.L.; Fikioris, G. Convergence analysis of the currents and fields involved in the method of auxiliary sources applied to scattering by PEC cylinders. IEEE Trans. Electromagn. Compat. 2021, 63, 454–462. [Google Scholar] [CrossRef]
- Tsitsas, N.L.; Alivizatos, E.G.; Anastassiu, H.T.; Kaklamani, D.I. Accuracy analysis of the method of auxiliary sources (MAS) for scattering from a two-layer dielectric circular cylinder. In Proceedings of the 2005 IEEE Antennas and Propagation Society International Symposium, Washington, DC, USA, 3–8 July 2005; Volume 3, pp. 356–359. [Google Scholar]
- Tsitsas, N.L.; Alivizatos, E.G.; Kaklamani, D.I.; Anastassiu, H.T. Optimization of the method of auxiliary sources (MAS) for oblique incidence scattering by an infinite dielectric cylinder. Electr. Eng. 2007, 89, 353–361. [Google Scholar] [CrossRef]
- Kouroublakis, M.; Tsitsas, N.L.; Fikioris, G. Shielding effectiveness of ideal monolayer graphene in cylindrical configurations with the method of auxiliary sources. IEEE Trans. Electromagn. Compat. 2022, 64, 1042–1051. [Google Scholar] [CrossRef]
- Kouroublakis, M.; Tsitsas, N.L.; Fikioris, G. Modeling of cylindrical configurations coated by monolayer graphene with a modified method of auxiliary sources. In Proceedings of the 2022 Microwave Mediterranean Symposium (MMS), Pizzo Calabro, Italy, 9–13 May 2022; pp. 1–5. [Google Scholar]
- Renaud, P.R.; Laurin, J.J. Shielding and scattering analysis of lossy cylindrical shells using an extended multifilament current approach. IEEE Trans. Electromagn. Compat. 1999, 41, 320–334. [Google Scholar] [CrossRef]
- Sankaran, K. Accurate Domain Truncation Techniques for Time-Domain Conformal Methods. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2007. [Google Scholar]
- Mai, W.; Li, P.; Bao, H.; Li, X.; Jiang, L.; Hu, J.; Werner, D.H. Prism-based DGTD with a simplified periodic boundary condition to analyze FSS With D 2n symmetry in a rectangular array under normal incidence. IEEE Antennas Wirel. Propag. Lett. 2018, 18, 771–775. [Google Scholar] [CrossRef]
- Li, P.; Jiang, L.J.; Zhang, Y.J.; Xu, S.; Bağci, H. An efficient mode-based domain decomposition hybrid 2-D/Q-2D finite-element time-domain method for power/ground plate-pair analysis. IEEE Trans. Microw. Theory Tech. 2018, 66, 4357–4366. [Google Scholar] [CrossRef]
- Lovat, G.; Hanson, G.W.; Araneo, R.; Burghignoli, P. Semiclassical spatially dispersive intraband conductivity tensor and quantum capacitance of graphene. Phys. Rev. B 2013, 87. [Google Scholar] [CrossRef]
- Li, P.; Jiang, L.J.; Bağcı, H. Discontinuous Galerkin time-domain modeling of graphene nanoribbon incorporating the spatial dispersion effects. IEEE Trans. Antennas Propag. 2018, 66, 3590–3598. [Google Scholar] [CrossRef]
- Tian, C.Y.; Shi, Y.; Chan, C.H. Interior penalty discontinuous Galerkin time-domain method based on wave equation for 3-D electromagnetic modeling. IEEE Trans. Antennas Propag. 2017, 65, 7174–7184. [Google Scholar] [CrossRef]
- Gustavsen, B.; Semlyen, A. Rational approximation of frequency domain responses by vector fitting. IEEE Trans. Power Deliv. 1999, 14, 1052–1061. [Google Scholar] [CrossRef]










| Mixed FEM-ITBC | FEM with Graphene Sheet | |
|---|---|---|
| DOF | 82,215 | 408,035 |
| CPU time | 29.9 s | 375.0 s |
| Memory | 0.07 GB | 0.18 GB |
| Mixed FEM-SCBC | FEM with Graphene Sheet | |
|---|---|---|
| DOF | 91,997 | 384,737 |
| CPU time | 31.4 s | 252.2 s |
| Mixed SEM-SCBC | FEM with Graphene Sheet | |
|---|---|---|
| DOF | 17,528 | 893,421 |
| CPU time | 13.8 s | 434.5 s |
| Memory | 0.06 GB | 3.17 GB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, Y.; Liu, N. Advanced Numerical Methods for Graphene Simulation with Equivalent Boundary Conditions: A Review. Photonics 2023, 10, 712. https://doi.org/10.3390/photonics10070712
Gong Y, Liu N. Advanced Numerical Methods for Graphene Simulation with Equivalent Boundary Conditions: A Review. Photonics. 2023; 10(7):712. https://doi.org/10.3390/photonics10070712
Chicago/Turabian StyleGong, Yansheng, and Na Liu. 2023. "Advanced Numerical Methods for Graphene Simulation with Equivalent Boundary Conditions: A Review" Photonics 10, no. 7: 712. https://doi.org/10.3390/photonics10070712
APA StyleGong, Y., & Liu, N. (2023). Advanced Numerical Methods for Graphene Simulation with Equivalent Boundary Conditions: A Review. Photonics, 10(7), 712. https://doi.org/10.3390/photonics10070712




