Abstract
A surface plasmonic waveguide made of metal–insulator–metal (MIM) capable of generating triple Fano resonances is proposed and numerically investigated for multi-biological parameter sensing as well as tunable slow light. The waveguide is made up of a bus waveguide with a silver baffle, a square split-ring cavity with a square center (SSRCSC), and a circular ring cavity with a square center (CRCSC). Based on the triple Fano resonances, human blood temperature and plasma concentration are measured simultaneously at different locations in the waveguide, and the maximum sensitivities were 0.25 nm/°C and 0.2 nm·L/g, respectively. Furthermore, the two biological parameters can be used to achieve tunable slow light, and it was found that the group delay responses to human blood temperature and plasma concentration all conformed to cubic functions. The MIM waveguide may have great applications in future nano-sensing of multiple biological parameters and information processing of optical chips or bio-optical chips.
1. Introduction
Since Ugo Fano initially proposed it in 1961, Fano resonance has established itself as one of the key components in the advancement of optical sensing [1,2,3,4]. Unlike conventional Lorentz resonance with a symmetric lineshape, Fano resonance, which emerges when a broad continuous state is connected to a narrow discrete state, usually has a sharp and asymmetric lineshape. Due to the unique lineshape, small changes in the geometry or environment can significantly affect Fano resonance [5,6,7,8,9]. Electromagnetic waves known as surface plasmon polaritons (SPPs) are found solely between a metal and a nonconductor, at their intersection. Molecular signals can be strengthened by strong SPPs at the metal–dielectric contact site, which is helpful in biomedicine [10,11,12], chemistry [13,14], and information technology [15]. Because the SPPs also have the excellent characteristic of breaking the classical diffraction limit [16,17], the combination of SPPs and Fano resonance has very important applications in modern micro- and nano-chip optics [18,19,20,21,22].
The SPPs in MIM waveguides, which have adequate propagation lengths, low bend losses, and ease of sample manufacturing, have gained significant study interest [23,24,25,26]. Fano-resonance-exciting MIM waveguide designs have gained popularity recently for use in filters [27,28,29], wavelength division multiplexers [30], all-optical switches [31,32], slow-light devices [33,34], and especially in sensors [6,35,36,37,38,39]. For instance, Chen et al. proposed an SSRC on a MIM waveguide that is non-through and could achieve multiple Fano resonances, and the highest sensing sensitivity for refractive index was up to 1290.2 nm/RIU [38]. A waveguide system with end coupling capable of Fano resonances was designed by Fang et al. The sensing sensitivity of the refractive index could reach 1059.2 nm/RIU [40]. In addition, Wang et al. achieved a square-ring and triangle-cavity MIM waveguide to obtain triple Fano resonances and a maximal sensitivity to refractive index of 2259.56 nm/RIU [41]. All of these results showed that Fano resonance could be effectively used for integrated optical sensing with high sensitivity.
In this study, we aimed to increase the parallel processing capability of biosensing and obtain tunable slow light, based on easily adjustable multiple Fano resonances. To implement the simultaneous measurement of multiple biological parameters and tuning of slow light effects at selected wavelengths, we proposed multi-ring cavities. This will also make it easier to use Fano resonances in integrated optical biosensing. A MIM surface plasmonic waveguide with ring cavities was designed to generate triple Fano resonances. By altering the refractive index, individual tuning of the triple Fano resonances was examined, and glucose solution concentration and plasma concentration were measured simultaneously using this waveguide. In addition, tunable slow light was achieved using these two biological parameters, and the response of the group delay to these biological parameters was fitted.
2. Materials and Methods
The envisioned waveguide for the MIM waveguide is shown in Figure 1, which is composed of a square split-ring cavity with a square center (SSRCSC), a circular ring cavity with a square center (CRCSC), and a waveguide with a silver baffle for a bus. Silver and air are represented by the white and green regions, respectively. A silver baffle was added to the upper part of the square ring, in order to obtain sufficient distances between Fano resonances for measuring multiple parameters at the same time, and increase the sharpness and transmittance of Fano resonances for realizing larger sensitivity and lower slow light. , , , , , and are the width of this silver baffle, the side length of the external square of the SSRCSC, the side length of the internal square of the SSRCSC, the radius of the external circle of the CRCSC, the side length of the internal square of the CRCSC, the distance between the SSRCSC and the bus waveguide, and the distance between the CRCSC and the bus waveguide, respectively. To ensure that only the basic transverse magnetic mode may exist in this configuration, the bus waveguide’s width is specified as 50 nm. The silver baffle in the center, whose width is given by , blocks the bus waveguide. The SSRCSC, CRCSC, and bus waveguide all have geometric centers that are on the reference line, so the overall waveguide is symmetrical about the reference line.
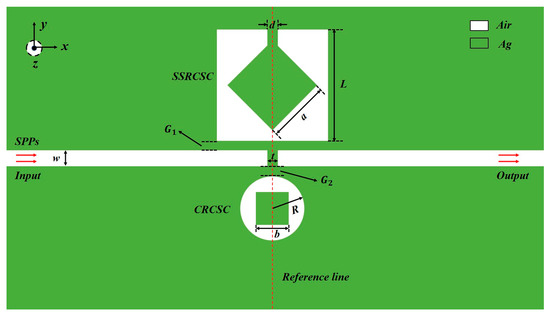
Figure 1.
A schematic diagram of a MIM waveguide composed of a square split-ring cavity, a bus waveguide with a silver baffle, and a circular ring cavity.
The Drude model represents the frequency-dependent complicated relative permittivity of silver [42,43]:
where , , , and represent the dielectric constant at infinite frequency, the plasma frequency of free conduction electrons, the angular frequency of the incident wave in vacuum, and the electron collision frequency, respectively.
The standing wave theory states that constructive interference should occur when the resonance condition is satisfied, and the transmitted wavelength is calculated by using the resonance condition [44,45]:
where , , , , and represent the resonant wavelength, the order of the resonant mode, the phase shift due to reflection, the real part of the effective refractive index, and the effective length of the resonant cavity, respectively.
The waveguide’s optical transmission characteristics are simulated by the finite element method (FEM), and the numerical values of the waveguide parameters utilized in the simulation are shown in Table 1. Here, all the parameters were optimized in order to obtain multiple Fano resonances with high transmittance. In order to absorb the escaping waves, perfect matching layers (PMLs) are positioned at the waveguide’s top and bottom. Moreover, fine triangular meshes with a maximum size of 10 nm were chosen to provide precise area segmentation in the simulation. In practice, the MIM waveguide may be fabricated in the following way: First, a thick enough Ag layer is prepared by the chemical vapor deposition (CVD) method on a silicon substrate [46]. Then, the SSRCSC, the CRCSC, and the bus waveguide with a silver baffle are etched on the Ag layer through electron beam etching.

Table 1.
A list of the simulation settings for the waveguide.
3. Results
3.1. Mechanism of Fano Resonance and Distribution of Magnetic Fields
As shown in Figure 2, we set the waveguide in SSRCSC with the CRCSC’s mode, single bus waveguide mode, and full waveguide mode to illustrate the mechanism of Fano resonance generation. The bus waveguide with the silver baffle removed produced three transmission dips at 1107 nm, 1849 nm, and 2428 nm, which, as represented by the red line, may be thought of as a narrow discrete state. The blue line represents the state produced by the bus waveguide, which is a wide continuous state. The entire waveguide generated three asymmetric and sharp Fano resonances at 1097 nm, 1795 nm, and 2407 nm, known as FR1, FR2, and FR3, as a consequence of interference between the discrete state and continuous state.
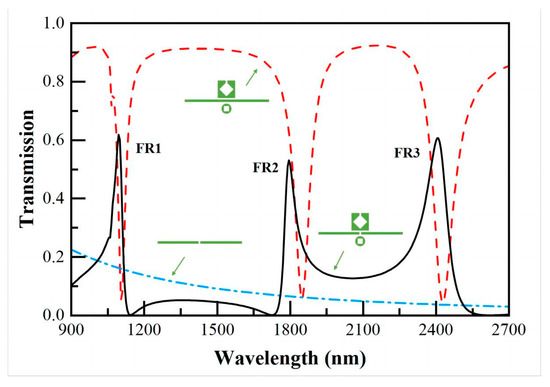
Figure 2.
Schematic diagram of the formation mechanism of the structurally excited Fano resonance proposed in this paper.
The dispersion of the magnetic fields () of FR1, FR2, and FR3 are shown in Figure 3a–c, and the corresponding heights are shown in Figure 3d–f. The distributions of magnetic field energy in the SSRCSC and the CRCSC are symmetric about the reference line parallel to the y-axis. For FR1, almost all of the energy was confined in the CRCSC, so FR1 is sensitive to the parameters of the CRCSC, while the majority of energy of FR2 and FR3 was confined in the SSRCSC, proving that the characteristics of the SSRCSC mostly impact FR2 and FR3. As a result, the SSRCSC and CRCSC characteristics may be individually changed to control the triple Fano resonances.
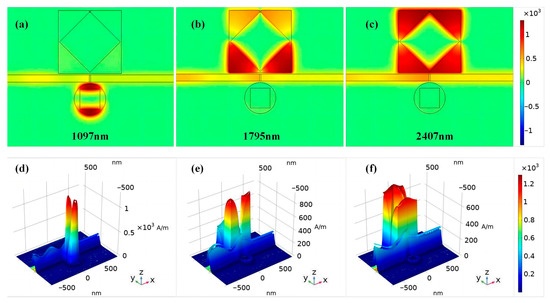
Figure 3.
(a–c) Patterns of the FR1, FR2, and FR3 magnetic fields. (d–f) Expressions in height for FR1, FR2, and FR3’s magnetic field patterns.
3.2. Refractive Index Sensing
For practical applications, it is difficult to change the structural parameters of waveguides, but the waveguide’s refractive index may be changed much more easily than its structural properties, which makes it possible to accomplish independent tuning of the Fano resonances that are more suited for sensing [47]. The following is the definition of the sensitivity of refractive index sensing [41,48]:
where denotes the alteration in resonance wavelength and denotes the alteration in the index of refraction.
In Figure 4 and Figure 5, the index of refraction of the SSRCSC and the index of refraction of the CRCSC both increased from 1.30 to 1.42 with an interval of 0.03. In biological parameter sensing, the chosen range of the index of refraction is easily attained. As the index of refraction of the SSRCSC increases, FR1 remained essentially unchanged, but FR2 and FR3 exhibited significant redshifts. In contrast, only FR1 exhibited a considerable redshift when the CRCSC’s refractive index increased, as shown in Figure 5a. According to the findings, it is possible to independently adjust the triple Fano resonances by altering the waveguide’s index of refraction.
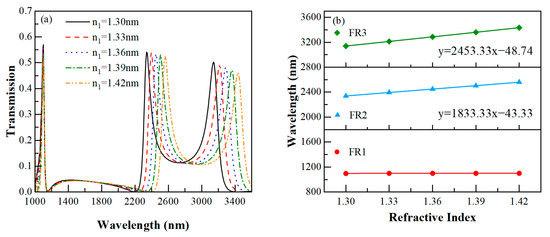
Figure 4.
(a) The effect of different refractive indexes of SSRCSC on waveguide Fano resonance (n2 =1.00). (b) Associations between the index of refraction of the SSRCSC and the resonance wavelengths of FR1, FR2, and FR3 are linear.
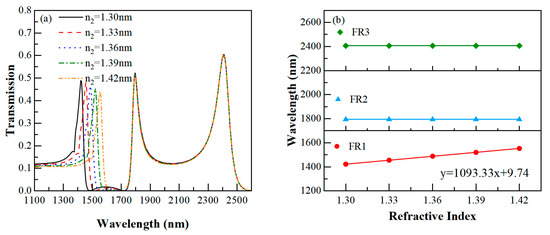
Figure 5.
(a) The effect of different refractive indexes of CRCSC on waveguide Fano resonance (n1 = 1.00). (b) Associations between the index of refraction of the CRCSC and the resonance wavelengths of FR1, FR2, and FR3 that are linear.
As shown in Figure 4b and Figure 5b, FR1, FR2, and FR3 all possessed strong linear correlations with linear correlation coefficients greater than 0.99999, and the sensitivities of FR1 and FR2 were 1093.33 nm/RIU and 1833.33 nm/RIU, respectively. According to Equations (3) and (4), the sensitivity is proportional to the proportion of the resonance mode order to the effective length of the resonant cavities, so the sensitivity of FR3 was 2453.33 nm/RIU greater than that of FR2, as shown in Figure 4b. Table 2 demonstrates that this waveguide has a relatively high sensitivity to refractive index sensing when compared to other architectures [38,47,49,50,51,52,53]. Based on the above analysis, the refractive index within the waveguide at different positions can be obtained by resonant wavelength measurements.

Table 2.
Utilizing different references to compare the sensitivity.
3.3. Multi-Biological Parameter Sensing
Next, two biological parameters, the temperature of human blood and the concentration of plasma, were chosen to be measured using this waveguide. The SSRCSC was filled with human blood, while the CRCSC was filled with plasma. Thus, the refractive indexes of the SSRCSC and the CRCSC were determined by the temperature and concentration of the biological parameters, respectively. In practice, human blood and plasma should be separated in advance, and then filled into the SSRCSC and CRCSC, respectively. In addition, it is unnecessary for the SSRCSC and CRCSC to be fully filled. When they are partially filled with human blood and plasma, the waveguide can still produce similar Fano resonances, just with different resonant wavelengths. The refractive indexes of human blood and plasma are expressed as [54,55]:
where is the temperature of human blood and is the concentration of plasma.
In Figure 6, the temperature of human blood in the SSRCSC was increased from 10 °C to 50 °C with an interval of 10 °C, while the concentration of plasma in the CRCSC was increased from 0 g/L to 400 g/L with an interval of 100 g/L. As a result, the SSRCSC’s refractive index dropped from 1.358954 to 1.35477 with an interval of 0.001046, whereas the CRCSC’s index of refraction change increased with an interval of 0.0184 from 1.32459 to 1.39819. It is evident that FR1 exhibited a redshift, and FR2 and FR3 exhibited blueshifts.
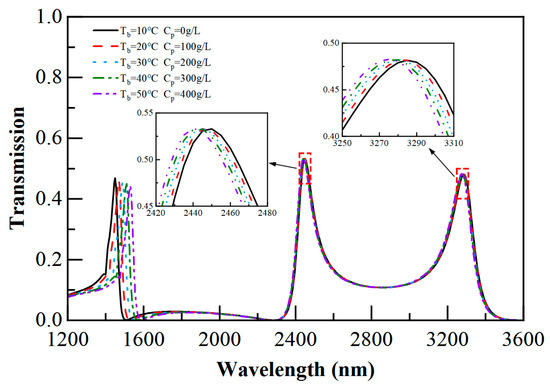
Figure 6.
The waveguide’s transmission spectra at various plasma concentrations and blood temperatures.
The linear fittings between the concentrations of the plasma and the resonant wavelengths are shown in Figure 7a, and Figure 7b displays the linear association between resonant wavelength and human blood temperature. For FR1, FR2, and FR3, each linear correlation coefficient was greater than 0.99. Here, the sensing sensitivity of the waveguide can be defined as as well as , where denotes the alteration in concentration and denotes the alteration in temperature. Thus, 0.2 nm·L/g was the sensitivity of plasma concentration sensing. Moreover, the sensitivity of human blood temperature to FR2 was 0.2 nm/°C, and the sensitivity to FR3 was 0.25 nm/°C. Obviously, the waveguide is far more sensitive to temperature than practically applied fiber grating sensors, which typically have a sensitivity of 0.01 nm/°C. In this way, the concentration of plasma and the temperature of human blood are simultaneously measured using this waveguide.
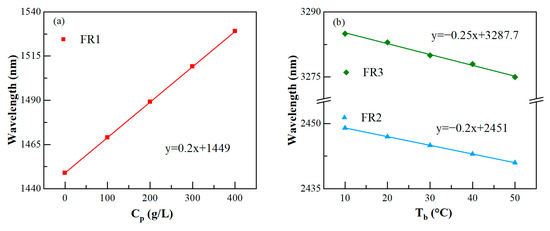
Figure 7.
(a) FR1’s resonant wavelength versus plasma concentration. (b) The resonant wavelengths of FR2 and FR3 versus human blood temperature.
3.4. Tunable Slow Light
Due to the sharp and asymmetric lineshape, Fano resonance is accompanied by an abrupt change in transmission phase, resulting in smaller group velocities, so the waveguide designed here can also be used to generate slow light, especially based on the effects of human blood temperature and plasma concentration on Fano resonance, which may achieve tunable slow light. The slow light characteristics can be described in terms of the group delay, which can be derived from the phase:
As a result of the sharp characteristics of Fano resonance, three group delay peaks can be found near the three Fano resonances, marked as GD1, GD2, and GD3. Then, we verified the proposed conjecture by measuring the biological parameters in the waveguide. In Figure 8, the human blood temperature in the SSRCSC increased with an interval of 10 °C, while the plasma concentration in the CRCSC increased with an interval of 10 g/L. It can be seen that GD1 experienced a redshift, while GD2 and GD3 experienced a blueshift. Subsequently, we locally enlarged GD1, GD2, and GD3, as shown in Figure 9a, Figure 10a, and Figure 11a. We selected the wavelength corresponding to the group delay peak at a temperature of 10 °C and concentration of 0 g/L as the reference wavelength, which was 1508 nm, 2287 nm, and 3585 nm for GD1, GD2, and GD3, respectively. We also plotted the response of the group delay to the biological parameters at each reference wavelength, as shown in Figure 9b, Figure 10b, and Figure 11b. The responses of the group delay to the two biological parameters were not exactly the same. For plasma concentration, it can be seen in Figure 9b that in the initial stage of concentration increase, group delay rapidly decreased. However, after the concentration was high, although the step size of concentration increase was still 10 g/L, the speed of the group delay decreased significantly. In b and 11b, it can be seen that for human blood temperature, the response of GD2 changed slowly during the low and high temperature stages, while the response of GD3 was different. For GD3, at relatively low temperatures, group delay slowly decreased with increasing temperature, and after a certain degree of temperature increase, the response of the group delay to temperature became faster.
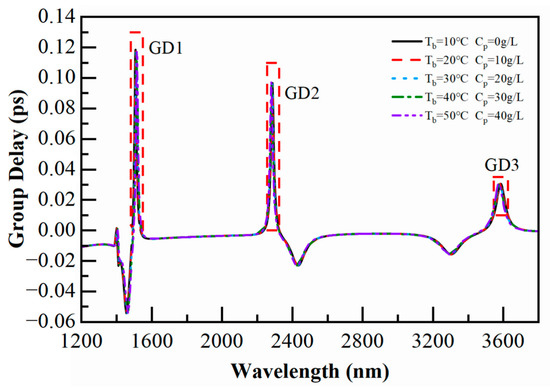
Figure 8.
The waveguide’s group delay at various plasma concentrations and blood temperatures.
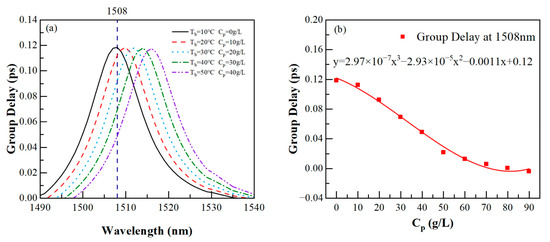
Figure 9.
(a) Partial enlarged view of GD1. (b) Response of group delay at 1508 nm to plasma concentration.
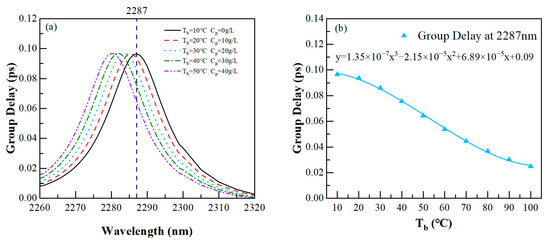
Figure 10.
(a) Partial enlarged view of GD2. (b) Response of group delay at 2287 nm to human blood temperature.
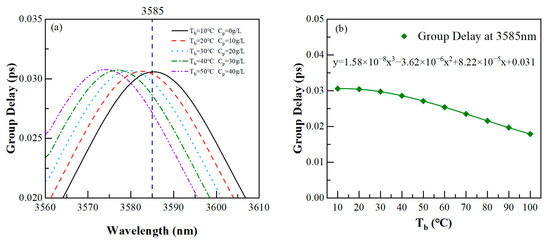
Figure 11.
(a) Partial enlarged view of GD3. (b) Response of group delay at 3585 nm to human blood temperature.
Next, we fit the response of the group delay to these two biological parameters. We first performed a quadratic fit on the response of the group delay to the biological parameters, and the residual sum of squares of the fit results were larger than the expected results. Then, we performed a cubic fit on the three responses, and the residual sum of squares of the fitting curves was much smaller, resulting in a significant improvement in the fitting effect. The results showed that the two biological parameters can be used to adjust slow light, and it is worth noting that the responses of the group delay to human blood temperature and plasma concentration all conformed to cubic functions. In this way, tunable slow light was achieved in this waveguide by varying the temperature of human blood and the concentration of blood plasma.
It should be noted that the largest group delay obtained in this paper was only about 0.1 ps. One reason is that the size of the waveguide was small. The other is that the structural parameters of the waveguide were optimized in order to obtain multiple Fano resonances with high transmittance, failing to take into account the group delay. One can obtain a large group delay by increasing the contrast of Fano resonance and reducing the bandwidth of Fano resonance. Here, only a potential solution for adjusting slow light in the MIM waveguide was proposed, combined with biological parameters.
From current research results, it can be seen that the coupling efficiency between a MIM waveguide and external optical devices is relatively low, due to the small width of the waveguide. If the coupling efficiency can be improved, the application of the MIM waveguide may be greatly promoted.
4. Discussion
Triple Fano resonances were achieved in the MIM waveguide made up of a SSRCSC, CRCSC, and bus waveguide. The refractive index may be changed to tune the Fano resonances individually. The maximum sensitivity of refractive index sensing was 2453.33 nm/RIU. The cavities of this waveguide can be filled with biological solutions as a biosensor, which make it possible to measure several biological parameters at once. Human blood temperature and plasma concentration sensing had maximal sensitivities of 0.25 nm/°C and 0.2 nm·L/g, respectively. Meanwhile, tunable slow light can be realized using this waveguide, and the group delay responses to human blood temperature and plasma concentration all conformed to cubic functions. The significant advantage of this waveguide is that two separate resonant cavities allow for the simultaneous measurement of multiple biological parameters and slow light tuning of multiple wavelengths. In conclusion, the waveguide proposed in this paper can play a role in biosensing and optical information processing in nanoscale applications.
Author Contributions
H.T.: conceptualization, resources, supervision, funding acquisition, and writing—review and editing. R.Z.: conceptualization, methodology, software, investigation, data curation, and writing—original draft. Y.L. and S.C.: visualization. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Innovation and Entrepreneurship Training Program for Undergraduates of Northeast Forestry University (DC-2023177).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fano, U. Effects of Configuration Interaction on Intensities and Phase Shifts. Phys. Rev. 1961, 124, 1866–1878. [Google Scholar] [CrossRef]
- Dai, X.; Ruan, B.; Xiang, Y. Self-Referenced Refractive Index Biosensing with Graphene Fano Resonance Modes. Biosensors 2021, 11, 400. [Google Scholar] [CrossRef]
- Limonov, M.F.; Rybin, M.V.; Poddubny, A.N.; Kivshar, Y.S. Fano resonances in photonics. Nat. Photonics 2017, 11, 543–554. [Google Scholar] [CrossRef]
- Luk’yanchuk, B.; Zheludev, N.I.; Maier, S.A.; Halas, N.J.; Nordlander, P.; Giessen, H.; Chong, C.T. The Fano resonance in plasmonic nanostructures and metamaterials. Nat. Mater. 2010, 9, 707–715. [Google Scholar] [CrossRef]
- Wan, F.; Qian, G.; Li, R.; Tang, J.; Zhang, T. High sensitivity optical waveguide accelerometer based on Fano resonance. Appl. Opt. 2016, 55, 6644–6648. [Google Scholar] [CrossRef]
- Li, J.; Chen, J.; Liu, X.; Tian, H.; Wang, J.; Cui, J.; Rohimah, S. Optical sensing based on multimode Fano resonances in metal-insulator-metal waveguide systems with X-shaped resonant cavities. Appl. Opt. 2021, 60, 5312–5319. [Google Scholar] [CrossRef] [PubMed]
- Ziauddin, J.R.; Chaung, Y.-L.; Rahmatullah. Tunable Fano resonances via optomechanical effect and gain -loss ratio in coupled microresonators. Laser Phys. 2018, 28, 116003. [Google Scholar] [CrossRef]
- Li, J.; Yu, R.; Wu, Y. Actively tunable double-Fano and Ramsey-Fano resonances in photonic molecules and improved sensing performance. Phys. Rev. A 2016, 94, 063822. [Google Scholar] [CrossRef]
- Deng, Y.; Cao, G.; Yang, H. Tunable Fano resonance and high-sensitivity sensor with high figure of merit in plasmonic coupled cavities. Photonics Nanostruct. Fundam. Appl. 2018, 28, 45–51. [Google Scholar] [CrossRef]
- Liu, G.; Cheng, D.; Zhang, B.; Shu, G.; Wang, J. A microwave biosensor based on spoof surface plasmon polaritons for in vivo measurement of the water content of human skin tissues. J. Phys. D Appl. Phys. 2019, 52, 205401. [Google Scholar] [CrossRef]
- Chen, Z.-Q.; Yin, Z.-X.; Xia, G.-Q.; Hong, L.-L.; Hu, Y.-L.; Liu, M.-H.; Hu, X.-W.; Kudryavtsev, A.A. Pulsed microwave-driven argon plasma jet with distinctive plume patterns resonantly excited by surface plasmon polaritons. Chin. Phys. B 2015, 24, 025203. [Google Scholar] [CrossRef]
- Balevicius, Z. Photonic Sensors in Chemical and Biological Applications. Biosensors 2022, 12, 1021. [Google Scholar] [CrossRef] [PubMed]
- Tong, L.; Wei, H.; Zhang, S.; Xu, H. Recent Advances in Plasmonic Sensors. Sensors 2014, 14, 7959–7973. [Google Scholar] [CrossRef]
- Xia, S.; Zhai, X.; Wang, L.; Wen, S. Plasmonically induced transparency in double-layered graphene nanoribbons. Photonics Res. 2018, 6, 692–702. [Google Scholar] [CrossRef]
- Ruffato, G.; Pasqualotto, E.; Sonato, A.; Zacco, G.; Silvestri, D.; Morpurgo, M.; De Toni, A.; Romanato, F. Implementation and testing of a compact and high-resolution sensing device based on grating-coupled surface plasmon resonance with polarization modulation. Sens. Actuators B Chem. 2013, 185, 179–187. [Google Scholar] [CrossRef]
- Wang, Y.; Jia, S.; Qin, J. Tunable Fano Resonance and Enhanced Sensing in Terahertz Metamaterial. Front. Phys. 2021, 8, 605125. [Google Scholar] [CrossRef]
- Choi, H.; Pile, D.F.P.; Nam, S.; Bartal, G.; Zhang, X. Compressing surface plasmons for nano-scale optical focusing. Opt. Express 2009, 17, 7519–7524. [Google Scholar] [CrossRef]
- Rohimah, S.; Tian, H.; Wang, J.; Chen, J.; Li, J.; Liu, X.; Cui, J.; Hao, Y. Tunable multiple Fano resonances based on a plasmonic metal-insulator-metal structure for nano-sensing and plasma blood sensing applications. Appl. Opt. 2022, 61, 1275–1283. [Google Scholar] [CrossRef]
- Kong, Y.; Cao, J.; Qian, W.; Liu, C.; Wang, S. Multiple Fano Resonance Based Optical Refractive Index Sensor Composed Of Micro-Cavity and Micro-Structure. IEEE Photonics J. 2018, 10, 6804410. [Google Scholar] [CrossRef]
- Zhang, D.; Cheng, L.; Shen, Z. Formation Laws of Direction of Fano Line-Shape in a Ring MIM Plasmonic Waveguide Side-Coupled with a Rectangular Resonator and Nano-Sensing Analysis of Multiple Fano Resonances. Crystals 2021, 11, 819. [Google Scholar] [CrossRef]
- Chen, J.; Li, J.; Liu, X.; Rohimah, S.; Tian, H.; Qi, D. Fano resonance in a MIM waveguide with double symmetric rectangular stubs and its sensing characteristics. Opt. Commun. 2021, 482, 126563. [Google Scholar] [CrossRef]
- Xia, S.; Zhai, X.; Wang, L.; Xiang, Y.; Wen, S. Plasmonically induced transparency in phase-coupled graphene nanoribbons. Phys. Rev. B 2022, 106, 075401. [Google Scholar] [CrossRef]
- Wang, T.-B.; Wen, X.-W.; Yin, C.-P.; Wang, H.-Z. The transmission characteristics of surface plasmon polaritons in ring resonator. Opt. Express 2009, 17, 24096–24101. [Google Scholar] [CrossRef]
- Park, J.; Kim, H.; Lee, B. High order plasmonic Bragg reflection in the metal-insulator-metal waveguide Bragg grating. Opt. Express 2008, 16, 413–425. [Google Scholar] [CrossRef]
- Rohimah, S.; Tian, H.; Wang, J.; Chen, J.; Li, J.; Liu, X.; Cui, J.; Xu, Q.; Hao, Y. Fano Resonance in the Plasmonic Structure of MIM Waveguide with r-Shaped Resonator for Refractive Index Sensor. Plasmonics 2022, 17, 1681–1689. [Google Scholar] [CrossRef]
- Wu, T.; Liu, Y.; Yu, Z.; Peng, Y.; Shu, C.; Ye, H. The sensing characteristics of plasmonic waveguide with a ring resonator. Opt. Express 2014, 22, 7669–7677. [Google Scholar] [CrossRef]
- Zhang, Q.; Huang, X.-G.; Lin, X.-S.; Tao, J.; Jin, X.-P. A subwavelength coupler-type MIM optical filter. Opt. Express 2009, 17, 7549–7555. [Google Scholar] [CrossRef]
- Lin, X.-S.; Huang, X.-G. Tooth-shaped plasmonic waveguide filters with nanometeric sizes. Opt. Lett. 2008, 33, 2874–2876. [Google Scholar] [CrossRef]
- Yun, B.; Hu, G.; Cui, Y. Theoretical analysis of a nanoscale plasmonic filter based on a rectangular metal-insulator-metal waveguide. J. Phys. D Appl. Phys. 2010, 43, 385102. [Google Scholar] [CrossRef]
- Feng, C.; Ying, Z.; Zhao, Z.; Gu, J.; Pan, D.Z.; Chen, R.T. Wavelength-division-multiplexing (WDM)-based integrated electronic-photonic switching network (EPSN) for high-speed data processing and transportation. Nanophotonics 2020, 9, 4579–4588. [Google Scholar] [CrossRef]
- Liu, X.; Li, J.; Chen, J.; Rohimah, S.; Tian, H.; Wang, J. Fano resonance based on D-shaped waveguide structure and its application for human hemoglobin detection. Appl. Opt. 2020, 59, 6424–6430. [Google Scholar] [CrossRef]
- Petrovszki, D.; Krekic, S.; Valkai, S.; Heiner, Z.; Der, A. All-Optical Switching Demonstrated with Photoactive Yellow Protein Films. Biosensors 2021, 11, 432. [Google Scholar] [CrossRef]
- Jiang, C.; Jiang, L.; Yu, H.; Cui, Y.; Li, X.; Chen, G. Fano resonance and slow light in hybrid optomechanics mediated by a two-level system. Phys. Rev. A 2017, 96, 053821. [Google Scholar] [CrossRef]
- Yi, X.; Tian, J.; Yang, R. Tunable Fano resonance in MDM plasmonic waveguide with a T-shaped resonator coupled to ring resonator. Mater. Res. Express 2019, 6, 035021. [Google Scholar] [CrossRef]
- Liu, Y.; Tian, H.; Zhang, X.; Wang, M.; Hao, Y. Quadruple Fano resonances in MIM waveguide structure with ring cavities for multisolution concentration sensing. Appl. Opt. 2022, 61, 10548–10555. [Google Scholar] [CrossRef]
- Liang, Z.; Wen, Y.; Zhang, Z.; Liang, Z.; Xu, Z.; Lin, Y.-S. Plasmonic metamaterial using metal-insulator-metal nanogratings for high-sensitive refraction index sensor. Results Phys. 2019, 15, 102602. [Google Scholar] [CrossRef]
- Rakhshani, M.R.; Mansouri-Birjandi, M.A. High-Sensitivity Plasmonic Sensor Based on Metal-Insulator-Metal Waveguide and Hexagonal-Ring Cavity. IEEE Sens. J. 2016, 16, 3041–3046. [Google Scholar] [CrossRef]
- Chen, J.; Lian, X.; Zhao, M.; Xie, C. Multimode Fano Resonances Sensing Based on a Non-Through MIM Waveguide with a Square Split-Ring Resonance Cavity. Biosensors 2022, 12, 306. [Google Scholar] [CrossRef]
- Qi, J.; Chen, Z.; Chen, J.; Li, Y.; Qiang, W.; Xu, J.; Sun, Q. Independently tunable double Fano resonances in asymmetric MIM waveguide structure. Opt. Express 2014, 22, 14688–14695. [Google Scholar] [CrossRef] [PubMed]
- Fang, Y.; Wen, K.; Qin, Y.; Li, Z.; Wu, B. Multiple fano resonances in an end-coupled MIM waveguide system. Opt. Commun. 2019, 452, 12–17. [Google Scholar] [CrossRef]
- Wang, M.; Tian, H.; Liu, X.; Li, J.; Liu, Y. Multiparameter Sensing Based on Tunable Fano Resonances in MIM Waveguide Structure with Square-Ring and Triangular Cavities. Photonics 2022, 9, 291. [Google Scholar] [CrossRef]
- Duc Duy, N.; Zhao, S. A new high order dispersive FDTD method for Drude material with complex interfaces. J. Comput. Appl. Math. 2015, 285, 1–14. [Google Scholar] [CrossRef]
- Gugger, H.; Jurich, M.; Swalen, J.D.; Sievers, A.J. Reply to “Comment on ‘Observation of an index-of-refraction-induced change in the Drude parameters of Ag films’”. Phys. Rev. B Condens. Matter 1986, 34, 1322–1324. [Google Scholar] [CrossRef] [PubMed]
- Wen, K.; Chen, L.; Zhou, J.; Lei, L.; Fang, Y. A Plasmonic Chip-Scale Refractive Index Sensor Design Based on Multiple Fano Resonances. Sensors 2018, 18, 3181. [Google Scholar] [CrossRef]
- Dong, S.; Liu, H.; Zheng, Y.; Zhang, J.; Xia, S.; Dong, C.; Shen, K.; Deng, C.; Luo, W.; Su, M.; et al. Numerical study on the biosensing in mid-infrared based on multiple Fano-resonance plasmonic waveguide. Optik 2022, 270, 170042. [Google Scholar] [CrossRef]
- Wang, Q.; Ouyang, Z.; Lin, M.; Liu, Q. Independently Tunable Fano Resonances Based on the Coupled Hetero-Cavities in a Plasmonic MIM System. Materials 2018, 11, 1675. [Google Scholar] [CrossRef]
- Liu, X.; Li, J.; Chen, J.; Rohimah, S.; Tian, H.; Wang, J. Independently tunable triple Fano resonances based on MIM waveguide structure with a semi-ring cavity and its sensing characteristics. Opt. Express 2021, 29, 20829–20838. [Google Scholar] [CrossRef]
- Al-Naib, I. Terahertz Asymmetric S-Shaped Complementary Metasurface Biosensor for Glucose Concentration. Biosensors 2022, 12, 609. [Google Scholar] [CrossRef]
- Zhang, Y.; Kuang, Y.; Zhang, Z.; Tang, Y.; Han, J.; Wang, R.; Cui, J.; Hou, Y.; Liu, W. High-sensitivity refractive index sensors based on Fano resonance in the plasmonic system of splitting ring cavity-coupled MIM waveguide with tooth cavity. Appl. Phys. A 2019, 125, 13. [Google Scholar] [CrossRef]
- Chen, Z.; Cao, X.; Song, X.; Wang, L.; Yu, L. Side-Coupled Cavity-Induced Fano Resonance and Its Application in Nanosensor. Plasmonics 2016, 11, 307–313. [Google Scholar] [CrossRef]
- Xiao, G.; Xu, Y.; Yang, H.; Ou, Z.; Chen, J.; Li, H.; Liu, X.; Zeng, L.; Li, J. High Sensitivity Plasmonic Sensor Based on Fano Resonance with Inverted U-Shaped Resonator. Sensors 2021, 21, 1164. [Google Scholar] [CrossRef]
- Wen, K.; Hu, Y.; Chen, L.; Zhou, J.; He, M.; Lei, L.; Meng, Z.; Wu, Y.; Li, J. Fano Resonance Based on End-Coupled Cascaded-Ring MIM Waveguides Structure. Plasmonics 2017, 12, 1875–1880. [Google Scholar] [CrossRef]
- Rakhshani, M.R. Refractive index sensor based on concentric triple racetrack resonators side-coupled to metal-insulator-metal waveguide for glucose sensing. J. Opt. Soc. Am. B Opt. Phys. 2019, 36, 2834–2842. [Google Scholar] [CrossRef]
- Yahya, M.; Saghir, M.Z. Empirical modelling to predict the refractive index of human blood. Phys. Med. Biol. 2016, 61, 1405–1415. [Google Scholar] [CrossRef] [PubMed]
- El-Khozondar, H.J.; Mahalakshmi, P.; El-Khozondar, R.J.; Ramanujam, N.R.; Amiri, I.S.; Yupapin, P. Design of one dimensional refractive index sensor using ternary photonic crystal waveguide for plasma blood samples applications. Phys. E Low Dimens. Syst. Nanostruct. 2019, 111, 29–36. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).