High-Precision Laser Self-Mixing Displacement Sensor Based on Orthogonal Signal Phase Multiplication Technique
Abstract
1. Introduction
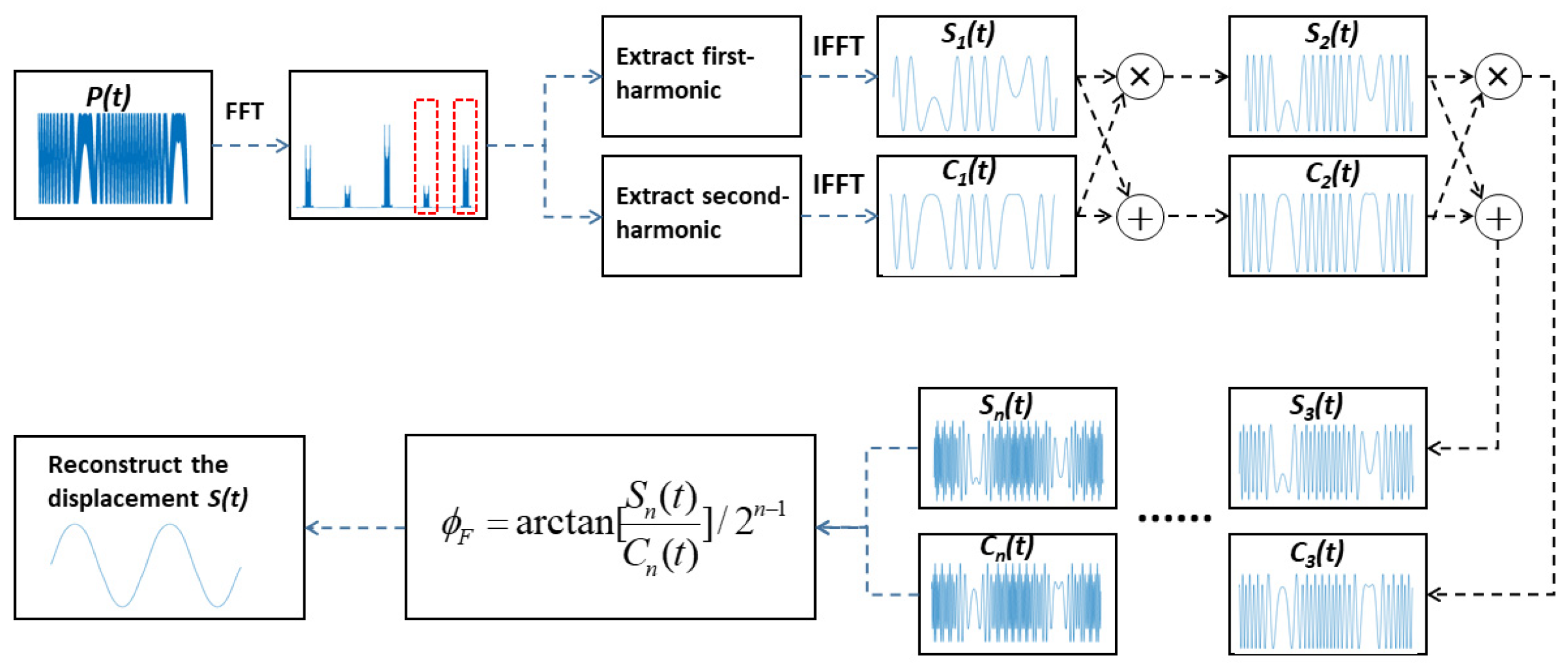
2. Measurement Principle
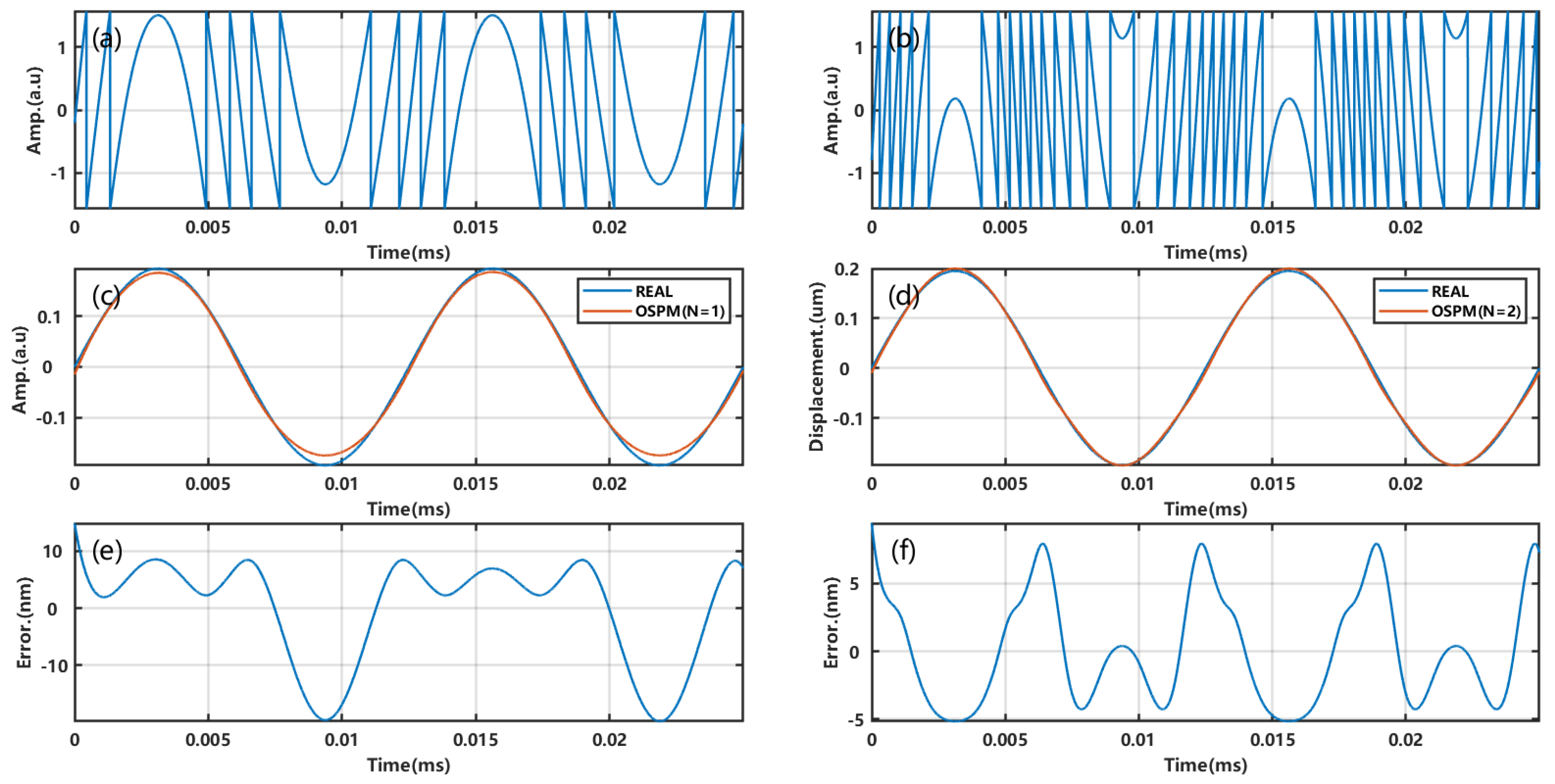
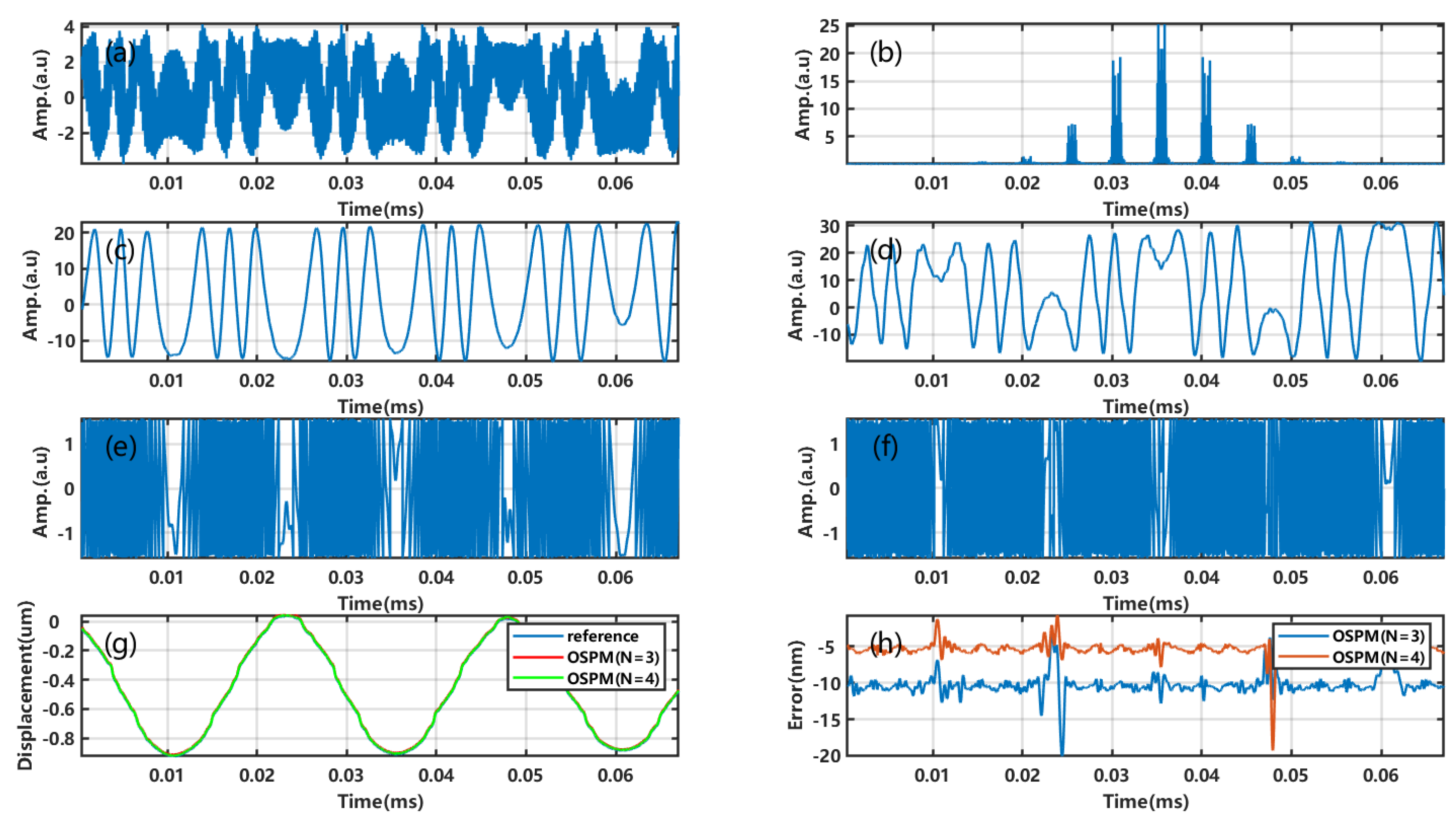
3. Simulations and Experiments
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, H.-J.; Deibel, J.; Nyberg, S.; Riles, K. High-precision absolute distance and vibration measurement with frequency scanned interferometry. Appl. Opt. 2005, 44, 3937–3944. [Google Scholar] [CrossRef] [PubMed]
- Pfister, T.; Buttner, L.; Czarske, J.; Krain, H.; Schodl, R. Turbo machine tip clearance and vibration measurements using a fibre optic laser Doppler position sensor. Meas. Sci. Technol. 2006, 17, 1693–1705. [Google Scholar] [CrossRef]
- Donati, S. Developing self-mixing interferometry for instrumentation and measurements. Laser Photonics Rev. 2012, 6, 393–417. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, S.; Long, X. Polarisation control through an optical feedback technique and its application in precise measurements. Sci. Rep. 2013, 3, 1992. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wang, R.; Wei, Z.; Wang, X.; Xu, H.; Sun, H.; Huang, W. Broad Range and High Precision Self-Mixing Interferometer Based on Spectral Analysis with Multiple Reflections. IEEE Sens. J. 2018, 19, 926–932. [Google Scholar] [CrossRef]
- Guo, D.; Wang, M. Self-mixing interferometry based on a double-modulation technique for absolute distance measurement. Appl. Opt. 2007, 46, 1486–1491. [Google Scholar] [CrossRef]
- Duan, Z.; Yu, Y.; Gao, B.; Jiang, C. Absolute distance measurement based on multiple self-mixing interferometry. Opt. Commun. 2017, 389, 270–274. [Google Scholar] [CrossRef]
- Kou, K.; Wang, C.; Liu, Y. All-phase FFT based distance measurement in laser self-mixing interferometry. Opt. Lasers Eng. 2021, 142, 106611. [Google Scholar] [CrossRef]
- Li, L.; Zhang, Y.; Zhu, Y.; Dai, Y.; Zhang, X.; Liang, X. Absolute Distance Measurement Based on Self-Mixing Interferometry Using Compressed Sensing. Appl. Sci. 2022, 12, 8635. [Google Scholar] [CrossRef]
- Donati, S.; Rossi, D.; Norgia, M. Single Channel Self-Mixing Interferometer Measures Simultaneously Displace0ment and Tilt and Yaw Angles of a Reflective Target. IEEE J. Quantum Electron. 2015, 51, 1–8. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, H. Angle measurement method based on speckle affected laser self-mixing interference signal. Opt. Commun. 2021, 482, 126569. [Google Scholar] [CrossRef]
- Xu, X.; Dai, Z.; Wang, Y.; Li, M.; Tan, Y. High Sensitivity and Full-Circle Optical Rotary Sensor for Non-Cooperatively Tracing Wrist Tremor with Nanoradian Resolution. IEEE Trans. Ind. Electron. 2021, 69, 9605–9612. [Google Scholar] [CrossRef]
- Wang, X.; Yuan, Y.; Chen, P.; Gao, B. Laser self-mixing based on peak–valley point detection algorithm for displacement reconstruction. Opt. Quantum Electron. 2020, 52, 34. [Google Scholar] [CrossRef]
- Amin, S.; Zabit, U.; Bernal, O.D.; Hussain, T. High Resolution Laser Self-Mixing Displacement Sensor Under Large Variation in Optical Feedback and Speckle. IEEE Sens. J. 2020, 20, 9140–9147. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Y.; Xu, X.; Tian, M.; Zhu, K.; Tan, Y. All-fiber laser feedback interferometry with 300 m transmission distance. Opt. Lett. 2021, 46, 821–824. [Google Scholar] [CrossRef]
- Ge, S.; Lin, Y.; Chen, H.; Kong, X.; Zhu, D.; Dong, Z.; Wang, X.; Huang, W. Signal extraction method based on spectral processing for a dual-channel SMI vibration sensor. Opt. Lasers Eng. 2023, 164, 107531. [Google Scholar] [CrossRef]
- Wu, S.; Wang, D.; Xiang, R.; Zhou, J.; Ma, Y.; Gui, H.; Liu, J.; Wang, H.; Lu, L.; Yu, B. All-Fiber Configuration Laser Self-Mixing Doppler Velocimeter Based on Distributed Feedback Fiber Laser. Sensors 2016, 16, 1179. [Google Scholar] [CrossRef]
- Jiang, C.; Geng, Y.; Liu, Y.; Liu, Y.; Chen, P.; Yin, S. Rotation velocity measurement based on self-mixing interference with a dual-external-cavity single-laser diode. Appl. Opt. 2019, 58, 604–608. [Google Scholar] [CrossRef]
- Wang, X.; Yang, H.; Hu, L.; Li, Z.; Chen, H.; Huang, W. Single Channel Instrument for Simultaneous Rotation Speed and Vibration Measurement Based on Self-Mixing Speckle Interference. IEEE Photonics J. 2021, 14, 6802405. [Google Scholar] [CrossRef]
- Tan, Y.; Zhang, S.; Xu, C.; Zhao, S. Inspecting and locating foreign body in biological sample by laser confocal feedback technology. Appl. Phys. Lett. 2013, 103, 101909. [Google Scholar] [CrossRef]
- Zhao, Y.; Xu, G.; Zhang, C.; Liu, K.; Lu, L. Vibration displacement immunization model for measuring the free spectral range by means of a laser self-mixing velocimeter. Appl. Opt. 2019, 58, 5540–5546. [Google Scholar] [CrossRef] [PubMed]
- Zhou, B.; Wang, Z.; Shen, X.; Zhang, L.; Tan, Y. High-sensitivity laser confocal tomography based on frequency-shifted feedback technique. Opt. Lasers Eng. 2020, 129, 106059. [Google Scholar] [CrossRef]
- Liu, B.; Ruan, Y.; Yu, Y. Determining System Parameters and Target Movement Directions in a Laser Self-Mixing Interferometry Sensor. Photonics 2022, 9, 612. [Google Scholar] [CrossRef]
- Donati, S.; Giuliani, G.; Merlo, S. Laser diode feedback interferometer for measurement of displacements without ambiguity. IEEE J. Quantum Electron. 1995, 31, 113–119. [Google Scholar] [CrossRef]
- Bes, C.; Plantier, G.; Bosch, T. Displacement Measurements Using a Self-Mixing Laser Diode Under Moderate Feedback. IEEE Trans. Instrum. Meas. 2006, 55, 1101–1105. [Google Scholar] [CrossRef]
- Guo, D.; Wang, M.; Tan, S. Self-mixing interferometer based on sinusoidal phase modulating technique. Opt. Express 2005, 13, 1537–1543. [Google Scholar] [CrossRef]
- Guo, D. Quadrature demodulation technique for self-mixing interferometry displacement sensor. Opt. Commun. 2011, 284, 5766–5769. [Google Scholar] [CrossRef]
- Xia, W.; Wang, M.; Yang, Z.; Guo, W.; Hao, H.; Guo, D. High-accuracy sinusoidal phase-modulating self-mixing interferometer using an electro-optic modulator: Development and evaluation. Appl. Opt. 2013, 52, B52–B59. [Google Scholar] [CrossRef]
- Ali, N.; Zabit, U.; Bernal, O.D. Nanometric Vibration Sensing Using Spectral Processing of Laser Self-Mixing Feedback Phase. IEEE Sens. J. 2021, 21, 17766–17774. [Google Scholar] [CrossRef]
- Lu, L.; Hu, L.; Li, Z.; Qiu, L.; Huang, W.; Wang, X. High Precision Self-Mixing Interferometer Based on Reflective Phase Modulation Method. IEEE Access 2020, 8, 204153–204159. [Google Scholar] [CrossRef]
- De Groot, P.J.; Gallatin, G.M.; Macomber, S.H. Ranging and velocimetry signal generation in a backscatter-modulated laser diode. Appl. Opt. 1988, 27, 4475–4480. [Google Scholar] [CrossRef] [PubMed]
- Cui, X.; Liu, Y.; Chen, P.; Li, C. Measuring two vibrations using dual-external-cavity structure in a self-mixing system. Opt. Lasers Eng. 2021, 141, 106557. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Zhong, Z.; Chen, H.; Zhu, D.; Zheng, T.; Huang, W. High-Precision Laser Self-Mixing Displacement Sensor Based on Orthogonal Signal Phase Multiplication Technique. Photonics 2023, 10, 575. https://doi.org/10.3390/photonics10050575
Wang X, Zhong Z, Chen H, Zhu D, Zheng T, Huang W. High-Precision Laser Self-Mixing Displacement Sensor Based on Orthogonal Signal Phase Multiplication Technique. Photonics. 2023; 10(5):575. https://doi.org/10.3390/photonics10050575
Chicago/Turabian StyleWang, Xiulin, Zhengjian Zhong, Hanqiao Chen, Desheng Zhu, Tongchang Zheng, and Wencai Huang. 2023. "High-Precision Laser Self-Mixing Displacement Sensor Based on Orthogonal Signal Phase Multiplication Technique" Photonics 10, no. 5: 575. https://doi.org/10.3390/photonics10050575
APA StyleWang, X., Zhong, Z., Chen, H., Zhu, D., Zheng, T., & Huang, W. (2023). High-Precision Laser Self-Mixing Displacement Sensor Based on Orthogonal Signal Phase Multiplication Technique. Photonics, 10(5), 575. https://doi.org/10.3390/photonics10050575




