Optogenetic Generation of Neural Firing Patterns with Temporal Shaping of Light Pulses
Abstract
1. Introduction
2. Methods
2.1. Photocurrent Model
2.2. Model for Optogenetic Excitation of Opsin-Expressing Neurons
2.3. Temporal Shapes of Light Pulses
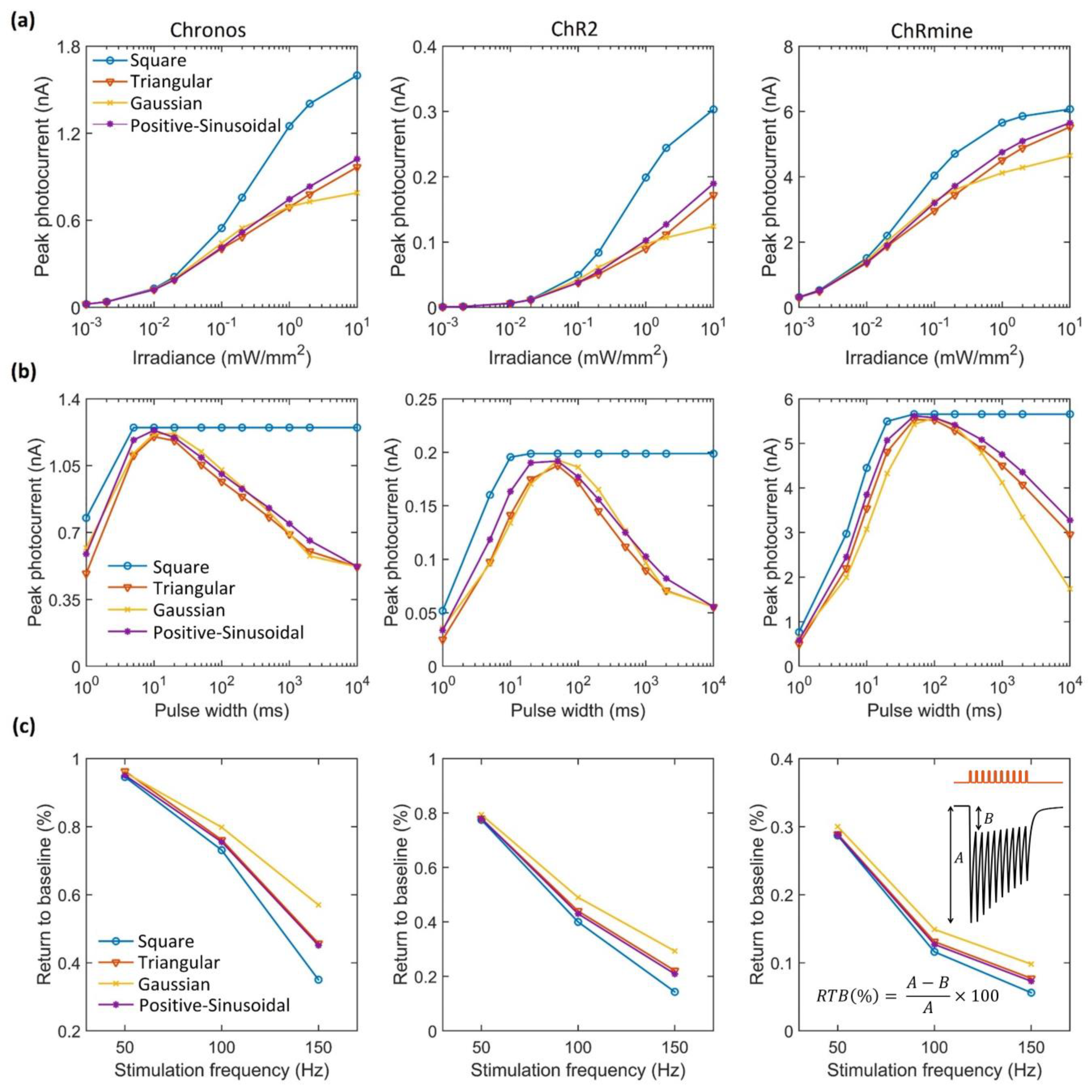
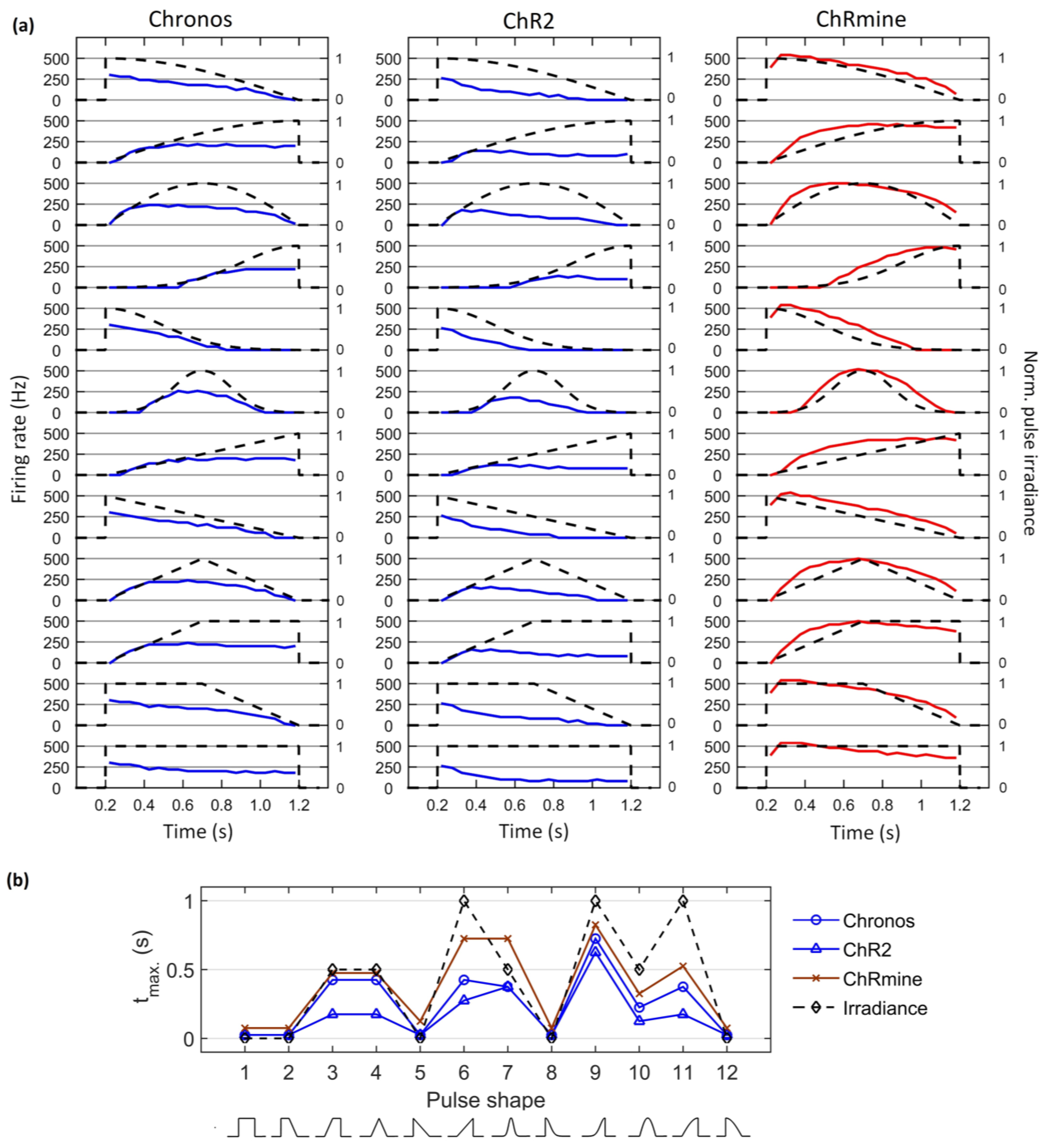
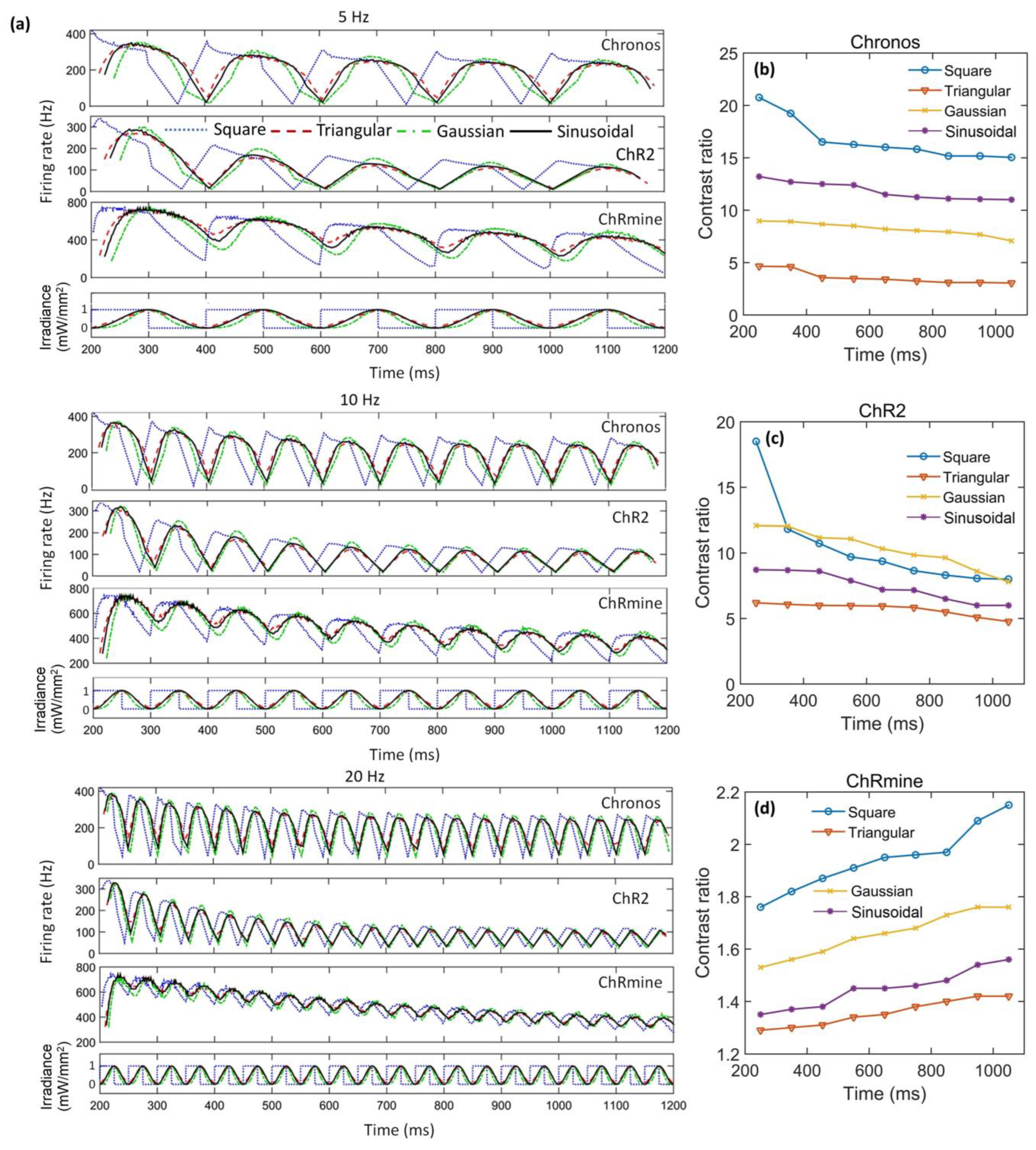
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Krohn, S.; von Schwanenflug, N.; Waschke, L.; Romanello, A.; Gell, M.; Garrett, D.D.; Finke, C. A spatiotemporal complexity architecture of human brain activity. Sci. Adv. 2023, 9, eabq3851. [Google Scholar] [CrossRef]
- Lin, A.; Witvliet, D.; Hernandez-Nunez, L.; Linderman, S.W.; Samuel, A.D.; Venkatachalam, V. Imaging whole-brain activity to understand behaviour. Nat. Rev. Phys. 2022, 4, 292–305. [Google Scholar] [CrossRef]
- Panzeri, S.; Moroni, M.; Safaai, H.; Harvey, C.D. The structures and functions of correlations in neural population codes. Nat. Rev. Neurosci. 2022, 23, 551–567. [Google Scholar] [CrossRef]
- Scangos, K.W.; State, M.W.; Miller, A.H.; Baker, J.T.; Williams, L.M. New and emerging approaches to treat psychiatric disorders. Nat. Med. 2023, 29, 317–333. [Google Scholar] [CrossRef]
- Tang, X.; Shen, H.; Zhao, S.; Li, N.; Liu, J. Flexible brain–computer interfaces. Nat. Electron. 2023, 6, 109–118. [Google Scholar] [CrossRef]
- Urai, A.E.; Doiron, B.; Leifer, A.M.; Churchland, A.K. Large-scale neural recordings call for new insights to link brain and behavior. Nat. Neurosci. 2022, 25, 11–19. [Google Scholar] [CrossRef] [PubMed]
- Cury, R.G.; Pavese, N.; Aziz, T.Z.; Krauss, J.K.; Moro, E. Neuromodulation of Gait Study Group from Movement Disorders Society. Gaps and roadmap of novel neuromodulation targets for treatment of gait in Parkinson’s disease. npj Park. Dis. 2022, 8, 8. [Google Scholar] [CrossRef]
- Bansal, A.; Shikha, S.; Zhang, Y. Towards translational optogenetics. Nat. Biomed. Eng. 2022, 7, 349–369. [Google Scholar] [CrossRef] [PubMed]
- Emiliani, V.; Entcheva, E.; Hedrich, R.; Hegemann, P.; Konrad, K.R.; Lüscher, C.; Mahn, M.; Pan, Z.H.; Sims, R.R.; Vierock, J.; et al. Optogenetics for light control of biological systems. Nat. Rev. Methods Primers 2022, 2, 55. [Google Scholar] [CrossRef]
- Montagni, E.; Resta, F.; Mascaro, A.L.A.; Pavone, F.S. Optogenetics in brain research: From a strategy to investigate physiological function to a therapeutic tool. Photonics 2019, 6, 92. [Google Scholar] [CrossRef]
- Adesnik, H.; Abdeladim, L. Probing neural codes with two-photon holographic optogenetics. Nat. Neurosci. 2021, 10, 1356–1366. [Google Scholar] [CrossRef] [PubMed]
- Cehajic-Kapetanovic, J.; Singh, M.S.; Zrenner, E.; MacLaren, R.E. Bioengineering strategies for restoring vision. Nat. Biomed. Eng. 2022, 7, 387–404. [Google Scholar] [CrossRef] [PubMed]
- Sahel, J.A.; Boulanger-Scemama, E.; Pagot, C.; Arleo, A.; Galluppi, F.; Martel, J.N.; Esposti, S.D.; Delaux, A.; de Saint Aubert, J.B.; de Montleau, C.; et al. Partial recovery of visual function in a blind patient after optogenetic therapy. Nat. Med. 2021, 7, 1223–1239. [Google Scholar] [CrossRef]
- Hsueh, B.; Chen, R.; Jo, Y.; Tang, D.; Raffiee, M.; Kim, Y.S.; Inoue, M.; Randles, S.; Ramakrishnan, C.; Patel, S.; et al. Cardiogenic control of affective behavioural state. Nature 2023, 615, 292–299. [Google Scholar] [CrossRef]
- Entcheva, E.; Kay, M.W. Cardiac optogenetics: A decade of enlightenment. Nat. Rev. Cardiol. 2021, 18, 349–367. [Google Scholar] [CrossRef] [PubMed]
- Cole, E.R.; Eggers, T.E.; Weiss, D.; Connolly, M.J.; Gombolay, M.C.; Laxpati, N.G.; Gross, R.E. Irregular optogenetic stimulation waveforms can induce naturalistic patterns of hippocampal spectral activity. bioRxiv 2022. [Google Scholar] [CrossRef]
- Khodagholy, D.; Ferrero, J.J.; Park, J.; Zhao, Z.; Gelinas, J.N. Large-scale, closed-loop interrogation of neural circuits underlying cognition. Trends Neurosci. 2022, 45, 968–983. [Google Scholar] [CrossRef]
- Newman, J.P.; Fong, M.F.; Millard, D.C.; Whitmire, C.J.; Stanley, G.B.; Potter, S.M. Optogenetic feedback control of neural activity. eLife 2015, 4, e07192. [Google Scholar] [CrossRef]
- Wilmerding, L.K.; Yazdanbakhsh, A.; Hasselmo, M.E. Impact of optogenetic pulse design on CA3 learning and replay: A neural model. Cell Rep. Methods 2022, 2, 100208. [Google Scholar] [CrossRef]
- Govorunova, E.G.; Sineshchekov, O.A.; Spudich, J.L. Emerging diversity of channelrhodopsins and their structure-function relationships. Front. Cell. Neurosci. 2022, 15, 800313. [Google Scholar] [CrossRef]
- Lehtinen, K.; Nokia, M.S.; Takala, H. Red light optogenetics in neuroscience. Front. Cell. Neurosci. 2022, 15, 778900. [Google Scholar] [CrossRef]
- Boyden, E.S.; Zhang, F.; Bamberg, E.; Nagel, G.; Deisseroth, K. Millisecond-timescale, genetically targeted optical control of neural activity. Nat. Neurosci. 2005, 8, 1263–1268. [Google Scholar] [CrossRef]
- Deisseroth, K. Optogenetics: 10 years of microbial opsins in neuroscience. Nat. Neurosci. 2015, 18, 1213–1225. [Google Scholar] [CrossRef] [PubMed]
- Bi, A.; Cui, J.; Ma, Y.P.; Olshevskaya, E.; Pu, M.; Dizhoor, A.M.; Pan, Z.H. Ectopic expression of a microbial-type rhodopsin restores visual responses in mice with photoreceptor degeneration. Neuron 2006, 50, 23–33. [Google Scholar] [CrossRef] [PubMed]
- Mattis, J.; Tye, K.M.; Ferenczi, E.A.; Ramakrishnan, C.; O’shea, D.J.; Prakash, R.; Gunaydin, L.A.; Hyun, M.; Fenno, L.E.; Gradinaru, V.; et al. Principles for applying optogenetic tools derived from direct comparative analysis of microbial opsins. Nat. Methods 2012, 9, 159–172. [Google Scholar] [CrossRef] [PubMed]
- Klapoetke, N.C.; Murata, Y.; Kim, S.S.; Pulver, S.R.; Birdsey-Benson, A.; Cho, Y.K.; Morimoto, T.K.; Chuong, A.S.; Carpenter, E.J.; Tian, Z.; et al. Independent optical excitation of distinct neural populations. Nat. Methods 2014, 11, 338–346. [Google Scholar] [CrossRef]
- Ronzitti, E.; Conti, R.; Zampini, V.; Tanese, D.; Foust, A.J.; Klapoetke, N.; Boyden, E.S.; Papagiakoumou, E.; Emiliani, V. Submillisecond optogenetic control of neuronal firing with two-photon holographic photoactivation of chronos. J. Neurosci. 2017, 37, 10679–10689. [Google Scholar] [CrossRef]
- Mager, T.; de la Morena, D.L.; Senn, V.; Schlotte, J.; Feldbauer, K.; Wrobel, C.; Jung, S.; Bodensiek, K.; Rankovic, V.; Browne, L.; et al. High frequency neural spiking and auditory signaling by ultrafast red-shifted optogenetics. Nat. Commun. 2018, 9, 1750. [Google Scholar] [CrossRef]
- Marshel, J.H.; Kim, Y.S.; Machado, T.A.; Quirin, S.; Benson, B.; Kadmon, J.; Raja, C.; Chibukhchyan, A.; Ramakrishnan, C.; Inoue, M.; et al. Cortical layer–specific critical dynamics triggering perception. Science 2019, 365, eaaw5202. [Google Scholar] [CrossRef]
- Kishi, K.E.; Kim, Y.S.; Fukuda, M.; Inoue, M.; Kusakizako, T.; Wang, P.Y.; Ramakrishnan, C.; Byrne, E.F.; Thadhani, E.; Paggi, J.M.; et al. Structural basis for channel conduction in the pump-like channelrhodopsin ChRmine. Cell 2022, 185, 672–689. [Google Scholar] [CrossRef]
- Akam, T.; Oren, I.; Mantoan, L.; Ferenczi, E.; Kullmann, D.M. Oscillatory dynamics in the hippocampus support dentate gyrus-CA3 coupling. Nat. Neurosci. 2012, 15, 763–768. [Google Scholar] [CrossRef]
- Kilias, A.; Canales, A.; Florien, U.P.; Park, S.; Egert, U.; Anikeeva, P. Optogenetic entrainment of neural oscillations with hybrid fiber probes. J. Neural Eng. 2018, 15, 056006. [Google Scholar] [CrossRef] [PubMed]
- Cole, S.R.; Voytek, B. Brain oscillations and the importance of waveform shape. Trends Cog. Sci. 2017, 21, 137–149. [Google Scholar] [CrossRef]
- Bitzenhofer, S.H.; Ahlbeck, J.; Hanganu-Opatz, I.L. Methodological approach for optogenetic manipulation of neonatal neuronal networks. Front. Cell. Neurosci. 2017, 11, 239. [Google Scholar] [CrossRef]
- Owen, S.F.; Liu, M.H.; Kreitzer, A.C. Thermal constraints on in vivo optogenetic manipulations. Nat. Neurosci. 2019, 22, 1061–1065. [Google Scholar] [CrossRef] [PubMed]
- Senova, S.; Scisniak, I.; Chiang, C.C.; Doignon, I.; Palfi, S.; Chaillet, A.; Martin, C.; Pain, F. Experimental assessment of the safety and potential efficacy of high irradiance photostimulation of brain tissues. Sci. Rep. 2017, 7, 43997. [Google Scholar] [CrossRef] [PubMed]
- Grossman, N.; Nikolic, K.; Toumazou, C.; Degenaar, P. Modeling study of the light stimulation of a neuron cell with channelrhodopsin-2 mutants. IEEE Trans. Biomed. Eng. 2011, 58, 1742–1751. [Google Scholar]
- Nikolic, K.; Grossman, N.; Grubb, M.S.; Burrone, J.; Toumazou, C.; Degenaar, P. Photocycles of channelrhodopsin-2. Photochem. Photobiol. 2009, 85, 400–411. [Google Scholar] [CrossRef]
- Grossman, N.; Simiaki, V.; Martinet, C.; Toumazou, C.; Schultz, S.R.; Nikolic, K. The spatial pattern of light determines the kinetics and modulates backpropagation of optogenetic action potentials. J. Comp. Neurosci. 2013, 34, 477–488. [Google Scholar] [CrossRef]
- Foutz, T.J.; Arlow, R.L.; McIntyre, C.C. Theoretical principles underlying optical stimulation of a channelrhodopsin-2 positive pyramidal neuron. J. Neurophysiol. 2012, 107, 3235–3245. [Google Scholar] [CrossRef]
- Arlow, R.L.; Foutz, T.J.; McIntyre, C.C. Theoretical principles underlying optical stimulation of myelinated axons expressing channelrhodopsin-2. Neuroscience 2013, 248, 541–551. [Google Scholar] [CrossRef]
- Saran, S.; Gupta, N.; Roy, S. Theoretical analysis of low-power fast optogenetic control of firing of Chronos-expressing neurons. Neurophotonics 2018, 5, 025009. [Google Scholar] [CrossRef] [PubMed]
- Gupta, N.; Bansal, H.; Roy, S. Theoretical optimization of high-frequency optogenetic spiking of red-shifted very fast-Chrimson-expressing neurons. Neurophotonics 2019, 6, 025002. [Google Scholar] [CrossRef]
- Bansal, H.; Gupta, N.; Roy, S. Comparison of low-power, high-frequency and temporally precise optogenetic inhibition of spiking in NpHR, eNpHR3. 0 and Jaws-expressing neurons. Biomed. Phys. Eng. Express. 2020, 6, 045011. [Google Scholar] [CrossRef] [PubMed]
- Bansal, H.; Gupta, N.; Roy, S. Theoretical analysis of low-power bidirectional optogenetic control of high-frequency neural codes with single spike resolution. Neuroscience 2020, 449, 165–188. [Google Scholar] [CrossRef]
- Bansal, H.; Gupta, N.; Roy, S. Theoretical analysis of optogenetic spiking with ChRmine, bReaChES and CsChrimson-expressing neurons for retinal prostheses. J. Neural Eng. 2021, 18, 0460b8. [Google Scholar] [CrossRef]
- Bansal, H.; Pyari, G.; Roy, S. Co-expressing Fast Channelrhodopsin with Step-Function Opsin Overcomes Spike Failure due to Photocurrent Desensitization in Optogenetics: A Theoretical Study. J. Neural Eng. 2022, 19, 026032. [Google Scholar] [CrossRef]
- Pyari, G.; Bansal, H.; Roy, S. Ultra-Low Power Deep Sustained Optogenetic Excitation of Human Ventricular Cardiomyocytes with Red-shifted Opsins: A Computational Study. J. Physiol. 2022, 600, 4653–4676. [Google Scholar] [CrossRef] [PubMed]
- Engelhard, C.; Chizhov, S.F.; Engelhard, M. Microbial halorhodopsins: Light-driven chloride pumps. Chem. Rev. 2018, 118, 10629–10645. [Google Scholar] [CrossRef]
- Roy, S.; Singh, C.P.; Reddy, K.P.J. Generalized model for all-optical light modulation in bacteriorhodopsin. J. Appl. Phys. 2001, 90, 3679–3688. [Google Scholar] [CrossRef]
- Roy, S.; Kikukawa, T.; Sharma, P.; Kamo, N. All-optical switching in pharaonis phoborhodopsin protein molecules. IEEE Trans. Nanobiosci. 2006, 5, 178–187. [Google Scholar] [CrossRef]
- Roy, S.; Yadav, C. All-optical sub-ps switching and parallel logic gates with bacteriorhodopsin (BR) protein and BR-gold nanoparticles. Laser Phys. Lett. 2014, 11, 12590. [Google Scholar] [CrossRef]
- Sharma, P.; Roy, S. All-optical light modulation in pharaonis phoborhodopsin and its application to parallel logic gates. J. Appl. Phys. 2004, 96, 1687–1695. [Google Scholar] [CrossRef]
- Evans, B.D.; Jarvis, S.; Schultz, S.R.; Nikolic, K. PyRhO: A multiscale optogenetics simulation platform. Front. Neuroinform. 2016, 10, 8. [Google Scholar] [CrossRef] [PubMed]
- Hemond, P.; Epstein, D.; Boley, A.; Migliore, M.; Ascoli, G.A.; Jaffe, D.B. Distinct classes of pyramidal cells exhibit mutually exclusive firing patterns in hippocampal area CA3b. Hippocampus 2008, 18, 411–424. [Google Scholar] [CrossRef] [PubMed]
- Alturki, A.; Feng, F.; Nair, A.; Guntu, V.; Nair, S.S. Distinct current modules shape cellular dynamics in model neurons. Neuroscience 2016, 334, 309–331. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.J.; Buzsáki, G. Gamma oscillation by synaptic inhibition in a hippocampal interneuronal network model. J. Neurosci. 1996, 16, 6402–6413. [Google Scholar] [CrossRef] [PubMed]
- Foutz, T.J.; McIntyre, C.C. Evaluation of novel stimulus waveforms for deep brain stimulation. J. Neural Eng. 2010, 7, 066008. [Google Scholar] [CrossRef] [PubMed]
- Rapp, J.; Braun, P.; Hemmert, W.; Gleich, B. Optimal pulse configuration for peripheral inductive nerve stimulation. Biomed. Phys. Eng. Exp. 2022, 8, 025020. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, X.; Wang, Q.; Wang, Q. A review of computational modeling and deep brain stimulation: Applications to Parkinson’s disease. Appl. Math. Mech. 2020, 41, 1747–1768. [Google Scholar] [CrossRef]
- Graupner, M.; Wallisch, P.; Ostojic, S. Natural firing patterns imply low sensitivity of synaptic plasticity to spike timing compared with firing rate. J. Neurosci. 2016, 36, 11238–11258. [Google Scholar] [CrossRef]
- Wick, C.Z.; Krook-Magnuson, E. Specificity, versatility, and continual development: The power of optogenetics for epilepsy research. Front. Cell. Neurosci. 2018, 12, 151. [Google Scholar] [CrossRef] [PubMed]
- Cohen, M.R.; Maunsell, J.H. Attention improves performance primarily by reducing interneuronal correlations. Nat. Neurosci. 2009, 12, 1594–1600. [Google Scholar] [CrossRef] [PubMed]
- Keppeler, D.; Merino, R.M.; Lopez de la Morena, D.; Bali, B.; Huet, A.T.; Gehrt, A.; Wrobel, C.; Subramanian, S.; Dombrowski, T.; Wolf, F.; et al. Ultrafast optogenetic stimulation of the auditory pathway by targeting-optimized Chronos. EMBO J. 2018, 37, e99649. [Google Scholar] [CrossRef]
- Jun, N.Y.; Cardin, J.A. Activation of distinct Channelrhodopsin variants engages different patterns of network activity. eNeuro 2019, 7, ENEURO.0222-18.2019. [Google Scholar] [CrossRef] [PubMed]
- Sridharan, S.; Gajowa, M.A.; Ogando, M.B.; Jagadisan, U.K.; Abdeladim, L.; Sadahiro, M.; Bounds, H.A.; Hendricks, W.D.; Turney, T.S.; Tayler, I.; et al. High-performance microbial opsins for spatially and temporally precise perturbations of large neuronal networks. Neuron 2022, 110, 1139–1155. [Google Scholar] [CrossRef]
- Chen, R.; Gore, F.; Nguyen, Q.A.; Ramakrishnan, C.; Patel, S.; Kim, S.H.; Raffiee, M.; Kim, Y.S.; Hsueh, B.; Krook-Magnusson, E.; et al. Deep brain optogenetics without intracranial surgery. Nat. Biotechnol. 2021, 39, 161–164. [Google Scholar] [CrossRef]
- Gunaydin, L.A.; Yizhar, O.; Berndt, A.; Sohal, V.S.; Deisseroth, K.; Hegemann, P. Ultrafast optogenetic control. Nat. Neurosci. 2010, 13, 387–392. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, L.P.; Brauner, M.; Liewald, J.F.; Kay, K.; Watzke, N.; Wood, P.G.; Bamberg, E.; Nagel, G.; Gottschalk, A.; et al. Multimodal fast optical interrogation of neural circuitry. Nature 2007, 446, 633–639. [Google Scholar] [CrossRef]
- Gradinaru, V.; Zhang, F.; Ramakrishnan, C.; Mattis, J.; Prakash, R.; Diester, I.; Goshen, I.; Thompson, K.R.; Deisseroth, K. Molecular and cellular approaches for diversifying and extending optogenetics. Cell 2010, 141, 154–165. [Google Scholar] [CrossRef]
- Chuong, A.S.; Miri, M.L.; Busskamp, V.; Matthews, G.A.; Acker, L.C.; Sørensen, A.T.; Young, A.; Klapoetke, N.C.; Henninger, M.A.; Kodandaramaiah, S.B.; et al. Noninvasive optical inhibition with a red-shifted microbial rhodopsin. Nat. Neurosci. 2014, 17, 1123–1129. [Google Scholar] [CrossRef] [PubMed]
- Raimondo, J.V.; Kay, L.; Ellender, T.J.; Akerman, C.J. Optogenetic silencing strategies differ in their effects on inhibitory synaptic transmission. Nat. Neurosci. 2012, 15, 1102–1104. [Google Scholar] [CrossRef] [PubMed]
- Wiegert, J.S.; Mahn, M.; Prigge, M.; Printz, Y.; Yizhar, O. Silencing neurons: Tools, applications, and experimental constraints. Neuron 2017, 95, 504–529. [Google Scholar] [CrossRef] [PubMed]
- Kuhne, J.; Vierock, J.; Tennigkeit, S.A.; Dreier, M.A.; Wietek, J.; Petersen, D.; Gavriljuk, K.; El-Mashtoly, S.F.; Hegemann, P.; Gerwert, K. Unifying photocycle model for light adaptation and temporal evolution of cation conductance in channelrhodopsin-2. Proc. Natl. Acad. Sci. USA 2019, 116, 9380–9389. [Google Scholar] [CrossRef]
- Sekulić, V.; Lawrence, J.J.; Skinner, F.K. Using multi-compartment ensemble modeling as an investigative tool of spatially distributed biophysical balances: Application to hippocampal oriens-lacunosum/moleculare (O-LM) cells. PLoS ONE 2014, 9, e106567. [Google Scholar] [CrossRef]
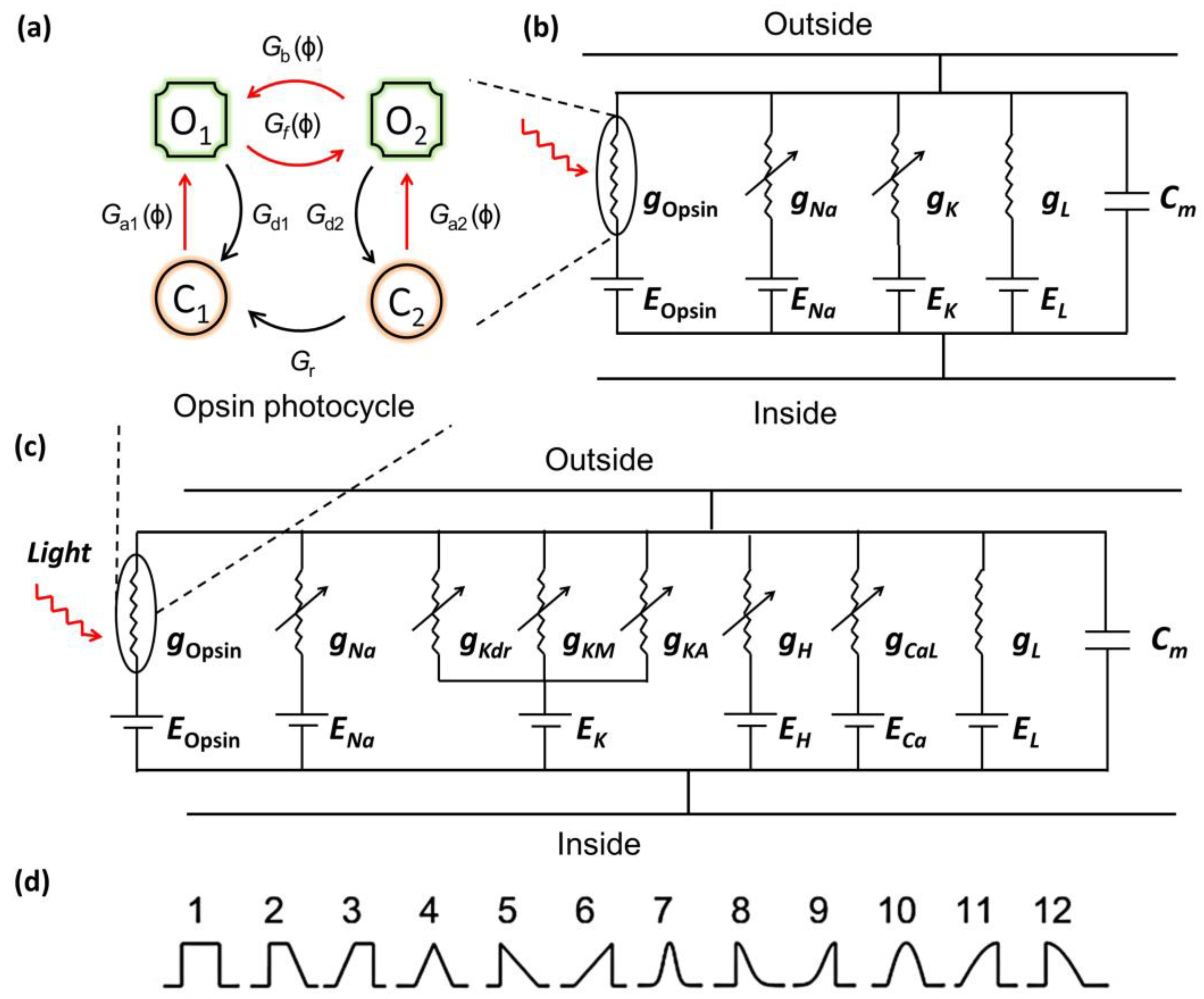


| Parameter | Chronos | ChR2 | ChRmine |
|---|---|---|---|
| (ms−1) | 0.278 | 0.09 | 0.02 |
| (ms−1) | 0.01 | 0.01 | 0.013 |
| (ms−1) | 1.2 × 10−3 | 0.5 × 10−3 | 5.9 × 10−4 |
| (nS) for photocurrent | 39 | 5.9 | 110 |
| (mS/cm2) for hippocampal neurons | 0.88 | 0.65 | 1.9 |
| (mS/cm2) for neocortical interneurons | 0.176 | 0.12 | 0.38 |
| (ph·mm−2·s−1) | 8 × 1015 | 4 × 1016 | 2.1 × 1015 |
| (ms−1) | 1.8 | 3 | 0.2 |
| (ms−1) | 0.01 | 0.18 | 0.01 |
| (ms−1) | 0.05 | 0.015 | 0.0027 |
| (ms−1) | 0.08 | 0.005 | 0.0005 |
| (ms−1) | 0.1 | 0.03 | 0.001 |
| (ms−1) | 0.01 | 0.003 | 0 |
| γ | 0.05 | 0.05 | 0.05 |
| p | 0.8 | 1 | 0.8 |
| q | 0.9 | 1 | 1 |
| λ (nm) | 470 | 470 | 590 |
| E (mV) | 0 | 0 | 5.64 |
| Gating Variable | |||||
|---|---|---|---|---|---|
| - | |||||
| Parameter | Unit | Value |
|---|---|---|
| 22 | ||
| 10 | ||
| 0.01 | ||
| 0.01 | ||
| 20 | ||
| 0.5 | ||
| 0.04 | ||
| −30 | ||
| 55 | ||
| −90 | ||
| −70 | ||
| 100 | ||
| 0 | ||
| 1.41 |
| Gating Variable | |||
|---|---|---|---|
| Parameter | Unit | Value |
|---|---|---|
| 35 | ||
| 9 | ||
| 0.1 | ||
| 55 | ||
| −90 | ||
| −65 | ||
| - | 7 | |
| −0.51 | ||
| 1.41 | ||
| −65 |
| Shape Name | Shape | |
|---|---|---|
| Square pulse |  | |
| Forward-Ramp |  | |
| Backward-Ramp |  | |
| Triangular |  | |
| Left-Triangular |  | |
| Right-Triangular |  | |
| Gaussian | 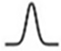 | ; |
| Left-Gaussian |  | ; |
| Right-Gaussian |  | ; |
| Positive-Sinusoidal |  | |
| Left-Positive-Sinusoidal | 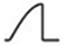 | |
| Right-Positive-Sinusoidal |  |
| Pulse Shape | Square | Triangular | Gaussian | Positive-Sinusoidal | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Condition | Irradiance/ Energy Density | Pulse Width | Ipeak (nA) | tpeak (ms) | Ipeak (nA) | tpeak (ms) | Ipeak (nA) | tpeak (ms) | Ipeak (nA) | tpeak (ms) |
| Chronos | ||||||||||
| Iso-max | 1 mW/mm2 | 5 ms | 1.24 | 5 | 1.10 | 3.7 | 1.06 | 3.6 | 1.18 | 3.9 |
| 1 mW/mm2 | 1 s | 1.25 | 4.3 | 0.68 | 160 | 0.69 | 310 | 0.74 | 130 | |
| Iso-energy density | 5 µJ/mm2 | 5 ms | 1.24 | 5 | 1.33 | 3.4 | 1.36 | 3.33 | 1.32 | 3.5 |
| 1 mJ/mm2 | 1 s | 1.24 | 4.3 | 0.778 | 110 | 0.74 | 250 | 0.803 | 80 | |
| ChR2 | ||||||||||
| Iso-max | 1 mW/mm2 | 5 ms | 0.16 | 5 | 0.098 | 4.42 | 0.08 | 3.92 | 0.11 | 4.5 |
| 1 mW/mm2 | 1 s | 0.19 | 13 | 0.089 | 160 | 0.096 | 330 | 0.1 | 140 | |
| Iso-energy density | 5 µJ/mm2 | 5 ms | 0.160 | 5 | 0.161 | 4.5 | 0.165 | 4.01 | 0.161 | 4.5 |
| 1 mJ/mm2 | 1 s | 0.19 | 13.6 | 0.111 | 110 | 0.110 | 260 | 0.118 | 100 | |
| ChRmine | ||||||||||
| Iso-max | 1 mW/mm2 | 5 ms | 2.97 | 5 | 2.21 | 4.94 | 1.82 | 4.77 | 2.45 | 4.96 |
| 1 mW/mm2 | 1 s | 5.65 | 29.2 | 4.50 | 120 | 4.11 | 260 | 4.74 | 100 | |
| Iso-energy density | 5 µJ/mm2 | 5 ms | 2.97 | 5 | 2.76 | 4.92 | 2.41 | 4.68 | 2.8 | 4.93 |
| 1 mJ/mm2 | 1 s | 5.65 | 28.1 | 4.88 | 90 | 4.34 | 210 | 4.98 | 80 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bansal, H.; Pyari, G.; Roy, S. Optogenetic Generation of Neural Firing Patterns with Temporal Shaping of Light Pulses. Photonics 2023, 10, 571. https://doi.org/10.3390/photonics10050571
Bansal H, Pyari G, Roy S. Optogenetic Generation of Neural Firing Patterns with Temporal Shaping of Light Pulses. Photonics. 2023; 10(5):571. https://doi.org/10.3390/photonics10050571
Chicago/Turabian StyleBansal, Himanshu, Gur Pyari, and Sukhdev Roy. 2023. "Optogenetic Generation of Neural Firing Patterns with Temporal Shaping of Light Pulses" Photonics 10, no. 5: 571. https://doi.org/10.3390/photonics10050571
APA StyleBansal, H., Pyari, G., & Roy, S. (2023). Optogenetic Generation of Neural Firing Patterns with Temporal Shaping of Light Pulses. Photonics, 10(5), 571. https://doi.org/10.3390/photonics10050571





