Toward Practical Optical Phased Arrays through Grating Antenna Engineering
Abstract
1. Introduction
2. Basic Structure and Principle
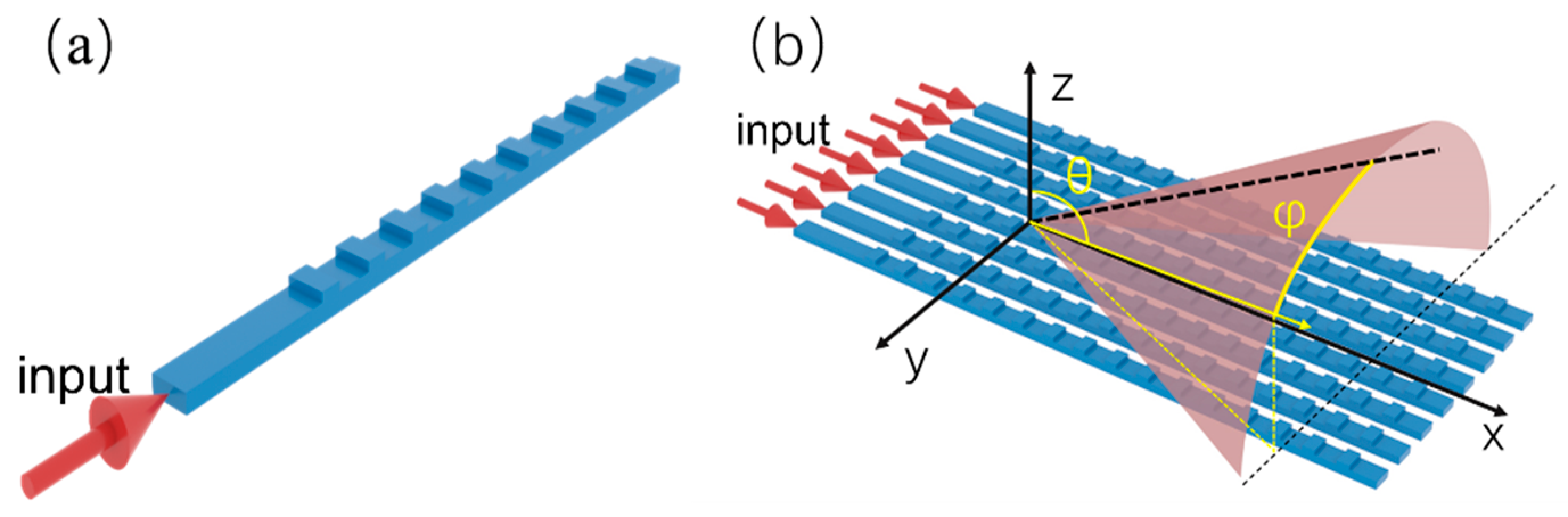
2.1. Basic Structure of Waveguide Grating Antenna
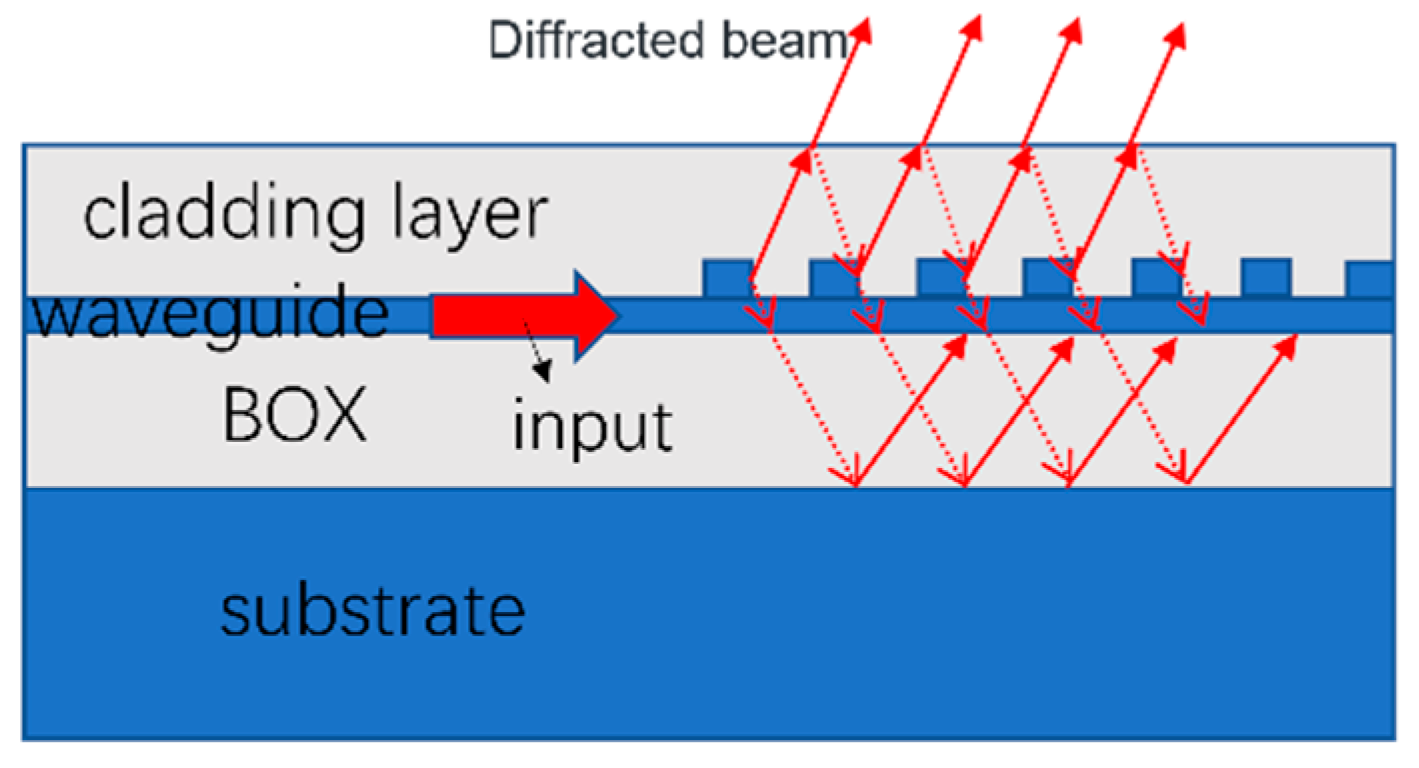
2.2. Basic Diffraction Principle of Waveguide Grating Antenna
3. The Main Research Directions of Waveguide Grating Antenna
3.1. The Effective Length of a Waveguide Grating Antenna
3.2. Uniform Radiation
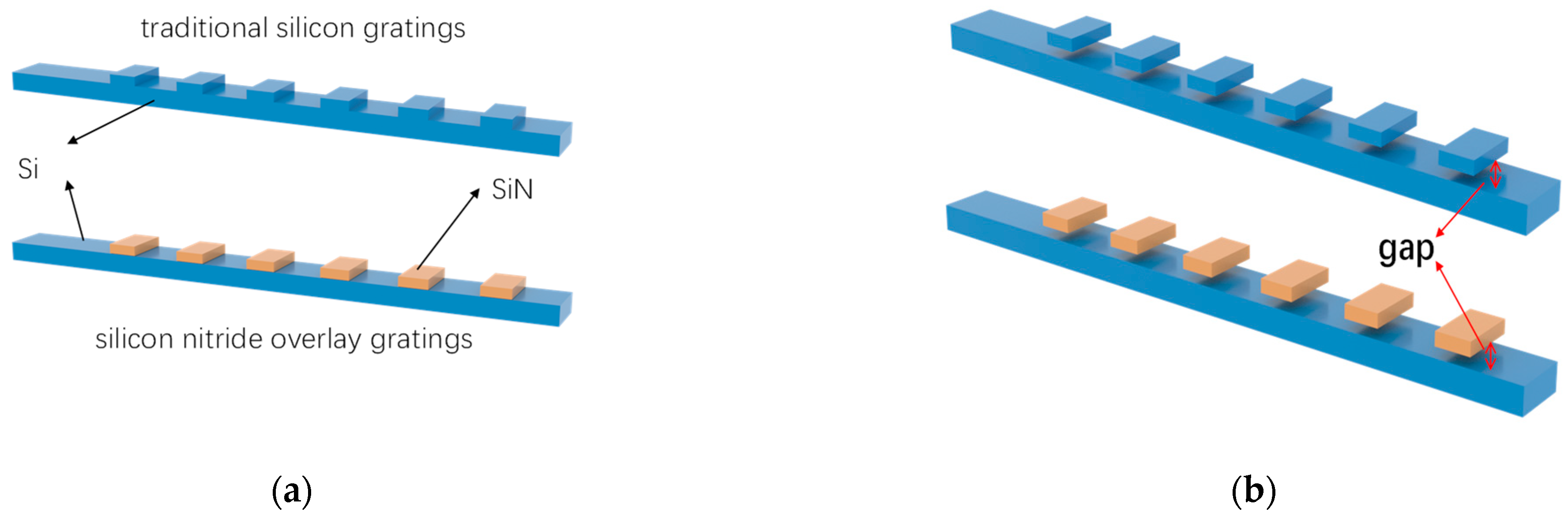
3.3. The Directivity of Diffraction
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yu, L.; Liu, L.; Zhou, Z.; Wang, X. High efficiency binary blazed grating coupler for perfectly-vertical and near-vertical coupling in chip level optical interconnections. Opt. Commun. 2015, 355, 161–166. [Google Scholar] [CrossRef]
- Liu, L.; Deng, Q.; Zhou, Z. Manipulation of beat length and wavelength dependence of a polarization beam splitter using a subwavelength grating. Opt. Lett. 2016, 41, 5126–5129. [Google Scholar] [CrossRef]
- Feng, J.; Zhou, Z. Polarization beam splitter using a binary blazed grating coupler. Opt. Lett. 2007, 32, 1662–1664. [Google Scholar] [CrossRef]
- Bai, B.; Yang, F.; Zhou, Z. Demonstration of an on-chip TE-pass polarizer using a silicon hybrid plasmonic grating. Photonics Res. 2019, 7, 289–293. [Google Scholar] [CrossRef]
- Meyer, R.A. Optical Beam Steering Using a Multichannel Lithium Tantalate Crystal. Appl. Opt. 1972, 11, 613. [Google Scholar] [CrossRef] [PubMed]
- Tien, P.K.; Riva Sanseverino, S.; Ballman, A.A. Light beam scanning and deflection in epitaxial LiNbO3 electro-optic waveguides. Appl. Phys. Lett. 1974, 25, 563–565. [Google Scholar] [CrossRef]
- Bhargava, P.; Kim, T.; Poulton, C.V.; Notaros, J.; Yaacobi, A.; Timurdogan, E.; Baiocco, C.; Fahrenkopf, N.; Kruger, S.; Ngai, T.; et al. Fully Integrated coherent LiDAR in 3D-Integrated Silicon Photonics/65nm CMOS. In Proceedings of the 2019 Symposium on VLSI Circuits, Kyoto, Japan, 9–14 June 2019. [Google Scholar] [CrossRef]
- Van Acoleyen, K.; Bogaerts, W.; Jagerska, J.; Le Thomas, N.; Houdre, R.; Baets, R. Off-chip beam steering with a one-dimensional optical phased array on silicon-on-insulator. Opt. Lett. 2009, 34, 1477–1479. [Google Scholar] [CrossRef]
- Kim, T.; Ngai, T.; Timalsina, Y.; Watts, M.R.; Stojanovic, V.; Bhargava, P.; Poulton, C.V.; Notaros, J.; Yaacobi, A.; Timurdogan, E.; et al. A Single-Chip Optical Phased Array in a Wafer-Scale Silicon Photonics/CMOS 3D-Integration Platform. IEEE J. Solid-State Circuits 2019, 54, 3061–3074. [Google Scholar] [CrossRef]
- Xu, W.; Guo, Y.; Li, X.; Liu, C.; Lu, L.; Chen, J.; Zhou, L. Fully Integrated Solid-State LiDAR Transmitter on a Multi-Layer Silicon-Nitride-on-Silicon Photonic Platform. J. Light. Technol. 2023, 41, 832–840. [Google Scholar] [CrossRef]
- Lin, S.; Chen, Y.; Wong, Z.J. High-performance optical beam steering with nanophotonics. Nanophotonics 2022, 11, 2617–2638. [Google Scholar] [CrossRef]
- Sayyah, K.; Sarkissian, R.; Patterson, P.; Huang, B.; Efimov, O.; Kim, D.; Elliott, K.; Yang, L.; Hammon, D. Fully Integrated FMCW LiDAR Optical Engine on a Single Silicon Chip. J. Light. Technol. 2022, 40, 2763–2772. [Google Scholar] [CrossRef]
- Kazemian, A.; Wang, P.; Zhuang, Y.; Yi, Y. Optimization of the silicon-based aperiodic optical phased array antenna. Opt. Lett. 2021, 46, 801–804. [Google Scholar] [CrossRef] [PubMed]
- Van Laere, F.; Roelkens, G.; Schrauwen, J.; Taillaert, D.; Dumon, P.; Bogaerts, W.; van Thourhout, D.; Baets, R. Compact grating couplers between optical fibers and Silicon-on-Insulator photonic wire waveguides with 69% coupling efficiency. In Proceedings of the Optical Fiber Communication Conference, Anaheim, CA, USA, 5–10 March 2006. [Google Scholar]
- Feng, J.; Zhou, Z. High efficiency compact grating coupler for integrated optical circuits. In Proceedings of the Asia-Pacific Optical Communications, Gwangju, Republic of Korea, 4 October 2006. [Google Scholar] [CrossRef]
- Sun, J.; Timurdogan, E.; Yaacobi, A.; Hosseini, E.S.; Watts, M.R. Large-scale nanophotonic phased array. Nature 2013, 493, 195–199. [Google Scholar] [CrossRef]
- Raval, M.; Poulton, C.V.; Watts, M.R. Unidirectional waveguide grating antennas with uniform emission for optical phased arrays. Opt. Lett. 2017, 42, 2563–2566. [Google Scholar] [CrossRef] [PubMed]
- Zadka, M.; Chang, Y.; Mohanty, A.; Phare, C.T.; Roberts, S.P.; Lipson, M. On-chip platform for a phased array with minimal beam divergence and wide field-of-view. Opt. Express 2018, 26, 2528. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, S.; Jia, L.; Cai, Y.; Yue, W.; Yu, M. Silicon nitride assisted 1 × 64 optical phased array based on a SOI platform. Opt. Express 2021, 29, 10509. [Google Scholar] [CrossRef]
- Xu, W.; Liu, C.; Guo, Y.; Li, X.; Lu, L.; Chen, J.; Zhou, L. Impact of Aperture Size on Beam Evolution of Optical Phased Arrays. In Proceedings of the Optical Fiber Communication Conference, Washington, DC, USA, 6–11 June 2021. [Google Scholar]
- Chen, J.; Wang, J.; Li, J.; Yao, Y.; Sun, Y.; Tian, J.; Zou, Y.; Zhao, X.; Xu, X. Subwavelength structure enabled ultra-long waveguide grating antenna. Opt. Express 2021, 29, 15133. [Google Scholar] [CrossRef]
- Ginel-Moreno, P.; Sánchez-Postigo, A.; De-Oliva-Rubio, J.; Hadij-ElHouati, A.; Ye, W.N.; Gonzalo Wangüemert-Pérez, J.; Molina-Fernández, Í.; Schmid, J.H.; Cheben, P.; Ortega-Moñux, A. Millimeter-long metamaterial surface-emitting antenna in the silicon photonics platform. Opt. Lett. 2021, 46, 3733–3736. [Google Scholar] [CrossRef]
- Ginel Moreno, P.; Hadij ElHouati, A.; Sánchez Postigo, A.; Wangüemert Pérez, J.G.; Molina Fernández, Í.; Schmid, J.H.; Cheben, P.; Ortega Moñux, A. On-Chip Metamaterial Antenna Array with Distributed Bragg Deflector for Generation of Collimated Steerable Beams. Laser Photonics Rev. 2022, 16, 2200164. [Google Scholar] [CrossRef]
- Yu, L.; Ma, P.; Luo, G.; Cui, L.; Zhou, X.; Wang, P.; Zhang, Y.; Pan, J. Adoption of large aperture chirped grating antennas in optical phase array for long distance ranging. Opt. Express 2022, 30, 28112. [Google Scholar] [CrossRef]
- Wang, H.; Sun, C.; Yang, L.; Nie, X.; Li, B.; Zhang, A. Uniform emission of large-scale optical phase arrays with wide wavelength tuning. In Proceedings of the Optical Fiber Communication, Washington, DC, USA, 6–11 June 2021. [Google Scholar]
- Shang, K.; Qin, C.; Zhang, Y.; Liu, G.; Xiao, X.; Feng, S.; Yoo, S.J.B. Uniform emission, constant wavevector silicon grating surface emitter for beam steering with ultra-sharp instantaneous field-of-view. Opt. Express 2017, 25, 19655. [Google Scholar] [CrossRef]
- Chen, Z.; Lü, H.; Chen, Y.; Liu, X. High-performance millimeter-scale silicon grating emitters for beam steering applications. Chin. Opt. Lett. 2022, 20, 121301. [Google Scholar] [CrossRef]
- Roelkens, G.; Van Thourhout, D.; Baets, R. High efficiency Silicon-on-Insulator grating coupler based on a poly-Silicon overlay. Opt. Express 2006, 14, 11622–11630. [Google Scholar] [CrossRef]
- Ma, P.; Luo, G.; Wang, P.; Ma, J.; Wang, R.; Yang, Z.; Zhou, X.; Zhang, Y.; Pan, J. Unidirectional SiN antenna based on dual-layer gratings for LiDAR with optical phased array. Opt. Commun. 2021, 501, 127361. [Google Scholar] [CrossRef]
- Chen, B.; Li, Y.; Zhang, L.; Li, Y.; Liu, X.; Tao, M.; Hou, Y.; Tang, H.; Zhi, Z.; Gao, F.; et al. Unidirectional large-scale waveguide grating with uniform radiation for optical phased array. Opt. Express 2021, 29, 20995. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, S.; Zeng, Y.; Wang, W.; Cai, Y.; Tu, Z.; Yue, W.; Wang, X.; Fang, Q.; Yu, M. Dual-layer waveguide grating antenna with high directionality for optical phased arrays. Appl. Opt. 2019, 58, 5807–5811. [Google Scholar] [CrossRef] [PubMed]
- Mei, C.; Liu, Q.; Huang, Q.; Zhang, X.; Shum, P.; Dong, J. Design of double-layer silicon nitride-based optical phased array. In Proceedings of the 13th International Photonics and Optoelectronics Meetings (POEM2021), Wuhan, China, 6–8 November 2021. [Google Scholar]
- Wang, P.F.; Luo, G.Z.; Yu, H.Y.; Li, Y.J.; Wang, M.Q.; Zhou, X.L.; Chen, W.X.; Zhang, Y.J.; Pan, J.Q. Improving the performance of optical antenna for optical phased arrays through high-contrast grating structure on SOI substrate. Opt. Express 2019, 27, 2703. [Google Scholar] [CrossRef]
- Zhang, Y.; Ling, Y.; Zhang, K.; Gentry, C.; Sadighi, D.; Whaley, G.; Colosimo, J.; Suni, P.; Ben Yoo, S.J. Sub-wavelength-pitch silicon-photonic optical phased array for large field-of-regard coherent optical beam steering. Opt. Express 2019, 27, 1929. [Google Scholar] [CrossRef] [PubMed]
- Khajavi, S.; Melati, D.; Cheben, P.; Schmid, J.H.; Ramos, C.A.A.; Ye, W.N. Highly efficient ultra-broad beam silicon nanophotonic antenna based on near-field phase engineering. Sci. Rep. 2022, 12, 18808. [Google Scholar] [CrossRef]
- Im, C.; Bhandari, B.; Lee, K.; Kim, S.; Oh, M.; Lee, S. Silicon nitride optical phased array based on a grating antenna enabling wavelength-tuned beam steering. Opt. Express 2020, 28, 3270. [Google Scholar] [CrossRef] [PubMed]
- Zhou, G.; Qu, S.; Wu, J.; Yang, S. High-efficiency unidirectional vertical emitter achieved by an aperture-coupling nanoslot antenna array. Opt. Express 2021, 29, 25399. [Google Scholar] [CrossRef]
- Sacher, W.D.; Huang, Y.; Ding, L.; Taylor, B.J.F.; Jayatilleka, H.; Lo, G.; Poon, J.K.S. Wide bandwidth and high coupling efficiency Si_3N_4-on-SOI dual-level grating coupler. Opt. Express 2014, 22, 10938. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Li, Y.; Hou, Y.; Wang, Y.; Tao, M.; Chen, B.; Na, Q.; Li, Y.; Zhi, Z.; Liu, X.; et al. Investigation and demonstration of a high-power handling and large-range steering optical phased array chip. Opt. Express 2021, 29, 29755. [Google Scholar] [CrossRef] [PubMed]
- Sun, C.; Li, B.; Shi, W.; Lin, J.; Ding, N.; Tsang, H.K.; Zhang, A. Large-Scale and Broadband Silicon Nitride Optical Phased Arrays. IEEE J. Sel. Top. Quant. 2022, 28, 1–10. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Z.; Sun, C.; Deng, S.; Tang, X.; Zhang, L.; Jiang, R.; Shi, W.; Chen, Z.; Li, Z.; et al. Broadband silicon nitride nanophotonic phased arrays for wide-angle beam steering. Opt. Lett. 2021, 46, 286–289. [Google Scholar] [CrossRef] [PubMed]




| Design Type | Effective Length/Manufacturing Length * | Divergence Angle |
|---|---|---|
| Double-layer misaligned SiN waveguide [17] | 3 mm | - |
| Apodized grating antennas [18] | 1 mm | 0.089° |
| SiN/Si double-layer design [19] | 1.5 mm | 0.075° |
| SiN/Si three-layer design [20] | 1 cm | - |
| Subwavelength structure [21] | 1 mm | 0.081° |
| Metamaterial surface-emitting [22] | 2 mm | 0.1° |
| Design Type | (Maximum) Emission Efficiency * |
|---|---|
| Double-layer misaligned silicon nitride waveguide [17] | 93% |
| Double-layer silicon nitride structure [29] | 96.7% |
| Single waveguide double-sided etching [30] | 95% |
| SiN/Si double layer [31] | 89% |
| Double-layer SiN [32] | 69% |
| High-contrast grating structure [33] | 93.94% |
| Bragg reflector structure [34,35] | 95% |
| 82% | |
| Nanoslot antenna [37] | 87.6% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shuai, Y.; Zhou, Z.; Su, H. Toward Practical Optical Phased Arrays through Grating Antenna Engineering. Photonics 2023, 10, 520. https://doi.org/10.3390/photonics10050520
Shuai Y, Zhou Z, Su H. Toward Practical Optical Phased Arrays through Grating Antenna Engineering. Photonics. 2023; 10(5):520. https://doi.org/10.3390/photonics10050520
Chicago/Turabian StyleShuai, Youqiang, Zhiping Zhou, and Hui Su. 2023. "Toward Practical Optical Phased Arrays through Grating Antenna Engineering" Photonics 10, no. 5: 520. https://doi.org/10.3390/photonics10050520
APA StyleShuai, Y., Zhou, Z., & Su, H. (2023). Toward Practical Optical Phased Arrays through Grating Antenna Engineering. Photonics, 10(5), 520. https://doi.org/10.3390/photonics10050520





