Application of Crossed Polarizer Method in the Measurement of Differential Group Delay of Optical Fibers
Abstract
1. Introduction
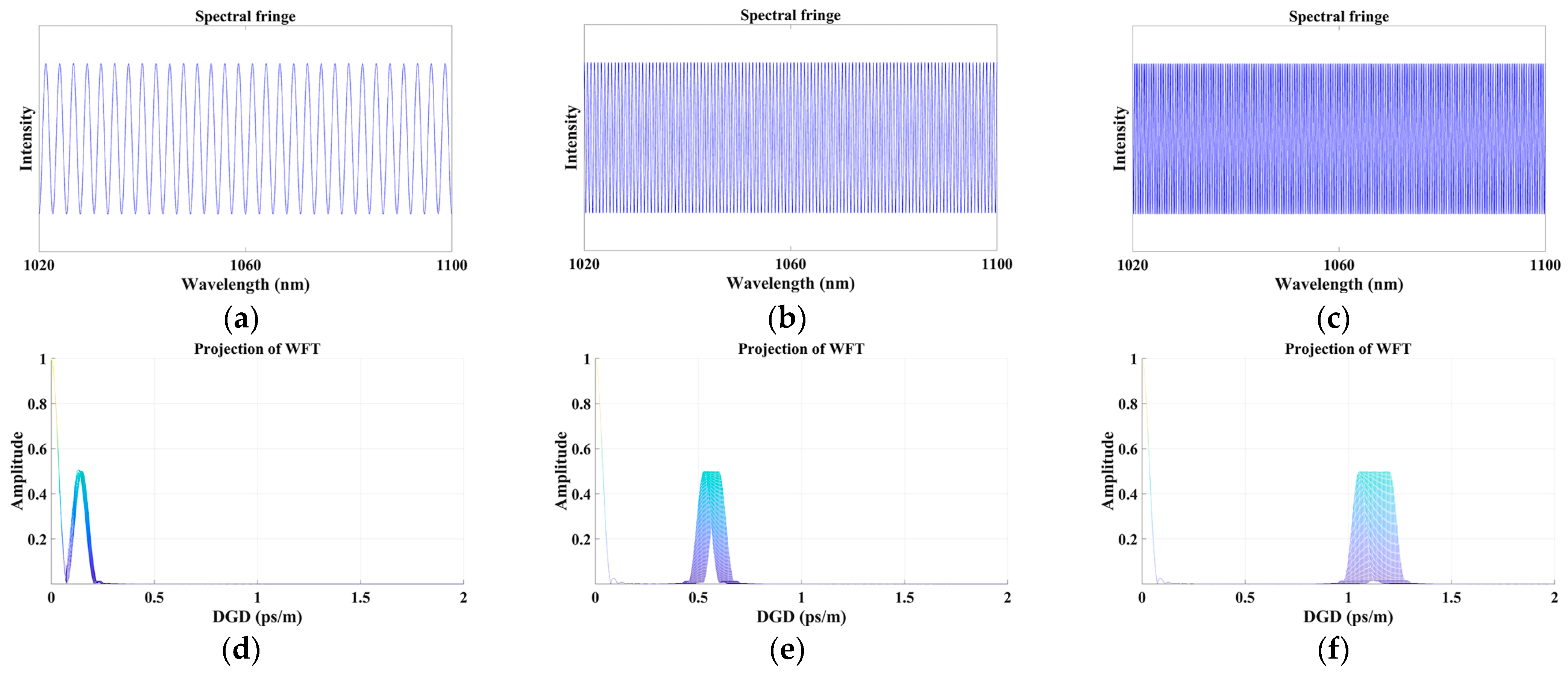
2. Experiment Setup and Theoretic Model
3. Experiment Result
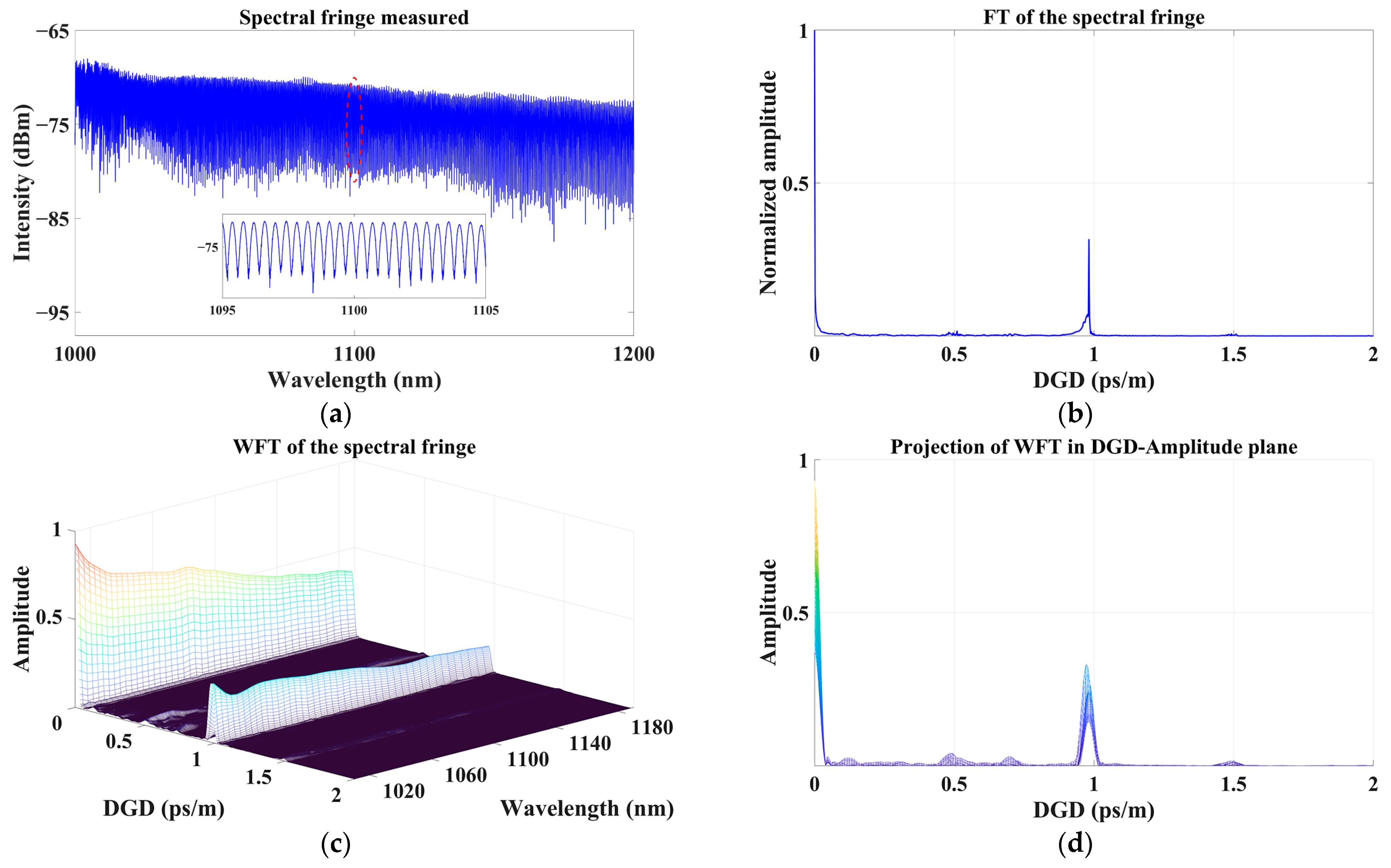
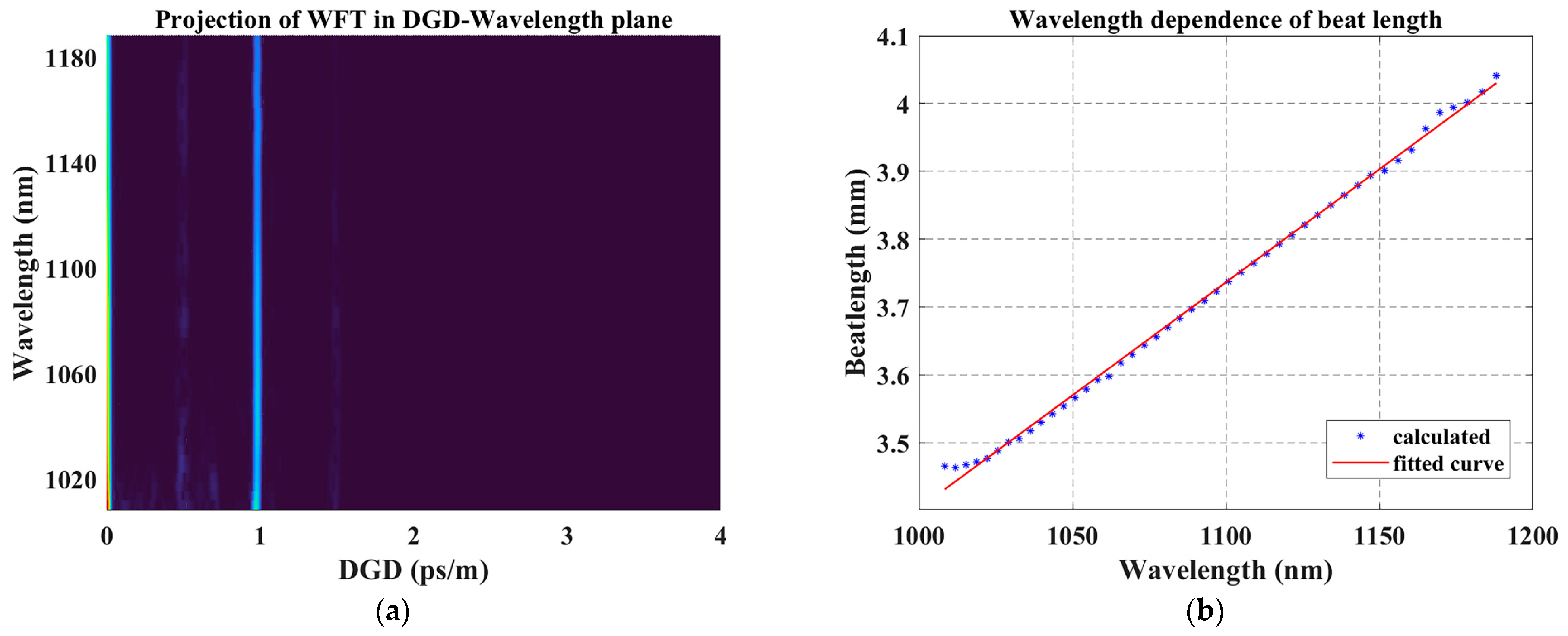
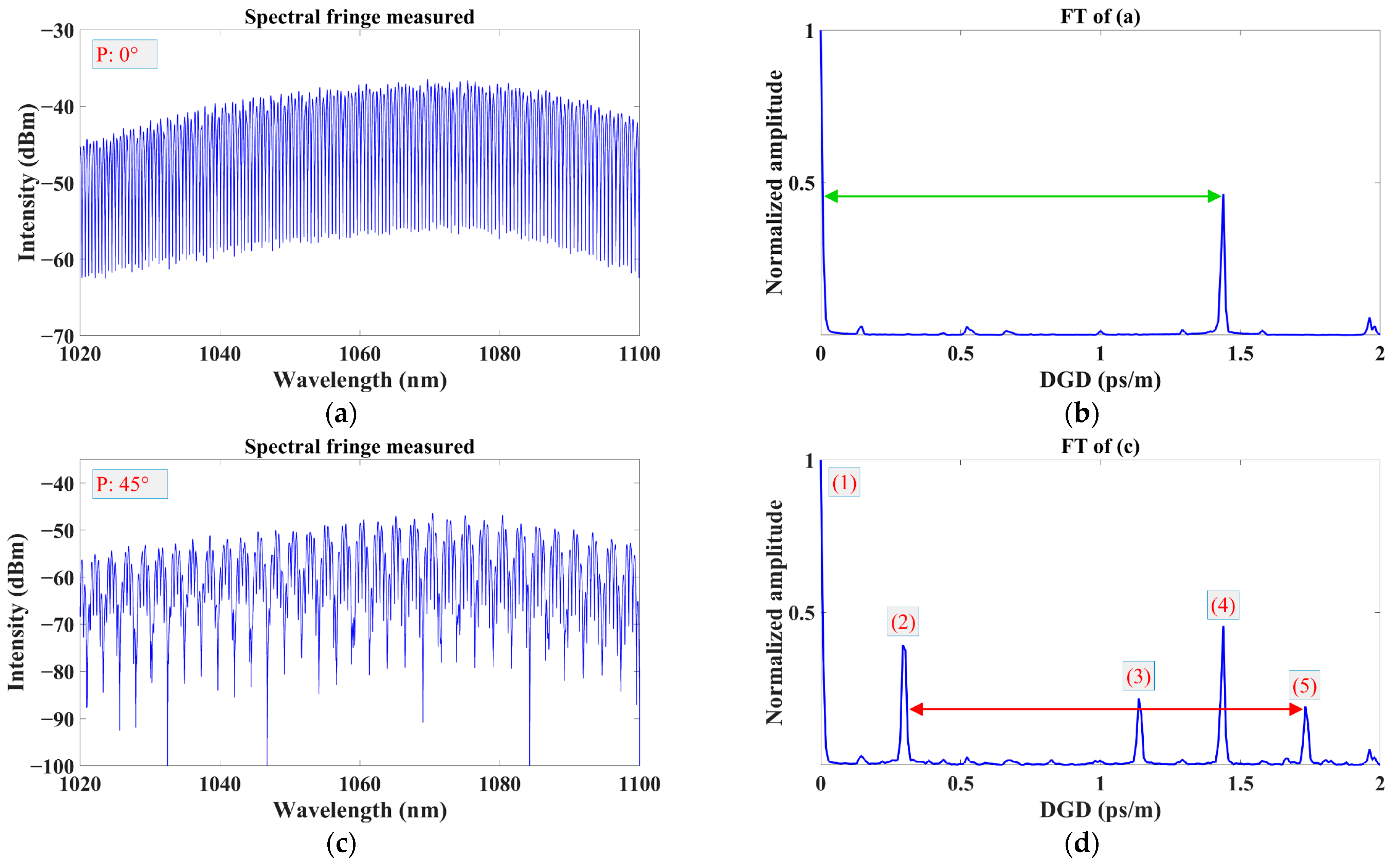
3.1. Characterization of Polarization-Maintaining Optical Fiber
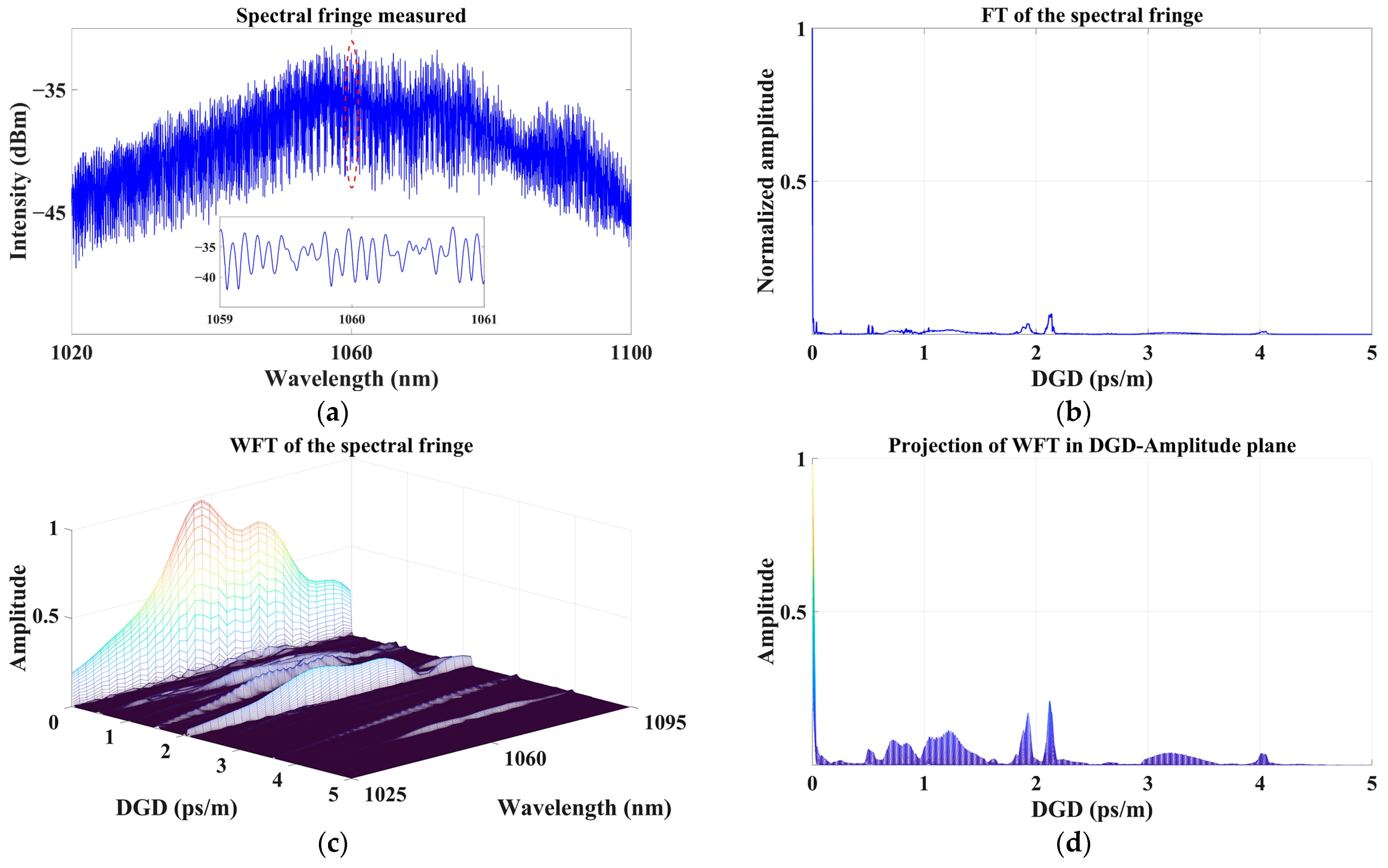
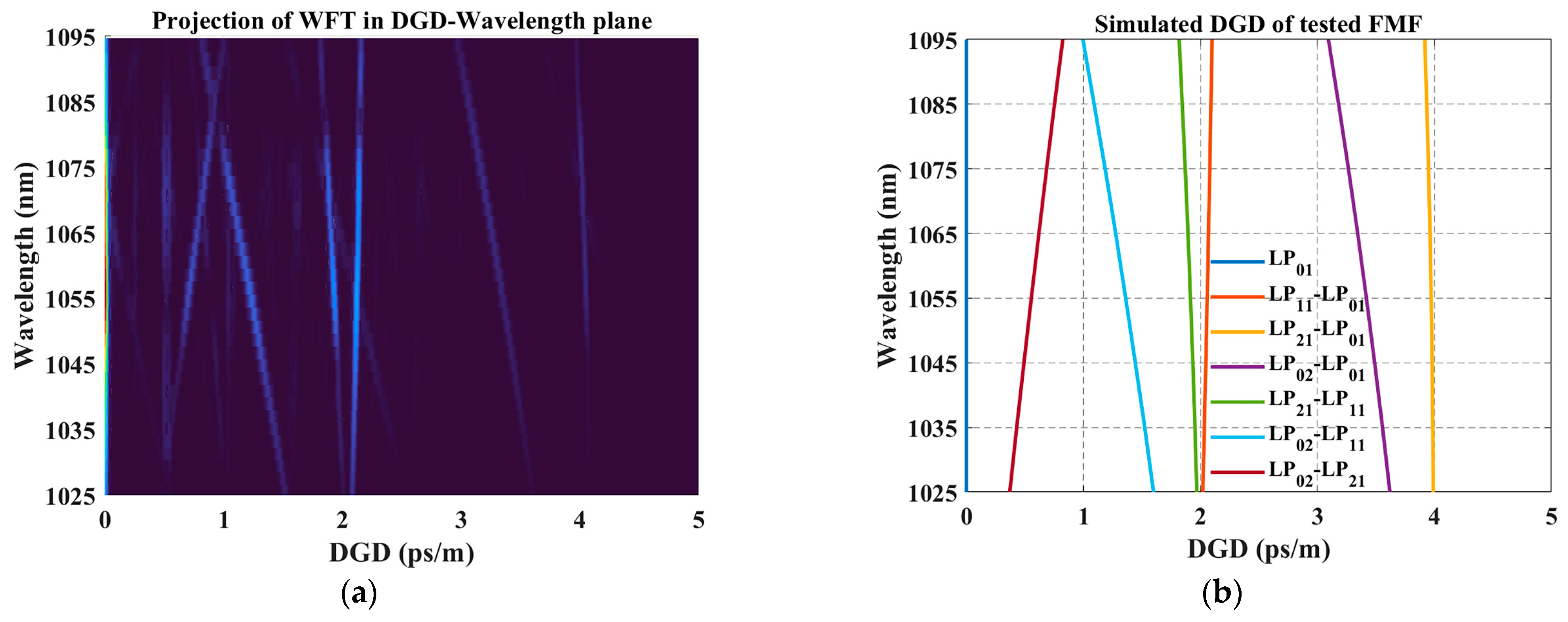
3.2. Characterization of Few-Mode Optical Fiber
4. Discussion
4.1. Noise Background of FT of Spectral Fringes
4.2. DGD Peak Width
4.3. Error Induced in the Optical Path
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, G.F.; Bai, N.; Zhao, N.B.; Xia, C. Space-division multiplexing: The next frontier in optical communication. Adv. Opt. Photonics 2014, 6, 413–487. [Google Scholar] [CrossRef]
- Huang, H.; Milione, G.; Lavery, M.P.J.; Xie, G.D.; Ren, Y.X.; Cao, Y.W.; Ahmed, N.; Nguyen, T.A.; Nolan, D.A.; Li, M.J.; et al. Mode division multiplexing using an orbital angular momentum mode sorter and MIMO-DSP over a graded-index few-mode optical fibre. Sci. Rep. 2015, 5, 14931. [Google Scholar] [CrossRef] [PubMed]
- Rademacher, G.; Ryf, R.; Fontaine, N.K.; Chen, H.S.; Essiambre, R.J.; Puttnam, B.J.; Luis, R.S.; Awaji, Y.; Wada, N.; Gross, S.; et al. Long-Haul Transmission Over Few-Mode Fibers With Space-Division Multiplexing. J. Light. Technol. 2018, 36, 1382–1388. [Google Scholar] [CrossRef]
- Ryf, R.; Randel, S.; Gnauck, A.H.; Bolle, C.; Sierra, A.; Mumtaz, S.; Esmaeelpour, M.; Burrows, E.C.; Essiambre, R.J.; Winzer, P.J.; et al. Mode-Division Multiplexing Over 96 km of Few-Mode Fiber Using Coherent 6 x 6 MIMO Processing. J. Light. Technol. 2012, 30, 521–531. [Google Scholar] [CrossRef]
- Kubota, H.; Morioka, T. Few-mode optical fiber for mode-division multiplexing. Opt. Fiber Technol. 2011, 17, 490–494. [Google Scholar] [CrossRef]
- Ming-Jun, L.; Hoover, B.; Shenping, L.; Bickham, S.; Ten, S.; Ip, E.; Yue-Kai, H.; Mateo, E.; Yin, S.; Ting, W. Low delay and large effective area few-mode fibers for mode-division multiplexing. In Proceedings of the 2012 Opto-Electronics and Communications Conference (OECC) 2012, Busan, Republic of Korea, 2–6 July 2012; pp. 495–496. [Google Scholar] [CrossRef]
- Li, M.J.; Ip, E.; Huang, Y.K. Large effective area FMF with low DMGD. In Proceedings of the IEEE-Photonics-Society Summer Topical Meeting, IEEE, Waikoloa, HI, USA, 8–10 July 2013; p. 86. [Google Scholar]
- Zhang, H.; Zhao, J.; Yang, Z.Q.; Peng, G.J.; Di, Z.X. Low-DMGD, Large-Effective-Area and Low-Bending-Loss 12-LP-Mode Fiber for Mode-Division-Multiplexing. IEEE Photonics J. 2019, 11, 1–8. [Google Scholar] [CrossRef]
- Li, K.M.; Chen, X.; Hurley, J.; Stone, J.; Li, M.J. Measuring modal delays of few-mode fibers using frequency-domain method. Opt. Fiber Technol. 2021, 62, 102474. [Google Scholar] [CrossRef]
- Chen, X.; Hurley, J.E.; Stone, J.S.; Li, M.J. Chromatic Dispersion Measurements of Single-Mode Fibers, Polarization-Maintaining Fibers, and Few-Mode Fibers Using a Frequency Domain Method. Photonics 2023, 10, 215. [Google Scholar] [CrossRef]
- Chen, X.; Li, K.M.; Hurley, J.E.; Li, M.J. Differential mode delay and modal bandwidth measurements of multimode fibers using frequency-domain method. Opt. Fiber Technol. 2022, 72, 102998. [Google Scholar] [CrossRef]
- Cheng, J.; Pedersen, M.E.V.; Wang, K.; Xu, C.; Gruner-Nielsen, L.; Jakobsen, D. Time-domain multimode dispersion measurement in a higher-order-mode fiber. Opt. Lett. 2012, 37, 347–349. [Google Scholar] [CrossRef]
- Liu, F.; Hu, G.J.; Chen, W.C.; Chen, C.G.; Song, C.C.; Chen, J.K. Simultaneous Measurement of MDL and DMGD in FMFs by Analyzing the Rayleigh Backscattering Amplitudes. IEEE Photonics J. 2019, 11, 1–13. [Google Scholar] [CrossRef]
- Veronese, R.; Galtarossa, A.; Palmieri, L. Distributed Characterization of Few-Mode Fibers Based on Optical Frequency Domain Reflectometry. J. Light. Technol. 2020, 38, 4843–4849. [Google Scholar] [CrossRef]
- Dallachiesa, L.; Veronese, R.; Fontaine, N.; Mazur, M.; Chen, H.S.; Ryf, R.; Palmieri, L.; Bigot, M.; Sillard, P. Measurement of Propagation Constants of Graded Index Multi-mode Fiber Using Rayleigh Backscattered Light. In Proceedings of the Optical Fiber Communications Conference and Exhibition (OFC), IEEE, Electr Network, Washington, DC, USA, 6–11 June 2021. [Google Scholar]
- Hamel, P.; Jaouen, Y.; Gabet, R.; Ramachandran, S. Optical low-coherence reflectometry for complete chromatic dispersion characterization of few-mode fibers. Opt. Lett. 2007, 32, 1029–1031. [Google Scholar] [CrossRef]
- Gabet, R.; Le Cren, E.; Jin, C.; Gadonna, M.; Ung, B.; Sillard, P.; Nguyen, H.G.; Jaouen, Y.; Thual, M.; LaRochelle, S. Complete Dispersion Characterization of Few Mode Fibers by OLCI Technique. J. Light. Technol. 2015, 33, 1155–1160. [Google Scholar] [CrossRef]
- Olsson, B.E.; Karlsson, M.; Andrekson, P.A. Polarization mode dispersion measurement using a sagnac interferometer and a comparison with the fixed analyzer method. IEEE Photonics Technol. Lett. 1998, 10, 997–999. [Google Scholar] [CrossRef]
- Yang, Y.H.; Duan, W.Q.; Ye, M. High precision measurement technology for beat length of birefringence optical fiber. Meas. Sci. Technol. 2013, 24, 025201. [Google Scholar] [CrossRef]
- Ou, Z.; Lu, L.; Zhu, X.; Zheng, G.; Li, J.; Liu, Y.; Yue, H.; Dai, Z.; Zhang, L. The research on beat length of polarization maintaining optical fiber with external pressure. Optik 2014, 125, 6058–6062. [Google Scholar] [CrossRef]
- Poole, C.D.; Favin, D.L. Polarization-mode dispersion measurements based on transmission spectra through a polarizer. J. Light. Technol. 1994, 12, 917–929. [Google Scholar] [CrossRef]
- Jian, M.I.; Chunxi, Z.; Zheng, L.I.; Zhanjun, W.U. Measuring the Beatlength of Polarization Maintaining Fiber by Broadband Light Source and Conoscopic Interference. J. Optoelectron. Laser 2006, 17, 1074–1077. [Google Scholar]
- Nicholson, J.W.; Yablon, A.D.; Ramachandran, S.; Ghalmi, S. Spatially and spectrally resolved imaging of modal content in large-mode-area fibers. Opt. Express 2008, 16, 7233–7243. [Google Scholar] [CrossRef]
- Xu, Y.; Ren, G.B.; Jiang, Y.C.; Gao, Y.X.; Li, H.S.; Jin, W.X.; Wu, Y.; Shen, Y.; Jian, S.S. Bending effect characterization of individual higher-order modes in few-mode fibers. Opt. Lett. 2017, 42, 3343–3346. [Google Scholar] [CrossRef]
- Xu, J.S.; Zhao, J.; Xu, T.H. Modified S2 schemes for estimating differential mode group delay in polarization-maintaining few-mode fiber. Opt. Fiber Technol. 2022, 70, 102887. [Google Scholar] [CrossRef]
- Flavin, D.A.; McBride, R.; Jones, J.D.C. Dispersion of birefringence and differential group delay in polarization-maintaining fiber. Opt. Lett. 2002, 27, 1010–1012. [Google Scholar] [CrossRef] [PubMed]
- Tang, F.; Wang, X.Z.; Zhang, Y.; Jing, W. Characterization of birefringence dispersion in polarization-maintaining fibers by use of white-light interferometry. Appl. Opt. 2007, 46, 4073–4080. [Google Scholar] [CrossRef] [PubMed]
- Hlubina, P.; Martynkien, T.; Urbanczyk, W. Dispersion of group and phase modal birefringence in elliptical-core fiber measured by white-light spectral interferometry. Opt. Express 2003, 11, 2793–2798. [Google Scholar] [CrossRef] [PubMed]
- Hlubina, P. White-light spectral interferometry to measure intermodal dispersion in two-mode elliptical-core optical fibres. Opt. Commun. 2003, 218, 283–289. [Google Scholar] [CrossRef]
- Yin, W.H.; Huang, S.J.; Yan, C. Beat length measurement study of few-mode polarization-maintaining fiber based on low coherence off-axis digital holography. Opt. Commun. 2021, 484, 126695. [Google Scholar] [CrossRef]
- Jasapara, J.; Yablon, A.D. Spectrogram approach to S2 fiber mode analysis to distinguish between dispersion and distributed scattering. Opt. Lett. 2012, 37, 3906–3908. [Google Scholar] [CrossRef]
- Nicholson, J.W.; Meng, L.; Fini, J.M.; Windeler, R.S.; DeSantolo, A.; Monberg, E.; DiMarcello, F.; Dulashko, Y.; Hassan, M.; Ortiz, R. Measuring higher-order modes in a low-loss, hollow-core, photonic-bandgap fiber. Opt. Express 2012, 20, 20494–20505. [Google Scholar] [CrossRef]
- Inoue, M.; Ohashi, M.; Kubota, H.; Miyoshi, Y.; Shibata, N. Differential group delay measurements of few-mode fibers using an interferometric technique. IEICE Commun. Express 2020, 9, 330–335. [Google Scholar] [CrossRef]
- Yu, J.X.; Tan, F.Z.; Yu, C.Y. Few-Mode Fiber Characterization System Based on the Spatially and Spectrally Imaging Technique. Sensors 2022, 22, 1809. [Google Scholar] [CrossRef] [PubMed]
- Hlubina, P. Spectral-domain intermodal interference under general measurement conditions. Opt. Commun. 2002, 210, 225–232. [Google Scholar] [CrossRef]
- Dong, F.; Da, F.; Huang, H. Windowed Fourier Transform Profilometry Based on Advanced S-Transform. Acta Opt. Sin. 2012, 32, 0512008. [Google Scholar] [CrossRef]
- Kemao, Q. Windowed Fourier transform for fringe pattern analysis. Appl. Opt. 2004, 43, 2695–2702. [Google Scholar] [CrossRef] [PubMed]
- Noda, J.; Okamoto, K.; Sasaki, Y. Polarization-Maintaining Fibers and Their Applications. J. Light. Technol. 1986, 4, 1071–1089. [Google Scholar] [CrossRef]
- Chau, Y.F.; Yeh, H.H.; Tsai, D.P. Significantly enhanced Birefringence of photonic crystal fiber using rotational binary unit cell in fiber cladding. Jpn. J. Appl. Phys. Part 2—Lett. Express Lett. 2007, 46, L1048–L1051. [Google Scholar] [CrossRef]
- Chau, Y.F.; Liu, C.Y.; Yeh, H.H.; Tsai, D.P. A comparative study of high birefringence and low confinement loss photonic crystal fiber employing elliptical air holes in fiber cladding with tetragonal lattice. Prog. Electromagn. Res. B (USA) 2010, 22, 39–52. [Google Scholar] [CrossRef]
- Okamoto, K.; Edahiro, T.; Shibata, N. Polarization properties of single-polarization fibers. Opt. Lett. 1982, 7, 569–571. [Google Scholar] [CrossRef]
- Gray, D.R.; Sandoghchi, S.R.; Wheeler, N.V.; Baddela, N.K.; Jasion, G.T.; Petrovich, M.N.; Poletti, F.; Richardson, D.J. Accurate calibration of S2 and interferometry based multimode fiber characterization techniques. Opt. Express 2015, 23, 10540–10552. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, C.; Yu, F.; Feng, S.; Yu, C.; Xu, L.; Zhai, R.; Jia, Z.; Hu, L. Application of Crossed Polarizer Method in the Measurement of Differential Group Delay of Optical Fibers. Photonics 2023, 10, 518. https://doi.org/10.3390/photonics10050518
Wu C, Yu F, Feng S, Yu C, Xu L, Zhai R, Jia Z, Hu L. Application of Crossed Polarizer Method in the Measurement of Differential Group Delay of Optical Fibers. Photonics. 2023; 10(5):518. https://doi.org/10.3390/photonics10050518
Chicago/Turabian StyleWu, Cheng, Fei Yu, Suya Feng, Chunlei Yu, Lixin Xu, Ruizhan Zhai, Zhongqing Jia, and Lili Hu. 2023. "Application of Crossed Polarizer Method in the Measurement of Differential Group Delay of Optical Fibers" Photonics 10, no. 5: 518. https://doi.org/10.3390/photonics10050518
APA StyleWu, C., Yu, F., Feng, S., Yu, C., Xu, L., Zhai, R., Jia, Z., & Hu, L. (2023). Application of Crossed Polarizer Method in the Measurement of Differential Group Delay of Optical Fibers. Photonics, 10(5), 518. https://doi.org/10.3390/photonics10050518





