Demonstration of 12.5 Mslot/s 32-PPM Underwater Wireless Optical Communication System with 0.34 Photons/Bit Receiver Sensitivity
Abstract
1. Introduction
2. System Characteristics
2.1. Absorption and Scattering
| Water Types | λ0 [nm] | a [m−1] | b [m−1] | c [m−1] | Lext [m] | Albedo ω0 |
|---|---|---|---|---|---|---|
| Jerlov I | 450 | 0.018 | 0.0038 | 0.022 | 45.87 | 0.17 |
| Jerlov IA | 450 | 0.0221 | 0.00631 | 0.028 | 35.71 | 0.23 |
| Jerlov IB | 450 | 0.0235 | 0.068 | 0.092 | 10.87 | 0.74 |
| Jerlov IC | 450 | 0.105 | 0.514 | 0.619 | 1.62 | 0.83 |
| Jerlov II | 450 | 0.0241 | 0.504 | 0.528 | 1.89 | 0.95 |
| Jerlov III | 450 | 0.0388 | 2.38 | 2.419 | 0.41 | 0.98 |
2.2. Underwater Turbulence
2.3. The Theoretical Analysis of M-PPM Photon-Counting Communication System
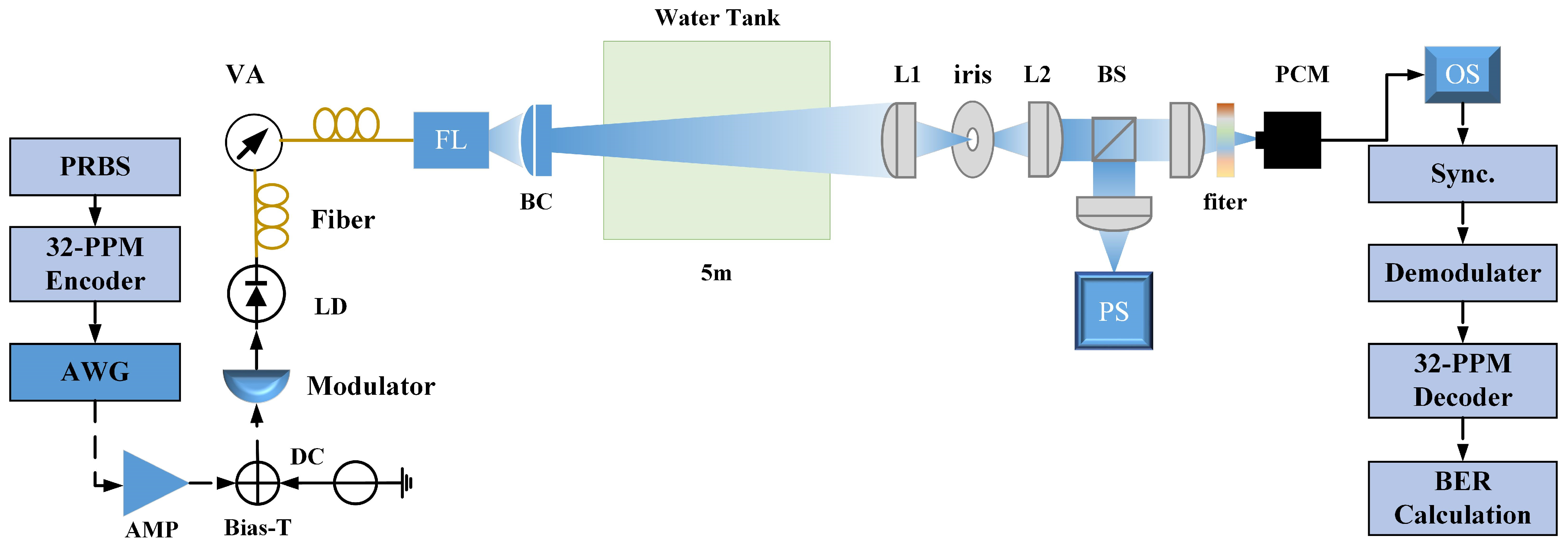
3. Experimental Setup
3.1. LD and Transmitter
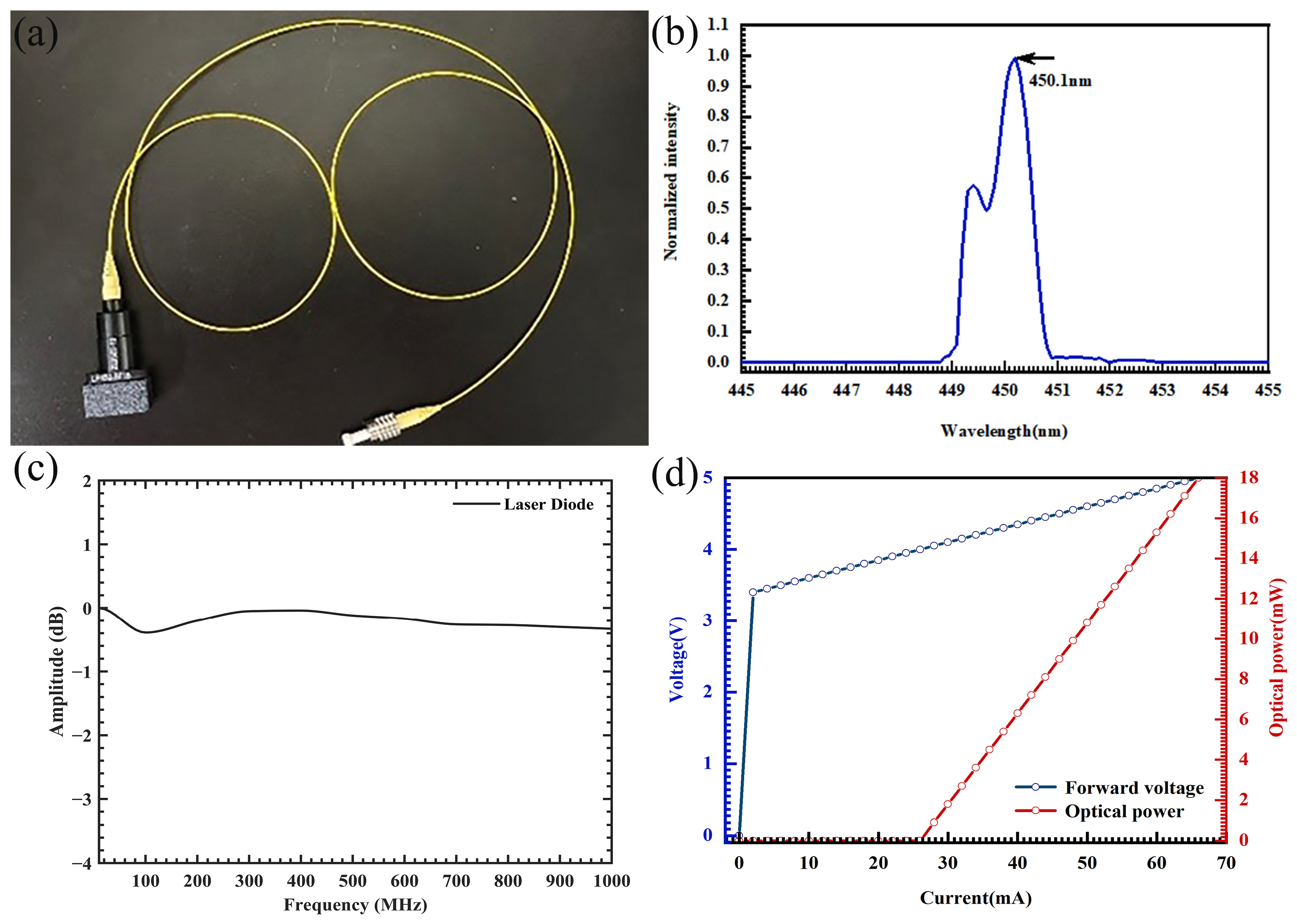
3.1.1. LD Light Source
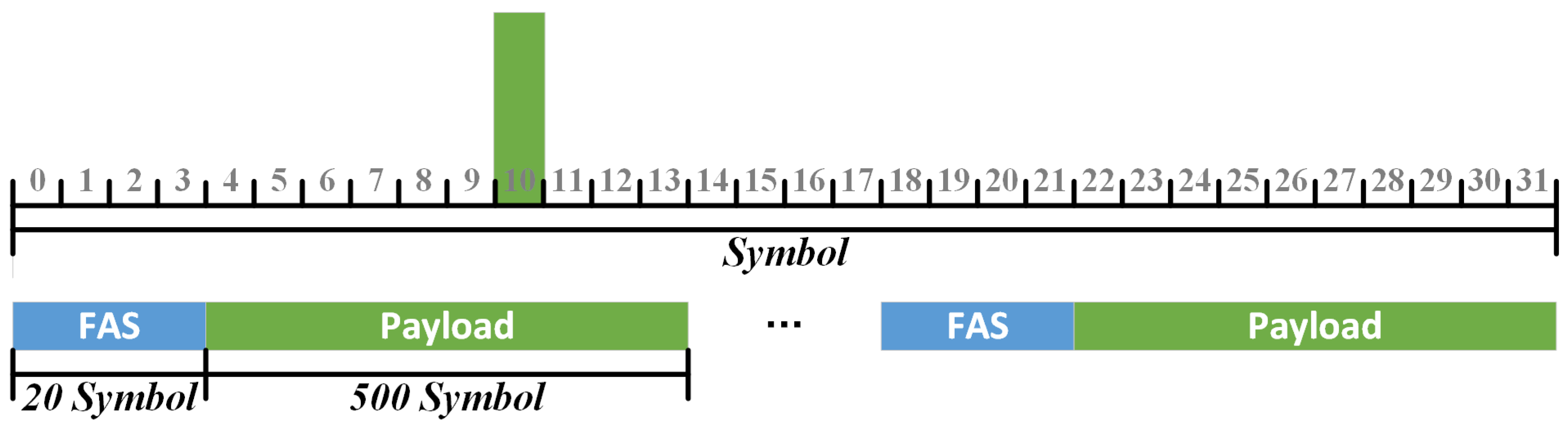
3.1.2. Transmitted Waveform
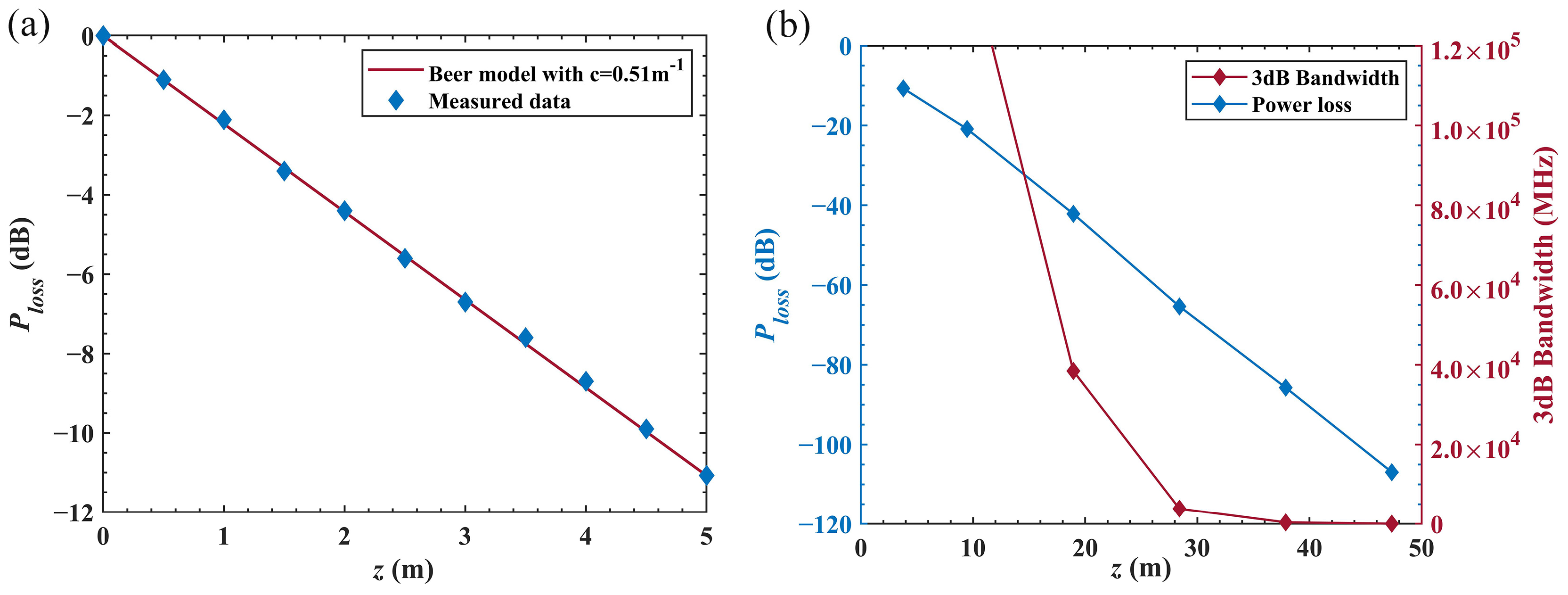
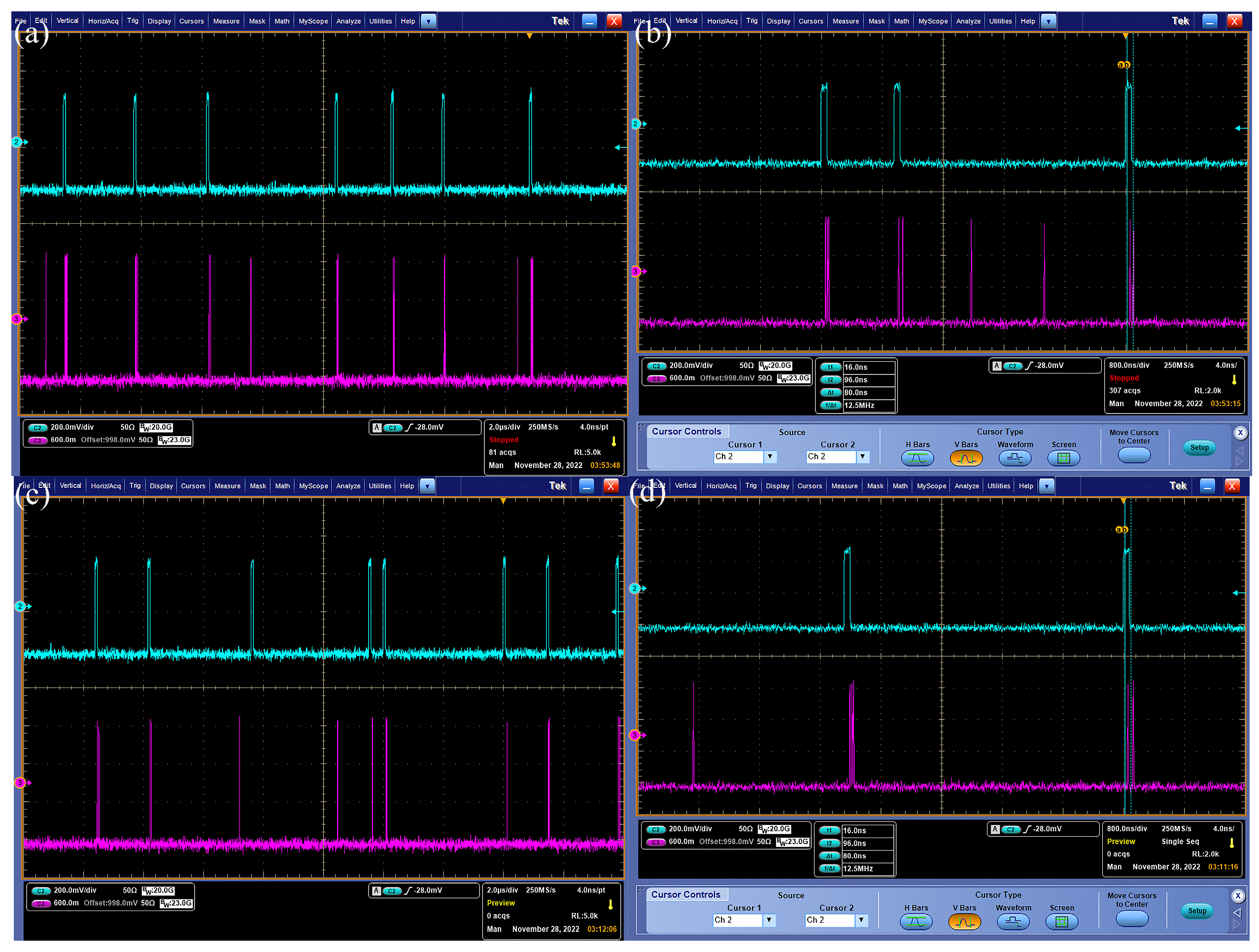
3.2. Underwater Channel Characterization
3.3. Photon Counting with PCM
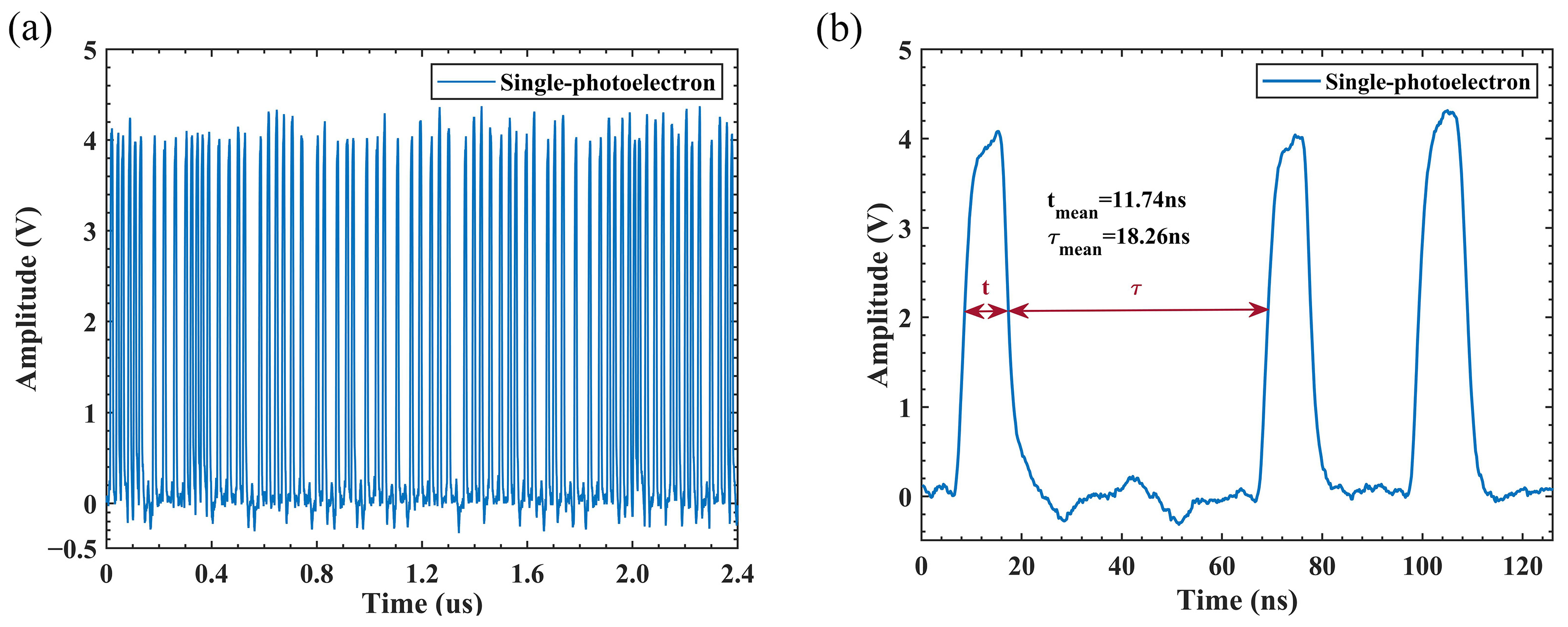
3.3.1. Output Pulse Width and Dead Time
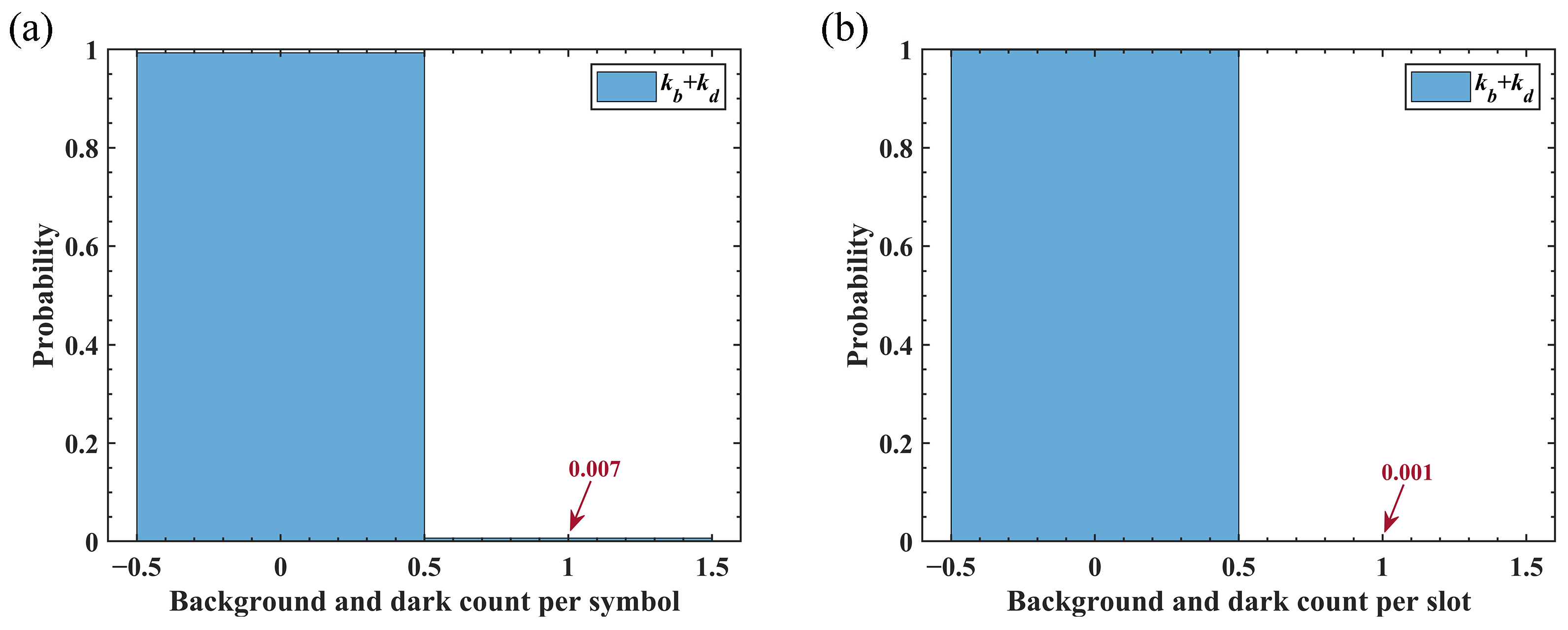
3.3.2. Background and Dark Counts
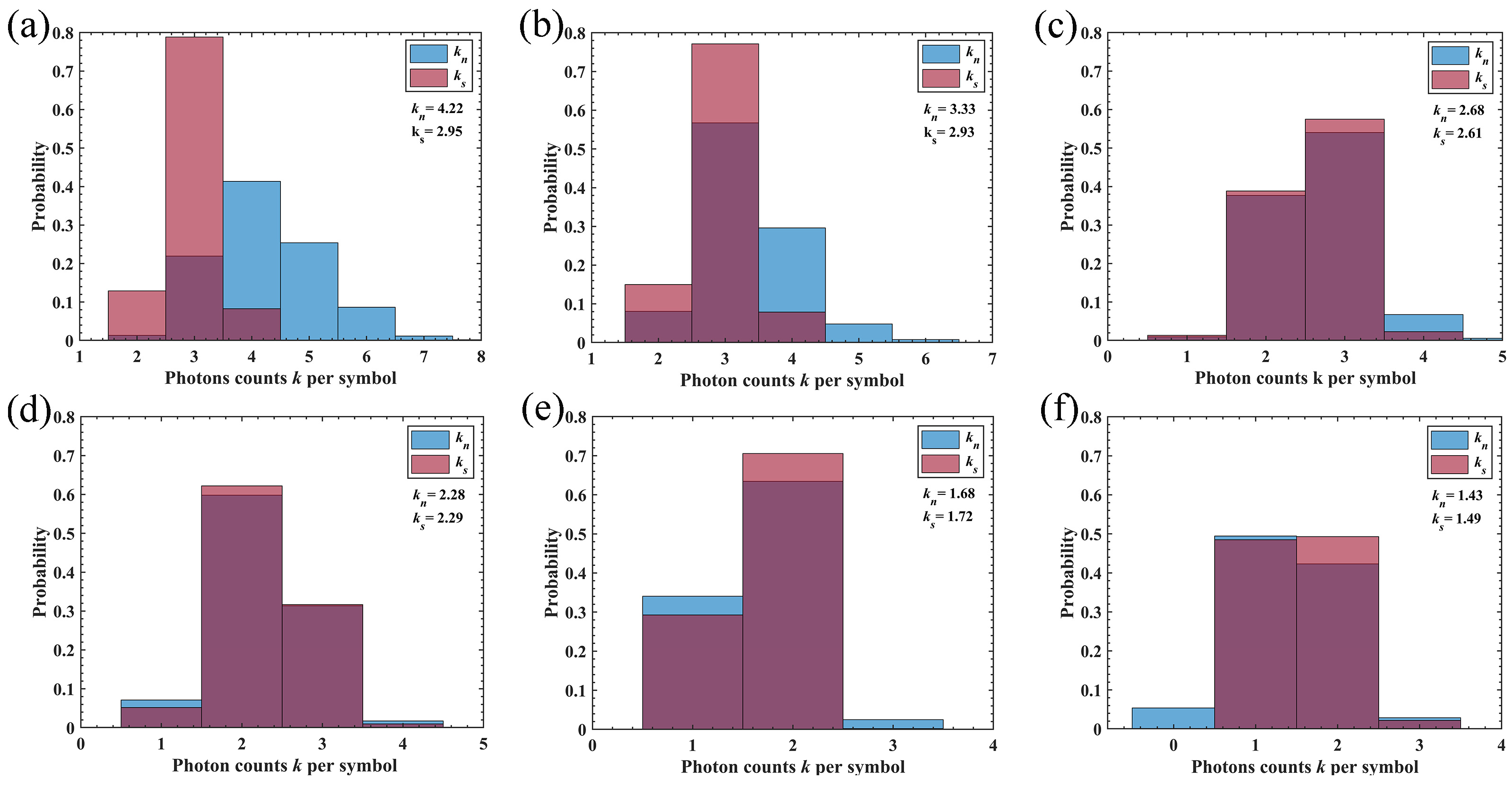
3.3.3. Distribution of Photocounts
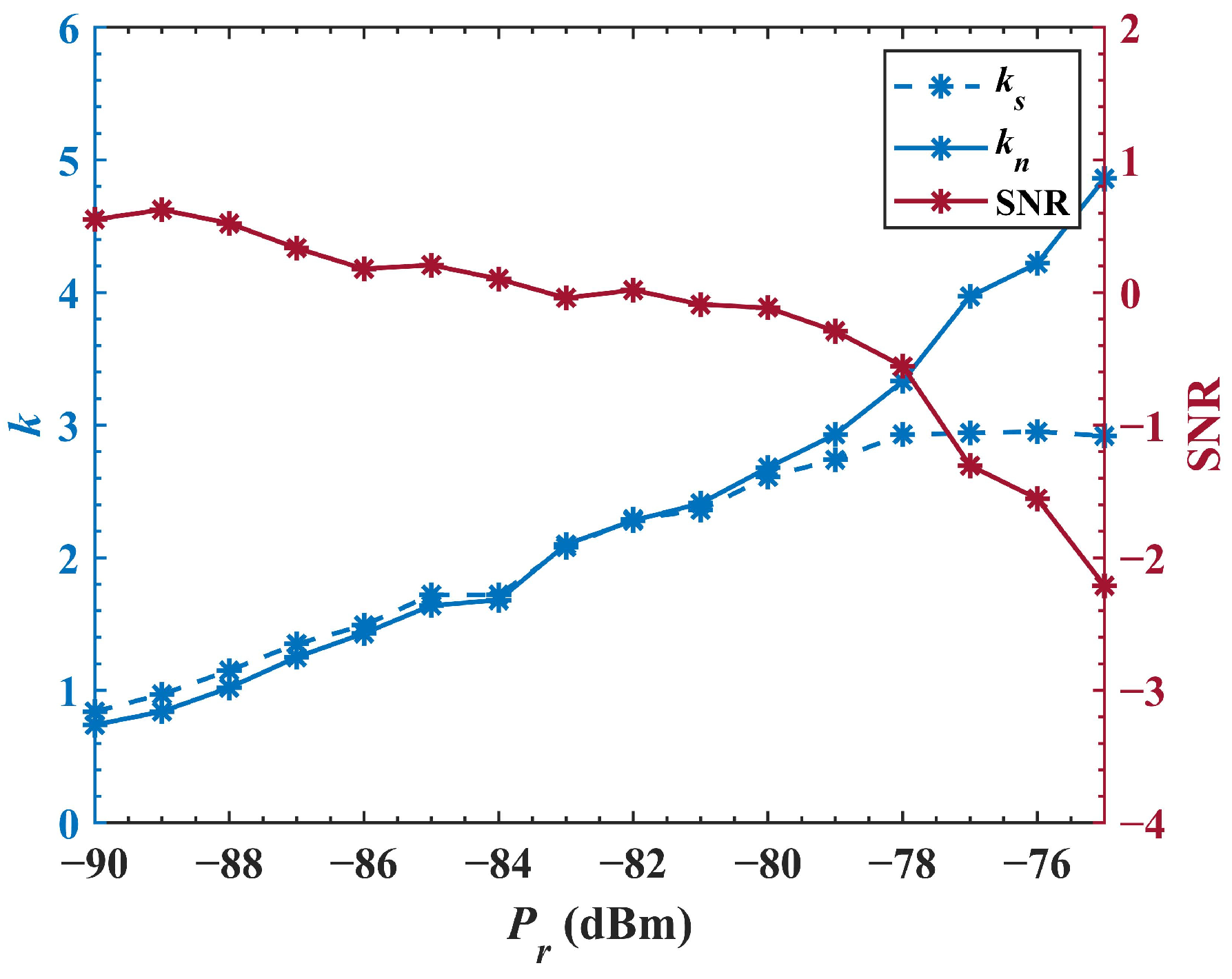
4. Results of the Water Tank Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhu, S.; Chen, X.; Liu, X.; Zhang, G.; Tian, P. Recent progress in and perspectives of underwater wireless optical communication. Prog. Quantum Electron. 2020, 73, 100274. [Google Scholar] [CrossRef]
- Ali, M.A.; Mohideen, S.K.; Vedachalam, N. Current status of underwater wireless communication techniques: A Review. In Proceedings of the 2022 Second International Conference on Advances in Electrical, Computing, Communication and Sustainable Technologies (ICAECT), Bhilai, India, 21–22 April 2022; pp. 1–9. [Google Scholar]
- Ali, M.F.; Jayakody, D.N.K.; Chursin, Y.A.; Affes, S.; Dmitry, S. Recent Advances and Future Directions on Underwater Wireless Communications. Arch. Comput. Methods Eng. 2020, 27, 1379–1412. [Google Scholar] [CrossRef]
- Ooi, B.S.; Kong, M.; Ng, T.K. Underwater wireless optical communications: Opportunity, challenges and future prospects commentary on “Recent progress in and perspectives of underwater wireless optical communication”. Prog. Quantum Electron. 2020, 73, 100275. [Google Scholar] [CrossRef]
- Yan, Z.-Q.; Hu, C.-Q.; Li, Z.-M.; Li, Z.-Y.; Zheng, H.; Jin, X.-M. Underwater photon-inter-correlation optical communication. Photon. Res. 2021, 9, 2360–2368. [Google Scholar] [CrossRef]
- Lin, Z.; Xu, G.; Zhang, Q.; Song, Z. Average symbol error probability and channel capacity of the underwater wireless optical communication systems over oceanic turbulence with pointing error impairments. Opt. Express 2022, 30, 15327–15343. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Cheng, C.; Zhang, C.; Wei, Z.; Wang, L.; Fu, H.Y.; Yang, Y. Net 4 Gb/s underwater optical wireless communication system over 2 m using a single-pixel GaN-based blue mini-LED and linear equalization. Opt. Lett. 2022, 47, 1976–1979. [Google Scholar] [CrossRef] [PubMed]
- Dai, Y.; Chen, X.; Yang, X.; Tong, Z.; Du, Z.; Lyu, W.; Zhang, C.; Zhang, H.; Zou, H.; Cheng, Y.; et al. 200-m/500-Mbps underwater wireless optical communication system utilizing a sparse nonlinear equalizer with a variable step size generalized orthogonal matching pursuit. Opt. Express 2021, 29, 32228–32243. [Google Scholar] [CrossRef]
- Hu, S.; Mi, L.; Zhou, T.; Chen, W. 35.88 attenuation lengths and 3.32 bits/photon underwater optical wireless communication based on photon-counting receiver with 256-PPM. Opt. Express 2018, 26, 21685–21699. [Google Scholar] [CrossRef]
- Abbas, G.L.; Chan, V.W.S.; Yee, T.K. Local-oscillator excess-noise suppression for homodyne and heterodyne detection. Opt. Lett. 1983, 8, 419–421. [Google Scholar] [CrossRef]
- Yuen, H.P.; Chan, V.W.S. Noise in homodyne and heterodyne detection. Opt. Lett. 1983, 8, 177–179. [Google Scholar] [CrossRef]
- Chen, W.; Sun, J.; Hou, X.; Zhu, R.; Hou, P.; Yang, Y.; Gao, M.; Lei, L.; Xie, K.; Huang, M.; et al. 5.12Gbps optical communication link between LEO satellite and ground station. In Proceedings of the 2017 IEEE International Conference on Space Optical Systems and Applications (ICSOS), Naha, Japan, 14–16 November 2017; pp. 260–263. [Google Scholar]
- Huang, J.; Li, C.; Dai, J.; Shu, R.; Zhang, L.; Wang, J. Real-Time and High-Speed Underwater Photon-Counting Communication Based on SPAD and PPM Symbol Synchronization. IEEE Photonics J. 2021, 13, 1–9. [Google Scholar] [CrossRef]
- Zhang, L.; Tang, X.; Sun, C.; Chen, Z.; Li, Z.; Wang, H.; Jiang, R.; Shi, W.; Zhang, A. Over 10 attenuation length gigabits per second underwater wireless optical communication using a silicon photomultiplier (SiPM) based receiver. Opt. Express 2020, 28, 24968–24980. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Ye, D.; Fu, K.; Wang, L.; Piao, J.; Wang, Y. Single-photon detection for MIMO underwater wireless optical communication enabled by arrayed LEDs and SiPMs. Opt. Express 2021, 29, 25922–25944. [Google Scholar] [CrossRef]
- Hemonth, G.R.; Catherine, E.D.; Andrew, S.F.; Igor, D.G.; Farhad, H.; Scott, A.H.; Nicholas, D.H.; John, G.I.; Richard, D.K.; John, D.M.; et al. A Burst-Mode Photon Counting Receiver with Automatic Channel Estimation and Bit Rate Detection; SPIE: San Francisco, CA, USA, 13 April 2016; p. 97390H. [Google Scholar]
- Liu, X.; Yi, S.; Zhou, X.; Fang, Z.; Qiu, Z.-J.; Hu, L.; Cong, C.; Zheng, L.; Liu, R.; Tian, P. 34.5 m underwater optical wireless communication with 2.70 Gbps data rate based on a green laser diode with NRZ-OOK modulation. Opt. Express 2017, 25, 27937–27947. [Google Scholar] [CrossRef]
- Shen, J.; Wang, J.; Chen, X.; Zhang, C.; Kong, M.; Tong, Z.; Xu, J. Towards power-efficient long-reach underwater wireless optical communication using a multi-pixel photon counter. Opt. Express 2018, 26, 23565–23571. [Google Scholar] [CrossRef]
- Wang, J.; Lu, C.; Li, S.; Xu, Z. 100 m/500 Mbps underwater optical wireless communication using an NRZ-OOK modulated 520 nm laser diode. Opt. Express 2019, 27, 12171–12181. [Google Scholar] [CrossRef] [PubMed]
- Tang, X.; Kumar, R.; Sun, C.; Zhang, L.; Chen, Z.; Jiang, R.; Wang, H.; Zhang, A. Towards underwater coherent optical wireless communications using a simplified detection scheme. Opt. Express 2021, 29, 19340–19351. [Google Scholar] [CrossRef] [PubMed]
- Scott, A.H.; Cathy, E.D.; Andrew, S.F.; Igor, D.G.; Farhad, H.; Nicholas, D.H.; Thomas, H.; Nathan, M.; Hemonth, G.R.; Marvin, S.S.; et al. Undersea Narrow-Beam Optical Communications Field Demonstration; SPIE: Anaheim, CA, USA, 22 May 2017; p. 1018606. [Google Scholar]
- Arnon, S.; Kedar, D. Non-line-of-sight underwater optical wireless communication network. J. Opt. Soc. Am. A 2009, 26, 530–539. [Google Scholar] [CrossRef]
- Cox, W.; Muth, J. Simulating channel losses in an underwater optical communication system. J. Opt. Soc. Am. A 2014, 31, 920–934. [Google Scholar] [CrossRef]
- Jiang, R.; Sun, C.; Zhang, L.; Tang, X.; Wang, H.; Zhang, A. Deep Learning Aided Signal Detection for SPAD-Based Underwater Optical Wireless Communications. IEEE Access 2020, 8, 20363–20374. [Google Scholar] [CrossRef]
- Boluda-Ruiz, R.; Rico-Pinazo, P.; Castillo-Vázquez, B.; García-Zambrana, A.; Qaraqe, K. Impulse Response Modeling of Underwater Optical Scattering Channels for Wireless Communication. IEEE Photonics J. 2020, 12, 1–14. [Google Scholar] [CrossRef]
- Zhu, H.; Qiurong, Y.; Zihang, L.; Weihui, D.; Ming, W. Monte Carlo Simulation and Implementation of Underwater Single Photon Communication System; SPIE: Changchun, China, 31 January 2020; p. 1142737. [Google Scholar]
- Henyey, L.G.; Greenstein, J.L. Diffuse radiation in the galaxy. Astrophys. J. 1941, 93, 70–83. [Google Scholar]
- Haltrin, V.I. One-parameter two-term Henyey-Greenstein phase function for light scattering in seawater. Appl. Opt. 2002, 41, 1022–1028. [Google Scholar] [CrossRef]
- Georges, R.F.; Forand, J.L. Analytic Phase Function for Ocean Water; SPIE: Bergen, Norway, 26 October 1994; pp. 194–201. [Google Scholar]
- Georges, R.F.; Miroslaw, J. Computer-Based Underwater Imaging Analysis; SPIE: Denver, CO, USA, 28 October 1999; pp. 62–70. [Google Scholar]
- Mobley, C.D.; Sundman, L.K.; Boss, E. Phase function effects on oceanic light fields. Appl. Opt. 2002, 41, 1035–1050. [Google Scholar] [CrossRef] [PubMed]
- Huber, E.; Frost, M. Light scattering by small particles. J. Water Supply Res. Technol. Aqua 1998, 47, 87–94. [Google Scholar] [CrossRef]
- Solonenko, M.G.; Mobley, C.D. Inherent optical properties of Jerlov water types. Appl. Opt. 2015, 54, 5392–5401. [Google Scholar] [CrossRef]
- Liu, W.; Xu, Z.; Yang, L. SIMO detection schemes for underwater optical wireless communication under turbulence. Photon. Res. 2015, 3, 48–53. [Google Scholar] [CrossRef]
- Andrews, L.C.; Phillips, R.L.; Hopen, C.Y. Laser Beam Scintillation with Applications; SPIE press: Bellingham, WA, USA, 2001; Volume 99. [Google Scholar]
- Vetelino, F.S.; Young, C.; Andrews, L.; Recolons, J. Aperture averaging effects on the probability density of irradiance fluctuations in moderate-to-strong turbulence. Appl. Opt. 2007, 46, 2099–2108. [Google Scholar] [CrossRef] [PubMed]
- Willis, M.M.; Robinson, B.S.; Stevens, M.L.; Romkey, B.R.; Matthews, J.A.; Greco, J.A.; Grein, M.E.; Dauler, E.A.; Kerman, A.J.; Rosenberg, D.; et al. Downlink synchronization for the lunar laser communications demonstration. In Proceedings of the 2011 International Conference on Space Optical Systems and Applications (ICSOS), Santa Monica, CA, USA, 11–13 May 2011; pp. 83–87. [Google Scholar]
- Ghassemlooy, Z.; Popoola, W.O.; Zvanovec, S. Optical Wireless Communications; Springer: New York, NY, USA, 2016; Volume 3, pp. 154–196. [Google Scholar]
- Gagliardi, R.M.; Karp, S. Optical Communications; Wiley-Interscience: New York, NY, USA, 1976; Volume 1. [Google Scholar]
- Sarbazi, E.; Safari, M.; Haas, H. Statistical modeling of single-photon avalanche diode receivers for optical wireless communications. IEEE Trans. Commun. 2018, 66, 4043–4058. [Google Scholar] [CrossRef]
- Sarbazi, E.; Haas, H. Detection statistics and error performance of SPAD-based optical receivers. In Proceedings of the 2015 IEEE 26th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), Hong Kong, China, 30 August–2 September 2015; pp. 830–834. [Google Scholar]
- Petersen, D.P.; Middleton, D. Sampling and reconstruction of wave-number-limited functions in N-dimensional euclidean spaces. Inf. Control 1962, 5, 279–323. [Google Scholar] [CrossRef]
- Hemmati, H. Deep Space Optical Communications; Jet Propulsion Laboratory California Institute of Technology: Pasadena, CA, USA, 2006; Volume 11. [Google Scholar]
- Book, B. Optical Communications Coding and Synchronization; National Aeronautics and Space Administration: Washington, DC, USA, 2019. [Google Scholar]
- Cox, W.C., Jr. Simulation, Modeling, and Design of Underwater Optical Communication Systems. Ph.D. Thesis, North Carolina State University, Raleigh, NC, USA, 2012. [Google Scholar]
- Oubei, H.M. Underwater Wireless Optical Communications Systems: From System-Level Demonstrations to Channel Modeling. Ph.D. Thesis, King Abdullah University of Science and Technology, Thuwal, Kingdom of Saudi Arabia, 2018. [Google Scholar]
- Fletcher, A.; Hardy, N.; Hamilton, S. Propagation Modeling Results for Narrow-Beam Undersea Laser Communications; SPIE LASE: Anaheim, CA, USA, 2016. [Google Scholar]
- Zhang, H.; Dong, Y. Impulse response modeling for general underwater wireless optical MIMO links. IEEE Commun. Mag. 2016, 54, 56–61. [Google Scholar] [CrossRef]
- Migdall, A.; Polyakov, S.V.; Fan, J.; Bienfang, J.C. Single-Photon Generation and Detection: Physics and Applications; Academic Press: Waltham, MA, USA, 2013; Volume 2. [Google Scholar]






| Light Source | Power | Modulation | Detectors | Rate | Received Optical Power | SNR | Received Photons per Bit | References |
|---|---|---|---|---|---|---|---|---|
| 517 nm LD | 100 mW | OOK | PCM | 1.30 Mbps | −84.1 dBm | +20 dB | ~1.0 | [16] |
| 520 nm LD | 19.4 mW | OOK | PD | 2.7 Gbps | −8.24 dBm | +1.8 dB | ~105 | [17] |
| 532 nm SSL | 1.5 W | 256-PPM | PCM | ~12 kbps | −105.04 dBm | +2.5 dB | ~0.33 | [9] |
| 450 nm LD | 174 μW | PPM | MPPC | 5 MHz | −39.19 dBm | +2.1 dB | ~104 | [18] |
| 520 nm LD | 7.3 mW | OOK | PD | 500 Mbps | −19.77 dBm | +2.6 dB | ~105 | [19] |
| 520 nm LD | 10 mW | OOK | SiPM | 1 Gbps | −40.9 dBm | - | ~102 | [14] |
| 532 nm LD | 10 mW | BPSK | SiPM | 500 Mbps | −48.2 dBm | - | ~102 | [20] |
| 450 nm LD | 0.47 mW | 32-PPM | PCM | 1.9 Mbps | −84.0 dBm | +0.1 dB | 0.34 | This work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, X.; Li, P.; Li, G.; Chang, C.; Jia, S.; Xie, Z.; Liao, P.; Nie, W.; Xie, X. Demonstration of 12.5 Mslot/s 32-PPM Underwater Wireless Optical Communication System with 0.34 Photons/Bit Receiver Sensitivity. Photonics 2023, 10, 451. https://doi.org/10.3390/photonics10040451
Han X, Li P, Li G, Chang C, Jia S, Xie Z, Liao P, Nie W, Xie X. Demonstration of 12.5 Mslot/s 32-PPM Underwater Wireless Optical Communication System with 0.34 Photons/Bit Receiver Sensitivity. Photonics. 2023; 10(4):451. https://doi.org/10.3390/photonics10040451
Chicago/Turabian StyleHan, Xiaotian, Peng Li, Guangying Li, Chang Chang, Shuaiwei Jia, Zhuang Xie, Peixuan Liao, Wenchao Nie, and Xiaoping Xie. 2023. "Demonstration of 12.5 Mslot/s 32-PPM Underwater Wireless Optical Communication System with 0.34 Photons/Bit Receiver Sensitivity" Photonics 10, no. 4: 451. https://doi.org/10.3390/photonics10040451
APA StyleHan, X., Li, P., Li, G., Chang, C., Jia, S., Xie, Z., Liao, P., Nie, W., & Xie, X. (2023). Demonstration of 12.5 Mslot/s 32-PPM Underwater Wireless Optical Communication System with 0.34 Photons/Bit Receiver Sensitivity. Photonics, 10(4), 451. https://doi.org/10.3390/photonics10040451




