Topological Charge Measurement of a Partially Coherent Vortex Beam Using Dual Cylindrical Lenses with an Arbitrary Angle
Abstract
1. Introduction
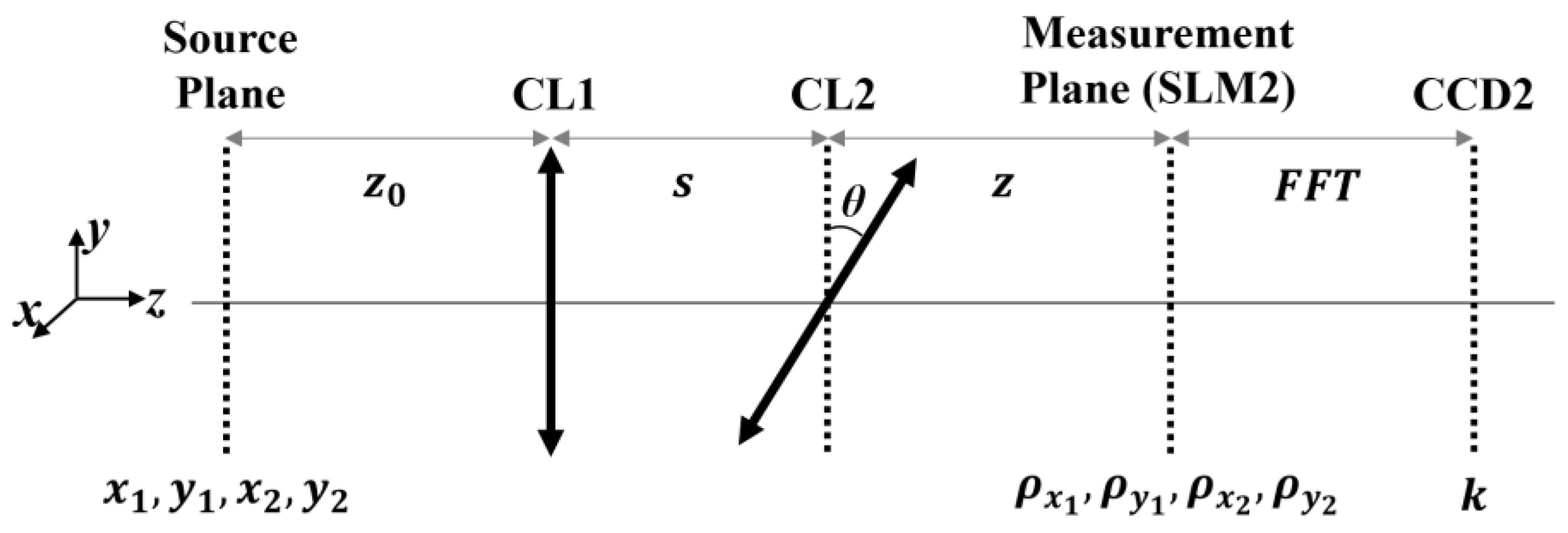
2. Theory
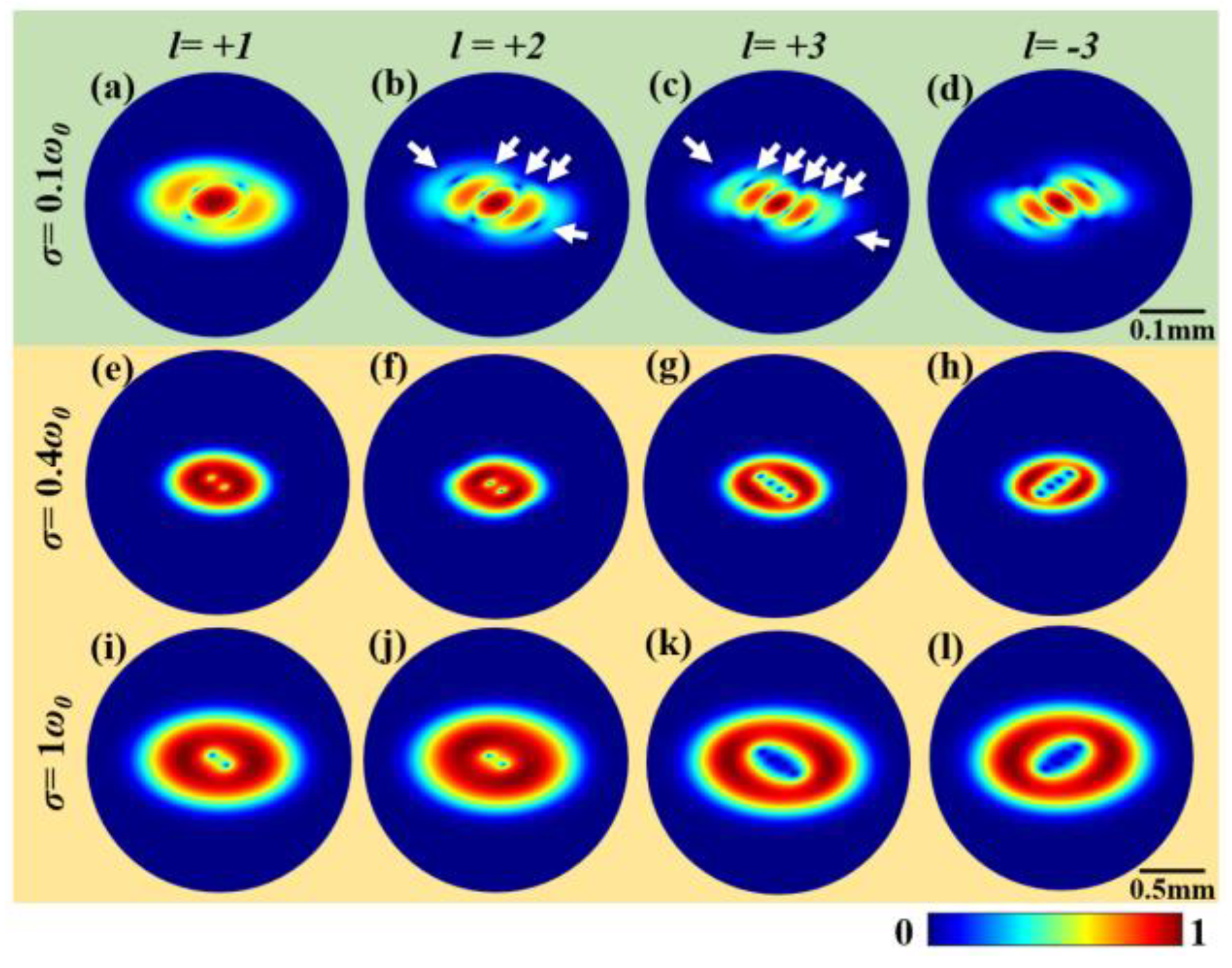
3. Simulation Results
4. Experiment
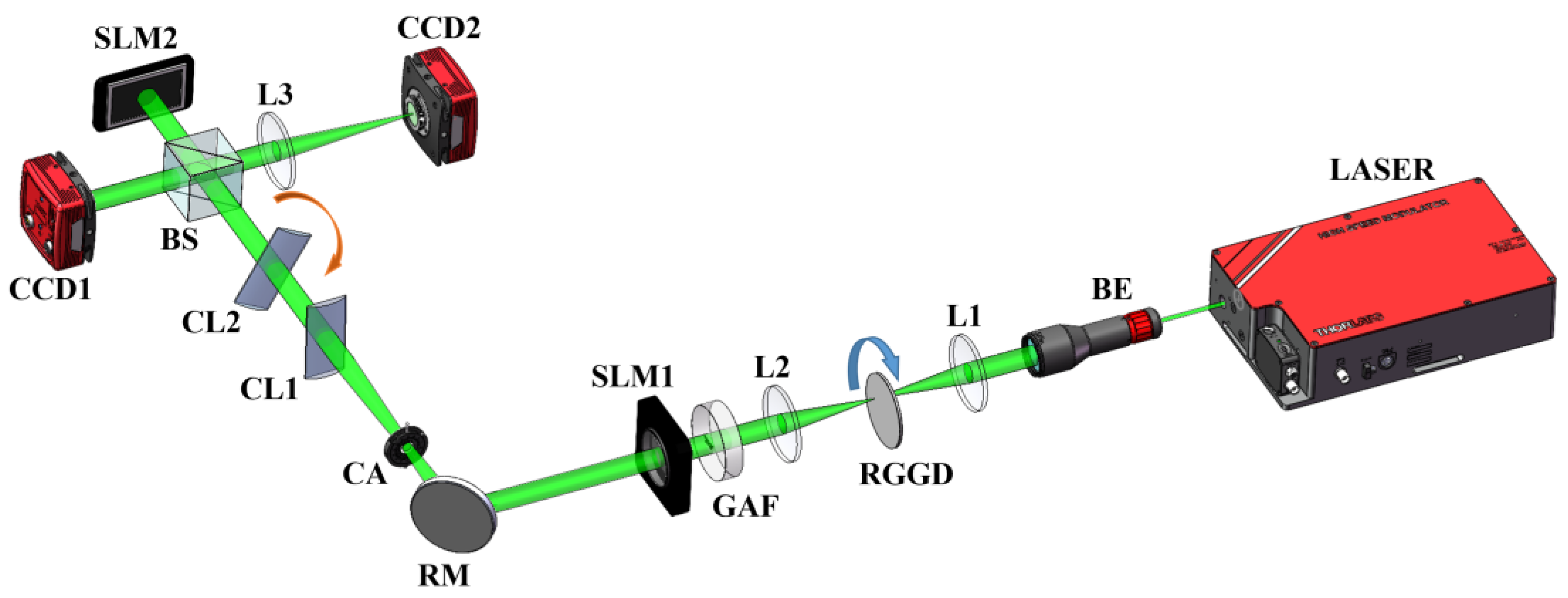
4.1. Experimental Setup
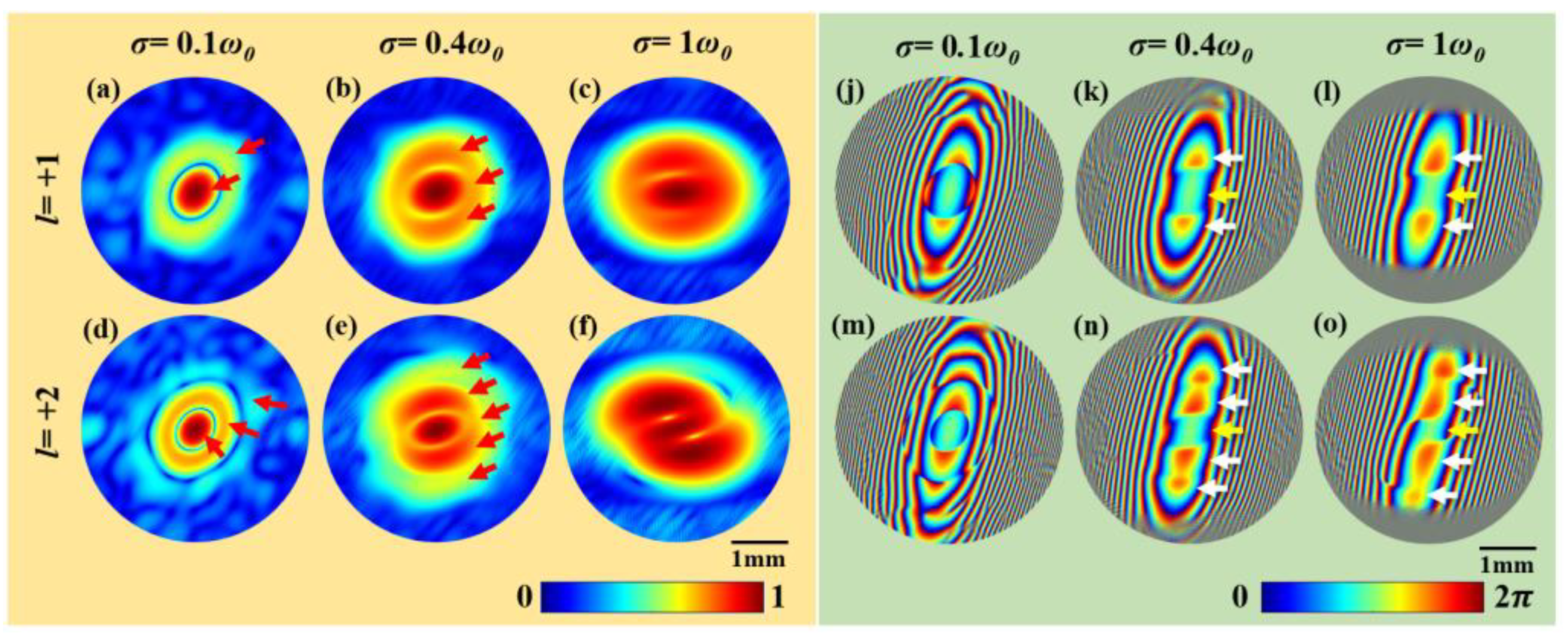
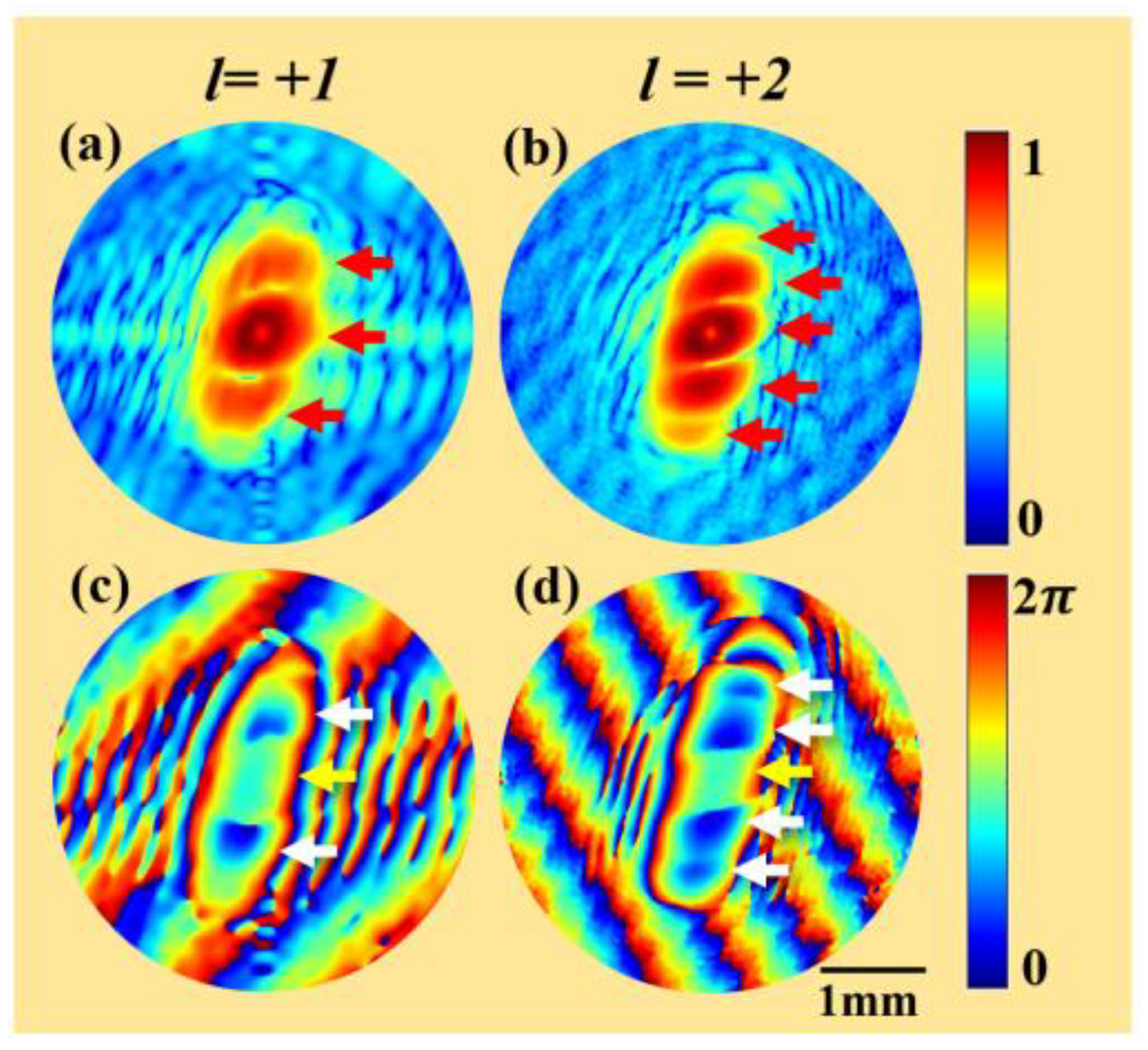
4.2. Experimental Results and Discussions
5. Discussions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Coullet, P.; Gil, L.; Rocca, F. Optical vortices. Opt. Commun. 1989, 73, 403–408. [Google Scholar] [CrossRef]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerd-man, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8196. [Google Scholar] [CrossRef] [PubMed]
- He, H.; Friese, M.E.J.; Heckenberg, N.R.; RubinszteinDunlop, H. Direct Observation of Transfer of Angular Momentum to Absorptive Particles from a Laser Beam with a Phase Singularity. Phys. Rev. Lett. 1995, 75, 826–831. [Google Scholar] [CrossRef] [PubMed]
- Dong, M.; Jiang, D.; Luo, N.; Yang, Y. Trapping two types of Rayleigh particles using a focused partially coherent anomalous vortex beam. Appl. Phys. B Lasers Opt. 2019, 125, 903–907. [Google Scholar] [CrossRef]
- Zhao, C.L.; Cai, Y.J.; Lu, X.H.; Eyyuboğlu, H.T. Radiation force of coherent and partially coherent flat-topped beams on a Rayleigh particle. Opt. Express 2009, 17, 1753–1765. [Google Scholar] [CrossRef]
- Wang, J. Advances in communications using optical vortices. Photonics Research. Photon. Res. 2016, 4, B14–B28. [Google Scholar] [CrossRef]
- Walker, G.; Arnold, A.S.; Franke-Arnold, S. Trans-spectral orbital angular momentum transfer via four-wave mixing in Rb vapor. Phys. Rev. Lett. 2012, 108, 243601. [Google Scholar] [CrossRef]
- Yousif, B.B.; Elsayed, E.E. Performance enhancement of an orbital-angular-momentum-multiplexed free-space optical link under atmospheric turbulence effects using spatial-mode multiplexing and hybrid diversity based on adaptive MIMO equalization. IEEE. Access 2019, 7, 84401–84412. [Google Scholar] [CrossRef]
- Liang, C.; Monfared, Y.E.; Liu, X.; Qi, B.; Wang, F.; Korotkova, O.; Cai, Y. Optimizing illumination’s complex coherence state for overcoming Rayleigh’s resolution limit. Chin. Opt. Lett. 2021, 19, 052601. [Google Scholar] [CrossRef]
- Willig, K.I.; Rizzoli, S.O.; Westphal, V.; Jahn, R.; Hell, S.W. STED microscopy reveals that synaptotagmin remains clustered after synaptic vesicle exocytosis. Nature 2006, 440, 935–939. [Google Scholar] [CrossRef]
- Wang, B.; Tanksalvala, M.; Zhang, Z.; Esashi, Y.; Jenkins, N.W.; Murnane, M.M.; Henry, C.K.; Liao, C.T. Coherent Fourier Scatterometry Using Orbital Angular Momentum Beams for Defect Detection. Opt. Express 2021, 29, 3342–3358. [Google Scholar] [CrossRef]
- McCarter, M.R.; Saleheen, A.I.; Singh, A.; Tumbleson, R.; Woods, J.S.; Tremsin, A.S.; Lance, E.D.L.; Hastings, J.T.; Morley, S.A.; Roy, S. Antiferromagnetic real-space configuration probed by dichroism in scattered X-ray beams with orbital angular momentum. Phys. Rev. B. 2023, 107, L060407. [Google Scholar] [CrossRef]
- Tamburini, F.; Thidé, B.; Della Valle, M. Measurement of the spin of the M87 black hole from its observed twisted light. Mon. Not. R. Astron. Soc. Lett. 2020, 492, 22–27. [Google Scholar] [CrossRef]
- Wang, B.; Brooks, N.J.; Johnsen, P.C.; Jenkins, N.W.; Esashi, Y.; Binnie, I.; Tanksalvala, M.; Kapteyn, H.C.; Murnane, M.M. High-fidelity ptychographic imaging of highly periodic structures enabled by vortex high harmonic beams. arXiv 2023, arXiv:2301.05563. [Google Scholar]
- Liu, X.; Shen, Y.; Liu, L.; Wang, F.; Cai, Y. Experimental demonstration of vortex phase-induced reduction in scintillation of a partially coherent beam. Opt. Lett. 2013, 38, 5323–5326. [Google Scholar] [CrossRef]
- Gori, F.; Santarsiero, M.; Borghi, R.; Vicalvi, S. Partially coherent sources with helicoidal modes. J. Mod. Opt. 1998, 45, 539–554. [Google Scholar] [CrossRef]
- Dogariu, A.; Amarande, S. Propagation of partially coherent beams: Turbulence-induced degradation. Opt. Lett. 2003, 28, 10–12. [Google Scholar] [CrossRef]
- Ge, D.; Cai, Y.; Lin, Q. Partially coherent flat-topped beam and its propagation. Appl. Opt. 2004, 43, 4732–4738. [Google Scholar] [CrossRef]
- Ricklin, J.C.; Davidson, F.M. Atmospheric turbulence effects on a partially coherent Gaussian beam: Implication for free-space laser communication. J. Opt. Soc. Am. A 2002, 19, 1794–1802. [Google Scholar] [CrossRef]
- Peng, X.; Lu, X.; Liu, X.; Zhao, C.; Lin, R.; Liu, L.; Cai, Y. Generation and Propagation of a Hermite-Gaussian Correlated Schell-Model LG0l Beam. Appl. Sci. 2019, 9, 610. [Google Scholar] [CrossRef]
- Cai, Y.; Chen, Y.; Wang, F. Generation and propagation of partially coherent beams with nonconventional correlation functions: A review. J. Opt. Soc. Am. A 2014, 31, 2083–2096. [Google Scholar] [CrossRef] [PubMed]
- Kovalev, A.A.; Kotlyar, V.V.; Nalimov, A.G. Topological charge and asymptotic phase invariants of vortex laser beams. Photonics 2021, 8, 445. [Google Scholar] [CrossRef]
- Lan, B.; Liu, C.; Rui, D.; Chen, M.; Shen, F.; Xian, H. The topological charge measurement of the vortex beam based on dislocation self-reference interferometry. Phys. Scr. 2019, 94, 055502. [Google Scholar] [CrossRef]
- Kovalev, A.A.; Kotlyar, V.V.; Kozlova, E.S.; Butt, M.A. Dividing the Topological Charge of a Laguerre–Gaussian Beam by 2 Using an Off-Axis Gaussian Beam. Micromachines 2022, 13, 1709. [Google Scholar] [CrossRef] [PubMed]
- Stoklasa, B.; Motka, L.; Rehacek, J.; Hradil, Z.; Sánchez-Soto, L.L. Wavefront sensing reveals optical coherence. Nat. Commun. 2014, 5, 3275. [Google Scholar] [CrossRef]
- Vaughan, J.M.; Willetts, D.V. Interference properties of a light beam having a helical wave surface. Opt. Commun. 1979, 30, 263–267. [Google Scholar] [CrossRef]
- Brandao, P.A.; Cavalcanti, S.B. Topological charge identification of partially coherent light diffracted by a triangular aperture. Phys. Lett. A 2016, 380, 4013–4017. [Google Scholar] [CrossRef]
- Berkhout, G.C.G.; Beijersbergen, M.W. Method for probing the orbital angular momentum of optical vortices in electromagnetic waves from astronomical objects. Phys. Rev. Lett. 2008, 101, 100801. [Google Scholar] [CrossRef]
- Mourka, A.; Baumgartl, J.; Shanor, C.; Dholakia, K.; Wright, E.M. Visualization of the birth of an optical vortex using diffraction from a triangular aperture. Opt. Express 2011, 19, 5760–5771. [Google Scholar] [CrossRef]
- Esashi, Y.; Liao, C.T.; Wang, B.; Brooks, N.; Dorney, K.M.; Hernández-García, C.; Kapteyn, H.; Adams, D.; Murnane, M. Ptychographic amplitude and phase reconstruction of bichromatic vortex beams. Opt. Express 2018, 26, 34007–34015. [Google Scholar] [CrossRef]
- Dong, M.; Lu, X.Y.; Zhao, C.; Cai, Y.; Yang, Y. Measuring topological charge of partially coherent elegant Laguerre-Gaussian beam. Opt. Express 2018, 26, 33035–33043. [Google Scholar] [CrossRef]
- Chen, J.; Liu, X.; Yu, J.; Cai, Y. Simultaneous determination of the sign and the magnitude of the topological charge of a partially coherent vortex beam. Appl. Phys. B 2016, 122, 201. [Google Scholar] [CrossRef]
- Lu, X.; Zhao, C.; Shao, Y.; Zeng, J.; Konijnenberg, S.; Zhu, X.; Popov, S.; Urbach, H.P.; Cai, Y. Phase detection of coherence singularities and determination of the topological charge of a partially coherent vortex beam. Appl. Phys. Lett. 2019, 114, 201106. [Google Scholar] [CrossRef]
- Chen, T.; Lu, X.; Zeng, J.; Wang, Z.; Zhang, H.; Zhao, C.; Hoenders, B.J.; Cai, Y. Young’s double-slit experiment with a partially coherent vortex beam. Opt. Express 2020, 28, 38106–38114. [Google Scholar] [CrossRef]
- Denisenko, V.; Shvedov, V.; Desyatnikov, A.S.; Neshev, D.N.; Krolikowski, W.; Volyar, A.; Soskin, M.; Kivshar, Y.S. Determination of topological charges of polychromatic optical vortices. Opt. Express 2009, 17, 23374–23379. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Kovalev, A.A.; Porfirev, A.P. Astigmatic transforms of an optical vortex for measurement of its topological charge. Appl. Opt. 2017, 56, 4095–4104. [Google Scholar] [CrossRef]
- Wang, F.; Cai, Y.; Korotkova, O. Partially coherent standard and elegant Laguerre-Gaussian beams of all orders. Opt. Express 2009, 17, 22366–22379. [Google Scholar] [CrossRef]
- Lin, Q.; Cai, Y. Tensor ABCD law for partially coherent twisted anisotropic Gaussian–Schell model beams. Opt. Lett. 2002, 27, 216–218. [Google Scholar] [CrossRef]
- Tong, R.; Dong, Z.; Chen, Y.; Wang, F.; Cai, Y.; Setälä, T. Fast calculation of tightly focused random electromagnetic beams: Controlling the focal field by spatial coherence. Opt. Express 2020, 28, 9713–9727. [Google Scholar] [CrossRef]
- Shao, Y.; Lu, X.; Sander, K.; Zhao, C.; Cai, Y.; Paul, U.H. Spatial coherence measurement and partially coherent diffractive imaging using self-referencing holography. Opt. Express 2018, 26, 4479–4490. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, X.; Wang, Z.; Lu, X.; Zhao, C.; Cai, Y. Topological Charge Measurement of a Partially Coherent Vortex Beam Using Dual Cylindrical Lenses with an Arbitrary Angle. Photonics 2023, 10, 444. https://doi.org/10.3390/photonics10040444
Lu X, Wang Z, Lu X, Zhao C, Cai Y. Topological Charge Measurement of a Partially Coherent Vortex Beam Using Dual Cylindrical Lenses with an Arbitrary Angle. Photonics. 2023; 10(4):444. https://doi.org/10.3390/photonics10040444
Chicago/Turabian StyleLu, Xiaotan, Zhuoyi Wang, Xingyuan Lu, Chengliang Zhao, and Yangjian Cai. 2023. "Topological Charge Measurement of a Partially Coherent Vortex Beam Using Dual Cylindrical Lenses with an Arbitrary Angle" Photonics 10, no. 4: 444. https://doi.org/10.3390/photonics10040444
APA StyleLu, X., Wang, Z., Lu, X., Zhao, C., & Cai, Y. (2023). Topological Charge Measurement of a Partially Coherent Vortex Beam Using Dual Cylindrical Lenses with an Arbitrary Angle. Photonics, 10(4), 444. https://doi.org/10.3390/photonics10040444





