Generation, Topological Charge, and Orbital Angular Momentum of Off-Axis Double Vortex Beams
Abstract
1. Introduction
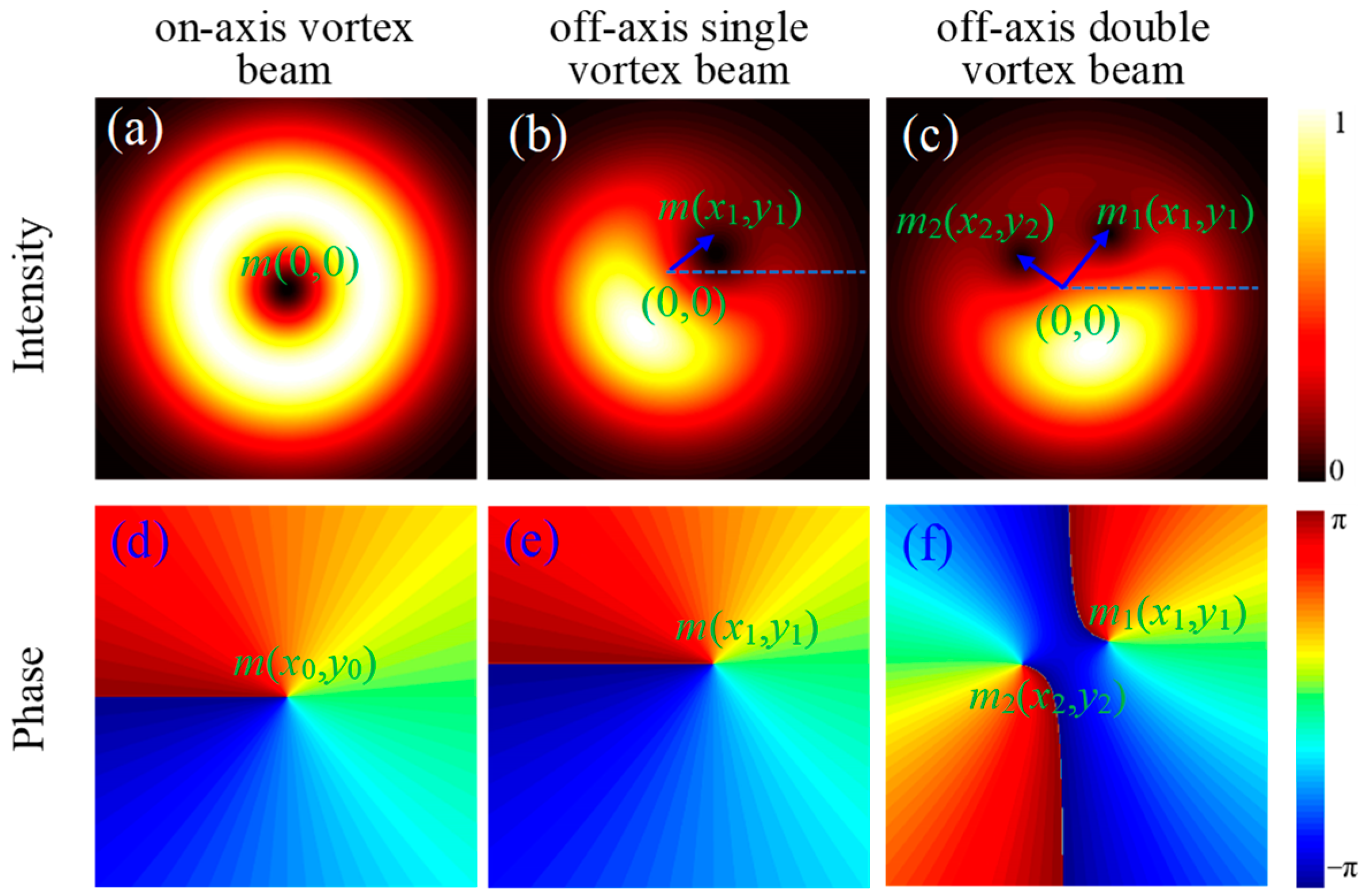
2. Generation of Off-Axis Double Vortex Beams
2.1. Mathematical Description
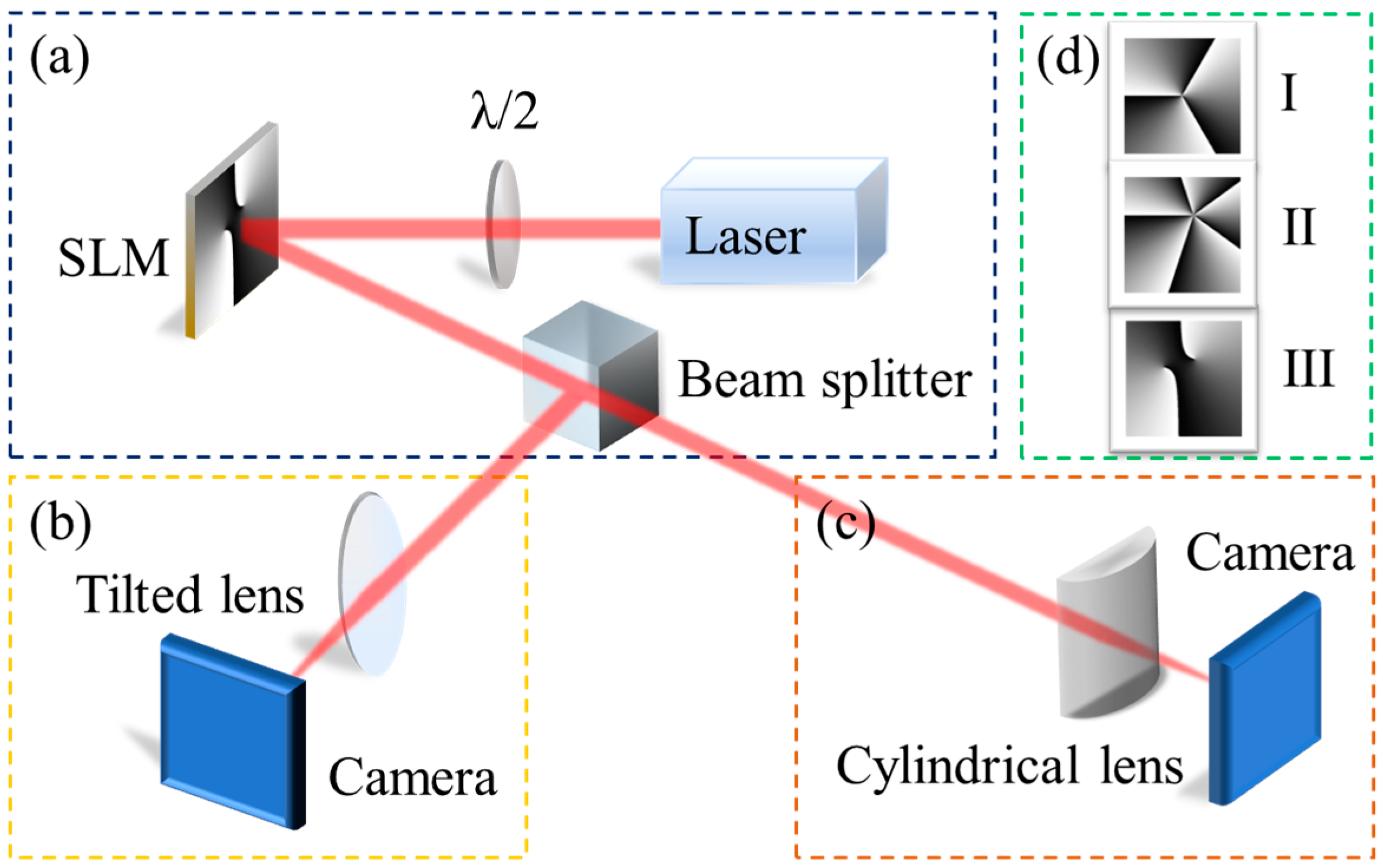
2.2. Experimental Arrangement
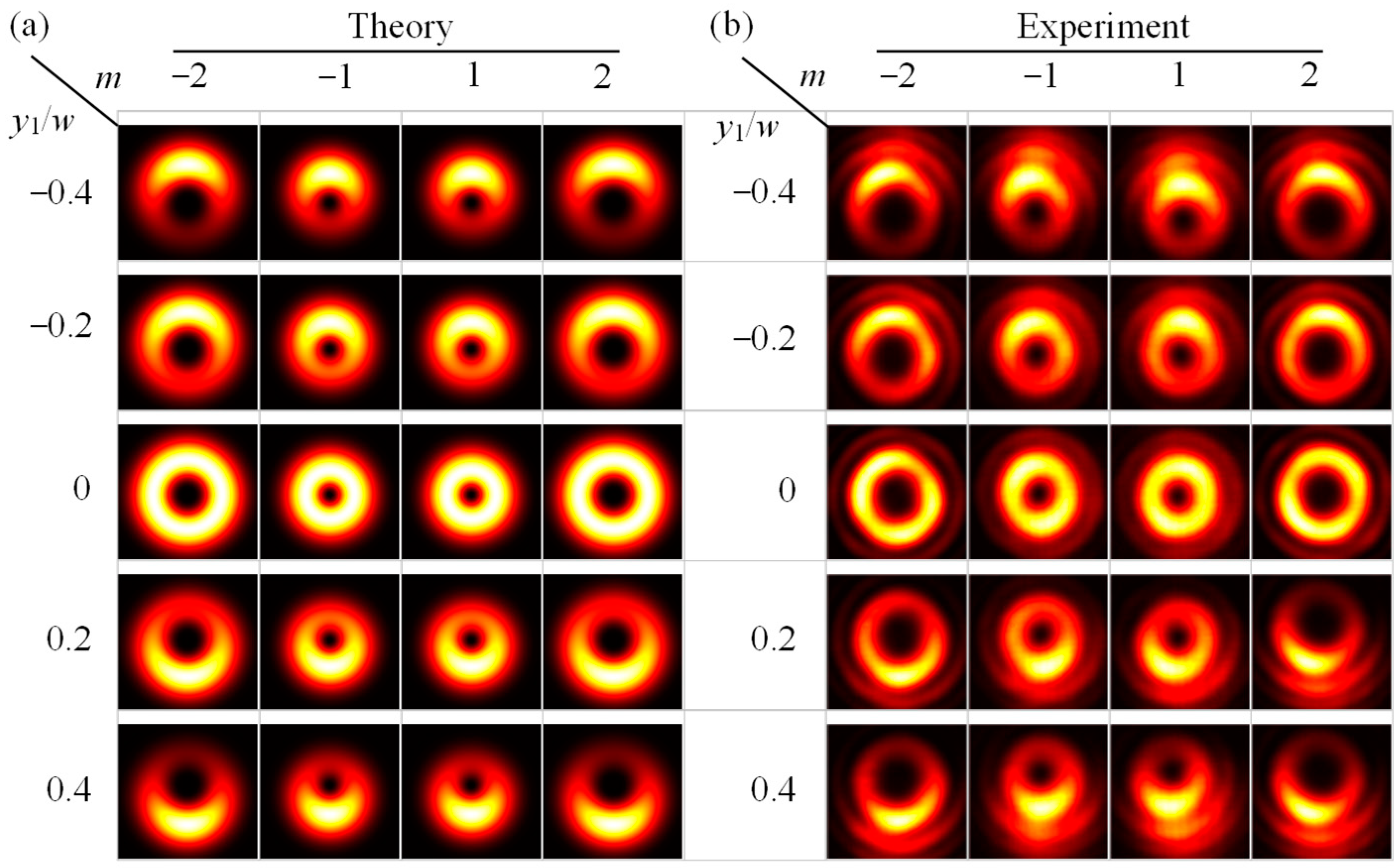
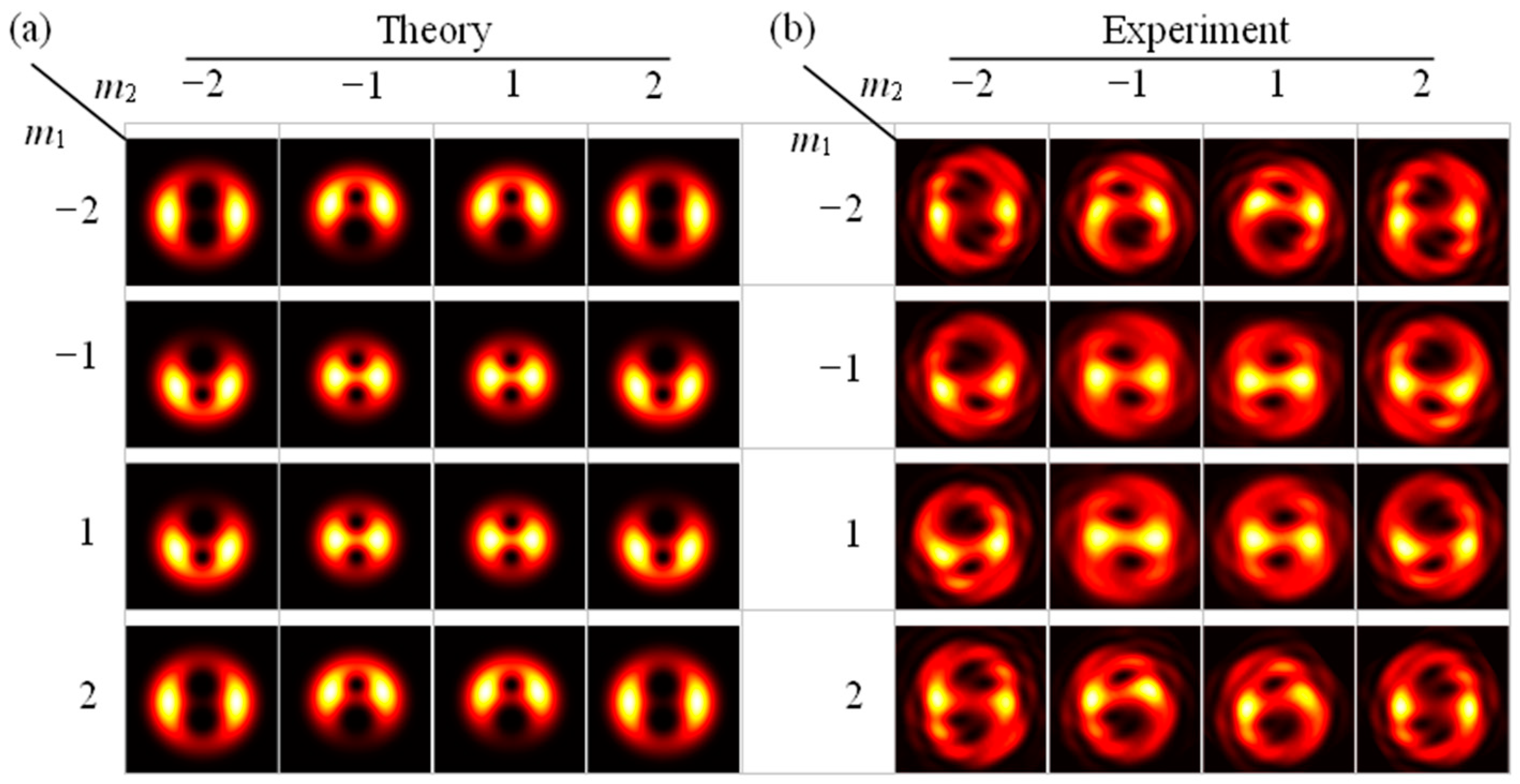
2.3. Results and Discussion
3. TCs of Off-Axis Double Vortex Beams
3.1. Calculation of the TC
3.2. Electric Field of the Off-Axis Vortex Beam Focused by a Tilted Convex Lens
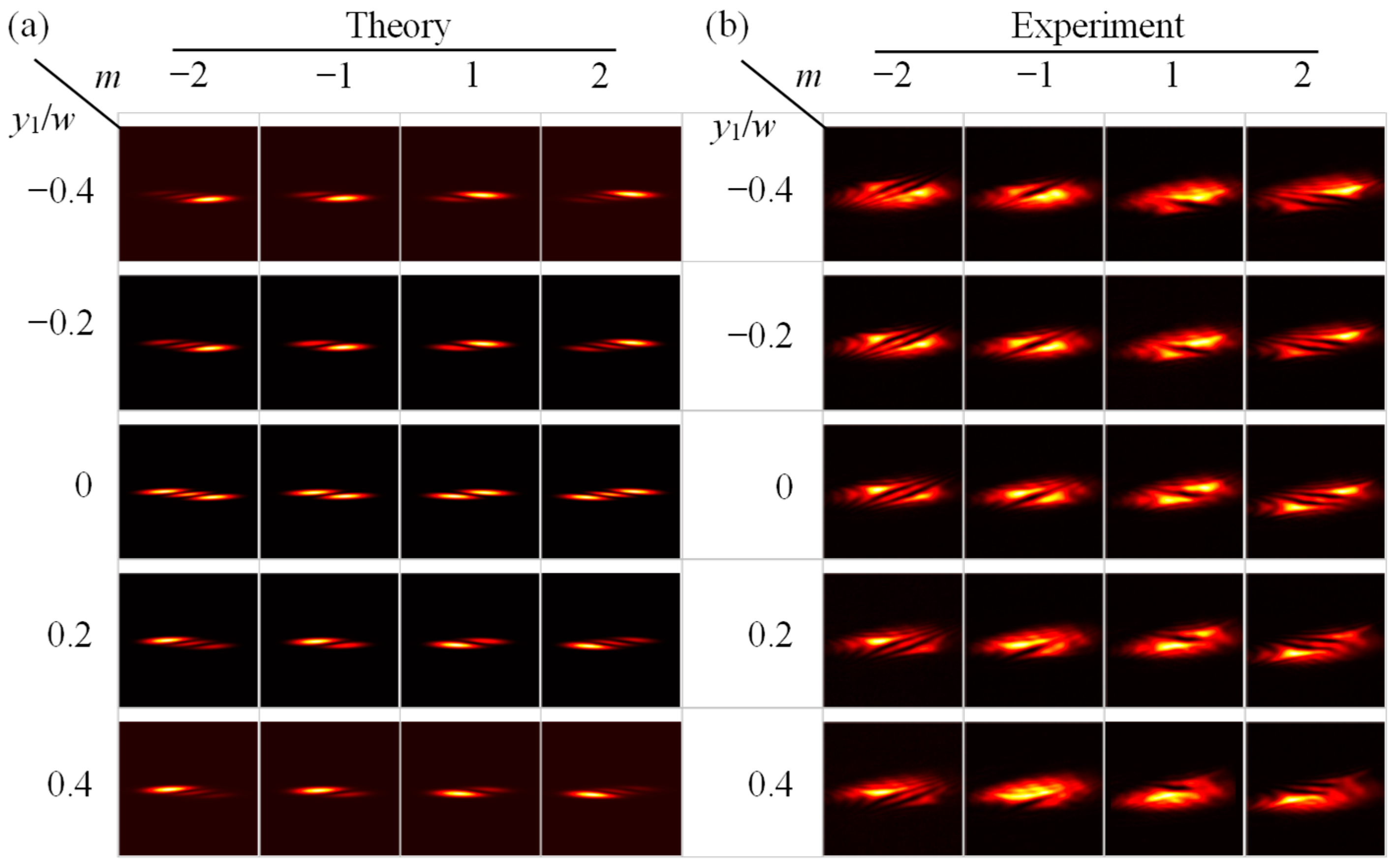
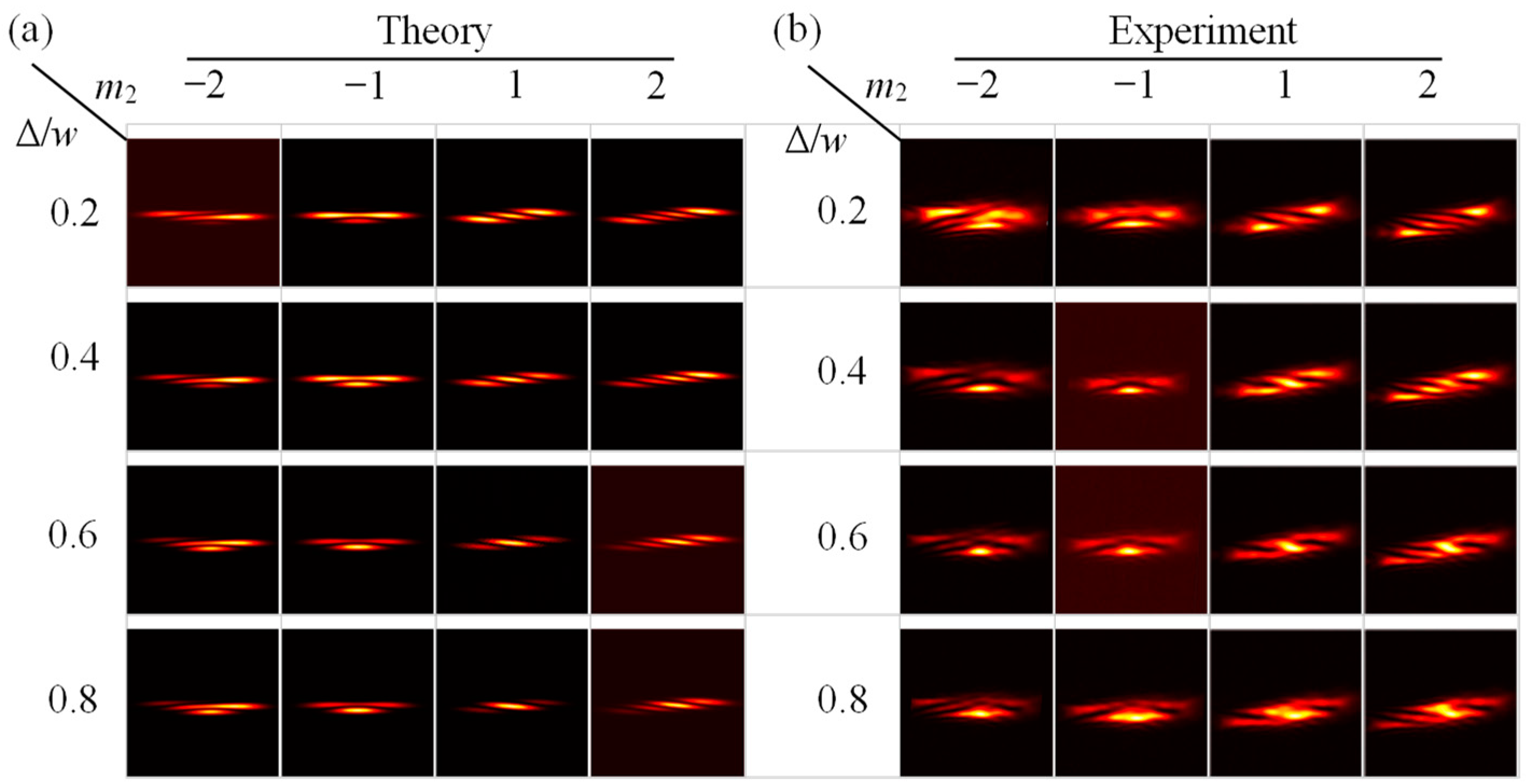
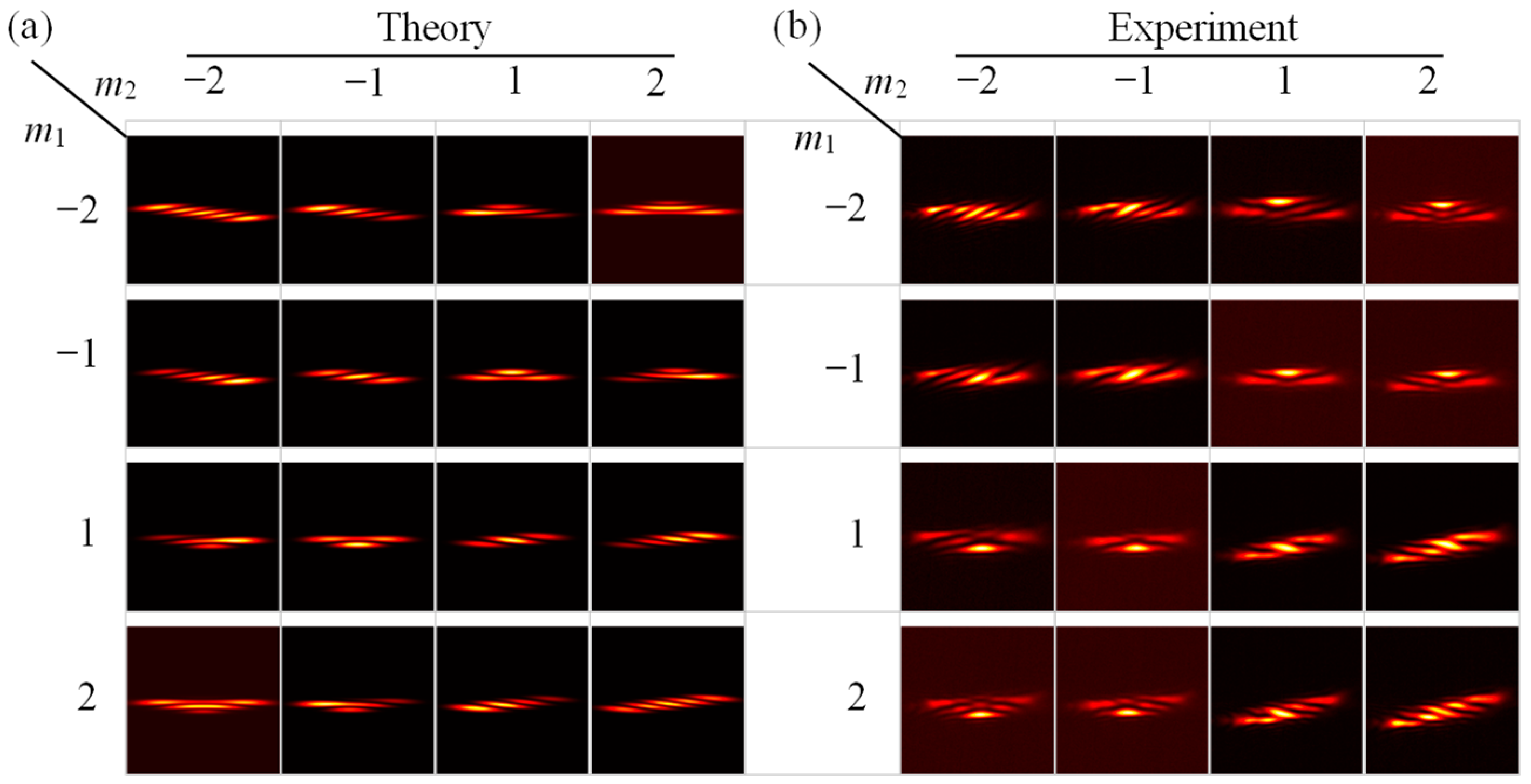
3.3. Detection of the TC
4. OAM of Off-Axis Double Vortex Beams
4.1. OAM Density and Average OAM
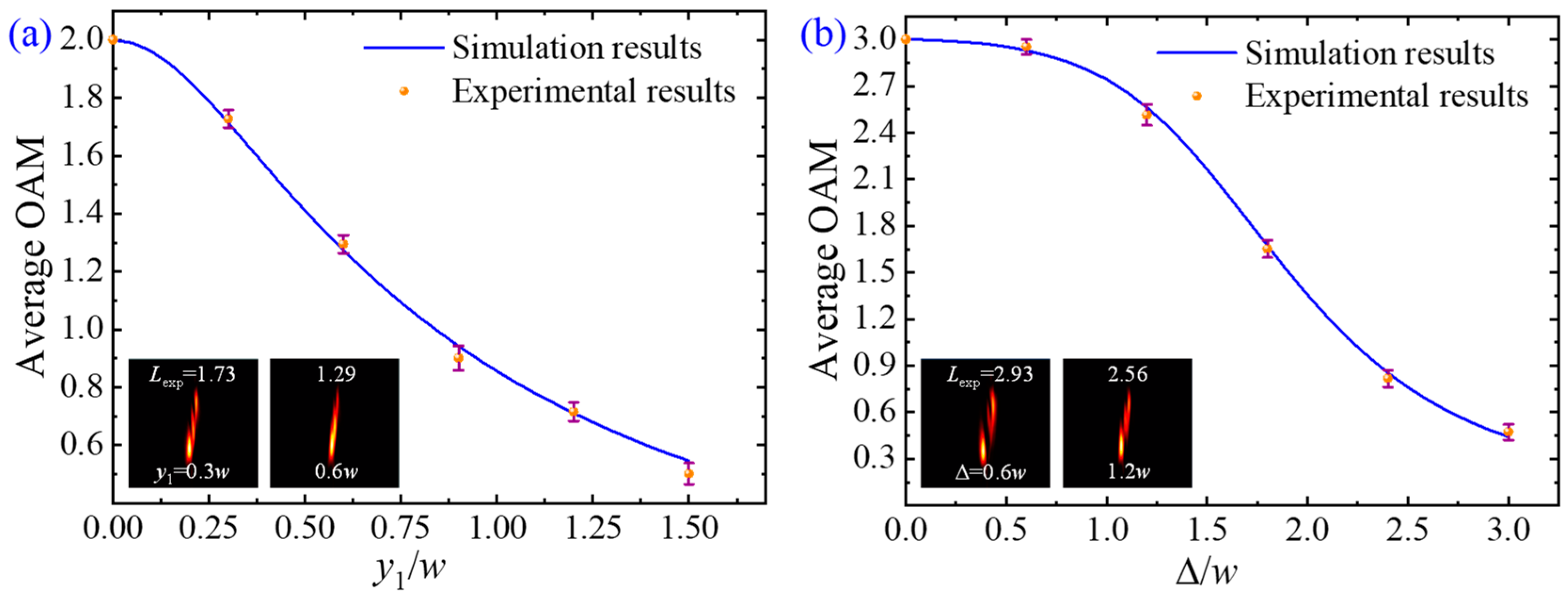
4.2. Average OAM Measurement
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shen, Y.; Wang, X.; Xie, Z.; Min, C.; Fu, X.; Liu, Q.; Gong, M.; Yuan, X. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light Sci. Appl. 2019, 8, 90. [Google Scholar] [CrossRef] [PubMed]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef] [PubMed]
- Tao, S.H.; Yuan, X.C.; Lin, J.; Peng, X.; Niu, H.B. Fractional optical vortex beam induced rotation of particles. Opt. Express 2005, 13, 7726–7731. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Li, X.; Ma, H.; Tang, M.; Li, H.; Tang, J.; Cai, Y. Grafted optical vortex with controllable orbital angular momentum distribution. Opt. Express 2019, 27, 22930–22938. [Google Scholar] [CrossRef]
- Vaity, P.; Rusch, L. Perfect vortex beam: Fourier transformation of a Bessel beam. Opt. Lett. 2015, 40, 597–600. [Google Scholar] [CrossRef]
- Marrucci, L.; Manzo, C.; Paparo, D. Optical spin-to-orbital angular momentum conversion in inhomogeneous anisotropic media. Phys. Rev. Lett. 2006, 96, 163905. [Google Scholar] [CrossRef]
- Chen, P.; Wei, B.-Y.; Ji, W.; Ge, S.-J.; Hu, W.; Xu, F.; Chigrinov, V.; Lu, Y.-Q. Arbitrary and reconfigurable optical vortex generation: A high-efficiency technique using director-varying liquid crystal fork gratings. Photonics Res. 2015, 3, 133–139. [Google Scholar] [CrossRef]
- Forbes, A.; Dudley, A.; McLaren, M. Creation and detection of optical modes with spatial light modulators. Adv. Opt. Photonics 2016, 8, 200–227. [Google Scholar] [CrossRef]
- Goorden, S.A.; Bertolotti, J.; Mosk, A.P. Superpixel-based spatial amplitude and phase modulation using a digital micromirror device. Opt. Express 2014, 22, 17999–18009. [Google Scholar] [CrossRef]
- Rozas, D.; Law, C.T.; Swartzlander, G.A. Propagation dynamics of optical vortices. J. Opt. Soc. Am. B 1997, 14, 3054–3065. [Google Scholar]
- Grier, D.G. A revolution in optical manipulation. Nature 2003, 424, 810–816. [Google Scholar] [CrossRef]
- Wang, J.; Yang, J.-Y.; Fazal, I.M.; Ahmed, N.; Yan, Y.; Huang, H.; Ren, Y.; Yue, Y.; Dolinar, S.; Tur, M.; et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics 2012, 6, 488–496. [Google Scholar] [CrossRef]
- Mair, A.; Vaziri, A.; Weihs, G.; Zeilinger, A. Entanglement of the orbital angular momentum states of photons. Nature 2001, 412, 313–316. [Google Scholar] [CrossRef]
- Fürhapter, S.; Jesacher, A.; Bernet, S.; Ritsch-Marte, M. Spiral phase contrast imaging in microscopy. Opt. Express 2005, 13, 689–694. [Google Scholar]
- Hnatovsky, C.; Shvedov, V.G.; Krolikowski, W.; Rode, A.V. Materials processing with a tightly focused femtosecond laser vortex pulse. Opt. Lett. 2010, 35, 3417–3419. [Google Scholar] [CrossRef]
- Popiołek-Masajada, A.; Frączek, E.; Frączek, W.; Masajada, J.; Makowski, M.; Suszek, J.; Włodarczyk, F.; Sypek, M. Vortex beam as a positioning tool. Opt. Express 2022, 30, 25830–25841. [Google Scholar] [CrossRef]
- Indebetouw, G. Optical vortices and their propagation. J. Mod. Opt. 1993, 40, 73–87. [Google Scholar] [CrossRef]
- Kovalev, A.A.; Kotlyar, V.V.; Porfirev, A.P. Optical trapping and moving of microparticles by using asymmetrical Laguerre-Gaussian beams. Opt. Lett. 2016, 41, 2426–2429. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, J.; Pang, X.; Wan, G. Properties of a strongly focused Gaussian beam with an off-axis vortex. Opt. Commun. 2017, 389, 275–282. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Kovalev, A.A.; Porfirev, A.P. Asymmetric Gaussian optical vortex. Opt. Lett. 2017, 42, 139–142. [Google Scholar] [CrossRef]
- Alam, S.U.I.; Rao, A.S.; Ghosh, A.; Vaity, P.; Samanta, G.K. Nonlinear frequency doubling characteristics of asymmetric vortices of tunable, broad orbital angular momentum spectrum. Appl. Phys. Lett. 2018, 112, 171102. [Google Scholar] [CrossRef]
- Kotlyar, V.; Kovalev, A.; Porfirev, A.; Kozlova, E. Orbital angular momentum of a laser beam behind an off-axis spiral phase plate. Opt. Lett. 2019, 44, 3673–3676. [Google Scholar] [CrossRef] [PubMed]
- Kovalev, A.A.; Kotlyar, V.V.; Porfirev, A.P. Orbital angular momentum and topological charge of a multi-vortex Gaussian beam. J. Opt. Soc. Am. A 2020, 37, 1740–1747. [Google Scholar] [CrossRef]
- Augustyniak, I.; Lamperska, W.; Masajada, J.; Płociniczak, Ł.; Popiołek-Masajada, A. Off-axis vortex beam propagation through classical optical system in terms of Kummer confluent hypergeometric function. Photonics 2020, 7, 60. [Google Scholar] [CrossRef]
- Hickmann, J.M.; Fonseca, E.J.S.; Soares, W.C.; Chávez-Cerda, S. Unveiling a truncated optical lattice associated with a triangular aperture using light’s orbital angular momentum. Phys. Rev. Lett. 2010, 105, 053904. [Google Scholar] [CrossRef] [PubMed]
- Tao, H.; Liu, Y.; Chen, Z.; Pu, J. Measuring the topological charge of vortex beams by using an annular ellipse aperture. Appl. Phys. B 2012, 106, 927–932. [Google Scholar] [CrossRef]
- Vaity, P.; Banerji, J.; Singh, R.P. Measuring the topological charge of an optical vortex by using a tilted convex lens. Phys. Lett. A 2013, 377, 1154–1156. [Google Scholar] [CrossRef]
- Shen, D.; Zhao, D. Measuring the topological charge of optical vortices with a twisting phase. Opt. Lett. 2019, 44, 2334–2337. [Google Scholar] [CrossRef]
- Yang, Y.; Niu, L.; Yang, Z.; Liu, J. Measuring the topological charge of terahertz vortex beams with a focal hyperbolic lens. Appl. Opt. 2020, 59, 4685–4691. [Google Scholar] [CrossRef]
- Zhao, J.; Jin, Y.; Kong, F.; He, D.; Cao, H.; Hao, W.; Wu, Y.; Shao, J. Measuring the topological charge of optical vortices with a single plate. Chin. Opt. Lett. 2022, 20, 110501. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Kovalev, A.A.; Porfirev, A.P. Astigmatic transforms of an optical vortex for measurement of its topological charge. Appl. Opt. 2017, 56, 4095–4104. [Google Scholar] [CrossRef]
- Basistiy, I.V.; Bazhenov, V.Y.; Soskin, M.S.; Vasnetsov, M.V. Optics of light beams with screw dislocations. Opt. Commun. 1993, 103, 422–428. [Google Scholar] [CrossRef]
- Denisenko, V.; Shvedov, V.; Desyatnikov, A.S.; Neshev, D.N.; Krolikowski, W.; Volyar, A.; Soskin, M.; Kivshar, Y.S. Determination of topological charges of polychromatic optical vortices. Opt. Express 2009, 17, 23374–23379. [Google Scholar] [CrossRef] [PubMed]
- Alperin, S.N.; Niederriter, R.D.; Gopinath, J.T.; Siemens, M.E. Quantitative measurement of the orbital angular momentum of light with a single, stationary lens. Opt. Lett. 2016, 41, 5019–5022. [Google Scholar] [CrossRef] [PubMed]
- Volyar, A.; Bretsko, M.; Akimova, Y.; Egorov, Y. Measurement of the vortex and orbital angular momentum spectra with a single cylindrical lens. Appl. Opt. 2019, 58, 5748–5755. [Google Scholar] [CrossRef] [PubMed]
- Berkhout, G.C.G.; Lavery, M.P.J.; Courtial, J.; Beijersbergen, M.W.; Padgett, M.J. Efficient sorting of orbital angular momentum states of light. Phys. Rev. Lett. 2010, 105, 153601. [Google Scholar] [CrossRef]
- Kovalev, A.A.; Kotlyar, V.V.; Nalimov, A.G. Topological charge and asymptotic phase invariants of vortex laser beams. Photonics 2021, 8, 445. [Google Scholar] [CrossRef]
- Chen, R.; Wang, Q. Propagation properties of off-axis double vortex single beam in nonlocal media. Laser Optoelectron. Prog. 2021, 58, 2119001. [Google Scholar]
- Berry, M.V. Optical vortices evolving from helicoidal integer and fractional phase steps. J. Opt. A Pure Appl. Opt. 2004, 6, 259–268. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Kovalev, A.A.; Volyar, A.V. Topological charge of a linear combination of optical vortices: Topological competition. Opt. Express 2020, 28, 8266–8281. [Google Scholar] [CrossRef]
- Berkhout, G.C.G.; Beijersbergen, M.W. Method for probing the orbital angular momentum of optical vortices in electromagnetic waves from astronomical objects. Phys. Rev. Lett. 2008, 101, 100801. [Google Scholar] [CrossRef] [PubMed]
- Lubk, A.; Guzzinati, G.; Börrnert, F.; Verbeeck, J. Transport of intensity phase retrieval of arbitrary wave fields including vortices. Phys. Rev. Lett. 2013, 111, 173902. [Google Scholar] [CrossRef] [PubMed]
- Gu, B.; Hu, Y.; Zhang, X.; Li, M.; Zhu, Z.; Rui, G.; He, J.; Cui, Y. Angular momentum separation in focused fractional vector beams for optical manipulation. Opt. Express 2021, 29, 14705–14719. [Google Scholar] [CrossRef] [PubMed]
- Kovalev, A.A.; Kotlyar, V.V.; Porfirev, A.P. Asymmetric Laguerre-Gaussian beams. Phys. Rev. A 2016, 93, 063858. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, M.; Le, W.; Wang, C.; Rui, G.; Zhu, Z.; He, J.; Gu, B. Generation, Topological Charge, and Orbital Angular Momentum of Off-Axis Double Vortex Beams. Photonics 2023, 10, 368. https://doi.org/10.3390/photonics10040368
Guo M, Le W, Wang C, Rui G, Zhu Z, He J, Gu B. Generation, Topological Charge, and Orbital Angular Momentum of Off-Axis Double Vortex Beams. Photonics. 2023; 10(4):368. https://doi.org/10.3390/photonics10040368
Chicago/Turabian StyleGuo, Mingxian, Wei Le, Chao Wang, Guanghao Rui, Zhuqing Zhu, Jun He, and Bing Gu. 2023. "Generation, Topological Charge, and Orbital Angular Momentum of Off-Axis Double Vortex Beams" Photonics 10, no. 4: 368. https://doi.org/10.3390/photonics10040368
APA StyleGuo, M., Le, W., Wang, C., Rui, G., Zhu, Z., He, J., & Gu, B. (2023). Generation, Topological Charge, and Orbital Angular Momentum of Off-Axis Double Vortex Beams. Photonics, 10(4), 368. https://doi.org/10.3390/photonics10040368





