Two-Dimensional Quantum Droplets in Binary Dipolar Bose-Bose Mixture
(This article belongs to the Section Quantum Photonics and Technologies)
Abstract
1. Introduction
2. Model
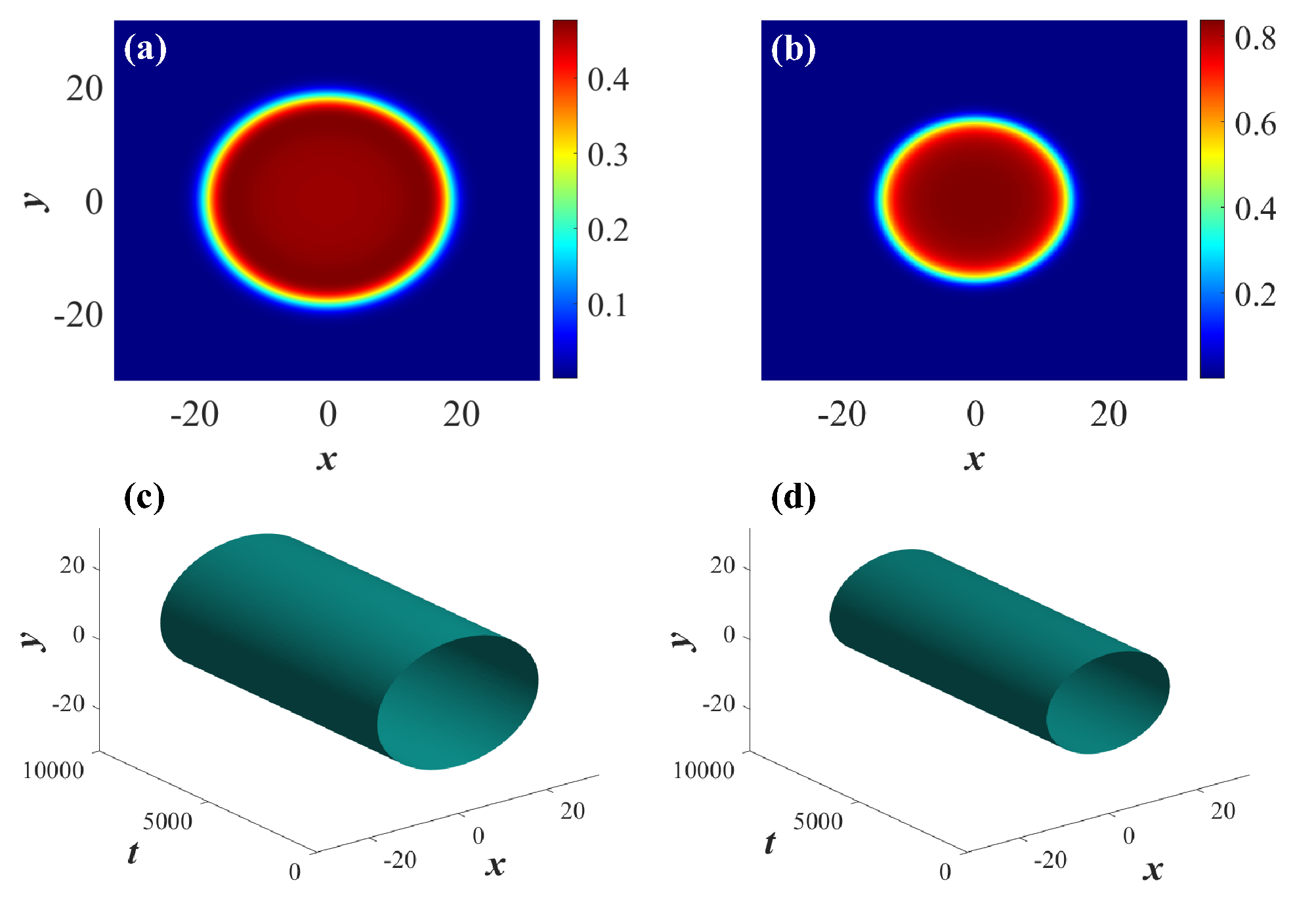
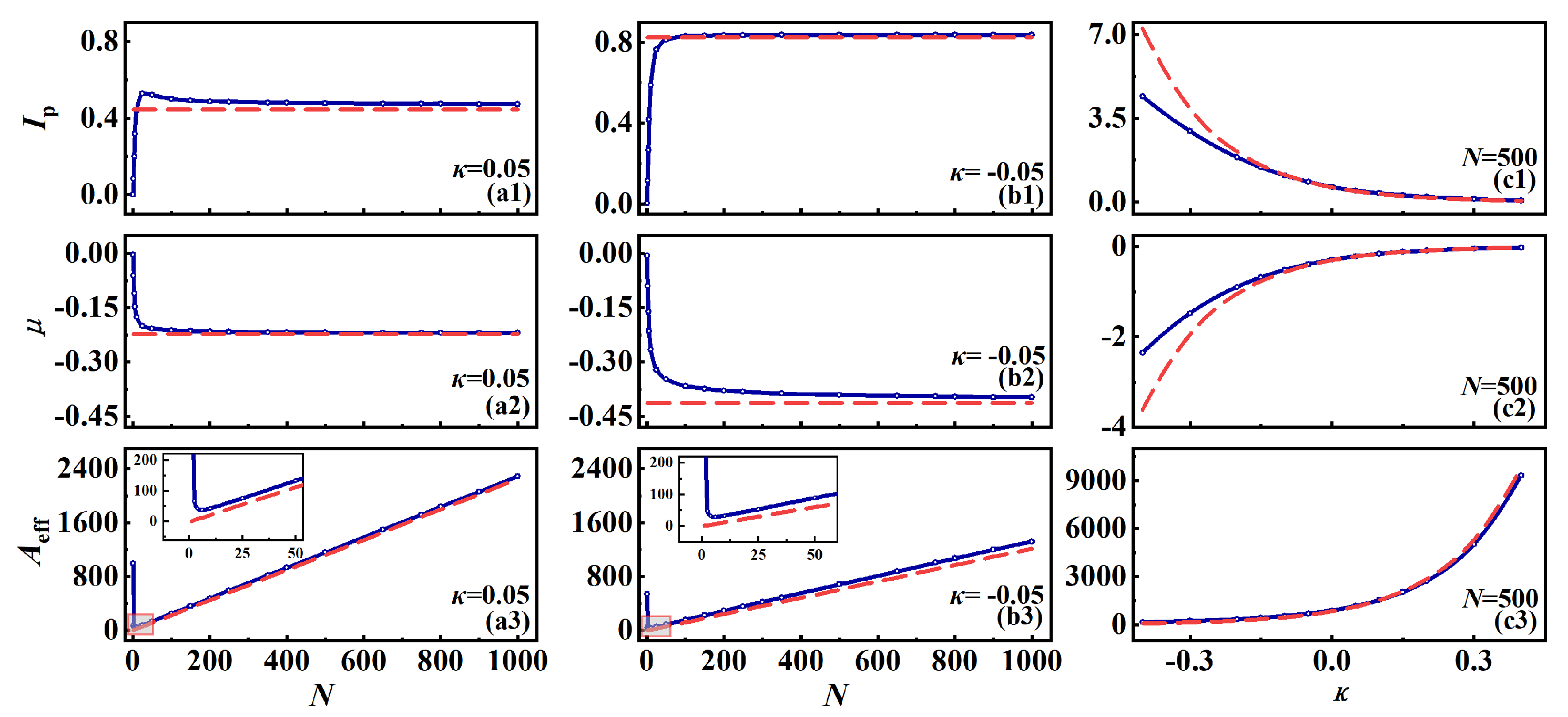
3. Stationary Solution of the Quantum Droplets
4. Collision between the Moving Quantum Droplets
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Donley, E.A.; Claussen, N.R.; Cornish, S.L.; Roberts, J.L.; Cornell, E.A.; Wieman, C.E. Dynamics of collapsing and exploding Bose–Einstein condensates. Nature 2001, 412, 295–299. [Google Scholar] [CrossRef] [PubMed]
- Malomed, B.A. Multidimensional Solitons: Well-Established Results and Novel Findings. Eur. Phys. J. Spec. Top. 2016, 225, 2507–2532. [Google Scholar] [CrossRef]
- Petrov, D.S. Quantum Mechanical Stabilization of a Collapsing Bose-Bose Mixture. Phys. Rev. Lett. 2015, 115, 155302. [Google Scholar] [CrossRef] [PubMed]
- Cabrera, C.R.; Tanzi, L.; Sanz, J.; Naylor, B.; Thomas, P.; Cheiney, P.; Tarruell, L. Quantum liquid droplets in a mixture of Bose–Einstein condensates. Science 2018, 359, 301–304. [Google Scholar] [CrossRef]
- Semeghini, G.; Ferioli, G.; Masi, L.; Mazzinghi, C.; Wolswijk, L.; Minardi, F.; Modugno, M.; Modugno, G.; Inguscio, M.; Fattori, M. Self-Bound Quantum Droplets of Atomic Mixtures in Free Space. Phys. Rev. Lett. 2018, 120, 235301. [Google Scholar] [CrossRef]
- Chomaz, L.; Baier, S.; Petter, D.; Mark, M.J.; Wächtler, F.; Santos, L.; Ferlaino, F. Quantum-Fluctuation-Driven Crossover from a Dilute Bose–Einstein Condensate to a Macrodroplet in a Dipolar Quantum Fluid. Phys. Rev. X 2016, 6, 041039. [Google Scholar] [CrossRef]
- Cheiney, P.; Cabrera, C.R.; Sanz, J.; Naylor, B.; Tanzi, L.; Tarruell, L. Bright soliton to quantum droplet transition in a mixture of Bose–Einstein condensates. Phys. Rev. Lett. 2018, 120, 135301. [Google Scholar] [CrossRef]
- Ferioli, G.; Giulia, S.; Masi, L.; Giusti, G.; Modugno, G.; Inguscio, M. Gallemí, A.; Recati, A.; Fattori, M. Collisions of Self-Bound Quantum Droplets. Phys. Rev. Lett. 2019, 122, 090401. [Google Scholar] [CrossRef]
- D’Errico, C.; Burchianti, A.; Prevedelli, M.; Salasnich, L.; Ancilotto, F.; Modugno, M.; Fort, C. Observation of quantum droplets in a heteronuclear bosonic mixture. Phys. Rev. Res. 2019, 1, 033155. [Google Scholar] [CrossRef]
- Ferrier-Barbut, I.; Kadau, H.; Schmitt, M.; Wenzel, M.; Pfau, T. Observation of Quantum Droplets in a Strongly Dipolar Bose Gas. Phys. Rev. Lett. 2016, 116, 215301. [Google Scholar] [CrossRef]
- Ferrier-Barbut, I.; Wenzel, M.; Schmitt, M.; Böttcher, F.; Pfau, T. Onset of a modulational instability in trapped dipolar Bose–Einstein condensates. Phys. Rev. A 2018, 97, 011604. [Google Scholar] [CrossRef]
- Ferrier-Barbut, I.; Wenze, M.; Bötcher, F.; Langen, T.; Isoard, M.; Stringari, S.; Pfau, T. Scissors Mode of Dipolar Quantum Droplets of Dysprosium Atoms. Phys. Rev. Lett. 2018, 120, 160402. [Google Scholar] [CrossRef] [PubMed]
- Böttcher, F.; Wenzel, M.; Schmidt, J.N.; Guo, M.; Langen, T.; Ferrier-Barbut, I.; Mazzanti, F. Dilute dipolar quantum droplets beyond the extended Gross–Pitaevskii equation. Phys. Rev. Res. 2019, 1, 033088. [Google Scholar] [CrossRef]
- Schmitt, M.; Wenzel, M.; Böttcher, F.; Ferrier-Barbut, I.; Pfau, T. Self-Bound Droplets of a Dilute Magnetic Quantum Liquid. Nature 2016, 539, 259–262. [Google Scholar] [CrossRef]
- Ferrier-Barbut, I.; Schmitt, M.; Wenzel, M.; Kadau, H.; Pfau, T. Liquid quantum droplets of ultracold magnetic atoms. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 214004. [Google Scholar] [CrossRef]
- Kadau, H.; Schmitt, M.; Wenzel, M.; Wink, C.; Maier, T.; Ferrier-Barbut, I.; Pfau, T. Observing the Rosensweig Instability of a Quantum Ferrofluid. Nature 2016, 530, 194–197. [Google Scholar] [CrossRef]
- Malomed, B.A. The Family of Quantum Droplets Keeps Expanding. Front. Phys. 2021, 16, 22504. [Google Scholar] [CrossRef]
- Guo, M.Y.; Pfau, T. A New State of Matter of Quantum Droplets. Front. Phys. 2021, 16, 32202. [Google Scholar] [CrossRef]
- Otajonov, S.R.; Otajonov, E.N.; Abdullaev, F.K. Modulational instability and quantum droplets in a two-dimensional Bose–Einstein condensate. Phys. Rev. A 2022, 106, 033309. [Google Scholar] [CrossRef]
- Böttcher, F.; Schmidt, J.N.; Hertkorn, J.; Ng, K.S.H.; Graham, S.D.; Guo, M.Y.; Langen, T.; Pfau, T. New States of Matter with Fine-Tuned Interactions: Quantum Droplets and Dipolar Supersolids. Rep. Prog. Phys. 2021, 84, 012403. [Google Scholar] [CrossRef]
- d’Errico, C.; Zaccanti, M.; Fattori, M.; Roati, G.; Inguscio, M.; Modugno, G.; Simoni, A. Feshbach resonances in ultracold 39K. New J. Phys. 2007, 9, 223. [Google Scholar] [CrossRef]
- Petrov, D.S.; Astrakharchik, G.E. Ultradilute Low-Dimensional Liquids. Phys. Rev. Lett. 2016, 117, 100401. [Google Scholar] [CrossRef]
- Zheng, Y.Y.; Chen, S.T.; Huang, Z.P.; Dai, S.X.; Liu, B.; Li, Y.Y.; Wang, S.R. Quantum Droplets in Two-Dimensional Optical Lattices. Front. Phys. 2021, 16, 22501. [Google Scholar] [CrossRef]
- Kartashov, Y.V.; Malomed, B.A.; Torner, L. Structured heterosymmetric quantum droplets. Phys. Rev. Res. 2020, 2, 033522. [Google Scholar] [CrossRef]
- Otajonov, S.R.; Tsoy, E.N.; Abdullaev, F.K. Variational approximation for two-dimensional quantum droplets. Phys. Rev. E 2020, 102, 062217. [Google Scholar] [CrossRef]
- Boudjemâa, A. Fluctuations and quantum self-bound droplets in a dipolar Bose-Bose mixture. Phys. Rev. A 2018, 98, 033612. [Google Scholar] [CrossRef]
- Dong, L.; Qi, W.; Peng, P.; Wang, L.; Zhou, H.; Huang, C. Multi-stable quantum droplets in optical lattice. Nonlinear Dyn. 2020, 102, 303. [Google Scholar] [CrossRef]
- Morera, I.; Astrakharchik, G.E.; Polls, A.; Juliá-Díaz, B. Quantum droplets of bosonic mixtures in a one-dimensional optical lattice. Phys. Rev. Res. 2020, 2, 022008. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, H.; Zhong, R.; Zhang, X.; Qin, X.; Huang, C.; Li, Y.; Malomed, B.A. Symmetry breaking of quantum droplets in a dual-core trap. Phys. Rev. A 2019, 99, 053602. [Google Scholar] [CrossRef]
- Chen, Y.; Cai, X.; Liu, B.; Jiang, X.; Li, Y. Hidden vortices of quantum droplets in quasi-two dimensional space. Acta Phys. Sin. 2022, 71, 200302. [Google Scholar] [CrossRef]
- Liu, B.; Chen, Y.; Yang, A.W.; Cai, X.Y.; Liu, Y.; Luo, Z.H.; Qin, X.Z.; Jiang, X.D.; Li, Y.Y.; Malomed, B.A. Vortex-ring quantum droplets in a radially-periodic potential. New J. Phys. 2022, 24, 123026. [Google Scholar] [CrossRef]
- Dong, L.; Kartashov, Y.V. Rotating Multidimensional Quantum Droplets. Phys. Rev. Lett. 2021, 126, 244101. [Google Scholar] [CrossRef]
- Huang, H.; Wang, H.; Chen, M.; Lim, C.; Wong, K. Binary-vortex quantum droplets. Chaos Solitons Fractals 2022, 158, 112079. [Google Scholar] [CrossRef]
- Zhou, Z.; Shi, Y.; Ye, F.; Chen, H.; Tang, S.; Deng, H.; Zhong, H. Self-bound states induced by the Lee-Huang-Yang effect in non-PT-symmetric complex potentials. Nonlinear Dyn. 2022, 110, 3769. [Google Scholar] [CrossRef]
- Zhou, Z.; Shi, Y.; Tang, S.; Deng, H.; Wang, H.; He, X.; Zhong, H. Controllable dissipative quantum droplets in one-dimensional optical lattices. Chaos Solitons Fractals 2021, 150, 111193. [Google Scholar] [CrossRef]
- Dong, L.W.; Liu, D.S.; Du, Z.J.; Shi, K.; Qi, W. Bistable multipole quantum droplets in binary Bose–Einstein condensates. Phys. Rev. A 2022, 105, 033321. [Google Scholar] [CrossRef]
- Dong, L.W.; Shi, K.; Huang, C.M. Internal modes of two-dimensional quantum droplets. Phys. Rev. A 2022, 106, 053303. [Google Scholar] [CrossRef]
- Xu, S.; Lei, Y.; Du, J.; Zhao, Y.; Hua, R.; Zeng, J. Three-dimensional quantum droplets in spin–orbit-coupled Bose–Einstein condensates. Chaos Solitons Fractals 2022, 164, 112665. [Google Scholar] [CrossRef]
- Li, Y.Y.; Luo, Z.H.; Liu, Y.; Chen, Z.P.; Huang, C.Q.; Fu, S.H.; Tan, H.S.; Malomed, B.A. Two-dimensional solitons and quantum droplets supported by competing self- and cross-interactions in spin–orbit-coupled condensates. New J. Phys. 2017, 19, 113043. [Google Scholar] [CrossRef]
- Cui, X. Spin-orbit-coupling-induced quantum droplet in ultracold Bose–Fermi mixtures. Phys. Rev. A 2018, 98, 023630. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, L.; Yi, S.; Shi, T. Theory for self-bound states of dipolar Bose–Einstein condensates. Phys. Rev. Res. 2020, 2, 043074. [Google Scholar] [CrossRef]
- Wang, J.; Hu, H.; Liu, X.J. Thermal destabilization of self-bound ultradilute quantum droplets. New J. Phys. 2020, 22, 103044. [Google Scholar] [CrossRef]
- Guo, Z.; Jia, F.; Li, L.; Ma, Y.; Hutson, J.; Cui, X.; Wang, D. Lee-Huang-Yang effects in the ultracold mixture of 23Na and 87Rb with attractive interspecies interactions. Phys. Rev. Res. 2021, 3, 033247. [Google Scholar] [CrossRef]
- Guebli, N.; Boudjemâa, A. Quantum self-bound droplets in Bose-Bose mixtures: Effects of higher-order quantum and thermal fluctuations. Phys. Rev. A 2021, 104, 023310. [Google Scholar] [CrossRef]
- Boudjemâa, A. Many-body and temperature effects in two-dimensional quantum droplets in Bose-Bose mixtures. Sci. Rep. 2021, 11, 21765. [Google Scholar] [CrossRef]
- Jiang, X.; Zeng, Y.; Ji, Y.; Liu, B.; Qin, X.; Li, Y. Vortex formation and quench dynamics of rotating quantum droplets. Chaos Solitons Fractals 2022, 161, 112368. [Google Scholar] [CrossRef]
- Wächtler, F.; Santos, L. Quantum filaments in dipolar Bose–Einstein condensates. Phys. Rev. A 2016, 93, 061603(R). [Google Scholar] [CrossRef]
- Wächtler, F.; Santos, L. Ground-state properties and elementary excitations of quantum droplets in dipolar Bose–Einstein condensates. Phys. Rev. A 2016, 94, 043618. [Google Scholar] [CrossRef]
- Sekino, Y.; Nishida, Y. Quantum droplet of one-dimensional bosons with a three-body attraction. Phys. Rev. A 2018, 97, 011602(R). [Google Scholar] [CrossRef]
- Bisset, R.N.; Wilson, R.M.; Baillie, D.; Blakie, P.B. Ground-state phase diagram of a dipolar condensate with quantum fluctuations. Phys. Rev. A 2016, 94, 033619. [Google Scholar] [CrossRef]
- Cidrim, A.; dos Santos, F.E.A.; Henn, E.A.L.; Macrì, T. Vortices in self-bound dipolar droplets. Phys. Rev. A 2018, 98, 023618. [Google Scholar] [CrossRef]
- Baillie, D.; Wilson, R.M.; Bisset, R.N.; Blakie, P.B. Self-bound dipolar droplet: A localized matter wave in free space. Phys. Rev. A 2016, 94, 021602(R). [Google Scholar] [CrossRef]
- Boudjemâa, A. Two-Dimensional Quantum Droplets in Dipolar Bose Gases. New J. Phys. 2019, 21, 093027. [Google Scholar] [CrossRef]
- Edler, D.; Mishra, C.; Wächtler, F.; Nath, R.; Sinha, S.; Santos, L. Quantum Fluctuations in Quasi-One-Dimensional Dipolar Bose–Einstein Condensates. Phys. Rev. Lett. 2017, 119, 050403. [Google Scholar] [CrossRef]
- Bland, T.; Poli, E.; Ardila, L.A.P.; Santos, L.; Ferlaino, F.; Bisset, R.N. Alternating-domain supersolids in binary dipolar condensates. Phys. Rev. A 2022, 106, 053322. [Google Scholar] [CrossRef]
- Bisset, R.N.; Ardila, L.A.P.; Santos, L. Quantum Droplets of Dipolar Mixtures. Phys. Rev. Lett. 2021, 126, 025301. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.C.; Baillie, D.; Blakie, P.B. Quantum Droplet States of a Binary Magnetic Gas. Phys. Rev. Lett. 2021, 126, 025302. [Google Scholar] [CrossRef]
- Scheiermann, D.; Ardila, L.A.P.; Bland, T.; Bisset, R.N.; Santos, L. Catalyzation of supersolidity in binary dipolar condensates. arXiv 2022, arXiv:2202.08259. [Google Scholar] [CrossRef]
- Tikhonenkov, I.; Malomed, B.A.; Vardi, A. Anisotropic solitons in dipolar Bose–Einstein Condensates. Phys. Rev. Lett. 2008, 100, 090406. [Google Scholar] [CrossRef] [PubMed]
- Li, G.L.; Jiang, X.D.; Liu, B.; Chen, Z.P.; Malomed, B.A.; Li, Y.Y. Anisotropic vortex quantum droplets in dipolar Bose–Einstein condensates. arXiv 2023, arXiv:2301.04305. [Google Scholar]
- Giovanazzi, S.; Görlitz, A.; Pfau, T. Tuning the Dipolar Interaction in Quantum Gases. Phys. Rev. Lett. 2002, 89, 130401. [Google Scholar] [CrossRef] [PubMed]
- Roati, G.; Zaccanti, M.; D’Errico, C.; Catani, J.; Modugno, M.; Simoni, A.; Inguscio, M.; Modugno, G. 39K Bose–Einstein condensate with tunable interactions. Phys. Rev. Lett. 2007, 99, 010403. [Google Scholar] [CrossRef] [PubMed]
- Tikhonenkov, I.; Malomed, B.A.; Vardi, A. Vortex Solitons in Dipolar Bose–Einstein Condensates. Phys. Rev. A 2008, 78, 043614. [Google Scholar] [CrossRef]
- Sinha, S.; Santos, L. Cold Dipolar Gases in Quasi-One-Dimensional Geometries. Phys. Rev. Lett. 2007, 99, 140406. [Google Scholar] [CrossRef]
- Cuevas, J.; Malomed, B.A.; Kevrekidis, P.G.; Frantzeskakis, D.J. Solitons in quasi-one-dimensional Bose–Einstein condensates with competing dipolar and local interactions. Phys. Rev. A 2009, 79, 053608. [Google Scholar] [CrossRef]
- Huang, C.Q.; Lyu, L.; Huang, H.; Chen, Z.P.; Fu, S.H.; Tan, H.S.; Malomed, B.A.; Li, Y.Y. Dipolar bright solitons and solitary vortices in a radial lattice. Phys. Rev. A 2017, 96, 053617. [Google Scholar] [CrossRef]
- Ramachandhran, B.; Opanchuk, B.; Liu, X.J.; Pu, H.; Drummond, P.D.; Hu, H. Half-quantum vortex state in a spin–orbit-coupled Bose–Einstein condensate. Phys. Rev. A 2021, 85, 023606. [Google Scholar] [CrossRef]
- Li, Y.; Liu, J.; Pang, W.; Malomed, B.A. Matter-wave solitons supported by field-induced dipole-dipole repulsion with spatially modulated strength. Phys. Rev. A 2013, 88, 053630. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Y.; Fan, Z.; Pang, W.; Fu, S.; Malomed, B.A. Two-dimensional dipolar gap solitons in free space with spin–Orbit coupling. Phys. Rev. A 2017, 95, 063613. [Google Scholar] [CrossRef]
- Huang, C.; Ye, Y.; Liu, S.; He, H.; Pang, W.; Malomed, B.A.; Li, Y. Excited states of two-dimensional solitons supported by spin–orbit coupling and field-induced dipole-dipole repulsion. Phys. Rev. A 2018, 97, 013636. [Google Scholar] [CrossRef]
- Chiofalo, L.M.; Succi, S.; Tosi, P.M. Ground state of trapped interacting Bose–Einstein condensates by an explicit imaginary-time algorithm. Phys. Rev. E 2000, 62, 7438. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Lakoba, T.I. Accelerated Imaginary-time Evolution Methods for the Computation of Solitary Waves. Stud. Appl. Math. 2008, 120, 265–292. [Google Scholar] [CrossRef]
- Vakhitov, N.G.; Kolokolov, A.A. Stationary solutions of the wave equation in the medium with nonlinearity saturation. Radiophys. Quantum Electron. 1973, 16, 783–789. [Google Scholar] [CrossRef]
- Hu, Y.M.; Fei, Y.F.; Chen, X.L.; Zhang, Y.B. Collisional Dynamics of Symmetric Two-Dimensional Quantum Droplets. Front. Phys. 2022, 17, 61505. [Google Scholar] [CrossRef]
- Luo, Z.H.; Pang, W.; Liu, B.; Li, Y.Y.; Malomed, B.A. A new form of liquid matter: Quantum droplets. Front. Phys. 2021, 16, 32201. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, A.; Li, G.; Jiang, X.; Fan, Z.; Chen, Z.; Liu, B.; Li, Y. Two-Dimensional Quantum Droplets in Binary Dipolar Bose-Bose Mixture. Photonics 2023, 10, 405. https://doi.org/10.3390/photonics10040405
Yang A, Li G, Jiang X, Fan Z, Chen Z, Liu B, Li Y. Two-Dimensional Quantum Droplets in Binary Dipolar Bose-Bose Mixture. Photonics. 2023; 10(4):405. https://doi.org/10.3390/photonics10040405
Chicago/Turabian StyleYang, Aowei, Guilong Li, Xunda Jiang, Zhiwei Fan, Zhaopin Chen, Bin Liu, and Yongyao Li. 2023. "Two-Dimensional Quantum Droplets in Binary Dipolar Bose-Bose Mixture" Photonics 10, no. 4: 405. https://doi.org/10.3390/photonics10040405
APA StyleYang, A., Li, G., Jiang, X., Fan, Z., Chen, Z., Liu, B., & Li, Y. (2023). Two-Dimensional Quantum Droplets in Binary Dipolar Bose-Bose Mixture. Photonics, 10(4), 405. https://doi.org/10.3390/photonics10040405




