Transmission Matrix-Inspired Optimization for Mode Control in a 6 × 1 Photonic Lantern-Based Fiber Laser
Abstract
1. Introduction
2. Materials and Methods
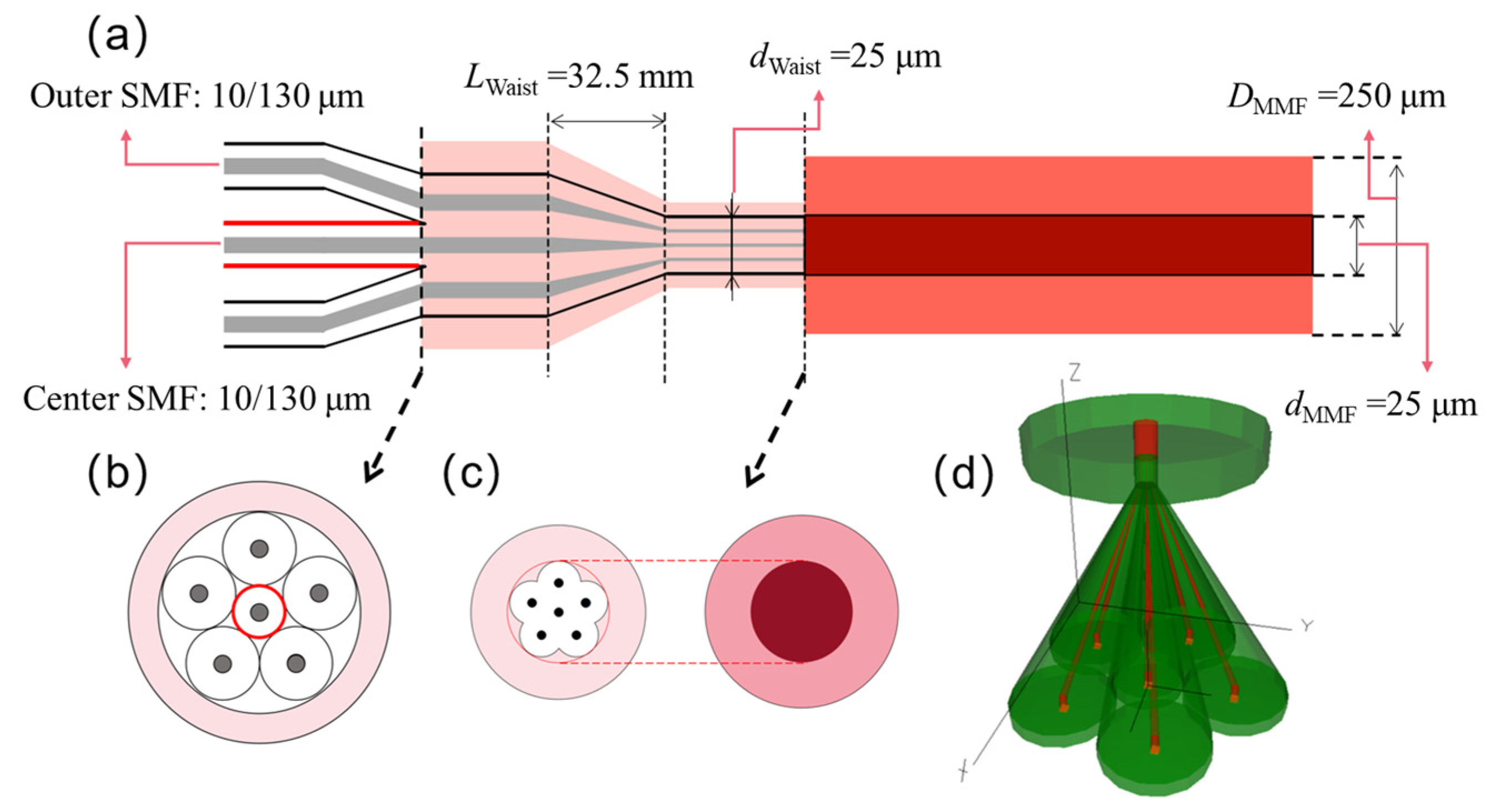
2.1. The Transmission Matrix of the Photonic Lantern
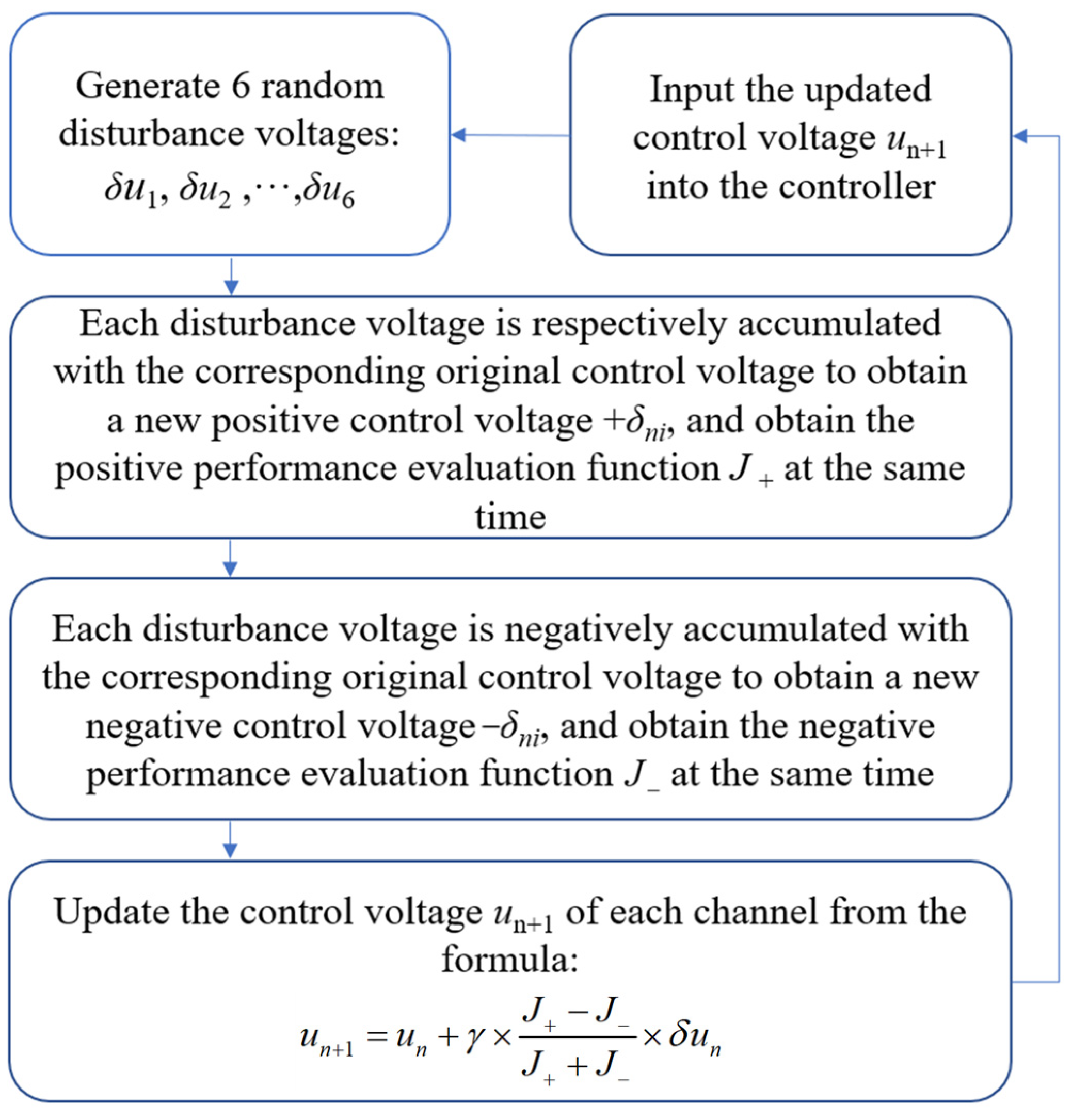
2.2. Stochastic Parallel Gradient Descent Algorithm
3. Results and Discussion
3.1. The 6 × 1 Photonic Lantern
3.2. Random Amplitude
3.3. Preset the Equal Amplitude
3.4. Preset Amplitude Based on Transmission Matrix
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Leon-Saval, S.G.; Argyros, A.; Bland-Hawthorn, J. Photonic lanterns: A study of light propagation in multimode to single-mode converters. Opt. Express 2010, 18, 8430–8439. [Google Scholar] [CrossRef] [PubMed]
- Leon-Saval, S.G.; Argyros, A.; Bland-Hawthorn, J. Photonic lanterns. Nanophotonics 2013, 2, 429–440. [Google Scholar] [CrossRef]
- Birks, T.A.; Gris-Sanchez, I.; Yerolatsitis, S.; Leon-Saval, S.G.; Thomson, R.R. The photonic lantern. Adv. Opt. Photonics 2015, 7, 107–167. [Google Scholar] [CrossRef]
- Noordegraaf, D.; Skovgaard, P.M.W.; Maack, M.D.; Bland-Hawthorn, J.; Haynes, R.; Laegsgaard, J. Multi-mode to single-mode conversion in a 61 port Photonic Lantern. Opt. Express 2010, 18, 4673–4678. [Google Scholar] [CrossRef] [PubMed]
- Leon-Saval, S.G.; Birks, T.A.; Bland-Hawthorn, J.; Englund, M. Multimode fiber devices with single-mode performance. Opt. Lett. 2005, 30, 2545–2547. [Google Scholar] [CrossRef] [PubMed]
- Bland-Hawthorn, J.; Ellis, S.C.; Leon-Saval, S.G.; Haynes, R.; Roth, M.M.; Lohmannsroben, H.G.; Horton, A.J.; Cuby, J.G.; Birks, T.A.; Lawrence, J.S.; et al. A complex multi-notch astronomical filter to suppress the bright infrared sky. Nat. Commun. 2011, 2, 581. [Google Scholar] [CrossRef]
- Leon-Saval, S.G.; Fontaine, N.K.; Salazar-Gil, J.R.; Ercan, B.; Ryf, R.; Bland-Hawthorn, J. Mode-selective photonic lanterns for spacedivision multiplexing. Opt. Express 2014, 22, 1036–1044. [Google Scholar] [CrossRef]
- Fontaine, N.K.; Leon-Saval, S.G.; Ryf, R.; Gil, J.R.S.; Ercan, B.; Bland-Hawthorn, J. Mode-selective dissimilar fiber photonic-lantern spatial multiplexers for few-mode fiber. In Proceedings of the 39th European Conference and Exhibition on Optical Communication (ECOC 2013), London, UK, 22–26 September 2013; pp. 1–3. [Google Scholar]
- Huang, B.; Fontaine, N.K.; Ryf, R.; Guan, B.; Leon-Saval, S.G.; Shubochkin, R.; Sun, Y.; Lingle, R.; Li, G.F. All-fiber mode-group-selective photonic lantern using graded-index multimode fibers. Opt. Express 2015, 23, 224–234. [Google Scholar] [CrossRef]
- Ryf, R.; Fontaine, N.K.; Montoliu, M.; Randel, S.; Ercan, B.; Chen, H.; Chandrasekhar, S.; Gnauck, A.H.; Leon-Saval, S.G.; Bland-Hawthorn, J.; et al. Photonic-Lantern-Based Mode Multiplexers for Few-Mode-Fiber Transmission. In Proceedings of the Optical Fiber Communications Conference and Exhibition (OFC), San Francisco, CA, USA, 9–13 March 2014. [Google Scholar]
- Lopez-Galmiche, G.; Eznaveh, Z.S.; Antonio-Lopez, J.E.; Benitez, A.M.V.; Asomoza, J.R.; Mondragon, J.J.S.; Gonnet, C.; Sillard, P.; Li, G.; Schulzgen, A.; et al. Few-mode erbium-doped fiber amplifier with photonic lantern for pump spatial mode control. Opt. Lett. 2016, 41, 2588–2591. [Google Scholar] [CrossRef]
- Arrizón, V.; Ruiz, U.; Carrada, R.; González, L.A. Pixelated phase computer holograms for the accurate encoding of scalar complex fields. J. Opt. Soc. Am. A 2007, 24, 3500–3507. [Google Scholar] [CrossRef]
- Goorden, S.A.; Bertolotti, J.; Mosk, A.P. Superpixel-based spatial amplitude and phase modulation using a digital micromirror device. Opt. Express 2014, 22, 17999–18009. [Google Scholar] [CrossRef] [PubMed]
- Forbes, A.; Dudley, A.; McLaren, M. Creation and detection of optical modes with spatial light modulators. Adv. Opt. Photonics 2016, 8, 200–227. [Google Scholar] [CrossRef]
- Rothe, S.; Daferner, P.; Heide, S.; Krause, D.; Schmieder, F.; Koukourakis, N.; Czarske, J.W. Benchmarking analysis of computer generated holograms for complex wavefront shaping using pixelated phase modulators. Opt. Express 2021, 29, 37602–37616. [Google Scholar] [CrossRef] [PubMed]
- Labroille, G.; Denolle, B.; Jian, P.; Genevaux, P.; Treps, N.; Morizur, J.-F. Efficient and mode selective spatial mode multiplexer based on multi-plane light conversion. Opt. Express 2014, 22, 15599–15607. [Google Scholar] [CrossRef] [PubMed]
- Fontaine, N.K.; Ryf, R.; Chen, H.; Neilson, D.; Carpenter, J. Design of High Order Mode-Multiplexers using Multiplane Light Conversion. In Proceedings of the 2017 European Conference on Optical Communication (ECOC), Gothenburg, Sweden, 17–21 September 2017; pp. 1–3. [Google Scholar]
- Montoya, J.; Aleshire, C.; Hwang, C.; Fontaine, N.K.; Velazquez-Benitez, A.; Martz, D.H.; Fan, T.Y.; Ripin, D. Photonic lantern adaptive spatial mode control in LMA fiber amplifiers. Opt. Express 2016, 24, 3405–3413. [Google Scholar] [CrossRef]
- Montoya, J.; Hwang, C.; Martz, D.; Aleshire, C.; Fan, T.Y.; Ripin, D.J. Photonic lantern kW-class fiber amplifier. Opt. Express 2017, 25, 27543–27550. [Google Scholar] [CrossRef]
- Taverner, D.; Galvanauskas, A.; Harter, D.; Richardson, D.; Dong, L. Generation of high-energy pulses using a large-mode-area erbium-doped fiber amplifier. In Proceedings of the Summaries of Papers Presented at the Conference on Lasers and Electro-Optics, Anaheim, CA, USA, 2–7 June 1996; pp. 496–497. [Google Scholar]
- Paschotta, R.; Nilsson, J.; Tropper, A.C.; Hanna, D.C. Ytterbium-doped fiber amplifiers. IEEE J. Quantum Electron. 1997, 33, 1049–1056. [Google Scholar] [CrossRef]
- Carter, C.; Samson, B.; Tankala, K.; Machewirth, D.P.; Khitrov, V.; Manyam, U.H.; Gonthier, F.; Seguin, F. Damage mechanisms in components for fibre lasers and amplifiers. In Proceedings of the 36th Annual Boulder Damage Symposium on Optical Materials for High Power Lasers, NIST, Boulder, CO, USA, 20–22 September 2004; pp. 561–571. [Google Scholar]
- Naderi, S.; Dajani, I.; Madden, T.; Robin, C. Investigations of modal instabilities in fiber amplifiers through detailed numerical simulations. Opt. Express 2013, 21, 16111–16129. [Google Scholar] [CrossRef]
- Gaida, C.; Gebhardt, M.; Heuermann, T.; Wang, Z.; Jauregui, C.; Limpert, J. Transverse mode instability and thermal effects in thulium-doped fiber amplifiers under high thermal loads. Opt. Express 2021, 29, 14963–14973. [Google Scholar] [CrossRef]
- Marcuse, D. Curvature loss formula for optical fibers. J. Opt. Soc. Am. 1976, 66, 216–220. [Google Scholar] [CrossRef]
- Tao, R.M.; Su, R.T.; Ma, P.F.; Wang, X.L.; Zhou, P. Suppressing mode instabilities by optimizing the fiber coiling methods. Laser Phys. Lett. 2017, 14, 025101. [Google Scholar] [CrossRef]
- Ward, B.; Robin, C.; Dajani, I. Origin of thermal modal instabilities in large mode area fiber amplifiers. Opt. Express 2012, 20, 11407–11422. [Google Scholar] [CrossRef] [PubMed]
- Smith, A.V.; Smith, J.J. Overview of a Steady-Periodic Model of Modal Instability in Fiber Amplifiers. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 14054984. [Google Scholar] [CrossRef]
- Su, R.T.; Yang, B.L.; Xi, X.M.; Zhou, P.; Wang, X.L.; Ma, Y.X.; Xu, X.J.; Chen, J.B. 500 W level MOPA laser with switchable output modes based on active control. Opt. Express 2017, 25, 23275–23281. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Shi, F.; Huang, Y.P.; Wen, J.X.; Luo, Z.Q.; Pang, F.F.; Wang, T.Y.; Zeng, X.L. High-order mode direct oscillation of few-mode fiber laser for high-quality cylindrical vector beams. Opt. Express 2018, 26, 11850–11858. [Google Scholar] [CrossRef] [PubMed]
- Otto, H.-J.; Jauregui, C.; Stutzki, F.; Jansen, F.; Limpert, J.; Tünnermann, A. Controlling mode instabilities by dynamic mode excitation with an acousto-optic deflector. Opt. Express 2013, 21, 17285–17298. [Google Scholar] [CrossRef]
- Yerolatsitis, S.; Gris-Sánchez, I.; Birks, T.A. Adiabatically-tapered fiber mode multiplexers. Opt. Express 2015, 22, 608–617. [Google Scholar] [CrossRef]
- Popoff, S.M.; Lerosey, G.; Carminati, R.; Fink, M.; Boccara, A.C.; Gigan, S. Measuring the Transmission Matrix in Optics: An Approach to the Study and Control of Light Propagation in Disordered Media. Phys. Rev. Lett. 2010, 104, 100601. [Google Scholar] [CrossRef]
- Li, S.; Horsley, S.A.R.; Tyc, T.; Čižmár, T.; Phillips, D.B.J.N.C. Memory effect assisted imaging through multimode optical fibres. Nat. Commun. 2020, 12, 3751. [Google Scholar] [CrossRef]
- Mounaix, M.; Carpenter, J.J.N.C. Control of the temporal and polarization response of a multimode fiber. Nat. Commun. 2019, 10, 5085. [Google Scholar] [CrossRef]
- Turtaev, S.; Leite, I.T.; Altwegg-Boussac, T.; Pakan, J.M.P.; Rochefort, N.L.; Čižmár, T. High-fidelity multimode fibre-based endoscopy for deep brain in vivo imaging. Light Sci. Appl. 2018, 7, 92. [Google Scholar] [CrossRef] [PubMed]
- Tzang, O.; Caravaca-Aguirre, A.M.; Wagner, K.; Piestun, R. Adaptive Wave-front shaping in Linear and Nonlinear Complex Media. In Proceedings of the Conference on Lasers and Electro-Optics, San Jose, CA, USA, 13 May 2018; p. FF3H.5. [Google Scholar]
- Kunimasa Saitoh, K.S.; Masanori Koshiba, M.K. Beam Propagation Method for Three-Dimensional Surface Acoustic Waveguides. Jpn. J. Appl. Phys. 2000, 39, 2999. [Google Scholar] [CrossRef]
- Liu, G.J.; Liang, B.M.; Li, Q.; Jin, G.L. Beam propagation in nonlinear multimode interference waveguide. J. Opt. A Pure Appl. Opt. 2005, 7, 457. [Google Scholar] [CrossRef]
- Lateef, Z.A. Design and Simulation of the Fourier Transform Beam Propagation Method in Different Optical Waveguides. IOP Conf. Ser. Mater. Sci. Eng. 2019, 518, 052019. [Google Scholar] [CrossRef]
- Aleshire, C.; Montoya, J.; Hwang, C.; Fontaine, N.K.; Martz, D.H.; Fan, T.Y.; Ripin, D.; Ieee. Photonic Lantern Mode Control in Few-Moded Fiber Amplifiers Using SPGD. In Proceedings of the Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 5–10 June 2016. [Google Scholar]
- Zhou, P.; Liu, Z.; Wang, X.; Ma, Y.; Xu, X. Theoretical and Experimental Investigation on Coherent Beam Combining of Fiber Lasers Using SPGD Algorithm. Acta Opt. Sin. 2009, 29, 2232–2237. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, P.; Ma, Y.; Leng, J.; Xu, X.; Liu, Z. Active phasing a nine-element 1.14 kW all-fiber two-tone MOPA array using SPGD algorithm. Opt. Lett. 2011, 36, 3121–3123. [Google Scholar] [CrossRef]
- Montoya, J.; Augst, S.J.; Creedon, K.; Kansky, J.; Fan, T.Y.; Sanchez-Rubio, A. External cavity beam combining of 21 semiconductor lasers using SPGD. Appl. Opt. 2012, 51, 1724–1728. [Google Scholar] [CrossRef]
- Geng, C.; Luo, W.; Tan, Y.; Liu, H.M.; Mu, J.B.; Li, X.Y. Experimental demonstration of using divergence cost-function in SPGD algorithm for coherent beam combining with tip/tilt control. Opt. Express 2013, 21, 25045–25055. [Google Scholar] [CrossRef] [PubMed]
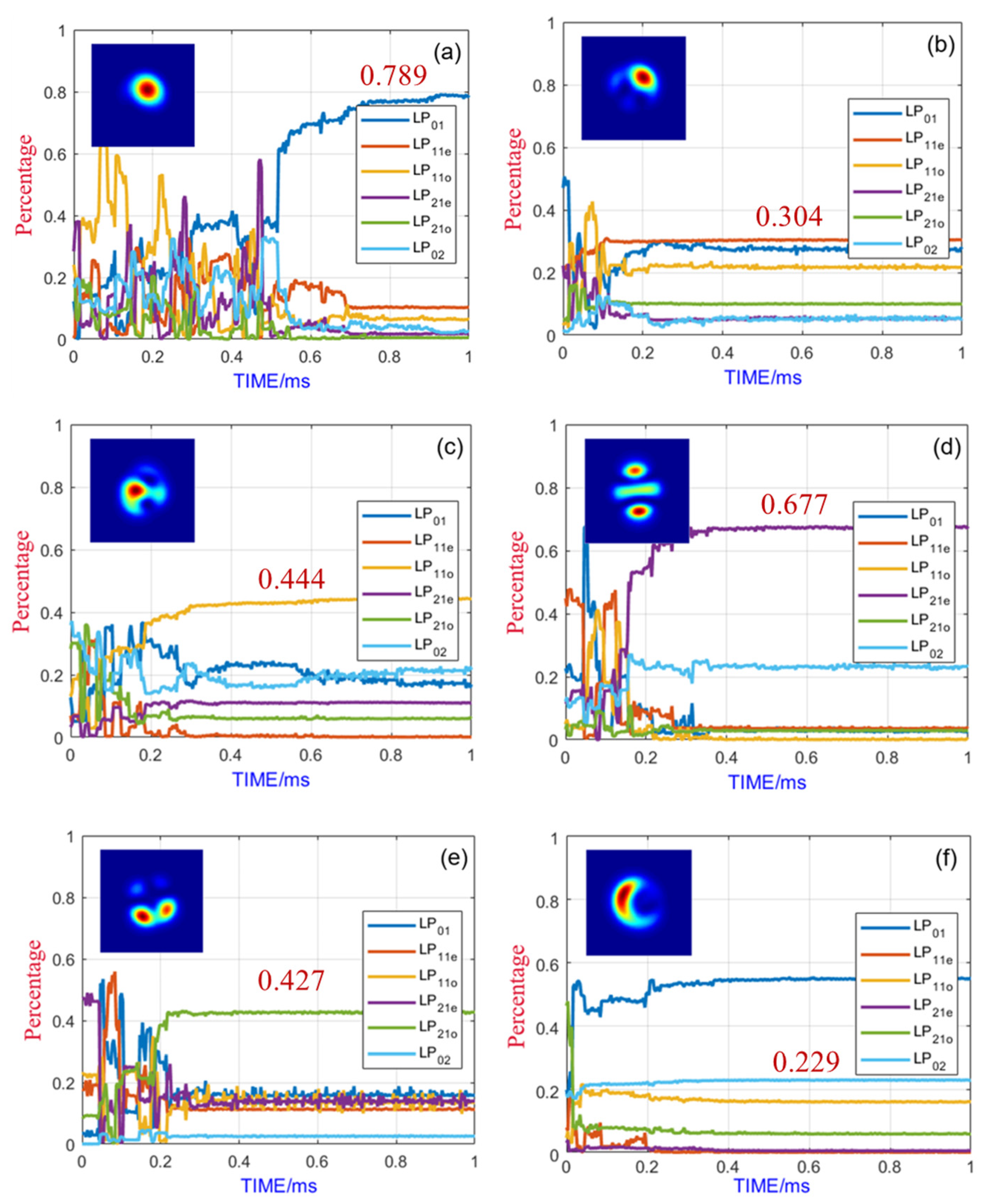

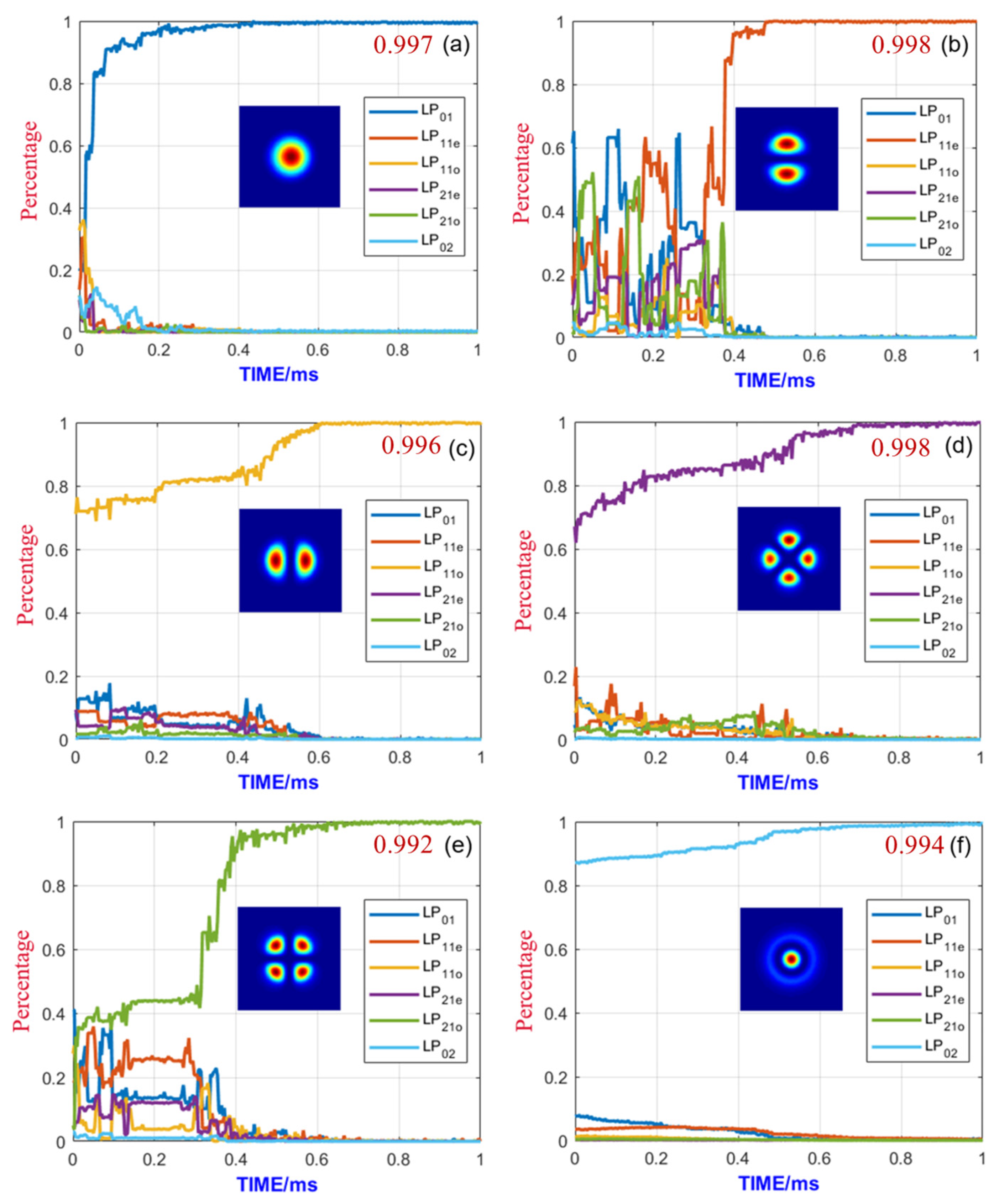
| Mode Content | Random | Equal | Transmission Matrix-Inspired |
|---|---|---|---|
| LP01 | 78.9% | 99.1% | 99.7% |
| LP11e | 30.4% | 70.0% | 99.8% |
| LP11o | 44.4% | 78.7% | 99.6% |
| LP21e | 67.7% | 65.0% | 99.8% |
| LP21o | 42.7% | 59.5% | 99.2% |
| LP02 | 22.9% | 30.0% | 99.4% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Q.; Lu, Y.; Li, C.; Chai, J.; Zhang, D.; Liu, P.; Zhang, J.; Jiang, Z.; Liu, W. Transmission Matrix-Inspired Optimization for Mode Control in a 6 × 1 Photonic Lantern-Based Fiber Laser. Photonics 2023, 10, 390. https://doi.org/10.3390/photonics10040390
Zhou Q, Lu Y, Li C, Chai J, Zhang D, Liu P, Zhang J, Jiang Z, Liu W. Transmission Matrix-Inspired Optimization for Mode Control in a 6 × 1 Photonic Lantern-Based Fiber Laser. Photonics. 2023; 10(4):390. https://doi.org/10.3390/photonics10040390
Chicago/Turabian StyleZhou, Qiong, Yao Lu, Changjin Li, Junyu Chai, Dan Zhang, Pengfei Liu, Jiangbin Zhang, Zongfu Jiang, and Wenguang Liu. 2023. "Transmission Matrix-Inspired Optimization for Mode Control in a 6 × 1 Photonic Lantern-Based Fiber Laser" Photonics 10, no. 4: 390. https://doi.org/10.3390/photonics10040390
APA StyleZhou, Q., Lu, Y., Li, C., Chai, J., Zhang, D., Liu, P., Zhang, J., Jiang, Z., & Liu, W. (2023). Transmission Matrix-Inspired Optimization for Mode Control in a 6 × 1 Photonic Lantern-Based Fiber Laser. Photonics, 10(4), 390. https://doi.org/10.3390/photonics10040390





