Design of Full Stokes Vector Polarimetry Based on Metasurfaces for Wide-Angle Incident Light
Abstract
1. Introduction
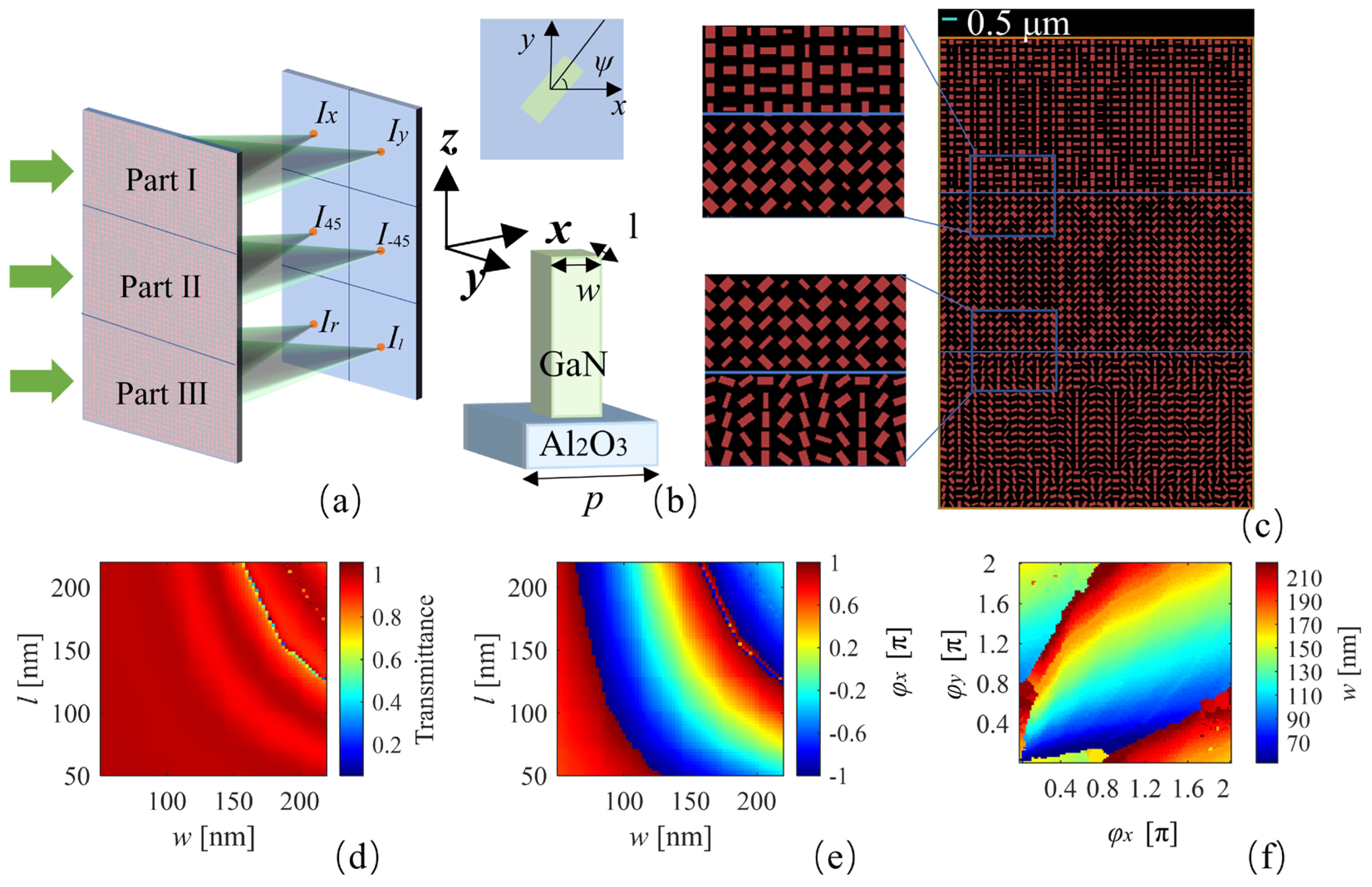
2. Proposed Metasurface-Based Polarimetry
3. Results and Discussion
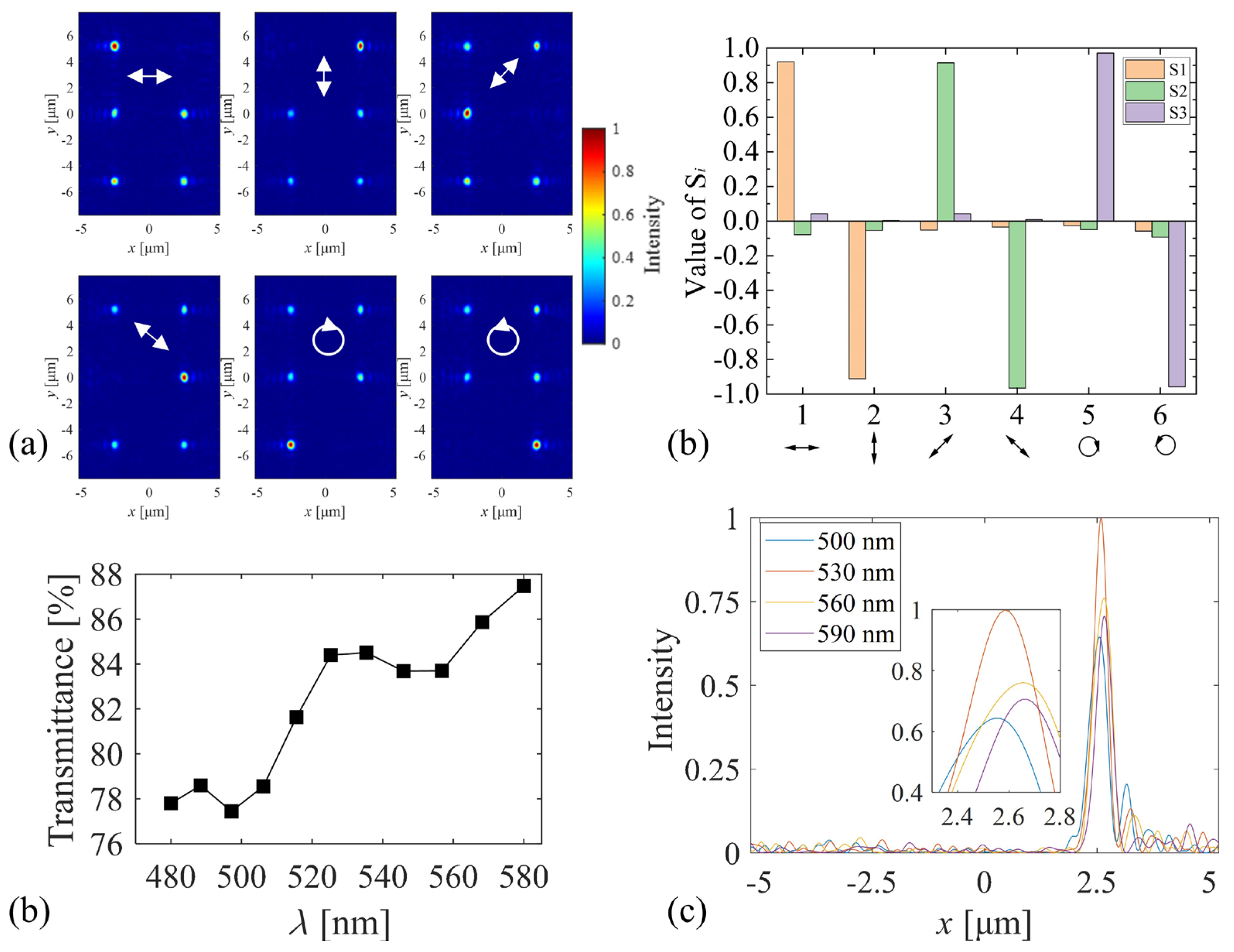
3.1. Stokes Vector Detection for Vertical Incident Light
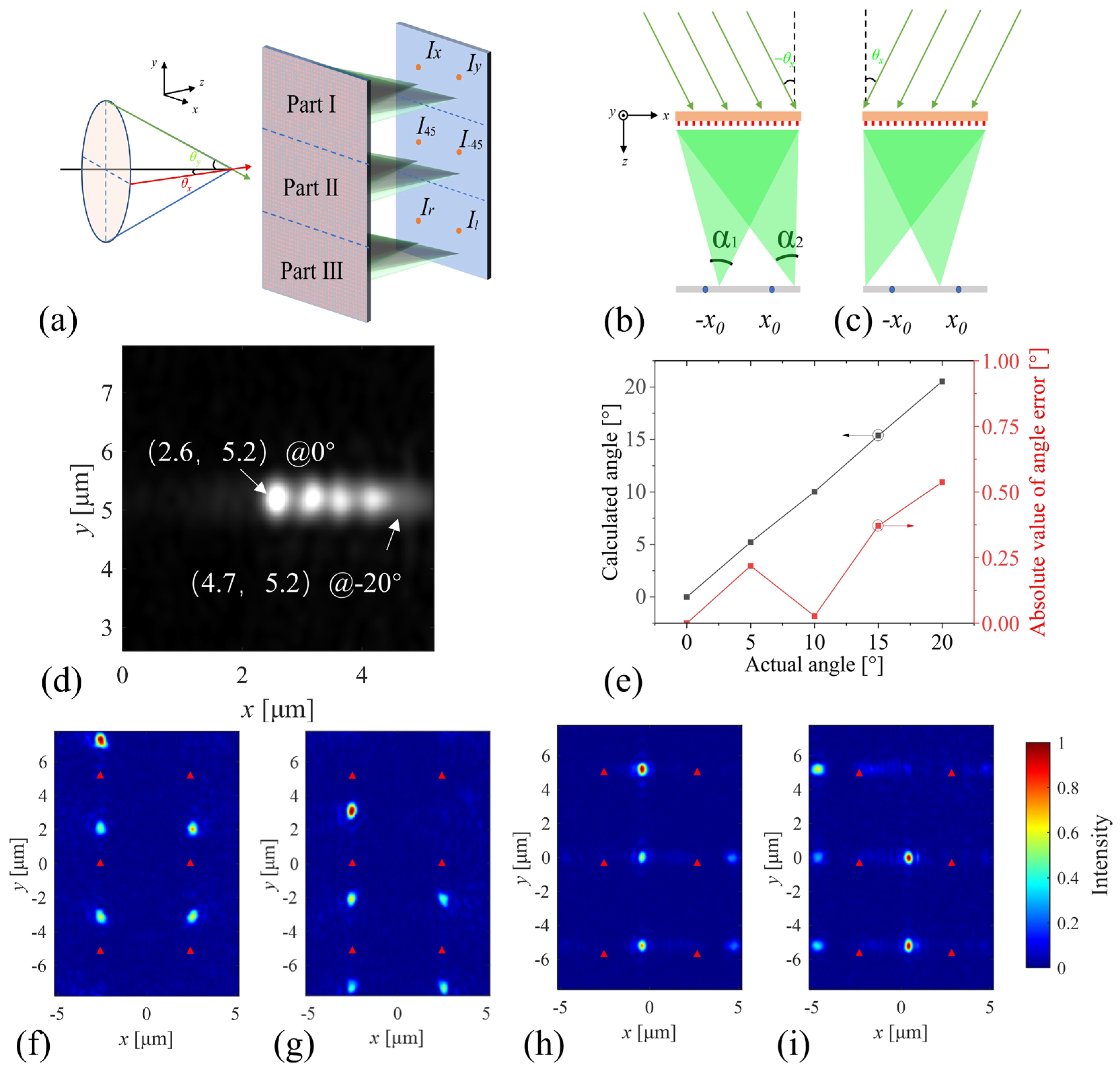
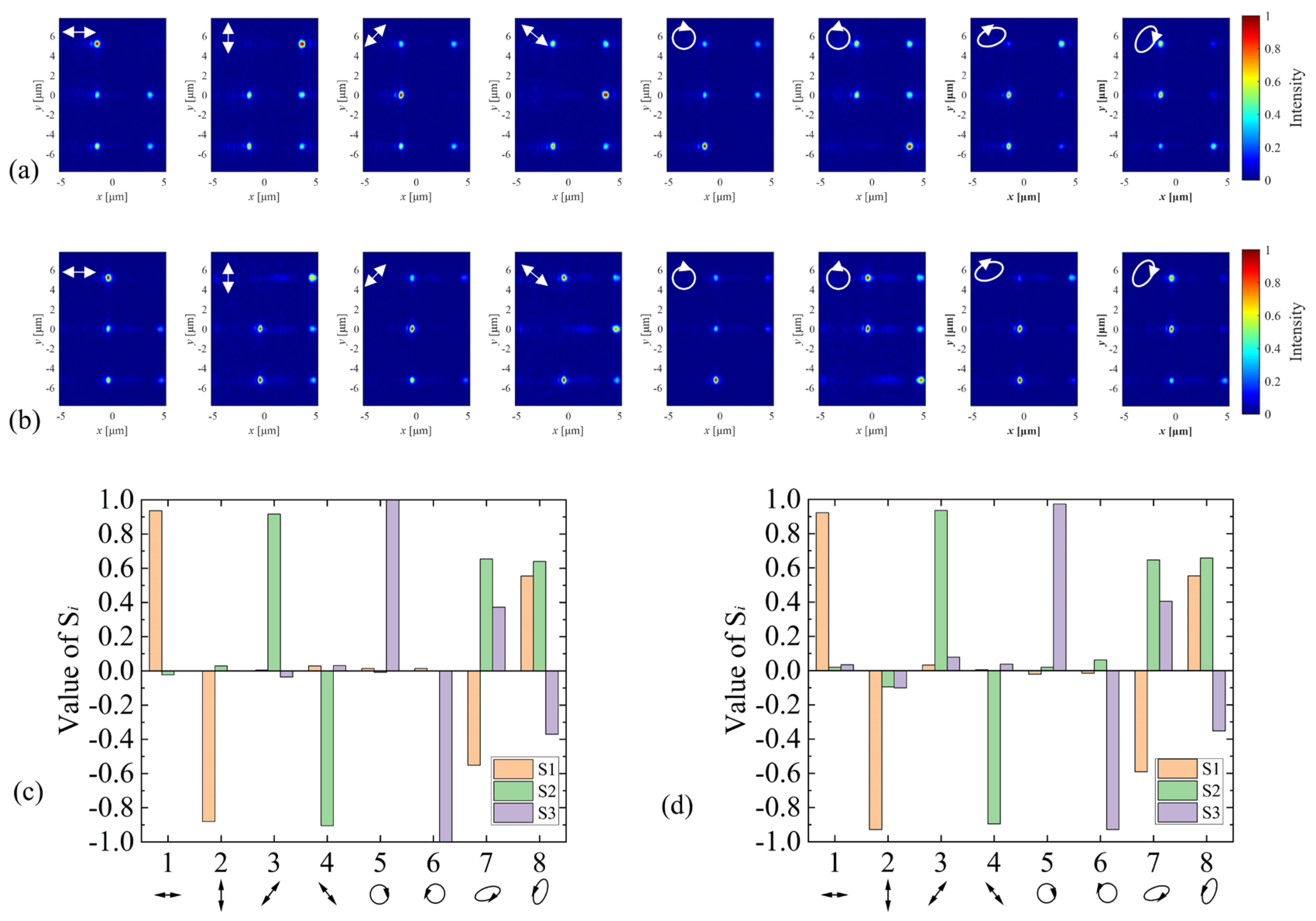
3.2. Stokes Vector Detection for Oblique Incident Light
3.3. Modified Coefficient for Oblique Incident Light
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dupeyroux, J.; Serres, J.R.; Viollet, S. AntBot: A six-legged walking robot able to home like desert ants in outdoor environments. Sci. Robot. 2019, 4, eaau0307. [Google Scholar] [CrossRef]
- Tyo, J.S.; Goldstein, D.L.; Chenault, D.B.; Shaw, J.A. Review of passive imaging polarimetry for remote sensing applications. Appl. Opt. 2006, 45, 5453–5469. [Google Scholar] [CrossRef] [PubMed]
- Dou, C.; Wang, S.; Zhang, Z.; Huang, Y.; Yang, X.; Li, B. The design of atmosphere polarimetry sensing with multi-bands. Opt. Commun. 2018, 410, 863–866. [Google Scholar] [CrossRef]
- Okoshi, T.; Kikuchi, K. Coherent Optical Fiber Communications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1988; Volume 4. [Google Scholar]
- Antonelli, M.-R.; Pierangelo, A.; Novikova, T.; Validire, P.; Benali, A.; Gayet, B.; De Martino, A. Mueller matrix imaging of human colon tissue for cancer diagnostics: How Monte Carlo modeling can help in the interpretation of experimental data. Opt. Express 2010, 18, 10200–10208. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Li, J.; Liao, R.; Chen, Y.; Liu, T.; Wang, Y.; Zhang, X.; Ma, H. Profile probing of suspended particles in water by Stokes vector polarimetry. Opt. Express 2022, 30, 14924–14937. [Google Scholar] [CrossRef]
- Shen, Y.; Lin, W.; Wang, Z.; Li, J.; Sun, X.; Wu, X.; Wang, S.; Huang, F. Rapid detection of camouflaged artificial target based on polarization imaging and deep learning. IEEE Photonics J. 2021, 13, 1–9. [Google Scholar] [CrossRef]
- Liu, T.; Yu, S.; Zhu, X.; Liao, R.; Zhuo, Z.; He, Y.; Ma, H. In-situ Detection Method for Microplastics in Water by Polarized Light Scattering. Front. Mar. Sci. 2021, 8, 739683. [Google Scholar] [CrossRef]
- Arteaga, O.; Kahr, B. Mueller matrix polarimetry of bianisotropic materials. J. Opt. Soc. Am. B 2019, 36, F72–F83. [Google Scholar] [CrossRef]
- Azzam, R. Photopolarimeter using two modulated optical rotators. Opt. Lett. 1977, 1, 181–183. [Google Scholar] [CrossRef]
- Gori, F. Measuring Stokes parameters by means of a polarization grating. Opt. Lett. 1999, 24, 584–586. [Google Scholar] [CrossRef]
- Krishnan, S.; Hampton, S.; Rix, J.; Taylor, B.; Azzam, R.M. Spectral polarization measurements by use of the grating division-of-amplitude photopolarimeter. Appl. Opt. 2003, 42, 1216–1227. [Google Scholar] [CrossRef] [PubMed]
- Pezzaniti, J.L.; Chenault, D.B. A division of aperture MWIR imaging polarimeter. In Proceedings of the Polarization Science and Remote Sensing II, San Diego, CA, USA, 31 July–4 August 2005; pp. 239–250. [Google Scholar]
- York, T.; Gruev, V. Characterization of a visible spectrum division-of-focal-plane polarimeter. Appl. Opt. 2012, 51, 5392–5400. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Mei, S.; Huang, K.; Qiu, C.W. Advances in full control of electromagnetic waves with metasurfaces. Adv. Opt. Mater. 2016, 4, 818–833. [Google Scholar] [CrossRef]
- Hsiao, H.H.; Chu, C.H.; Tsai, D.P. Fundamentals and applications of metasurfaces. Small Methods 2017, 1, 1600064. [Google Scholar] [CrossRef]
- Overvig, A.C.; Shrestha, S.; Malek, S.C.; Lu, M.; Stein, A.; Zheng, C.; Yu, N. Dielectric metasurfaces for complete and independent control of the optical amplitude and phase. Light Sci. 2019, 8, 92. [Google Scholar] [CrossRef] [PubMed]
- Myhre, G.; Hsu, W.-L.; Peinado, A.; LaCasse, C.; Brock, N.; Chipman, R.A.; Pau, S. Liquid crystal polymer full-stokes division of focal plane polarimeter. Opt. Express 2012, 20, 27393–27409. [Google Scholar] [CrossRef]
- Mueller, J.P.B.; Rubin, N.A.; Devlin, R.C.; Groever, B.; Capasso, F. Metasurface Polarization Optics: Independent Phase Control of Arbitrary Orthogonal States of Polarization. Phys. Rev. Lett. 2017, 118, 113901. [Google Scholar] [CrossRef]
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.-P.; Capasso, F.; Gaburro, Z. Light propagation with phase discontinuities: Generalized laws of reflection and refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef]
- Yu, N.; Capasso, F. Flat optics with designer metasurfaces. Nat. Mater. 2014, 13, 139–150. [Google Scholar] [CrossRef]
- Zheng, G.; Mühlenbernd, H.; Kenney, M.; Li, G.; Zentgraf, T.; Zhang, S. Metasurface holograms reaching 80% efficiency. Nat. Nanotechnol. 2015, 10, 308–312. [Google Scholar] [CrossRef]
- Kamali, S.M.; Arbabi, E.; Arbabi, A.; Faraon, A. A review of dielectric optical metasurfaces for wavefront control. Nanophotonics 2018, 7, 1041–1068. [Google Scholar] [CrossRef]
- Erçağlar, V.; Hajian, H.; Serebryannikov, A.E.; Ozbay, E. Multifunctional tunable gradient metasurfaces for terahertz beam splitting and light absorption. Opt. Lett. 2021, 46, 3953–3956. [Google Scholar] [CrossRef]
- Park, C.-S.; Koirala, I.; Gao, S.; Shrestha, V.R.; Lee, S.-S.; Choi, D.-Y. Structural color filters based on an all-dielectric metasurface exploiting silicon-rich silicon nitride nanodisks. Opt. Express 2019, 27, 667–679. [Google Scholar] [CrossRef] [PubMed]
- Pors, A.; Nielsen, M.G.; Bozhevolnyi, S.I. Plasmonic metagratings for simultaneous determination of Stokes parameters. Optica 2015, 2, 716–723. [Google Scholar] [CrossRef]
- Guo, Z.; Xu, H.; Guo, K.; Shen, F.; Zhou, H.; Zhou, Q.; Gao, J.; Yin, Z. High-efficiency visible transmitting polarizations devices based on the GaN metasurface. Nanomaterials 2018, 8, 333. [Google Scholar] [CrossRef]
- Arbabi, E.; Kamali, S.M.; Arbabi, A.; Faraon, A. Full-Stokes imaging polarimetry using dielectric metasurfaces. ACS Photonics 2018, 5, 3132–3140. [Google Scholar] [CrossRef]
- Zhang, Y.; Jin, J.; Pu, M.; He, Q.; Guo, Y.; Li, X.; Ma, X.; Luo, X. Full Stokes Polarimetry for Wide-Angle Incident Light. Phys. Status Solidi-Rapid Res. Lett. 2020, 14, 2000044. [Google Scholar] [CrossRef]
- Solonenko, M.G.; Mobley, C.D. Inherent optical properties of Jerlov water types. Appl. Opt. 2015, 54, 5392–5401. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, R.; Fan, Y.; Cheng, H.; Guan, C.; Chu, J. A novel method for the design of a full Stokes polarimeter based on dielectric metasurfaces. Optik 2022, 261, 169198. [Google Scholar] [CrossRef]
- Li, X.; Wang, H.; Xu, X.; Ju, L.; Fan, Z.; Chen, S. Mid-infrared full-Stokes polarization detection based on dielectric metasurfaces. Opt. Commun. 2021, 484, 126690. [Google Scholar] [CrossRef]
- Yu, G.; Wang, G.; Ishikawa, H.; Umeno, M.; Soga, T.; Egawa, T.; Watanabe, J.; Jimbo, T. Optical properties of wurtzite structure GaN on sapphire around fundamental absorption edge (0.78–4.77 eV) by spectroscopic ellipsometry and the optical transmission method. Appl. Phys. Lett. 1997, 70, 3209–3211. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Zhang, Z.; Cheng, J.; Wang, X.; Sun, S.; Xu, J. Design of Full Stokes Vector Polarimetry Based on Metasurfaces for Wide-Angle Incident Light. Photonics 2023, 10, 382. https://doi.org/10.3390/photonics10040382
Liu S, Zhang Z, Cheng J, Wang X, Sun S, Xu J. Design of Full Stokes Vector Polarimetry Based on Metasurfaces for Wide-Angle Incident Light. Photonics. 2023; 10(4):382. https://doi.org/10.3390/photonics10040382
Chicago/Turabian StyleLiu, Songjie, Zejun Zhang, Jingxuan Cheng, Xiyin Wang, Shixiao Sun, and Jing Xu. 2023. "Design of Full Stokes Vector Polarimetry Based on Metasurfaces for Wide-Angle Incident Light" Photonics 10, no. 4: 382. https://doi.org/10.3390/photonics10040382
APA StyleLiu, S., Zhang, Z., Cheng, J., Wang, X., Sun, S., & Xu, J. (2023). Design of Full Stokes Vector Polarimetry Based on Metasurfaces for Wide-Angle Incident Light. Photonics, 10(4), 382. https://doi.org/10.3390/photonics10040382





