Abstract
The transmission properties in two-dimensional plasma photonic crystal composed of plasma and yttrium–iron–garnet rods with square lattices are demonstrated under different electron densities and external magnetic fields. The TE and TM modes respond to the permittivity tensor and the permeability tensor produced by the magnetic field. For TM polarization, two distinct attenuation peaks appear in the ranges of 3.4–3.62 GHz and 3.78–4 GHz, induced by the external magnetic fields, and the location of these attenuation peaks can be modulated by modifying the electron densities. For TE polarization, a flat transmission spectrum was obtained in the range of 4–4.6 dB by increasing the electron density to . Then, a Y-shaped plasma photonic crystal waveguide is designed. The transmission path can be modulated by changing the direction of the external magnetic field. By regulating the electron density, switching the Y-shaped waveguide on and off can be achieved.
1. Introduction
Photonic crystals (PCs) consist of dielectric materials with periodic structures, which produce a photonic bandgap due to the Bragg scattering effect [,]. The band structure in PCs is analogous to the electron dispersion relationship in solids, and the operating wavelength of photonic crystals is comparable to the lattice constant. Owing to their unique ability to manipulate electromagnetic waves, PCs have been studied extensively. Numerous interesting phenomena have been discovered, including super-transmission, slow light, super-prismatic and topological effects [,,,,]. Subsequently, practical devices have been developed such as optical splitters, slow light waveguides, and optical isolators based on these extraordinary effects [,,]. Once the material parameters or lattice constants of the PCs have been determined, their band structures are also confirmed, significantly limiting their practical applications.
Plasma, as a metamaterial, is widely used in space communication and device stealth due to its tunable and reconfigurable properties [,,,]. H. Hojo theoretically constructed a one-dimensional plasma photonic crystal (PPC) by periodically arranging quartz and plasma. It was found that periodic attenuation peaks appeared in the microwave range, and that the positions of the peaks could be adjusted by means of electron density []. This novel design endowed PCs with tunable properties, attracting a lot of attention. O. Sakai creatively constructed a two-dimensional periodic array of microplasma columns by means of dielectric barrier discharge [,]. The designed PPC attenuated the electromagnetic signal of the TM mode at 33 GHz and enhanced the signal of the TE mode. Meanwhile, dynamic T-junctions controlled by plasma could be used to regulate the transmittance of electromagnetic waves. A tunable double negative-refractive-index device consisting of discharge tubes and split-ring resonators was constructed to study the transmission properties of electromagnetic waves. The transmission peak of the device could be regulated by controlling the discharge currents []. B. Wang designed a reconfigurable plasma photonic crystal device by introducing a layer of eight plasma discharge tubes into the spherical silicon nitride elements. The resonance peaks were regulated by switching the plasma tubes on and off []. W. Fan used the dielectric barrier discharge method to generate periodic microplasma structures. A Lieb lattice was formed between the mesh electrode and the water electrode, which is a form of self-organization. The Dirac flat band was found at the M point of the reduced Brillouin zone. The experimental results showed that the center frequency of the attenuation peak shifted from 29.5 GHz to 30 GHz, and could be adjusted using the applied voltage []. In general, tuning and reconfiguration of the properties of PPCs are realized by adjusting the electron density, which can be controlled easily by means of the discharge current, gas pressure, and gas composition. In a stable uniform magnetic field, the response function of the plasma to the electromagnetic field is a gyrodielectric tensor. This property, in turn, is able to modulate the propagation of electromagnetic waves. M. Lin designed a PC structure composed of plasma and ferrite. By controlling the magnetic field, high isolation and insertion loss were achieved for TE and TM polarizations []. A. H. M. Almawgani proposed a photonic crystal filter with a magnetized plasma defect layer in the terahertz range. The defect layer was sensitive to the TM modes, and the defect mode was investigated under different plasma densities, layer thicknesses, and magnetic fields. Meanwhile, the full width at half maximum of the defect mode was enhanced by means of the applied magnetic field []. Plasma can achieve metallic () or dielectric properties () by tuning the electron density. In addition, magnetized plasmas with anisotropic permittivity can lead to gyrotropic responses. These behaviors enable the realization of tunable and reconfigurable microwave devices.
In this work, a plasma photonic crystal is presented consisting of plasma and yttrium–iron–garnet (YIG) rods with square lattices. The transmittance of electromagnetic waves is calculated using the finite element method. Furthermore, the role of the magnetic field, electron density, and collision frequency in PPCs is theoretically analyzed. Finally, the designed Y-shaped waveguide can be controlled by using different electron densities and magnetic fields.
2. Physical Model
Figure 1 shows a schematic diagram of the two-dimensional plasma photonic crystal. A square lattice was selected for this work, and a composite structure is constructed within the unit cell. The red area represents the YIG and the violet area represents the plasma. The focus of this work is on the propagation of electromagnetic waves in PPCs in the microwave range. Therefore, the lattice constant of a unit cell was set as , the radius of the YIG rod was , and the outer radius of the plasma ring was . For the non-magnetized discharge plasma, the relative permittivity of the gaseous plasma was expressed using the Drude equation [,]:
where represents the plasma frequency, represents the angular frequency of the incident wave, and represents the collision frequency between the electrons and molecules. The plasma frequency is typically denoted as
where denote the plasma electron density, the unit charge, the vacuum relative permittivity, and the electron mass. Fluorescent lamps are remarkably stable devices for generating gaseous plasma, and are widely used for the construction of plasma-related tunable devices such as microwave modulators, filters, and plasma antennas [,,,]. The measured electron density for the fluorescent lamp is between and , and the collision frequency is close to 15 GHz []. Experimental parameters were defined in line with this reference in order to facilitate subsequent practical applications.
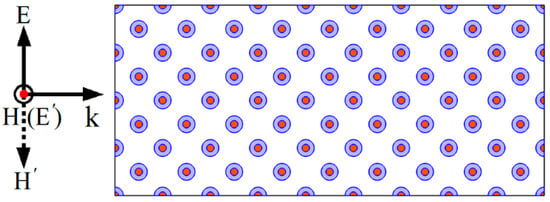
Figure 1.
Schematic of a two-dimensional plasma photonic crystal. YIG rods (red), plasma (violet). Solid lines represent TE () polarization and dashed lines represent TM ( ) polarization.
Magnetic fields provide a flexible method for manipulating electromagnetic waves []. When considering a uniform and a stable magnetic field, the response function of the plasma to the electromagnetic field is that of a gyrodielectric tensor [], which is expressed as
where and represent the components parallel and perpendicular to the magnetic fields. The off-diagonal term describes the gyroscopic strength of the magnetized plasma. The expressions are as follows:
where the cyclotron frequency is controlled by the applied magnetic fields, which are given by . In this case, the TE () mode responds to a permittivity tensor according to the electric displacement vector . However, when the direction of the applied magnetic field is perpendicular to the z-axis, both the TE and TM polarizations of the electromagnetic waves may be affected []. At the same time, the response of the gyromagnetic materials YIG to the magnetic field is also in tensor form, as follows:
YIG materials exhibit anisotropy under stronger magnetic fields. The tensor elements are usually taken as and when the applied field is 1600 Gauss []. The permeability tensor is valid for TM () modes. The wave-optics module of Comsol was used in the simulation. To solve the Maxwell equations, the electromagnetic wave frequency domain interface was chosen. Periodic ports were used to generate plane waves with an incident angle of 0°, ensuring that the electromagnetic waves were incident perpendicular to the boundary. The Drude–Lorentz dispersive model was used to define the plasma permittivity. Meanwhile, the mesh setting is important for obtaining a precise solution. The maximum cell size of the YIG and plasma area was set to . The remainder were set to , where denotes the smallest wavelength in the simulated range. The model was divided by free triangulation.
3. Results and Discussion
3.1. The Effect of Magnetic Field and Electron Density for the TM Polarization
Firstly, we consider collisionless plasma () and investigate the effects of the magnetic field and electron density on the transmission properties. In this case, an incident wave with TM polarization was employed. When the magnetic field was absent and the plasma electron density was set as , the transmittance was extremely high—in the range of 3.4 GHz to 4.2 GHz, as shown by the black line in Figure 2. When a magnetic field of 1600 Gauss was applied in the z-direction, the Bragg scattering effect of the plasma–YIG composite was modified by the permeability tensor, resulting in two distinct attenuation peaks in the ranges of 3.4–3.62 GHz and 3.78–4 GHz (see red curve). We next increased the electron density to , and found that the attenuation peaks shifted to high frequencies. Thus, we realized the propagation and attenuation of electromagnetic waves by controlling the magnetic field, and the position of the peak could be modulated by adjusting the electron density.
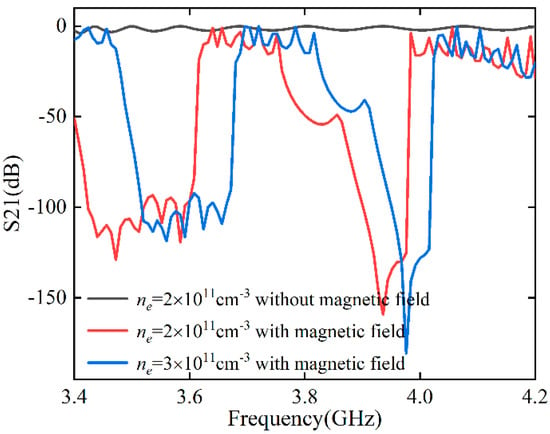
Figure 2.
Transmission spectra of the PPC for different electron densities with or without magnetic fields when considering TM polarization.
According to the Drude model, the permittivity of plasma is complex. Collisions between electrons and neutral examples can result in the attenuation of electromagnetic waves. When electromagnetic waves propagate through a large area of plasma, the incident waves are attenuated in a broad frequency range. However, this situation would be different in periodic structures. Next, we investigated the effect of collision frequency on transmittance in the presence of a magnetic field and with electron density fixed at . The results are shown in Figure 3. It can be seen that the electromagnetic waves are strongly attenuated with a collision frequency of . The energy of the electromagnetic wave decays gradually from left to right, as shown in the electric field distributions, and the energy is concentrated on the YIG rods. It is worth noting that the original attenuation peaks are still present due to the Bragg scattering effect.
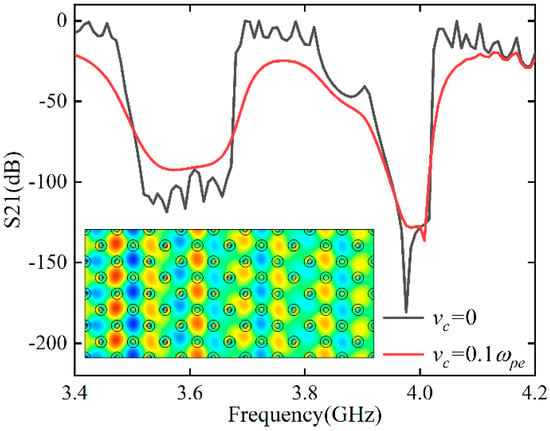
Figure 3.
Transmission spectra of the PPC for the TM mode considering a collision frequency of .
3.2. The Effect of Magnetic Field and Electron Density for the TE Polarization
In this section, we mainly focus on of the incident waves with TE polarization, i.e., magnetic induction along the z-axis direction, because the permittivity tensor caused by the applied magnetic field affects the TE mode. The influence of magnetic fields when the electron density was fixed at is shown in Figure 4. There is a wide attenuation peak in the range of 4.3–4.75 GHz when the magnetic field strength is 0. The position of the attenuation peak shifts to the right when the magnetic field strength is increased to 100 Gauss. When the magnetic field strength is fixed at 300 Gauss, the original attenuation peak disappears, and a new attenuation peak emerges in the range of 5.2–5.4 GHz.
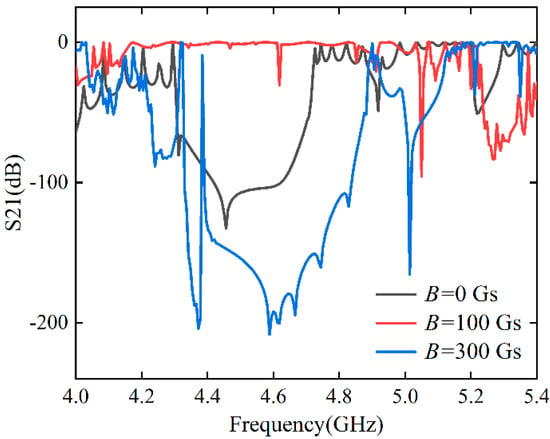
Figure 4.
The transmission spectra of the PPC at different magnetic fields considering TE polarization.
The influence of electron density on transmittance when the magnetic field strength is 300 Gauss is shown in Figure 5. When the electron density is increased to , the original attenuation peak at 5.2–5.4 GHz disappears, and a new attenuation peak emerges at around 5.05 GHz. This is not a simple frequency shift, but the creation of a new forbidden band structure. More interestingly, the transmittance is close to 0 dB in the range of 4–4.6 GHz with weak Fabry–Perot resonance, as seen in the red line, which facilitates the design of tunable devices with high transmittance.
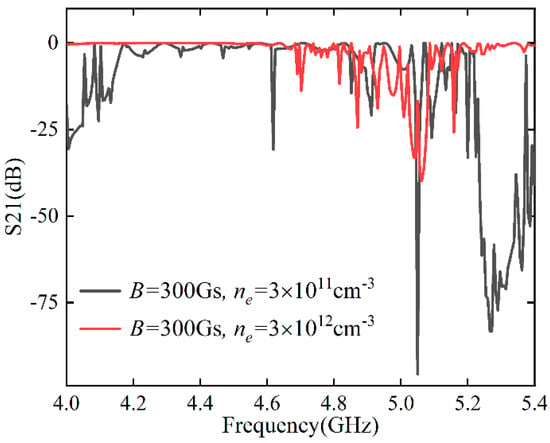
Figure 5.
For TE polarization, the transmission spectra of the PPC at different electron densities.
3.3. The Y-Shaped Tunable PPC Waveguide
Subsequently, we designed a Y-shaped PPC waveguide and investigated the TM mode as an example. The PPC waveguide was also composed of plasma–YIG composites with square lattices, with the insertion of a Y-shaped metal plate. The scattering boundary condition was imposed on the outer edges. The plane wave was emitted from the left boundary. The electric distribution with an electron density of and the application of an external magnetic field of 1600 Gauss along the +z direction is shown in Figure 6a. Before the electromagnetic wave encounters the metal plate, it propagates uniformly through the waveguide structure and is gradually attenuated on both sides. When the electromagnetic wave encounters the metal plate, it is squeezed into the upper part due to the gyromagnetic properties of the YIG. In the other part, electromagnetic waves are completely prohibited. When the applied magnetic field is changed along the -z direction, the energy of the electromagnetic wave becomes concentrated in the lower part. The upper channel prohibits the propagation of electromagnetic waves. Therefore, we achieve effective regulation of electromagnetic waves in the Y-shaped PPC waveguide by regulating the direction of the external magnetic field.
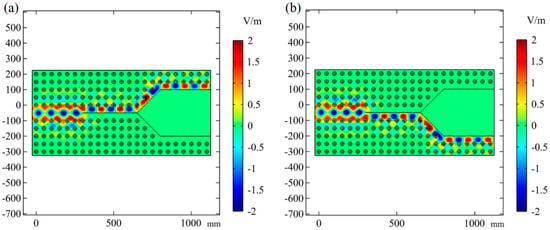
Figure 6.
The electric field distribution for the Y-shaped waveguide when the magnetic field is along the (a) +z direction; (b) −z direction.
In addition to the effect of applying a magnetic field, the plasma electron density is a similarly effective tuning parameter in plasma photonic crystal waveguides. The simulation results for when the plasma was turned off, i.e., when the plasma electron density was 0, are shown in Figure 7a. In contrast with Figure 6, it can be seen that the electromagnetic wave propagates only in the waveguide in front of the Y-shaped metal, while propagation in the upper and lower channels is forbidden. It is worth noting that the electromagnetic waves spread to the inside of the PPC and are gradually attenuated. In this way, the opening and closing of the PPC waveguide can be controlled by turning the plasma on or off. Next, the magnetic field was turned off while maintaining the electron density at , and the results are shown in Figure 7b. It can be seen that electromagnetic waves also propagate in the front part of the metal plate, but are forbidden at metal boundaries. From this, it can be concluded that only the cooperation of plasma and external magnetic field are able to effectively control the Y-shaped PPC waveguide. By controlling the plasma parameters and the applied magnetic field, we theoretically studied the effects of electron density, collision frequency and magnetic field strength on the propagation of electromagnetic waves. A Y-shaped waveguide was designed to support different paths of energy flow. At the same time, our research is also easy to implement experimentally. Plasma can be generated using gas discharge techniques such as capacitively coupled discharge and inductively coupled discharge, while electron density and collision frequency are adjusted by external voltage. A Helmholtz coil can be employed to generate a uniform magnetic field. The entire plasma photonic crystal can be placed in a waveguide to prevent free-space scattering.
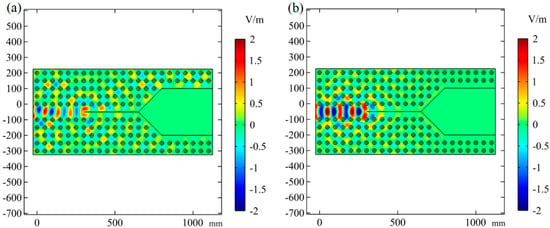
Figure 7.
The electric field distribution for the Y-shaped waveguide when (a) the plasma is absent or (b) the external magnetic field is absent.
4. Conclusions
In the present work, we focused on the effects of an external magnetic field, plasma electron density, and collision frequency on the transport properties of two-dimensional plasma photonic crystals. The external magnetic field causes the permittivity of the plasma and the permeability of the YIG to take a tensor form, which can significantly affect the transmission characteristics of electromagnetic waves. Because of the dependence of permittivity or permeability tensors on polarization, we investigated the TM and TE modes separately under the applied magnetic field. The transmittance and field distribution of the incident waves in PPC were calculated by means of full-wave simulation (COMSOL Multiphysics). For the TM polarization, the external magnetic fields induced two distinct attenuation peaks in the ranges of 3.4–3.62 GHz and 3.78–4 GHz when the collision frequency was ignored. With increasing electron density, the position of the peak moved toward higher frequencies. By this method, it was possible to arbitrarily control the transmission of electromagnetic waves and block them in specific frequencies by regulating the electron density. In addition, the electromagnetic waves were strongly attenuated when the collision frequency was considered. However, the location of the prohibition for electromagnetic waves did not change. For the TE polarization, the transmission rules were affected by the applied magnetic field. When the magnetic field strength was fixed at 300 Gauss, it was possible to obtain a flat transmission spectrum (near 0 dB) in the range of 4–4.6 dB by increasing the electron density by an order of magnitude. Based on the above research, we designed a Y-shaped PPC waveguide. When the electron was and the external magnetic field was along the +z direction, electromagnetic waves were able to propagate in the upper part of the waveguide. The electromagnetic wave energy was concentrated in the lower part of the waveguide when the magnetic field was in the opposite direction. The opening and closing of the PPC waveguide could be controlled by turning on or off the plasma. More importantly, achieving effective modulation of electromagnetic waves in the designed Y-shaped PPC waveguide required both the magnetic field and the plasma electron density to be set.
Author Contributions
Conceptualization, J.Y. and H.-P.L.; methodology, H.W. and J.Y.; software, H.W.; validation, J.L., L.G. and D.M.; formal analysis, H.-P.L.; investigation, H.W.; resources, L.G.; data curation, J.Y.; writing—original draft preparation, H.W.; writing—review and editing, H.W.; visualization, D.M.; supervision, H.-P.L.; project administration, L.G.; funding acquisition, J.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of China (Nos. 12205067).
Institutional Review Board Statement
The study did not require ethical approval.
Informed Consent Statement
The study did not involve humans.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author.
Acknowledgments
All individuals agree to the acknowledgement.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yablonovitch, E. Inhibited Spontaneous Emission in Solid-State Physics and Electronics. Phys. Rev. Lett. 1987, 58, 2059. [Google Scholar] [CrossRef] [PubMed]
- John, S. Strong Localization of Photons in Certain Disordered Dielectric Super Lattices. Phys. Rev. Lett. 1987, 58, 2486–2489. [Google Scholar] [CrossRef] [PubMed]
- Kosaka, H.; Kawashima, T.; Tomita, A.; Notomi, M.; Tamamura, T.; Sato, T.; Kawakami, S. Superprism phenomena in photonic crystals. Phys. Rev. B 1998, 58, R10096. [Google Scholar] [CrossRef]
- Hu, X.; Chan, C.T. Photonic crystals with silver nanowires as a near-infrared superlens. Appl. Phys. Lett. 2004, 85, 1520–1522. [Google Scholar] [CrossRef]
- Xie, X.; Yan, S.; Dang, J.; Yang, J.; Xiao, S.; Wang, Y.; Shi, S.; Yang, L.; Dai, D.; Yuan, Y.; et al. Topological Cavity Based on Slow-Light Topological Edge Mode for Broadband Purcell Enhancement. Phys. Rev. Appl. 2021, 16, 014036. [Google Scholar] [CrossRef]
- Lu, L.; Joannopoulos, J.D.; Soljačić, M. Topological photonics. Nat. Photonics 2014, 8, 821–829. [Google Scholar] [CrossRef]
- Liu, G.; Wang, F.; Gao, Y.; Jia, B.; Guan, X.; Lu, P.; Song, H. Topology Optimization of Low-Loss Z-Bend 2D Photonic Crystal Waveguide. Photonics 2023, 10, 202. [Google Scholar] [CrossRef]
- He, C.; Chen, X.-L.; Lu, M.-H.; Li, X.-F.; Wan, W.-W.; Qian, X.-S.; Yin, R.-C.; Chen, Y.-F. Tunable one-way cross-waveguide splitter based on gyromagnetic photonic crystal. Appl. Phys. Lett. 2010, 96, 111111. [Google Scholar] [CrossRef]
- Le Thomas, N.; Zhang, H.; Jágerská, J.; Zabelin, V.; Houdré, R.; Sagnes, I.; Talneau, A. Light transport regimes in slow light photonic crystal waveguides. Phys. Rev. B 2009, 80, 125332. [Google Scholar] [CrossRef]
- Yu, Z.; Wang, Z.; Fan, S. One-way total reflection with one-dimensional magneto-optical photonic crystals. Appl. Phys. Lett. 2007, 90, 121133. [Google Scholar] [CrossRef]
- Wen, Y.; Liu, S.; Zhang, H.; Wang, L. The absorber realized by 2D photonic crystals with plasma constituents. J. Phys. Appl. Phys. 2018, 51, 025108. [Google Scholar] [CrossRef]
- Kamboj, G.K.; Yadav, R.P.; Kaler, R.S. Development of Reconfigurable Plasma Column Antenna. IEEE Trans. Plasma Sci. 2021, 49, 656–662. [Google Scholar] [CrossRef]
- Li, J.; Yao, J.; Yuan, C.; Wang, Y.; Zhou, Z.; Zhang, J. Tunable transmission near Dirac-like point in the designed plasma photonic crystal. Phys. Plasmas 2022, 29, 033505. [Google Scholar] [CrossRef]
- Liang, Y.; Liu, Z.; Peng, J.; Lin, L.; Lin, R.; Lin, Q. Study on Transmission Characteristics and Bandgap Types of Plasma Photonic Crystal. Photonics 2021, 8, 401. [Google Scholar] [CrossRef]
- Hojo, H.; Mase, A. Dispersion Relation of Electromagnetic Waves in One-Dimensional Plasma Photonic Crystals. J. Plasma Fusion Res. 2004, 80, 89–90. [Google Scholar] [CrossRef]
- Sakai, O.; Sakaguchi, T.; Ito, Y.; Tachibana, K. Interaction and control of millimetre-waves with microplasma arrays. Plasma Phys. Control. Fusion 2005, 47, B617–B627. [Google Scholar] [CrossRef]
- Sakai, O.; Sakaguchi, T.; Tachibana, K. Photonic bands in two-dimensional microplasma arrays. I. Theoretical derivation of band structures of electromagnetic waves. J. Appl. Phys. 2007, 101, 073304. [Google Scholar] [CrossRef]
- Iwai, A.; Righetti, F.; Wang, B.; Sakai, O.; Cappelli, M.A. A tunable double negative device consisting of a plasma array and a negative-permeability metamaterial. Phys. Plasmas 2020, 27, 023511. [Google Scholar] [CrossRef]
- Wang, B.; Rodríguez, J.A.; Miller, O.; Cappelli, M.A. Reconfigurable plasma-dielectric hybrid photonic crystal as a platform for electromagnetic wave manipulation and computing. Phys. Plasmas 2021, 28, 043502. [Google Scholar] [CrossRef]
- Fan, W.; Jia, M.; Zhu, P.; Liu, C.; Hou, X.; Zhang, J.; He, Y.; Liu, F. Realization of tunable plasma Lieb lattice in dielectric barrier discharges. APL Photonics 2022, 7, 116105. [Google Scholar] [CrossRef]
- Lin, M.; Fu, L.; Ahmed, S.; Wang, Q.; Zheng, Y.; Liang, Z.; Ouyang, Z. Polarization-Independent Circulator Based on Composite Rod of Ferrite and Plasma in Photonic Crystal Structure. Nanomaterials 2021, 11, 381. [Google Scholar] [CrossRef]
- Almawgani, A.H.M.; Alhamss, D.N.; Taya, S.A.; Colak, I.; Sharma, A.; Alhawari, A.R.H.; Patel, S.K. The properties of a tunable terahertz filter based on a photonic crystal with a magnetized plasma defect layer. Phys. Fluids 2022, 34, 082020. [Google Scholar] [CrossRef]
- Drude, P. Zur Elektronentheorie der Metalle. Ann. Phys. 1900, 306, 566–613. [Google Scholar] [CrossRef]
- Wu, S.; Chen, Y.; Liu, M.; Yang, L.; Zhang, C.; Liu, S. Numerical study on the modulation of THz wave propagation by collisional microplasma photonic crystal. Plasma Sci. Technol. 2020, 22, 115402. [Google Scholar] [CrossRef]
- Wang, B.; Cappelli, M.A. A plasma photonic crystal bandgap device. Appl. Phys. Lett. 2016, 108, 161101. [Google Scholar] [CrossRef]
- Wang, B.; Cappelli, M.A. A tunable microwave plasma photonic crystal filter. Appl. Phys. Lett. 2015, 107, 171107. [Google Scholar] [CrossRef]
- Howlader, M.K.; Yang, Y.; Roth, J.R. Time-resolved measurements of electron number density and collision frequency for a fluorescent lamp plasma using microwave diagnostics. IEEE Trans. Plasma Sci. 2005, 33, 1093–1099. [Google Scholar] [CrossRef]
- Li, J.; Zhou, C.; Yao, J.; Yuan, C.; Wang, Y.; Zhou, Z.; Zhang, J.; Kudryavtsev, A.A. Valley-dependent topological edge states in plasma photonic crystals. Plasma Sci. Technol. 2023, 25, 035001. [Google Scholar] [CrossRef]
- Guo, Z.; Long, Y.; Jiang, H.; Ren, J.; Chen, H. Anomalous unidirectional excitation of high-k hyperbolic modes using all-electric metasources. Adv. Photonics 2021, 3, 036001. [Google Scholar] [CrossRef]
- Houriez, L.S.; Mehrpour Bernety, H.; Rodríguez, J.A.; Wang, B.; Cappelli, M.A. Experimental study of electromagnetic wave scattering from a gyrotropic gaseous plasma column. Appl. Phys. Lett. 2022, 120, 223101. [Google Scholar] [CrossRef]
- Hu, S.; Song, J.; Guo, Z.; Jiang, H.; Deng, F.; Dong, L.; Chen, H. Omnidirectional nonreciprocal absorber realized by the magneto-optical hypercrystal. Opt. Express. 2022, 30, 12104–12119. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Chong, Y.D.; Joannopoulos, J.D.; Soljačić, M. Reflection-Free One-Way Edge Modes in a Gyromagnetic Photonic Crystal. Phys. Rev. Lett. 2008, 100, 013905. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).