Exclusive Effect in Rydberg Atom-Based Multi-Band Microwave Communication
Abstract
1. Introduction
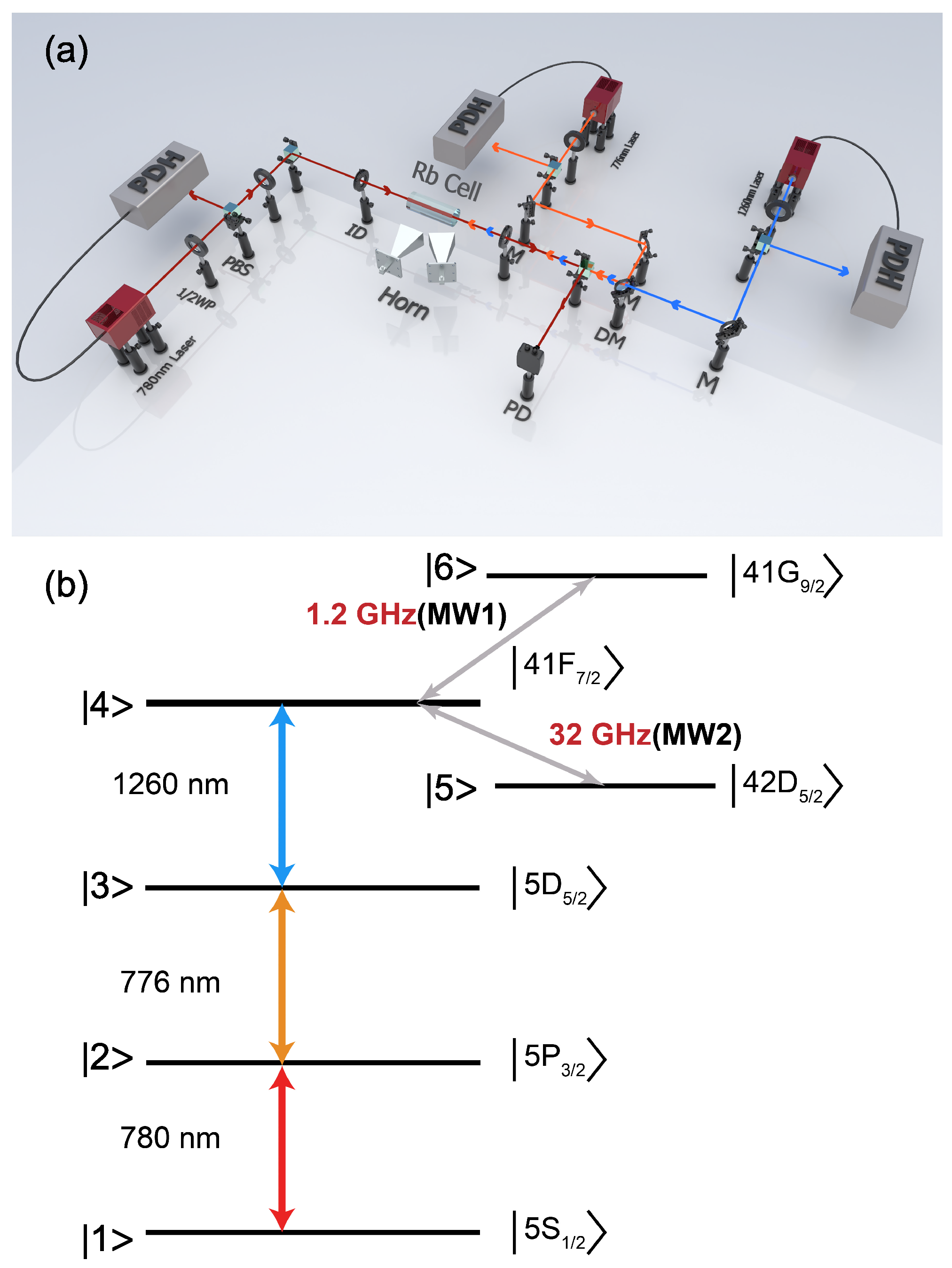
2. Experiment Setup
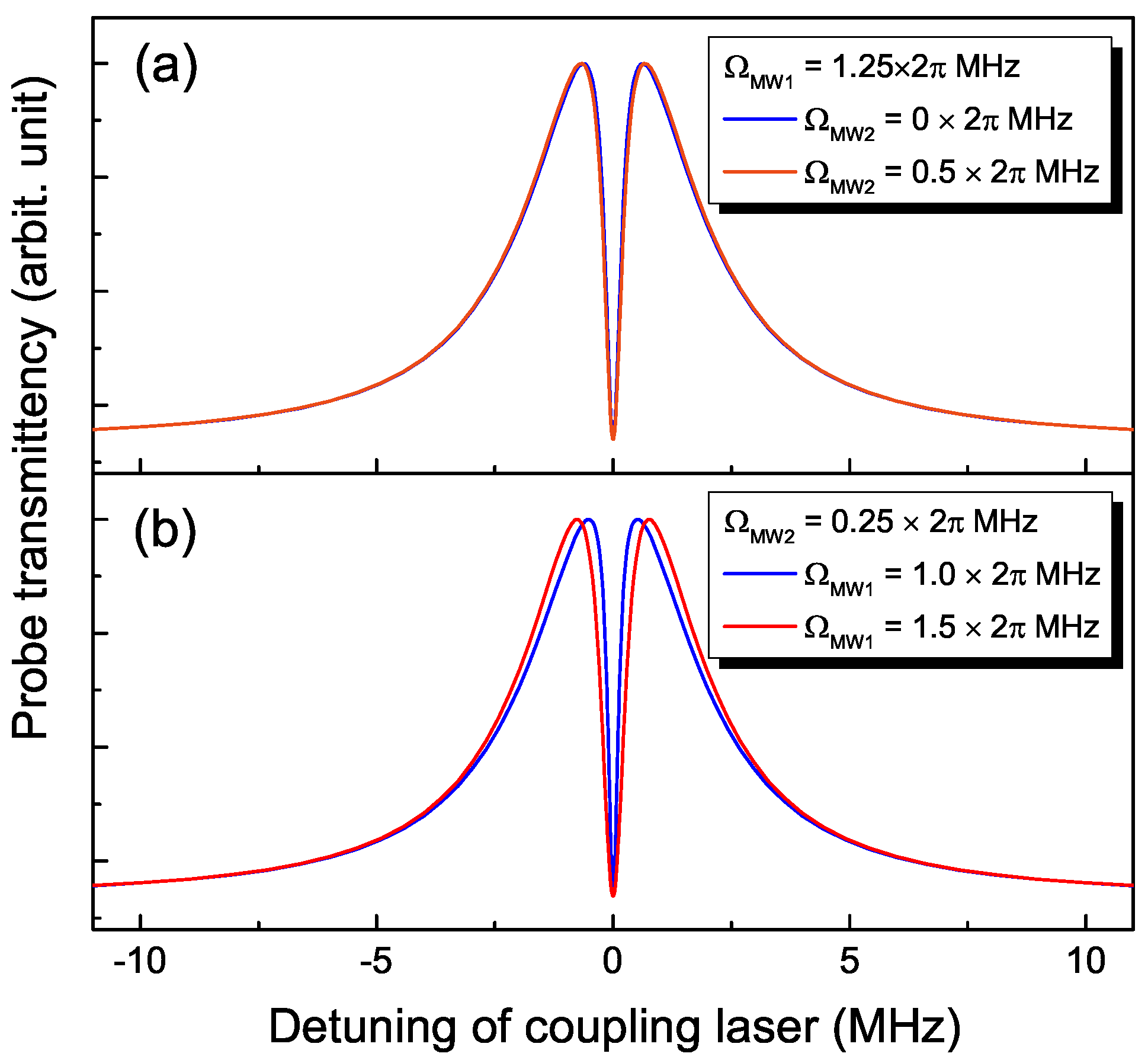
3. Theory
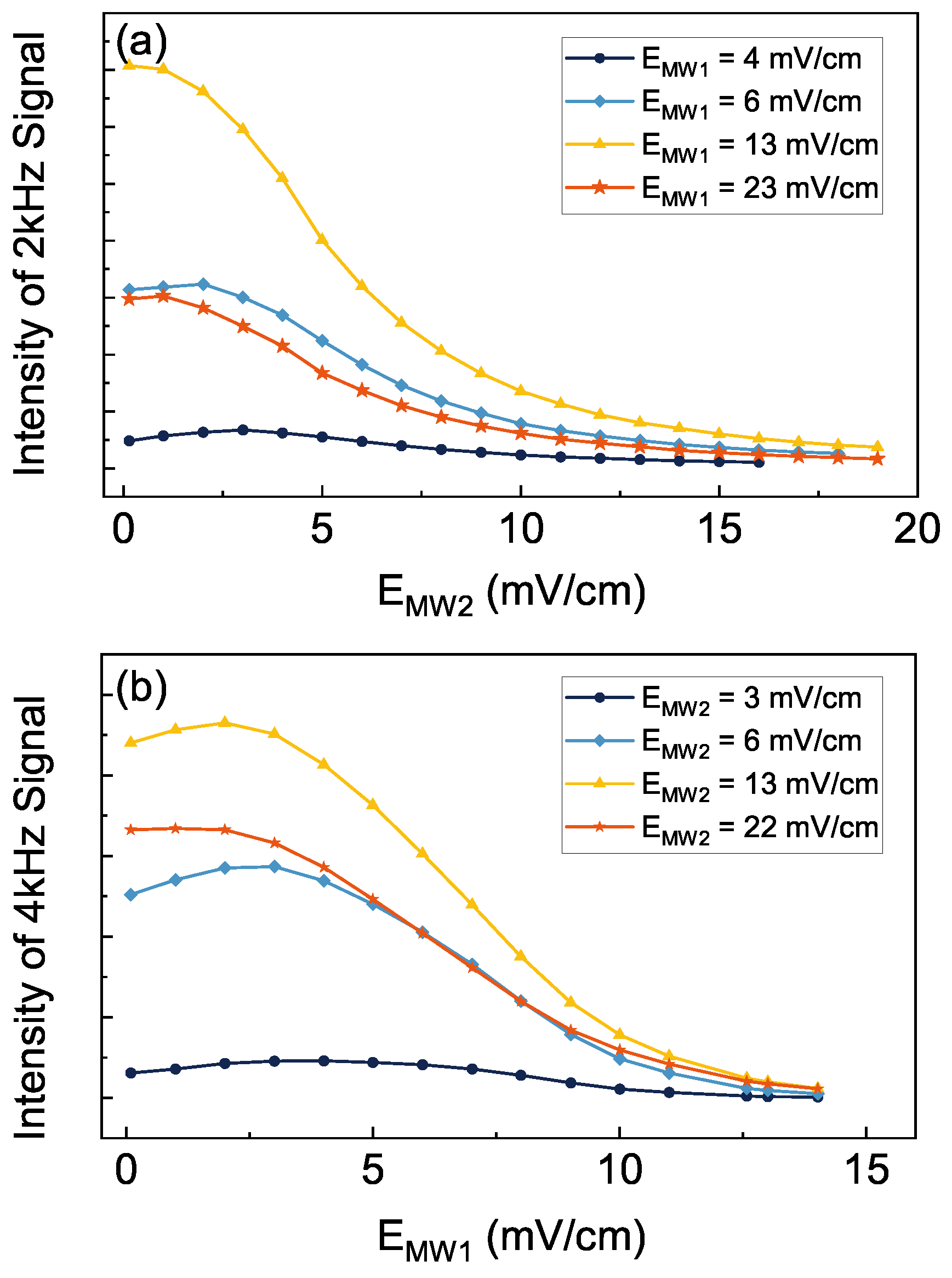
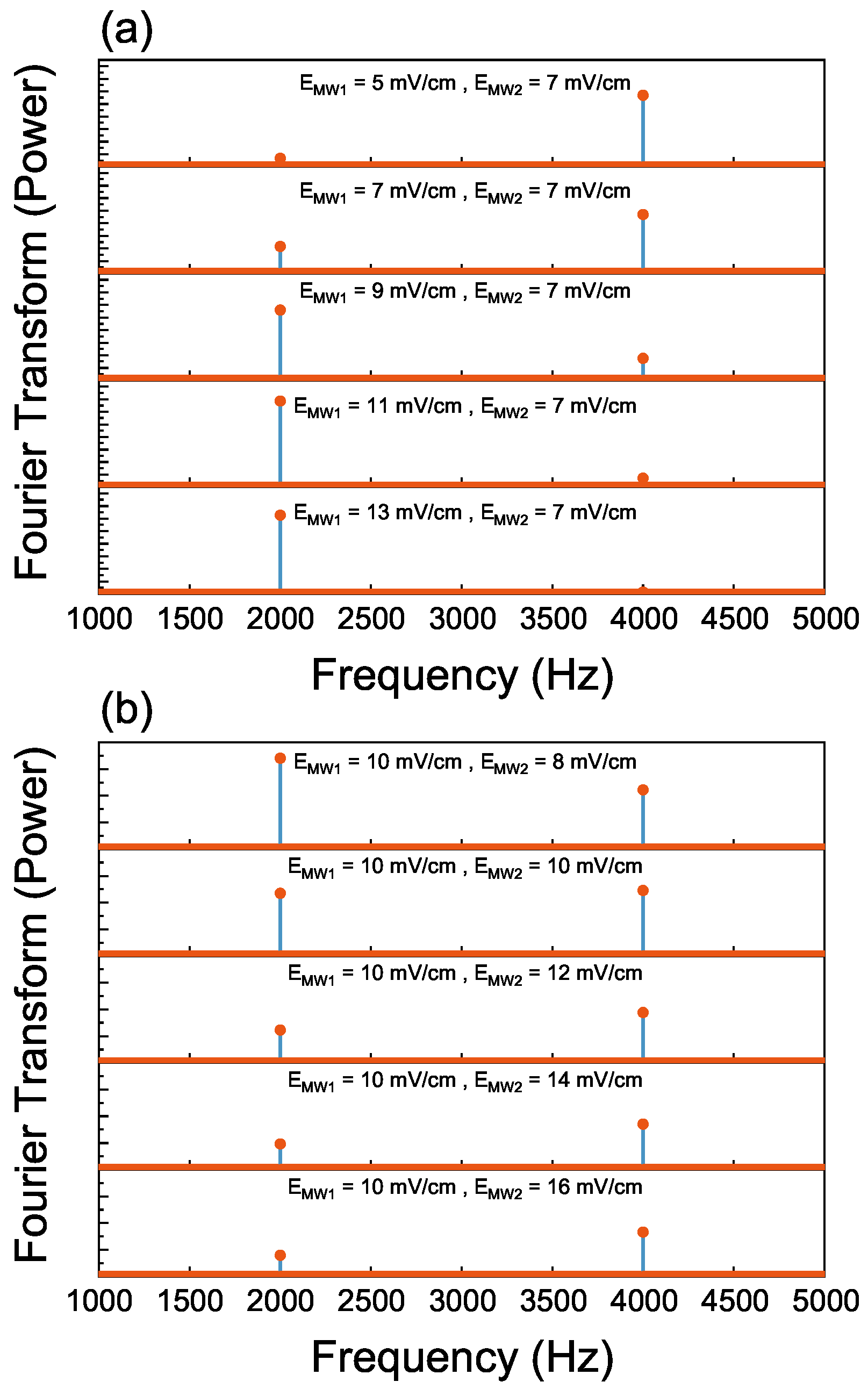
4. Result and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Osterwalder, A.; Merkt, F. Using High Rydberg States as Electric Field Sensors. Phys. Rev. Lett. 1999, 82, 1831–1834. [Google Scholar] [CrossRef]
- Mohapatra, A.K.; Jackson, T.R.; Adams, C.S. Coherent Optical Detection of Highly Excited Rydberg States Using Electromagnetically Induced Transparency. Phys. Rev. Lett. 2007, 98, 113003. [Google Scholar] [CrossRef]
- Kübler, H.; Shaffer, J.P.; Baluktsian, T.; Löw, R.; Pfau, T. Coherent excitation of Rydberg atoms in micrometre-sized atomic vapour cells. Nat. Photon. 2010, 4, 112–116. [Google Scholar] [CrossRef]
- Holloway, C.L.; Gordon, J.A.; Jefferts, S.; Schwarzkopf, A.; Anderson, D.A.; Miller, S.A.; Thaicharoen, N.; Raithel, G. Broadband Rydberg atom-based electric-field probe for SI-traceable, self-calibrated measurements. IEEE Trans. Antennas Propag. 2014, 62, 6169–6182. [Google Scholar] [CrossRef]
- Holloway, C.L.; Simons, M.T.; Gordon, J.A.; Wilson, P.F.; Cooke, C.M.; Anderson, D.A.; Raithel, G. Atom-Based RF Electric Field Metrology: From Self-Calibrated Measurements to Subwavelength and Near-Field Imaging. IEEE Trans. Antennas Propag. 2017, 59, 717–728. [Google Scholar] [CrossRef]
- Anderson, D.A.; Sapiro, R.E.; Raithel, G. A Self-Calibrated SI-Traceable Rydberg Atom-Based Radio Frequency Electric Field Probe and Measurement Instrument. IEEE Trans. Antennas Propag. 2021, 69, 5931–5941. [Google Scholar] [CrossRef]
- Jing, M.; Hu, Y.; Ma, J.; Zhang, H.; Zhang, L.; Xiao, L.; Jia, S. Atomic superheterodyne receiver based on microwave-dressed Rydberg spectroscopy. Nat. Phys. 2020, 16, 911–915. [Google Scholar] [CrossRef]
- Cai, M.; Xu, Z.; You, S.; Liu, H. Sensitivity Improvement and Determination of Rydberg Atom-Based Microwave Sensor. Photonics 2022, 9, 250. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, L.H.; Liu, Z.K.; Zhang, Z.Y.; Zhu, Z.H.; Gao, W.; Guo, G.C.; Ding, D.S.; Shi, B.S. Highly Sensitive Measurement of a Megahertz rf Electric Field with a Rydberg-Atom Sensor. Phys. Rev. Appl. 2022, 18, 014045. [Google Scholar] [CrossRef]
- Meyer, D.H.; Kunz, P.D.; Cox, K.C. Waveguide-Coupled Rydberg Spectrum Analyzer from 0 to 20 GHz. Phys. Rev. Appl. 2021, 15, 014053. [Google Scholar] [CrossRef]
- Lin, Y.; She, Z.; Chen, Z.; Li, X.; Zhang, C.; Liao, K.; Zhang, X.; Huang, W.; Yan, H.; Zhu, S. The Room-Temperature Rydberg-Atom Receiver For Terahertz Wireless Communications. arXiv 2022, arXiv:2205.11021. [Google Scholar] [CrossRef]
- Wade, C.G.; Šibalić, N.; de Melo, N.R.; Kondo, J.M.; Adams, C.S.; Weatherill, K.J. Real-time near-field terahertz imaging with atomic optical fluorescence. Nat. Photon. 2017, 11, 40–43. [Google Scholar] [CrossRef]
- Downes, L.A.; MacKellar, A.R.; Whiting, D.J.; Bourgenot, C.; Adams, C.S.; Weatherill, K.J. Full-Field Terahertz Imaging at Kilohertz Frame Rates Using Atomic Vapor. Phys. Rev. X 2020, 10, 011027. [Google Scholar] [CrossRef]
- Sedlacek, J.A.; Schwettmann, A.; Kübler, H.; Löw, R.; Pfau, T.; Shaffer, J.P. Microwave electrometry with Rydberg atoms in a vapour cell using bright atomic resonances. Nat. Phys. 2012, 8, 819–824. [Google Scholar] [CrossRef]
- Kumar, S.; Fan, H.; Kübler, H.; Sheng, J.; Shaffer, J.P. Atom-Based Sensing of Weak Radio Frequency Electric Fields Using Homodyne Readout. Sci. Rep. 2017, 7, 42981. [Google Scholar] [CrossRef]
- Simons, M.T.; Haddab, A.H.; Gordon, J.A.; Holloway, C.L. A Rydberg atom-based mixer: Measuring the phase of a radio frequency wave. Appl. Phys. Lett. 2019, 114, 114101. [Google Scholar] [CrossRef]
- Koepsell, J.; Thiele, T.; Deiglmayr, J.; Wallraff, A.; Merkt, F. Measuring the polarization of electromagnetic fields using Rabi-rate measurements with spatial resolution: Experiment and theory. Phys. Rev. A 2017, 95, 053860. [Google Scholar] [CrossRef]
- Sedlacek, J.A.; Schwettmann, A.; Kubler, H.; Shaffer, J.P. Atom-based vector microwave electrometry using rubidium Rydberg atoms in a vapor cell. Phys. Rev. Lett. 2013, 111, 063001. [Google Scholar] [CrossRef] [PubMed]
- Robinson, A.K.; Prajapati, N.; Senic, D.; Simons, M.T.; Holloway, C.L. Determining the angle-of-arrival of a radio-frequency source with a Rydberg atom-based sensor. Appl. Phys. Lett. 2021, 118, 114001. [Google Scholar] [CrossRef]
- Simons, M.T.; Gordon, J.A.; Holloway, C.L. Fiber-coupled vapor cell for a portable Rydberg atom-based radio frequency electric field sensor. Appl. Opt. 2018, 57, 6456. [Google Scholar] [CrossRef]
- Holloway, C.L.; Gordon, J.A.; Schwarzkopf, A.; Anderson, D.A.; Miller, S.A.; Thaicharoen, N.; Raithel, G. Sub-wavelength imaging and field mapping via electromagnetically induced transparency and Autler-Townes splitting in Rydberg atoms. Appl. Phys. Lett. 2014, 104, 244102. [Google Scholar] [CrossRef]
- Meyer, D.H.; Cox, K.C.; Fatemi, F.K.; Kunz, P.D. Digital communication with Rydberg atoms and amplitude-modulated microwave fields. Appl. Phys. Lett. 2018, 112, 211108. [Google Scholar] [CrossRef]
- Jiao, Y.; Han, X.; Fan, J.; Raithel, G.; Zhao, J.; Jia, S. Atom-based receiver for amplitude-modulated baseband signals in high-frequency radio communication. Appl. Phys. Express 2019, 12, 126002. [Google Scholar] [CrossRef]
- Li, S.; Yuan, J.; Wang, L. Improvement of Microwave Electric Field Measurement Sensitivity via Multi-Carrier Modulation in Rydberg Atoms. Appl. Sci. 2020, 10, 8110. [Google Scholar] [CrossRef]
- Kumar, S.; Fan, H.; Kubler, H.; Jahangiri, A.J.; Shaffer, J.P. Rydberg-atom based radio-frequency electrometry using frequency modulation spectroscopy in room temperature vapor cells. Opt. Express 2017, 25, 8625–8637. [Google Scholar] [CrossRef]
- Anderson, D.A.; Sapiro, R.E.; Raithel, G. An atomic receiver for AM and FM radio communication. IEEE Trans. Antennas Propag. 2020, 69, 2455–2462. [Google Scholar] [CrossRef]
- Holloway, C.L.; Simons, M.T.; Gordon, J.A.; Novotny, D. Detecting and Receiving Phase-Modulated Signals With a Rydberg Atom-Based Receiver. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 1853–1857. [Google Scholar] [CrossRef]
- Simons, M.T.; Artusio-Glimpse, A.B.; Holloway, C.L.; Imhof, E.; Jefferts, S.R.; Wyllie, R.; Sawyer, B.C.; Walker, T.G. Continuous radio-frequency electric-field detection through adjacent Rydberg resonance tuning. Phys. Rev. A 2021, 104, 032824. [Google Scholar] [CrossRef]
- Li, H.; Hu, J.; Bai, J.; Shi, M.; Jiao, Y.; Zhao, J.; Jia, S. Rydberg atom-based AM receiver with a weak continuous frequency carrier. Opt. Express 2022, 30, 13522–13529. [Google Scholar] [CrossRef]
- Holloway, C.L.; Simons, M.T.; Haddab, A.H.; Williams, C.J.; Holloway, M.W. A “real-time” guitar recording using Rydberg atoms and electromagnetically induced transparency: Quantum physics meets music. AIP Adv. 2019, 9, 065110. [Google Scholar] [CrossRef]
- Zou, H.; Song, Z.; Mu, H.; Feng, Z.; Qu, J.; Wang, Q. Atomic Receiver by Utilizing Multiple Radio-Frequency Coupling at Rydberg States of Rubidium. Appl. Sci. 2020, 10, 1346. [Google Scholar] [CrossRef]
- Jia, F.D.; Liu, X.B.; Mei, J.; Yu, Y.H.; Zhang, H.Y.; Lin, Z.Q.; Dong, H.Y.; Zhang, J.; Xie, F.; Zhong, Z.P. Span shift and extension of quantum microwave electrometry with Rydberg atoms dressed by an auxiliary microwave field. Phys. Rev. A 2021, 103, 063113. [Google Scholar] [CrossRef]
- Du, Y.; Cong, N.; Wei, X.; Zhang, X.; Luo, W.; He, J.; Yang, R. Realization of multiband communications using different Rydberg final states. AIP Adv. 2022, 12, 065118. [Google Scholar] [CrossRef]
- Meyer, D.H.; Hill, J.C.; Kunz, P.D.; Cox, K.C. Simultaneous Multiband Demodulation Using a Rydberg Atomic Sensor. Phys. Rev. Appl. 2023, 19. [Google Scholar] [CrossRef]
- Liu, Z.K.; Zhang, L.H.; Liu, B.; Zhang, Z.Y.; Guo, G.C.; Ding, D.S.; Shi, B.S. Deep learning enhanced Rydberg multifrequency microwave recognition. Nat. Commun. 2022, 13, 1997. [Google Scholar] [CrossRef]
- Orazbayev, B.; Fleury, R. Far-field subwavelength acoustic imaging by deep learning. Phys. Rev. X 2020, 10, 031029. [Google Scholar] [CrossRef]
- Carr, C.; Tanasittikosol, M.; Sargsyan, A.; Sarkisyan, D.; Adams, C.S.; Weatherill, K.J. Three-photon electromagnetically induced transparency using Rydberg states. Opt. Lett. 2012, 37, 3858–3860. [Google Scholar] [CrossRef]
- Shaffer, J.; Kübler, H. A read-out enhancement for microwave electric field sensing with Rydberg atoms. Proc. SPIE 2018, 10674, 106740C. [Google Scholar]
- You, S.H.; Cai, M.H.; Zhang, S.S.; Xu, Z.S.; Liu, H.P. Microwave-field sensing via electromagnetically induced absorption of Rb irradiated by three-color infrared lasers. Opt. Express 2022, 30, 16619–16629. [Google Scholar] [CrossRef] [PubMed]
- Black, E.D. An introduction to Pound–Drever–Hall laser frequency stabilization. Am. J. Phys. 2001, 69, 79–87. [Google Scholar] [CrossRef]
- Liao, K.Y.; Tu, H.T.; Yang, S.Z.; Chen, C.J.; Liu, X.H.; Liang, J.; Zhang, X.D.; Yan, H.; Zhu, S.L. Microwave electrometry via electromagnetically induced absorption in cold Rydberg atoms. Phys. Rev. A 2020, 101, 053432. [Google Scholar] [CrossRef]
- Robinson, A.K.; Artusio-Glimpse, A.B.; Simons, M.T.; Holloway, C.L. Atomic spectra in a six-level scheme for electromagnetically induced transparency and Autler-Townes splitting in Rydberg atoms. Phys. Rev. A 2021, 103, 023704. [Google Scholar] [CrossRef]
- Thaicharoen, N.; Moore, K.R.; Anderson, D.A.; Powel, R.C.; Peterson, E.; Raithel, G. Electromagnetically induced transparency, absorption, and microwave-field sensing in a Rb vapor cell with a three-color all-infrared laser system. Phys. Rev. A 2019, 100, 063427. [Google Scholar] [CrossRef]
- Xu, Z.S.; Wang, H.M.; Cai, M.H.; You, S.H.; Liu, H.P. High resolution spectroscopy of Rb in magnetic field by far-detuning electromagnetically induced transparency. Chin. Phys. B 2022, 31, 123201. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, S.; Cai, M.; Zhang, H.; Xu, Z.; Liu, H. Exclusive Effect in Rydberg Atom-Based Multi-Band Microwave Communication. Photonics 2023, 10, 328. https://doi.org/10.3390/photonics10030328
You S, Cai M, Zhang H, Xu Z, Liu H. Exclusive Effect in Rydberg Atom-Based Multi-Band Microwave Communication. Photonics. 2023; 10(3):328. https://doi.org/10.3390/photonics10030328
Chicago/Turabian StyleYou, Shuhang, Minghao Cai, Haoan Zhang, Zishan Xu, and Hongping Liu. 2023. "Exclusive Effect in Rydberg Atom-Based Multi-Band Microwave Communication" Photonics 10, no. 3: 328. https://doi.org/10.3390/photonics10030328
APA StyleYou, S., Cai, M., Zhang, H., Xu, Z., & Liu, H. (2023). Exclusive Effect in Rydberg Atom-Based Multi-Band Microwave Communication. Photonics, 10(3), 328. https://doi.org/10.3390/photonics10030328




