High-Performance Dual-Channel Photonic Crystal Terahertz Wave Modulator Based on the Defect Mode Disappearance of a Combined Microcavity
Abstract
1. Introduction
2. Modulator Structure and Working Mechanism
3. Simulation Results and Discussion
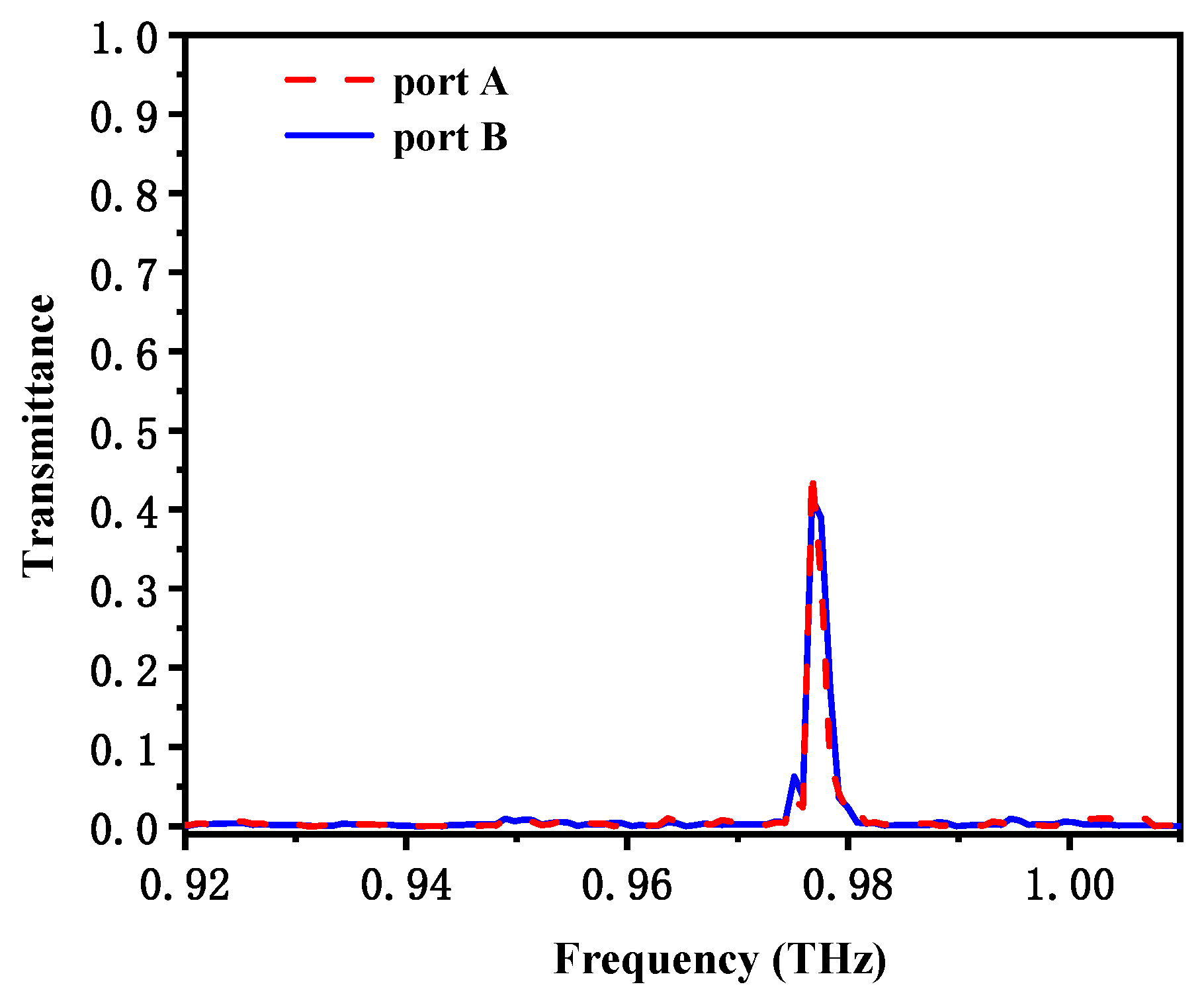
3.1. Selection of Operating Frequency
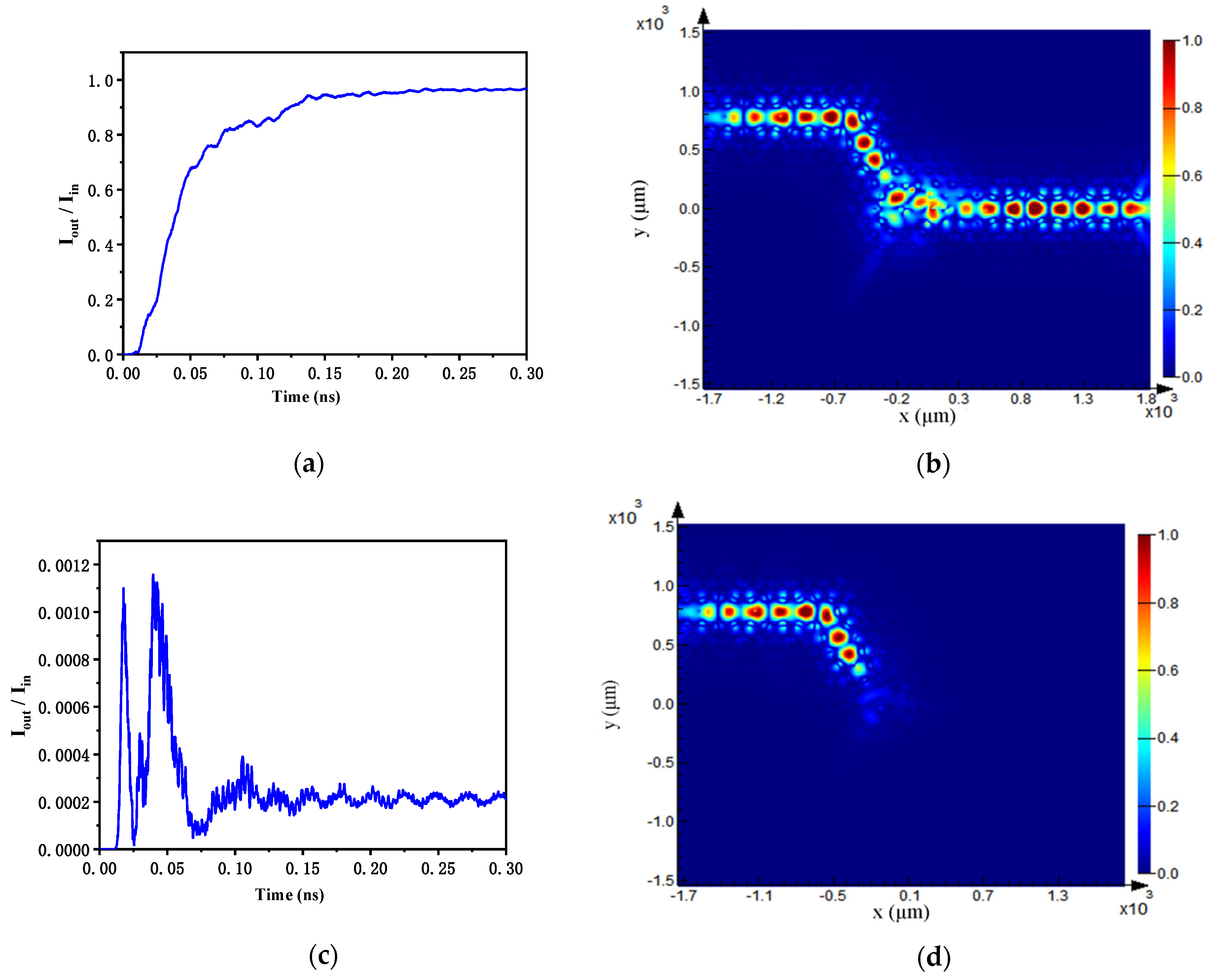
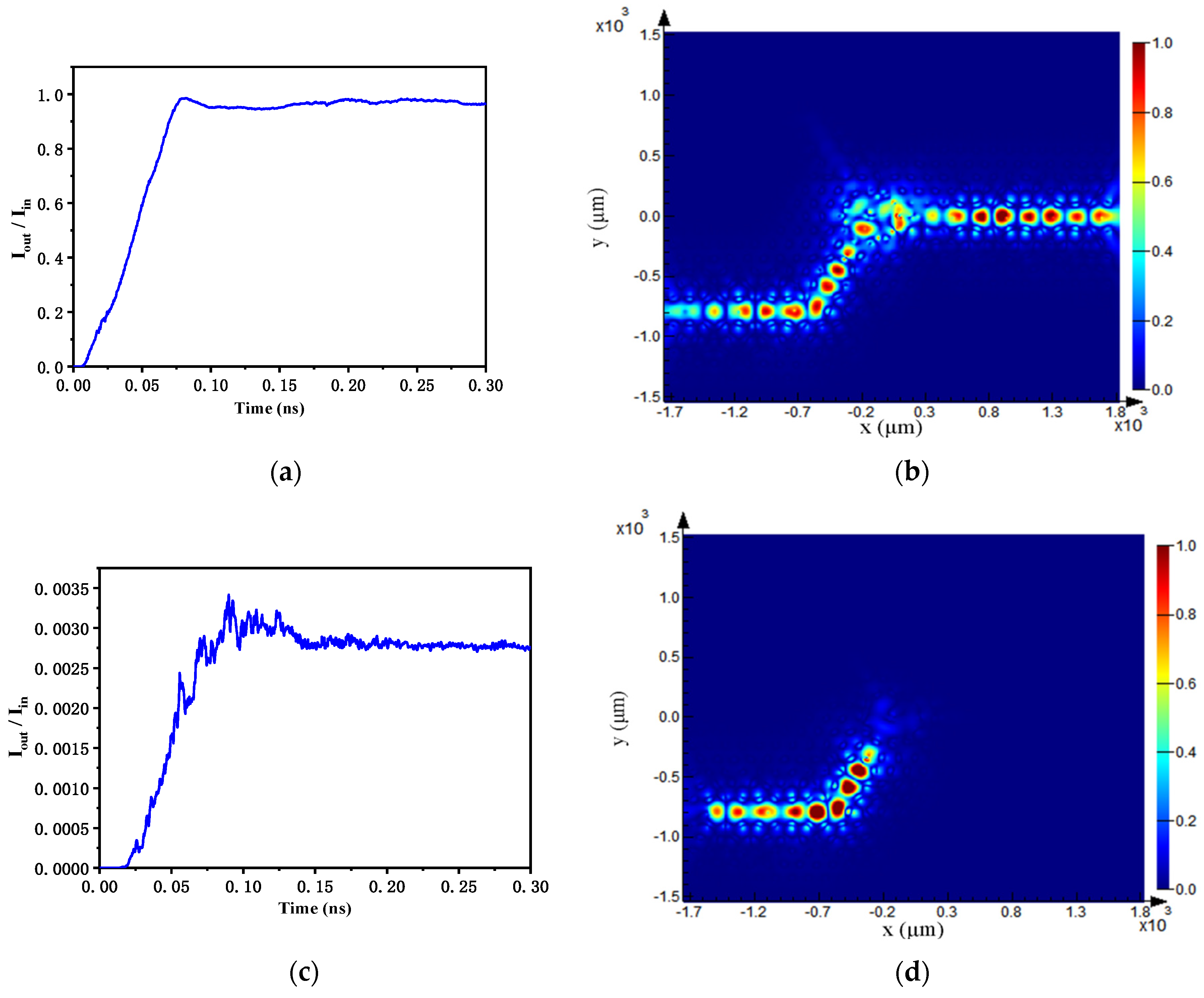
3.2. Modulator Performance Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Victor, P.P. Terahertz technologies and its applications. Electronics 2021, 10, 268. [Google Scholar]
- Ke, L.; Zhang, L. Corneal elastic property investigated by terahertz technology. Sci. Rep. 2022, 12, 19229. [Google Scholar] [CrossRef] [PubMed]
- Willner, A.E.; Su, X.Z. High capacity terahertz communication systems based on multiple orbital-angular-momentum beams. J. Opt.-UK 2022, 24, 124002. [Google Scholar] [CrossRef]
- Wei, M.; Zhang, D. High-performance all-optical terahertz modulator based on graphene/TiO2/Si trilayer heterojunctions. Nanoscale Res. Lett. 2019, 14, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Ma, H.; Wang, Y. A flexible, multifunctional, active terahertz modulator with an ultra-low triggering threshold. J. Mater. Chem. C 2020, 8, 10213–10220. [Google Scholar] [CrossRef]
- Vitor, D.; Geraldo, M. Tunable THz switch-filter based on magneto-plasmonic graphene nanodisk. IEEE Trans. Magn. 2021, 57, 2900209. [Google Scholar]
- Liu, J.B.; Li, P.J. Flexible terahertz modulator based on coplanar-gate graphene field-effect transistor structure. Opt. Lett. 2016, 41, 816–819. [Google Scholar] [CrossRef]
- Huang, J.W.; Song, Z.Y. Terahertz graphene modulator based on hybrid plasmonic waveguide. Phys. Scr. 2021, 96, 1402–4896. [Google Scholar] [CrossRef]
- Huang, Y.D.; Yu, Y. Plasmonic terahertz modulator based on a grating-coupled two-dimensional electron system. Appl. Phys. Lett. 2016, 109, 201110. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Qiao, S. Gbps terahertz external modulator based on a composite metamaterial with a double-channel heterostructure. Nano Lett. 2015, 15, 3501–3506. [Google Scholar] [CrossRef]
- Zheng, W.; Fan, F. Optically pumped terahertz wave modulation in MoS2-Si heterostructure metasurface. AIP Adv. 2016, 6, 075105. [Google Scholar] [CrossRef]
- Wang, H.X.; Ling, F.R. A terahertz wave all-optical modulator based on quartz-based MAPbI3 thin film. Opt. Mater. 2022, 127, 112235. [Google Scholar] [CrossRef]
- Kowerdziej, R.; Jaroszewicz, L. Active control of terahertz radiation using a metamaterial loaded with a nematic liquid crystal. Liq. Cryst. 2016, 43, 1120–1125. [Google Scholar] [CrossRef]
- Li, J.S. Terahertz modulator using photonic crystals. Opt. Commun. 2007, 269, 98–101. [Google Scholar] [CrossRef]
- Faramarz, A.; Zahra, H. Design and analysis of a high-performance terahertz photoconductive modulator enhanced by photonic crystal cavity. Appl. Phys. B-Lasers Opt. 2022, 128, 211. [Google Scholar]
- Chen, H.M.; Su, J. Optically-controlled high-speed terahertz wave modulator based on nonlinear photonic crystals. Opt. Express 2011, 19, 3599. [Google Scholar] [CrossRef]
- Moradi, M.; Mohammadi, M. Design and simulation of a fast all-optical modulator based on photonic crystal using ring resonators. Silicon 2022, 14, 765–771. [Google Scholar] [CrossRef]
- Wu, F.; Chen, M.Y. Omnidirectional terahertz photonic band gap broaden effect in one-dimensional photonic crystal containing few-layer graphene. Opt. Commun. 2021, 490, 126898. [Google Scholar]
- Wang, Y.L.; Chen, S.Y. Omnidirectional absorption properties of a terahertz one-dimensional ternary magnetized plasma photonic crystal based on a tunable structure. Results Phys. 2020, 18, 103298. [Google Scholar] [CrossRef]
- Osswa, S.; Sebastien, F. Tunable polychromatic filters based on semiconductor-superconductor-dielectric periodic and quasi-periodic hybrid photonic crystal. Opt. Mater. 2021, 111, 110690. [Google Scholar]
- Rakhshani, M.R.; Mansouri-Birjandi, M.A. Design and simulation of wavelength demultiplexer based on heterostructure photonic crystals ring resonators. Physica E 2013, 50, 97–101. [Google Scholar] [CrossRef]
- Mansouri-Birjandi, M.A.; Rakhshani, M.R. A new design of tunable four-port wavelength demultiplexer by photonic crystal ring resonators. Optik 2013, 124, 5923–5926. [Google Scholar] [CrossRef]
- Rakhshani, M.R.; Mansouri-Birjandi, M.A. Realization of tunable optical filter by photonic crystal ring resonators. Optik 2013, 124, 5377–5380. [Google Scholar] [CrossRef]
- Yan, D.X.; Li, J.S. Light-controlled tunable terahertz filters based on photoresponsive liquid crystals. Laser Phys. 2019, 29, 025401. [Google Scholar] [CrossRef]
- Gao, Y.F.; Wang, L.S. Transmission properties of one-dimensional magneto-optical photonic crystals containing graphene nanolayers. J. Supercond. Nov. Magn. 2019, 32, 1049–1055. [Google Scholar] [CrossRef]
- Jiang, Z.D.; Li, P.L. Light-control splitting ratio tunable Y-type Terahertz waves to beam splitter based on two-dimensional photonic crystal. J. Infrared Millim. W. 2020, 39, 561–566. [Google Scholar]
- Wang, Z.M.; Qiao, J. Recent progress in terahertz modulation using photonic structures based on two-dimensional materials. InfoMat. 2021, 3, 1110–1133. [Google Scholar] [CrossRef]
- Huang, Y.J.; Wang, Y. Tunable electro-optical modulator based on a photonic crystal fiber selectively filled with liquid crystal. J. Light. Technol. 2019, 37, 1903–1908. [Google Scholar] [CrossRef]
- Li, Z.J.; Kim, T.H. Wide-bandgap perovskite/gallium arsenide tandem solar cells. Adv. Energy Mater. 2020, 10, 1903085. [Google Scholar] [CrossRef]
- Mangla, O.; Savita, R. Synthesis of gallium arsenide nanostructures for solar cell applications. Mater. Lett. 2020, 274, 128036. [Google Scholar] [CrossRef]
- Yang, H.; Yun, G.H. Effects of point defect shapes on defect modes in two-dimensional magnonic crystals. J. Magn. Magn. Mater. 2014, 356, 32–36. [Google Scholar] [CrossRef]
- Ge, D.H.; Zhang, J.H.; Zhang, L.Q. Effect of Point and Linear Defects on Band-gap Properties in Triangular-Honeycomb Structure Photonic Crystals. In IOP Conference Series: Materials Science and Engineering; IOP Publishing Ltd.: Guangzhou, China, 2017; Volume 170, p. 012005. [Google Scholar]
- Kleine-Ostmann, T.; Koch, M. Modulation of THz radiation by semiconductor nanostructures. Microw. Opt. Technol. Lett. 2002, 35, 343–345. [Google Scholar] [CrossRef]
- Tiedje, H.F.; Haugen, H.K. Measurement of nonlinear absorption coefficients in GaAs, InP and Si by an optical pump THz probe technique. Opt. Commun. 2007, 274, 187–197. [Google Scholar] [CrossRef]
- Neamen, D.A. Semiconductor Physics and Devices, 2nd ed.; McGraw Hill Higher Education: New York, NY, USA, 2002. [Google Scholar]
- Fekete, L.; Kadlec, F. Ultrafast opto-terahertz photonic crystal modulator. Opt. Lett. 2007, 32, 680–682. [Google Scholar] [CrossRef]
- Javan, M.A.R.; Granpayeh, N. Fast terahertz wave switch/modulator based on photonic crystal structures. J. Electromagnet. Waves Appl. 2009, 23, 203–212. [Google Scholar] [CrossRef]
- Yablonovitch, A. Inhibited spontaneous emission in solid-state physics and electronics. Phy. Rev. Lett. 1987, 58, 2059–2062. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Wang, D.; Chen, Y.F. Physics of Optoelectronic Devices, 2nd ed.; Publishing House of Electronics Industry: Beijing, China, 2009. [Google Scholar]
- He, Y.; Wang, Y. Enhanced performance of a fast GaAs-based terahertz modulator via surface passivation. Photonics Res. 2021, 9, 2230–2236. [Google Scholar] [CrossRef]
- Kuzel, P.; Kadlec, F. Propagation of terahertz pulses in photoexcited media: Analytical theory for layered systems. J. Chem. Phys. 2007, 127, 024506. [Google Scholar] [CrossRef]
- Zhao, Y.C.; Wang, L. High-speed efficient terahertz modulation based on tunable collective-individual state conversion within an active 3 nm two-dimensional electron Gas metasurface. Nano Lett. 2019, 19, 7588–7597. [Google Scholar] [CrossRef]
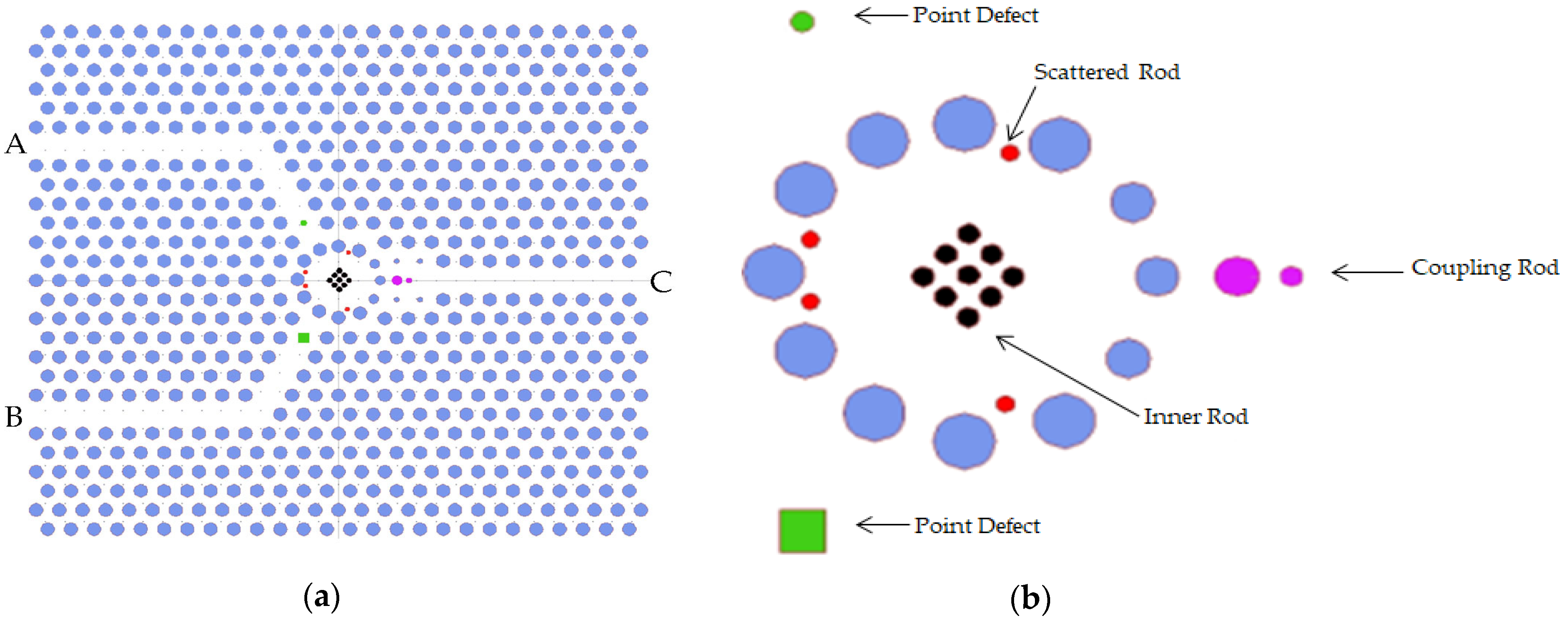



| Name | Symbol | Attribute |
|---|---|---|
| The lattice constant | a | 119 μm |
| The radius of circular silicon rods | R | 0.28a |
| The refractive index of silicon | n | 3.4 |
| The circular rod (green color) | r | 0.1a |
| The square rod (green color) | l | 0.42a |
| The inner rods (black color) | b | 0.1a |
| The scattered rods (red color) | s | 0.08a |
| The coupling rods (purple color) | p | 0.2a |
| Modulation | Input Port | Transmissivity (%) | Modulation Depth (%) | Modulation Rate (GHz) | Insertion Loss (dB) | |
|---|---|---|---|---|---|---|
| [24] | No input port | Not provided | Not provided | Not provided | 0.46 | |
| [40] | One input port | Not provided | 94 | 0.069 | Not provided | |
| [42] | One input port | Not provided | 93 | 3 | Not provided | |
| [15] | One input port | Not provided | 99 | 3 | 2.2 | |
| dual-channel modulator | A | ON | 93 | 100 | 4.05 | 0.31 |
| OFF | 0.02 | |||||
| B | ON | 96 | 99.7 | 4.17 | 0.18 | |
| OFF | 0.27 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Tan, J.; Xu, Y.; Cui, H.; Tang, B.; Jiao, Z.; Zhou, W.; Zeng, J.; Xia, N. High-Performance Dual-Channel Photonic Crystal Terahertz Wave Modulator Based on the Defect Mode Disappearance of a Combined Microcavity. Photonics 2023, 10, 298. https://doi.org/10.3390/photonics10030298
Li G, Tan J, Xu Y, Cui H, Tang B, Jiao Z, Zhou W, Zeng J, Xia N. High-Performance Dual-Channel Photonic Crystal Terahertz Wave Modulator Based on the Defect Mode Disappearance of a Combined Microcavity. Photonics. 2023; 10(3):298. https://doi.org/10.3390/photonics10030298
Chicago/Turabian StyleLi, Gaofang, Jie Tan, Yanxia Xu, Haoyang Cui, Bo Tang, Zhejing Jiao, Wei Zhou, Jundong Zeng, and Nenghong Xia. 2023. "High-Performance Dual-Channel Photonic Crystal Terahertz Wave Modulator Based on the Defect Mode Disappearance of a Combined Microcavity" Photonics 10, no. 3: 298. https://doi.org/10.3390/photonics10030298
APA StyleLi, G., Tan, J., Xu, Y., Cui, H., Tang, B., Jiao, Z., Zhou, W., Zeng, J., & Xia, N. (2023). High-Performance Dual-Channel Photonic Crystal Terahertz Wave Modulator Based on the Defect Mode Disappearance of a Combined Microcavity. Photonics, 10(3), 298. https://doi.org/10.3390/photonics10030298




