Tunable Transparency and Group Delay in Cavity Optomechanical Systems with Degenerate Fermi Gas
Abstract
1. Introduction
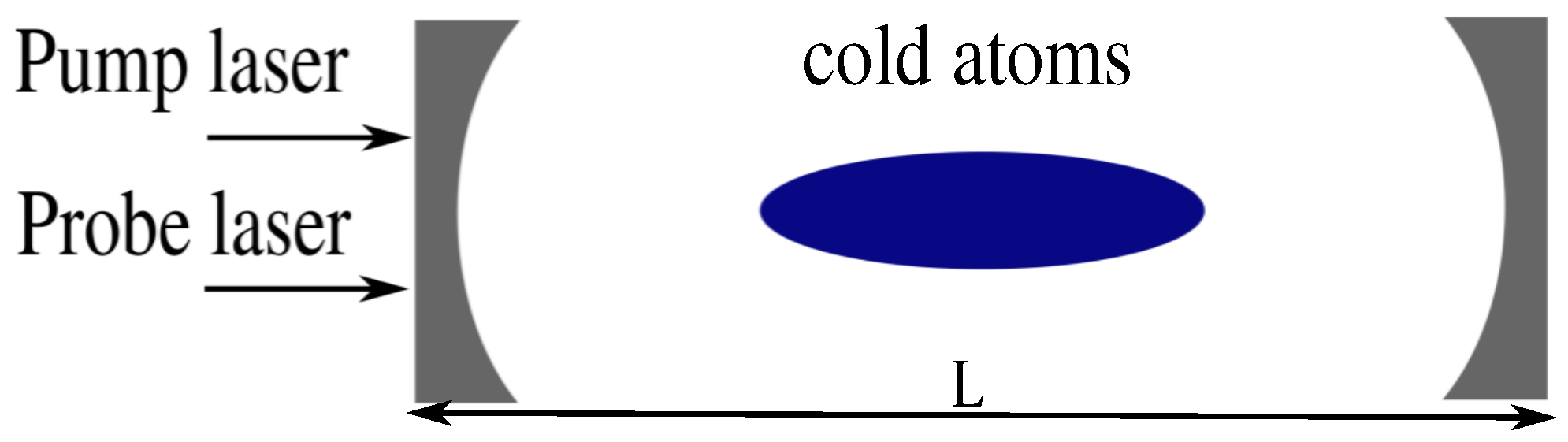
2. Model and Hamiltonian of the System
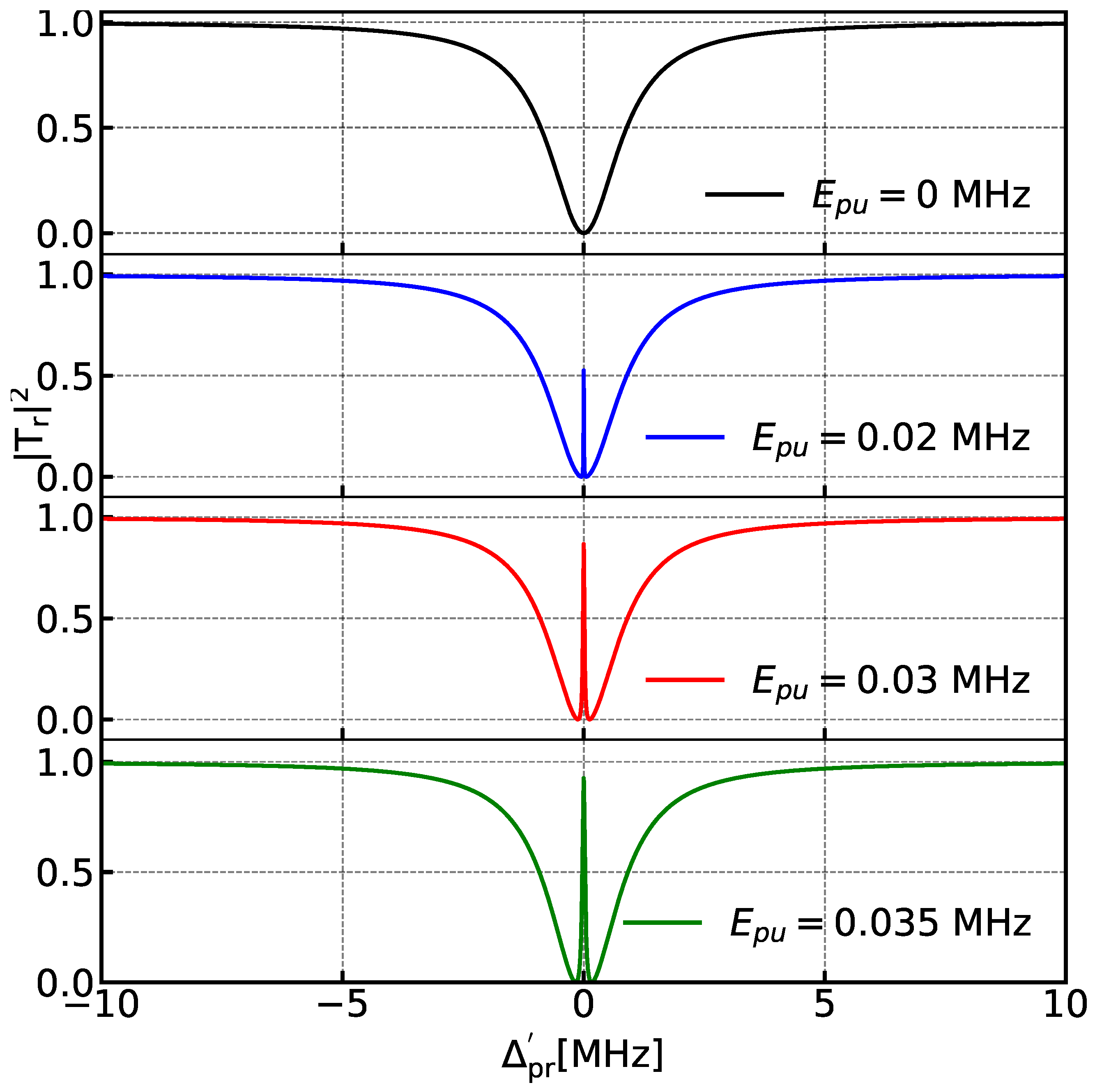
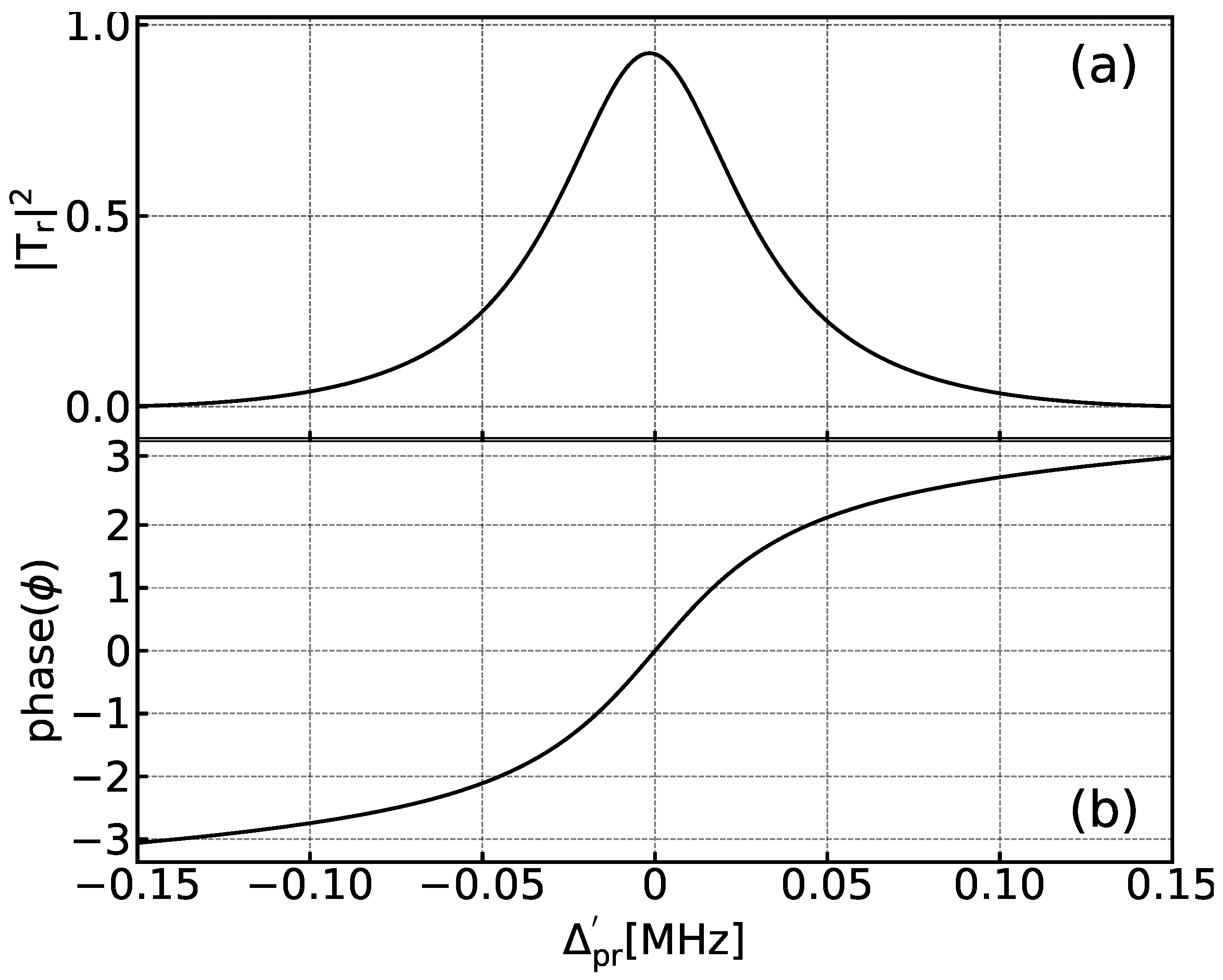
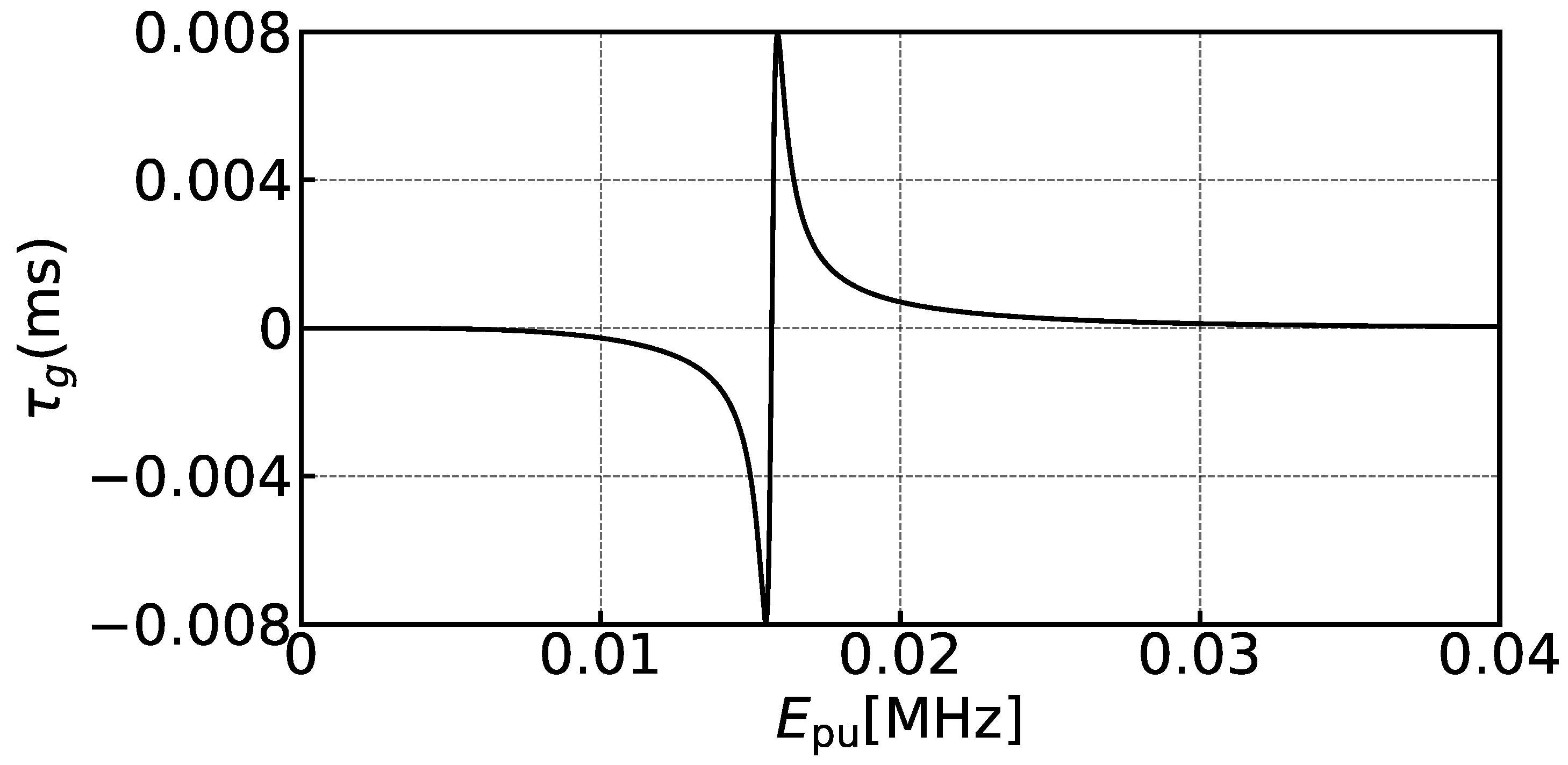
3. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kippenberg, T.J.; Vahala, K.J. Cavity Optomechanics: Back-Action at the Mesoscale. Science 2008, 321, 1172–1176. [Google Scholar] [CrossRef] [PubMed]
- Rugar, D.; Budakian, R.; Mamin, H.J.; Chui, B.W. Single Spin Detection by Magnetic Resonance Force Microscopy. Nature 2004, 430, 329–332. [Google Scholar] [CrossRef] [PubMed]
- Braginsky, V.; Vyatchanin, S.P. Low quantum noise tranquilizer for Fabry–Perot interferometer. Phys. Lett. A 2002, 293, 228–234. [Google Scholar] [CrossRef]
- Weis, S.; Rivière, R.; Deléglise, S.; Gavartin, E.; Arcizet, O.; Schliesser, A.; Kippenberg, T.J. Optomechanically induced transparency. Science 2010, 330, 1520–1523. [Google Scholar] [CrossRef] [PubMed]
- Vitali, D.; Gigan, S.; Ferreira, A.; Bohm, H.R.; Tombesi, P.; Guerreiro, A.; Vedral, V.; Zeilinger, A.; Aspelmeyer, M. Optomechanical entanglement between a movable mirror and a cavity field. Phys. Rev. Lett. 2007, 98, 030405. [Google Scholar] [CrossRef]
- Asjad, M.; Tombesi, P.; Vitali, D. Feedback control of two-mode output entanglement and steering in cavity optomechanics. Phys. Rev. A 2016, 94, 052312. [Google Scholar] [CrossRef]
- Asjad, M.; Tombesi, P.; Vitali, D. Quantum phase gate for optical qubits with cavity quantum optomechanics. Opt. Express 2015, 23, 7786–7794. [Google Scholar] [CrossRef]
- Asjad, M.; Zippilli, S.; Tombesi, P.; Vitali, D. Large distance continuous variable communication with concatenated swaps. Phys. Scr. 2015, 90, 074055. [Google Scholar] [CrossRef]
- Manninen, J.; Asjad, M.; Selenius, E.; Ojajarvi, R.; Kuusela, P.; Massel, F. Clauser-Horne-Shimony-Holt Bell inequality test in an optomechanical device. Phys. Rev. A 2018, 98, 043831. [Google Scholar] [CrossRef]
- Teufel, J.D.; Donner, T.; Castellanos-Beltran, M.A.; Harlow, J.W.; Lehnert, K.W. Nanomechanical motion measured with an imprecision below that at the standard quantum limit. Nanomech. Nat. Nanotechnol. 2009, 4, 820–823. [Google Scholar] [CrossRef]
- Arvanitaki, A.; Geraci, A.A. Detecting high-frequency gravitational waves with optically levitated sensors. Phys. Rev. Lett. 2013, 110, 071105. [Google Scholar] [CrossRef] [PubMed]
- Asjad, M.; Zippilli, S.; Vitali, D. Mechanical Einstein-Podolsky-Rosen entanglement with a finite-bandwidth squeezed reservoir. Phys. Rev. A 2016, 93, 062307. [Google Scholar] [CrossRef]
- Asjad, M.; Saif, F. Engineering entanglement mechanically. Phys. Lett. A 2012, 376, 2608–2612. [Google Scholar] [CrossRef]
- Asjad, M.; Saif, F. Steady-state entanglement of a Bose-Einstein condensate and a nanomechanical resonator. Phys. Rev. A 2011, 84, 033606. [Google Scholar] [CrossRef]
- Singh, S.K.; Peng, J.-X.; Asjad, M.; Mazaheri, M. Entanglement and coherence in a hybrid Laguerre–Gaussian rotating cavity optomechanical system with two-level atoms. J. Phys. B At. Mol. Opt. Phys. 2021, 54, 215502. [Google Scholar] [CrossRef]
- Jin, L.; Peng, J.-X.; Yuan, Q.-Z.; Feng, X.-L. Macroscopic quantum coherence in a spinning optomechanical system. Opt. Express 2021, 29, 41191–41205. [Google Scholar] [CrossRef]
- Chen, Z.; Peng, J.-X.; Fu, J.-J.; Feng, X.-L. Entanglement of two rotating mirrors coupled to a single Laguerre-Gaussian cavity mode. Opt. Express 2019, 27, 29479–29490. [Google Scholar] [CrossRef]
- Singh, S.K.; Ooi, C.H.R. Quantum correlations of quadratic optomechanical oscillator. J. Opt. Soc. Am. B 2014, 31, 2390–2398. [Google Scholar] [CrossRef]
- Singh, S.K.; Muniandy, S.V. Temporal Dynamics and Nonclassical Photon Statistics of Quadratically Coupled Optomechanical Systems. Int. J. Theor. Phys. 2016, 55, 287–301. [Google Scholar] [CrossRef]
- Singh, S.K. Heisenberg-Langevin Formalism for Squeezing Dynamics of Linear Hybrid Optomechanical System. Int. J. Theor. Phys. 2019, 58, 2418–2427. [Google Scholar]
- Peng, J.-X.; Chen, Z.; Yuan, Q.-Z.; Feng, X.-L. Optomechanically induced transparency in a Laguerre-Gaussian rotational-cavity system and its application to the detection of orbital angular momentum of light fields. Phys. Rev. A 2019, 99, 043817. [Google Scholar] [CrossRef]
- Singh, S.K.; Asjad, M.; Ooi, C.H.R. Tunable optical response in a hybrid quadratic optomechanical system coupled with single semiconductor quantum well. Quantum Inf. Process. 2022, 21, 47. [Google Scholar] [CrossRef]
- Singh, S.K.; Parvez, M.; Abbas, T.; Peng, J.-X.; Mazaheri, M.; Asjad, M. Tunable optical response and fast (slow) light in optomechanical system with phonon pump. Phys. Lett. A 2022, 442, 128181. [Google Scholar] [CrossRef]
- Hocke, F.; Zhou, X.; Schliesser, A.; Kippenberg, T.J.; Huebl, H.; Gross, R. Electromechanically induced absorption in a circuit nano-electromechanical system. New J. Phys. 2012, 14, 123037. [Google Scholar] [CrossRef]
- Qu, K.N.; Agarwal, G.S. Phonon-mediated electromagnetically induced absorption in hybrid opto-electromechanical systems. Phys. Rev. A 2013, 87, 031802. [Google Scholar] [CrossRef]
- Singh, V.; Bosman, S.J.; Schneider, B.H.; Blanter, Y.M.; Castellanos-Gomez, A.; Steele, G.A. Optomechanical coupling between a multilayer graphene mechanical resonator and a superconducting microwave cavity. Nat. Nanotechnol. 2014, 9, 820–824. [Google Scholar] [CrossRef]
- Groblacher, S.; Hammerer, K.; Vanner, M.R.; Aspelmeyer, M. Observation of strong coupling between a micromechanical resonator and an optical cavity field. Nature 2009, 460, 724–727. [Google Scholar] [CrossRef]
- Wilson-Rae, I.; Nooshi, N.; Zwerger, W.; Kippenberg, T.J. Theory of ground state cooling of a mechanical oscillator using dynamical back-action. Phys. Rev. Lett. 2007, 99, 093901. [Google Scholar] [CrossRef]
- Agarwal, G.S.; Huang, S. Electromagnetically induced transparency in mechanical effects of light. Phys. Rev. A 2007, 81, 041803. [Google Scholar] [CrossRef]
- Braginskii, V.B.; Manukin, A.B. Measurement of Weak Forces in Physics Experiments; University of Chicago Press: Chicago, IL, USA, 1977. [Google Scholar]
- Mancini, S.; Giovannetti, V.; Vitali, D.; Tombesi, P. Entangling macroscopic oscillators exploiting radiation pressure. Phys. Rev. Lett. 2002, 88, 120401. [Google Scholar] [CrossRef]
- Zhang, J.; Peng, K.; Braunstein, S.L. Quantum-state transfer from light to macroscopic oscillators. Phys. Rev. A 2003, 68, 013808. [Google Scholar] [CrossRef]
- Thompson, J.D.; Zwickl, B.M.; Jayich, A.M.; Marquardt, F.; Girvin, S.M.; Harris, J.G.E. Strong dispersive coupling of a high-finesse cavity to a micromechanical membrane. Nature 2008, 452, 72–75. [Google Scholar] [CrossRef] [PubMed]
- Sankey, J.C.; Yang, C.; Zwickl, B.M.; Jayich, A.M.; Harris, J.G.E. Strong and tunable nonlinear optomechanical coupling in a low-loss system. Nat. Phys. 2010, 6, 707–712. [Google Scholar] [CrossRef]
- Asjad, M.; Vitali, D. Reservoir engineering of a mechanical resonator: Generating a macroscopic superposition state and monitoring its decoherence. J. Phys. B At. Mol. Opt. Phys. 2013, 47, 045502. [Google Scholar] [CrossRef]
- Asjad, M.; Agarwal, G.S.; Kim, M.S.; Tombesi, P.; Giuseppe, G.D.; Vitali, D. Robust stationary mechanical squeezing in a kicked quadratic optomechanical system. Phys. Rev. A 2014, 89, 023849. [Google Scholar] [CrossRef]
- Tian, L.; Zoller, P. Coupled ion-nanomechanical systems. Phys. Rev. Lett. 2004, 93, 266403. [Google Scholar] [CrossRef] [PubMed]
- Naik, A.; Buu, O.; LaHaye, M.D.; Armour, A.D.; Clerk, A.A.; Blencowe, M.P.; Schwab, K.C. Cooling a nanomechanical resonator with quantum back-action. Nature 2006, 443, 193–196. [Google Scholar] [CrossRef] [PubMed]
- Ian, H.; Gong, Z.R.; Liu, Y.X.; Sun, C.P.; Nori, F. Cavity optomechanical coupling assisted by an atomic gas. Phys. Rev. A 2008, 78, 013824. [Google Scholar] [CrossRef]
- Genes, C.; Vitali, D.; Tombesi, P. Emergence of atom-light-mirror entanglement inside an optical cavity. Phys. Rev. A 2008, 77, 050307. [Google Scholar] [CrossRef]
- Meiser, D.; Meystre, P. Coupled dynamics of atoms and radiation-pressure-driven interferometers. Phys. Rev. A 2006, 73, 033417. [Google Scholar] [CrossRef]
- Genes, C.; Ritsch, H.; Vitali, D. Micromechanical oscillator ground-state cooling via resonant intracavity optical gain or absorption. Phys. Rev. A 2009, 80, 061803. [Google Scholar] [CrossRef]
- Singh, S.K.; Abak, M.K.; Tasgin, M.E. Enhancement of four-wave mixing via interference of multiple plasmonic conversion paths. Phys. Rev. B 2016, 93, 035410. [Google Scholar] [CrossRef]
- Teufel, J.D.; Li, D.; Allman, M.S.; Cicak, K.; Sirois, A.J.; Whittaker, J.D.; Simmonds, R.W. Circuit cavity electromechanics in the strong coupling regime. Nature 2011, 471, 204–208. [Google Scholar] [CrossRef] [PubMed]
- Safavi-Naeini, A.H.; Mayer Alegre, T.P.; Chan, J.; Eichenfield, M.; Winger, M.; Lin, Q.; Hill, J.T.; Chang, D.E.; Painter, O. Electromagnetically induced transparency and slow light with optomechanics. Nature 2011, 472, 69–73. [Google Scholar] [CrossRef] [PubMed]
- Grünwald, P.; Singh, S.K.; Vogel, W. Raman-assisted Rabi resonances in two-mode cavity QED. Phys. Rev. A 2011, 83, 063806. [Google Scholar] [CrossRef]
- Singh, S.K. Quantum dynamics and nonclassical photon statistics of coherently driven Raman transition in bimodal cavity. J. Mod. Opt. 2019, 66, 562–570. [Google Scholar] [CrossRef]
- Brennecke, F.; Ritter, S.; Donner, T.; Esslinger, T. Cavity optomechanics with a Bose-Einstein condensate. Science 2008, 322, 235–238. [Google Scholar] [CrossRef]
- Ritter, S.; Brennecke, F.; Baumann, K.; Donner, T.; Guerlin, C.; Esslinger, T. Dynamical coupling between a Bose–Einstein condensate and a cavity optical lattice. Appl. Phys. B Lasers Opt. 2009, 95, 213–218. [Google Scholar] [CrossRef]
- Asjad, M. Cavity optomechanics with a Bose–Einstein condensate: Normal mode splitting. J. Mod. Opt. 2012, 59, 917–922. [Google Scholar] [CrossRef]
- Asjad, M.; Saif, F. Normal mode splitting in hybrid BEC-optomechanical system. Optik 2014, 125, 5455–5460. [Google Scholar] [CrossRef]
- Mabuchi, H.; Doherty, A.C. Cavity quantum electrodynamics: Coherence in context. Science 2000, 298, 1372–1377. [Google Scholar] [CrossRef] [PubMed]
- Kanamoto, R.; Meystre, P. Optomechanics of a Quantum-Degenerate Fermi Gas. Phys. Rev. Lett. 2010, 104, 0603601. [Google Scholar] [CrossRef]
- Kanamoto, R.; Meystre, P. Optomechanics of ultracold atomic gases. Phys. Scr. 2010, 82, 038111. [Google Scholar] [CrossRef]
- Asjad, M.; Shahzad, M.A.; Saif, F. Quantum degenerate Fermi gas entanglement in optomechanics. Eur. Phys. J. D 2013, 67, 198. [Google Scholar] [CrossRef]
- Gibble, K.; Verhaar, B.J. Eliminating cold-collision frequency shifts. Phys. Rev. A 1995, 52, 3370. [Google Scholar] [CrossRef]
- Katori, H.; Takamoto, M.; Palchikov, V.G.; Ovsiannikov, V.D. Ultrastable Optical Clock with Neutral Atoms in an Engineered Light Shift Trap. Phys. Rev. Lett. 2003, 91, 173005. [Google Scholar] [CrossRef]
- Giamarchi, T. Quantum Physics in One Dimension; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Xiong, H.; Wu, Y. Fundamentals and applications of optomechanically induced transparency. Appl. Phys. Rev. 2018, 5, 031305. [Google Scholar] [CrossRef]
- Asjad, M. Optomechanically dark state in hybrid BEC–optomechanical systems. J. Russ. Laser Res. 2013, 34, 278–287. [Google Scholar] [CrossRef]
- Asjad, M. Electromagnetically-Induced Transparency in Optomechanical Systems with Bose–Einstein Condensate. J. Russ. Laser Res. 2013, 34, 159–165. [Google Scholar] [CrossRef]
- Gardiner, C.W.; Zoller, P. Quantum Noise: A Handbook of Markovian and Non-Markovian Quantum Stochastic Methods with Applications to Quantum Optics; Springer Science & Business Media: Berlin, Germany, 2004. [Google Scholar]
- Boyd, R.W. Slow and fast light: Fundamentals and applications. J. Mod. Opt. 2009, 56, 1908–1915. [Google Scholar] [CrossRef]
- Milonni, P.W. Fast Light, Slow Light and Left handed Light; Institute of Physics: Bristol, UK, 2005. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yusoff, F.N.; Zulkifli, M.A.; Ali, N.; Singh, S.K.; Abdullah, N.; Ahmad Hambali, N.A.M.; Edet, C.O. Tunable Transparency and Group Delay in Cavity Optomechanical Systems with Degenerate Fermi Gas. Photonics 2023, 10, 279. https://doi.org/10.3390/photonics10030279
Yusoff FN, Zulkifli MA, Ali N, Singh SK, Abdullah N, Ahmad Hambali NAM, Edet CO. Tunable Transparency and Group Delay in Cavity Optomechanical Systems with Degenerate Fermi Gas. Photonics. 2023; 10(3):279. https://doi.org/10.3390/photonics10030279
Chicago/Turabian StyleYusoff, Fatin Nadiah, Muhammad Afiq Zulkifli, Norshamsuri Ali, Shailendra Kumar Singh, Nooraihan Abdullah, Nor Azura Malini Ahmad Hambali, and Collins Okon Edet. 2023. "Tunable Transparency and Group Delay in Cavity Optomechanical Systems with Degenerate Fermi Gas" Photonics 10, no. 3: 279. https://doi.org/10.3390/photonics10030279
APA StyleYusoff, F. N., Zulkifli, M. A., Ali, N., Singh, S. K., Abdullah, N., Ahmad Hambali, N. A. M., & Edet, C. O. (2023). Tunable Transparency and Group Delay in Cavity Optomechanical Systems with Degenerate Fermi Gas. Photonics, 10(3), 279. https://doi.org/10.3390/photonics10030279





