Research on Magnetic-Induced Error of Small-Sized Fiber Optic Gyro Fiber Coil in Space Environment

Abstract

Spacecraft is severely limited in weight and volume, resulting in a small bending radius of the fiber coil used by IFOG (Interference Fiber Optic Gyroscope). The fiber coil has such a size that the influence of bending on fiber birefringence cannot be ignored. In this paper, we research magnetic-induced errors of small-sized IFOG working in low orbit space. Firstly, we use the Jones matrix to analyze the effects of radial magnetic field and axial magnetic field on IFOG. Secondly, we establish a three-dimensional model for the radial magnetic-induced errors and magnetic-induced errors of minor radius fiber coil. Using the finite element method, we analyze the magnetic-induced error between different levels of the fiber coil. Combined with the birefringence distribution of the minor radius fiber coil, an accurate three-dimensional magnetic-induced error model is established. Thirdly, in the experiment, we design the magnetic-induced error test platform that includes the Fluke standard current source, transconductance amplifier, and Helmholtz coil. The experimental results show that, compared with the traditional calculation method, the three-dimensional magnetic-induced error model reduces the RMSE (Root Mean Square Error) of the radial magnetic field by 56.9% and the RMSE of the axial magnetic field by 35.7%, respectively.

1. Introduction

With the development of aerospace technology, the exploration tasks undertaken by new spacecraft have also become diversified. In space exploration, gyroscope is an important optical device that provides position and attitude information for spacecraft. The miniaturization of the fiber coil is required due to strict restrictions on the dimension and weight of gyroscope equipped in the spacecraft. As the sensitive unit of the IFOG, the fiber coil directly affects the positioning accuracy of the system.

Nowadays, magnetic-induced errors have become an essential issue in miniaturization and lightweight of IFOG. From 1982 to 2005, Böhm. K [1] of AEG-Telefunken, Blake. J.N. [2] of Honeywell Systems and Research Center, Kazuo Hotate [3,4] of Tokyo University, I.A. Andronova [5] of Russian Academy of Sciences, and Wang Xiaxiao [6] of Beihang University conducted in-depth theoretical analyses on the magnetically induced errors in fiber coils. It is proposed and verified that the magnetic-induced error in IFOG is a phase error caused by the fiber torsion and the environmental magnetic field. In 2011, C.N. Zhang et al. [7] demonstrated the drift characteristics of IFOG under axial magnetic field. The mathematical model of the IFOG non-reciprocal phase difference and the polarization state of the incident light is verified by experiments. The research shows that the magnetic error induced by the axial magnetic field on the IFOG is closely related to the torsion distribution of the fiber in the fiber coil. In 2018, Y. Zhou et al. [8] proposed an optical method to reduce the radial magnetic error by adding a suppressing cross-section fiber in the optical path, and they achieved the suppression of the radial magnetic error.

In 2016, E. deToldi et al. carried out a research on magnetic shielding technology and developed a method to measure the shielding efficiency of metal enclosures using fiber coils [9]. In 2017, H.X.Liu et al. proposed an open magnetic shielding protection method, utilizing several layers of coaxial permanent magnet foil tubes to replace the traditional heavy shielding shell to reduce the weight of the magnetic shielding device [10]. Therefrom, the researchers observed that an efficient way to reduce the magnetically induced error is to add a magnetic shielding enclosure outside the fiber coil.

In previous work, we discussed the distribution of birefringence in a fiber coil with quadrupole symmetrical winding method [11]. Based on it, this paper analyzes the principle of the magnetically induced error of the radial magnetic field and the axial magnetic field in IFOG, and proposes a three-dimensional magnetically induced error model of a small fiber coil. The model considers the effect of the bending radius between different layers in a small-sized fiber coil on fiber birefringence. Compared with the traditional magnetic-induced error calculation method, it can more accurately reflect the influence of the magnetic field on the small fiber optic gyroscope for space use.

In the space environment, we establish a three-dimensional magnetic-induced error model of the fiber optic gyroscope with small radius fiber coil. Firstly, according to the magneto-optical Faraday effect, the magnetic error mechanism of the fiber optic gyroscope in the radial and axial magnetic field is analyzed by using the Jones matrix, respectively; Secondly, given the influence of the birefringence distribution of the fiber coil on the magnetic error, the refractive index and birefringence distribution models for the small fiber coil with a bending radius of 10–20 mm are introduced, and the expression of the three-dimensional magnetic error of the small IFOG is derived. The simulation work has been carried out to analyze the influence of the axial and radial magnetic field on the IFOG under the same magnetic induction intensity. Finally, based on the theoretical analysis, a magnetic-induced error experimental measuring system is designed. The Helmholtz coil is used as the magnetic field generating device, powered from the combination of the Fluke standard current source and transconductance amplifier which provides stable current to ensure the high stability of the output magnetic field. In the experiment setup, the fiber coil is placed in the Helmholtz coil separately, and the magnitude of current is changed to obtain system outputs with different magnetic induction intensities. Both the simulation results and the experimental data prove that the birefringence model of the small-sized fiber coil proposed in this paper can more accurately reflect the influence of the magnetic field on the IFOG compared with the commonly used calculation method of magnetic-induced error.

2. Materials and Methods

2.1. Magnetic Error Analysis of Radial Magnetic Field

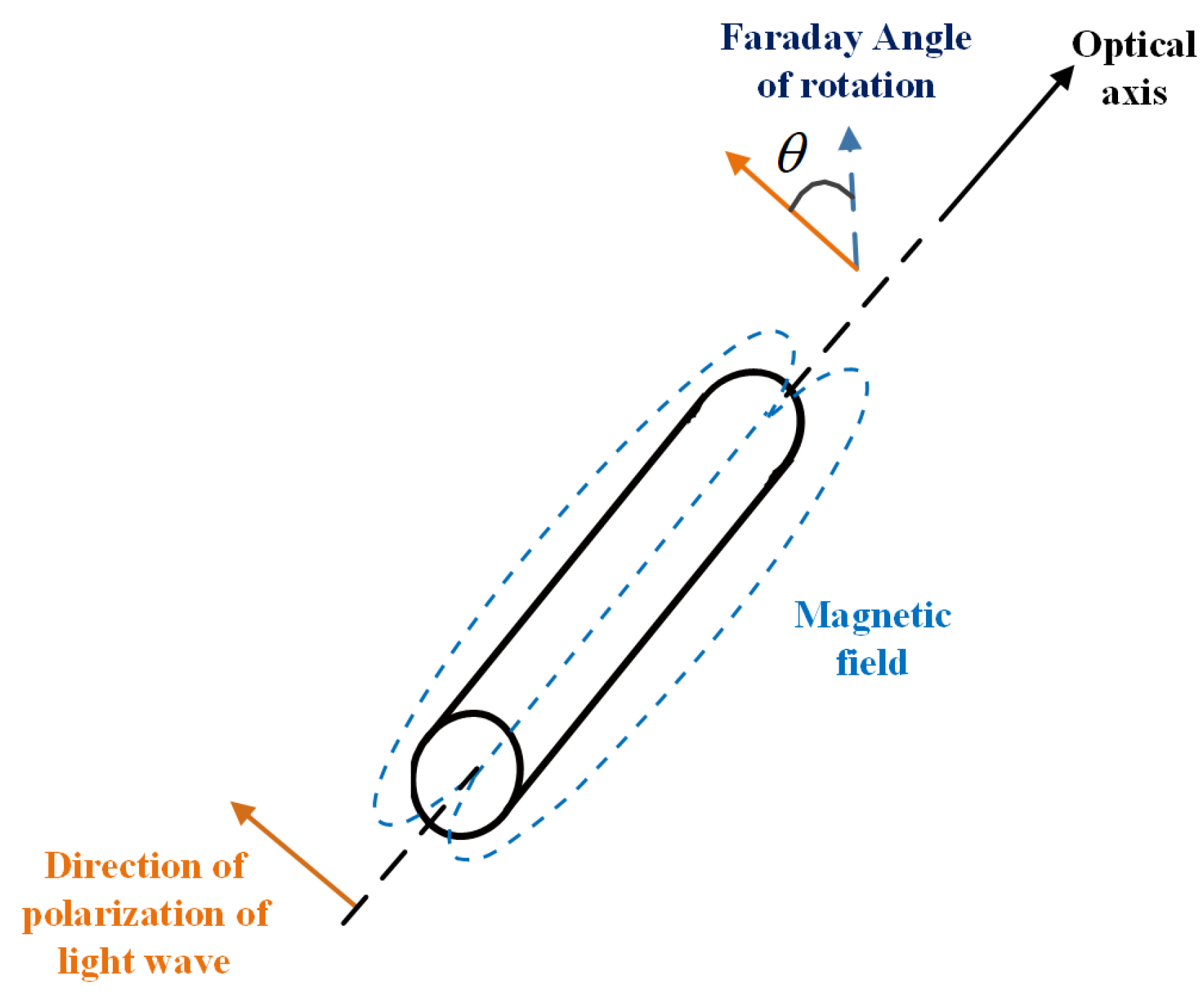
The linearly polarized light can be decomposed into a left-handed circularly polarized light and a right-handed circularly polarized light in the optical fiber. In consideration of the non-interference external environment, there will be no relative phase difference between two beams of circularly polarized light after propagating for a certain distance. Therefore, the polarization plane of the combined linearly polarized light remains unchanged. When the parallel magnetic field applied on the propagation direction of the light wave, the relative phase of the left and right circularly polarized light changes due to the non-diagonal component of the dielectric constant tensor, and the polarization plane of the light is rotated after the linearly polarized light emerges again. As is shown in Figure 1, the optical rotation angle caused by the magneto-optical Faraday effect can be expressed as:

$$\theta =V{B}_{//}L$$

(1)

where $\theta$ denotes the Faraday rotation angle, V denotes the Verdet constant, $B_{//}$ represents the parallel magnetic induction, and L represents the transmission distance.

The Verdet constant of the polarization maintaining fiber (PMF) used in the fiber optic gyroscope is 6.4 × 10⁻⁴ rad/(m·mT). The magneto-optical Faraday rotation angle is proportional to the magnetic field strength and propagation distance. In addition, the magneto-optical Faraday rotation angle is related to the propagation position of light. Figure 2 shows the decomposition of the radial magnetic field at any position in the XOY plane. ${\theta }_{\mathrm{r}}$ is the angle between the radial magnetic field and the X-axis of the coordinate axis, and the parallel component $B_{\mathrm{r}}{}_{//}$ in the vibration plane is extracted at the z point (its vertical component will not affect the beam). The magnetic induction of the radial magnetic field is: $B_{\mathrm{r}}{}_{//}=B_{\mathrm{r}}\sin (z/r-{\theta }_{\mathrm{r}})$. When the direction of the magnetic field is fixed with the included angle of the fiber coil, the magneto-Faraday rotation angle is related to the position of the fiber in the coil.

In order to establish the radial magnetic-induced error model, it is a common method to analyze the phase change generated by clockwise (CW) and counterclockwise (CCW) beams through the Jones matrix. The infinitesimal element method is employed to analyze the birefringence of the fiber coil. The fiber coil can be decomposed into a micro-element with length z, and the magneto-Faraday rotation angle of fiber coil units with length z can be considered as uniformly generated. Therefore, the electric field component of the polarized light incident into the fiber coil can be expressed as:

$$\left[\begin{array}{c}{E}_{\mathrm{x}}(z)\\ E_{\mathrm{y}}(z)\end{array}\right]=\exp (-i{\beta }_{\mathrm{a}}z)C_{+}(t_{\mathrm{wi}},{\xi }_{\mathrm{i}})\left[\begin{array}{c}{E}_{\mathrm{x}}(0)\\ E_{\mathrm{y}}(0)\end{array}\right]$$

(2)

$$C_{+}(t_{\mathrm{wi}},{\xi }_{\mathrm{i}})=\left[\begin{array}{cc}\cos {\eta }_{+}z-j\frac{\mathsf{\Delta }\beta }{2{\eta }_{+}}\sin \eta & \frac{{\xi }_{\mathrm{i}}-t_{\mathrm{wi}}}{{\eta }_{+}}\sin {\eta }_{+}z\\ \frac{t_{wi}-{\xi }_i}{{\eta }_{+}}\sin {\eta }_{+}z& \cos {\eta }_{+}z+j\frac{\mathsf{\Delta }\beta }{2{\eta }_{+}}\sin {\eta }_{+}z\end{array}\right]$$

(3)

$${\eta }_{+}=\sqrt{{(\frac{\mathsf{\Delta }\beta }{2})}^2+{({\xi }_i+t_{wi})}^2}$$

(4)

where E_x(z) and E_y(z) are the electric field components in the X-axis and Y-axis directions at z point, respectively. E_x(0) and E_y(0) are the electric field components in the X-axis and Y-axis directions when the fiber enters the cavity, respectively. Δβ represents the inherent linear birefringence of the fiber, t_wi represents the circular birefringence caused by twisting, and ξ_i denotes the circular birefringence caused by the magneto-optical Faraday effect.

Then, in the i-th micro-element fiber, the circular birefringence caused by the magneto-optical Faraday effect can be expressed as:

$${\xi }_{\mathrm{i}}=V{B}_{\mathrm{r}}{}_{//}=V{B}_{\mathrm{r}}\sin (z/r-{\theta }_{\mathrm{r}})$$

(5)

It can be seen from the above formula that in addition to the circular birefringence generated by the Faraday rotation effect for the CW and CCW directions, there is also a torsional circular birefringence due to the torsional circular birefringence introduced by the fiber during the drawing process. Typically, the fiber torsion introduced by fiber drawing process is sinusoidally periodic. Assuming that the fiber is CW twisted, the circular birefringence caused by the magneto-optical Faraday effect and the fiber torsion towards the same direction are superposed when the light wave propagates CW, and, on the contrary, cancel each other out when the light wave propagates CCW. The Jones matrix for CCW propagation can be expressed as:

$$C_{-}(t_{\mathrm{wi}},{\xi }_{\mathrm{i}})=\left[\begin{array}{cc}\cos {\eta }_{-}z-j\frac{\mathsf{\Delta }\beta }{2{\eta }_{-}}\sin {\eta }_{-}z& -\frac{{\xi }_{\mathrm{i}}-t_{\mathrm{wi}}}{{\eta }_{-}}\sin {\eta }_{-}z\\ \frac{{\xi }_{\mathrm{i}}-t_{\mathrm{wi}}}{{\eta }_{-}}\sin {\eta }_{-}z& \cos {\eta }_{-}z+j\frac{\mathsf{\Delta }\beta }{2{\eta }_{-}}\sin {\eta }_{-}z\end{array}\right]$$

(6)

$${\eta }_{-}=\sqrt{{(\frac{\mathsf{\Delta }\beta }{2})}^2+{({\xi }_{\mathrm{i}}-t_{\mathrm{wi}})}^2}$$

(7)

The light wave in the CW direction is injected from the port on one side of the fiber coil through n micro-units and then exits from the port on the other side, while the light wave in the CCW direction propagates in the fiber coil along the opposite direction. Then, the electric field component E₊ of the light wave in the CW direction and the electric field component E_- in the CCW direction can be expressed as [6]:

$$\begin{array}{l}{E}_{+}=\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right]{\displaystyle \prod _{i=1}^n{C}_{+}(t_{\mathrm{wi}},{\xi }_{\mathrm{i}})\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right]}{E}_0{e}^{-j\varphi }\hfill \\ E_{-}=\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right]{\displaystyle \prod _{i=1}^n{C}_{-}(t_{\mathrm{wi}},{\xi }_{\mathrm{i}})\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right]}{E}_0\hfill \end{array}$$

(8)

Put Formulas (4) and (7) into the above formula, according to the Sagnac effect, the phase difference $\mathsf{\Delta }{\varphi }_{\mathrm{R}}$ generated by CW and CCW light waves can be expressed as:

$$\mathsf{\Delta }{\varphi }_R={\displaystyle \sum _{i=1}^n\frac{4{\xi }_{\mathrm{i}}{t}_{\mathrm{wi}}z}{({\eta }_{+}+{\eta }_{-})}}={\displaystyle {\int }_0^L\frac{4\xi (z)t_{\mathrm{w}}(z)}{\mathsf{\Delta }\beta }}dz$$

(9)

Then, the magnetic error of the radial magnetic field generated by the Faraday magneto-optical effect is:

$${\mathsf{\Omega }}_{\mathrm{R}}=\frac{\lambda \mathrm{c}V{B}_{\mathrm{r}}}{\pi R\mathsf{\Delta }\beta L}{\displaystyle {\int }_0^L{t}_{\mathrm{w}}(z)\sin (\frac{z}{R}-{\theta }_{\mathrm{r}})}dz$$

(10)

where λ denotes the wavelength of light wave, c denotes the speed of light in vacuum, B_r represents the radial magnetic induction, R represents the coil radius.

2.2. Magnetic Error Analysis of Axial Magnetic Field

In addition to the radial magnetic field, the fiber optic gyroscope will also be affected by the axial magnetic field. It can be seen from the previous analysis that the mode field distribution is asymmetric on the cross-section of the bending fiber. Therefore, the off-diagonal component of the dielectric constant tensor of the fiber is not zero. When the transverse magnetic field is applied, the transverse magnetic modes propagating CW and CCW cause a magneto-optical non-reciprocal phase shift, which will lead to magnetic-induced errors.

When an axial magnetic field is applied to a single-mode fiber, the propagation constants of CW ${\rho }_{+}$ and CW light waves ${\rho }_{-}$ can be expressed as:

$$\begin{array}{l}{\rho }_{+}=[\frac{\omega {\epsilon }_0}{4}{\displaystyle \int {\displaystyle \int E_{+}^{*}}}K{E}_{+}dxdy+\frac{\omega {\mu }_0}{4}{\displaystyle \int {\displaystyle \int H_{+}^{*}{H}_{+}dxdy}}\\ +\frac{j}{4}{\displaystyle \int {\displaystyle \int (E_{+}^{*}}}\cdot \nabla \times H_{+}-H_{+}^{*}\cdot \nabla \times H_{+})dxdy]/[\frac{1}{2}{\displaystyle \int {\displaystyle \int \mathrm{Re}(E_{+}\times H_{+}^{*})}}\cdot (+\widehat{z})dxdy]\end{array}$$

(11)

$$\begin{array}{l}{\rho }_{-}=[\frac{\omega {\epsilon }_0}{4}{\displaystyle \int {\displaystyle \int E_{-}^{*}}}K{E}_{-}dxdy+\frac{\omega {\mu }_0}{4}{\displaystyle \int {\displaystyle \int H_{-}^{*}{H}_{-}dxdy}}\\ +\frac{j}{4}{\displaystyle \int {\displaystyle \int (E_{-}^{*}}}\cdot \nabla \times H_{-}-H_{-}^{*}\cdot \nabla \times H_{-})dxdy]/[\frac{1}{2}{\displaystyle \int {\displaystyle \int \mathrm{Re}(E_{-}\times H_{-}^{*})}}\cdot (+\widehat{z})dxdy]\end{array}$$

(12)

where ω represents the spatial angular frequency, ε₀ represents the vacuum permittivity, K denotes the relative permittivity, μ₀ denotes the relative permeability of the fiber, and $+\widehat{z}$ and $-\widehat{z}$ are the light wave unit vectors in the CW and CCW directions, respectively.

The integral area in the above formula is the entire cross-section of the fiber, and its denominator is the Poynting power in this mode. After normalizing the denominator and decomposing the relative permittivity K into a diagonal matrix K₀ and an off-diagonal matrix ΔK, we get:

$${\rho }_{\pm }={\rho }_0+\frac{\omega {\epsilon }_0}{4}{\displaystyle \iint E_{\pm }^{*}\cdot \mathsf{\Delta }K{E}_{\pm }dxdy}$$

(13)

The longitudinal electric field components of the CW light wave and the CCW light wave are equal in magnitude and opposite in sign, and the transverse electric field components are equal in magnitude and sign. The propagation constants of CW and CCW light waves can be obtained:

$${\rho }_{\pm }={\rho }_0\pm \frac{\omega {\epsilon }_0}{2}{\displaystyle \iint \mathrm{Im}(n\lambda V{B}_{\mathrm{a}}/\mathsf{\pi }{E}_{\mathrm{x}}^{*}{E}_{\mathrm{z}})dxdy}$$

(14)

Then, the difference Δρ between the propagation constants of CW and CCW light waves is described as:

$$\mathsf{\Delta }\rho ={\rho }_{+}-{\rho }_{-}=\omega {\epsilon }_0{\displaystyle \iint \mathrm{Im}(n\lambda V{B}_{\mathrm{a}}/\mathsf{\pi }{E}_{\mathrm{x}}^{*}{E}_{\mathrm{z}})dxdy}$$

(15)

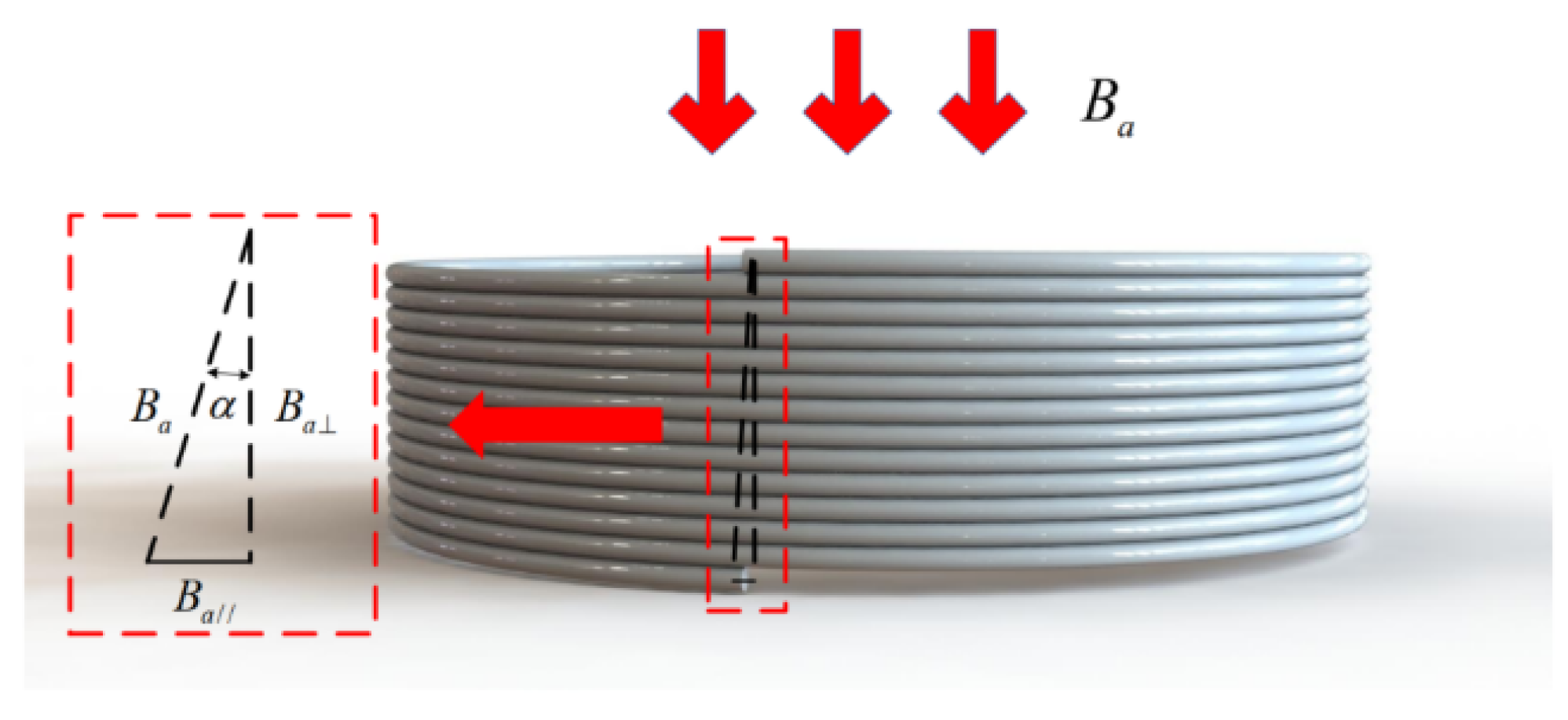
which shows the electric field component of the light wave is not symmetrical about the center point on the fiber cross-section when dielectric constant of a single-mode fiber has an off-diagonal component in axial magnetic field, resulting in a phase shift of the CW and CCW light waves. The magnitude of this phase shift is related to the strength of the magnetic field and the central asymmetry. Since the fiber coil is spirally rising close to the fiber skeleton during the winding process, as shown in Figure 3. Each turn of fiber has a slight tilt angle relative to the central axis of the fiber coil. Therefore, when the axial magnetic field acts on the fiber coil, there is a parallel component and a vertical component of the axial magnetic field, which can be expressed as:

$$\left\{\begin{array}{c}{B}_{\mathrm{a}//}=B_{\mathrm{a}}\sin \alpha \\ B_{\mathrm{a}\perp }=B_{\mathrm{a}}\cos \alpha \end{array}\right.$$

(16)

The helix angle α of the fiber coil is expressed as:

$$\sin \alpha =\frac{h}{2\mathsf{\pi }NR}$$

(17)

where h, N, and R represent coil height, number of turns, and radius, respectively.

For a fiber coil with a height of 13 mm, 72 turns in a single layer, and a winding radius of 30 mm, the helix angle is 0.052°. It can be determined by Equation (17) that the vertical component of the axial magnetic field is 1102 times that of the parallel component. Since the magnitude of the magnetic field referred to in this paper is that of the Earth’s magnetic field, the effect of the parallel component can be ignored. The homogeneous scalar wave equation obtained from the induced vector $\overrightarrow{D}$ in the single-mode fiber and Maxwell’s equation on the magnitude of the Earth’s magnetic field is:

$$\left\{\begin{array}{c}\overrightarrow{D}=\epsilon \overrightarrow{E}\\ {\nabla }^2{\overrightarrow{E}}_0+k^2\epsilon {\overrightarrow{E}}_0=0\end{array}\right.$$

(18)

where ε represents the dielectric constant of the fiber, and k represents the wave number in the fiber.

In general, the dielectric constant of the fiber is ε = n², in which n is the index of refraction. In order to facilitate the calculation, let the Z-axis direction of the fiber be the light wave propagation direction, and the X-axis direction be the fiber bending direction, then the relationship between the longitudinal component ${\overrightarrow{E}}_{0\mathrm{z}}$ and the transverse component ${\overrightarrow{E}}_{0\mathrm{x}}$ of the electric field inside the bent fiber is:

$${\overrightarrow{E}}_{0\mathrm{z}}=-\frac{j\lambda }{2\mathsf{\pi }n}\frac{\partial {\overrightarrow{E}}_{0\mathrm{x}}}{\partial x}$$

(19)

The transverse component of the electric field exhibits as Gaussian distribution, and the transverse electric field component ${\overrightarrow{E}}_{0x}$ in the bent fiber is expressed as:

$${\overrightarrow{E}}_{0\mathrm{x}}(x,y)=\exp \left(-\frac{x^2+y^2}{2w^2}\right)$$

(20)

where w represents the mode spot size.

When the axial magnetic field B_a is applied on the fiber, paralleled to the y-direction, the induced vector $\overrightarrow{D}$ can be expressed as:

$$\left\{\begin{array}{c}\overrightarrow{D}=n^2\overrightarrow{E}+j(\overrightarrow{\delta }\times \overrightarrow{E})\\ \overrightarrow{\delta }=V\overrightarrow{B}\lambda n/\pi \end{array}\right.$$

(21)

The resulting homogeneous scalar wave equation is:

$${\nabla }^2\overrightarrow{E}+n^2{k}^2\overrightarrow{E}=\nabla (\nabla \overrightarrow{E})-j{k}^2(\overrightarrow{\delta }\times \overrightarrow{E})$$

(22)

Substituting Equation (22) Into Equation (19), the wave equation corresponding to the transverse electric field component can be obtained as:

$${\nabla }^2\overrightarrow{E}+n^2{k}^2{\overrightarrow{E}}_{\mathrm{x}}=\frac{j\overrightarrow{\delta }}{n^2}\frac{{\partial }^2{E}_{\mathrm{x}}}{\partial x\partial z}-\frac{j\overrightarrow{\delta }}{n^2}\frac{{\partial }^2{E}_{\mathrm{z}}}{\partial x^2}-j{k}^2(\overrightarrow{\delta }\times {\overrightarrow{E}}_{\mathrm{z}})$$

(23)

Taking Equation (20) into the above equation and simplifying it, we calculated it as:

$${\nabla }^2\overrightarrow{E}+n^2{k}^2{\overrightarrow{E}}_{\mathrm{x}}=-\frac{j\overrightarrow{\delta }}{n^2}\frac{{\partial }^2{\overrightarrow{E}}_{\mathrm{z}}}{\partial x^2}$$

(24)

The right side of the equation is the perturbation component of ${\overrightarrow{E}}_{\mathrm{z}}$ induced by the axial magnetic field. Use Gaussian approximation for the transverse electric field in Equation (24), the mode field distribution is expressed as:

$${\nabla }^2\overrightarrow{E}+n^2{k}^2{\overrightarrow{E}}_{\mathrm{x}}\left(1+\frac{3\overrightarrow{\delta }x}{k^3{n}^5{w}^4}\right){\overrightarrow{E}}_{\mathrm{x}}=0$$

(25)

Putting Equation (21) into the above equation, we obtained:

$$\left\{\begin{array}{c}{\overrightarrow{E}}_{\mathrm{x}}(x,y)={\overrightarrow{E}}_{0\mathrm{x}}(x,y)\times (1+ax)\\ a=\frac{3V{B}_{\mathrm{a}}\lambda }{2\mathsf{\pi }{n}^2{w}^{2}k}\end{array}\right.$$

(26)

The propagation constant of the CW and CCW light waves change along the bent fiber. By normalizing $E_{\mathrm{x}}\left(x,y\right)$ in the fiber section, the mode field offset $\mathsf{\Delta }x$ of the bent fiber under the action of the axial magnetic field is expressed as [12]:

$$\mathsf{\Delta }x=\frac{{\displaystyle \iint x{E}_{\mathrm{x}}(x,y)dxdy}}{{\displaystyle \iint {\left|E_{0\mathrm{x}}(x,y)\right|}^{2}dxdy}}=\frac{3V{B}_{\mathrm{a}}{\lambda }^2}{2{\mathsf{\pi }}^2{n}^2}$$

(27)

Since the mode field offset of the CW and CCW light waves in the fiber are equal in magnitude and opposite in direction, for the entire fiber coil, the phase difference caused by the axial magnetic field can be expressed as:

$$\mathsf{\Delta }{\varphi }_{\mathrm{A}}=\frac{8{\mathsf{\pi }}^{2}n}{\lambda }\mathsf{\Delta }x=\frac{12V{B}_{\mathrm{a}}\lambda }{n}$$

(28)

From the above formula, the expression of the axial magnetic-induced error of the fiber optic gyroscope can be deduced as:

$${\mathsf{\Omega }}_{\mathrm{A}}=\frac{\lambda c}{4\mathsf{\pi }RL}\mathsf{\Delta }{\varphi }_{\mathrm{A}}=\frac{3{\lambda }^{2}cV{B}_{\mathrm{a}}}{4\mathsf{\pi }nRL}$$

(29)

2.3. Establishment of a Small IFOG Three-Dimensional Magnetically Induced Error Model

The bending fiber is subjected to both axial tension and radial compressive stress, which can be regarded as a curved cylindrical quartz rod. The stress distribution in the fiber is given by [13]:

$$\left\{\begin{array}{l}{\sigma }_{\mathrm{s}}=\frac{Y}{2R^2}[\frac{7-6v}{8(1-v)}(x^2-y^2-d^2)-\frac{1-2v}{2(1-v)}{y}^2]\\ {\sigma }_{\mathrm{f}}=\frac{1-2v}{16(1-v)}\frac{Y}{R^2}(x^2+y^2-d^2)\end{array}\right.$$

(30)

where Y represent the Young’s modulus of the fiber, ν represent Poisson’s ratio of the fiber.

The cladding diameter is fixed when the PMF is drawn from the preform, and the bending radius is related to both the initial radius of the fiber coil and the winding method. The bending radius of the fiber coil is required to be designed between 10 mm and 20 mm in the aerospace field. For such a bending radius, the difference in the bending radius between different layers cannot be ignored. Our previous work showed that for a fiber coil using the orthocyclic quadrupolar winding, the relationship between fiber length and fiber bending radius, as well as the refractive index and birefringence distribution models, can be expressed as [9]:

$$\left\{\begin{array}{c}{R}_{\mathrm{i}}=R_{\mathrm{in}}+\frac{\sqrt{3}}{2}id\\ L_{\mathrm{i}}=N·2\pi R_{\mathrm{i}}\\ \mathsf{\Delta }\beta =\frac{n^3}{2}(p_{11}-2v{p}_{12})\times [\frac{(6-4v)}{16R^2(1-v)}{d}^2]\left\{i=1,2,...,M\right\}\\ \mathsf{\Delta }{n}_{\mathrm{si}}=\frac{n^3}{2}(p_{11}-2v{p}_{12})\times [\frac{(7-6v)d^2}{16R_{\mathrm{i}}{}^2(1-v)}]\\ \mathsf{\Delta }{n}_{\mathrm{fi}}=\frac{n^3}{2}(p_{11}-2v{p}_{12})\times [\frac{(1-2v)d^2}{16R_{\mathrm{i}}{}^2(1-v)}]\end{array}\right.$$

(31)

where R_in represents the innermost radius of the fiber coil, R_i represents the radius of the first layer of the fiber coil, L_i represents the total length of the fiber wrapped around the fiber coil at the first layer, N represents the number of turns of the fiber coil, and M is the number of layers of the fiber coil, p₁₁ and p₁₂ represent the elastic optical coefficient of the fiber.

Take YOFC-PM-1310 80-18/135 panda PMF as an example. The specific parameters of the fiber are listed in

Table 1. Key parameters of the YOFC-PM-1310 80-18/135 PMF.

Fiber Parameters	Parameter Setting Value
Inner diameter of stress zone	0.021 mm
Outside diameter of stress zone	0.084 mm
Young’s modulus Y	7830 kg/mm2
Poisson’s ratio ν	0.186

. Figure 4 shows the relationship between birefringence and fiber length with a different winding radius where the birefringence increases first and then decreases with fiber length increasing. Additionally, it is illustrated that the bending radius of the fiber increases in a stepwise manner with length increasing, which is due to the fiber coil increases in length at different turns within the same layer while the bend radius remains the same. Moreover, since the fiber winding is from the midpoint to both ends, the smallest radius is found at the midpoint of the fiber coil, where the birefringence varies the most significantly. With the bending radius gradually increasing, the variation of birefringence is gradually decreasing. The smaller the initial bending radius, the greater the birefringence change.

As shown in Figure 5, the magnetic field applied to the fiber optic gyro can be decomposed into two directions and calculated separately and then accumulated. Decompose the magnetic field B with an angle η to the vertical axis into an axial magnetic field and a radial magnetic field, and the magnetic error caused by the magnetic field at any angle can be expressed as:

$${\mathsf{\Omega }}_{\mathrm{B}}={\mathsf{\Omega }}_{\mathrm{R}}+{\mathsf{\Omega }}_{\mathrm{A}}=\frac{\lambda cVB\sin \eta }{\mathsf{\pi }R\mathsf{\Delta }\beta L}{\displaystyle {\int }_0^L{t}_{\mathrm{w}}(z)\sin (\frac{z}{R}-{\theta }_0)}dz+\frac{3{\lambda }^{2}cVB\cos \eta }{4\mathsf{\pi }nRL}$$

(32)

Since the optical fiber is a non-magnetic conductive material, the intensity of the magnetic field will not change after passing through the multi-layer fiber, so the variation of the birefringence and refractive index caused by the bending radius varying only affect the magnitude of the magnetic error. The number of turns can be simplified when thebending radius of the fibers in the same layer is the same, only carrying out the accumulation calculation based on the layer. The expression of the three-dimensional magnetic induction error of the small IFOG can be given as follows:

$${\mathsf{\Omega }}_{\mathrm{B}}={\displaystyle \sum _{i=1}^M\frac{N\lambda \mathrm{c}V{B}_{\mathrm{r}}}{\pi R_{\mathrm{i}}\mathsf{\Delta }{\beta }_{\mathrm{i}}L}{\displaystyle {\int }_0^{l_{\mathrm{i}}}{t}_{\mathrm{w}}(z)\sin (\frac{z}{R_{\mathrm{i}}}-{\theta }_{\mathrm{r}})}dz}+{\displaystyle \sum _{i=1}^M\frac{N3{\lambda }^{2}cV{B}_{\mathrm{a}}}{4\pi n_{\mathrm{i}}{R}_{\mathrm{i}}L}}$$

(33)

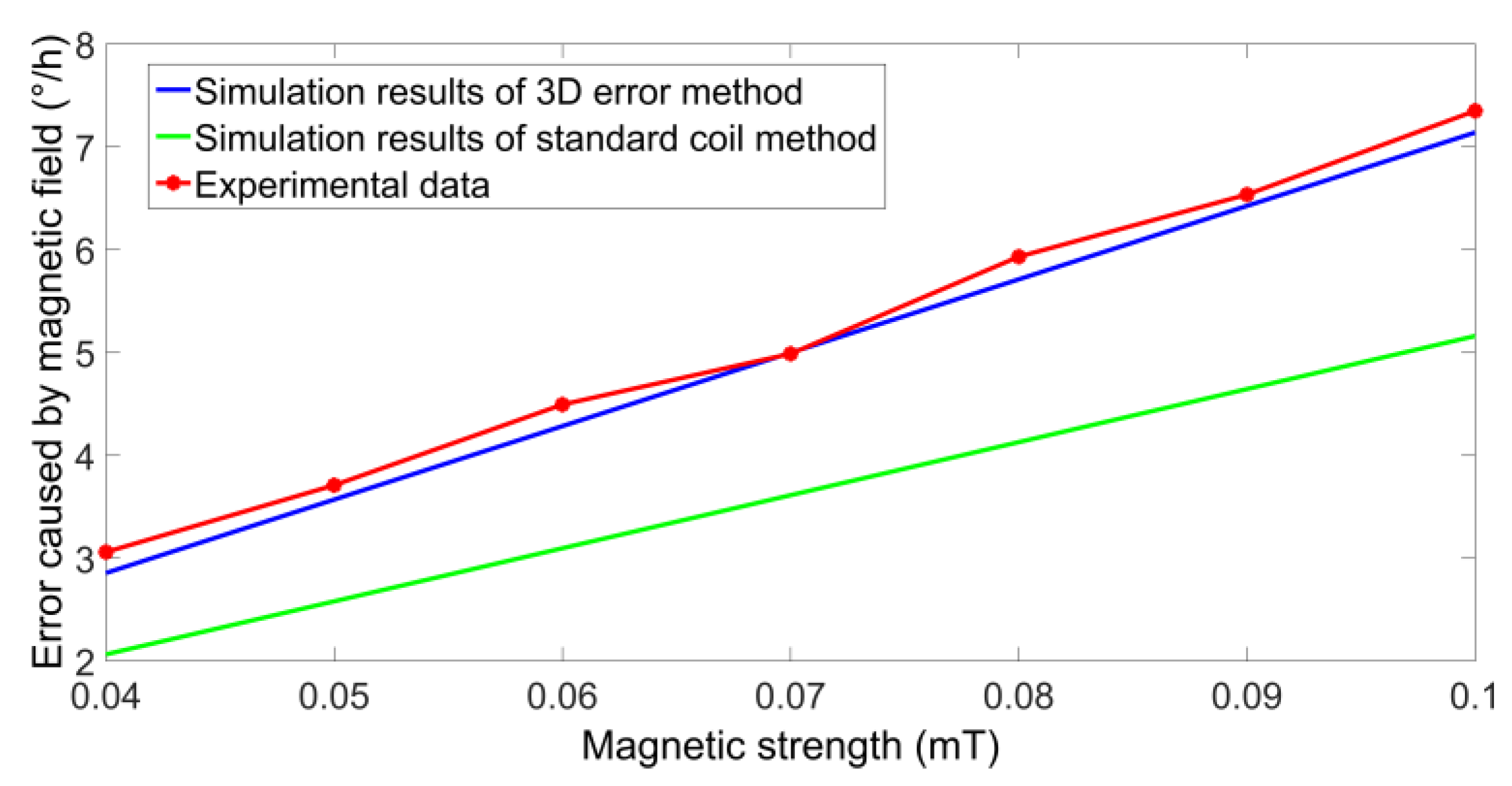
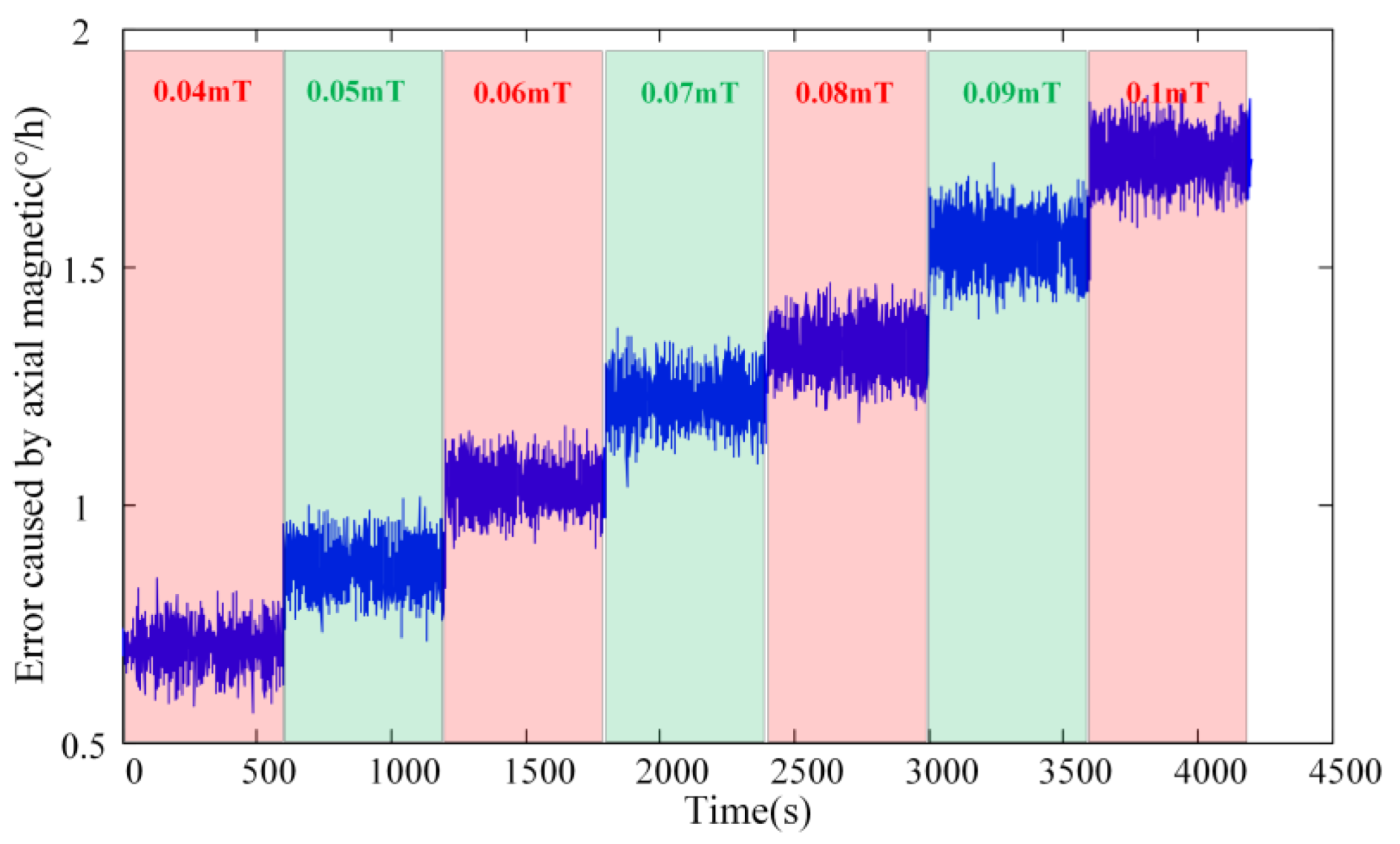
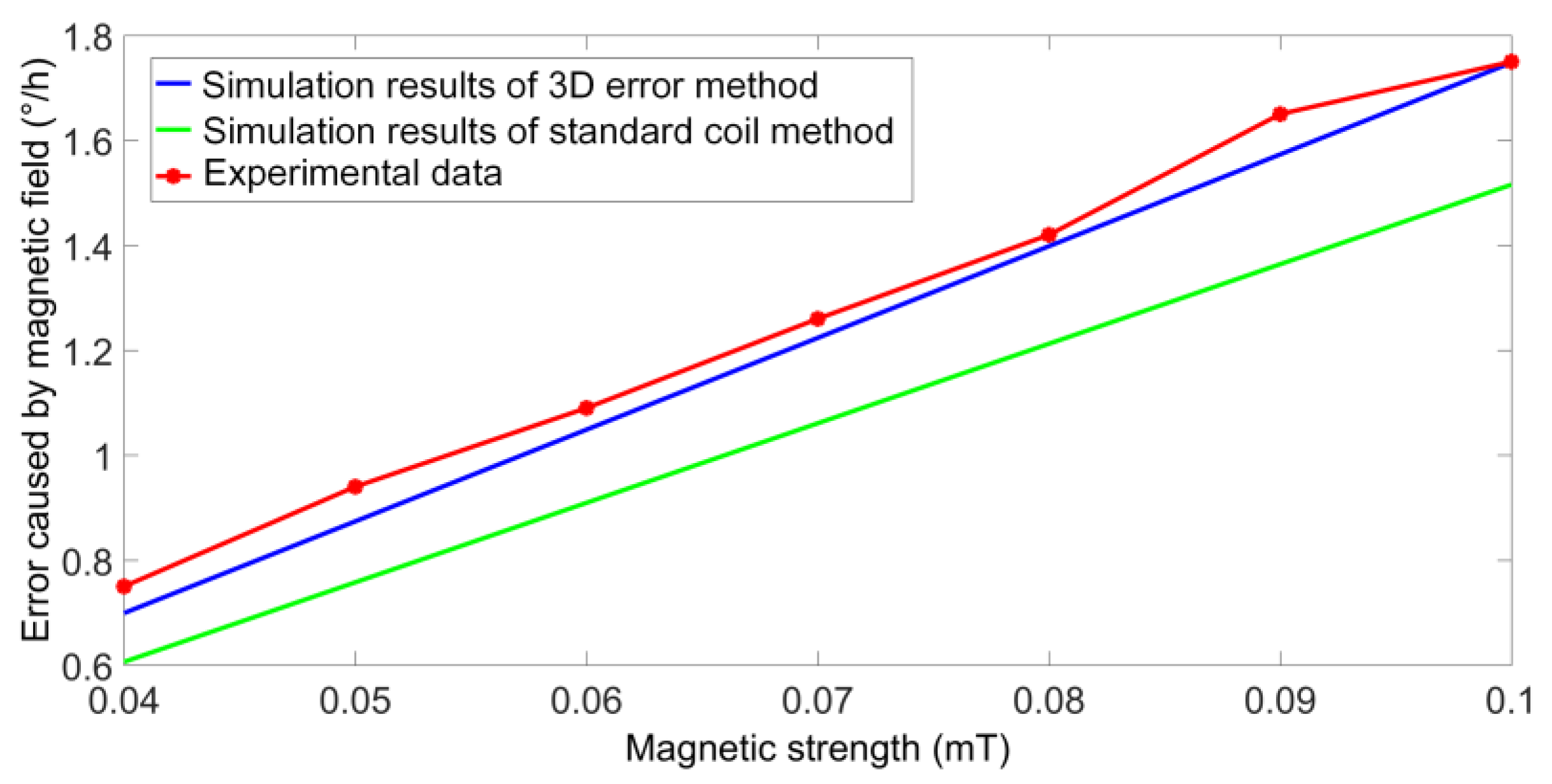
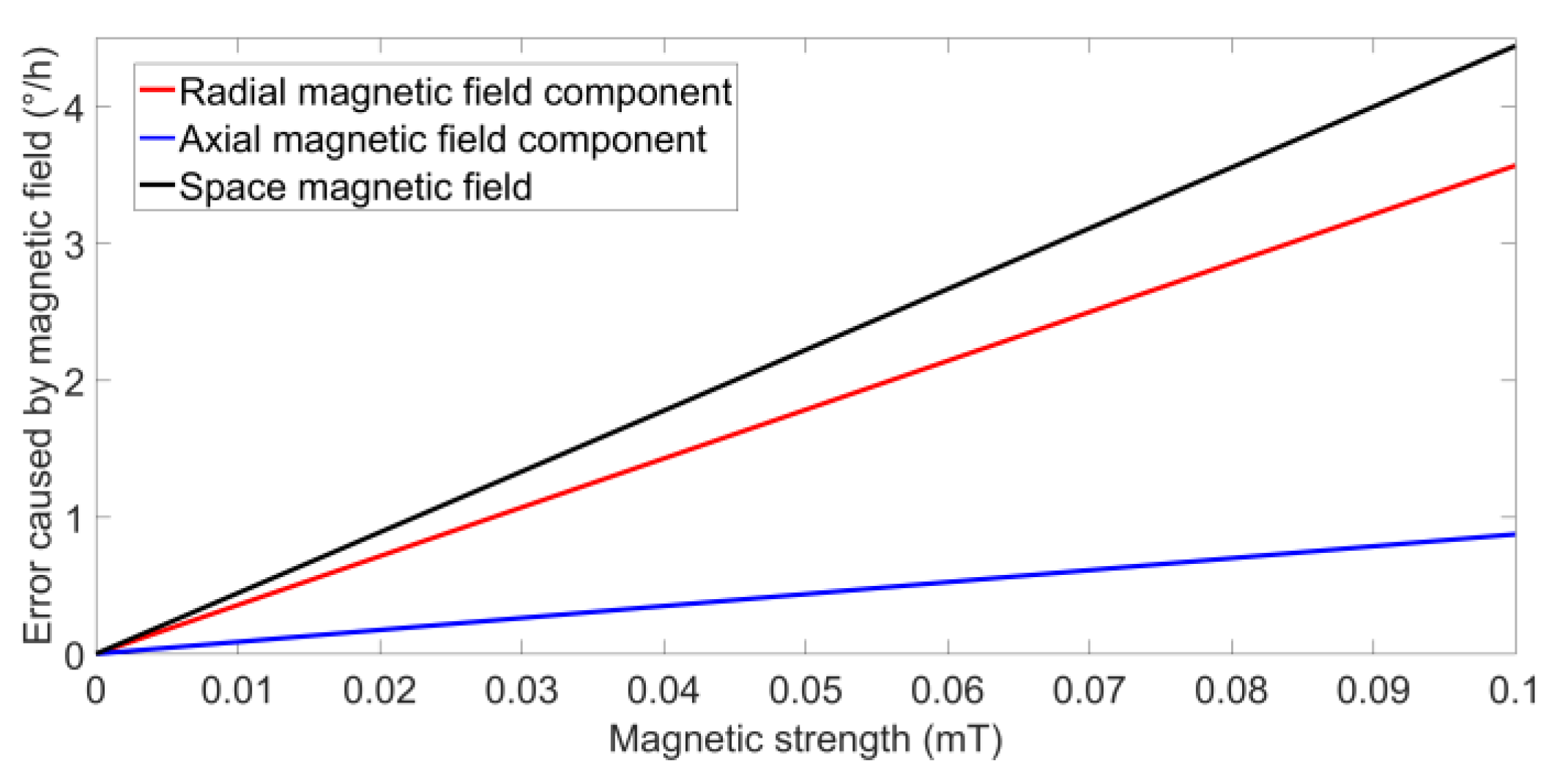
Next, the simulation analysis of the small IFOG fiber coil is carried out. The fiber is YOFC-PM-1310 80-18/135 panda-type PMF. The total length of the fiber coil is 300 m, the inner diameter is 0.026 m, the number of layers is 42, and the number of turns is 72. During the winding process, the torsional period of the fiber amplitude t_w(z) is about 0.2. To make the radial and axial magnetic field equal in intensity, the angle between the magnetic field and the fiber coil is set to 45°. The simulation results of the three-dimensional magnetic induced error under the magnetic field with the magnetic induction intensity of 0–0.1 mT are depicted in Figure 6.

In Figure 6, the black line is the magnitude of the magnetic error caused by the magnetic field, the red line is the magnitude of the magnetic error induced by the radial magnetic field, and the blue line is the magnitude of the magnetic error induced by the axial magnetic field. Since the intensity of the magnetic field in the radial and axial directions are equal, the radial magnetic field has a greater impact on the gyro.

3. Results and Discussion

To test the output change of the gyroscope under different magnetic field strengths, it is elementary to establish a controllable magnetic field environment. We choose the Helmholtz coil as the magnetic field generating device of the magnetic-induced error test system. The schematic diagram of the Helmholtz coil is shown in Figure 7. The distance between the two coils is equal to the radius r of the two circular coils. Based on the Biot-Savart law, the relationship between the magnitude of the magnetic induction dB of a certain point in space and current element Idl and coil radius r is described as:

$$dB=\frac{\mu }{4\mathsf{\pi }}\frac{Idl}{r^2}$$

(34)

where μ is the vacuum permeability.

According to the above theoretical derivation and actual experimental requirements, a Helmholtz coil with a size of 220 mm × 125 mm × 2700 mm is designed, the inner diameter of the energized coil is 150 mm, and the number of turns is 112. The inner diameter of the Helmholtz coil is 150 mm, the outer diameter is 220 mm, the diameter of the copper enameled wire is 2 mm, and the DC resistance at room temperature is about 0.5 Ω. The size of the central magnetic field area is 40 mm × 40 mm × 40 mm, and the variation of the magnetic induction intensity is less than 1%.

To avoid the influence of the magnetic field on the circuit, a separated test system is applied. The experimental test system setup is shown in Figure 8. The beam emitted by the superluminescent diode (SLD) laser is incident into the MIOC. After being polarized and split in MIOC, the light beam enters the fiber coil and is converted into a digital information by the photodetector, finally collected by the computer.

Figure 8 shows the test method of radial magnetic induced error. The fiber coil is placed horizontally in a uniform magnetic field, and the current generating device is controlled to generate currents of 80 mA, 100 mA, 120 mA, 140 mA, 160 mA, 180 mA, and 200 mA, and the corresponding magnetic induction intensity is 0.04 mT, 0.05 mT, 0.06 mT, 0.07 mT, 0.08 mT, 0.09 mT, and 0.1 mT, respectively. The zero offset value is subtracted from the collected data to eliminate the influence of the earth’s rotation speed and regional magnetic field on the FOG. Finally, the 300–400 s part of the data is taken and averaged as the zero error of the radial experiment.

The experimental results are shown in Figure 9. Each step represents the output of the IFOG subjected to different magnetic induction intensities within 600 s. The three-dimensional error simulation method proposed in this paper and the traditional error simulation method are compared with the experimental data, and the results are shown in Figure 10. The green line in the figure is the simulation result of the standard coil method (that is, the fiber coil is used as a unified coil to calculate the error) [14]. The blue line is the three-dimensional error simulation result, and the red line is the experimental data. It can be clearly seen from the comparison results that the error value calculated by the 3D error method is closer to the experimental data.

This paper gives the RMSE of the two simulation results as the judging standard. The RMSE represents the fitting degree between the theoretical value and the true value. The smaller the RMSE, the higher the measurement accuracy. As shown in Figure 10, the RMSE of the three-dimensional error method model is 0.424°/h, and the RMSE of the standard coil method model error is 1.01°/h. Compared with the traditional model, the RMSE of the three-dimensional error simulation method model is reduced by 56.9%.

Figure 11 shows the test method of the axial magnetic-induced error. The fiber coil is placed horizontally in a uniform magnetic field. The test process is the same as that of the radial magnetic-induced error. The current generating devices output currents are 80 mA, 100 mA, 120 mA, 140 mA, 160 mA, 180 mA, and 200 mA, respectively, and the corresponding magnetic induction intensities are, respectively, 0.04 mT, 0.05 mT, 0.06 mT, 0.07 mT, 0.08 mT, 0.09 mT, and 0.1 mT. The 300–400 s part of the collected 600 s data was intercepted and processed in the computer. It has been discovered that the value of the axial magnetic error is smaller than the radial magnetic error, which is consistent with the theoretical deduction.

The experimental results are demonstrated in Figure 12. For the axial magnetically induced error, the results obtained by the three-dimensional error method are closer to the real value than the simulation results of the standard coil. The blue line in Figure 13 represents the three-dimensional error simulation result, the green line represents the standard coil method error simulation result, and the red line represents the experimental data. The RMSE of the three-dimensional error method model is 0.101°/h, and the RMSE of the standard coil method model is 0.157°/h. In comparison, the RMSE of the three-dimensional error method is reduced by 35.7%.

4. Conclusions

In this paper, we analyze the effects of axial magnetic field and radial magnetic field on the bias of a small fiber optic gyroscope for space, respectively. The bending will change the birefringence of the fiber, and then affect the magnitude of the magnetic-induced error of the IFOG. After considering the fiber birefringence varying with the small bending radius, we established a three-dimensional magnetic-induced error model of a small fiber coil. A magnetic field test system composed of Fluke standard current source, transconductance amplifier and Helmholtz coil is designed to verify the model. The experimental results show that the RMSE of the radial magnetic induced error model is reduced by 56.9% compared with the standard coil method, and the RMSE of the axial magnetic induced error model is reduced by 35.7% compared with the standard coil method at room temperature. Both the simulation results and the experimental data prove that the birefringence model of the small-sized fiber coil can more accurately reflect the influence of the magnetic field compared with the commonly used calculation method of magnetic-induced error.