Optical Chirality of Gold Chiral Helicoid Nanoparticles in the Strong Coupling Region
Abstract
1. Introduction
2. Results and Discussion
2.1. Modes Analysis and Chirality of the Single GHNP
2.2. Strong Coupling Systems Composed of Bright Modes and Emitters
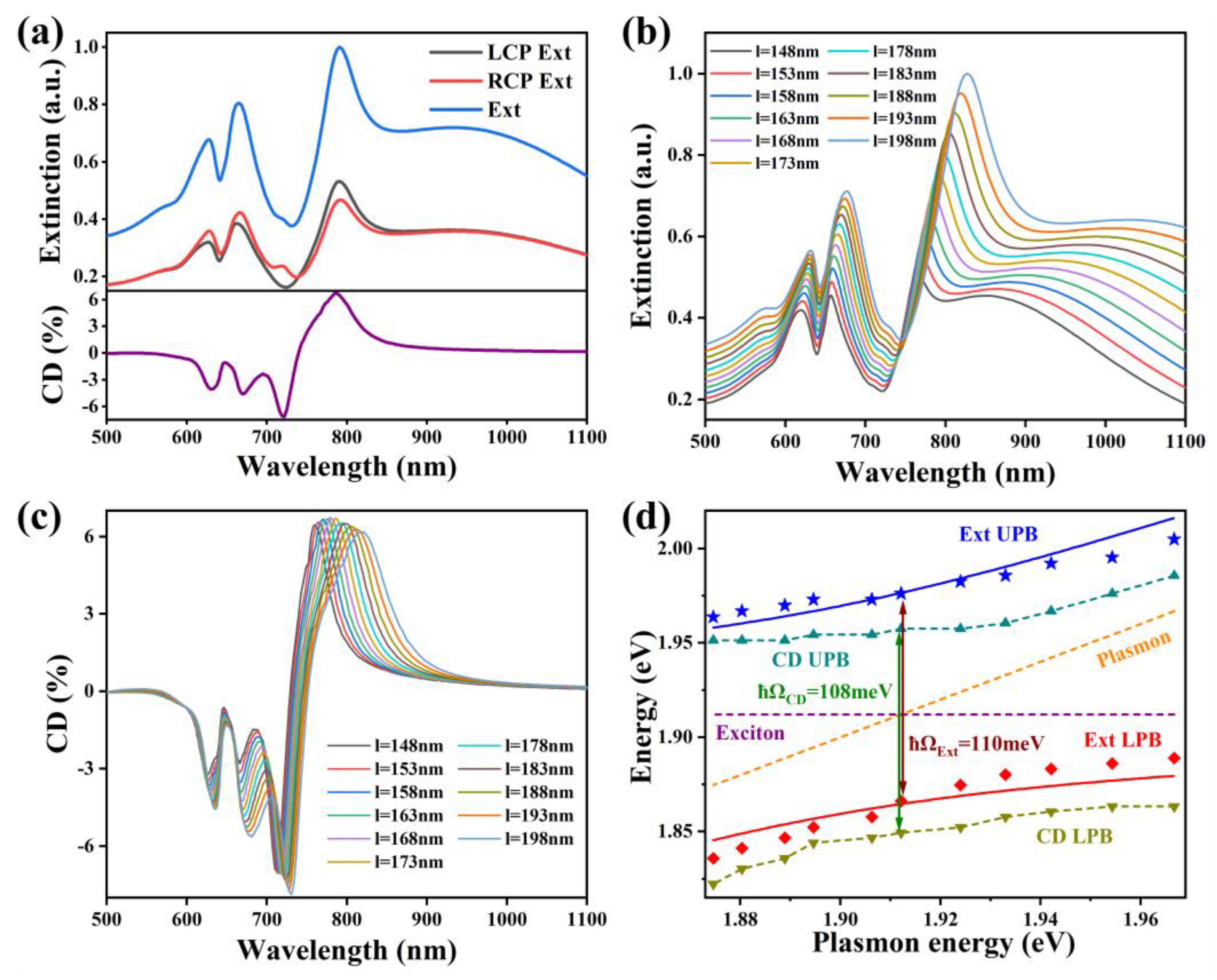
2.3. Chirality Analysis of GHNP in the Strong Coupling Region
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Electromagnetic and Chiral Optical Simulation
References
- Luo, Y.; Chi, C.; Jiang, M.; Li, R.; Zu, S.; Li, Y.; Fang, Z. Plasmonic chiral nanostructures: Chiroptical effects and applications. Adv. Opt. Mater. 2017, 5, 1700040. [Google Scholar] [CrossRef]
- Zhao, Y.; Belkin, M.; Alù, A. Twisted optical metamaterials for planarized ultrathin broadband circular polarizers. Nat. Commun. 2012, 3, 870. [Google Scholar] [CrossRef]
- Kaschke, J.; Blume, L.; Wu, L.; Thiel, M.; Bade, K.; Yang, Z.; Wegener, M. A helical metamaterial for broadband circular polarization conversion. Adv. Opt. Mater. 2015, 3, 1411–1417. [Google Scholar] [CrossRef]
- Hendry, E.; Carpy, T.; Johnston, J.; Popland, M.; Mikhaylovskiy, R.; Lapthorn, A.; Kelly, S.; Barron, L.; Gadegaard, N.; Kadodwala, M. Ultrasensitive detection and characterization of biomolecules using superchiral fields. Nat. Nanotechnol. 2010, 5, 783–787. [Google Scholar] [CrossRef]
- Zhang, S.; Zhou, J.; Park, Y.-S.; Rho, J.; Singh, R.; Nam, S.; Azad, A.K.; Chen, H.-T.; Yin, X.; Taylor, A.J.; et al. Photoinduced handedness switching in terahertz chiral metamolecules. Nat. Commun. 2012, 3, 942. [Google Scholar] [CrossRef]
- Pendry, J. A chiral route to negative refraction. Science 2004, 306, 1353–1355. [Google Scholar] [CrossRef]
- Tamura, M.; Fujihara, H. Chiral bisphosphine binap-stabilized gold and palladium nanoparticles with small size and their palladium nanoparticle-catalyzed asymmetric reaction. J. Am. Chem. Soc. 2003, 125, 15742–15743. [Google Scholar] [CrossRef]
- Zhan, P.; Wang, Z.-G.; Li, N.; Ding, B. Engineering gold nanoparticles with dna ligands for selective catalytic oxidation of chiral substrates. ACS Catal. 2015, 5, 1489–1498. [Google Scholar] [CrossRef]
- Jeong, H.; Mark, A.G.; Alarcón-Correa, M.; Kim, I.; Oswald, P.; Lee, T.C.; Fischer, P. Dispersion and shape engineered plasmonic nanosensors. Nat. Commun. 2016, 7, 11331. [Google Scholar] [CrossRef]
- Kumar, J.; Erana, H.; López-Martínez, E.; Claes, N.; Martín, V.F.; Solís, D.M.; Bals, S.; Cortajarena, A.L.; Castilla, J.; Liz-Marzán, L.M. Detection of amyloid fibrils in parkinsonąŕs disease using plasmonic chirality. Proc. Natl. Acad. Sci. USA 2018, 115, 3225–3230. [Google Scholar] [CrossRef]
- Nguyen, L.A.; He, H.; Pham-Huy, C. Chiral drugs: An overview. Int. J. Biomed. Sci. 2006, 2, 85–100. [Google Scholar] [PubMed]
- Tang, Y.; Liu, Z.; Deng, J.; Li, K.; Li, J.; Li, G. Nano-kirigami metasurface with giant nonlinear optical circular dichroism. Laser Photonics Rev. 2020, 14, 2000085. [Google Scholar] [CrossRef]
- Ohnoutek, L.; Cho, N.H.; Allen Murphy, A.W.; Kim, H.; Rasadean, D.M.; Pantos, G.D.; Nam, K.T.; Valev, V.K. Single nanoparticle chiroptics in a liquid: Optical activity in hyper-rayleigh scattering from au helicoids. Nanoletters 2020, 20, 5792–5798. [Google Scholar] [CrossRef] [PubMed]
- Kuzyk, A.; Schreiber, R.; Fan, Z.; Pardatscher, G.; Roller, E.-M.; Hogele, A.; Simmel, F.C.; Govorov, A.O.; Liedl, T. Dna-based self-assembly of chiral plasmonic nanostructures with tailored optical response. Nature 2012, 483, 311–314. [Google Scholar] [CrossRef]
- Long, G.; Adamo, G.; Tian, J.; Klein, M.; Krishnamoorthy, H.N.; Feltri, E.; Wang, H.; Soci, C. Perovskite metasurfaces with large superstructural chirality. Nat. Commun. 2022, 13, 1551. [Google Scholar] [CrossRef]
- Chen, J.; Gao, X.; Zheng, Q.; Liu, J.; Meng, D.; Li, H.; Cai, R.; Fan, H.; Ji, Y.; Wu, X. Bottom-up synthesis of helical plasmonic nanorods and their application in generating circularly polarized luminescence. ACS Nano 2021, 15, 15114–15122. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.-E.; Ahn, H.-Y.; Mun, J.; Lee, Y.Y.; Kim, M.; Cho, N.H.; Chang, K.; Kim, W.S.; Rho, J.; Nam, K.T. Amino-acid-and peptide-directed synthesis of chiral plasmonic gold nanoparticles. Nature 2018, 556, 360–365. [Google Scholar] [CrossRef]
- Spreyer, F.; Mun, J.; Kim, H.; Kim, R.M.; Nam, K.T.; Rho, J.; Zentgraf, T. Second harmonic optical circular dichroism of plasmonic chiral helicoid-iii nanoparticles. ACS Photonics 2022, 9, 784–792. [Google Scholar] [CrossRef]
- He, Z.; Li, F.; Liu, Y.; Yao, F.; Xu, L.; Han, X.; Wang, K. Principle and applications of the coupling of surface plasmons and excitons. Appl. Sci. 2020, 10, 1774. [Google Scholar] [CrossRef]
- Li, S.; Li, Y.; Lv, H.; Ji, C.; Gao, H.; Sun, Q. Chiral Dual-Core Photonic Crystal Fiber for an Efficient Circular Polarization Beam Splitter. Photonics 2023, 10, 45. [Google Scholar] [CrossRef]
- Sollner, I.; Mahmoodian, S.; Hansen, S.L.; Midolo, L.; Javadi, A.; Kiršanske, G.; Pregnolato, T.; El-Ella, H.; Lee, E.H.; Song, J.D.; et al. Deterministic photon–emitter coupling in chiral photonic circuits. Nat. Nanotechnol. 2015, 10, 775–778. [Google Scholar] [CrossRef] [PubMed]
- Lodahl, P.; Mahmoodian, S.; Stobbe, S.; Rauschenbeutel, A.; Schneeweiss, P.; Volz, J.; Pichler, H.; Zoller, P. Chiral quantum optics. Nature 2017, 541, 473–480. [Google Scholar] [CrossRef] [PubMed]
- Aiello, A.; Banzer, P.; Neugebauer, M.; Leuchs, G. From transverse angular momentum to photonic wheels. Nat. Photonics 2015, 9, 789–795. [Google Scholar] [CrossRef]
- Guo, J.; Song, G.; Huang, Y.; Liang, K.; Wu, F.; Jiao, R.; Yu, L. Optical chirality in a strong coupling system with surface plasmons polaritons and chiral emitters. ACS Photonics 2021, 8, 901–906. [Google Scholar] [CrossRef]
- Guo, J.; Wu, F.; Song, G.; Huang, Y.; Jiao, R.; Yu, L. Diverse axial chiral assemblies of j-aggregates in plexcitonic nanoparticles. Nanoscale 2021, 13, 15812–15818. [Google Scholar] [CrossRef]
- Wu, F.; Guo, J.; Huang, Y.; Liang, K.; Jin, L.; Li, J.; Deng, X.; Jiao, R.; Liu, Y.; Zhang, J.; et al. Plexcitonic optical chirality: Strong exciton–plasmon coupling in chiral j-aggregate-metal nanoparticle complexes. ACS Nano 2020, 15, 2292–2300. [Google Scholar] [CrossRef]
- Zhu, J.; Wu, F.; Han, Z.; Shang, Y.; Liu, F.; Yu, H.; Yu, L.; Li, N.; Ding, B. Strong light–matter interactions in chiral plasmonic–excitonic systems assembled on dna origami. Nano Lett. 2021, 21, 3573–3580. [Google Scholar] [CrossRef]
- Thomaschewski, M.; Yang, Y.; Wolff, C.; Roberts, A.S.; Bozhevolnyi, S.I. On-Chip Detection of Optical Spin–Orbit Interactions in Plasmonic Nanocircuits. Nano Lett. 2019, 19, 1166–1171. [Google Scholar] [CrossRef]
- Ren, H.; Wang, X.; Li, C.; He, C.; Wang, Y.; Pan, A.; Maier, S.A. Orbital-Angular-Momentum-Controlled Hybrid Nanowire Circuit. Nano Lett. 2021, 21, 6220–6227. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, B.; Huang, Z.; Li, J.; Han, Z.; Wu, D.; Zhou, J.; Ma, Y.; Wu, Q.; Maeda, H. High-directionality spin-selective routing of photons in plasmonic nanocircuits. Nanoscale 2022, 14, 428–432. [Google Scholar] [CrossRef]
- Bhaskar, S.; Srinivasan, V.; Ramamurthy, S.S. Nd2O3-Ag Nanostructures for Plasmonic Biosensing, Antimicrobial, and Anticancer Applications. ACS Appl. Nano Mater. 2023, 6, 1129–1145. [Google Scholar] [CrossRef]
- Bhaskar, S.; Das, P.; Srinivasan, V.; Bhaktha, S.B.N.; Ramamurthy, S.S. Plasmonic-Silver Sorets and Dielectric-Nd2O3 nanorods for Ultrasensitive Photonic Crystal-Coupled Emission. Mater. Res. Bull. 2022, 145, 111558. [Google Scholar] [CrossRef]
- Feng, W.; Kim, J.-Y.; Wang, X.; Calcaterra, H.A.; Qu, Z.; Meshi, L.; Kotov, N.A. Assembly of mesoscale helices with near-unity enantiomeric excess and light-matter interactions for chiral semiconductors. Sci. Adv. 2017, 3, e1601159. [Google Scholar] [CrossRef] [PubMed]
- Berova, N.; Nakanishi, K.; Woody, R.W. Circular Dichroism: Principles and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- García-Guirado, J.; Svedendahl, M.; Puigdollers, J.; Quidant, R. Enantiomer-selective molecular sensing using racemic nanoplasmonic arrays. Nano Lett. 2018, 18, 6279–6285. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Deng, L.; Guo, Y.; Yang, W.; Xia, S.; Yan, W.; Yang, Y.; Qin, J.; Bi, L. Enhanced chiral sensing in achiral nanostructures with linearly polarized light. Opt. Express 2022, 30, 26306–26314. [Google Scholar] [CrossRef]
- Zhao, Y.; Askarpour, A.N.; Sun, L.; Shi, J.; Li, X.; Alù, A. Chirality detection of enantiomers using twisted optical metamaterials. Nat. Commun. 2017, 8, 14180. [Google Scholar] [CrossRef]
- Kelly, C.; Tullius, R.; Lapthorn, A.J.; Gadegaard, N.; Cooke, G.; Barron, L.D.; Karimullah, A.S.; Rotello, V.M.; Kadodwala, M. Chiral plasmonic fields probe structural order of biointerfaces. J. Am. Chem. Soc. 2018, 140, 8509–8517. [Google Scholar] [CrossRef]
- Das, R.; Sarkar, S. Optical properties of silver nano-cubes. Opt. Mater. 2015, 48, 203–208. [Google Scholar] [CrossRef]
- Rai, A.; Bhaskar, S.; Ganesh, K.M.; Ramamurthy, S.S. Hottest Hotspots from the Coldest Cold: Welcome to Nano 4.0. ACS Appl. Nano Mater. 2022, 5, 12245–12264. [Google Scholar] [CrossRef]
- Bhaskar, S.; Thacharakkal, D.; Ramamurthy, S.S.; Subramaniam, C. Metal–Dielectric Interfacial Engineering with Mesoporous Nano-Carbon Florets for 1000-Fold Fluorescence Enhancements: Smartphone-Enabled Visual Detection of Perindopril Erbumine at a Single-molecular Level. ACS Sustain. Chem. Eng. 2023, 11, 78–91. [Google Scholar] [CrossRef]
- Kelf, T.A.; Sugawara, Y.; Baumberg, J.J.; Abdelsalam, M.; Bartlett, P.N. Plasmonic Band Gaps and Trapped Plasmons on Nanostructured Metal Surfaces. Phys. Rev. Lett. 2005, 95, 116802. [Google Scholar] [CrossRef] [PubMed]
- Schäferling, M. Chiral nanophotonics. Springer Ser. Opt. Sci. 2017, 205, 159. [Google Scholar]
- Tang, Y.; Cohen, A.E. Enhanced enantioselectivity in excitation of chiral molecules by superchiral light. Science 2011, 332, 333–336. [Google Scholar] [CrossRef] [PubMed]
- Baranov, D.G.; Wersäll, M.; Cuadra, J.; Antosiewicz, T.J.; Shegai, T. Novel nanostructures and materials for strong light–matter interactions. ACS Photonics 2018, 5, 24–42. [Google Scholar] [CrossRef]
- Cao, E.; Lin, W.; Sun, M.; Liang, W.; Song, Y. Exciton-plasmon coupling interactions: From principle to applications. Nanophotonics 2018, 7, 145–167. [Google Scholar] [CrossRef]
- Johnson, P.B.; Christy, R.-W. Optical constants of the noble metals. Phys. Rev. B 1972, 6, 4370. [Google Scholar] [CrossRef]
- Song, G.; Guo, J.; Duan, G.; Jiao, R.; Yu, L. Interactions between a single metallic nanoparticle and chiral molecular j-aggregates in the strong coupling regime and the weak coupling regime. Nanotechnology 2020, 31, 345202. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, H.; Liang, K.; Deng, X.; Jin, L.; Shangguan, J.; Zhang, J.; Guo, J.; Yu, L. Optical Chirality of Gold Chiral Helicoid Nanoparticles in the Strong Coupling Region. Photonics 2023, 10, 251. https://doi.org/10.3390/photonics10030251
Cheng H, Liang K, Deng X, Jin L, Shangguan J, Zhang J, Guo J, Yu L. Optical Chirality of Gold Chiral Helicoid Nanoparticles in the Strong Coupling Region. Photonics. 2023; 10(3):251. https://doi.org/10.3390/photonics10030251
Chicago/Turabian StyleCheng, Haowei, Kun Liang, Xuyan Deng, Lei Jin, Jingcheng Shangguan, Jiasen Zhang, Jiaqi Guo, and Li Yu. 2023. "Optical Chirality of Gold Chiral Helicoid Nanoparticles in the Strong Coupling Region" Photonics 10, no. 3: 251. https://doi.org/10.3390/photonics10030251
APA StyleCheng, H., Liang, K., Deng, X., Jin, L., Shangguan, J., Zhang, J., Guo, J., & Yu, L. (2023). Optical Chirality of Gold Chiral Helicoid Nanoparticles in the Strong Coupling Region. Photonics, 10(3), 251. https://doi.org/10.3390/photonics10030251




