Sub-40 GHz Broadband Polarization Chaos Generation Using Mutually Coupled Free-Running VCSELs
Abstract
1. Introduction
2. System Model and Theory
3. Simulation Results and Analysis
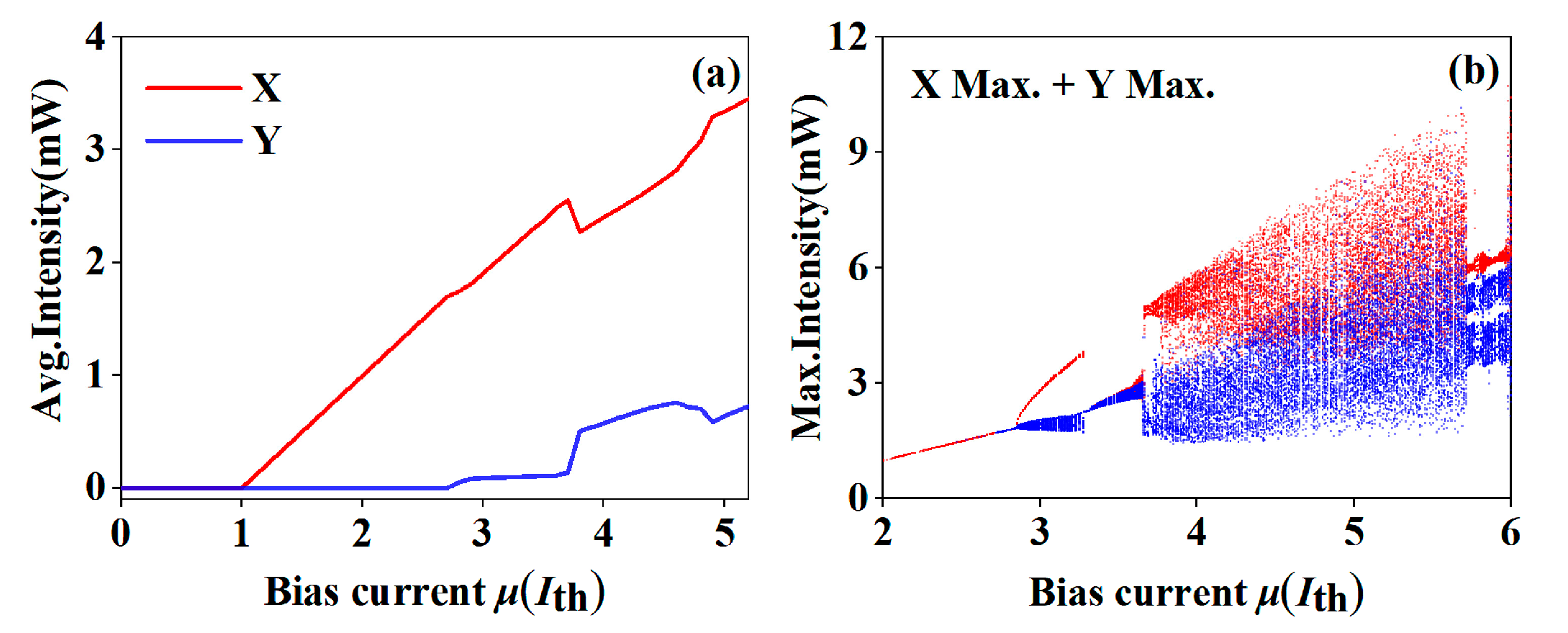
3.1. Basic Characteristics of Polarization Chaos from Free-Running VCSEL
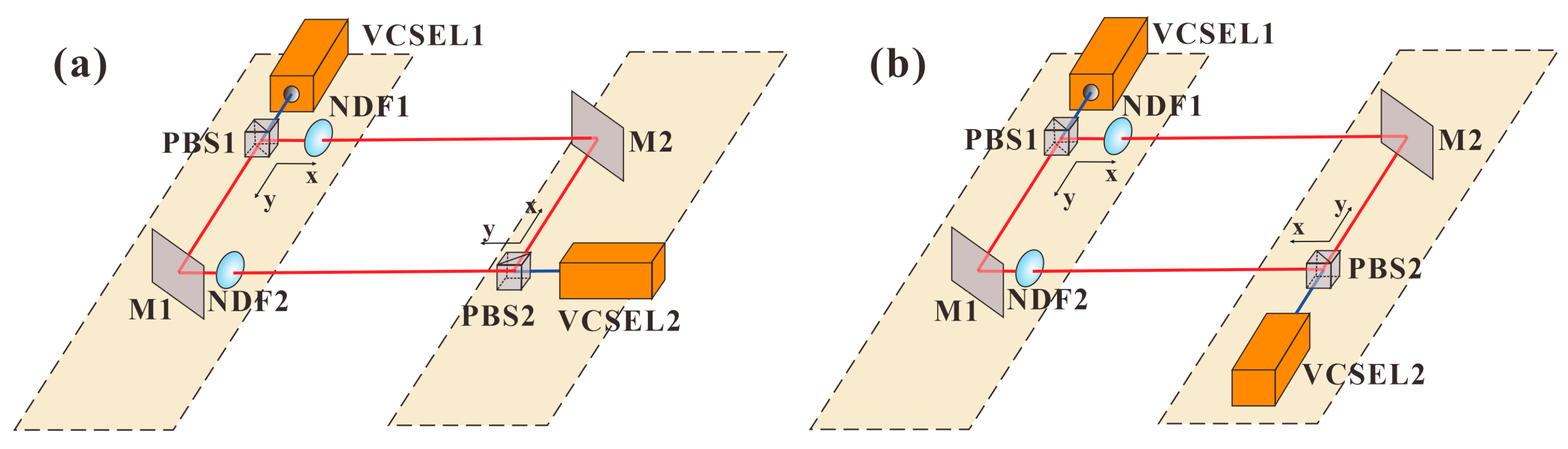
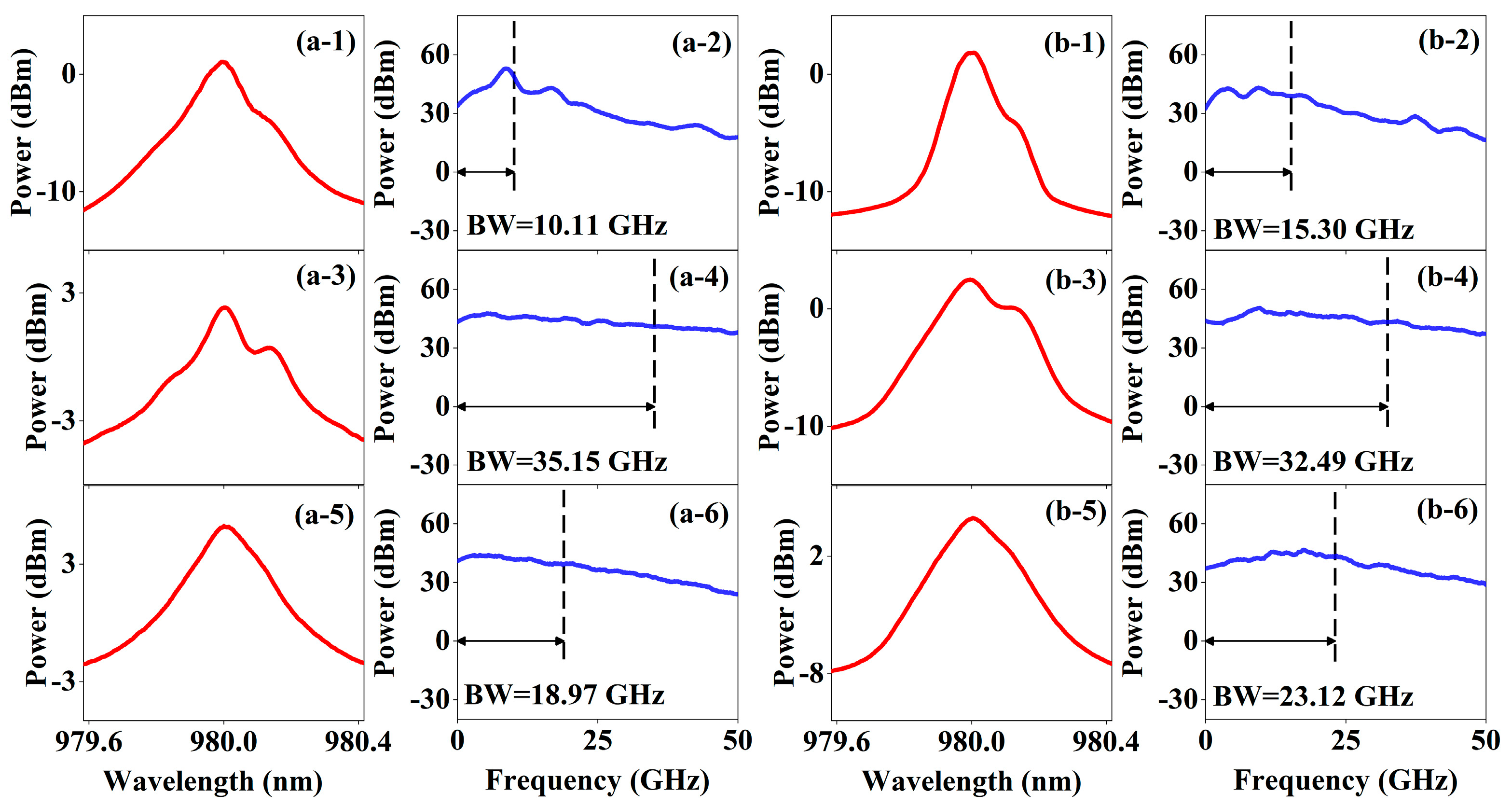
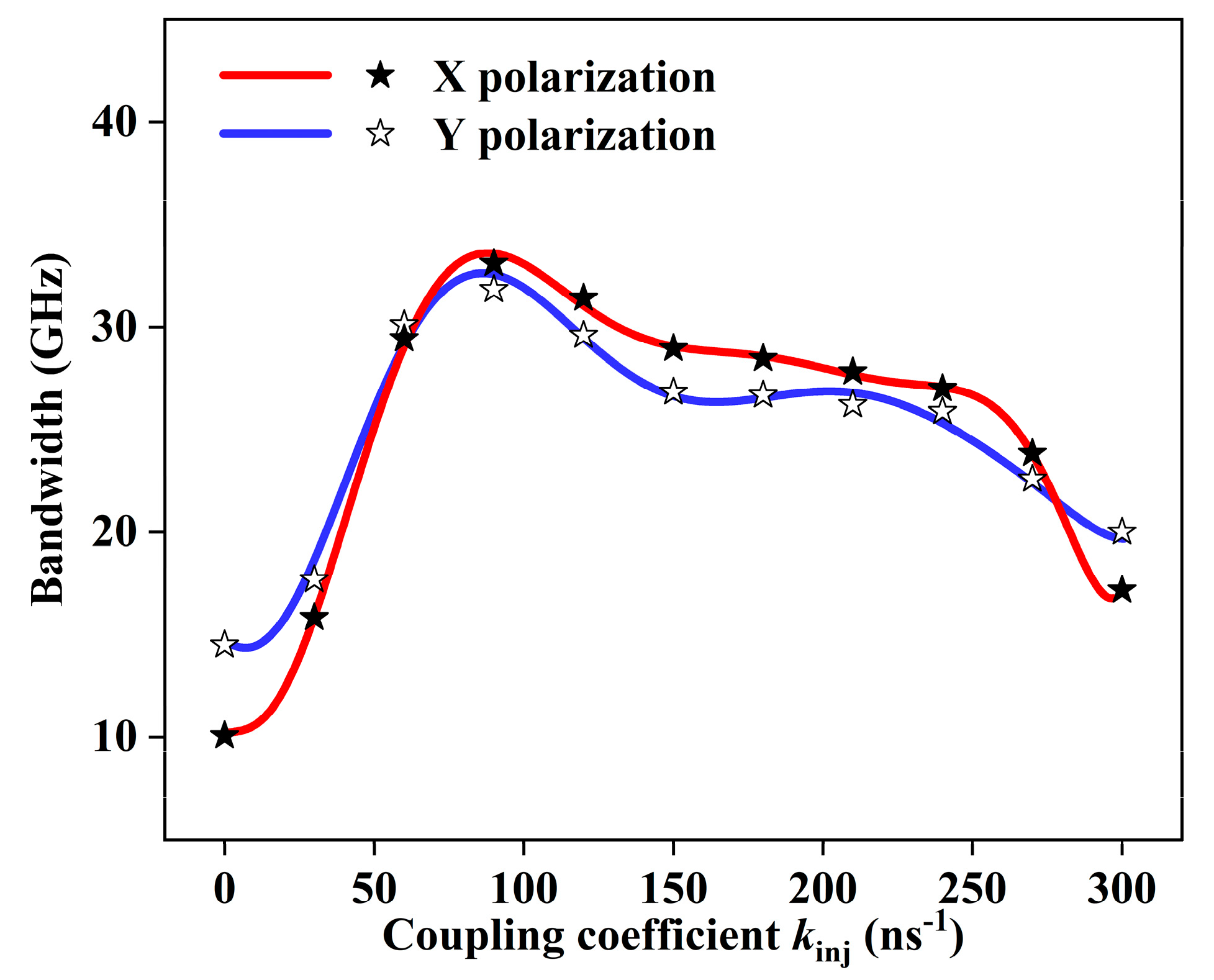
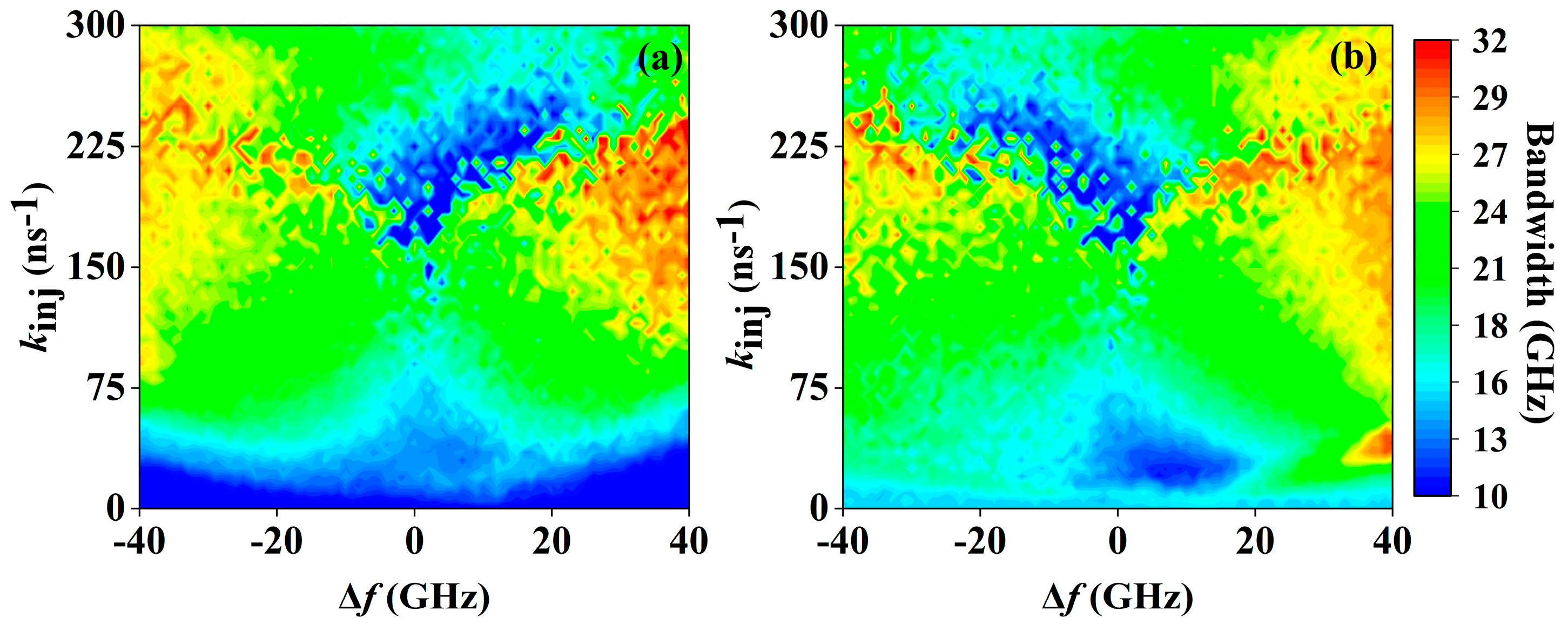
3.2. Enhanced Polarization Chaos Bandwidth by Parallel Injection
3.3. Enhanced Polarization Chaos Bandwidth by Orthogonal Injection
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Uchida, A.; Amano, K.; Inoue, M.; Hirano, K.; Naito, S.; Someya, H.; Oowada, I.; Kurashige, T.; Shiki, M.; Yoshimori, S.; et al. Fast physical random bit generation with chaotic semiconductor lasers. Nat. Photonics 2008, 2, 728–732. [Google Scholar] [CrossRef]
- Kanter, I.; Aviad, Y.; Reidler, I.; Cohen, E.; Rosenbluh, M. An optical ultrafast random bit generator. Nat. Photonics 2010, 4, 58–61. [Google Scholar] [CrossRef]
- Hirano, K.; Yamazaki, T.; Morikatsu, S.; Okumura, H.; Aida, H.; Uchida, A.; Yoshimori, S.; Yoshimura, K.; Harayama, T.; Davis, P. Fast random bit generation with bandwidth-enhanced chaos in semiconductor lasers. Opt. Express 2010, 18, 5512–5524. [Google Scholar] [CrossRef]
- Li, N.; Kim, B.; Chizhevsky, V.; Locquet, A.; Bloch, M.; Citrin, D.; Pan, W. Two approaches for ultrafast random bit generation based on the chaotic dynamics of a semiconductor laser. Opt. Express 2014, 22, 6634–6646. [Google Scholar] [CrossRef]
- Li, P.; Guo, Y.; Guo, Y.; Fan, Y.; Guo, X.; Liu, X.; Shore, K.A.; Dubrova, E.; Xu, B.; Wang, Y.; et al. Self-balanced real-time photonic scheme for ultrafast random number generation. APL Photonics 2018, 3, 061301. [Google Scholar] [CrossRef]
- Masoller, C. Anticipation in the synchronization of chaotic semiconductor lasers with optical feedback. Phys. Rev. Lett. 2001, 86, 2782. [Google Scholar] [CrossRef]
- Argyris, A.; Syvridis, D.; Larger, L.; Annovazzi-Lodi, V.; Colet, P.; Fischer, I.; Garcia-Ojalvo, J.; Mirasso, C.R.; Pesquera, L.; Shore, K.A. Chaos-based communications at high bit rates using commercial fibre-optic links. Nature 2005, 438, 343–346. [Google Scholar] [CrossRef]
- Hong, Y.; Lee, M.W.; Paul, J.; Spencer, P.S.; Shore, K.A. GHz bandwidth message transmission using chaotic vertical-cavity surface-emitting lasers. J. Light. Technol. 2009, 27, 5099–5105. [Google Scholar] [CrossRef]
- Ke, J.; Yi, L.; Xia, G.; Hu, W. Chaotic optical communications over 100-km fiber transmission at 30-Gb/s bit rate. Opt. Lett. 2018, 43, 1323–1326. [Google Scholar] [CrossRef]
- Jiang, N.; Zhao, A.; Xue, C.; Tang, J.; Qiu, K. Physical secure optical communication based on private chaotic spectral phase encryption/decryption. Opt. Lett. 2019, 44, 1536–1539. [Google Scholar] [CrossRef]
- Lin, F.Y.; Liu, J.M. Chaotic lidar. IEEE J. Sel. Top. Quantum Electron. 2004, 10, 991–997. [Google Scholar] [CrossRef]
- Piracha, M.U.; Nguyen, D.; Mandridis, D.; Yilmaz, T.; Ozdur, I.; Ozharar, S.; Delfyett, P.J. Range resolved lidar for long distance ranging with sub-millimeter resolution. Opt. Express 2010, 18, 7184–7189. [Google Scholar] [CrossRef]
- Cheng, C.H.; Chen, C.Y.; Chen, J.D.; Pan, D.K.; Ting, K.T.; Lin, F.Y. 3D pulsed chaos lidar system. Opt. Express 2018, 26, 12230–12241. [Google Scholar] [CrossRef] [PubMed]
- Mork, J.; Tromborg, B.; Mark, J. Chaos in semiconductor lasers with optical feedback: Theory and experiment. IEEE J. Quantum Electron. 1992, 28, 93–108. [Google Scholar] [CrossRef]
- Wang, A.; Wang, Y.; He, H. Enhancing the bandwidth of the optical chaotic signal generated by a semiconductor laser with optical feedback. IEEE Photon. Technol. Lett. 2008, 20, 1633–1635. [Google Scholar] [CrossRef]
- Sciamanna, M.; Shore, K.A. Physics and applications of laser diode chaos. Nat. Photonics 2015, 9, 151–162. [Google Scholar] [CrossRef]
- Uchida, A.; Heil, T.; Liu, Y.; Davis, P.; Aida, T. High-frequency broad-band signal generation using a semiconductor laser with a chaotic optical injection. IEEE J. Quantum Electron. 2003, 39, 1462–1467. [Google Scholar] [CrossRef]
- Lin, F.; Liu, J. Nonlinear dynamical characteristics of an optically injected semiconductor laser subject to optoelectronic feedback. Opt. Commun. 2003, 221, 173–180. [Google Scholar] [CrossRef]
- Schires, K.; Gomez, S.; Gallet, A.; Duan, G.H.; Grillot, F. Passive chaos bandwidth enhancement under dual-optical feedback with Hybrid III–V/Si DFB laser. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 1801309 . [Google Scholar] [CrossRef]
- Bouchez, G.; Uy, C.H.; Macias, B.; Wolfersberger, D.; Sciamanna, M. Wideband chaos from a laser diode with phase-conjugate feedback. Opt. Lett. 2019, 44, 975–978. [Google Scholar] [CrossRef]
- Zhao, A.; Jiang, N.; Liu, S.; Xue, C.; Tang, J.; Qiu, K. Wideband complex-enhanced chaos generation using a semiconductor laser subject to delay-interfered self-phase-modulated feedback. Opt. Express 2019, 27, 12336–12348. [Google Scholar] [CrossRef] [PubMed]
- Hong, Y. Flat broadband chaos in mutually coupled vertical-cavity surface-emitting lasers. IEEE J. Sel. Top. Quantum Electron. 2015, 21, 652–658. [Google Scholar] [CrossRef]
- Chai, M.; Qiao, L.; Zhang, M.; Wang, A.; Yang, Q.; Zhang, J.; Wang, T.; Gao, S. Simulation of monolithically integrated semiconductor laser subject to random feedback and mutual injection. IEEE J. Quantum Electron. 2020, 56, 2001008. [Google Scholar] [CrossRef]
- Zhang, W.L.; Pan, W.; Luo, B.; Wang, M.Y.; Zou, X.H. Synchronization performance comparison of vertical-cavity surface-emitting lasers with two different feedback chaos schemes. Semicond. Sci. Technol 2005, 20, 979. [Google Scholar] [CrossRef]
- Rontani, D.; Locquet, A.; Sciamanna, M.; Citrin, D.S.; Ortin, S. Time-delay identification in a chaotic semiconductor laser with optical feedback: A dynamical point of view. IEEE J. Quantum Electron. 2009, 45, 879–1891. [Google Scholar] [CrossRef]
- Soriano, M.C.; García-Ojalvo, J.; Mirasso, C.R.; Fischer, I. Complex photonics: Dynamics and applications of delay-coupled semiconductors lasers. Rev. Mod. Phys 2013, 85, 421. [Google Scholar] [CrossRef]
- Virte, M.; Panajotov, K.; Thienpont, H.; Sciamanna, M. Deterministic polarization chaos from a laser diode. Nat. Photonics 2013, 7, 60–65. [Google Scholar] [CrossRef]
- Virte, M.; Panajotov, K.; Sciamanna, M. Bifurcation to nonlinear polarization dynamics and chaos in vertical-cavity surface-emitting lasers. Phys. Rev. Appl. 2013, 87, 013834. [Google Scholar] [CrossRef]
- Mu, P.; Pan, W.; Li, N. Analysis and characterization of chaos generated by free-running and optically injected VCSELs. Opt. Express 2018, 26, 15642–15655. [Google Scholar] [CrossRef]
- Martin-Regalado, J.; Prati, F.; San Miguel, M.; Abraham, N. Polarization properties of vertical-cavity surface-emitting lasers. IEEE J. Quantum Electron. 1997, 33, 765–783. [Google Scholar] [CrossRef]




| Parameter | Symbol | Value |
|---|---|---|
| Field decay rate | κ | 300 ns−1 |
| Linewidth enhancement factor | α | 3 |
| Linear dichroism | γa | 0.5 ns−1 |
| Linear birefringence | γp | 30 ns−1 |
| Carrier decay rate | γN | 1 ns−1 |
| Spin-flip relaxation rate | γS | 50 ns−1 |
| coupling coefficient | kinj | 0~300 ns−1 |
| Propagation time delay | τ | 3 × 10−9 s |
| Bias current | μ | 1~6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bian, H.; Zhang, X.; Li, P.; Jia, Z.; Ma, L.; Xu, B.; Shore, K.A.; Qin, Y.; Wang, Y. Sub-40 GHz Broadband Polarization Chaos Generation Using Mutually Coupled Free-Running VCSELs. Photonics 2023, 10, 219. https://doi.org/10.3390/photonics10020219
Bian H, Zhang X, Li P, Jia Z, Ma L, Xu B, Shore KA, Qin Y, Wang Y. Sub-40 GHz Broadband Polarization Chaos Generation Using Mutually Coupled Free-Running VCSELs. Photonics. 2023; 10(2):219. https://doi.org/10.3390/photonics10020219
Chicago/Turabian StyleBian, Haofan, Xiaomai Zhang, Pu Li, Zhiwei Jia, Li Ma, Bingjie Xu, Keith Alan Shore, Yuwen Qin, and Yuncai Wang. 2023. "Sub-40 GHz Broadband Polarization Chaos Generation Using Mutually Coupled Free-Running VCSELs" Photonics 10, no. 2: 219. https://doi.org/10.3390/photonics10020219
APA StyleBian, H., Zhang, X., Li, P., Jia, Z., Ma, L., Xu, B., Shore, K. A., Qin, Y., & Wang, Y. (2023). Sub-40 GHz Broadband Polarization Chaos Generation Using Mutually Coupled Free-Running VCSELs. Photonics, 10(2), 219. https://doi.org/10.3390/photonics10020219





