Abstract
Laser-based medical techniques for evaluating blood flow (BF), such as laser Doppler flowmetry, laser speckle contrast imaging, etc., are known, but expensive and have some disadvantages. Recently, we have proposed a new technique—incoherent optical fluctuation flowmetry (IOFF), which is realized using a LED-based optical probe. This work aims to theoretically study the dependence of BF registered by IOFF on the source-detector distance (SDD) in the probe. For this purpose, we developed a three-layer optical model of skin and used Monte Carlo (MC) simulations of light propagation. All computations were performed for a wavelength of 810 nm and several SDDs from 1 to 14 mm. MC results showed that the BF depends nonlinearly on the SDD. Herewith, the BF is strongly correlated with the mean photon path length in a tissue (R = 0.92). Thus, flowmeters with different SDDs can give different BF values on the same patient. Based on the study results, to standardize BF measurements, it has been justified that BF magnitudes measured should be normalized to the exponential function of the SDD in the used optical probe in the form of [1 − exp(−b·SDD)], where b is a constant.
Keywords:
optical; non-invasive; flowmetry; blood flow; Monte Carlo simulation; source-detector distance; skin 1. Introduction
Optical methods for evaluating blood flow (BF) in biological tissues for medical purposes are well known today. Most of them use lasers as a source of light. Such methods include laser Doppler flowmetry (LDF), laser speckle contrast imaging, diffuse correlation spectroscopy, etc. [1,2]. One of the most used methods among them is the LDF, which is based on the Doppler effect induced by moving red blood cells at a coherent illumination [3]. A laser Doppler instrument’s output usually is BF, velocity, and/or concentration of the moving red blood cells, which are extracted from the spectrum of photocurrent power fluctuations produced by optical fields’ beatings of backscattered light on a surface of a square-law detector [3,4]. However, the LDF technique has some disadvantages. One of the significant limitations of the method is the small diagnostic volume in a tissue, which makes it possible to explore only superficial skin vessels. As a result, the method has a low reproducibility of basal skin BF recorded at rest [5]. In general, LDF has low diagnostic significance when making a diagnostic conclusion for one person. It does not yet allow the use of this technology for a wide clinical practice [6]. Moreover, the LDF technique is quite expensive due to the use of lasers and optical fibers. In addition, it is an operator-dependent technology due to the ambiguity and complexity of fiber positioning on the patient’s skin surface [7,8].
A simpler and cheaper optical technique can be realized with the use of incoherent light to illuminate skin. In this case, fluctuations in the blood volume in the skin lead to corresponding fluctuations in the optical properties of the skin (mainly absorption), which, in turn, modulates the intensity of optical radiation backscattered by the skin [9]. In particular, the photoplethysmography (PPG) technique, in which a pulse wave signal is recorded, is based on this principle [10]. The registered PPG signal consists of a slowly varying component (DC), due to the absorption of light by motionless tissue structures as well as by an average blood volume, and a variable (alternating) component (AC), which is formed due to blood volume fluctuations.
Recently, we have proposed a new method to record BF in skin based on incoherent illumination and a spectral analysis of AC components similar to the LDF technique [11]. The method was named “Incoherent Optical Fluctuation Flowmetry” (IOFF). It is close to the PPG technique with the flowmetry function [12], i.e., with the calculation of the peripheral perfusion index (PFI), but differs from that in the data processing algorithm. The term BF (or perfusion) describes the amount of blood delivered to the capillary bed of tissues in a certain period of time [13]. Since blood flows nonuniformly, but with pulsations, any movement of blood will lead to blood volume changes. Thus, in IOFF the considered BF is proportional to the rate of the blood volume increment in a tissue per unit time. BF is computed as the first moment of the AC photocurrent amplitude spectrum normalized to the DC photocurrent component [11]:
Where k0 is the proportional coefficient, n is the total number of all low-frequency harmonics in the registered AC photocurrent, is the AC photocurrent amplitude of the k-th harmonic, is the frequency of this k-th harmonic, is an amplitude of the DC photocurrent component. The frequency range of the registered signal is from 0 Hz to about 10 Hz. It includes approximately 5–8 harmonics [11] and all of them should be taken into account. Thus, the data processing algorithm in IOFF is closer to the LDF computations, but unlike all known laser-based flowmetry techniques, IOFF does not require any optical fibers, lasers, or coherent light, and makes it possible to obtain a signal from a larger diagnostic volume of tissues (tens of mm3) [14].
However, when developing a tissue optical probe for the IOFF or other similar technologies, it is necessary to select and substantiate the basic design parameters of the probe, i.e., to select wavelengths for probing radiation, to determine the distance between a light source and a photodetector, etc. It is well known, that to implement a flowmetry technique, one of the isosbestic points is preferable as the light source wavelength because, near this point, the absorption of light by oxy-hemoglobin (HbO2) and de-oxyhemoglobin (Hb) is practically the same [11]. This is necessary to eliminate the difference in measured results associated with unequal light absorption by arterial and venous blood. The wavelengths of ~525, 568, and 805 nm can serve as such points [14]. For example, due to different penetration depths, the green light at wavelengths of 525 and 568 nm can be used to register superficial skin BF, whereas IR light at a wavelength of ~805 nm can be used to analyze deeper subcutaneous BF [15].
At the same time, the problem of the most effective source-detector distance (SDD) in the optical probe for the IOFF technique has not yet been studied at all. In particular, this problem was studied in LDF earlier [16]. It was shown in a number of experiments with the use of different phantoms that BF measured by LDF grows nonlinearly with increasing SDD. However, measurements in LDF are usually limited to the distance of 1.4 mm between emitting and receiving optical fibers [16,17]. Due to a small receiving aperture of an optical fiber, a longer SDD leads to a large signal power loss. Therefore, in LDF short SDDs are used, and this problem is not so important. However, the problem of optimal SDDs also exists in cerebral BF measurements with the use of optical heterodyne detections combined with interferometric diffusing wave spectroscopy [18].
The IOFF method makes it possible to separate a light source and a detector at a greater distance due to the ability to use light-emitted chips and photodiodes directly on the surface of the skin. However, it requires an additional study of the backscattered signal characteristics depending on the geometry of tissue illumination and a reasonable choice of SDDs. A useful tool for this purpose is the Monte Carlo (MC) method, which allows us to theoretically simulate the propagation of “photons” inside a tissue [19,20].
Our work aims to study the dependence of BF registered by the IOFF technique on the geometry of tissue illumination (on the SDD in an optical probe) using numerical MC simulations.
2. Materials and Methods
2.1. Optical Model of the IOFF Signal Formation
In this study, we consider the illumination of biological tissue in the backscattering geometry in which a detector is located at some distance from a light source (see Figure 1). We represented the skin as a three-layer heterogeneous medium consisting of the epidermis, dermis, and deeper subcutaneous fat [21]. The epidermis is 0.2 mm thick, the dermis is 0.7 mm thick and the subcutaneous fat layer is semi-infinite [22]. Both the dermis and the subcutis are also characterized by a level of blood volume Vb, which can be considered as a relative total hemoglobin fraction (Hb and HbO2) in the diagnostic volume of tissue [23].
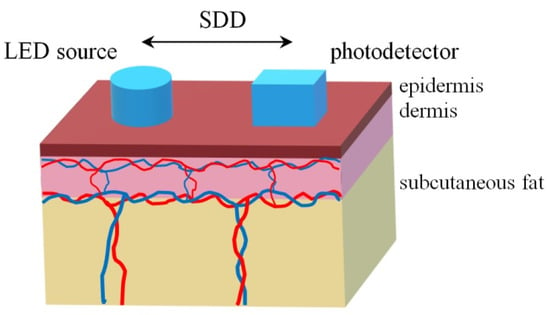
Figure 1.
The location of a light source and a photodetector at the simulation of light propagation in the three-layer skin model. SDD—source-detector distance.
The epidermis does not contain blood vessels and consists of connective tissue, melanin, and water. Thus, we can represent the absorption coefficient of the epidermal layer as follows [24]:
where λ is a wavelength, Vmel and Vw are the volume fractions of melanin and water in the epidermis, respectively, μa,mel and μa,w are the absorption coefficients of melanin and water, μa,baseline is the baseline absorption coefficient, which characterizes the absorption by connective tissue in the absence of other chromophores. μa,baseline depends on a wavelength and can be expressed by the following equation [25,26]:
We computed the absorption coefficient of the dermal layer as in [27,28]:
where Vb,A and Vb,V are the volume fractions of arterial and venous blood in the dermis, respectively, μa,A and μa,V are the absorption coefficients of the arterial and venous blood. The value of Vb in the entire dermis, which is defined as the sum of Vb,A and Vb,V, is 0.1 rel. units. μa,A and μa,V, in turn, can be expressed in terms of arterial (SaO2) and venous (SvO2) oxygen saturation, respectively, as [27]:
where μa,HbO2 and μa,Hb are the absorption coefficients of HbO2 and Hb.
Since the subcutaneous fat layer consists mainly of fat, we determine the absorption coefficient of this layer as:
where μa,fat is the absorption coefficient of fat.
To simulate BF according to Equation (1), it is necessary to model different increments of Vb,A with various spectral components in the dermal layer, since the main blood pulsations occur in the dermis. For this, we represented the time pulsations in the arterial blood volume in Equation (4) inside the dermal layer as a sum of harmonic oscillations:
where Vb0,A is an average level of arterial blood volume, ΔVb,A(t) is the variable component of the arterial blood volume, n is the number of harmonics of Vb,A, mk is a relative amplitude of the k-th harmonic, Ωk is the angular frequency of the k-th harmonic, mk is defined as Ak/Vb0,A, where Ak is the absolute amplitude of this k-th harmonic.
2.2. Monte Carlo Simulation
We performed 3D MC simulations to calculate backscattered optical fluxes at different levels of Vb,A in the dermal layer. The numerical model applied uses a photon weighting technique and is based on the well-known principles of MC simulation of photon transport in biological tissues [29,30]. Laterally symmetrical skin model allows the use of detectors with the square-form sensitive surface to improve computation accuracy [14,31,32]. At the simulation, 109 photon packets were launched in the medium. A round source with a diameter of 1 mm and a 1 × 1 mm square sensitive surface were used. The registered flux was calculated relative to the incident one illuminating the tissue. Thus, the relative backscattered flux was determined. The simulations were performed in Matlab R2022a software (MathWorks, Natick, MA, USA).
We calculated the power of backscattered fluxes at the average arterial blood volume of the dermal layer Vb0,A = 0.05 rel. units, and at different ΔVb,A which modeled harmonics in (7). We simulated 5 harmonics with the following amplitudes mk: 20, 10, 5, 2, and 1%. These amplitudes correspond to the following increments of Vb,A relative to the average level: 0.01, 0.005, 0.0025, 0.001, and 0.0005 rel. units. Harmonic frequencies were set from 1 to 5 Hz with a step of 1 Hz. Calculations were carried out for SDDs from 1 to 14 mm with a step of 1 mm. As a result, we have obtained a backscattered flux value for each SDD and each harmonic. In addition, we detected the photon path length from a source to a detector for each SDD. The mean optical path length (MPL) was calculated as the sum of all paths of photons, registered by the detector, divided by their number.
It is known that the registered photocurrent is proportional to the power of the optical flux incident on the surface of the square-law photodetector [4]. Thus, the power of the backscattered flux at the average level of Vb,A (Fluxaver) corresponds to , and the difference between Fluxaver and the power of the backscattered flux at a k-th increment of Vb,A (Fluxk) corresponds to in (1). Therefore, we can calculate the BF level that corresponds to the k-th harmonic in (1) provided at k0 = 1 as follows:
Finally, we calculated the total BF over all harmonics as:
where fk = {1, 2… 5} Hz are frequencies of these harmonics.
We also estimated the error of simulations. For this, we first calculated the error of the power of backscattered flux at the average level of Vb,A as a standard deviation over 5 measurements. Let us denote X = Fluxaver − Fluxk and Y = 1/Fluxaver in (8) for convenience. Assuming the errors of Fluxaver and Fluxk are equal, the error of X was defined as s(X) = . Further, we calculated the error of each harmonic in the following form:
where E(X) and E(Y) are the expected values of X and Y, respectively. Assuming that harmonics are independent of each other, we finally calculated the error of total BF as follows:
2.3. Optical Properties of Skin Layers
In this study, we simulated the light propagation in the skin by MC calculations using the developed three-layer model at the wavelength of 810 nm. Absorption coefficients of melanin, oxyhemoglobin, deoxyhemoglobin, water, and fat were selected from literature sources [27,33,34,35,36]. When calculating absorption coefficients of arterial and venous blood according to (5), SaO2 was set at 97% and SvO2 was set at 30% lower, i.e., 67% [37]. The ratio of volume fractions of arterial and venous blood in dermal and subcutaneous fat layers was 1:1 [27]. The scattering coefficient of each layer was determined as a combination of the Mie and Rayleigh theories [38]. The anisotropy factor and the refractive index were assumed to be 0.8 and 1.4 correspondingly for all skin layers [39]. The anatomical and optical parameters of skin layers are summarized in Table 1 and Table 2, respectively.

Table 1.
Anatomical properties of model skin layers.

Table 2.
Optical properties of tissue chromophores and model layers for the wavelength of 810 nm.
3. Results and Discussion
Firstly, it is interesting to estimate the MPL at different distances between the source and the detector. Figure 2 illustrates MPL and a registered flux calculated for different SDDs at the average arterial blood volume Vb0,A = 0.05 rel. units. As can be seen, MPL grows linearly with the increasing SDD and strongly correlates with it. The Pearson correlation coefficient between MPL and the SDD is 0.99. The registered flux decreases strongly with the increasing SDD. It should be noted that similar results were obtained by S. Chatterjee et al. earlier [27]. They investigated the optical path for photons in the application to PPG at wavelengths of both 660 and 880 nm and obtained a similar linear dependence of the optical path on the SDD at small distances.
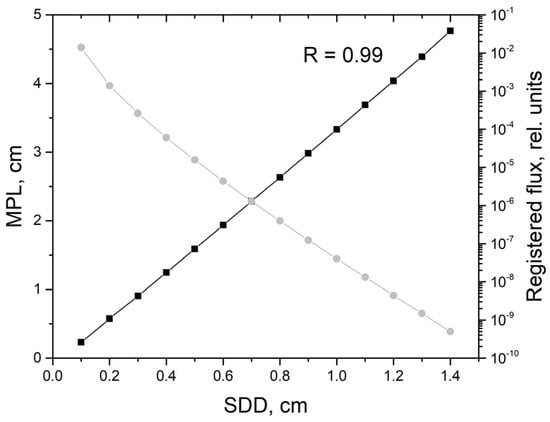
Figure 2.
Mean optical path length (MPL) (black line, left scale) and the registered flux (gray line, right scale) versus the source-detector distance (SDD) obtained by MC simulation at the average arterial blood volume Vb0,A = 0.05 rel. units.
Further, we plotted the dependences of the BF level on the SDD for each of the blood volume harmonics (see Figure 3a). As can be seen, the BF level increases with decreasing the harmonic number. Herewith, the level of BF for all harmonics increases with the increasing SDD. It reaches some maximum and drops to almost zero by a distance of 1.4 cm. The total BF as a function of SDD is shown in Figure 3b. This dependence has a pronounced maximum at the SDD of 1.1 cm. After 1.3 cm, BF rapidly drops to almost zero due to the strong attenuation of the registered flux. At a distance of 1.4 cm, the registered flux is 9 orders of magnitude less than the incident one (see the gray line in Figure 2). It is also worth noting that, after a distance of 1.1 cm, the simulation error increases greatly. In general, it can be concluded that the most sensitive measurements of BF can be performed inside the SDD range from 0.8 to 1.2 cm.
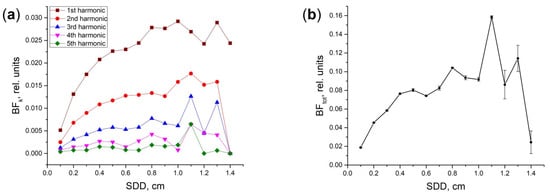
Figure 3.
Dependence of BF on the SDD for: (a) individual harmonics BFk of Vb,A pulsations; (b) the total BF. Amplitudes of the 1, 2… 5th harmonics correspond to the following increments of Vb,A in a dermal layer: 0.01, 0.005, 0.0025, 0.001, and 0.0005 rel. units. The simulation error is shown as vertical bars in (b).
Since the BF grows with the increasing distance in the range of 0.1–1.0 cm, most likely this is due to the optical path growing when photons travel from the source to the detector. Therefore, the dependence of BF level on the MPL is of interest. It was also computed in our study. This dependence is presented in the form of a scatterplot in Figure 4. In addition, we carried out both a linear and nonlinear approximation of the obtained dependence. Nonlinear approximation was performed with the use of the exponential function of the form a·(1 − exp(−b·MPL)). These approximation results are shown in Figure 4 with red and blue curves. As can be seen below, the nonlinear function better reflects the dependence of BF on the MPL than the linear one. The Spearman correlation coefficient between the BF and the mean optical path is 0.92. The nonlinear fitting curve is given by the equation:
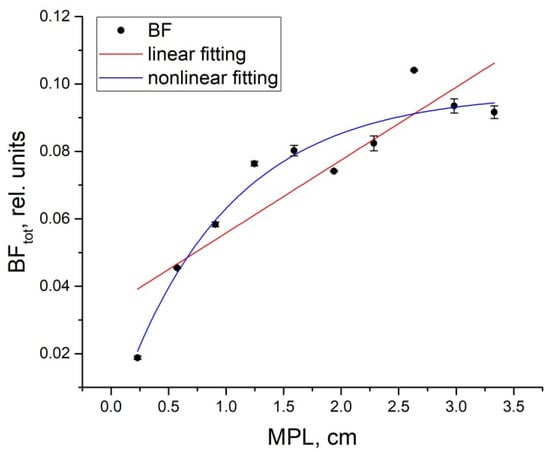
Figure 4.
Dependence of the total BF on MPL at SDDs from 0.1 to 1.0 cm (black dots). The linear fitting curve (red line) has the equation BFtot = 0.034 + 0.022·MPL and the nonlinear fitting curve (blue line) is determined by the equation BFtot = 0.1·(1 − exp(−1.04·MPL)).
Since the MPL is strongly a linear function on SDD (see Figure 2), then the same exponential relationship should exist between the BF and the SDD, but with other coefficients a and b. As a result, we determined the dependence of BF on SDD by the following equation:
As one can see in Figure 4, at SDDs up to 1 cm a level of BF increases with increasing optical path length. This is a completely logical and physiologically justified result. It is known that the greater the distance between the light source and the photodetector, the deeper the light penetrates a tissue [40]. As a result, more vessels enter the area of illumination (diagnostic volume). Since there are larger vessels in deeper layers of the dermis, with deeper penetration of photons into tissues, the total BF registered increases due to the entry of a larger number of vessels with larger diameters into the diagnostic volume. As mentioned above, this effect was observed in LDF earlier [16]. All dependencies plotted in [16] were limited to the SDD of 1.4 mm. At such distances, as was shown in [17], the measurement depth is approximately 0.6–0.8 mm at the wavelength of 780 nm (in [17], calculations in the near IR region were carried out only for a wavelength of 780 nm, but it is close to our 810 nm). In accordance with our model, in this case, the light does not cover the deep vascular plexuses of the dermis. Moreover, such a small diagnostic volume determines the well-known drawback of the LDF—the problem of the dependence of device readings on the individual architecture of the microvascular bed in the examined volume of tissues. Fredriksson I. et al. discussed this problem in [17] and proposed that the model of homogeneous skin with a homogeneous vasculature may not be correct at such small distances. However, the result obtained is close to ours.
The IOFF technique does not use fibers or lasers, and the SDD may be larger. In our hardware realization [11] the SDD is deliberately chosen in the range of a few millimeters to avoid the effect of inhomogeneity of the vessels’ microarchitecture. Therefore, IOFF allows us to evaluate the BF in deeper layers of skin, as well as to look even deeper—into the subcutaneous tissue. That is why we studied by analogy a wider range of distances. Nevertheless, we obtained a similar result. The main result of this study—the nonlinear dependence of BF measured by IOFF on the SDD in optical probes—is the most important for the usage of the IOFF method in clinical practice.
From the point of view of standardization of IOFF measurements, this is not an inspiring result. It complicates the problem because IOFF instruments with different SDDs in their optical probes can give different outputs. If we do not take into consideration the problem of registering BF over all layers of the skin, then for the standardization and unification of measurements it is necessary to require that all flowmeters have the same SDD. Alternatively, it is necessary to do some kind of normalization when comparing results.
We tried to normalize the registered BFs by the exponential function:
These results are presented in Figure 5. As can be seen, after the normalization all magnitudes of BFs measured converged approximately to the same level up to a distance of 1 cm and become independent of SDDs. Thus, the normalization procedure is possible. Within a short range of SDDs, inside the 0.3–1.0 cm interval, it allows standardized BF measurements to be made regardless of the real SDDs used in flowmeters’ optical probes.
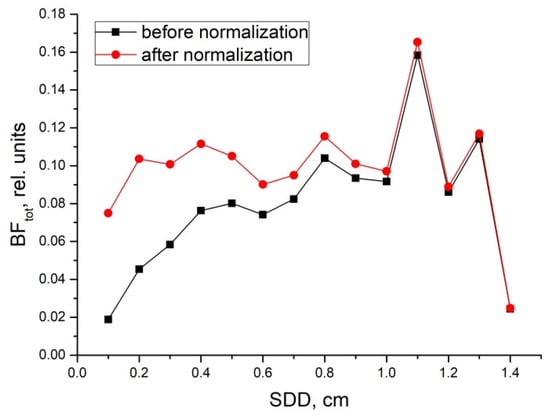
Figure 5.
Dependence of the total BF on the SDD before (black line) and after (red line) normalization to the exponential function of the distance in the form of 1 − exp(−2.9·SDD).
Indeed, such a result must be proven experimentally. But, this requires the creation of additional equipment (various optical probes with different SDDs) and in vivo trials in clinics. It is a long and complex process, but possible. We intend to do this in the next phase of our research.
4. Conclusions
We theoretically investigated the problem of dependence of the blood flow (BF) registered by the new IOFF technique on the source-detector distance (SDD) in the optical probe used. A three-layer optical model of skin and the Monte Carlo simulation technique was used for this purpose. The main result of the study is the nonlinear dependence of BF on the mean optical path length and the SDD in optical probes. It was shown that the BF depends on these quantities in the main form of the exponential function 1 − exp(−b·x), where b is a constant. This makes it quite difficult to compare results for different flowmeters with different SDDs. Therefore, we proposed the procedure for normalizing the registered BFs to this function of the actual SDD in a probe. Within a short range of SDDs, inside the 0.3–1.0 cm interval, which is usually of interest in clinics for evaluation of cutaneous BFs, it allows standardized BF measurements to be made regardless of the real SDDs used in flowmeters’ optical probes. However, these theoretical results and proposals need to be approved in further experimental trials.
Author Contributions
Conceptualization, D.G.L.; Methodology, D.G.L.; Simulation, A.P.T.; Investigation, D.G.L.; Writing—Original Draft Preparation, D.G.L.; Writing—Review & Editing, D.A.R. and A.P.T.; Project Administration, D.G.L.; Funding Acquisition, D.G.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Russian Science Foundation (project No. 21-75-00037).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Briers, J.D. Laser Doppler, speckle and related techniques for blood perfusion mapping and imaging. Physiol. Meas. 2001, 22, R35. [Google Scholar] [CrossRef] [PubMed]
- Yu, G. Diffuse correlation spectroscopy (DCS): A diagnostic tool for assessing tissue blood flow in vascular-related diseases and therapies. Curr. Med. Imaging 2012, 8, 194–210. [Google Scholar] [CrossRef]
- Rajan, V.; Varghese, B.; van Leeuwen, T.G.; Steenbergen, W. Review of methodological developments in laser Doppler flowmetry. Lasers Med. Sci. 2009, 24, 269–283. [Google Scholar] [CrossRef]
- Lapitan, D.G.; Rogatkin, D.A.; Tarasov, A.P. Model of Doppler scattering with variable blood volume in laser Doppler flowmetry. Proc. SPIE 2017, 10417, 104170V. [Google Scholar] [CrossRef]
- Lapitan, D.G.; Rogatkin, D.A. Functional studies on blood microcirculation system with laser Doppler flowmetry in clinical medicine: Problems and prospects. Alm. Clin. Med. 2016, 44, 249–259. [Google Scholar] [CrossRef]
- Kulikov, D.; Glazkov, A.; Dreval, A.; Kovaleva, Y.; Rogatkin, D.; Kulikov, A.; Molochkov, A. Approaches to improve the predictive value of laser Doppler flowmetry in detection of microcirculation disorders in diabetes mellitus. Clin. Hemorheol. Microcirc. 2018, 70, 173–179. [Google Scholar] [CrossRef]
- Rogatkin, D.A.; Lapaeva, L.G.; Bychenkov, O.A.; Tereshchenko, S.G.; Shumskii, V.I. Principal sources of errors in noninvasive medical spectrophotometry. Part 1. Physicotechnical sources and factors of errors. Meas. Technol. 2013, 56, 201–210. [Google Scholar] [CrossRef]
- Rogatkin, D.A.; Lapaeva, L.G.; Bychenkov, O.A.; Tereshchenko, S.G.; Shumskii, V.I. Principal sources of errors in noninvasive medical spectrophotometry. Part 2. Medicobiological factors of errors. Meas. Technol. 2013, 56, 455–463. [Google Scholar] [CrossRef]
- Reisner, A.; Shaltis, P.A.; McCombie, D.; Asada, H.H.; Warner, D.S.; Warner, M.A. Utility of the photoplethysmogram in circulatory monitoring. Anesthesiology 2008, 108, 950–958. [Google Scholar] [CrossRef]
- Allen, J. Photoplethysmography and its application in clinical physiological measurement. Physiol. Meas. 2007, 28, R1–R39. [Google Scholar] [CrossRef]
- Lapitan, D.; Rogatkin, D. Optical incoherent technique for noninvasive assessment of blood flow in tissues: Theoretical model and experimental study. J. Biophotonics 2021, 14, e202000459. [Google Scholar] [CrossRef] [PubMed]
- Lima, A.; Bakker, J. Noninvasive monitoring of peripheral perfusion. Intensive Care Med. 2005, 31, 1316–1326. [Google Scholar] [CrossRef]
- Thomas, D.L.; Lythgoe, M.F.; Pell, G.S.; Calamante, F.; Ordidge, R.J. The measurement of diffusion and perfusion in biological systems using magnetic resonance imaging. Phys. Med. Biol. 2000, 45, R97–R138. [Google Scholar] [CrossRef] [PubMed]
- Tarasov, A.; Lapitan, D.; Rogatkin, D. Combined non-invasive optical oximeter and flowmeter with basic metrological equipment. Photonics 2022, 9, 392. [Google Scholar] [CrossRef]
- Lapitan, D.G.; Raznitsyn, O.A. A method and a device prototype for noninvasive measurements of blood perfusion in a tissue. Instrum. Exp. Technol. 2018, 61, 745–750. [Google Scholar] [CrossRef]
- Liebert, A.; Leahy, M.; Maniewski, R. Multichannel laser-Doppler probe for blood perfusion measurements with depth discrimination. Med. Biol. Eng. Comput. 1998, 36, 740–747. [Google Scholar] [CrossRef] [PubMed]
- Fredriksson, I.; Larsson, M.; Strömberg, T. Measurement depth and volume in laser Doppler flowmetry. Microvasc. Res. 2009, 78, 4–13. [Google Scholar] [CrossRef]
- Han, G.; Feng, H.; Chen, S.; Guo, Q.; Wang, H. Optimization of source-detector separation for non-invasive regional cerebral blood flow sensing. Infrared Phys. Technol. 2021, 117, 103843. [Google Scholar] [CrossRef]
- Rogers, D.W.O. Fifty years of Monte Carlo simulations for medical physics. Phys. Med. Biol. 2006, 51, R287. [Google Scholar] [CrossRef]
- Tuchin, V.V. Tissue Optics; Society of Photo-Optical Instrumentation Engineers (SPIE): Bellingham, WA, USA, 2015. [Google Scholar]
- Lapitan, D.G.; Tarasov, A.P.; Rogatkin, D.A. Justification of the photoplethysmography sensor configuration by Monte Carlo modeling of the pulse waveform. J. Biomed. Photonics Eng. 2022, 8, 030306. [Google Scholar] [CrossRef]
- Reuss, J.L. Multilayer modeling of reflectance pulse oximetry. IEEE Trans. Biomed. Eng. 2005, 52, 153–159. [Google Scholar] [CrossRef]
- Dunaev, A.V.; Zherebtsov, E.A.; Rogatkin, D.A.; Stewart, N.A.; Sokolovski, E.U. Substantiation of medical and technical requirements for noninvasive spectrophotometric diagnostic devices. J. Biomed. Opt. 2013, 18, 107009. [Google Scholar] [CrossRef] [PubMed]
- Jacques, S.L. Skin Optics Summary. 1998. Available online: https://omlc.org/news/jan98/skinoptics.html (accessed on 30 November 2022).
- Saidi, I.S. Transcutaneous Optical Measurement of Hyperbilirubinemia in Neonates. Ph.D. Thesis, Rice University, Houston, TX, USA, 1992. [Google Scholar]
- Jacques, S.L. Origins of tissue optical properties in the UVA, visible, and NIR regions. OSA TOPS Adv. Opt. Imaging Phot. Migr. 1996, 2, 364–369. [Google Scholar]
- Chatterjee, S.; Budidha, K.; Kyriacou, P.A. Investigating the origin of photoplethysmography using a multiwavelength Monte Carlo model. Physiol. Meas. 2020, 41, 084001. [Google Scholar] [CrossRef] [PubMed]
- Meglinski, I.V.; Matcher, S.J. Computer simulation of the skin reflectance spectra. Comput. Methods Programs Biomed. 2003, 70, 179–186. [Google Scholar] [CrossRef]
- Prahl, S.A.; Keijzer, M.; Jacques, S.L.; Welch, A.J. A Monte Carlo model of light propagation in tissue. In Dosimetry of Laser Radiation in Medicine and Biology; Müller, G., Sliney, D., Eds.; SPIE Institute Series; SPIE: Bellingham, WA, USA, 1989; pp. 102–111. [Google Scholar]
- Wang, L.; Jacques, S.L.; Zheng, L. MCML—Monte Carlo modeling of light transport in multi-layered tissues. Comput. Meth. Programs Biomed. 1995, 47, 131–146. [Google Scholar] [CrossRef]
- Tarasov, A.P. Acceleration of Monte Carlo simulation of light transport in tissues using disk-detector geometry in the backscattering problem. In Proceedings of the 2020 International Conference Laser Optics (ICLO), Saint Petersburg, Russia, 2–6 November 2020. [Google Scholar] [CrossRef]
- Tarasov, A.P. Using disk-detector geometry for calculation of optical path length by Monte Carlo simulation of light transport in turbid media. In Proceedings of the 2022 International Conference Laser Optics (ICLO), St. Petersburg, Russia, 20–24 June 2022. [Google Scholar] [CrossRef]
- Bosschaart, N.; Edelman, G.J.; Aalders, M.C.; van Leeuwen, T.G.; Faber, D.J. A literature review and novel theoretical approach on the optical properties of whole blood. Lasers Med. Sci. 2014, 29, 453–479. [Google Scholar] [CrossRef]
- Hale, G.M.; Querry, M.R. Optical constants of water in the 200-nm to 200-m wavelength region. Appl. Opt. 1973, 2, 555–563. [Google Scholar] [CrossRef]
- Simpson, C.R.; Kohl, M.; Essenpreis, M.; Cope, M. Near-infrared optical properties of ex vivo human skin and subcutaneous tissues measured using the Monte Carlo inversion technique. Phys. Med. Biol. 1998, 43, 2465–2478. [Google Scholar] [CrossRef]
- Bashkatov, A.N.; Genina, E.A.; Tuchin, V.V. Optical properties of skin, subcutaneous, and muscle tissues: A review. J. Innov. Opt. Health Sci. 2011, 4, 9–38. [Google Scholar] [CrossRef]
- Moço, A.V.; Stuijk, S.; de Haan, G. New insights into the origin of remote PPG signals in visible light and infrared. Sci. Rep. 2018, 8, 8501. [Google Scholar] [CrossRef]
- Jacques, S.L. Optical properties of biological tissues: A review. Phys. Med. Biol. 2013, 58, R37–R61. [Google Scholar] [CrossRef] [PubMed]
- Salomatina, E.; Jiang, B.; Novak, J.; Yaroslavsky, A.N. Optical properties of normal and cancerous human skin in the visible and near-infrared spectral range. J. Biomed. Opt. 2006, 11, 064026. [Google Scholar] [CrossRef] [PubMed]
- Weiss, G.H.; Nossal, R.; Bonner, R.F. Statistics of penetration depth of photons re-emitted from irradiated tissue. J. Mod. Opt. 1989, 36, 349–359. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).