Experimental Demonstration of Attoseconds-at-Harmonics at the SASE3 Undulator of the European XFEL

Abstract

We report on observations of single spike spectra (3–13% of events) upon employing a previously proposed method for single spike generation via harmonic conversion. The method was tested at the soft X-ray SASE3 undulator of the European XFEL. The first part of the undulator allows one to amplify bunching at the fundamental as well as the higher harmonics. The downstream undulator is tuned to a harmonic, the fourth in our case, to amplify pulses with a shorter duration. We estimate the generated pulse duration within such a subset of short pulses at a level of 650 as. Considering the demonstrated probability of single spike events, this method is attractive for high repetition-rate free electron lasers.

1. Introduction

Bunching at harmonics driven by amplification of the fundamental has drawn the attention of researchers in the past and has been described in numerous publications, e.g., [1,2,3,4]. The authors of [4] proposed to use this effect for generating single spike sub-femtosecond pulses at free-electron laser facilities. The proposed setup requires minimal hardware manipulations and only the availability of variable gap undulator cells. In our contribution, we present an experimental demonstration of obtaining these nearly single-mode radiation pulses at the SASE3 undulator of the European XFEL with a two stage setup. For brevity, we shall call this the “attoseconds-at-harmonics” method.

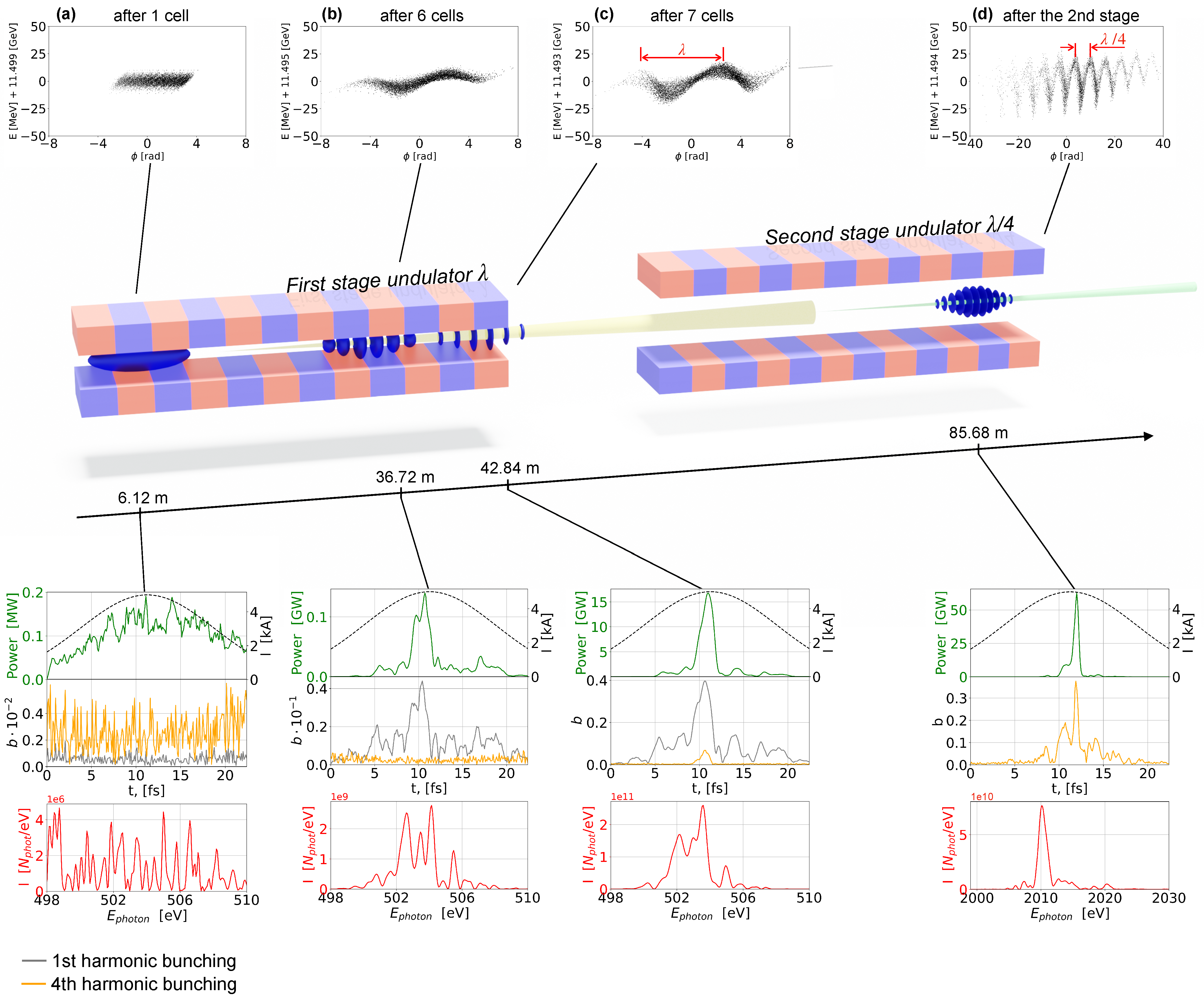
During the amplification process in free-electron lasers (FELs), see Figure 1, the longitudinal phase space of the electron beam evolves along the undulator: in the linear regime it gradually undergoes sinusoidal energy and density modulations at the wavelength of the fundamental harmonics, as the electrons “rotate” in an FEL bucket; see the upper panels in Figure 2. At the onset of saturation, these modulations become non-linear and deviate from the sinusoidal shape. This leads to the growth of a rich harmonic content, shown in Figure 1A. The growth of bunching at harmonics is rapid and non-linear, which is characterized by a power law dependence with respect to the fundamental ($b_n\left(t\right)\sim b_1^n\left(t\right)$), see Figure 1B, where $b_n$ denotes the bunching at the corresponding n-th harmonic.

We illustrate the amplification process with snapshots of the electron beam and radiation properties in the bottom panels of Figure 2, which show the radiation power dependence, bunching factors, and radiation spectra. Up to the 6th undulator cell, before reaching saturation, we observe growth at the fundamental harmonic while the bunching at the 4th harmonic remains at the noise level. This corresponds to a long plateau in Figure 1B, where each mapped point corresponds to the bunching factor calculated at a given position along the electron beam. At the 8th cell, we see a rapid harmonic growth. This corresponds to the linear part of the graph on the right panel of Figure 1B, which confirms (actually, this relation $b_n\left(t\right)\sim b_1^n\left(t\right)$ strictly holds in steady state regime, while for the time-dependent simulation results, Figure 1, the slope for the 4th harmonic deviates from 4, although this is still the power law dependence) the power law dependence of the higher harmonic bunching with respect to the fundamental. A deviation from this linear dependence indicates saturation.

Upon reaching saturation at 42 m, shown in Figure 2, the bunching at the 4th harmonic is proportional to that at the fundamental raised to the power of 4. Afterwards, the beam radiates in the downstream radiator tuned to the given harmonic, as depicted at Figure 2d. The power law dependence leads to effective suppression of spikes with low values of bunching and to an increase in the relative height of the dominant spikes which results in the reduction of the width of the spike and total pulse duration.

The authors of [4] proposed to use this effect for generating sub-femtosecond pulses with two or multi-stage undulator schemes. In the first stage, one creates bunching at the harmonic of the fundamental $\lambda$. The following stages are successively tuned to the wavelengths that correspond to the harmonics of the previous stages ($\lambda /n$). These can be sequences, for example, 1→2→4, 1→4, 1→3, etc. In this way, lasing at the harmonics starts from a substantial level of bunching created at the previous stages.

The idea behind this scheme is to generate the events with a minimum number of spikes in the first stage and to reduce their effective number and width further by exploiting prominent bunching at the harmonics in the following stages. This way, pre- and post-spikes are greatly mitigated, as we show in Figure 2c. This allows for the generation of single spike sub-femtosecond pulses on a statistical basis, at the level of several percent of the total number of pulses [4]. This method is attractive for high repetition rate machines, since one can post-select the ensemble of events with desired pulse duration and other properties using non-invasive spectral or temporal diagnostics.

2. Experiment at SASE3 Undulator at the European XFEL

We performed two separate experiments using the two stage setup at the SASE3 undulator of the European XFEL. The second stage was set to the 4th harmonic of the first one. In

Table 1. Experimental parameters.

Experiment	${\mathit{E}}_{\mathit{ebeam}}$ (GeV)	${\mathit{E}}_{1\mathit{h}}$ (eV)	Cells${}_{1\mathit{h}}$	XGM${}_{1\mathit{h}}$ ($\mathsf{\mu }$J)	${\mathit{E}}_{4\mathit{h}}$ (eV)	Cells${}_{4\mathit{h}}$
675h4 (#1 and #2)	14	675	10	18	2700	1
503h4 (#1 and #2)	11.5	503	9	52	2012	6 → 8

, we present the experimental parameters.

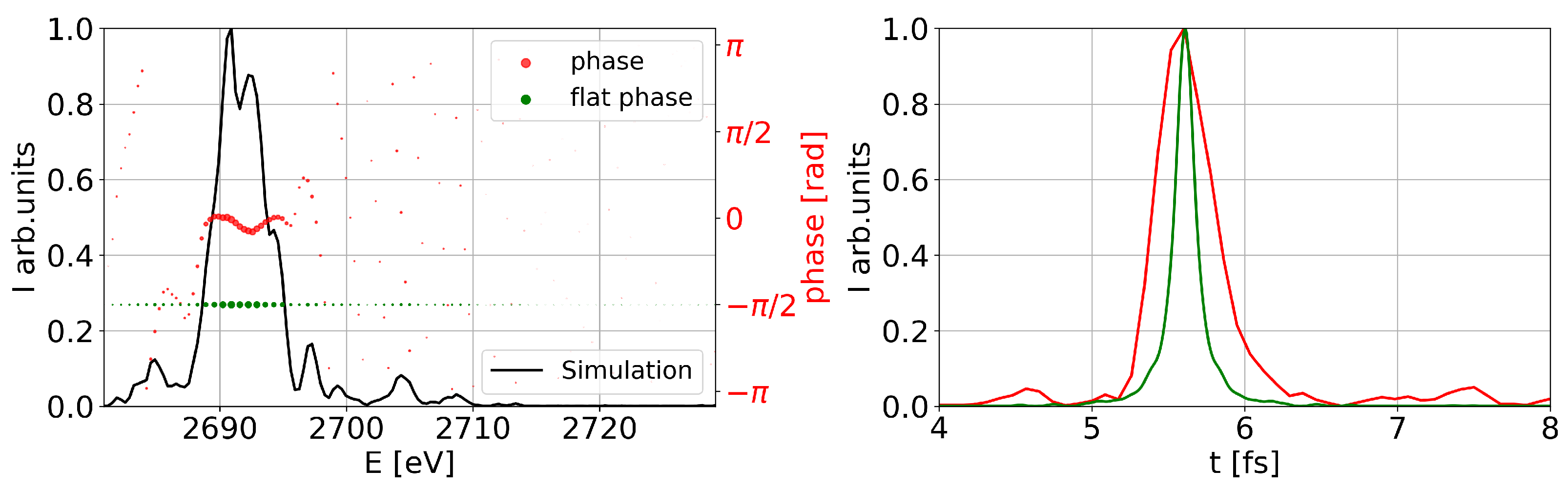
During the first experiment (October 2020), we used a compressed 100 pC electron beam to minimize the amount of SASE spikes in the first stage tuned to the fundamental photon energy of 675 eV, the spectrometer resolution was $0.13$ eV [6]. The pulse energy downstream from 10 active undulator cells was at the level of 18 $\mathsf{\mu }$J. We recorded spectra of the fundamental, finding their relative bandwidth at a level of 0.5 %, see Figure A1a. To optimize the performance of the high harmonic bunching, we stopped FEL amplification at the fundamental at the beginning of the nonlinear regime. The second stage was set to $4\times 675$ eV $=2700$ eV with one undulator closed. The spectrometer resolution at this photon energy was $0.7$ eV. We aimed at seeing only the effect of coherent radiation at the harmonic without further amplification. In the recorded spectra, as expected, we observed sporadic events with spikes dominant over their satellites, Figure 3a. The data from this experiment are represented by the run identifier 675h4#1 in the present article (notation like 675h4#1 encodes the main parameters of an experimental run; the first number stands for the energy at the fundamental harmonic, h4 represents which particular harmonic is considered, and #1 is the number of the run). The results were reproducible after optimization attempts, run 675h4#2.

One of the challenges of the experiment was the diagnostics of the pulse energy. It was measured with an X-ray Gas Monitor (XGM) [7]. In two pulse operation, this device is sensitive not only to the fundamental but also at its harmonics.

During the second experiment (September 2021), we tuned nine undulator cells to the fundamental photon energy of 503 eV with a spectrometer resolution of $0.2$ eV. Similarly, we optimized the electron beam compression to minimize the number of spectral spikes and acquired spectra, run 503h4#1, Figure 3b. We tuned the second stage to the fourth harmonic, and recorded radiation spectra again, with a resolution of $1.2$ eV at 2012 eV. In run 503h4#2, we used six closed cells; after closing two more cells, we observed a minor increase in pulse energy from 57 $\mathsf{\mu }$J by 11 $\mathsf{\mu }$J.

Data Analysis

During the experiments, we collected raw spectra from the SASE3 soft X-ray spectrometer [6]. We filtered this set of spectra for single spike events only. We relied on the fact that, on a statistical basis, a single spike event in a spectrum corresponds to a single spike event in the time domain.

At first, we extracted raw data from the SASE3 spectrometer, see Figure 4a, subtracted the background, and proceeded with the application of a noise reduction algorithm, see Figure 4b. The last step was needed to facilitate the finding of peaks in the spectra, see Figure 4c. The number of single spike events was at the level of 11–13 % for the first experiment and 3% for the second experiment. The filtered events and the corresponding values for the minimal pulse duration are presented in Figure 3.

We refer to minimal pulse duration because the actual time domain power distribution is unknown in these experiments; in fact, we plan to conduct measurements with the angular streaking technique [8] to measure the actual temporal duration. At the moment, we lack direct temporal diagnostics for the attoseconds-at-harmonics experiments, and we can only provide the lower estimate of the pulse duration under the assumption of Fourier limit. We performed a Fourier transform of the spectral amplitude, in other words, we assumed a flat phase across the spectrum. Therefore, we only obtained the minimal possible pulse duration. Results are presented in

Table 2. Experimental results.

	675h4#1 (as)	675h4#2 (as)	503h4#1 (as)	503h4#2 (as)
${\left(\mathsf{\Delta }{t}_{eFT}\right)}_{FWHM}$	$234\pm 29$	$234\pm 27$	$338\pm 27$	$319\pm 18$
${\left(\mathsf{\Delta }{t}_e\right)}_{FWHM}$	$650\pm 140$

with the spread expressed with median absolute deviation; we also report here our estimate of the real pulse duration ${\left(\mathsf{\Delta }{t}_e\right)}_{FWHM}$ based on the reasoning in Appendix B.

3. Discussion

As we indicated before, the attoseconds-at-harmonics method will be particularly suitable for high repetition-rate machines. For example, the European XFEL allows generating up to 27,000 photon pulses per second (2700 per train of electron bunched, trains go at 10 Hz repetition rate) [9]. Such a high repetition rate is a unique feature of superconducting FEL drivers. In this case, the attoseconds-at-harmonic method can potentially provide from 80 up to 350 single spike events per train, ten times per second.

The numbers in Table 2 provide only a rough estimation for the pulse duration. In these results, we evaluated both the minimal possible ${\left(\mathsf{\Delta }{t}_{eFT}\right)}_{FWHM}$ and the actually expected pulse duration ${\left(\mathsf{\Delta }{t}_e\right)}_{FWHM}$. The estimations on the minimal possible pulse duration are based on a Fourier transform of the spectral amplitude and on the measure of the spread of the resulting distributions. The estimation for the actually expected pulse duration is more intricate and is explained in detail in Appendix B.

We expect to conduct further experiments: firstly, we aim to provide an absolute measurement of the harmonic pulse energy with the XGM diagnostic and, secondly, to perform angular streaking experiments to reveal the time domain of such pulses. The latter will give us a clear indication of the real pulse duration and validate the analysis of the present paper. Additionally, further theoretical analysis on statistical properties of such pulses may be possible.

Finally, we should place the attoseconds-at-harmonic method in the context of the many techniques for obtaining sub-fs level single spike pulses that have been proposed and/or tested at different facilities. A comprehensive overview of these methods is given in [10]. Given the statistical nature of the attoseconds-at-harmonics method, it should be clear that this technique might not be useful for every user’s experiment, as it is based on a “post-selection” of short pulses out of an ensemble. Nevertheless, one of the benefits of the attoseconds-at-harmonics method is that it is free to implement and does not require any additional hardware to be installed, except for the availability of variable gap undulators.

4. Conclusions

In this paper, we show experimental results on the generation of quasi-single spike FEL pulses by applying the attoseconds-at-harmonics method. We estimate that a fraction (3–13%) of such pulses can be as short as several hundred attoseconds (650 as). We expect that this work will be followed up, in the future, by direct time-domain measurements with the angular streaking technique at the European XFEL.