Abstract
Lensless imaging represents a significant advancement in imaging technology, offering unique benefits over traditional optical systems due to its compact form factor, ideal for applications within the Internet of Things (IoT) ecosystem. Despite its potential, the intensive computational requirements of current lensless imaging reconstruction algorithms pose a challenge, often exceeding the resource constraints typical of IoT devices. To meet this challenge, a novel approach is introduced, merging multi-level image restoration with the pix2pix generative adversarial network architecture within the lensless imaging sphere. Building on the foundation provided by U-Net, a Multi-level Attention-based Lensless Image Restoration Network (MARN) is introduced to further augment the generator’s capabilities. In this methodology, images reconstructed through Tikhonov regularization are perceived as degraded images, forming the foundation for further refinement via the Pix2pix network. This process is enhanced by incorporating an attention-focused mechanism in the encoder--decoder structure and by implementing stage-wise supervised training within the deep convolutional network, contributing markedly to the improvement of the final image quality. Through detailed comparative evaluations, the superiority of the introduced method is affirmed, outperforming existing techniques and underscoring its suitability for addressing the computational challenges in lensless imaging within IoT environments. This method can produce excellent lensless image reconstructions when sufficient computational resources are available, and it consistently delivers optimal results across varying computational resource constraints. This algorithm enhances the applicability of lensless imaging in applications such as the Internet of Things, providing higher-quality image acquisition and processing capabilities for these domains.
1. Introduction
In the design of traditional lens-based imaging systems, factors such as focal length, material, and the refractive index of the optical lens must be taken into account. These constraints often make it challenging to design lenses that are compact. Furthermore, the inherent optical characteristics of lenses typically necessitate a protruding shape (e.g., mobile phone cameras), complicating the concealment and portability of lens-based imaging systems. With the advancement of IoT technology, the design of covert and miniaturized imaging devices has encountered significant challenges.
Lensless imaging technology [1] has emerged as a promising solution to these issues. This approach involves placing an optical modulation device in front of the image sensor. The modulation of light, traditionally performed using the optical lens, is achieved through a combination of the optical modulation device and a back-end solution algorithm, thus enabling a lensless imaging system. Imaging systems based on lensless technology, when compared to their lens-based counterparts, are not only more cost-effective and compact but also offer a larger field of view and improved concealability. A variant of lensless imaging technology, lensless microscopic imaging, has been widely used in the medical field. Unlike lensless imaging structures based on optical modulation devices, the observed targets are usually placed on a transparent substrate located between the light source and the image sensor [2,3].
Furthermore, the design of lensless imaging systems is less constrained by material requirements. Various substances have been employed in the creation of optically modulating devices, including chromium masks on quartz [4], diffusers [5], phase masks [6], and an assortment of programmable modulators [7]. The versatility of lensless imaging technology extends to applications such as 3D imaging [8] and face recognition [9].
Significant advancements in the field have been documented. For instance, images of a cityscape were reconstructed by DeWeert et al. [7]. A novel lensless opto-electronic neural network architecture was proposed by Wanxin Shi et al. [10], resulting in effective computational resource conservation. The FlatScope, a lensless microscope, was designed by Jesse K. Adams et al. [11]. Additionally, compression sensing was applied to lensless imaging by Guy Satat et al. [12]. Given these innovative developments, lensless imaging technology demonstrates substantial potential and a wide range of applicability across various domains.
In the realm of the IoT, imaging systems equipped on terminal devices occasionally necessitate image reconstruction and restoration at the terminal itself. However, existing end-to-end lensless image reconstruction algorithms often demand substantial computational resources, rendering them unsuitable for terminals with limited capabilities. On the other hand, in different application scenarios, such as those with sufficient available computational resources, there is a need to obtain reconstructed images with the best possible quality. To address and reconcile this challenge, a multi-stage lensless image restoration algorithm is introduced within the proposed method, leveraging the pix2pix architecture and deep neural networks. This ensures the high-quality reconstruction and restoration of lensless images across varying computational resources. For instance, the rapid reconstruction of lensless images in low-computational resource settings and obtaining the best possible lensless image reconstruction results when computational resources and time are abundant, achieving adaptive computing power for lensless imaging.
Within the proposed method, the lensless image, initially reconstructed through Tikhonov regularization, is perceived as a degraded image. Restoration is then initiated by employing a generative adversarial network built on the pix2pix architecture. Subsequently, images produced using the deep neural network, acting as a generator, are treated as degraded images subject to further restoration processes. Throughout the iterative image restoration, the network’s breadth is systematically expanded, and supervisory modules are instituted at each output juncture, a strategic move designed to uphold the integrity and quality of the images rendered at every phase.
This methodology underscores a nuanced approach to lensless image processing, acknowledging the computational restrictions present in certain terminal devices within the Internet of Things ecosystem. By adopting a multi-tiered restoration algorithm, the process not only adapts to the constraints of device-specific resources but also iteratively enhances image quality, effectively balancing performance requirements with available computational assets.
In the context of lensless imaging systems, employing analytical solutions for deriving reconstructed images exhibits increased robustness against variable illumination conditions, distinguishing it as a more adaptable approach compared with conventional end-to-end image reconstruction algorithms. The image restoration algorithms based on this methodology demonstrate substantial environmental adaptability.
The pivotal contributions of this article are manifold:
The application of generative adversarial networks for the restoration of noise-free images constitutes another major contribution, refining the quality of reconstructed images beyond the capabilities of deep convolutional networks alone.
The introduction of multi-stage image restoration techniques to the domain of lensless imaging marks a significant advancement. This innovation enables lensless imaging systems to execute high-caliber image restoration within a diverse array of IoT scenarios, irrespective of the variance in available computing resources.
A novel multi-tiered lensless image restoration network architecture is articulated and used as a generator of the GAN, known as the Multi-level Attention-based Lensless Image Restoration Network (MARN). This framework is instrumental in enhancing the image quality procured from FlatCam systems and affords the network the flexibility for continuous cascading, contingent on the computational resources at its disposal.
The compilation of a comprehensive lensless dataset, derived from ImageNet [13], featuring 60,000 images with an initial resolution of 5120 × 5120. These images, captured via our proprietary FlatCam, were subsequently downsampled to a resolution of 512 × 512, followed by meticulous calibration and reconstruction. The potency of the proposed method was rigorously affirmed through its application to this dataset, and its performance was benchmarked against alternative methodologies, showcasing its superior effectiveness.
Collectively, these contributions underscore the significant strides made in the realm of lensless imaging, particularly in enhancing the robustness and adaptability of imaging systems confronted with diverse environmental conditions and computational constraints. This research not only paves the way for more resilient and efficient imaging methodologies but also broadens the horizons for the practical, real-world applications of lensless imaging technologies.
2. Lensless Imaging System
FlatCam is a lensless camera based on an amplitude mask designed by Asif et al [14]. It is also one of the most studied camera models in the field of lensless imaging. FlatCam has shown great potential in areas such as compression sensing based on a lensless imaging [15], face recognition based on a lensless system [16,17], lensless image reconstruction [18,19,20,21,22], and 3D imaging based on a lensless system [23]. Our lensless imaging system is built on the FlatCam prototype, as shown in Figure 1.

Figure 1.
The lensless camera system we built.
2.1. Theoretical Model
In lensless imaging systems, distinct from their lens-based counterparts, light that carries scene information undergoes modulation using an optical device prior to its interaction with the sensor. This process is mathematically represented by Equation (1).
Here, denotes the image as captured by the sensor, with representing the system transfer matrix, and signifying the original image information. The term is indicative of additive noise. The pursuit then becomes a quest to extract an accurate measure of x through the utilization of Equation (1).
Given the nature of this challenge as an ill-posed inverse problem, the optimization of the algorithm becomes essential in effectively approximating a solution. Several strategies for this optimization dilemma have been proposed [24,25]. In this study, the Tikhonov regularization algorithm is employed as the optimization technique [26]. The post-optimization problem is articulated as follows in Equation (2):
In this context, and are the decomposed left and right system transfer matrices of , achieved through the use of a separable coding mask [4]. The term quantifies the squared residual norm, and stands as the regularization term, with being the regularization parameter. The reconstructed image is then computable via Equation (2), and the impact of this reconstruction is demonstrable through the degraded image, as illustrated in Figure 2. This methodology illuminates the intricacies of handling ill-posed inverse problems in lensless imaging systems, underscoring the necessity for meticulous algorithm optimization. By doing so, it enables a more precise reconstruction of images, even when they are subject to conditions that typically complicate image capture and processing.
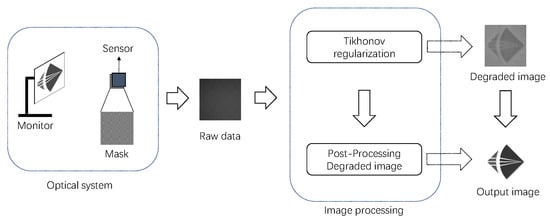
Figure 2.
Framework of this study.
2.2. Calibration
Calibration remains a critical step for lensless cameras, akin to their lens-based counterparts. Some lensless cameras employ end-to-end deep neural network image reconstruction algorithms in the imaging process. While these systems do not undergo an explicit calibration phase, calibration is inherently integrated into the deep neural network’s training regimen [27,28,29].
Particularly for FlatCam-based lensless cameras, the calibration process fundamentally involves acquiring the left and right system transmission matrices, and , of the camera system. The methodology adopted here parallels that of [14], utilizing ’n’ separable patterns to ascertain and . These matrices are subsequently computed via Equations (4) and (5), respectively.
where are the approximate terms of the image captured by the sensor through truncating the singular value decomposition, ’H’ denotes the Hadamard matrix, and ’N’ represents the total count of separable patterns. The term stands for the measured image of the displayed image . Significantly, Equation (3) corresponds to the rank-1 approximation acquired through TSVD (Truncated Singular Value Decomposition).
This procedural delineation emphasizes the nuanced calibration required for lensless cameras, particularly those based on the FlatCam design. By integrating these systematic calibration steps [14], lensless imaging technology becomes more precise, contributing to the advancement of this emerging field and enhancing the reliability of the imaging systems employed across various applications.
2.3. Image Reconstruction
The algorithm employed in reconstructing images within a lensless imaging system is pivotal, directly influencing the quality of the resultant lensless images. This aspect remains a focal point of research within the domain of lensless imaging. Currently, the algorithms utilized for image reconstruction in lensless imaging systems predominantly fall into two categories: those based on convex optimization and those that are data-driven [30].
Convex optimization-based image reconstruction algorithms offer the advantage of speed, facilitating quicker image processing. However, they often compromise on the quality of the reconstructed images. On the other hand, data-driven image reconstruction strategies, while typically more time-consuming, consistently yield higher quality reconstructed images, surpassing their convex optimization-based counterparts [14,20,29,31,32].
This dichotomy highlights an essential trade-off in the field of lensless image reconstruction: the balance between the processing speed and the quality of the reconstructed images. The choice between these methodologies can significantly impact practical applications, making it a critical consideration in the ongoing development and refinement of lensless imaging technologies.
In order to better balance computational complexity and image quality, we propose a progressive multi-stage image restoration algorithm for lensless image restoration: pix2pix-MARN. This algorithm treats the reconstructed image [14] as a degraded image, accesses a progressive deep neural network at the back end, and continuously optimizes and outputs the image in stages, finally obtaining a better quality reconstructed image. The details of the deep neural network will be given in Section 3.1.
3. Proposed Method
3.1. Generate Adversarial Network Structure: Pix2pix
The proposed method for lensless image restoration is primarily based on a generative adversarial network architecture: pix2pix [33], as illustrated in Figure 3. Furthermore, the generator component employs a U-Net network structure with an integrated attention mechanism. Within the pix2pix network framework, the discriminator receives two categories of image pairs: one consists of the degraded image coupled with the restored image from the generator, signifying ’FAKE’, while the other pairs the degraded image with the ground truth, indicating ’REAL’. The objective of the generator is to augment the quality of the produced images via an ongoing learning process, aspiring to eventually “deceive” the discriminator. Through this iterative enhancement, the generator aims to reach a level of proficiency where its outputs are indistinguishable from the authentic images, thereby misleading the discriminator effectively. Through extensive training and learning, the generator progressively refines the restored images derived from the degraded ones, bringing them increasingly closer to the ground truth. This continual improvement enhances the generator’s capability, which is instrumental in the image restoration process.
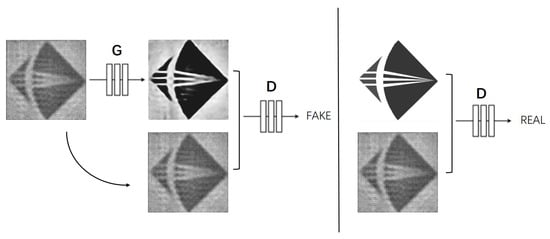
Figure 3.
The pix2pix architecture for lensless image restoration.
A prevalent and fitting selection for the generator component is the U-Net, characterized by its encoder–decoder structure. Convolutional neural networks of similar design have demonstrated proficiency in recovering noise-free images. Building on the foundation provided by U-Net, a Multi-level Attention-based Lensless Image Restoration Network(MARN) is introduced to further augment the generator’s capabilities. This enhanced approach will be delineated in upcoming sections.
3.2. Multi-Stage Architecture
The image restoration framework, shown in Figure 4, restores the image step by step in three stages. The main component of these three stages is the U-net network architecture [34] based on the attention mechanism [35,36]. In the first stage, the entire image is taken as input, considering only one patch per image. In the next stage, the output of the first stage is used as input to the second stage, and the input image is divided into four patches of equal size, which are fed into the encoder–decoder architecture and stitched together to form the complete image. In this way, the amount of data can be increased to allow the network to be fully trained, and the image can be restored at a lower scale, allowing more detail to be restored. In the third stage, the output of the previous stage is still used as input. To increase the perceptual field, the decoder architecture of the third stage receives the feature maps from the first and second stages, respectively.
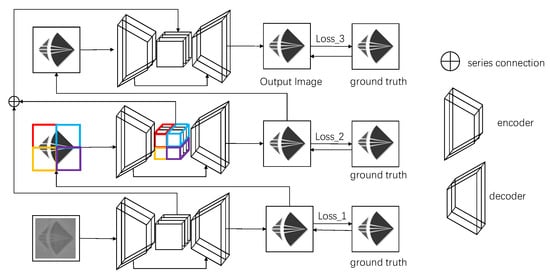
Figure 4.
The MARN algorithm framework.
Let us consider the input lensless reconstructed image . We denote the j-th patch in the i-th stage as . If the image is not separated into any patches at the i-th stage, we define the image as . Thus, the input image for the first stage can be denoted as , the input image for the second stage can be denoted as ,,,, and the input image for the third stage can be denoted as . Encoders and decoders at the i-th stage are denoted as and , respectively.
For our deep neural network, at the first stage, the lensless reconstructed image is input into the to obtain the corresponding feature image .
Then, is input to the to get the first stage of the lensless restoration image .
At the second stage, we need to split F into four patches of the same size. The relationship between the input at the second stage and can be expressed as Equation (8).
where ± and ∓ do not represent adding the images pixel by pixel, ± represents stitching the images left and right, and ∓ represents stitching the images top and bottom.
We can obtain the feature map for the second stage by feeding ,,, into the and stitching together the feature maps from the output.
As with the first stage, the second stage of the lensless restoration of images is obtained by using the as input to the .
At stage 3, we use the obtained at stage 2 directly as the input to the .
To enhance the details of the image and prevent the loss of image information in the first and second stages of processing, we concatenate the three stages of feature maps as input to the .
where + stands for series connection. is the final restoration image.
3.3. Encoder and Decoder Architecture
The architecture for encoding and decoding is depicted in Figure 5. The attention module employed integrates the Convolutional Block Attention Module as presented in [35].
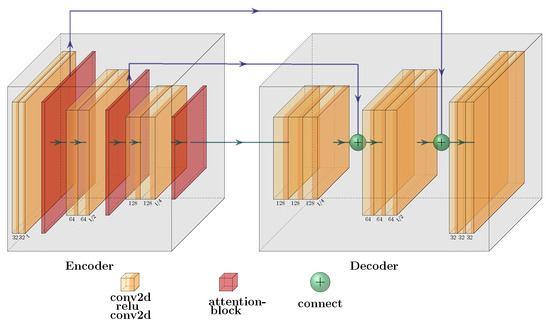
Figure 5.
The architecture for encoding and decoding.
Encoding encompasses the process of feature extraction from input data using a convolutional neural network, culminating in a feature map rich in channels. Conversely, decoding involves the restoration of this feature map to its initial size and channel density through a structure that mirrors the encoder. Skip-connections established between encoders and decoders facilitate the transmission of information across all phases of encoding, significantly expediting network convergence and gradient propagation [34,37].
The principles of encoding and decoding are foundational to numerous deep neural network structures, with a myriad of effective methodologies drawing on these elements [36,38,39,40,41,42,43,44]. Diverging from a direct application of the encoding and decoding framework, an attention mechanism is incorporated into this architecture, akin to the approach in [36]. This integration aims to optimize the attention module’s efficacy and augment the intricacies of the restored image, prompting the positioning of the attention module within the encoder segment.
3.4. Loss Function
Using mean squared error (MSE) directly as a loss function would result in a loss of high-frequency detail in the image. To improve image quality, we let the Charbonnier penalty function help us design our loss function [45]. We optimize our deep neural network with the following loss function:
where Y represents the ground truth, and represent Charbonnier loss and edge loss respectively, and and d are system parameters; set to 0.05 and , , and to 0.1, 0.4, and 1, respectively, according to experience. and are calculated in Equations (18) and (19).
In the context of lensless imaging, the pix2pix network and the convolutional neural network functioning as generators share the goal of minimizing the discrepancy between the restored image and the ground truth. Consequently, the same loss function is adopted for both networks.
3.5. Supervision Module
The supervision module is mainly represented in the loss function. When calculating the total loss, we first calculate the loss in different stages, and then accumulate and sum them through a certain proportion to obtain the total loss, and modify our model parameters through the backward transfer algorithm. In Section 4.4, we demonstrate the effectiveness of this approach through ablation experiments.
4. Experimental Results and Analysis
4.1. Dataset
A lensless camera is built to capture the ImageNet dataset [13] in a dark room and downsampled the captured images to a size of 512 × 512. Due to experimental constraints, we were unable to capture all of the ImageNet dataset and only 60,000 of the images were captured. Among them, 47,880 images were used as the training set and 12,000 images were used as the validation set. The remaining 120 images from the ImageNet dataset and 500 images other than the dataset were used as the test set.
In the training set, we reconstruct each captured image using Tikhonov regularization and then form a data pair from the reconstructed image to the captured image. This data pair will be used to train our deep neural network. Figure 6 shows two sample sets of data pairs.

Figure 6.
Two sets of samples from the training set.
In the test set, we also reconstructed each of the acquired images using Tikhonov regularization, using the reconstructed images as the test set images.
The FlatCam used to collect the data is the same as that in [46]. The system parameters of FlatCam are shown in Table 1. We disassembled a camera and placed the mask close to the sensor. According to our measurements, the distance between the sensor and the mask is less than 3 mm.

Table 1.
Flatcom system parameters.
It is important to highlight that, in the comparative experiments involving convolutional neural networks, including FCN-8s, U-Net, and others, a consistent variable control was maintained by conducting all tests within the pix2pix architecture framework. This standardization ensures that the performance differences are attributable to the neural network structures and strategies themselves, rather than variations in the overarching experimental setup.
4.2. Experimental Details
Unless otherwise specified, all our image restoration experiments were performed on a server equipped with an NVIDIA GeForce RTX 3090 graphics card and Intel i9-10940X CPU. In deep neural network training, we used a fixed learning rate () and Adam optimizer to train until the network converged. Our network was completely convoluted. Any size of image can be used as input as long as the GPU memory allows. Specifically, we used the input image size of 512 × 512 pixel dataset. If not otherwise specified, all network performances mentioned in this paper are measured conditional to the input and output being 512 × 512 images.
4.3. Comparison with Other Algorithms
To evaluate the performance of the proposed algorithm, we have reconstructed and restored lensless images on our dataset and compared them with other algorithms, including U-net [34], FCN-8s [47], and Dense-U-net [48].
Figure 7a is an image from the test set, which we first reconstructed using Tikhonov regularization to obtain Figure 7b, and we then used Figure 7b as input for each algorithm to obtain each of the remaining images in Figure 7, respectively. As can be seen from the objective evaluation metrics, the proposed algorithm significantly outperforms FCN-8s and U-net. In the first stage, the PSNR of Dense-U-Net was higher than that of our proposed algorithm, but in the second and third stages, the PSNR of the proposed algorithm exceeded that of Dense-U-Net. It is worth mentioning that the size of the proposed model is much smaller than that of Dense-U-Net. In terms of running speed, the proposed algorithm is almost 18% faster than Dense-U-Net in the first stage, but there is not much difference in image quality. The sizes and running times of the individual models are given in Table 2. Figure 8 gives a comparison of the results of using different algorithms for some sample test sets.

Figure 7.
A sample result from the test set.

Table 2.
Model size and run time.

Figure 8.
Seven images from the test set were restored using FCN-8s, Unet, Dense-U-Net, and the proposed method.
The quantitative evaluation of 120 images is summarized in Figure 9 from the perspective of PSNR and SSIM, respectively. Based on the curves, it can be seen that the proposed method outperforms other algorithms on almost all images. The average quantization metrics for each of the 120 images are given in Table 3. It is clear that the proposed method improves, on average, 8.5968, 1.4225 (dB), and 0.0365 over the existing methods for the three metrics MSE, PSNR, and SSIM, respectively.
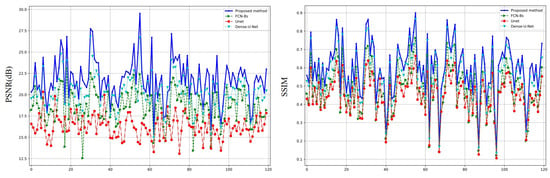
Figure 9.
The quantitative evaluations of PSNR and SSIM for 120 images.

Table 3.
Comparison of quantitative indicators.
4.4. Ablation Experiment
In order to verify the effectiveness of the monitoring module and the attention module, we conducted ablation experiments. The experimental results are shown in Table 4. Since the supervision module directly affects the output of multi-stage restored images, without the supervision module, our model can only restore images once, so there is only the output of MARN-3-stage in the table.

Table 4.
Ablation results.
It can be seen from Table 4 that removing the supervision module not only destroys the multi-level output of the network, but also makes the network training more difficult and the model parameters difficult to fully train; the effect of removing the attention module is not obvious. We think this may be related to the insufficient details of the data set we selected.
5. Discussion
This study introduces a multi-stage image restoration algorithm into the field of lensless imaging. By combining the pix2pix architecture and deep neural networks, it achieves high-quality image reconstruction and restoration under varying computational resource conditions. This has a positive impact on image processing and sensing applications in domains like IoT, with the potential to enhance the performance and adaptability of imaging systems.
The proposed method provides a solution for image processing requirements on terminal devices, enabling them to independently perform image reconstruction and restoration. This is particularly significant for IoT terminal devices, such as smart cameras and sensors, as it can improve their autonomy and performance.
Despite demonstrating good performance under different computational resource conditions, the method may still require significant computational resources in some cases and may not achieve real-time reconstruction. This limitation could restrict its application in resource-constrained terminal devices. For IoT devices, actual deployment and performance validation are crucial. Future work could involve deploying this method on real terminal devices and conducting large-scale performance validation and practical application case studies.
In summary, this work provides strong support for the development and application of lensless imaging technology, particularly in the context of IoT. However, there are still challenges to overcome, and future research can further improve and expand upon this method.
6. Conclusions
This paper pioneers the integration of the pix2pix architecture and multi-stage image restoration within the realm of lensless imaging, adeptly catering to the demand for high-quality image acquisition in lensless imaging systems amidst varying computational resources in the Internet of Things (IoT) landscape.
The methodology advanced in this study facilitates more comprehensive training of deep neural networks. By implementing supervised multi-stage image restoration, this ensures the pinnacle of image restoration quality in lensless systems when adequate computational resources are available. The efficacy and superiority of the proposed method have been substantiated through both comparative and ablation experiments. It is anticipated that the algorithm’s applicability extends beyond merely lensless image restoration. There is an expectation that its potential could be further realized in tasks involving lensless image inference, broadening its scope of influence within the field.
Author Contributions
Conceptualization, M.L. and X.Y.; methodology, M.L.; software, X.Y.; validation, W.Z. and W.Z.; data curation, X.S.; writing—original draft preparation, M.L. and X.Y.; writing—review and editing, X.S.; project administration, X.S. and W.H.; funding acquisition, X.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the strategic high-tech innovation fund of CAS: GQRS 19-23.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Boominathan, V.; Adams, J.K.; Asif, M.S.; Avants, B.W.; Robinson, J.T.; Baraniuk, R.G.; Sankaranarayanan, A.C.; Veeraraghavan, A. Lensless Imaging: A computational renaissance. IEEE Signal Process. Mag. 2016, 33, 23–35. [Google Scholar] [CrossRef]
- Xiong, Z.; Melzer, J.E.; Garan, J.; McLeod, E. Optimized sensing of sparse and small targets using lens-free holographic microscopy. Opt. Express 2018, 26, 25676–25692. [Google Scholar] [CrossRef] [PubMed]
- Ozcan, A.; McLeod, E. Lensless Imaging and Sensing. Annu. Rev. Biomed. Eng. 2016, 18, 77–102. [Google Scholar] [CrossRef]
- Wei, Z.; Su, X.; Zhu, W. Lensless Computational Imaging with Separable Coded Mask. In Proceedings of the 2018 IEEE 3rd International Conference on Image, Vision and Computing (ICIVC), Chongqing, China, 27–29 June 2018; pp. 614–617. [Google Scholar] [CrossRef]
- Kuo, G.; Antipa, N.; Ng, R.; Waller, L. DiffuserCam: Diffuser-Based Lensless Cameras. In Proceedings of the Imaging and Applied Optics 2017 (3D, AIO, COSI, IS, MATH, pcAOP), San Francisco, CA, USA, 26–29 June 2017; Optica Publishing Group: Washington, DC, USA, 2017; p. CTu3B.2. [Google Scholar] [CrossRef]
- Boominathan, V.; Adams, J.K.; Robinson, J.T.; Veeraraghavan, A. PhlatCam: Designed Phase-Mask Based Thin Lensless Camera. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 1618–1629. [Google Scholar] [CrossRef] [PubMed]
- DeWeert, M.J.; Farm, B.P. Lensless coded-aperture imaging with separable Doubly-Toeplitz masks. Opt. Eng. 2015, 54, 1–9. [Google Scholar] [CrossRef]
- Antipa, N.; Kuo, G.; Ng, R.; Waller, L. 3D DiffuserCam: Single-Shot Compressive Lensless Imaging. In Proceedings of the Imaging and Applied Optics 2017 (3D, AIO, COSI, IS, MATH, pcAOP), San Francisco, CA, USA, 26–29 June 2017; Optica Publishing Group: Washington, DC, USA, 2017; p. CM2B.2. [Google Scholar] [CrossRef]
- Tan, J.; Niu, L.; Adams, J.K.; Boominathan, V.; Robinson, J.T.; Baraniuk, R.G.; Veeraraghavan, A. Face Detection and Verification Using Lensless Cameras. IEEE Trans. Comput. Imaging 2019, 5, 180–194. [Google Scholar] [CrossRef]
- Shi, W.; Huang, Z.; Huang, H.; Hu, C.; Chen, M.; Yang, S.; Chen, H. LOEN: Lensless opto-electronic neural network empowered machine vision. Light. Sci. Appl. 2022, 11, 121. [Google Scholar] [CrossRef]
- Adams, J.K.; Boominathan, V.; Avants, B.W.; Vercosa, D.G.; Ye, F.; Baraniuk, R.G.; Robinson, J.T.; Veeraraghavan, A. Single-frame 3D fluorescence microscopy with ultraminiature lensless FlatScope. Sci. Adv. 2017, 3, e1701548. [Google Scholar] [CrossRef] [PubMed]
- Satat, G.; Tancik, M.; Raskar, R. Lensless Imaging With Compressive Ultrafast Sensing. IEEE Trans. Comput. Imaging 2017, 3, 398–407. [Google Scholar] [CrossRef]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Asif, M.S.; Ayremlou, A.; Sankaranarayanan, A.; Veeraraghavan, A.; Baraniuk, R.G. Flatcam: Thin, lensless cameras using coded aperture and computation. IEEE Trans. Comput. Imaging 2016, 3, 384–397. [Google Scholar] [CrossRef]
- Nguyen Canh, T.; Nagahara, H. Deep Compressive Sensing for Visual Privacy Protection in FlatCam Imaging. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision Workshop (ICCVW), Seoul, Republic of Korea, 27–28 October 2019; pp. 3978–3986. [Google Scholar] [CrossRef]
- Tan, J. Face Detection and Verification with FlatCam Lensless Imaging System. Ph.D. Thesis, Rice University, Houston, TX, USA, 2018. [Google Scholar]
- Anushka, R.L.; Jagadish, S.; Satyanarayana, V.; Singh, M.K. Lens less Cameras for Face Detection and Verification. In Proceedings of the 2021 6th International Conference on Signal Processing, Computing and Control (ISPCC), Solan, India, 7–9 October 2021; pp. 242–246. [Google Scholar] [CrossRef]
- Asif, M.S.; Ayremlou, A.; Veeraraghavan, A.; Baraniuk, R.; Sankaranarayanan, A. FlatCam: Replacing Lenses with Masks and Computation. In Proceedings of the 2015 IEEE International Conference on Computer Vision Workshop (ICCVW), Santiago, Chile, 7–13 December 2015; pp. 663–666. [Google Scholar] [CrossRef]
- Tan, J.; Boominathan, V.; Veeraraghavan, A.; Baraniuk, R. Flat focus: Depth of field analysis for the FlatCam lensless imaging system. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 6473–6477. [Google Scholar] [CrossRef]
- Khan, S.S.; Adarsh, V.; Boominathan, V.; Tan, J.; Veeraraghavan, A.; Mitra, K. Towards photorealistic reconstruction of highly multiplexed lensless images. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 7860–7869. [Google Scholar]
- Zhou, H.; Feng, H.; Hu, Z.; Xu, Z.; Li, Q.; Chen, Y. Lensless cameras using a mask based on almost perfect sequence through deep learning. Opt. Express 2020, 28, 30248–30262. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Feng, H.; Xu, W.; Xu, Z.; Li, Q.; Chen, Y. Deep denoiser prior based deep analytic network for lensless image restoration. Opt. Express 2021, 29, 27237–27253. [Google Scholar] [CrossRef]
- Asif, M.S. Lensless 3D Imaging Using Mask-Based Cameras. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 6498–6502. [Google Scholar] [CrossRef]
- Chan, T.; Esedoglu, S.; Park, F.; Yip, A. Total variation image restoration: Overview and recent developments. In Handbook of Mathematical Models in Computer Vision; Springer: Berlin/Heidelberg, Germany, 2006; pp. 17–31. [Google Scholar]
- Eckstein, J.; Yao, W. Augmented Lagrangian and alternating direction methods for convex optimization: A tutorial and some illustrative computational results. RUTCOR Res. Rep. 2012, 32, 44. [Google Scholar]
- Tihonov, A.N. Solution of incorrectly formulated problems and the regularization method. Sov. Math. 1963, 4, 1035–1038. [Google Scholar]
- Bae, D.; Jung, J.; Baek, N.; Lee, S.A. Lensless Imaging with an End-to-End Deep Neural Network. In Proceedings of the 2020 IEEE International Conference on Consumer Electronics-Asia (ICCE-Asia), Seoul, Republic of Korea, 1–3 November 2020; pp. 1–5. [Google Scholar]
- Pan, X.; Chen, X.; Takeyama, S.; Yamaguchi, M. Image reconstruction with transformer for mask-based lensless imaging. Opt. Lett. 2022, 47, 1843–1846. [Google Scholar] [CrossRef]
- Wu, J.; Cao, L.; Barbastathis, G. DNN-FZA camera: A deep learning approach toward broadband FZA lensless imaging. Opt. Lett. 2021, 46, 130–133. [Google Scholar] [CrossRef] [PubMed]
- Boominathan, V.; Robinson, J.T.; Waller, L.; Veeraraghavan, A. Recent advances in lensless imaging. Optica 2022, 9, 1–16. [Google Scholar] [CrossRef]
- Monakhova, K.; Yurtsever, J.; Kuo, G.; Antipa, N.; Yanny, K.; Waller, L. Learned reconstructions for practical mask-based lensless imaging. Opt. Express 2019, 27, 28075–28090. [Google Scholar] [CrossRef] [PubMed]
- Haris, M.; Shakhnarovich, G.; Ukita, N. Deep back-projection networks for super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1664–1673. [Google Scholar]
- Dong, H.; Neekhara, P.; Wu, C.; Guo, Y. Unsupervised image-to-image translation with generative adversarial networks. arXiv 2017, arXiv:1701.02676. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Oktay, O.; Schlemper, J.; Folgoc, L.L.; Lee, M.; Heinrich, M.; Misawa, K.; Mori, K.; McDonagh, S.; Hammerla, N.Y.; Kainz, B.; et al. Attention u-net: Learning where to look for the pancreas. arXiv 2018, arXiv:1804.03999. [Google Scholar]
- Mao, X.; Shen, C.; Yang, Y.B. Image restoration using very deep convolutional encoder-decoder networks with symmetric skip connections. Adv. Neural Inf. Process. Syst. 2016, 29. [Google Scholar]
- Zhang, H.; Dai, Y.; Li, H.; Koniusz, P. Deep stacked hierarchical multi-patch network for image deblurring. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5978–5986. [Google Scholar]
- Das, S.D.; Dutta, S. Fast deep multi-patch hierarchical network for nonhomogeneous image dehazing. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 13–19 June 2020; pp. 482–483. [Google Scholar]
- Schuler, C.J.; Hirsch, M.; Harmeling, S.; Schölkopf, B. Learning to deblur. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 1439–1451. [Google Scholar] [CrossRef] [PubMed]
- Zamir, S.W.; Arora, A.; Khan, S.; Hayat, M.; Khan, F.S.; Yang, M.H.; Shao, L. Multi-stage progressive image restoration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 14821–14831. [Google Scholar]
- Tao, X.; Gao, H.; Shen, X.; Wang, J.; Jia, J. Scale-recurrent network for deep image deblurring. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 8174–8182. [Google Scholar]
- Zhang, K.; Luo, W.; Zhong, Y.; Ma, L.; Stenger, B.; Liu, W.; Li, H. Deblurring by realistic blurring. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 2737–2746. [Google Scholar]
- Jiang, K.; Wang, Z.; Yi, P.; Chen, C.; Huang, B.; Luo, Y.; Ma, J.; Jiang, J. Multi-scale progressive fusion network for single image deraining. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 8346–8355. [Google Scholar]
- Lai, W.S.; Huang, J.B.; Ahuja, N.; Yang, M.H. Deep Laplacian Pyramid Networks for Fast and Accurate Super-Resolution. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5835–5843. [Google Scholar] [CrossRef]
- Yao, X.; Liu, M.; Su, X.; Zhu, W. Influence of exposure time on image reconstruction by lensless imaging technology. In Proceedings of the 2022 7th International Conference on Intelligent Computing and Signal Processing (ICSP), Xi’an, China, 15–17 April 2022; pp. 1978–1981. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 5–12 June 2015; pp. 3431–3440. [Google Scholar]
- Chen, P.; Su, X.; Liu, M.; Zhu, W. Lensless computational imaging technology using deep convolutional network. Sensors 2020, 20, 2661. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).