Abstract
To improve the imaging speed of ghost imaging and ensure the accuracy of the images, an adaptive ghost imaging scheme based on 2D-Haar wavelets has been proposed. This scheme is capable of significantly retaining image information even under under-sampling conditions. By comparing the differences in light intensity distribution and sampling characteristics between Hadamard and 2D-Haar wavelet illumination patterns, we discovered that the lateral and longitudinal information detected by the high-frequency 2D-Haar wavelet measurement basis could be used to predictively adjust the diagonal measurement basis, thereby reducing the number of measurements required. Simulation and experimental results indicate that this scheme can still achieve high-quality imaging results with about a 25% reduction in the number of measurements. This approach provides a new perspective for enhancing the efficiency of computational ghost imaging.
1. Introduction
Computational ghost imaging(CGI) [1] has garnered widespread attention due to its simple construction and innovative image reconstruction techniques. In a CGI system, a series of pre-set illumination patterns are used as reference signals and projected onto the object under observation. The light beams reflected from the object’s surface are captured by a bucket detector. Subsequently, the image information can be reconstructed by correlating these bucket signals with the reference signals. Ghost imaging is characterized by its non-locality and strong anti-interference capabilities, offering broad application prospects in fields such as medical imaging [2,3,4], remote sensing [5,6], and defense [7,8,9].
However, achieving high efficiency and a high signal-to-noise ratio in image reconstruction remains a challenge in the field of ghost imaging. For an image containing N pixels, ghost imaging requires at least N samples to recover the image, which is the measurement’s Nyquist limit. Notably, ghost imaging using random speckle patterns often requires more samples than N. Therefore, for high-resolution imaging, the need for a large number of samples leads to lower imaging speeds, which becomes a limiting factor in the application of ghost imaging. In 2006, Candès et al. introduced the theory of Compressive Sensing (CS). In 2009, Katz et al. successfully integrated CS theory with Ghost Imaging technology, significantly reducing the number of samples required for CGI [10]. Subsequently, numerous studies have proposed various models and algorithms within the framework of CS to enhance the efficiency of CGI [11,12,13,14]. The core idea of CS is that a sparse or compressible signal can be almost perfectly recovered through a small number of non-adaptive linear measurements, surpassing the limitations of the traditional Nyquist sampling theorem. However, the essence of CS lies in solving a series of convex optimization problems iteratively, a process that consumes considerable computational resources and time. Additionally, this method has specific requirements for the characteristics of the sparse basis. These factors jointly affect the imaging speed and stability of ghost imaging.
Measurement based on orthogonal transformation matrices is another effective method to enhance imaging efficiency [15]. It employs correlation algorithms and matrix inversion algorithms, requiring less from hardware performance, thus enabling fast and stable imaging. Common orthogonal speckle-based ghost imaging techniques include discrete Fourier ghost imaging [16,17], discrete cosine ghost imaging [18,19,20], Hadamard CGI (HCGI) [21,22], and wavelet transform ghost imaging [23,24,25,26]. Among these, the Hadamard transform is notable for its simplicity in constructing the observation matrix and can easily project speckle patterns on high-speed spatial light modulators. This type of speckle has a strong intensity, thereby enhancing the robustness of the imaging. However, the Hadamard transform method requires the number of measurements to be equal to the number of pixels in the image for a perfect reconstruction, making compressed sampling unachievable. Some studies have reduced the number of samples by changing the arrangement of the Hadamard measurement basis. For example, Walsh-Hadamard CGI (WHCGI) [27] involves rearranging each row of the Hadamard matrix in order of increasing frequency of “1” and “−1” transitions. This approach treats the two-dimensional image as a one-dimensional signal, allowing the image’s information to be extracted progressively by frequency. Other approaches, such as the “cake-cutting” ordering for Hadamard CGI [28] and the “Russian doll” ordering for Hadamard CGI (RDHCGI) [29], reorder based on the coherence between each illumination speckle pattern and the two-dimensional image under test. These strategies allow the measurement process to stop as soon as the reconstructed image meets observational requirements, thereby reducing the number of sampling instances. However, while reducing the number of samples, these methods may also lead to a significant loss of detailed information in the reconstructed images. Therefore, how to reconstruct rich detailed information under under-sampling conditions remains the focus of our work.
The wavelet transform has the characteristic of multi-scale analysis, which can separate the localized features of an image and also has good decorrelation in image reconstruction. This paper proposes an Adaptive Ghost Imaging method based on 2D-Haar wavelets (2DHW-AGI). This method extracts different scale information of the image using 2D-Haar wavelets, then evaluates the diagonal information of a region using the horizontal and vertical information of that region, and selects the required diagonal measurement basis. This achieves the purpose of reducing the number of measurements. Through numerical simulations and experimental verification, we have demonstrated the effectiveness of this scheme in reducing the number of samples while significantly preserving the detailed information of the image.
2. Methodology
The schematic diagram of the traditional CGI system is illustrated in Figure 1. A series of pre-modulated patterns are projected onto the target object, denoted as , where m and n represent the discrete spatial coordinates in the horizontal and vertical directions, respectively. These projections are measured by a bucket detector. Each measurement base within a pattern is represented by . The signal detected by the detector for each projection is denoted by . In essence, the signal obtained during each measurement can be formulated as the inner product between the pattern and the object. Thus, can be articulated as follows:
the image can be reconstructed by calculating the second-order correlation function as:
If the set of all measurement bases is denoted as ‘’, then the second-order correlation function can be expressed as follows:
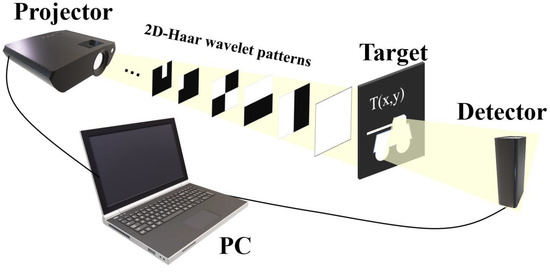
Figure 1.
Schematic diagram of CGI.
When is a measurement set modulated by an orthogonal matrix, the result of the second-order correlation function is the image information.
Given that an element of the 2D-Haar wavelet measurement base comprises “1”, “0”, and “−1”, and considering the projector’s inability to project negative elements, it typically becomes essential to segregate the measurement base into positive and negative patterns for separate measurement. The detection signals in the standard mode are acquired by executing the measurement process twice. To enhance imaging efficiency, we adopt a single-fold measurement strategy for sampling [30], as follows:
where denotes the positive pattern, denotes the smallest element in the measurement basis ( = “−1” for the 2D-Haar wavelet measurement basis), denotes an all “1” matrix of the same size as that of the target object, and denotes the detector signal obtained under the positive pattern irradiation. The first measurement basis of the 2D-Haar wavelet is an all “1” matrix. So, .This allows for the acquisition of accurate detection signals through a single measurement cycle.
The computational ghost imaging experiment can be conducted in two distinct phases. Initially, a sequence of patterns is projected onto the object using a projector, a step referred to as image sampling, with the patterns being measured by a bucket detector. Subsequently, the image is derived by correlating the measured patterns with the corresponding signals from the bucket detector, a step known as image reconstruction. The sampling phase necessitates the coordinated operation of both the projector and the bucket detector, rendering it a time-intensive process. Minimizing the number of samples during the experiment can significantly enhance the imaging efficiency of ghost imaging.
We believe that the 2D-Haar wavelet possesses the potential to retain substantial image information under conditions of under-sampling, a capability closely related to its construction and sampling characteristics. The 1D-Haar basis consists of a scaling function and a wavelet function :
Based on the 1D-Haar wavelet, we can define the scaling function of the 2D-Haar wavelet as follows:
For a fixed scaling factor j, the set of two-dimensional scaling functions can be represented as:
Unlike the 1D-Haar wavelet, the 2D-Haar wavelet has three mother wavelets, namely, the diagonal (D) mother wavelet, vertical (V) mother wavelet, and horizontal (H) mother wavelet. The frequency behavior of these three wavelet filters is such that they can capture the corner, vertical, and horizontal details of an image with a particular dilation. The three wavelets that give these details of images can be expressed as:
Given that there are three mother wavelets at each scaling level, let 1 ≤ k ≤ 3. Hence, the set of 2D-Haar mother wavelets can be represented as:
A certain basis vector of the 2D-Haar wavelet can be expressed as , where j denotes the scaling level whose maximum value depends on the total number of elements N (), and s denotes the three mother wavelets (s = H, V, D).
In the ghost imaging experiment utilizing 2D-Haar wavelets, the Haar wavelet matrix is initially constructed as per Equation (9). For illustrative purposes, we examine a 16 × 16 Haar wavelet matrix, as depicted in Figure 2a. The matrix rows are sequentially arranged by incrementing the scaling factor j, following the order of the three mother wavelets—horizontal, vertical, and diagonal—within the same scaling level. Subsequently, each row is isolated and transformed into an illumination pattern, with the pattern’s configuration illustrated in Figure 2b, showcasing illumination patterns modulated by the 2D-Haar wavelet matrix. As the scaling level escalates, the physical dimensions of each illumination pattern diminish, enhancing the resolution of the resultant image. Figure 2c presents the Hadamard illumination patterns.
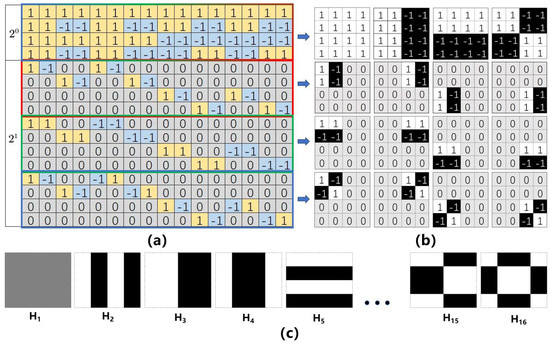
Figure 2.
(a) 2D-Haar wavelet matrix of size 16 × 16, (b) Illumination patterns modulated by a 2D-Haar wavelet matrix, and (c) Hadamard illumination patterns.
As illustrated in Figure 3, upon comparing the two types of illumination patterns, it is observed that the illumination area of the 2D-Haar wavelets gradually decreases, making many measurements redundant during the sampling process. In contrast, the illumination area of each Hadamard speckle corresponds to the entire object under observation. Hence, each detector signal contains information within the range covered by the illumination pattern. Therefore, reducing the number of sampling measurements will result in a significant loss of information about the target object.
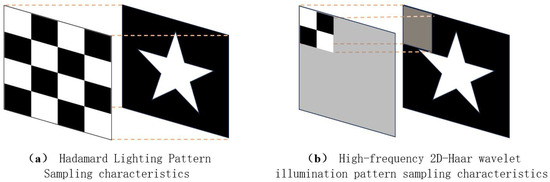
Figure 3.
Schematic illustration of the sampling characteristics of Hadamard and 2D-Haar wavelet illumination patterns.
The H, V, and D mother wavelets are designed to detect the horizontal, vertical, and diagonal directions, functioning as three high-frequency filters, respectively. They filter out low-frequency information while retaining high-frequency details. This principle underlies the implementation of the 2DHW-AGI scheme. In Figure 4, we analyze several cases where wavelet measurement bases irradiate an image and explain the 2DHW-AGI scheme’s principle by calculating the change in the signal caused by the bucket detector (indicated by the colored portion in the figure). Since the grayscale values in (a) are uniform, the convolution result using the high-frequency filter is zero, leading to a very small detector measurement value in the experiment. In (b), the grayscale values on the left and right sides differ, containing horizontal information. Here, only the H-series wavelets can generate a strong detection signal to extract this horizontal information. Similarly, only the V-series wavelets can detect the vertical information in (c). However, for the edge information as illustrated in (d), all three mother wavelets can produce strong detection signals. Therefore, in experiments, we first use the H- and V-series wavelets to measure the object. If both H- and V-series wavelets produce strong detection signals at a certain location, it indicates the presence of diagonal information. If only the H-series or V-series wavelet generates a strong signal at a specific location, it suggests the absence of diagonal information. Consequently, we can exclude the D-series wavelet measurement bases, thus reducing the sample count. The pattern observed can be attributed to the composition of the three types of mother wavelet illumination speckle elements shown in Figure 4. Taking the H-series illumination speckle as an example, it is composed of “1” on the left half and “−1” on the right half. Therefore, in the process of extracting information, it effectively divides the illumination area into left and right parts and calculates the difference between these two parts. The greater the difference, the larger the wavelet coefficient will be. In the case of edge and corner information shown in Figure 4d, where there are differences both left to right and top to bottom, it would be detected by both H-series and V-series wavelets. This method of detection leverages the inherent differences across the illuminated regions to extract and amplify relevant information, thereby facilitating the identification and reconstruction of image features with high fidelity.
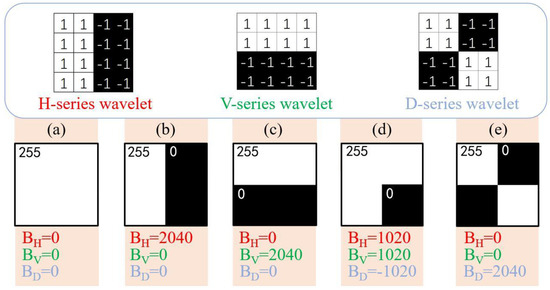
Figure 4.
Schematic diagram of 2D-Haar wavelet-based detection information principle. (a) denotes background information, (b) denotes horizontal information, (c) denotes vertical information, (d) denotes marginal information, and (e) denotes diagonal information.
It should be noted that (e) represents a special case where neither the H- nor V-series wavelet measurement bases yield a significant detector signal at this position, while the D-series wavelet measurement bases might affect the image quality in practical imaging. This scenario is uncommon in grayscale images and typically occurs only if the black and white boundaries of the measurement base and the object under observation perfectly align. Moreover, as long as the pattern in (e) does not consist of a high-frequency (alternating black and white pattern composed of four-pixel points), it can be detected. Conversely, if the image contains the highest frequency, only the four-pixel points of imaging will involve an error, which does not significantly impact the image quality.
Building on the properties of 2D-Haar wavelets discussed previously, we introduce the 2DHW-AGI scheme. The 2DHW-AGI approach is a direct imaging method that does not incorporate a plethora of complex algorithms into the image reconstruction process. By reducing the number of samples, we streamline the image reconstruction process without adding to its complexity, ensuring that the number of samples matches the number of image reconstructions.
3. Simulation Results and Analysis
To verify the feasibility of the 2DHW-AGI scheme, we selected “Cameraman” as the test object and performed numerical simulations following the experimental steps outlined in Figure 5. Considering the original image as a reference, this study selected the Peak Signal-to-Noise Ratio (PSNR) and Structure Similarity Index Measure (SSIM) as evaluation metrics. PSNR is a widely used standard to measure the difference between the reconstructed image and the original, offering a numerical reflection of the loss in image quality. On the other hand, SSIM is a metric for assessing the fidelity of image structure. It more precisely measures the visual effects of an image by simulating the human eye’s sensitivity to changes in image structure. The combination of these two metrics allows for a comprehensive evaluation of the quality of image reconstruction from various dimensions [31]. We compared the two Hadamard illumination pattern based fast imaging schemes, WHCGI and RDHCGI, with the 2DHW-AGI scheme. In addition, given that the 2DHW-AGI scheme relies on the 2D-Haar wavelet measurement-based CGI (2D-Haar CGI), we juxtaposed its imaging results with those of the 2D-Haar CGI scheme under full sampling conditions to underscore the 2DHW-AGI scheme’s imaging quality. We define the number of samples by and the number of reconstructions by . The WHCGI, RDHCGI, and 2D-Haar CGI schemes allow for direct setting of the sampling rate. In contrast, the 2DHW-AGI scheme requires initial basic measurements using H-series and V-series wavelets, with these basic measurements accounting for one-third of the total sampling instances. In our simulation experiments, we did not account for the impact of noise. However, after wavelet transformation, images tend to contain a large amount of redundant information that has a negligible effect on the imaging results. We have chosen to use 5% of the absolute value of the largest wavelet coefficients at each scale level as a threshold for selection. This method takes into account the differences in frequency components and allows for targeted selection and rejection of information at different scale levels, ultimately reducing the number of samples required. Therefore, the sampling rate for the 2DHW-AGI scheme should exceed 66.7%, with the actual rate determined by the threshold value.
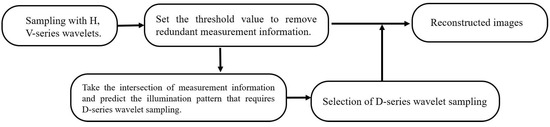
Figure 5.
Experimental procedure.
The simulation results are shown in Figure 6, the original image was 128 × 128 pixels, which means for a measurement basis based on orthogonality, the total number of samplings reached 16,384. Due to the 2DHW-AGI scheme’s requirement for foundational measurements using both horizontal and vertical wavelet bases, we chose to compare sampling rates of 67%, 75%, 85%, and 95%. At a 67% sampling rate, both the WHCGI and RDHCGI schemes could reconstruct most of the image information, but due to insufficient measurements, significant distortions occurred at the image edges. The imaging clarity under the 2DHW-AGI scheme at a 67% sampling rate was not satisfactory because this scheme necessitates 66.7% of the sampling rate for basic measurements. This implies that only an additional 0.3% of diagonal measurement bases are involved in the sampling and reconstruction of the image. Consequently, the reconstructed image lacks crucial diagonal information, which significantly impacts the quality of the image. However, when the sampling rate exceeds 75%, most of the important diagonal information is reconstructed, which leads to an improvement in image quality. In contrast, the quality improvements in the WHCGI and RDHCGI schemes were more uniform. To highlight the great preservation of detailed information and compare the subtle differences in the reconstructed images, we magnified parts of the images. At a 95% sampling rate, all three schemes had high SSIM values, but significant visual differences were still present upon magnifying the images. The WHCGI scheme still showed noticeable edge distortions. The RDHCGI scheme, by adjusting the order of the measurement bases to prioritize those more closely aligned with the target information, reduced distortion intensity but still exhibited slight distortions. Notably, the creases in the character’s black clothing conveyed a sense of three-dimensionality, representing some of the more detailed content in the images. The WHCGI and RDHCGI schemes did not significantly reconstruct these details, marking the most distinct difference between the three schemes. At a 75% sampling rate, the 2DHW-AGI imaging scheme was capable of reconstructing detailed information, but the quality was lower due to the lack of diagonal information. Magnifying the elbow area of the character in the 95% sampling rate reconstruction clearly shows that the 2DHW-AGI imaging scheme could reconstruct information almost identical to the original image.

Figure 6.
Comparison of imaging results of three schemes, 2DHW-AGI, WHCGI, and RDHCGI, and comparison of SSIM at different sampling rates.
In Figure 7, two graphs illustrate the relationship between SSIM and PSNR with the sampling rate. The results reveal that the differences in the reconstruction outcomes of the three schemes are reflected in the trends of SSIM and PSNR, both of which show a high degree of consistency. As the sampling rate gradually increases, the quality of the reconstructed images also increases. The improvements in image quality are relatively steady for both RDHCGI and WHCGI schemes, with the RDHCGI scheme outperforming the WHCGI scheme. For the 2DHW-AGI scheme, after reaching a 67% sampling rate, the image quality rapidly improves, stabilizing at around 78% and resulting in higher reconstructed image quality. This is consistent with the visual effects shown in Figure 6 and our analytical results. However, the specific sampling rate at which image quality stabilizes is determined by the amount of edge and corner information in the image being tested. Additionally, beyond a certain sampling rate, the image quality reconstructed by the 2DHW-AGI scheme surpasses that of the other two schemes. We believe this is because the 2D-Haar wavelet basis has a higher de-correlation effect, meaning the measurement bases that are filtered out have a minimal impact on the overall image quality. Although the RDHCGI and WHCGI schemes filter out some illumination patterns that do not match well with the target object, every Hadamard measurement basis affects the imaging of every area of the entire picture, thus having a more significant impact on image quality. Visually, this is manifested as distortions around the edges of the reconstructed objects.
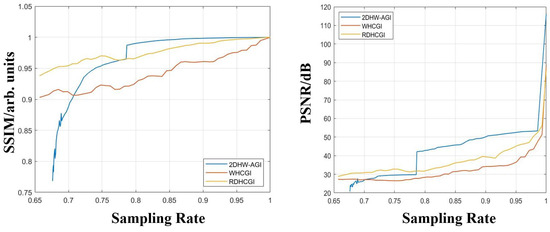
Figure 7.
“Cameraman” compares SSIM and PSNR at different sample rates using 2DHW-AGI, WHCGI and RDHCGI schemes.
Additionally, we selected “roses” and the more detail-rich “mandrill” as target images, applying the same comparative method mentioned above. The results, as shown in Figure 8, are consistent with those discussed earlier, demonstrating a clear advantage of the 2DHW-AGI scheme over the WHCGI and RDHCGI schemes after a 75% sampling rate. Moreover, we discovered that the 2DHW-AGI scheme could reconstruct high-quality images of objects with simpler backgrounds at a 70% sampling rate. For objects with richer details, it was also capable of reconstructing images very close to the original at around a 75% sampling rate.
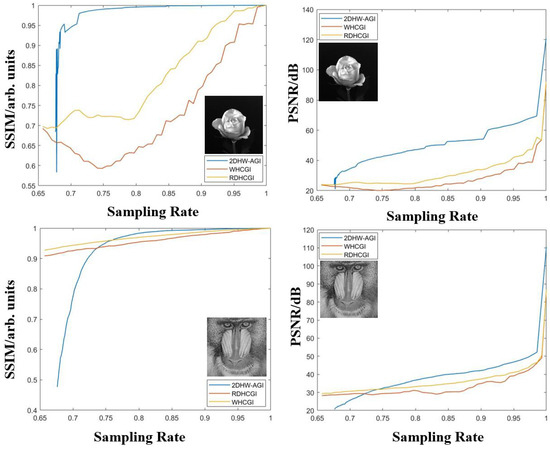
Figure 8.
Comparison of SSIM and PSNR of “roses” and “mandrill” using 2DHW-AGI, WHCGI, and RDHCGI schemes at different sampling rates.
4. Experimental Results and Analysis
To assess the practical effectiveness of our research approach, we conducted experiments using two distinct targets: a metal plate with a pentagram cutout at its center and a resolution board with more detailed information. The imaging area was set to 64 × 64 pixels, leading to a total of 4096 sampling instances. In the experimental setup, the XGIMI-XE11F model projector was utilized to project the illumination patterns, and a PDA100A2 photodetector from Thorlabs was employed for detection. For the 2DHW-AGI scheme, to more evenly process the image thresholds, the threshold was set to 20% of the average measured wavelet coefficients, resulting in actual sampling rates of 69.4% for the “pentagram” and 70.8% for the “resolution board”. Consequently, the sampling rates for the WHCGI and RDHCGI schemes were adjusted to 70% to facilitate a comparative analysis of the reconstructed images.
In the reconstruction results of the resolution board, to more distinctly observe the differences in noise and contrast, we set the image color to “Parula” mode. The experimental results were closely aligned with the numerical simulation outcomes. The WHCGI and RDHCGI schemes exhibited more pronounced distortion and noise due to insufficient measurements, leading to blurred images and low contrast. The advantages of the 2DHW-AGI scheme were more apparent; at the same sampling rate, the impacts of noise in Figure 9c,g were not significant, and the contrast was higher. Compared to the 2D-Haar CGI scheme under full sampling conditions, the image quality reconstructed by the 2DHW-AGI scheme under undersampling conditions was superior. This can be attributed to the filtering capabilities of the 2D-Haar wavelets, which eliminate some of the redundancy. Consequently, the influence of noise during measurement is reduced, enhancing the contrast and clarity of the reconstructed image.
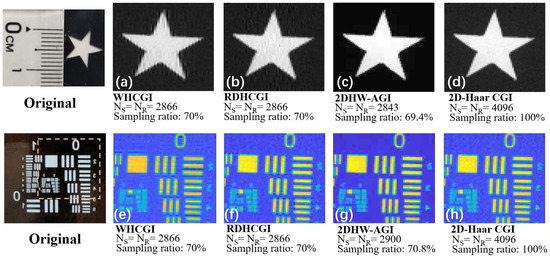
Figure 9.
Comparison of “Pentagram” and “Resolution board” reconstructed images using WHCGI, RDHCGI, 2DHW-AGI, and 2D-Haar CGI schemes. (a,e) are the imaging effects of the WHCGI scheme at a sampling rate of 70%. (b,f) are the imaging effects of the RDHCGI scheme at a sampling rate of 70%. (c,g) are the imaging effects of the 2DHW-AGI scheme at a sampling rate of about 70%. (d,h) are the imaging effects of the 2D-Haar CGI scheme at a sampling rate of 100%.
5. Discussion
From our experimental results, it is evident that the 2DHW-AGI scheme significantly retains image information under under-sampling conditions, marking its greatest advantage over other methods. However, the imaging process is inevitably affected by environmental noise, so the ’lossless’ aspect we discuss is theoretical, preserving more information than actual. In the previous section, we compared it with orthogonal speckle-based ghost imaging schemes, not with the latest deep learning-based ghost imaging (DLGI) approaches. We believe that 2DHW-AGI and DLGI are not directly comparable. On the one hand, 2DHW-AGI is universally applicable across various scenes, focusing on accurately capturing scene information and improving imaging speed without compromising information accuracy. On the other hand, DLGI prioritizes imaging speed, often at the expense of detailed image information. Therefore, these two approaches differ significantly in their application scenarios. Moreover, in terms of sampling rate, 2DHW-AGI does not show a significant advantage over current deep learning-based computational ghost imaging methods, and may even lag behind. However, we do not view DLGI’s efficiency as unattainable for 2DHW-AGI. A mere comparison of sampling rates is not rigorous. The efficiency of most DLGI schemes is constrained by various factors such as the quality and quantity of training datasets, neural network architecture, and computational resources. Thus, implementing DLGI in a random scenario necessitates considering the time cost of preliminary preparation, scene complexity, and hardware computational capacity.
A regrettable aspect of 2DHW-AGI we acknowledge is the lack of an appropriate threshold for different frequency measurement bases during high-pixel target object imaging, which could have refined the measurement bases from the previous scaling level. Hence, an important future task is to conduct further data fitting for the detection signals corresponding to each group of high-frequency measurement bases to identify a more suitable threshold.
6. Conclusions
In this study, we introduce a novel approach aimed at reducing the sample count required for CGI through the application of the 2D-Haar wavelet transform. The Haar wavelet, characterized by its ability to locally scan a target object sequentially at each scaling level, facilitates the prediction of D-series wavelet sequences with enhanced accuracy by leveraging both H-series and V-series wavelets. This capability enables a significant reduction in the required number of samples. Our experimental findings indicate that the 2DHW-AGI scheme is capable of reconstructing high-quality images with 25% fewer samples than traditionally necessary. This approach holds considerable potential for augmenting the efficiency of ghost imaging techniques, serving as a valuable reference for future research in the field.
Author Contributions
Conceptualization, Z.Y. (Zhuo Yu) and C.G.; methodology, Z.Y. (Zhuo Yu); software, Z.Y. (Zhuo Yu); validation, Z.Y. (Zhuo Yu) and H.Z.; formal analysis, X.W.; investigation, H.W.; resources, X.W.; data curation, Z.Y. (Zhuo Yu); writing—original draft preparation, Z.Y. (Zhuo Yu); writing—review and editing, Z.Y. (Zhuo Yu); visualization, Z.Y. (Zhuo Yu) and H.W.; supervision, Z.Y. (Zhihai Yao); project administration, C.G.; funding acquisition, Z.Y. (Zhihai Yao) and C.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Science & Technology Development Project of Jilin Province with grand (No. YDZJ202101ZYTS030).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Shapiro, J.H. Computational ghost imaging. Phys. Rev. A 2008, 78, 061802. [Google Scholar] [CrossRef]
- Zhang, A.X.; He, Y.H.; Wu, L.A.; Chen, L.M.; Wang, B.B. Tabletop X-ray ghost imaging with ultra-low radiation. Optica 2018, 5, 374–377. [Google Scholar] [CrossRef]
- Chen, S. X-ray ‘ghost images’ could cut radiation doses. Science 2018, 359, 1452. [Google Scholar] [CrossRef] [PubMed]
- Stantchev, R.I.; Mansfield, J.C.; Edginton, R.S.; Hobson, P.; Palombo, F.; Hendry, E. Subwavelength hyperspectral THz studies of articular cartilage. Sci. Rep. 2018, 8, 6924. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Peng, M.; Liu, F.; Tang, C. Protecting compressive ghost imaging with hyperchaotic system and DNA encoding. Complexity 2020, 2020, 8815315. [Google Scholar] [CrossRef]
- Wang, X.; Lin, Z. Nonrandom microwave ghost imaging. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4747–4764. [Google Scholar] [CrossRef]
- Erkmen, B.I. Computational ghost imaging for remote sensing. JOSA A 2012, 29, 782–789. [Google Scholar] [CrossRef] [PubMed]
- Cecconi, V.; Kumar, V.; Pasquazi, A.; Gongora, J.S.T.; Peccianti, M. Nonlinear field-control of terahertz waves in random media for spatiotemporal focusing. Open Res. Eur. 2022, 2, 32. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Hou, W.; Ye, Z.; Yuan, T.; Shao, S.; Xiong, J.; Sun, T.; Sun, X. Resolution-enhanced X-ray ghost imaging with polycapillary optics. Appl. Phys. Lett. 2023, 123, 141101. [Google Scholar] [CrossRef]
- Katz, O.; Bromberg, Y.; Silberberg, Y. Compressive ghost imaging. Appl. Phys. Lett. 2009, 95, 131110. [Google Scholar] [CrossRef]
- Zhang, H.; Xia, Y.; Duan, D. Computational ghost imaging with deep compressed sensing. Chin. Phys. B 2021, 30, 124209. [Google Scholar] [CrossRef]
- Magaña-Loaiza, O.S.; Howland, G.A.; Malik, M.; Howell, J.C.; Boyd, R.W. Compressive object tracking using entangled photons. Appl. Phys. Lett. 2013, 102, 231104. [Google Scholar] [CrossRef]
- Yu, W.K.; Li, M.F.; Yao, X.R.; Liu, X.F.; Wu, L.A.; Zhai, G.J. Adaptive compressive ghost imaging based on wavelet trees and sparse representation. Opt. Express 2014, 22, 7133–7144. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Cheng, Z.; Fan, X.; Cheng, Y.; Liang, Z. Compressive sensing ghost imaging based on image gradient. Optik 2019, 182, 1021–1029. [Google Scholar] [CrossRef]
- Luo, B.; Yin, P.; Yin, L.; Wu, G.; Guo, H. Orthonormalization method in ghost imaging. Opt. Express 2018, 26, 23093–23106. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Lu, R.; Han, S.; Xie, H.; Du, G.; Xiao, T.; Zhu, D. Fourier-transform ghost imaging with hard X-rays. Phys. Rev. Lett. 2016, 117, 113901. [Google Scholar] [CrossRef]
- Zhang, Z.; Ma, X.; Zhong, J. Single-pixel imaging by means of Fourier spectrum acquisition. Nat. Commun. 2015, 6, 6225. [Google Scholar] [CrossRef]
- Khamoushi, S.M.M.; Nosrati, Y.; Tavassoli, S.H. Sinusoidal ghost imaging. Opt. Lett. 2015, 40, 3452–3455. [Google Scholar] [CrossRef]
- Yu, W.; Shah, S.A.A.; Li, D.; Guo, K.; Liu, B.; Sun, Y.; Yin, Z.; Guo, Z. Polarized computational ghost imaging in scattering system with half-cyclic sinusoidal patterns. Opt. Laser Technol. 2024, 169, 110024. [Google Scholar] [CrossRef]
- Liu, B.L.; Yang, Z.H.; Liu, X.; Wu, L.A. Coloured computational imaging with single-pixel detectors based on a 2D discrete cosine transform. J. Mod. Opt. 2017, 64, 259–264. [Google Scholar] [CrossRef]
- Wu, H.; Wang, R.; Li, C.; Chen, M.; Zhao, G.; He, Z.; Cheng, L. Influence of intensity fluctuations on Hadamard-based computational ghost imaging. Opt. Commun. 2020, 454, 124490. [Google Scholar] [CrossRef]
- Mizuno, T.; Iwata, T. Hadamard-transform fluorescence-lifetime imaging. Opt. Express 2016, 24, 8202–8213. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; He, R.; Chen, Q.; Gu, G.; Zhang, W. Research on ghost imaging method based on wavelet transform. J. Opt. 2017, 19, 095202. [Google Scholar] [CrossRef]
- Alemohammad, M.; Stroud, J.R.; Bosworth, B.T.; Foster, M.A. High-speed all-optical Haar wavelet transform for real-time image compression. Opt. Express 2017, 25, 9802–9811. [Google Scholar] [CrossRef] [PubMed]
- Duan, D.; Zhu, R.; Xia, Y. Color night vision ghost imaging based on a wavelet transform. Opt. Lett. 2021, 46, 4172–4175. [Google Scholar] [CrossRef] [PubMed]
- Kim, B.H.; Kim, H.; Park, T. Nondestructive damage evaluation of plates using the multi-resolution analysis of two-dimensional Haar wavelet. J. Sound Vib. 2006, 292, 82–104. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, S. Fast reconstructed and high-quality ghost imaging with fast Walsh–Hadamard transform. Photonics Res. 2016, 4, 240–244. [Google Scholar] [CrossRef]
- Nie, X.; Zhao, X.; Peng, T.; Scully, M.O. Sub-Nyquist computational ghost imaging with orthonormal spectrum-encoded speckle patterns. Phys. Rev. A 2022, 105, 043525. [Google Scholar] [CrossRef]
- Sun, M.J.; Meng, L.T.; Edgar, M.P.; Padgett, M.J.; Radwell, N. A Russian Dolls ordering of the Hadamard basis for compressive single-pixel imaging. Sci. Rep. 2017, 7, 3464. [Google Scholar] [CrossRef]
- Yu, Z.; Wang, X.Q.; Gao, C.; Li, Z.; Zhao, H.; Yao, Z. Differential Hadamard ghost imaging via single-round detection. Opt. Express 2021, 29, 41457–41466. [Google Scholar] [CrossRef]
- Sara, U.; Akter, M.; Uddin, M.S. Image quality assessment through FSIM, SSIM, MSE and PSNR—A comparative study. J. Comput. Commun. 2019, 7, 8–18. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).