Multi-Frequency Doppler Velocimetry Based on a Mode-Locked Distributed Bragg Reflector Laser
Abstract
:1. Introduction
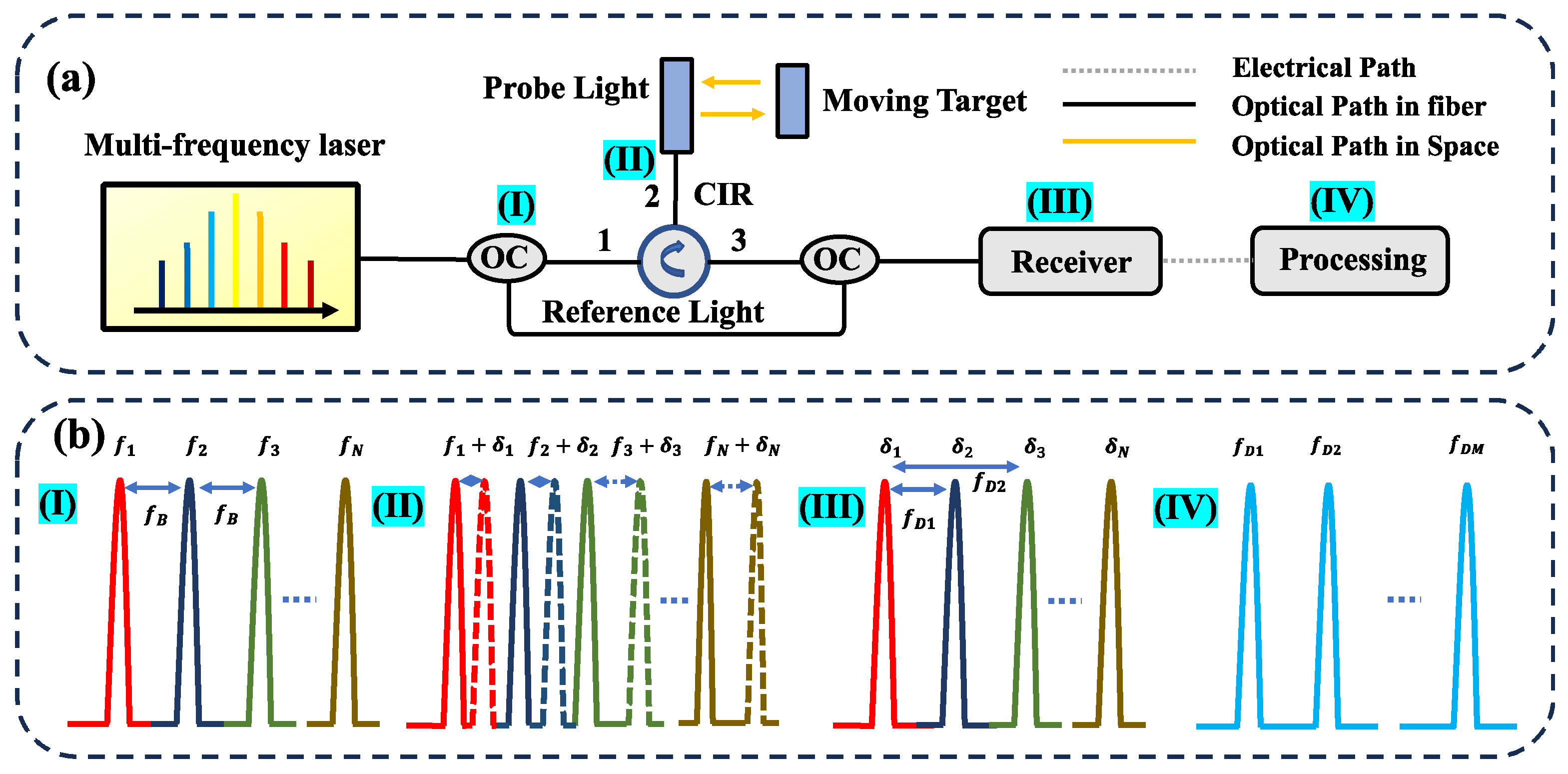
2. Principle
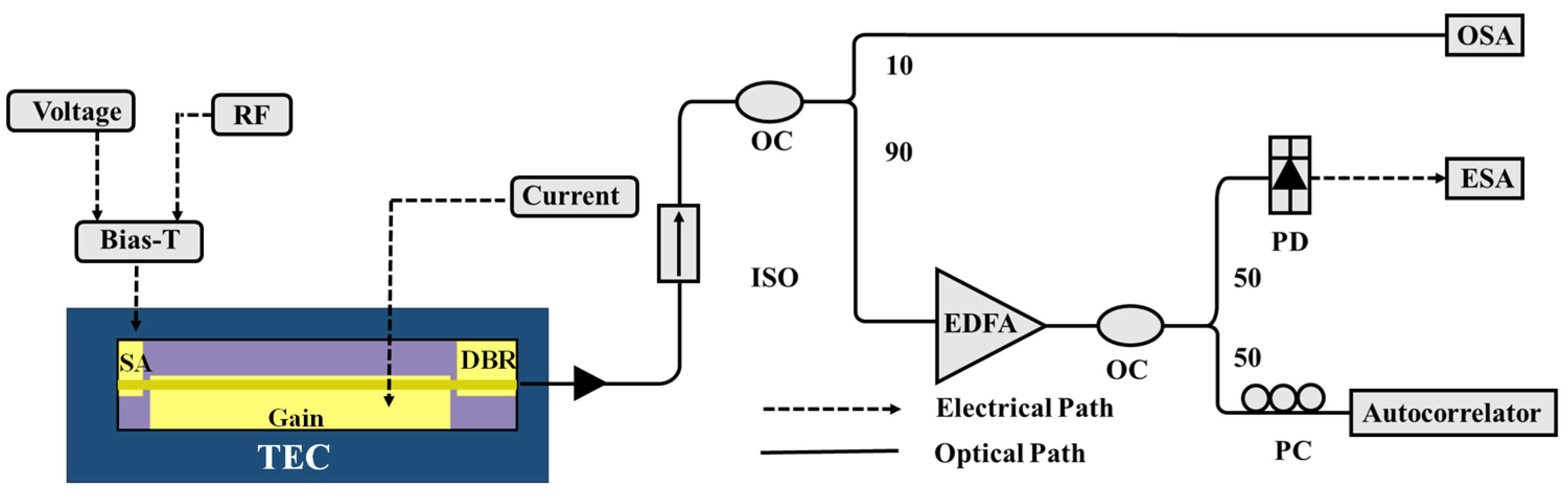
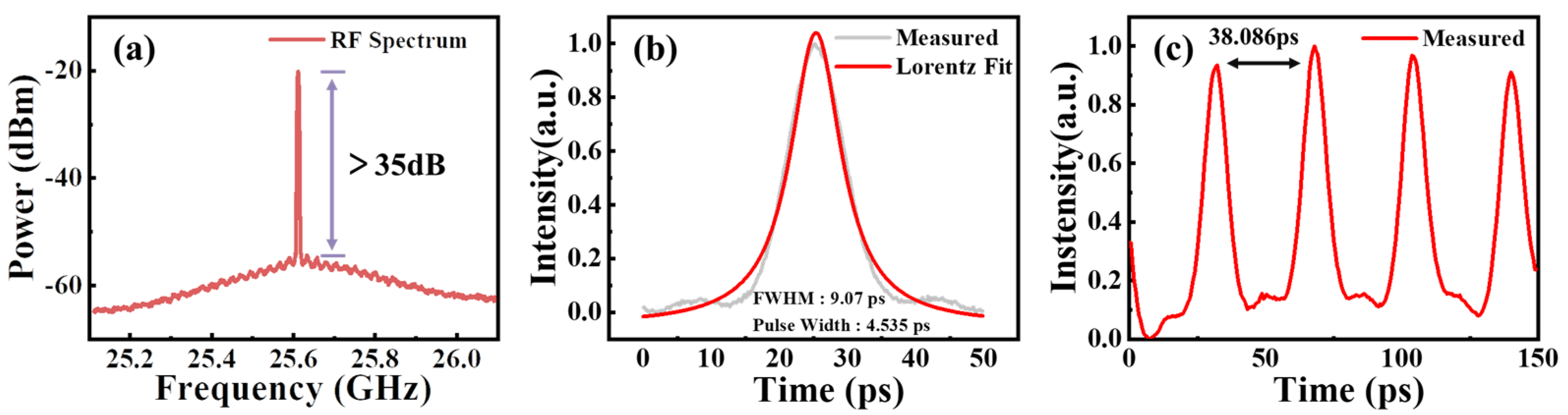
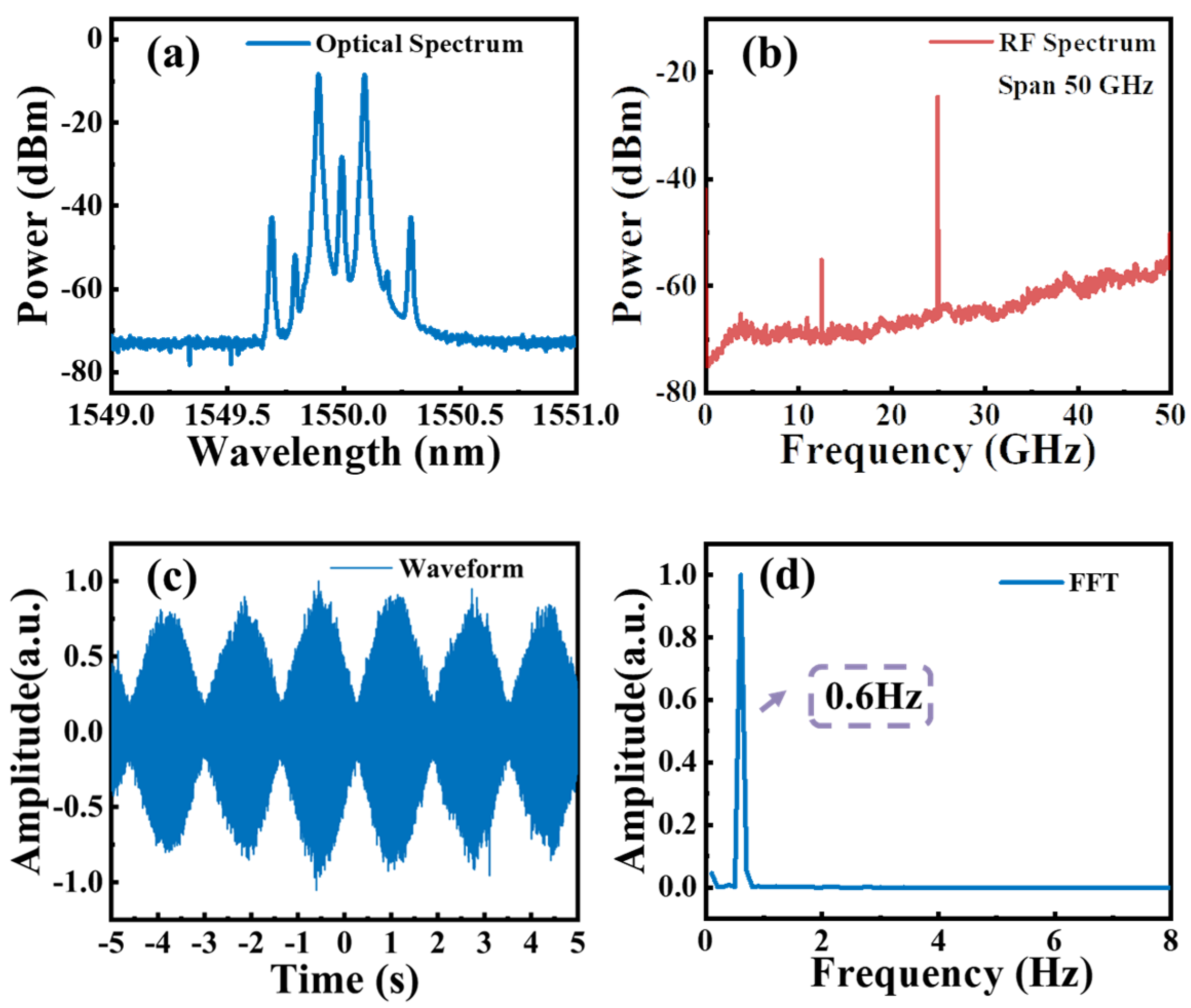
3. Device Characterization and Experimental Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vaughan, J.M. Coherent Laser Spectroscopy and Doppler Lidar Sensing in theAtmosphere. Phys. Scr. 1998, T78, 73. [Google Scholar] [CrossRef]
- Thobois, L.; Cariou, J.P.; Gultepe, I. Review of Lidar-Based Applications for Aviation Weather. Pure Appl. Geophys. 2019, 176, 1959–1976. [Google Scholar] [CrossRef]
- Zheng, Z.; Zhao, C.; Zhang, H.; Yang, S.; Zhang, D.; Yang, H.; Liu, J. Phase Noise Reduction by Using Dual-Frequency Laser in Coherent Detection. Opt. Laser Technol. 2016, 80, 169–175. [Google Scholar] [CrossRef]
- Mocker, H.W.; Bjork, P.E. High Accuracy Laser Doppler Velocimeter Using Stable Long-Wavelength Semiconductor Lasers. Appl. Opt. 1989, 28, 4914. [Google Scholar] [CrossRef]
- Churnside, J.H. Laser Doppler Velocimetry by Modulating a CO2 Laser with Backscattered Light. Appl. Opt. 1984, 23, 61. [Google Scholar] [CrossRef] [PubMed]
- Morvan, L.; Lai, N.D.; Dolfi, D.; Huignard, J.-P.; Brunel, M.; Bretenaker, F.; Le Floch, A. Building Blocks for a Two-Frequency Laser Lidar-Radar: A Preliminary Study. Appl. Opt. 2002, 41, 5702. [Google Scholar] [CrossRef] [PubMed]
- Diaz, R.; Chan, S.-C.; Liu, J.-M. Lidar Detection Using a Dual-Frequency Source. Opt. Lett. 2006, 31, 3600. [Google Scholar] [CrossRef] [PubMed]
- Lavrič, A.; Batagelj, B.; Vidmar, M. Calibration of an RF/Microwave Phase Noise Meter with a Photonic Delay Line. Photonics 2022, 9, 533. [Google Scholar] [CrossRef]
- Diaz, R.; Chan, S.-C.; Liu, J.-M. Dual-Frequency Multifunction Lidar; Mecherle, S., Korotkova, O., Eds.; SPIE: San Jose, CA, USA, 2007; p. 64570O. [Google Scholar]
- Chen, G.; Lu, D.; Guo, L.; Zhao, W.; Wang, H.; Zhao, L. Dual-Frequency Laser Doppler Velocimeter Based on Integrated Dual-Mode Amplified Feedback Laser. In Proceedings of the 2018 Asia Communications and Photonics Conference (ACP), Hangzhou, China, 26–29 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–3. [Google Scholar]
- Onori, D.; Scotti, F.; Scaffardi, M.; Bogoni, A.; Laghezza, F. Coherent Interferometric Dual-Frequency Laser Radar for Precise Range/Doppler Measurement. J. Light. Technol. 2016, 34, 4828–4834. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, L.; Zhang, Y.; Wu, Y.; Xia, H. Tunable Dual-Frequency Coherent Doppler Lidar Using Bi-Directional Electro-Optic Modulation in a Sagnac Loop. Opt. Commun. 2023, 526, 128852. [Google Scholar] [CrossRef]
- Cheng, C.-H.; Lee, C.-W.; Lin, T.-W.; Lin, F.-Y. Dual-Frequency Laser Doppler Velocimeter for Speckle Noise Reduction and Coherence Enhancement. Opt. Express 2012, 20, 20255–20265. [Google Scholar] [CrossRef] [PubMed]
- Vercesi, V.; Onori, D.; Laghezza, F.; Scotti, F.; Bogoni, A.; Scaffardi, M. Frequency-Agile Dual-Frequency Lidar for Integrated Coherent Radar-Lidar Architectures. Opt. Lett. 2015, 40, 1358. [Google Scholar] [CrossRef] [PubMed]
- Bai, Y.; Ren, D.; Zhao, W.; Qu, Y.; Qian, L.; Chen, Z. Heterodyne Doppler Velocity Measurement of Moving Targets by Mode-Locked Pulse Laser. Opt. Express 2012, 20, 764–768. [Google Scholar] [CrossRef] [PubMed]
- Jang, Y.-S.; Kim, S.-W. Distance Measurements Using Mode-Locked Lasers: A Review. Nanomanuf. Metrol. 2018, 1, 131–147. [Google Scholar] [CrossRef]




| Mode Spacing (Hz) | DDS (Hz) for Speed of 1.5 m/s | Speed Resolution (m/s) for DDS of 1 Hz |
|---|---|---|
| 100 M | 1 | 1.5 |
| 1 G | 10 | 0.15 |
| 10 G | 100 | 0.015 |
| 20 G | 200 | 0.0075 |
| 100 G | 1000 | 0.0015 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, H.; Lu, D.; Zhang, Z.; Guo, F.; Zhou, D.; Zhao, L. Multi-Frequency Doppler Velocimetry Based on a Mode-Locked Distributed Bragg Reflector Laser. Photonics 2023, 10, 1254. https://doi.org/10.3390/photonics10111254
Song H, Lu D, Zhang Z, Guo F, Zhou D, Zhao L. Multi-Frequency Doppler Velocimetry Based on a Mode-Locked Distributed Bragg Reflector Laser. Photonics. 2023; 10(11):1254. https://doi.org/10.3390/photonics10111254
Chicago/Turabian StyleSong, Hao, Dan Lu, Zhihao Zhang, Fei Guo, Daibing Zhou, and Lingjuan Zhao. 2023. "Multi-Frequency Doppler Velocimetry Based on a Mode-Locked Distributed Bragg Reflector Laser" Photonics 10, no. 11: 1254. https://doi.org/10.3390/photonics10111254
APA StyleSong, H., Lu, D., Zhang, Z., Guo, F., Zhou, D., & Zhao, L. (2023). Multi-Frequency Doppler Velocimetry Based on a Mode-Locked Distributed Bragg Reflector Laser. Photonics, 10(11), 1254. https://doi.org/10.3390/photonics10111254







